The coupling system of Kirchhoff and Euler-Bernoulli plates with logarithmic source terms: Strong damping versus weak damping of variable-exponent type

1.   Introduction

From an ecological and financial perspective, toxicants have emerged as a major threat to terrestrial and aquatic environments. With increasing demand, industries are cranking out a flood of toxic chemicals. Toxic chemicals and substances, such as cadmium, arsenic, copper, lead, etc., are often dumped into lakes, rivers and oceans, where they can have a devastating effect on aquatic life ^[1]. Toxic oil, metals and synthetic organic chemicals are common contaminants of river, lake, and sea water ^[2]. A significant loss of biodiversity occurs in ecosystems where toxic contaminants are present ^[3]. Fish, birds and mammals that eat contaminated marine life can be exposed to the toxins themselves. Therefore, many species have become extinct, and many more are on the verge of extinction, due to the unchecked release of toxic substances into the environment. There are numerous species in the ocean that produce toxins, and these toxins, if released into the environment, can have serious consequences for the development of other organisms. For example, the grazing pressure of zooplankton can be greatly reduced by phytoplankton that are naturally toxic. Therefore, research into the effects of toxic substances on ecological communities is becoming increasingly significant from both an environmental and a conservationist point of view.

The mathematical modeling of the impact of toxicants on a population was a newly established area in the early 1980s ^[4,5,6]. In order to effectively estimate the qualitative impact of toxic substances on species, mathematical models are a great tool to use. Das et al. ^[7] investigated a predator-prey fishery model with harvesting and the effects of toxicants which are released by some other species. Chakraborty and Das ^[8] studied a two-zooplankton one-phytoplankton system in the presence of toxicity. Ang and Safuan ^[9] discussed an intraguild fishery model in which predators are thought to become infected through their prey, while fish are thought to be infected directly by an anthropogenic toxicant in the environment. Juneja and Agnihotri ^[10] addressed the issue of two competing fish species, each of which releases a harmful chemical for the other.

It is noted that in biological populations, delay plays an important role. In the last few years, theoretical and mathematical ecologists have paid a lot of attention to research on differential equations with time delays ^{[11,12,13,14,15]}. Even so, studying the effects of time delay on the dynamics of a system can be very complicated. For example, it can cause the system to lose its stability and lead to periodic solutions and chaotic behavior. Pal and Mahapatra ^[16] studied the combined effect of a toxicant and delay on the dynamical behaviors of a delayed two-species competitive system with imprecise biological parameters. Pal et al. ^[17] took into account two fish species that are in competition with one another, each of which releases a toxin that is poisonous to the other and each of which obeys the law of logistic growth. Meanwhile, in reality, species are spatially heterogeneous, so individuals seek out low population densities where they have a better chance of survival. As a result, the reaction-diffusion predator-prey model with toxic effects has been considered by some researchers. Zhang and Zhao ^[18] investigated a diffusive predator-prey model with toxins, and their research results show that toxic substances have a great impact on the dynamics of the model. Zhu et al. ^[19] investigated a delayed diffusive predator-prey model affected by a toxic substance. However, we find that the research results about the delayed diffusive predator-prey model with toxic substances are rare.

Motivated by these pioneer works, we hypothesize that prey produce toxins for predators, and that this process is not instantaneous but rather follows a discrete time lag that can be thought of as the species' maturation period. Toxic substances released by prey into the environment have a half-life of $\tau$, which we introduce here. We consider a diffusive predator-prey model as follows

where $u(x, t)$, $v(x, t)$ denote the density of the prey and the predator, respectively. $r$ is the birth rate of prey. $\frac{u}{a+u^2}$ is the Holling type-Ⅳ function. $\alpha$ is the maximum predator per capita consumption rate of $u$ due to $v$. $\beta$ is the conversion of the biomass constant. The parameter $d$ is the death rate of predator. $\gamma v^2$ is the functional response of the $u$ population to the density of the $v$ population.

To explore the dynamics of system (1.1), we first do the non-dimensionalization described below

Thus, system (1.1) is simplified (by removing the bars) to be

In this study, we will study the dynamics of system (1.2), such as the existence of the solutions, local/global stability of the equilibria, and Hopf bifurcation induced by delay. In addition, we will also discuss the existence and non-existence of non-constant positive solutions of the following elliptic system

The structure of this paper is as follows. In Section 2, the existence of solutions and the persistence of system (1.2) are studied. In Section 3, the stability of the equilibria, Turing bifurcation, and Hopf bifurcation induced by delay are discussed. In Section 4, the global stability of the equilibria are investigated by using the Lyapunov functional method. In Section 5, the non-existence and existence of the non-constant steady state are studied. In Section 6, theoretical results are verified through numerical simulations. Finally, a brief conclusion is given in Section 7.

2.   Basic dynamics

Theorem 2.1. Assume that $u_0(x, t)\geq0$, $v_0(x, t)\geq0$, and $u_0(x, t)\not\equiv0$, $v_0(x, t)\not\equiv0$. There is a unique solution $(u(x, t), v(x, t)) > (0, 0)$, $(t > 0, x\in \bar{\Omega})$ of system (1.2), and

Additionally,

where $\Vert u(x, t)\Vert_{C(\overline{\Omega})} = \mathop{\max}\limits_{x\in\overline{\Omega}, t\in[-\tau, 0]} u(x, t)$, $\Vert v(x, t)\Vert_{C(\overline{\Omega})} = \mathop{\max}\limits_{x\in\overline{\Omega}} v(x, t)$, $K_1 = \max\{1, \max\limits_{\bar{\Omega}, t\in[-\tau, 0]}u_0(x, t)\}$ and $K_2$ depends upon $\beta$, $a$, $d$, $\gamma$, $u_0(x, t)$, $v_0(x, t)$ and $\Omega$.

Proof. We consider the following auxiliary system

Obviously, $(\underline{u}(x, t), \underline{v}(x, t)) = (0, 0)$ and $(\bar{u}(x, t), \bar{v}(x, t)) = (\tilde{u}(t), \tilde{v}(t))$ are the lower and upper solutions of system (2.3), respectively, where $(\tilde{u}(t), \tilde{v}(t))$ is the unique solution of

where $\bar{u}_0 = \max\limits_{\overline{\Omega}}u_0(x)$, $\bar{v}_0 = \max \limits_{\overline{\Omega}}v_0(x)$. As a result, according to Theorem 8.3.3 in ^[20], we obtain that system (1.2) has a unique globally defined solution which satisfies $0\leq u(x, t) \leq \tilde{u}(t), 0\leq v(x, t)\leq \tilde{v}(t).$ By the strong maximum principle, we have that $u(x, t), v(x, t) > 0$ $(t > 0, x\in \bar{\Omega})$.

Evidently, from the first equation of system (2.4) we have that $\lim \limits_{t\to+\infty}{u(t)}\leq1$, which implies $\mathop {\lim \sup \max }\limits_{t \to + \infty \quad x \in \bar{\Omega}} u(x, t) \leq 1$. Therefore, $||u(\cdot, t) ||_{C(\bar{\Omega})}\leq K_1$ for all $t\geq 0$.

For $v(x, t)$, we let $U(t) = \int_\Omega u(x, t)dx$ and $V(t) = \int_\Omega v(x, t)dx$; then,

Multiplying Eq (2.5) by $\beta$, and then addin it to Eq (2.6), we have

$||u(\cdot, t) ||_{C(\bar{\Omega})}\leq K_1$, so we have that $U(t)\leq K_1 |\Omega|$. Thus,

where $M_2 = (1+d\beta)|\Omega|$. Integrating the inequality (2.7), we obtain

This means that $||v(\cdot, t) ||_{L^1(\Omega)}\leq \beta ||u_0(\cdot) ||_{L^1(\Omega)}+||v_0(\cdot) ||_{L^1(\Omega)}+\frac{M_2}{d}.$ According to Theorem 3.1 ^[21], there is an $M_3$ such that $||v(\cdot, t) ||_{L^\infty(\Omega)}\leq M_3$. Therefore, there exists a $K_2$ such that $||v(\cdot, t) ||_{C(\overline{\Omega})}\leq K_2$. □

Theorem 2.2. If $1-\frac{K_2}{a} > 0$ and $\frac{\beta (1-\frac{K_2}{a})}{\gamma K_2(a+K_1)}-\frac{d}{\gamma K_2} > 0$, then system (1.2) has the persistence property.

Proof. From system (1.2), we obtain

For small enough $\varepsilon > 0$, it holds that $1-\frac{K_2}{a}- \varepsilon > 0$. Therefore, there is a $t_1$ such that

The second equation of system (1.2) is then solved using the upper and lower bounds of $u$, yielding

for $t > t_1+\tau$. Then there exists $t_2 > t_1+\tau$ such that for any $t > t_2$,

From (2.10) and (2.12), we can easily obtain that

They are evidence that the system (1.2) is persistent. Regardless of the diffusion coefficients, this indicates that, from a biological point of view, a predator and its prey will always coexist within the habitable domain at any given time and in any given location. □

3.   Local stability and bifurcation analysis

Obviously, model (1.2) has a trivial equilibrium $E_0 = (0, 0)$ and a predator-free equilibrium $E_1 = (1, 0)$, and the interior equilibrium must simultaneously meet the two non-trivial prey and predator nullcline conditions below:

From (3.2), we obtain that $v = -{\left(u^2 +a\right)}\, {\left(u-1\right)}$, and substituting this into (3.1), we have

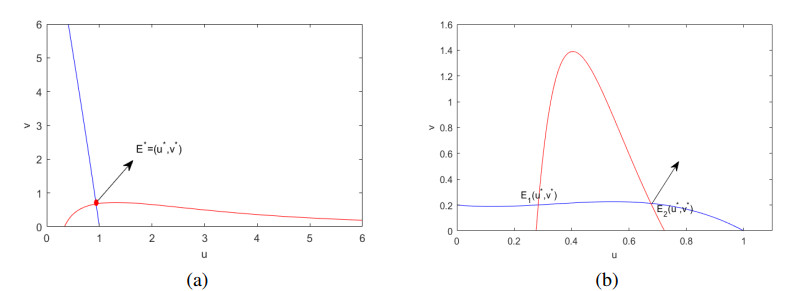
Obviously, Eq (3.3) has at least a positive root. Therefore, system (1.2) has at least an interior equilibrium $E^* = (u^*, v^*)$. To illustrate this, isoclines (3.1) and (3.2) are shown in Figure 1. Figure 1(a) shows that isoclines (3.1) and (3.2) intersect uniquely in the interior of the positive quadrant, i.e., system (1.2) has a unique interior equilibrium, and Figure 1(b) shows that isoclines (3.1) and (3.2) intersect two times in the interior of the positive quadrant, i.e., the system has two equilibria.

In order to study the stability of the equilibria. First, we define the real-valued Sobolev space

Then $(X, < \cdot, \cdot > )$ is a Hilbert space. In $C([-\tau, 0], X)$, system (1.2) can be thought of as a functional differential equation in abstract form.

Let $U(t) = (u(\cdot, t), v(\cdot, t))^{T}.$ Thus, we linearize system (1.2) around a constant solution $E = (u, v)$; we get

where $D = {\rm diag}(d_1, d_2)$,

and $U_t = {\bf col}(u(x, t), v(x, t))\in \mathcal{C}_\tau$ and $L: C([-\tau, 0] \rightarrow X$ is given by

with $\varphi = (\varphi_1, \varphi_2)^T\in C([-\tau, 0]$ and

Therefore, the characteristic equation of system (3.4) is

We know that with the corresponding eigenfunctions $\psi_n(x)$ the problem

has eigenvalues $0 = \mu_0 < \mu_1\leq \mu_2\leq \cdots\leq \mu_n\leq\mu_{n+1}\leq \cdots$. Substituting

into Eq (3.4), we have

Hence, Eq (3.6) equals

where

For the extinct equilibrium $E_0 = (0, 0)$, $J_{(0, 0)} = \left(\begin{array}{cc} 1 & 0 \\ 0 & -d \end{array}\right)$. When $n = 0$, the eigenvalue $\lambda = 1 > 0$, therefore, $E_0$ is a saddle point, which is always unstable.

For the predator free equilibrium $E_1 = (1, 0)$, $J_{(1, 0)} = \left(\begin{array}{cc} -1 & -\frac{1}{a+1} \\ 0 & \frac{\beta}{a+1}-d \end{array}\right)$. Therefore, if $\frac{\beta}{a+1}-d < 0$, then $E_1$ is stable.

In what follows, we first discuss the stability of the interior equilibrium of system (1.2) with $\tau = 0$. When $\tau = 0$, the characteristic equation (3.7) becomes

Theorem 3.1. Assume that the conditions

hold; then, the following results are true:

(i) If $d_1a_{22}-d_2a_{11} > 0$, then the interior equilibrium is locally asymptotically stable.

(ii) If $d_1a_{22}-d_2a_{11} < 0$ and $\Delta_1 < 0$, then the interior equilibrium is locally asymptotically stable, where

(iii) If $d_1a_{22}-d_2a_{11} < 0$ and $\Delta_1 > 0$, but there is no $n\in N_0$ such that $\mu_n\in (\mu^-, \mu^+)$, then the interior equilibrium is asymptotically stable, where

Proof. Obviously, if $a_{22}-a_{11} > 0$, then $A_n\leq A_0 > 0$ for $n\in N_0$. $a_{12}a_{21}-a_{11}a_{22}-a_{12}b > 0$ holds, so $B_0+C = hb_3(b_2b_3-b_1) > 0$.

(ⅰ) If $d_1a_{22}-d_2a_{11} > 0$, then $B_n+C\geq B_0+C$, which implies that all roots of the characteristic equation (3.9) have negative real parts. Therefore, the interior equilibrium is locally asymptotically stable.

(ⅱ) $d_1a_{22}-d_2a_{11} < 0$ and $\Delta_1 < 0$ hold, which implies that the equation

for any $y\geq0$. That is $B_n+C > 0$ for any $\mu_n$. Similar to the discussion in (i), we have that the interior equilibrium is locally asymptotically stable.

(ⅲ) There is no $n\in N_0$ such that $\mu_n\in (\mu^-, \mu^+)$. So, $B_n+C > 0$ for any $\mu_n$. Consequently, we have the results.

□

Theorem 3.2. Suppose that the conditions (3.10) and (3.11) hold, and assume further that

hold, then the Turing bifurcation occurs.

Proof. The condition (3.10) is satisfied, so $E^*$ of the ODE model corresponding to model (1.2) is locally asymptotically stable.

The condition (3.10) holds, so $A_n < 0$. Therefore, when $E^*$ of model (1.2) is unstable i.e., Eq (3.9) has at least one positive real root i.e., $B_n+C = 0$ has two true roots, one positive and one negative. Note that

It is easy to see that $B_n+C$ reaches its minimal value at $\mu_n = \mu_{\min} = \frac{d_2a_{11}-d_1a_{22}}{2d_1d_2}$ with $d_1 a_{22}- d_2 a_{11} < 0$.

It implies that

Hence, $D_n$ is negative when Eq (3.14) is met, and it applies for $\mu$ close to $\mu_{\min}$. By Eq (3.14), we obtain

which completes the proof. □

Let $\lambda = \pm i\omega\ (\omega > 0)$ be a pure imaginary pair of eigenvalues of Eq (3.7). Thus, $\omega$ satisfies

Therefore, we have

From the above equation, we obtain

From Eq (3.8), we know that if the condition (3.11) holds, then $B_n-C > B_n+C > 0$. Therefore, $B_n^2-C^2 > 0$. We discuss the existence of roots of Eq (3.18) in two cases.

Case Ⅰ. Suppose that

Thus, Eq (3.18) has two positive real roots $\omega^\pm(n) = \sqrt{\frac{-(A_n^2-2B_n)\pm\sqrt{\Delta_n}}{2}}$. Substituting $\omega^\pm(n)$ into Eq (3.17), we have

Case Ⅱ. Suppose that either of the following two conditions are met

So, Eq (3.18) does not have a positive real root.

We summarize the above discussions, and we have the following theorem.

Theorem 3.3. Assume that the conditions (3.10) and (3.11) hold and the following is true:

(i) When

Eq (3.18) has two positive real roots $\omega^\pm(n)$; then, Eq (3.7) has a pair of pure imaginary roots $\pm i \omega^\pm(n)$, when $\tau = \tau_{j}^\pm(n)$.

(ii) If either $\Delta_n < 0$ or $\Delta_n\geq0, P_{1n}\geq 0$; then, Eq (3.7) has no pure imaginary roots.

Lemma 3.1. Let $\lambda(\tau) = \xi(\tau)\pm i\eta(\tau)$ be the root of Eq (3.7) satisfying $\alpha(\tau_{j}^\pm(n)) = 0, \xi(\tau_{j}^\pm(n)) = \omega^\pm(n))$. Then the following transversality conditions are satisfied:

Proof. When both sides of Eq (3.7) are differentiated with regard to $\lambda$, the result is

Therefore,

Combining with (3.17), we get

□

Denote

For a given $n\in \Gamma$, it is seen that $\tau_{j}^+(n)$ grows with respect to $j$. As a result, we can deduce that $\tau_{0}^+(n) = \mathop {\min }\limits_{j\in\mathbb{N}_0}\tau_{j}^+(n)$ for some fixed $n$. We define

Theorem 3.4. Assume that the conditions (3.10) and (3.11) hold; we have the following results

(i) If either of the following two conditions are met

then the interior equilibrium $E^*$ is locally asymptotically stable for $\tau\geq 0$;

(ii) If $A_n^2-2B_n > 0$ and $\Delta_n > 0$, then the interior equilibrium $E^*$ is locally asymptotically stable when $\tau \in[0, \tau^*)$ and system (1.2) experiences a Hopf bifurcation at $E^*$. In addition, before it becomes unstable, the interior equilibrium $E*$ will go through $k$ changes from stable to unstable and back to stable.

4.   Global stability

Theorem 4.1. Suppose that $\frac{\beta K_1}{a} < d$ and $E_1 = (1, 0)$ is globally asymptotically stable.

Proof. Define a Lyapunov functional as follows

Differentiating $V(t)$ with respect to $t$, we have

$\frac{\beta}{a} < d$, so $\frac{{\rm d}V}{{\rm d}t}\leq 0$, and $\frac{{\rm d}V}{{\rm d}t} = 0$ if and only if $(u, v) = (1, 0)$. We conclude that $E_1 = (1, 0)$ is globally asymptotically stable. □

Theorem 4.2. Assume that the conditions

hold. Then the unique interior equilibrium $E^* = (u^*, v^*)$ is globally asymptotically stable.

Proof. Define a Lyapunov function as follows

where

Thus, we have

Note that

Therefore, we obtain

From Eq (4.2), we know that $\frac{{\rm d}W}{{\rm d}t}\leq 0$, and $\frac{{\rm d}W}{{\rm d}t} = 0$ if and only if $(u, v) = (u^*, v^*)$. Therefore, the interior equilibrium $E^*$ is globally asymptotically stable. □

5.   Non-constant positive steady states

In this section, we investigate the existence and non-existence of non-constant positive solutions of system (1.3). First, we will give a priori upper and lower bounds for the positive solutions of system (1.3).

5.1.   A priori estimates

Lemma 5.1 (Harnack inequality). ^[22] Assume that $c(x)\in C(\bar{\Omega})$ and $\phi \in C^2(\Omega)\cap C^1(\bar{\Omega})$ is a positive solution to

Then there exists a positive constant $C_* = C_*(\Vert c\Vert_\infty)$ such that

Theorem 5.1 (Upper bound). Any positive solution $(u, v)$ of system (1.3) satisfies

Proof. By the strong maximum principle, we know that if there is a $x_0\in \bar{\Omega}$ such that $v(x_0) = 0$, then $v(x)\equiv 0$ and $u$ satisfies

From the well known result, $u\equiv 0$ or $u\equiv 1$. Hence, if $(u, v)$ is not $(0, 0)$ or $(1, 0)$, then $u(x) > 0$ and $v(x) > 0$ for $x\in \bar{\Omega}$.

From the maximum principle, we easily obtained that $u(x)\leq 1$ in $\Omega$. Multiplying the first equation of Eq (1.3) by $\beta$ and adding it to the second equation of Eq (1.3), we have

Then from the maximum principle,

which leads to

□

Theorem 5.2 (Lower bound). There exists a positive constant $\underline{C}$ depending on $d_1$, $d_2$, $a$, $\beta$, $d$ and $\gamma$, such that any positive solution $(u(x), v(x))$ of Eq (1.3) satisfies

Proof.

Let

Then

A positive constant $C$ can be derived from Lemma 5.1 in such a way that

Therefore, it must now show that there is some $c > 0$ such that

On the other hand, suppose that the outcome is incorrect. Then there exists a series of affirmative solutions $(u_n(x), v_n(x))$ such that

By standard elliptic regularity, we obtain that there exists a subsequence of $\{(u_n, v_n)\}$, which is again denoted by $\{(u_n, v_n)\}$, such that $\{(u_n, v_n)\}\rightarrow (u_\infty, v_\infty)$ in $C^2(\bar{\Omega})$ as $n\rightarrow +\infty$. Noting that $u_\infty\leq 1$, since Eq (5.7) holds, $u_\infty\equiv0$ or $v_\infty\equiv0$. So, we have the following:

(ⅰ) $u_\infty\equiv0$, $v_\infty\not\equiv0$; or $u_\infty\equiv0$, $v_\infty\equiv0$;

(ⅱ) $u_\infty\not\equiv0$, $v_\infty\equiv0$.

Moreover, we get the following two integral equations:

(ⅰ) Case: $u_\infty\equiv0$, so we have

and $v_n > 0$. But, we integrate the equation of $v_n$; then, we have

This is a contradiction.

(ⅱ) $u_\infty\not\equiv0$ and $v_\infty\equiv0$, so $u_\infty$ satisfies Eq (5.1). So, $u_\infty\equiv 1$, and for a large $n$, we have

Thus, the second equation of Eq (5.9) does not hold, which is a contradiction. So, $\sup\limits_{\bar{\Omega}} u(x) > 0$, $\sup\limits_{\bar{\Omega}} v(x) > 0$, and consequently Eq (5.3) holds. □

Theorem 5.3. There is a large constant $d^*$ for which there is no non-constant positive solution to the problem (1.3) if $d_1, d_2\geq d^*$.

Proof. Suppose that $(u(x), v(x))$ is a non-constant positive solution of system (1.3). Denote

Then

Multiplying the first equation in Eq (1.3) by $u-\bar{u}$ and applying system (1.3), we get

Multiplying the second equation in system (1.3) by $v-\bar{v}$ and applying Theorem 5.1, we get

From Eqs (5.11) and (5.12), we get

By the $Poincar\acute{e}$ inequality, we have

where

These equations mean that if

then

and $(u, v)$ must be a constant solution. □

5.2.   Existence of non-constant positive steady states

For simplicity, denote

By the maximum principle and the standard elliptic regularity, the embedding theorems, and the assumption that $\partial \Omega \in C^{2+\alpha}$, we obtain that $(u, v)\in C^2\times C^2$ for the elliptic system (1.3). Therefore, there is a positive constant $M_1$, such that $\|\nabla u\|_{C^1}\leq M_1$ and $\|\nabla v\|_{C^1}\leq M_1$. So, there exists a sufficiently large positive constant $M$ such that $-d_1\Delta u-u(1-u-\frac{v}{a+u^2})+Mu$ and $-d_2\Delta v-\frac{\beta uv}{a+u^2}+dv+\gamma u v^2+Mv$ are monotonically increasing functions with respect to $u$ and $v$.

Define $\mathcal{A}:[C^1(\overline{\Omega})]^2\rightarrow [C^1(\overline{\Omega})]^2$ by

where $f_1(u, v) = u(1-u-\frac{v}{a+u^2})$ and $f_2(u, v) = \frac{\beta uv}{a+u^2}-dv-\gamma u v^2$.

It is worth noting that solving system (1.3) equates to finding positive solutions to the equation ${(M{\bf I}-{\bf \mathcal{A})u} = 0}$. We investigate the eigenvalue of the following problem using index theory.

where $\Psi = (\psi_1, \psi_2)^T$ and ${\bf u^*} = (u^*, v^*)$.

The following lemma is used to calculate the index of ($M{\bf I}-\mathcal{A}, {\bf u^*}$).

Lemma 5.2. ^[23] Assume that $(M{\bf I}-\mathcal{A}_u(u^*))\neq 0$. Then ${\rm index}(M{\bf I}-\mathcal{A}, {\bf u^*}) = (-1)^\sigma, \sigma = \sum_{\lambda > 0}m_{\lambda},$ where $m_\lambda$ is the multiplicity of $\lambda$.

By direct calculation, Eq (5.15) can be written as

Notice that Eq (5.16) has a non-trivial solution if and only if $Q_n(\lambda; d_1, d_2) = 0$ for some $\lambda\geq0$ and $n\geq0$, where

Then, $\lambda$ is an eigenvalue of Eqs (5.15) and (5.16) if and only if $\lambda$ is a positive root of the characteristic equation $Q_n(\lambda; d_1,$ $d_2) = 0$ for $n\geq0$.

Lemma 5.3. (i) When $n = 0$, $Q_0(\lambda, d_1, d_2) = 0$ may have no positive root, or exactly one positive root with a multiplicity of two, or two positive roots with a multiplicity of one.

(ii) If $d_1 > \frac{a_{11} }{M\mu_1}: = \hat{d}_1$, then $Q_n(\lambda, d_1, d_2) = 0$ has no positive root for $n\geq1$.

Proof. (ⅰ) It is easily obtained that $Q_0(\lambda, d_1, d_2) = \lambda^2- {\rm trace}({ {\bf{F}}_{\bf{u}}({\bf{u}}^*)})\lambda + {\rm{det}}({ {\bf{F}}_{\bf{u}}({\bf{u}}^*)}).$ Obviously, the result holds.

(ⅱ) It is clear that for $n\geq1$,

Since $a_{12} > 0$, $b_{1} < 0$ and $a_{22} > 0$, then the polynomial $Q_n(\lambda, d_1, d_2) > 0$. So, if $d_2$ is big enough, the desired result is reached. □

Lemma 5.4. Suppose that

holds; then, the following is true:

(i) The quadratic equation $M^2d_1d_2\mu_n^2+(a_{22}Md_1-a_{11}Md_2)\mu_n+b_{1}a_{12}-a_{11}a_{22} = 0$ has two roots. One is positive, say $\mu_1^*$, and the other is negative.

(ii) For some $n_1^*\geq1$, suppose that $\mu_1^*\in(\mu_{n_1^*}, \mu_{n_1^*+1})$. Then, there is a $\hat{d}_1: = \hat{d}_1(\Gamma, d_1, d_2)$ such that the characteristic equation $Q_n(\lambda, d_1, d_2) = 0$ has a unique positive root for $1\leq n\leq n_1^*$ and has no positive root for $n_1^*+1\leq n$ provided that $d_1\geq \hat{d}_1$.

Proof. (ⅰ) The condition (5.17) holds; then, $b_{1}a_{12}-a_{11}a_{22} < 0$, which implies that the result is true.

(ⅱ) Obviously, according to the definitions of $n_1^*$, $Q_n(\lambda, d_1, d_2) = 0$ has a unique root with a multiplicity of one for $1\leq b\leq n_1^*$, and it has no positive root for $n\geq n_1^*+1$ if $d_1\geq \hat{d}_1$. □

Theorem 5.4. Assume that $\mu_1^*\in(\mu_{n_1^*}, \mu_{n_1^*+1})$ for some $n_1^*\geq1$, and that $\sum_{k = 1}^{n^*}n_k$ is even. Thus, there is a $\hat{d}_1$ such that for any $d_1 > \hat{d}_1$, system (1.3) has at least one non-constant positive solution.

Proof. Assume, on the other hand, that the assertion is false for some $d_1 > \hat{d}_1$.

where $d_1^*$ and $d_2^*$ are constants that are positive and will be found out later.

Consider the problem

Its positive solution is contained in

By the homotopy invariance of the Leray-Schauder degree,

Notice that ${\bf u}$ is a non-constant positive solution of Eq (1.3) if and only if it is such a solution of (5.18) for $t = 1$. And for any $t\in[0, 1]$, ${\bf u}^*$ is a constant solution of Eq (5.18).

Since we assumed that there are no non-constant positive solutions of system (1.3), $\mathcal{A}_t({\bf u}) = {\bf u}$ has only the constant solution $u^*$ in $\Lambda$. By Lemmas 5.3 and 5.4, we can obtain

Thus, $\sigma = \sum_{k = 1}^{k_1^*}n_k+ 1\:(\:{\rm{or}}\: 3\:)\: = \:{\rm{an}}\: {\rm{odd}}\: {\rm{number}}.$ So that

Let us take

where $\hat{d}_1$ and $\hat{d}_2$ are defined in Lemma 5.3. By Theorem 5.3, $\mathcal{A}_0({\bf u}) = {\bf u}$ has only the positive constant solution $u^*$. In addition, by investigating the existence of positive roots $\lambda_k$ of $Q_k(\lambda, D_0,$ $D_I, D_P) = 0$, we get

since Lemma 5.3 gives $\sigma = l_{\lambda_0} = 0\; {\rm or}\; 2$. Therefore, Eqs (5.19) and (5.20) contradict Eq (5.21). This completes the proof. □

6.   Numerical simulations

In this section, we use numerical simulations of a few different scenarios to illustrate our theoretical findings.

6.1.   The effect of delay $\tau$

We choose the parameters $a = 1$, $\beta = 0.96$, $d = 0.01$, $\gamma = 0.3$, $d_1 = 0.2$, $d_2 = 2$ and $\Omega = (0, \pi)$. By a direct calculation, we get that system (1.2) has a unique equilibrium $E^* = (0.0151, 0.9852)$, and Eq (3.18) has two positive roots: $\omega_1 = 0.1336$ and $\omega_2 = 0.1018$. According to Eq (3.20), we obtain the critical values of $\tau$

and

In addition, from Eq (3.1), we obtain

When $\tau = \tau _1^j$, a pair of eigenvalues crosses the imaginary axis from left to right. Figure 2 shows the delay time histories for different locations. When $\tau \in [0, \tau_1^1)\bigcup(\tau_2^1, \tau_1^2)\bigcup(\tau_2^2, \tau_1^3)$, the equilibrium of system (1.2) is asymptotically stable, but it becomes unstable when $\tau \in (\tau_1^1, \tau_2^1)\bigcup(\tau_1^2, \tau_2^2)\bigcup (\tau_1^3, +\infty)$. In other words, the delay $\tau$ causes the system (1.2) to exhibit the phenomenon of multiple switching events, in which the state of system (1.2) alternates between stable and unstable and vice versa, and the equilibrium $E^*$ is ultimately unstable.

If we keep the other parameters unchanged, only changing the value of $\gamma$ to $0.1$, we find that the positive equilibrium $E^*$ is locally stable for all $\tau\geq0$ (see Figure 3).

6.2.   Turing instability

We apply the parameters $a = 0.3$, $\beta = 0.3$, $d = 0.2$, $\gamma = 0.3$, $d_1 = 0.002$, $d_2 = 4$ and $\Omega = (0, 60)$ By some calculations, we obtain that system (1.2) has a unique positive equilibrium $E^* = (0.2824, 0.2725)$. According to Theorem 3.1, by perturbing the initial value at the equilibrium $E^*$, we find that Turing bifurcation occurs (see Figure 4). Figure 4 shows that system (1.2) has a stable non-constant steady state. But, if we increase the value of $\tau$ to $12$, we find that the stable non-constant steady state disappears, and that the system has a period solution (see Figure 5). However, if we further increase the value of $\tau$ to $81$, we find that the system has chaotic behavior (see Figure 6); the bifurcation diagrams of system (1.2) are shown in Figure 7.

7.   Conclusions

The focus of this paper is on analyzing the effects of the toxins on a delayed diffusive predator-prey model. Overall, the paper provides a thorough analysis of the dynamic behavior of the system, considering various steady states and their stability. The incorporation of a delay in the model allows for an exploration of the effects of time lags in the predator-prey interaction, which adds realism to the study. The findings are interesting and reasonable.

Our system's dynamics were investigated in detail at and near all feasible steady states. We demonstrated that the system is persistent under specific conditions, where both the prey and the predator can survive. Conditions for the Turing bifurcation and global stability of the system at all equilibria are derived and presented. With respect to the delay $\tau$, we found that the system displays a Hopf bifurcation near its interior equilibrium. Non-constant steady states were also discussed, along with the conditions under which they do and do not exist.

The theoretical findings are then illustrated by means of some numerical simulations. These results demonstrate that the system (1.2) displays spatial patterns and that a delay can lead to Hopf bifurcation and chaos. The findings might be useful for future qualitative research into a similar natural system.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Social Science Fund Youth Project of China (Grant No. 21CJY040).

Conflict of interest

The authors declare that they have no conflicts of interest.