1.
Introduction
With the accelerated pace of global urbanization, the scale of transportation networks continues to expand, and their structures are becoming increasingly intricate. A primary consequence of this development is the escalating number of traffic accidents [1]. These accidents not only result in considerable casualties and economic damages [2], they also impede urban transportation efficiency and degrade the quality of residents' lives [3]. According to World Health Organization statistics, approximately 1 million individuals experience traffic accidents each year, positioning them as one of the predominant causes of death globally [4]. Concurrently, tens of millions sustain varied degrees of injuries, with many facing enduring disabilities.
In light of this context, traffic accident prediction has emerged as a salient research topic that intersects transportation studies, statistics, and data science. By assessing and forecasting the risks of traffic accidents at specified times or locations under certain conditions, one can obtain a foundational basis for informed decisions in traffic safety management [5]. In the short term, accurate and reliable accident prediction can offer timely alerts for drivers and pedestrians, mitigating accident risks. They also allow governmental and relevant agencies to pre-emptively allocate resources, ensuring effective traffic planning and administration. In the long run, such predictions offer invaluable data support for urban transportation planning, infrastructure investments, and public transit strategies, helping stakeholders and policymakers to shape a safer, more efficient, and sustainable urban transit environment.
Transportation data, typically sourced from intelligent transportation system (ITS) [6] sensors or collected by professionals at fixed intervals, possesses distinct time-series characteristics. Time-series forecasting [7], a cornerstone of statistics and data science, seeks to discern patterns in historical data and predict future trends and fluctuations. Incorporating time-series forecasting techniques into traffic accident prediction allows researchers to capture cyclical, seasonal, and trend variations more accurately. However, traffic accidents, influenced by multifaceted external factors like traffic volumes, weather conditions, and societal activities, possess a strong stochastic and uncertain nature. Traditional process-based machine learning techniques struggle to meet the growing stakeholder demand for predictive reliability and precision. With the progression of artificial intelligence and rapid advancements in computational power, data-driven machine learning methods, exemplified by artificial neural networks (ANNs) [8], dominate the realm of time-series forecasting. These models, independent of specialist expertise, showcase robust generalization capabilities and exceptional accuracy, finding extensive applications in financial systems and the energy sector. Within the transportation domain, ANN-based models have also seen preliminary adoption.
In [9], an ANN-based model was utilized to predict the number of traffic accidents on the Erzurum highway in Turkey. This model considered several factors that influence traffic accidents, such as the weather conditions, date, road conditions, and traffic volume. Experimental analysis also revealed the significance of these factors and the number of traffic accidents. On the other hand, Alkheder et al.[10] introduced an ANN-based model for classification of the severity of traffic accidents. By modeling 48 attributes collected from accident sites, this model could categorize accidents into four distinct severity levels. Tests on a traffic accident dataset from Abu Dhabi city showed that the classification accuracy of the ANN model increased by almost 25% relative to the traditional ordered probit model. It was clear that, owing to its powerful nonlinear processing capability, the ANN exhibited superior performance on both regression and classification tasks compared to traditional models. However, there were some limitations in the extensive use of basic ANNs across various domains. For example, as the network depth increased, deep neural networks often encountered the vanishing/exploding gradient problem. Additionally, the large number of parameters could significantly increase the computational costs. Notably, basic ANNs tend to struggle with handling time-series inputs, which meant, for traffic datasets with temporal data, they might not effectively capture the underlying relationships in the time dimension, limiting the model's efficacy. The field of neural networks is rapidly evolving, with new architectures continuously being proposed to address these challenges. convolutional neural network (CNNs) [11] and long short-term memory (LSTM) networks [12], two of the most prominent variants of ANNs, have become the cornerstone models in the domain of intelligent transportation. In [13], a traffic accident severity prediction model named TASP-CNN was introduced. Innovatively, this model transformed the feature data of traffic accidents into grayscale images by using the feature matrix to gray image algorithm. By leveraging the powerful image feature extraction capability of CNNs, the model was able to comprehensively learn the intricate abstract hidden relationships within traffic accident data. Through tests on a dataset encompassing eight years of traffic accident data recorded in Leeds, UK, the authors demonstrated that their proposed model significantly outperformed traditional models. In the study presented in [14], a data-driven multi-feature traffic flow prediction model, termed MF-CNN, was proposed based on CNNs. This model integrated a variety of self-features that influence traffic flow. Depending on their temporal scale, these features were further divided into short-term and long-term attributes, and they were mapped onto a two-dimensional spatio-temporal matrix. The CNN excelled in extracting high-order spatio-temporal abstract features from this matrix. Once these features were merged with multiple external attributes, a prediction was obtained. Experimental results from [14] suggested that the MF-CNN, endowed with multi-feature fusion capabilities, surpassed the vanilla CNN and other baseline models, recording a performance boost of over 20% on several traffic datasets. As compared to the CNN, the LSTM possessed the ability to selectively remember contextual information in input sequences, thus, they are currently the most frequently utilized neural network models in the domain of time series prediction, including traffic accident forecasting. Zhang et al.[15] proposed an LSTM and the gradient boosting regression tree (GBRT) based model LSTM-GBRT, for traffic accident trend prediction. The integration strategy employed by GBRTs could alleviate, to some extent, the subpar performance of LSTM in the area of predicting inflection points in data, thus endowing the proposed model with enhanced fitting capabilities. In order to fully leverage the respective advantages of CNNs and LSTM, and to compensate for their limitations, various scholars have attempted to combine the CNN and LSTM to achieve superior model performance. Both [16] and [17] employed the hybrid CNN-LSTM model for traffic prediction and demonstrated through multiple experiments that the efficacy of the hybrid model significantly surpassed that of a single model. Advancing beyond the LSTM framework, gate recurrent units (GRUs) have emerged as a variant that simplifies and integrates the original gated units of LSTM networks. This adaptation preserves the strong time series forecasting ability of LSTM while significantly reducing the model's parameters. As a result, the GRU has become one of the most successful derivatives of LSTM, being widely utilized in time series forecasting. Jin et al. [18] developed an air quality prediction method based on a GRU network, establishing an interpretable multivariate data filtering structure to extract crucial information from various external variables that impact air quality prediction, as well as optimizing feature selection via an embedded self-filtering layer within the network. Subsequently, an enhanced variational Bayesian GRU network was employed for multidimensional, multi-step time series forecasting. Shi et al. [19] tackled non-stationary time series by proposing a forecasting method that integrates data decomposition with parallel deep networks. This method initially segments the input non-stationary series into several groups, each further decomposed into cyclical, trend, and residual components. A GRU network is employed for to predict each component, with the predictions finally merged by using covariance intersection fusion. Moreover, Jin et al. [20] combined graph neural networks [21] with GRUs to propose the Bayesian graph gate recurrent network, a model capable of accurately modeling spatiotemporal features within the input vector and enhancing the performance of time series forecasting models from multiple dimensions, offering additional insights for current research.
Building upon the foundational work of CNNs and LSTM, which have laid the groundwork for neural network applications in traffic accident prediction, the advent of the Transformer architecture [22] represents a significant leap forward. This state-of-the-art model introduces a paradigm shift through its unique self-attention mechanism, setting a new benchmark for handling the intricacies of sequential data in the predictive modeling domain. Initially conceived to address the limitations of recurrent neural network (RNN) algorithms like LSTM in sequence-to-sequence (Seq2Seq) tasks [23], particularly in machine translation within the domain of natural language processing (NLP) [24], the Transformer architecture has gained favor among researchers for its unique self-attention mechanism. This mechanism effectively captures long-term dependencies within sequential inputs and allows for parallel processing, thereby enhancing efficiency. Consequently, the Transformer's influence has progressively extended beyond its original scope to penetrate diverse fields, including computer vision (CV) [25] and time series forecasting [26]. Dosovitskiy et al. [27] proposed a novel adaptation of the Transformer for image processing: the Vision Transformer (ViT). Aimed at transferring the quintessential Transformer architecture to the field of CV with minimal modifications, ViT ingeniously reconfigured the model's input stage. It dissects the input images into fixed-size patches and reconstituts these sub-patches into a linear embedding sequence through the use of a trainable linear projection, supplemented with positional encodings to encapsulate spatial information. Consequently, an image is effectively transformed into a sequence, which is then processed by the Transformer in a sequential manner. Meanwhile, Yin et al[28] advanced a Transformer-based model for rainfall-runoff forecasting, dubbed RR-Former. Upholding the integrity of the standard Transformer architecture, this model deftly sequenced historical hydrological and meteorological data as input to the Transformer, thereby enabling precise runoff forecasting. Zheng et al. [29] proposed a traffic prediction model based on graph CNN (GCN) and Transformer, referred to as virtual dynamic GCN and Transformer with gate and attention mechanisms (VDGCNeT). This model initially constructs a virtual dynamic road graph, and then models the spatio-temporal data in road datasets by using a GCN and Transformer. It integrates temporal and spatial features through a gating mechanism. Experiments demonstrated that the VDGCNeT achieves up to 96.77% accuracy on the PEMS-BAY road dataset, setting a new benchmark in the industry.
The impressive performance of the Transformer across various domains and application scenarios [30] has illuminated its substantial potential and practical value for traffic accident prediction. Nevertheless, the application of the Transformer in this area remains insufficiently explored. To address this gap, we introduce a Transformer-based model for traffic accident forecasting, namely, the Traffic Transformer. This model has been designed to capture historical traffic accident data and harness the Transformer's formidable sequence modeling capabilities to accurately predict traffic accidents over multiple future short-term periods. The contributions and innovations of this work are detailed as follows:
(1) We innovatively adopt the Transformer architecture, incorporating the Seq2Seq framework, to supplant commonly utilized neural network algorithms such as CNNs and LSTM in traffic accident prediction. Additionally, we employ a temporal discretization approach to transform irregularly intervaled raw datasets of traffic accidents into regularly sampled time series, thereby constructing serialized inputs that complements the Transformer model.
(2) Owing to the exceptional ability of the proposed Traffic Transformer to capture long-term dependencies, the model is capable of multi-step forecasting and exhibits temporal robustness across various forecast horizons.
(3) We conducted training and testing on a traffic accident dataset collected by Qatar's ITS and the police force; it is a valuable real-world dataset encompassing a diverse array of traffic data under various weather and road conditions in both urban and rural settings. This dataset has allowed the proposed model to thoroughly learn the underlying patterns of traffic accident occurrences across different conditions.
The remainder of this paper is organized as follows: Section 2 elucidates the motivation, architecture, and principles underpinning the Traffic Transformer; Section 3 details the specific implementation nuances of our model; Section 4 presents the experimental setup along with a comprehensive discussion of the results and their analysis; and Section 5 concludes the paper with a summary and an outlook on future research directions.
2.
Transformer-based traffic prediction model: An in-depth analysis of the architecture
2.1. From the CNN/LSTM to the Transformer
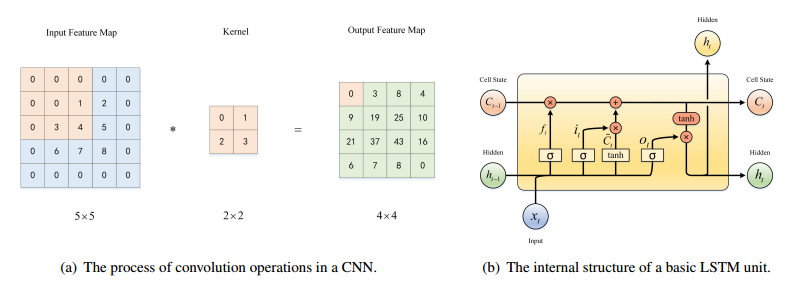
As seminal models in neural network research, CNN- and LSTM-based have become dominant forces in hot-button artificial intelligence domains such as CV, NLP, and time series forecasting. These architectures are the most frequently employed backbone networks in contemporary traffic forecasting models. The structure of a CNN, depicted in Figure 1(a), mimics the human visual system's approach to observing the external world; particularly, it is capable of accurately recognizing the layered structure of input data to extract specific features. The remarkable capabilities of CNNs are largely due to two key characteristics: weight sharing and sparse connectivity [31]. Unlike fully connected neural networks, CNNs utilize convolutional filters that move across the feature map at a defined stride, sharing filter weights across the entire feature map and thereby significantly reducing the model's parameter count. Additionally, each neuron in a CNN layer is connected only to a subset of neurons in the previous layer, which ensures focus on local features. Through the stacking of multiple layers, CNNs can gradually learn more complex and global features; this is achieved via a hierarchical learning mechanism that gives CNNs a superior feature extraction capacity compared to fully connected neural networks. The LSTM network structure, shown in Figure 1(b), consists of a unit known as a cell. This cell contains three gate structures: the forget gate, input gate, and output gate. The cooperative action of these gates allows the LSTM to selectively remember and forget information, thereby effectively avoiding the issues of gradient vanishing and explosion that are common in traditional RNNs [32]. Therefore, LSTM can model longer input sequences and extract sequential abstract information, which is an ability that has led to their extensive application in sequence modeling. Their flexible memory capacity makes them particularly well-suited for tasks that require maintaining sequential information over long durations.
In light of its commendable attributes, CNNs nonetheless possess considerable limitations in terms of its operational paradigm. The mechanism of feature extraction in CNNs is predicated on the convolutional traversal of kernels over the spatial extent of feature maps, which confines the receptive scope. To effectively navigate and assimilate long-term dependencies within sequential data, the architecture necessitates a linear superposition of numerous strata, culminating in a proliferation of parameters. This architectural profundity may precipitate a regression in network performance known as degradation. Conversely, LSTM networks equipped with intricate gated units demonstrate superior proficiency in deciphering dependencies that span greater temporal expanses than those within the purview of a CNN. Nevertheless, constrained by its intrinsic design as a recurrent architecture, each LSTM cell is compelled to sequentially await the computational outputs of its antecedent, thereby constraining the potential for parallel data processing. Such a sequential dependency introduces pronounced inefficiencies in the context of large-scale traffic data analytics. Moreover, despite the LSTM network's advanced capability to model long-term dependencies as compared to RNNs and CNNs, it is not immune to diminished performance when tasked with the processing of extensive sequential inputs, revealing a persistent challenge in the modeling of expansive temporal sequences.
In response to the inherent limitations observed within extant traffic prediction models, we propose the Traffic Transformer, a bespoke framework that has been meticulously engineered for the prediction of traffic accidents. Figure 2 delineates the composite structure of the Traffic Transformer. At the input juncture of the Traffic Transformer, a temporal discretization technique transmutes the multivariate, irregularly intervaled data of raw traffic accidents into a structured sampling of temporal sequences that are amenable to sequence forecasting. This transformation is further enhanced by input embedding and positional encoding, which collectively procure representational vectors for each constituent of the input sequence. The matrix composed of these vectors constitutes the input to the Traffic Transformer. Given the quintessential nature of traffic accident prediction as a time series forecasting problem, the Traffic Transformer employs the Seq2Seq architecture, which comprises an encoder and a decoder. The encoder is tasked with transfiguring the time series data into fixed-size context vectors that are instrumental in the learning and capturing of the covert interconnections among input sequences. The decoder, in turn, incrementally constructs the entire output sequence by generating predictions for subsequent temporal elements, drawing on the context vectors obtained from the encoder and the output of the preceding temporal step. Both the encoder and the decoder are constituted by a series of identical layers, each layer featuring a multi-head attention mechanism, concomitant residual connections [33], layer normalization [34], and a fully connected layer. The cornerstone of the Traffic Transformer is the self-attention mechanism, which allows the model to discern correlations between any two elements within the input sequence, and thus, obtain the long-term dependencies across arbitrary intervals. The assemblage of self-attention heads, termed multi-head attention, allows the model to concurrently concentrate on disparate sequence positions and thus learn the inherent associations within sequence information from a multiplicity of perspectives. It is noteworthy that the multi-head attention mechanism within the encoder and decoder blocks of the Traffic Transformer are not entirely identical. As is discernible from Figure 2, the first instance of multi-head attention module in each decoder layer employs a masking operation to ensure that sequence modeling is contingent solely on known observations, thereby preventing information leakage. Following each multi-head attention, residual connections and layer normalization are applied. Layer normalization stabilizes the gradients by normalizing the outputs from the multi-head attention or the feed-forward layers, thus reducing variability across the outputs of different layers and accelerating the training process. The application of residual connections, which constitutes a staple technique in neural networks, creates a direct pathway between the input and output, effectively preventing the problems of vanishing/exploding gradients and network degradation in a deep network. Each encoder and decoder layer also includes a fully connected feedforward network with an activation function, consequently introducing non-linearity and enhancing the model's capability for parallel processing. Conclusively, the decoder's output is passed through a linear transformation to allow the Traffic Transformer to generate the final traffic accident predictions.
The Traffic Transformer framework that we propose is notable for its innovative replacement of recurrent and convolutional structures, which are commonly found in LSTM and CNNs, with a self-attention mechanism. This pivotal shift allows for the establishment of direct correlations between any two elements in the input sequence, which enables the consideration of the model to consider the entire sequence when evaluating each element. Consequently, the Traffic Transformer possesses a global receptive field, which ensures the effective capture of long-term dependencies across sequences of any length without information loss and thereby fundamentally addresses the inherent shortcomings associated with CNNs and LSTM. Moreover, the Traffic Transformer is endowed with the capability of parallel processing and facilitates an enhancement of model interpretability through the visualization of attention weights, elucidating the rationale behind the model's predictive outcomes. These advantages confer upon the Traffic Transformer a distinct superiority over existing mainstream models in the domain of traffic accident prediction. The ensuing sections of this chapter will delve into a comprehensive exposition of the individual modules constituting the Traffic Transformer.
2.2. Self-atttention: The soul of the Transformer
The self-attention mechanism represents the cornerstone of the Transformer architecture and signifies a milestone advancement in the field of sequence modeling. It transcends the inherent limitations associated with traditional sequential data processing approaches. For instance, neural network algorithms based on recurrent architecture, such as LSTM, process sequences incrementally, which often impairs their ability to capture long-term dependencies. Self-attention has fundamentally addressed this issue by modeling without the constraints of a limited context window. It eschews the conventional paradigms of analyzing elements in isolation or through restricted proximal interactions. Instead, it models the entire input sequence, evaluating and expressing the significance of the interrelation between any two positional elements in the sequence through the implementation of a weighting scheme. This spectrum-wide analytical capacity endows the Transformer with a global receptive field that is superior to those CNNs and LSTM networks, which enables the recognition of relevant patterns across the full extent of the sequence, unfettered by immediate context.
Within the Transformer, self-attention is facilitated through the sophisticated interplay of query (Q), key (K), and value (V) matrices. Each input token is projected into these matrices via the linear transformation matrices WQ, WK and WV, fulfilling the following distinct functional purposes: Q captures each token's unique inquiry regarding other elements; K serves as the token's identifier, providing a contextual anchor; V holds the substantive content of each token, readying it for contextual weighting. In order to calculate the attention scores between elements within a sequence, the model executes a dot product operation between the row vectors of Q and K. A scaling mechanism is also employed to prevent excessively large dot product values. This necessitates the division of the dot product by the square root of the vector dimension dk within Q and K. A subsequent softmax operation ensures that these scores are proportionally distributed, summing to one. The normalized attention scores then determine the weighting of V, yielding an output that integrates these weighted contributions and compelling the model to prioritize the most significant portions of the input from a global informational perspective. The modeling process of self-attention can be formalized as follows:
For the prediction of traffic accidents, to accurately forecast across multiple future time periods, multi-variate long sequences, which often embed complex high-order abstract hidden relations, are utilized as inputs for the model. As the essence of the Traffic Transformer, the self-attention mechanism is precisely poised to effectively capture both short-term and long-term dependencies among any two elements in the sequence, which yields more precise and reliable multi-step predictions.
2.3. Diversifying attention with multiple heads
While the self-attention mechanism is capable of capturing the hidden relationships between any two elements within an input sequence from a global perspective, in essence, a single self-attention module possesses only a univocal viewpoint. However, complex input sequences may embody diverse patterns, and consequently, self-attention could potentially overlook the subtleties and intricacies embedded within the sequences. The Traffic Transformer model integrates the multi-head attention mechanism, allowing the architecture to not only observe data from a single standpoint but also to concurrently maintain multiple independent perspectives, thus attending to different segments of the input sequence to discern the potential diversity of connections among sequence elements.
Figure 3 delineates the structure of multi-head attention, which reveals that it consists of several self-attention units. Fundamentally, multi-head attention splits each attention head, and these newly derived heads function in a manner that is conceptually similar to the basic self-attention mechanism by upholding their independent sets of query, key, and value matrices. These matrices are critical as they dictate the relationships that are identified by each head within the data. By allocating distinct matrices to each head, the model ensures that different heads can potentially concentrate on various patterns and relationships within the sequence. This approach yields a rich array of perspectives on the input data. After these multiple heads process the data, a crucial integration step ensues. The outputs from each head, infused with their unique perspectives, are concatenated. This amalgamated output embodies the insights from all of the different attention heads, providing a multidimensional view of the sequence. Nonetheless, to guarantee that this collective output is effectively assimilable by subsequent layers, it undergoes a linear transformation for re-projection. This transformation aligns the diverse insights into a unified format, priming it for further processing.
The application of multi-head attention within the Traffic Transformer allows the model to compute the diversified dependencies within the input sequence in parallel during a single time step, significantly bolstering the model's representational capabilities. In our traffic accident prediction scenario, multi-head attention is particularly good at handling complex time-series data with multiple dependencies. For instance, seemingly sporadic traffic incidents on a city's roads are influenced by a myriad of factors e.g., the time of day, current events, weather conditions, and even subtle elements such as the start or end times of schools. A singular attention mechanism might predominantly focus on the most conspicuous patterns, such as traffic volume. In contrast, multi-head attention allows the model to comprehend multiple simultaneous influences, like the collective impact of rush hour, a sudden downpour, and a local event causing a detour. This capability renders it especially powerful for the analysis of data in the real world, which is influenced by a multitude of factors; thus, the attention module is the most accurate and reliable learning mechanism within the Traffic Transformer.
2.4. Constructing inputs for the Traffic Transformer model
Using the dataset employed in this study as a case in point, owing to the stochastic nature of traffic accidents, the raw traffic data set constitutes a multivariate irregularly intervaled dataset chronicling the time of accidents, weather conditions, and regional information, which cannot be directly fed into the Traffic Transformer for prediction. We employ a temporal discretization approach, initially transforming the raw dataset into a regular sampling time series with each interval spanning one hour. This endows the traffic accident data with temporal characteristics. Subsequently, we applied feature engineering to the transformed dataset to extract and generate additional novel features that better encapsulate the essence of the traffic accident prediction problem, which helps the model with learning and forecasting. Specifically, we performed a rolling calculation of the maximum, mean, sum, and exponential weighted moving average over multivariate features across a defined historical time span. These generated features were incorporated into the dataset to assist the model in more effectively capturing trends and cyclical patterns within the time series. Moreover, we employed a sliding window technique to construct input features and label values for multi-step forecasting. The size of the sliding window can be adjusted according to different forecast horizons, enhancing the model's efficiency in data utilization. We also applied min-max normalization to the dataset to normalize data of different dimensions on the same scale for processing. This approach significantly improved the convergence speed and performance of the model.
The multivariate time-series input sequences, having undergone data preprocessing and feature engineering, require transformation into vector matrices via input embedding and positional encoding to facilitate the multi-head attention computations within the encoder. Input embeddings convert each element of the input sequence into fixed-length vectors in a high-dimensional space, and these vectors are enriched with semantic information acquired during the model training process. The employment of input embeddings offers an efficient representational format wherein the vectors' distances and directions reflect the associations and similarities among the original elements, allowing the model to adaptively learn and capture the latent relationships between elements.
However, the Traffic Transformer eschews a recurrent architecture that is similar to LSTM in favor of parallel global information modeling, which inherently lacks the capacity to utilize the sequential order of input elements, which is a critical facet in time-series forecasting. To impart the Traffic Transformer with essential sequential recognition capability in the absence of inherent order perception, positional encoding is integrated after the input embedding, thereby providing the model with the positional context of input elements within the overall sequence. The introduction of positional encoding circumvents the need for architectural modifications and instead endows the Traffic Transformer with sequence recognition by infusing additional information into the model input. Utilizing sinusoidal functions for positional encoding conveys the precise location of each sequence element without distorting the original data. These encodings, derived from periodic mathematical functions, can suitably represent cyclic patterns in the data and ensure distinct positional discernibility within longer sequences. The formulation for positional embedding is as follows:
where pos denotes the position of an element within the overall sequence, while d represents the number of dimensions of the positional encoding. Subsequently, positional encodings are added to the input embeddings, ensuring that each element's vector representation encompasses not only its inherent semantic information but also its positional information within the sequence. As such, when these embedded vectors are fed into the self-attention modules of the subsequent encoders or decoders, the model can process the sequence based on this information, capturing the complex dependencies between the elements. This amalgamation of word embeddings and positional encodings constitute one of the key reasons why the Traffic Transformer model can demonstrate robust performance in traffic accident prediction.
3.
Implementation details
In the architecture of our proposed Traffic Transformer, we employ the rectified linear unit (ReLU) [35] activation function within the fully connected neural networks of each encoder and decoder layer to perform non-linear transformations; its formula can be expressed as follows:
Compared to traditional activation functions such as Sigmoid, the ReLU activation function is computationally more efficient as it simply thresholds the inputs. Additionally, with a constant gradient in the positive interval, the ReLU mitigates the issue of vanishing gradients, rendering it the most prevalently utilized activation function in neural networks.
The primary application of the Traffic Transformer is traffic accident forecasting, which falls within the domain of time series forecasting. Consequently, the mean absolute error (MAE) is employed as the loss function to evaluate performance, with the formula given as follows:
where n represents the number of samples and yi and ˆyi denote the actual and predicted values for the ith instance, respectively. The primary function of the MAE is to calculate the average of the absolute differences between predicted values and true values. Its advantage lies in the equal weighting of all prediction errors. However, constructing datasets for time series forecasting often results in missing values due to sensor malfunctions or human errors. To address this, we have adapted the MAE to create the masked-MAE. The masked-MAE disregards and masks out missing data points when calculating the loss, assessing the model's performance solely on available data. Traditional linear or polynomial interpolation methods require the assumption that missing values are uniform and regular. In contrast, the Masked-MAE does not rely on such strong assumptions, which enables a more flexible handling of data with random missing values and thus enhances the performance of the model.
In the evaluation of model performance, not only is the MAE utilized as a loss function, but two commonly employed metrics in time series forecasting, i.e., the mean squared error (MSE) and mean absolute percentage error (MAPE), are also adopted to provide a more comprehensive assessment of the model's efficacy. The formulas for these metrics are expressed as follows:
These equations serve to quantify the deviation of the model's predictions from the actual observed values, with the MSE providing a measure of the variance and squaring the prediction errors; this consequently penalizes larger errors more severely. Alternatively, the MAPE offers an insight into the relative error by comparing the absolute percentage difference between predicted and actual values. These three evaluation metrics each possess unique characteristics, enabling a comprehensive assessment of time-series forecasting models from multiple perspectives. Consequently, they are the preferred metrics in the field of traffic forecasting due to their ability to holistically evaluate model performance.
To verify the multi-step forecasting ability of the proposed Traffic Transformer, we have utilized multivariate historical data from the preceding 12 steps to predict traffic accident data for the subsequent 1, 3, and 6 steps. To expedite the convergence of the model, we have adoptd the adaptive moment estimation (Adam) optimizer [36], which combines the momentum from gradient descent with RMSprop, with an initial learning rate set at 0.005 and a weight decay configured to 1×10−4. Within the Traffic Transformer, we have determined through extensive testing that an optimal balance between performance and efficiency is achieved with two layers in both the encoder and decoder, and four attention heads in the multi-head attention module. If computational resources are abundant, an increment in the number of layers for both the encoder and decoder is feasible, which, albeit at the cost of increased computational demand, would yield a substantial improvement in performance. The construction of the Traffic Transformer and the comparative models for the experimental section were realized by using Pytorch 1.10.2+cu113 and Python 3.7, with the experiments being conducted on hardware comprising an Intel I7-12700F CPU and NVIDIA RTX 3070 GPU.
4.
Experimental results and analysis
4.1. Dataset and hyperparameter settings
In this study, we chose to utilize the traffic dataset from Qatar for model training and testing. Situated on the eastern coast of the Arabian Peninsula, Qatar has an approximate population of 2.68 million. The nation's traffic accident dataset is particularly advantageous for analysis and predictive modeling due to its highly modernized transportation infrastructure, the high-quality data collected by the government, its high geographical concentration, and its relatively small population. These attributes, combined with Qatar's unique climate and significant investment in technology, render the dataset an exemplary choice for traffic accident prediction; this contributes to enhance the precision of the models and the effectiveness of preventive measures. The dataset chronicles traffic accidents that occurred in Qatar from July 2018 to August 2019. After excluding samples with missing values, it contained a total of 332,766 valid records, each detailing the time of the accident, weather conditions, and area codes. To facilitate predictions across different subareas of Qatar, the country was segmented into 98 subareas, coded 1–98. For the purposes of experimentation, subareas coded 45, 55, and 56 were randomly selected, containing 6,257, 7,725, and 8,315 samples, respectively. The dataset was partitioned such that 75% was dedicated to training, while the remaining 25% was utilized for testing.
For the experiments, to thoroughly assess the proposed Traffic Transformer, we introduced two prevalent models for traffic accident prediction: the LSTM-S2S with a Seq2Seq structure and the LSTM-S2S-AM, which augments the former with an attention mechanism. Serving as the most widely utilized neural network architectures for traffic accident prediction, these LSTM-based comparator models offer significant benchmarking value. Table 1 displays the hyperparameter configurations employed by the models in the experiments. We conducted comparative analyses on datasets from various areas within Qatar; also, to ascertain the multi-step forecasting prowess of the models, we executed tests across different forecast horizons. To ensure fairness and consistency in the experiments, a uniform forecast horizon of six steps was adopted for predictions across multiple distinct areas. Furthermore, for the purposes of multi-step forecasting, area 45 was consistently utilized as the dataset.
4.2. Predictive outcomes and analysis of models across different areas in Qatar
Table 2 presents the results of comparative experiments conducted in areas coded 45, 55, and 56, from which it is readily apparent that despite adopting the same Seq2Seq architecture, the LSTM-based LSTM-S2S and its attention-augmented counterpart LSTM-S2S-AM lag considerably behind our proposed Traffic Transformer across multiple evaluation metrics. Regarding the MAE metric, the Traffic Transformer maintained a marginal error of only 0.26 in area 56, which is its least impressive performance, marking error reductions of 88% and 84% relative to LSTM-S2S and LSTM-S2S-AM, respectively. This underscores a pronounced advantage in prediction accuracy, particularly demonstrating a more robust mean level forecast. The significant enhancement in the MSE metric further accentuates the robustness of the Traffic Transformer against outliers or noise. Given that the MSE assigns greater weight to larger errors, the model's marked superiority in this metric indicates that the improvement in predictive accuracy is not confined to average levels, but it extends across the entire error distribution. Lastly, as shown in Figure 4, the MAPE metric reflects the proportion of the model's prediction error in relation to actual values, where the Traffic Transformer's performance is notably superior in all areas, especially excelling in area 55 with an error rate of only 4.43%. This signifies that in terms of relative predictive accuracy, the Transformer model captures changes in the data trend more precisely, which is particularly critical for traffic accident forecasting where accurately grasping the trend of occurrences is vital for the development of effective prevention and control strategies.
The experimental data compellingly suggest that the proposed Traffic Transformer model significantly outperforms LSTM models based on the Seq2Seq architecture—both the basic version and the one enhanced with attention mechanism on the multi-area traffic accident prediction task in Qatar. The performance disparity is primarily attributed to the unique self-attention mechanism of the Traffic Transformer, which captures long-term dependencies throughout the input sequence. In contrast, even the LSTM-S2S-AM model, with its attention mechanism, is limited in its understanding and modeling of complex spatiotemporal relationships due to its inherent sequential data processing approach. Furthermore, the Traffic Transformer's multi-head attention mechanism captures diverse data characteristics across different representational spaces, offering a more comprehensive understanding of the intricate dynamics in traffic flow. This significant improvement in prediction accuracy indicates that multidimensional feature comprehension is crucial for traffic accident forecasting. Moreover, the architecture of the Traffic Transformer prevents the occurence of the vanishing gradient problem, a common issue with RNNs on long sequences; this allows it to learn and predict the time series data for traffic accidents more efficiently. In contrast, the LSTM network must process each time step sequentially, limiting its efficiency in the process of capturing temporal dependencies. The Traffic Transformer's capacity to consider the entire input sequence at each decoding step allows for a global perspective of information integration, which provides a richer and more nuanced spatiotemporal context for traffic accident prediction. These factors combined not only provide a cogent explanation for the superior predictive performance of the Traffic Transformer, they also highlight the importance of a model's inherent global understanding capability and feature capturing precision when addressing complex and variable real-world issues like traffic accident prediction.
4.3. Predictive outcomes and analysis of models over different forecast horizons
The superior performance of the Traffic Transformer across various forecasting intervals is clearly evidenced by the data in Table 3 and Figure 5. For forecast horizons of 1, 3, and 6 steps, the Traffic Transformer consistently outperformed LSTM-S2S and LSTM-S2S-AM in terms of the MAE, MSE, and MAPE metrics. Notably, in the case of MAE and MSE indicators, the Traffic Transformer yielded values that were an order of magnitude lower than its counterparts, signifying a significant leap in prediction accuracy. For instance, for a 1-step forecast, the MAE and MSE for LSTM-S2S and LSTM-S2S-AM were 1.12 and 1.14, and 3.52 and 3.57, respectively, while for the Traffic Transformer, these values were markedly lower at 0.24 and 0.33, respectively. The same trend is also evident in longer-range forecasts; for example, the 6-step forecast results show that, although the MAE and MSE for the LSTM base model and its attention-augmented version remained constant, the Traffic Transformer still yielded substantially lower levels of error.
These findings reveal that our proposed model not only has an advantage in single-step forecasting, but it also sustains a high level of performance for multi-step predictions. This underscores the benefit of the Traffic Transformer's self-attention mechanism, which processes all elements in the input sequence in parallel and captures global dependencies effectively. Moreover, the architecture of the Traffic Transformer prevents occurences of the potential vanishing gradient problem associated with RNNs on long sequences, which improves the learning and predicting of time series data for traffic accidents. In contrast, LSTM-S2S and its attention-enhanced variant show a lack of sensitivity to the prediction period's length. Their performance did not vary significantly with different step lengths in the forecast; this may be attributed to the recursive nature of these models, which caused information to gradually diminish with the increase in time steps, a phenomenon that is especially pronounced in multi-step predictions. Additionally, while the attention mechanism slightly improved the performance of the LSTM-S2S-AM model on some metrics, it did not translate into a marked enhancement in multi-step predictions. This indicates that despite the attention mechanism's ability to somewhat bolster the model's capacity to seize crucial temporal information, it is still constrained by the inherent limitations of the LSTM's recursive characteristics, which do not measure up to the Traffic Transformer's parallel processing prowess.
5.
Conclusions
Accurate prediction of traffic accidents is vital for urban development and the safeguarding of lives and property. Therefore, we have proposed the Traffic Transformer for precise multidimensional and multi-step forecasting of traffic accidents. The Traffic Transformer utilizes an advanced multi-head attention mechanism, supplanting the conventional recurrent architecture that is prevalent in mainstream models, to realize the multi-faceted parallel modeling of the global information embedded in input sequences. Testing on a dataset of traffic accidents from Qatar, the results consistently demonstrate the superior predictive performance of the Traffic Transformer, as it outperformed existing models in terms of accuracy and robustness for various forecast horizons and areas. In subsequent research, emphasis will not only be placed on further enhancing the model's accuracy, it will also be on its efficiency, computational cost, and interpretability, with the objective of developing trustworthy, high-performance traffic accident prediction models.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in writing the paper.
Conflict of interest
The authors declare no conflict of interest.









 DownLoad:
DownLoad:







