Estimation of the coefficients of variation for inverse power Lomax distribution

1.   Introduction

In a number of fields of study, including engineering, telecommunications, chemistry, physics, finance, and medical sciences, the CV has long been extensively utilized as both a descriptive and inferential measure. It is frequently employed in chemical studies as a scale for measurement precision. The CV is an essential measure for characterizing the variance. It offers a substitute index in place of the most widely used measurements of variation, such as variance or standard deviation, which are problematic when comparing variations across populations with dissimilar units of measurement. Take, for instance, the variability between newborn weights (measured in grams) and adult sizes (measured in centimeters). Whatever the unit of measurement applied to the numbers, the CV calculates the variability of a set of numbers. The CV can be utilized as a relative risk indicator in the finance industry; see Bhoj and Ahsanullah ^[1] and Reh and Scheffler ^[2]. The homogeneity of bone samples can be tested in physiological research using the CV (Hamer et al. ^[3]). It has been applied to the assessment of ceramic strength and the uncertainty analysis of fault trees; see Ahn ^[4] and Gong and Li ^[5]. Several writers have employed many methods to derive the CV estimator; for more information, see Pang et al. ^[6,7] and Mohie El-Din et al. ^[8].

According to Lomax ^[9], the Pareto Type-Ⅱ distribution, also referred to as the Lomax model, is an essential structure for lifetime analysis. The Lomax distribution finds widespread use in various fields, including life testing, biological sciences, modeling business failure data, and analysis of wealth and income data (see ^{[10,11,12,13,14]}, among others). One specific example of the generalized beta distribution of the second sort is the inverse Lomax distribution. Among the important lifetime models in statistical applications is this one. Additionally, as mentioned by Kleiber and Kotz ^[15], it has applications in actuarial sciences, economics, stochastic modeling, and life testing.

The IPL distribution, a three-parameter lifetime distribution, was first presented by Hassan and Abd-Allah ^[16]. It has the following probability density function (PDF)

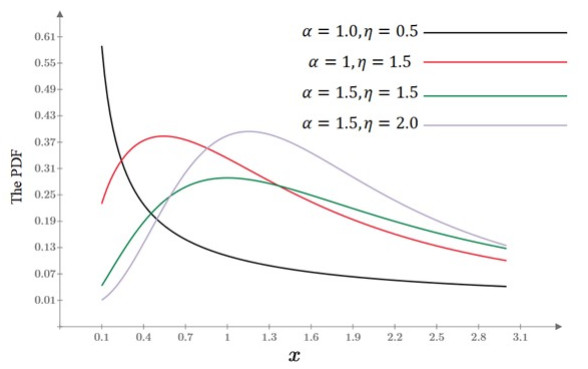
where the scale parameter is $\gamma$ and the shape parameters are $\alpha$ and $\eta$. Figure 1 shows plots of the PDF for a few chosen shape parameter values.

The IPL distribution's survival (reliability) function is provided by

When studying situations with a realized non-monotonic failure rate, the IPL is incredibly adaptable. As a result, ^[16] discussed how the IPL model can be used for various real-world data modeling and analytic applications. ^[16] investigated several statistical features for the IPL distribution in order to aid engineering applications. A comparison study in ^[16] showed that the IPL model fits essential data better than other models, such as the Lomax, power Lomax, and inverse Lomax models, inverse Weibull, generalized inverse Weibull, and exponentiated Lomax models. Despite its obvious advantages, the IPL distribution has some drawbacks, such as the lack of versatility of its left tail, which prevents the capture of some characteristics for small values in data, and the low diversity of shapes of its hazard rate function, which prevents optimal modeling of some phenomena with complex attributes.

Researchers often struggle when studying a complete sample of data because waiting for the entire sample to fail is expensive and time-consuming. Therefore, researchers obtain an incomplete data set through the censoring system. There are several sorts of censored tests: Type-Ⅰ censoring, which ends the life-testing experiment at a certain time $\tau$. Type-Ⅱ censoring, which ends the experiment on the $r^{th}$ failure in life testing. However, the flexibility to delete units at sites other than the experiment's endpoint is a limitation of typical Type-Ⅰ and Type-Ⅱ censoring approaches. This lack of adaptability led to the development of a more generic censoring method known as progressive Type-Ⅱ right censoring; for in-depth analyses of the literature on progressive censoring, see Balakrishnan and Aggarwala ^[17]. Let $n$ units be used in an experiment and let $r$ be the predetermined number of failed units, in order to discuss the mechanism of this technique. Let the timing of the $i^{th}$ failure be indicated by $X_{i:r:n}, \; i = 1, 2, \cdots, r$. The leftover units at $X_{1:r; n}$ are then randomly removed from their $R_1$ units. Once more units at $X_{2:r:n}$, are randomly selected to eliminate $R_2$ units, and so on. All of the leftover $n-r-\sum_{i = 1}^{r-1} R_i$ units are withdrawn at $X_{r:r:n}$.

In order to assure the number of failures, Ng et al. ^[18] propose an adaptive Type-Ⅱ progressive censoring. It is a mixture of Type-Ⅰ censoring and Type-Ⅱ progressive censoring schemes. In this censoring, a properly planned adaptive progressively censored life testing experiment can save both the total test time and the cost induced by failure of the units and increase the efficiency of statistical analysis. With this censoring, a well-designed adaptive progressively censored life testing experiment can reduce the general test time and the cost associated with unit failure while also improving the effectiveness of statistical analysis. Prior to commencing the experiment, let $r$ be predetermined. Then, let the test to run $\tau$ using a progressive censoring strategy $R = (R_1, R_2, \cdots, R_r)$, whose values are predetermined but available to change during the duration of the test. Employing the adaptive Type-Ⅱ progressive censoring scheme, if the $r^{th}$ failure happens before $\tau$ (i.e., $X_{r:r:n} < \tau$), the experiment stops at $X_{r:r:n}$. Otherwise, if $X_{s:r; n} < \tau < X_{s+1:r:n}$, where $s+1 < r$ and $X_{s:r:n}$ represent the failure time seen before to $\tau$, we would want to terminate the experiment as soon as possible, the researcher sets $R_{s+1} = \cdots = R_{r-1} = 0$ to ensure that no live units are removed from the experiment, $R_r = n-r-\sum_{i = 1}^s R_i$. Control of the experiment is ensured by this procedure once the required number of failures, $r$, is acquired. Let $\{x, R\} = \{(X_{1:r:n}, R_1), (X_{2:r:n}, R_2), \cdots, (X_{s:r:n}, R_s), \tau, (X_{s+1:r:n}, 0), \cdots, (X_{r-1:r:n}, 0), (X_{s:r:n}, R_r)\}$ be an adaptive Type-Ⅱ progressive censoring sample from a continuous population with PDF. The value of $\tau$ plays an important role in the determination of the values of $R$ and also as a compromise between a shorter experimental time and a higher chance to observe extreme failures. One case is when $\tau \to \infty$, which means time is not the main consideration for the experimenter, then we will have a usual progressive Type-Ⅱ censoring scheme with the pre-fixed progressive censored scheme $R$. Another case can occur when $\tau = 0$, which means we always want to end the experiment as soon as possible. Then we will have $R_1 = \cdots = R_r = 0$ and $R_r = n-r$, which results in the conventional Type-Ⅱ censoring scheme.

By setting $X_i = X_{i:r:n}, i = 1, \cdots, r$, for the purpose of simplicity, the adaptive Type-Ⅱ progressive censored data's probability function can be written as

where $c_s = \prod_{i = 1}^r (n-i+1-\sum_{k = 1}^{\min(i-1, s)} R_k)$ and the vector representing the unknown parameters is ${\bf{\Omega}}$. Numerous studies using adaptive Type-Ⅱ progressive censoring have been carried out; see ^{[19,20,21,22,23,24,25]} and the references cited therein.

Therefore, under consideration of the latent failure time following two parameters, IPL is partially observed. Our aim is to develop the statistical inferences of CV of IPL under adaptive Type-Ⅱ progressive censoring. Therefore, the point estimate discusses different methods of estimation such as MLE, bootstrapping and Bayesian estimations. Also, the approximate interval estimate is discussed with respected ML, bootstrapping, and Bayes approaches. The developed results are assessed through numerical computations under the formulation of the Monte Carlo simulation study and data analysis.

The remaining sections of the paper are arranged as follows: Section 2 presents the model and its basic presumptions. In Section 2, we were able to obtain the maximum likelihood estimation (MLE) and the Bayesian analysis with squared error loss (SEL) function. These two methods also cover interval estimation; the results include the bootstrap interval, the highest posterior density (HPD) credible interval, and approximate confidence intervals (ACIs) based on the MLEs. In Section 3, we simulate a data set, look at real data, and conduct a simulation study to show the methods of estimation covered in this paper. The final remarks are contained in Section 4.

2.   Methodology

The model considered here has an IPL distribution for the unit lifetime. The MLE and Bayesian techniques are used to formulate the point estimates of the model parameters. Additionally, interval estimators are developed using the HPD credible intervals, bootstrap methods, and the asymptotic property of MLEs.

2.1.   Modeling

The following relation provides the kth moments for the three-parameter IPL distribution

The CV is defined as

From (2.1), for $k = 1, 2$, the first two moments are as follows:

Then the theoretical CV for the IPL distribution is

2.2.   Point estimation

2.2.1.   Maximum likelihood estimation

To determine the point estimation, let $\pmb{x} = (x_{1:r; n}, x_{2:r:n} < \cdots < x_{r:r:n})$ be adaptive Type-Ⅱ progressive censored order statistics using censored scheme $R$ from the IPL distribution. From Eqs (1.1)–(1.3), by setting $\ell(\alpha, \eta, \gamma| \pmb{x}) = \ell({\bf{\Omega}})$, the likelihood function without normalized constant given by

where,

The log-likelihood function is

Calculating the normal equations, $\frac{\partial L}{\partial \Omega_i } = 0, \; {\bf{\Omega}} = (\alpha, \eta, \gamma)$ as follows:

The MLEs, $\hat{\alpha }, \, \hat{\eta }$, and $\hat{\gamma }$ of the parameters can be obtained by solving the three nonlinear Eqs (2.5)–(2.7). It is possible to use some numerical techniques, such as Newton's method. Consequently, the MLE of CV is

where $H(\hat{\alpha}, \hat{\eta})$ as given in Eq (2.2) after replacing $\alpha$ and $\eta$ by $\hat{\alpha}$ and $\hat{\eta}$, respectively.

2.2.2.   Bayes estimations

In this part, we explain the process of deriving the Bayes estimators for parameters $\alpha$, $\eta$, and $\gamma$ in the case where neither is known. Non-informative prior distribution is a useful instrument in cases where we lack sufficient prior information. This especially applies to the research we did. After that, the joint posterior density will match the likelihood function in proportion; see ^{[26,27,28,29]}.

Prior assumptions

For the parameter vector ${\bf{\Omega}} = (\alpha, \eta, \gamma)$, independent gamma priors characterize the prior information ${\bf{\Omega}} = (\alpha, \eta, \gamma)$. As a result, the joint prior of vector ${\bf{\Omega}}$ is as follows:

where $a_i, b_i$ are the hyperparameters for $\Omega_i, \; i = 1, 2, 3$.

Posterior analysis

Given the data, the joint posterior density of ${\bf{\Omega}} = (\alpha, \eta, \gamma)$ is

From Eqs (2.3) and (2.8), the posterior distribution has the following form:

The model parameters' Bayes estimators are dependent on the loss function selection. As several loss functions can be applied, we take into consideration the SEL function without losing generality. The theoretical structure of Bayes estimators for any function ${\bf{\Omega}} = (\alpha, \eta, \gamma)$ under the SEL function is defined by

In general, especially in a high-dimensional cause, the integration shown by Eqs (2.9) and (2.11) is harder and does not provide closed form formulations. As a result, approximation techniques like computational integration and Lindely approximation can be used. However, an important method like MCMC depends on building the empirical posterior distribution, which can be done by using the posterior distribution to simulate a large sample, as stated in ^[30]. A variety of techniques, including the more general Metropolis–Hastings (MH) algorithm within Gibbs sampling, or Gibbs sampling algorithms alone, can be utilized. Furthermore, the significance sampling method.

Bayesian estimation using MCMC

A popular method for simulating stochastic events with probability densities known up to a constant of proportionality is MCMC, which uses the MH-within-Gibbs sampler algorithm; see ^{[31,32,33,34]}.

Metropolis et al. ^[35] made the initial introduction of the MH algorithm. It can be used to calculate the estimated results from Eq (2.10), which can then be utilized to construct the association credible interval and get the Bayesian estimator. It is possible to write the posterior distribution provided by Eq (2.11) as

where,

and

Algorithm (1):

$1)$ Select an arbitrary beginning point $\alpha_0 = \hat{\alpha}, \eta_0 = \hat{\eta}$ and $\gamma_0 = \hat{\gamma}$.

$2)$ Generate $\alpha_1$ from $\pi_\alpha (\alpha|\eta, \gamma, \underline{x})$ using the MH algorithm.

$3)$ Generate $\eta_1$ from $\pi_\eta (\eta|\alpha, \gamma, \underline{x})$ using the MH algorithm.

$4)$ Generate $\gamma_1$ from $\pi_\gamma (\gamma|\alpha, \eta, \underline{x})$ using the MH algorithm.

$5)$ Compute $CV_1 = H(\alpha_1, \eta_1)$ $6)$ Repeat steps 2 and 5, $N$ times to obtain $CV_1, CV_2, \cdots, CV_N$.

$7)$ Using the SEL function as an example, find the Bayes estimate of $CV$ as

Consequently, the posterior variance of $CV$ is calculated by

2.2.3.   Interval estimation

(1) Asymptotic confidence intervals

The asymptotic normality of MLE is used to construct the ACIs of the parameters. In terms of model parameters, the Fisher information matrix defines the negative expectation of second derivatives of the log-likelihood function. In general, the expectation of the second derivative is more serious in more situations. Next, an appropriate approximation is shown by the observed Fisher information matrix, which may be utilized to build interval estimation in the manner described below

where

The asymptotic distribution theory of MLE indicates that $\widehat{{\bf{\Omega}}} = (\hat{\alpha}, \hat{\eta}, \hat{\gamma})$ may be distributed as a multivariate normal distribution with mean ${\bf{\Omega}} = (\alpha, \eta, \gamma$) given conventional regularity rules and variance covariance matrix $I_0^{-1} (\widehat{{\bf{\Omega}}})$ presented by $\widehat{{\bf{\Omega}}} \to N({\bf{\Omega}}, I_0^{-1} (\widehat{{\bf{\Omega}}}))$.

See Greene ^[36] for an estimated method of estimating the variance of $\widehat{CV}$ using the delta approach. Let

where $\frac{\partial CV}{\partial \alpha}, \frac{\partial CV}{\partial \eta}$ and $\frac{\partial CV}{\partial \gamma}$ are the first derivatives of the $CV$ with respect to $\alpha$, $\eta$ and $\gamma$.

where $\psi (x) = \frac{d}{dx}\log \left(\Gamma (x) \right) = \frac{{\Gamma }'(x)}{\Gamma (x)}.$

The approximate asymptotic variance of $\widehat{CV}$ is given by

where $H_1^T$ is the transpose of $H_1$.

The asymptotic distribution of the MLE ($\widehat{CV}$) of CV satisfies:

This implies that the asymptotic $100(1-\nu)\%$ confidence interval for CV is given by

(2) Bootstrap confidence intervals

This section derives confidence intervals for the unknown parameters $\alpha, \eta, \gamma$, and CV using the parametric bootstrap approach and the percentile interval; for further information, refer to Efron ^[37]. The algorithm that follows is designed to produce a bootstrap sample.

Algorithm (2):

$1)$ Starting with the first two samples, $\{x_1, x_2, \cdots, x_n\}$ compute MLEs $\hat{\alpha}, \hat{\eta}, \hat{\gamma}$ and $\widehat{CV}$.

$2)$ Generating a bootstrap sample $\{x_1^{*}, x_2^{*}, \cdots, x_n^{*}\}$ and computing the bootstrap estimate of $\tilde{\alpha}, \tilde{\eta}, \tilde{\gamma}$ and $\widetilde{CV}$ using $\hat{\alpha}, \hat{\eta}, \hat{\gamma}$ and $\widehat{CV}$.

$3)$ For obtaining the bootstrap samples, repeat steps (1) through (2), $N$, arranging each estimate in ascending order $\{\widehat{CV}_{M+1}, \widehat{CV}_{M+2}, \cdots, \widehat{CV}_{N-M} \}$.

$\left(\widehat{CV}_{Boot\, i(N-M) \frac{\nu}{2}}, \widehat{CV}_{Boot \, i(N-M)(1-\frac{\nu}{2}) } \right)$ provides the estimated confidence interval for $(\widehat{CV})$ and $i = M+1, \cdots, N$.

$4)$ $\left(\widehat{CV}_{Boot\, i(N-M) \frac{\nu}{2}}, \widehat{CV}_{Boot \, i(N-M)(1-\frac{\nu}{2}) } \right)$ provides the estimated $100(1-\nu)\%$ confidence interval for $(\widehat{CV})$.

(3) MCMC credible confidence intervals

A $100(1-\nu)\%$ posterior interval for a random quantity in the Bayesian credible theory is the interval with the posterior probability that $\Omega_i$ is within the interval, is denoted by $\Omega_i$ lies in the interval, ${\bf{\Omega}} = (\alpha, \eta, \gamma)$. The procedure that follows is used to produce credible CV confidence intervals.

Algorithm (3):

$1)$ In Algorithm (1), repeat steps (1) through (5).

$2)$ Then, using the resulting MCMC samples, the Bayesian credible interval for the CV is calculated using the algorithm suggested by Chen and Shao ^[38]. The posterior sample is arranged as $CV_{M+1}, CV_{M+2}, \cdots, CV_{N-M}$. This yields the $100(1-\nu)\%$ HPD credible intervals for CV.

where $\nu$ presents the standard normal values with probability-tailed $\nu$.

3.   Data analysis and simulation study

3.1.   Applications to real life data set

To illustrate our approach, we examined data on the survival times (in days) of 72 guinea pigs infected with virulent tubercle bacilli. The data set is as follows: {0.1, 0.33, 0.44, 0.56, 0.59, 0.59, 0.72, 0.74, 0.92, 0.93, 0.96, 1, 1, 1.02, 1.05, 1.07, 1.07, 1.08, 1.08, 1.08, 1.09, 1.12, 1.13, 1.15, 1.16, 1.2, 1.21, 1.22, 1.22, 1.24, 1.3, 1.34, 1.36, 1.39, 1.44, 1.46, 1.53, 1.59, 1.6, 1.63, 1.63, 1.68, 1.71, 1.72, 1.76, 1.83, 1.95, 1.96, 1.97, 2.02, 2.13, 2.15, 2.16, 2.22, 2.3, 2.31, 2.4, 2.45, 2.51, 2.53, 2.54, 2.54, 2.78, 2.93, 3.27, 3.42, 3.47, 3.61, 4.02, 4.32, 4.58, 5.55}.

This dataset was previously analyzed and reported by Bjerkedal ^[39]. Based on this data, the fitted survival functions and empirical survival functions are presented for IPL and Weibull distributions, as seen in Figures 2 and 3.

Table 1 contains the Kolmogorov–Smirnov (K-S) test and p-values.

Based on Figures 2, 3, and Table 1, the IPL distribution is the best fit for this data.

In this case we take $r = 49, \tau = 0.92$ and $R = \{0^7, 6, 0^7, 6, 0^7, 6, 0^7, 5, 0^17\}$, the adaptive progressive censored sample is {0.33, 0.44, 0.56, 0.59, 0.92, 0.93, 0.96, 1, 1.02, 1.05, 1.07, 1.08, 1.08, 1.08, 1.09, 1.12, 1.13, 1.15, 1.16, 1.21, 1.22, 1.22, 1.3, 1.34, 1.46, 1.59, 1.63, 1.63, 1.68, 1.72, 1.76, 1.95, 1.96, 1.97, 2.02, 2.13, 2.15, 2.16, 2.22, 2.3, 2.4, 2.45, 2.51, 2.53, 2.78, 3.27, 3.42, 4.58, 5.55}.

We compute the estimate of the MLE and the Bayes estimate using MCMC methods with MCMC samples in light of this assumption using the adaptive Type-Ⅱ progressive censoring data, and we ignore the first values as 'burn-in'. When computing the Bayes estimate, we use the assumption that the unknown parameters have non-informative gamma priors because we don't know anything about them beforehand. The non-informative gamma priors of the unknown parameters $(a_i = b_i = 0, \, i = 1, 2, 3)$ and the final results for this example are presented in Table 2.

The MCMC method produces an empirical posterior distribution that approaches convergence, as seen by the plots of the data's histogram and list-line plot from Figures 4 and 5.

3.2.   Numerical explorations

Comparing the performance of the methods theoretically impossible, we carry out a Monte Carlo simulation study in this section to compare the performance of the various estimating methods. In terms of mean-squared errors (MSE), we compare Bayes and MLEs under the SEL function with informative and non-informative priors. We analyze multiple confidence intervals, depending on length and coverage probability, such as asymptotic, bootstrap, and HPD credible intervals. To investigate and assess the proposed Bayes estimate in relation to the MLE, Monte Carlo simulation research utilizing the IPL distribution and the value of parameters $(\alpha, \eta, \gamma) = (1.5, 3, 0.5)$ is run.

Using the hyper-parameters $a_i = b_i = 0.0001, \, i = 1, 2, 3$, prior 0 for non-informative priors and prior 1 for informative priors. In the case of prior 1, the hyper-parameters are set up so that the real values of the parameters and the prior means are precisely identical to the real values of the parameters. We examine three sets of true values of parameters $(\alpha, \eta, \gamma) = (1.5, 3, 0.5)$ and related informative hyper-parameters $a_1 = 1.5, b_1 = 1, a_2 = 3, b_2 = 1, a_3 = 0.5, b_3 = 1$. Also, we consider $\tau = 0.9, 2.7$, effective sample sizes $r$, $(n, r) = (30, 15), (30, 20), (40, 20)$, and three different progressive-censoring schemes (CS):

● Ⅰ: $R_1 = n-r$, $R_i = 0$ for $i\neq 1$.

● Ⅱ: $R_{\frac{r+1}{2}} = n-r$, $R_i = 0$ for $i \neq \frac{r+1}{2}$; if $r$ odd, and $R_{\frac{r}{2}} = n-r$, $R_i = 0$ for $i \neq \frac{r}{2}$ if $r$ even.

● Ⅲ: $R_r = n-r$, $R_i = 0$ for $i\neq r$.

All calculations are performed using Mathematica 10. Table 3 shows the averages mean and MSEs of the estimates in parenthesis. The coverage percentages (CP) and average length (AL) of the 95% asymptotic, bootstrap confidence intervals, and HPD credible interval of CV are presented in Table 4. For the MCMC approach, we choose $N = 11000$ with a burn-in time period $M = 1000$.

4.   Concluding Remarks

The theoretical sampling distribution of the CV is not easily derived analytically within the frequentist framework, which makes making inferences about the CV challenging in many situations. We developed a method for estimating the CV for IPL distribution using adaptive Type-Ⅱ progressive censored data. We discussed the MLEs, as well as the Bootstrap and Bayes estimates of the CV. Given that explicit Bayes estimates are not possible, the MCMC approach was taken into consideration. We utilize the SEL function in the Bayesian technique. To evaluate the performance of the suggested approaches, we undertake a Monte Carlo simulation study and analyze a real data set. Based on the numerical outcome, we can see from the numerical result that Bayes estimates and MLEs yield results that are comparable. Compared to non-informative and informative prior, the Bayes estimates perform better. The estimates produced using the MCMC approach perform well in terms of MSEs and average widths for every combination of sample size and affected sample size. Tables 3 and 4 demonstrate how effectively the suggested Bayes estimates work for various $n, r$ and censoring schemes $R$. The results that are displayed in Tables 3 and 4 more clearly show the superiority of the Bayesian techniques over traditional methods in cases where appropriate prior information does become accessible. Tables 3 and 4 present the simulation research findings. These tables make these ideas obvious:

$1)$ In terms of MSE, the Bayes estimate of the CV performs better than the MLE for non-informative priors and is superior when using informative priors.

$2)$ As the sample size $r$ increases, the MSEs decrease for both ML and Bayes estimation approaches.

$3)$ The AL of asymptotic, bootstrap confidence, and HPD credible intervals decrease with increasing failure proportion ($r/n$).

$4)$ For AL and CP, boot confidence intervals outperformed asymptotic confidence intervals.

$5)$ HPD credible intervals perform better than any other confidence intervals, even when there are informative priors.

Author contributions

Samah M. Ahmed: Formal analysis, Validation, Writing-original draft & editing, Visualization, Software, Methodology, Data curation; Abdelfattah Mustafa: Conceptualization, Investigation, Writing-review & editing, Supervision, Resources. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors would like to thank the reviewers for their valuable comments that improved the original draft of the paper.

Conflict of interest

The authors declare no conflicts of interest.