Numerical analysis of the frequency-dependent Jiles-Atherton hysteresis model using the example of Terfenol-D material

Cheng Zhang; Guangming Xue; Cheng Zhang; Guangming Xue

doi:10.3934/math.20241517

AIMS Mathematics

2024, Volume 9, Issue 11: 31532-31552. doi: 10.3934/math.20241517

Previous Article Next Article

Research article Special Issues

Numerical analysis of the frequency-dependent Jiles-Atherton hysteresis model using the example of Terfenol-D material

Cheng Zhang ,
Guangming Xue ^,

School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350116, China

Received: 18 September 2024 Revised: 30 October 2024 Accepted: 31 October 2024 Published: 06 November 2024
MSC : 34A34, 34C55, 65L03, 65L05, 74N30

The Jiles-Atherton model has been widely used in describing the hysteretic property of a magnetic material or device. However, the calculation errors are not so easily discovered. With a complex expression, the frequency-dependent Jiles-Atherton model should be solved numerically with appropriate settings. This paper proposes an effective solving method for this model and describes some necessary analysis built on the numerical results. In the numerical method proposed in this manuscript, the anhysteretic magnetization was calculated by the secant method, and the trapezoidal rule was utilized to form the implicit function, which can be calculated by the fixed-point iteration. Compared to the other common methods, the proposed one has a friendly expression and fast computation speed. The Terfenol-D material was taken as an example for the numerical analysis. The feasible region was determined and the commonly used approximation that neglects the term of the magnetic field when calculating the magnetic induction intensity was tested. At last, the required number of sampling points per period was reached to guarantee high precision from analyzing its influence on the computation precision. The proposed numerical method is helpful for high-precision solutions of the frequency-dependent Jiles-Atherton model. The results from the numerical analysis can also help users avoid some incorrect calculations when employing this hysteresis model.

Keywords:

frequency-dependent Jiles-Atherton model,
numerical analysis,
feasible region,
approximation,
number of sampling points

Citation: Cheng Zhang, Guangming Xue. Numerical analysis of the frequency-dependent Jiles-Atherton hysteresis model using the example of Terfenol-D material[J]. AIMS Mathematics, 2024, 9(11): 31532-31552. doi: 10.3934/math.20241517

Related Papers:

[1]	Jeong-Kweon Seo, Byeong-Chun Shin . Reduced-order modeling using the frequency-domain method for parabolic partial differential equations. AIMS Mathematics, 2023, 8(7): 15255-15268. doi: 10.3934/math.2023779
[2]	Zhoujin Cui, Xiaorong Zhang, Tao Lu . Resonance analysis and time-delay feedback controllability for a fractional horizontal nonlinear roller system. AIMS Mathematics, 2024, 9(9): 24832-24853. doi: 10.3934/math.20241209
[3]	Erlin Guo, Cuixia Li, Patrick Ling, Fengqin Tang . Convergence rate for integrated self-weighted volatility by using intraday high-frequency data with noise. AIMS Mathematics, 2023, 8(12): 31070-31091. doi: 10.3934/math.20231590
[4]	Ahmed Alshehri, Miled El Hajji . Mathematical study for Zika virus transmission with general incidence rate. AIMS Mathematics, 2022, 7(4): 7117-7142. doi: 10.3934/math.2022397
[5]	Rahat Zarin, Amir Khan, Pushpendra Kumar, Usa Wannasingha Humphries . Fractional-order dynamics of Chagas-HIV epidemic model with different fractional operators. AIMS Mathematics, 2022, 7(10): 18897-18924. doi: 10.3934/math.20221041
[6]	Zihan Yue, Wei Jiang, Boying Wu, Biao Zhang . A meshless method based on the Laplace transform for multi-term time-space fractional diffusion equation. AIMS Mathematics, 2024, 9(3): 7040-7062. doi: 10.3934/math.2024343
[7]	Ibrahim-Elkhalil Ahmed, Ahmed E. Abouelregal, Doaa Atta, Meshari Alesemi . A fractional dual-phase-lag thermoelastic model for a solid half-space with changing thermophysical properties involving two-temperature and non-singular kernels. AIMS Mathematics, 2024, 9(3): 6964-6992. doi: 10.3934/math.2024340
[8]	Salma M. Al-Tuwairqi, Asma A. Badrah . Modeling the dynamics of innate and adaptive immune response to Parkinson's disease with immunotherapy. AIMS Mathematics, 2023, 8(1): 1800-1832. doi: 10.3934/math.2023093
[9]	Zhoujin Cui . Primary resonance and feedback control of the fractional Duffing-van der Pol oscillator with quintic nonlinear-restoring force. AIMS Mathematics, 2023, 8(10): 24929-24946. doi: 10.3934/math.20231271
[10]	Ishtiaq Ali, Sami Ullah Khan . Dynamics and simulations of stochastic COVID-19 epidemic model using Legendre spectral collocation method. AIMS Mathematics, 2023, 8(2): 4220-4236. doi: 10.3934/math.2023210

Abstract

1. Introduction

Hysteresis behavior widely exists in magnetic materials ^[1,2], devices ^[3,4], and systems ^[5,6]. Plenty of models for this complex nonlinear property and their solutions or controlling methods have been discussed comprehensively. Generally, the hysteresis model ^[7] can be divided into two types: the physics-based model type ^[8,9] and the phenomenological one ^[10,11]. The former explains the hysteresis behavior by use of the micro-magnetism theory to form a nonlinear equation in differential or integral form. Moreover, most parameters in this type of model have predetermined physical means ^[12].

The Jiles-Atherton model ^[13,14,15] is a kind of physics-based model and has been used in describing the hysteresis occurring in ferromagnetic material ^[16,17], amorphous material ^[18], giant magnetostrictive material ^[19,20], magnetic composite ^[21], electrical steel ^[22,23,24], transformers ^[25,26], and some other conditions ^[27]. The model expression has also been widely discussed from various perspectives, such as the vector form extension ^[9,28], energy conservation correction ^[24,29,30], and dynamic extension ^[31,32,33]. Though with various expressions, the basic mathematical construction is followed by several nonlinear and differential equations. There are several intermediate variables, parameters, and signum functions where the Jiles-Atherton model is not so easily solved. Szewczyk ^[34] and Michał Nowicki et al. ^[35,36] proposed that the Jiles-Atherton model has no analytical solutions and that some numerical methods should be employed. Among these numerical methods, the accumulated errors should be processed carefully when the numerical integrations are employed. Yining Li et al. ^[37] and Guangming Xue et al. ^[38,39] proposed some fitting functions built on the calculated magnetizations calculated from the Jiles-Atherton model. Mathematical fitting can improve the computation speed greatly while the applicability should be further discussed, as the fitted result was just suitable to the specified material or device. According to the expression of the Jiles-Atherton model, Guangming Xue et al. ^[40] also took the fixed-point iteration or secant method to solve anhysteretic magnetization. With the help of the Aitken or Steffensen method, the convergence can be accelerated while using the limit on the iterative numbers in order to guarantee high-precision results. Derived from Maxwell's equations, S. Azzaoui et al. ^[41] proposed a generalization method for nonlinear magnetic field calculation applied on two-dimensional finite volume geometry embedded with the Jiles-Atherton model. L. Perkkiö et al. ^[42] proposed a quasi-Newton method, namely a variant of sparse Broyden's method, to accelerate the solution of the nonlinear equation arising from the finite element method coupled with the Jiles-Atherton model. The two types of solutions can be treated as the application of finite element analysis in solving the model embedded with a hysteresis ^[43,44]. The neural network modeling process can also be employed to form solutions for the hysteresis model ^[45,46,47]. With effective training, the artificial neural network can track the hysteresis loop with quite high precision while the trade-off between the fast-solving speed and high computation precision should be noticed. Besides these methods, some other mathematical approximations or novel methods ^[7,48,49] can also provide effective references for easily solving the model, such as employing modified differential evolution ^[50], approximating the anhysteretic or irreversible magnetization ^[51], treating the global variable as the response of a linear time-invariant system ^[52,53], extending the use of the arctangent model ^[54], and using current software ^[55].

The mathematically strict discussion on the dynamic Jiles-Atherton model is absent as most model users just employed the hysteresis results for the future computations as long as they look like some standard loops. The dynamic Jiles-Atherton model ^[56,57,58] is extended from the quasi-static one to be suitable to the frequency-dependent condition. With strongly nonlinear terms including the nonlinear equation and nonlinear differential equation, the frequency-dependent Jiles-Atherton hysteresis model should be solved numerically, and the numerical method is necessary and quite important for accurate modeling or controlling in the future. The computation error is influenced by the employed methods and the parameter settings, especially the increment of the magnetic field. If the calculating method or parameter value were designed unreasonably, the error would be quite high. This kind of error is not so easily discovered as the calculated result can also form a hysteresis loop very similar to the exact solution, which will lead to different parameter values for the same material. For Terfenol-D, various parameters are provided in different references ^[59,60,61]. In addition, the model has an infeasible region (influencing the searching interval length in parameter identification ^[62]) while rarely cared about as the parameter value is generally specified to a small range. The mathematical discussions on the convergences or extensions of other models ^[10,63] are also helpful.

This manuscript executes numerical analysis of the frequency-dependent Jiles-Atherton model. The anhysteretic magnetization is calculated by the secant method and its derivative is solved from the analytical expression. Then the trapezoidal rule is utilized to form the implicit function related to the magnetization differential to be solved. In conjunction with the fixed-point iteration, the magnetization-magnetic field loop can be reached. Taking the Terfenol-D material as an example, the feasible region and the commonly used approximation of the model are discussed, and the required number of sampling points per period is analyzed to guarantee high precision. The proposed numerical solving method can solve the complex model fast and accurately, and applicable conditions for the model and solving method are also provided from the numerical analysis.

2. Numerical method to solve the Jiles-Atherton model

2.1. Expression of the frequency-dependent Jiles-Atherton model

From a mathematical viewpoint, the Jiles-Atherton model utilizes several strongly nonlinear equations to describe the relationships between the applied magnetic field H and magnetization M (or magnetic induction intensity B). In this model, there are some intermediate variables, and they are as follows:

$\left\{ \begin{array}{l} M = {M_{irr}} + {M_{rev}}, \hfill \\ {M_{rev}} = c\left( {{M_{an}} - {M_{irr}}} \right), \hfill \\ {H_e} = H + \alpha M, \hfill \\ \end{array} \right.$

(1)

where M_irr and M_rev are the irreversible and reversible magnetization, respectively, M_an is the anhysteretic magnetization, H_e is the effective magnetic field, c is the reversibility coefficient, and α is the quantified domain interaction parameter.

An implicit Langevin function is employed to described M_an and is written as

${M_{an}} = {M_s}\left[ {\coth \left( {\frac{{H + \alpha {M_{an}}}}{a}} \right) - \frac{a}{{H + \alpha {M_{an}}}}} \right] ,$

(2)

where M_s is the saturation magnetization, α is the quantified domain interaction, and a is the shape parameter for M_an.

The energy conservation equation to predict the energy losses per unit volume in the magnetizing process is generally written as

${\mu _0}{\delta _M}\int {M{\text{d}}{H_e}} = {\mu _0}{\delta _M}\int {{M_{an}}{\text{d}}{H_e}} - {\mu _0}\delta k{M_{irr}} - \int {\frac{{d_m^2}}{{2\rho {D_m}}}{{\left( {\frac{{{\text{d}}B}}{{{\text{d}}t}}} \right)}^2}{\text{d}}t} - \int {\sqrt {\frac{{G{S_m}{V_0}}}{\rho }} {{\left| {\frac{{{\text{d}}B}}{{{\text{d}}t}}} \right|}^{\frac{3}{2}}}{\text{d}}t} ,$

(3)

where k is the pinning parameter to quantify the average energy required to break the pinning site, d_m and S_m are the thickness and cross-sectional area of the stack, respectively, D_m is the coefficient influenced by the structural style of the magnetic core, ρ is the material resistivity, G = 0.1356, V₀ is another constant from statistics, and μ₀ is the permeability of the vacuum.

Equation (3) has no analytical solution and should be solved using some numerical methods. To avoid the numerical integrations, the differential form of the energy conservation equation is reached by taking the derivatives of both sides of Eq (3) with respect to t and is written as

${\mu _0}{\delta _M}M\frac{{{\text{d}}{H_e}}}{{{\text{d}}t}} = {\mu _0}{\delta _M}{M_{an}}\frac{{{\text{d}}{H_e}}}{{{\text{d}}t}} - {\mu _0}\delta k\frac{{{\text{d}}{M_{irr}}}}{{{\text{d}}t}} - \frac{{d_m^2}}{{2\rho {D_m}}}{\left( {\frac{{{\text{d}}B}}{{{\text{d}}t}}} \right)^2} - \sqrt {\frac{{G{S_m}{V_0}}}{\rho }} {\left| {\frac{{{\text{d}}B}}{{{\text{d}}t}}} \right|^{\frac{3}{2}}} .$

(4)

Considering the relationship that B = μ₀(H+M) and substituting Eq (1) into Eq (4), one gets

$\begin{array}{l} {\mu _0}{\delta _M}\left( {{M_{an}} - M} \right)\left( {\frac{{{\text{d}}H}}{{{\text{d}}t}} + \alpha \frac{{{\text{d}}M}}{{{\text{d}}t}}} \right) - \frac{{{\mu _0}\delta k}}{{1 - c}}\left( {\frac{{{\text{d}}M}}{{{\text{d}}t}} - c\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}}} \right) \hfill \\ - \frac{{d_m^2}}{{2\rho {D_m}}}\mu _0^2{\left( {\frac{{{\text{d}}H}}{{{\text{d}}t}} + \frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)^2} - \sqrt {\frac{{G{S_m}{V_0}}}{\rho }} \mu _0^{3/2}{\left| {\frac{{{\text{d}}H}}{{{\text{d}}t}} + \frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|^{\frac{3}{2}}} = 0. \hfill \\ \end{array}$

(5)

Combining Eqs (2) and (5), the frequency-dependent Jiles-Atherton model can predict the time-dependent magnetizations at various frequencies.

2.2. Numerical method to solve the Jiles-Atherton model

2.2.1. Solving the anhysteretic magnetization and its derivative

M_an can be directly solved from Eq (2) by any iteration method. Here, we employ the secant method to do this work. Define f_an(x) as

${f_{an}}(x) = x - {M_{\text{s}}}\left[ {\coth \left( {\frac{{H + \alpha x}}{a}} \right) - \frac{a}{{H + \alpha x}}} \right] .$

(6)

Then the iteration equation built on the secant method is

$\begin{aligned} {M_{an}}^{(j + 1)} &= {M_{an}}^{(j)} - \frac{{{f_{an}}({M_{an}}^{(j)})\left( {{M_{an}}^{(j)} - {M_{an}}^{(j - 1)}} \right)}}{{{f_{an}}({M_{an}}^{(j)}) - {f_{an}}({M_{an}}^{(j - 1)})}} \\ &= {M_{an}}^{(j)} - \frac{{\left[ {\coth \left( {\frac{{H + \alpha {M_{an}}^{(j)}}}{a}} \right) - \frac{a}{{H + \alpha {M_{an}}^{(i)}}}} \right]\left( {{M_{an}}^{(j)} - {M_{an}}^{(j - 1)}} \right)}}{{\left[ \begin{array}{l} \coth \left( {\frac{{H + \alpha {M_{an}}^{(j)}}}{a}} \right) - \hfill \\ \frac{a}{{H + \alpha {M_{an}}^{(j)}}} \hfill \\ \end{array} \right] - \left[ \begin{array}{l} \coth \left( {\frac{{H + \alpha {M_{an}}^{(j - 1)}}}{a}} \right) - \hfill \\ \frac{a}{{H + \alpha {M_{an}}^{(j - 1)}}} \hfill \\ \end{array} \right]}} \\ \end{aligned} ,$

(7)

where the superscript j represents the iterative number, j ≥ 1, and M_an⁽⁰⁾ and M_an⁽¹⁾ are two unequal initial values of M_an. The termination condition of the iteration is set as |M_an^(j) – M_an^(j–1)| < M_an^(j) ×10^-6 and the relative error between M_an^(j) and M_an^(j–1) is not higher than 1×10^–6. It should be noted that Eq (7) should be executed at all time points that the time t has been previously, equally segmented from 0 to the end time.

After solving M_an, its derivative with respect to H can be calculated by

$\begin{aligned} \frac{{{\text{d}}{M_{an}}}}{{{\text{d}}H}} & = \frac{{{a^2}{{\sinh }^2}\left( {\frac{{H + \alpha {M_{an}}}}{a}} \right) - {{\left( {H + \alpha {M_{an}}} \right)}^2}}}{{\frac{a}{{{M_s}}}{{\left( {H + \alpha {M_{an}}} \right)}^2}{{\sinh }^2}\left( {\frac{{H + \alpha {M_{an}}}}{a}} \right) - \alpha \left[ {{a^2}{{\sinh }^2}\left( {\frac{{H + \alpha {M_{an}}}}{a}} \right) - {{\left( {H + \alpha {M_{an}}} \right)}^2}} \right]}} \\ & = \frac{{{{\sinh }^2}\left( {\frac{{H + \alpha {M_{an}}}}{a}} \right) - {{\left( {\frac{{H + \alpha {M_{an}}}}{a}} \right)}^2}}}{{\frac{a}{{{M_s}}}{{\left( {\frac{{H + \alpha {M_{an}}}}{a}} \right)}^2}{{\sinh }^2}\left( {\frac{{H + \alpha {M_{an}}}}{a}} \right) - \alpha \left[ {{{\sinh }^2}\left( {\frac{{H + \alpha {M_{an}}}}{a}} \right) - {{\left( {\frac{{H + \alpha {M_{an}}}}{a}} \right)}^2}} \right]}} \\ & = \frac{{{{\sinh }^2}{H_f} - H_f^2}}{{\frac{a}{{{M_s}}}H_f^2{{\sinh }^2}{H_f} - \alpha \left( {{{\sinh }^2}{H_f} - H_f^2} \right)}}, \\ \end{aligned}$

(8)

where H_f = (H + α M_an) / a and it is easily concluded that H_f (H = 0) = 0.

Considering that the following computations built on M_an are time dependent, the derivative of M_an with respect to t is calculated built on

$\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}} = \frac{{{\text{d}}{M_{an}}}}{{{\text{d}}H}}\frac{{{\text{d}}H}}{{{\text{d}}t}} = \frac{{{{\sinh }^2}{H_f} - H_f^2}}{{\frac{a}{{{M_s}}}H_f^2{{\sinh }^2}{H_f} - \alpha \left( {{{\sinh }^2}{H_f} - H_f^2} \right)}}\frac{{{\text{d}}H}}{{{\text{d}}t}} .$

(9)

2.2.2. Solving the magnetization

Regarding the strongly nonlinear differential expression given by Eq (5), it is not easily solved just from the classic numerical methods as it is an implicit equation with respect to dM/dt. So, besides the numerical method for differential equations to solve M from dM/dt, an effective iteration method to solve dM/dt from the nonlinear expression is also indispensable.

Built on Eq (5), transpose one dM/dt out to the right-hand side and define a new function f_M as

$\begin{aligned} \frac{{{\text{d}}M}}{{{\text{d}}t}} & = {f_M}\left\{ {t, M, {{{\text{d}}M} \mathord{\left/ {\vphantom {{{\text{d}}M} {{\text{d}}t}}} \right. } {{\text{d}}t}}, \left( {H, {{{\text{d}}H} \mathord{\left/ {\vphantom {{{\text{d}}H} {{\text{d}}t}}} \right. } {{\text{d}}t}}, {M_{an}}, {{{\text{d}}{M_{an}}} \mathord{\left/ {\vphantom {{{\text{d}}{M_{an}}} {{\text{d}}t}}} \right. } {{\text{d}}t}}} \right)} \right\} \\ & = \frac{{\left( {1 - c} \right){\delta _M}}}{{\delta k}}\left( {{M_{an}} - M} \right)\left( {\frac{{{\text{d}}H}}{{{\text{d}}t}} + \alpha \frac{{{\text{d}}M}}{{{\text{d}}t}}} \right) + c\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}} \\ &- \frac{{\left( {1 - c} \right){K_{edd}}}}{{\delta k}}{\left( {\frac{{{\text{d}}H}}{{{\text{d}}t}} + \frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)^2} - \frac{{\left( {1 - c} \right){K_{exc}}}}{{\delta k}}{\left| {\frac{{{\text{d}}H}}{{{\text{d}}t}} + \frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|^{\frac{3}{2}}}, \\ \end{aligned}$

(10)

where K_edd = μ₀d_m²/(2ρD_m), K_exc = (GS_mV₀μ₀/ρ)^1/2, and both of the parameters are determined by the structural style, dimension, resistivity, and preassumed statistical characteristics. When solving the values of dM/dt and M at each point, the four variables have been predetermined according to the above calculations.

Equation (10) provides a natural fixed-point iteration format for solving dM/dt while the value of M at the same time is unknown such that the iteration cannot be executed in its current form. Considering that the iteration process is unavoidable, the implicit trapezoidal rule can be utilized here to solve the differential equation:

${\left. M \right|_{i + 1}} = {\left. M \right|_i} + \frac{{\Delta t}}{2}\left( {{{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i} + {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right) ,$

(11)

where M|_i is the value of M at the i^th point with the time t equally spaced from zero to the end.

From Eq (11), M|_i+1 can be calculated from dM/dt|_i+1, where dM/dt|_i and M|_i are previously known. Then the iteration at the (i+1)^th point can be done through substituting Eq (11) into Eq (10), and the nonlinear equation is

$\begin{aligned} {\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|_{i + 1}}& = {f_M}\left\{ {{{\left. t \right|}_{i + 1}}, {{\left. M \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_{i + 1}}, \left\langle {{{\left. H \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}}, {{\left. {{M_{an}}} \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right\rangle } \right\} \\ & = {f_M}\left\{ {{{\left. t \right|}_{i + 1}}, {{\left. M \right|}_i} + \frac{{\Delta t}}{2}\left( {{{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i} + {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right), {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_{i + 1}}, \left\langle {{{\left. H \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}}, {{\left. {{M_{an}}} \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right\rangle } \right\} \\ & = \frac{{\left( {1 - c} \right){\delta _{{{\left. M \right|}_{i + 1}}}}}}{{\delta k}}\left( {{{\left. {{M_{an}}} \right|}_{i + 1}} - \left[ {{{\left. M \right|}_i} + \frac{{\Delta t}}{2}\left( {{{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i} + {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right)} \right]} \right)\left( {{{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}} + \alpha {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right) + c{\left. {\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}}} \right|_{i + 1}} \\ &- \frac{{\left( {1 - c} \right){K_{edd}}}}{{\delta k}}{\left( {{{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}} + {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right)^2} - \frac{{\left( {1 - c} \right){K_{exc}}}}{{\delta k}}{\left| {\left( {{{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}} + {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right)} \right|^{\frac{3}{2}}} \\ &\triangleq {f_{M2}}\left\{ {{{\left. t \right|}_{i + 1}}, {{\left. M \right|}_i}, {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i}, {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_{i + 1}}, \left\langle {{{\left. H \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}}, {{\left. {{M_{an}}} \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right\rangle } \right\}. \\ \end{aligned}$

(12)

Equation (12) is the nonlinear equation dependent on dM/dt|_i+1. Utilizing the fixed-point method, the value of dM/dt at the (i+1)^th point can be calculated from

${\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|_{i + 1}}^{(j + 1)} = {f_{M2}}\left\{ {{{\left. t \right|}_{i + 1}}, {{\left. M \right|}_i}, {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i}, {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_{i + 1}}^{(j)}, \left\langle {{{\left. H \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}}, {{\left. {{M_{an}}} \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right\rangle } \right\} ,$

(13)

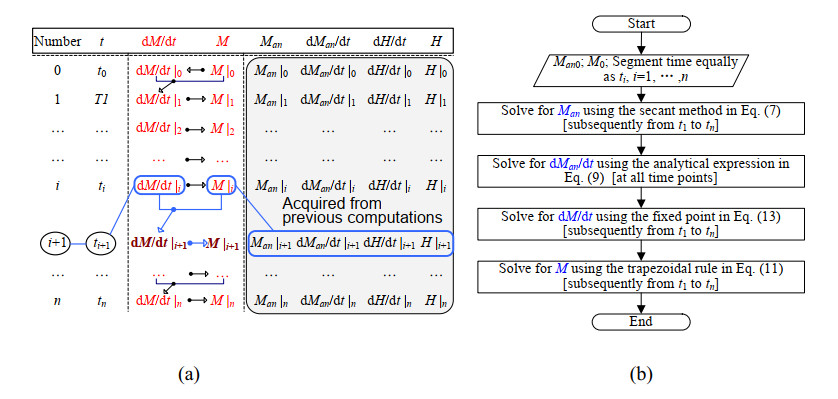
The solving process from M|₀ to M|_n is displayed in Figure 1(a). When calculating the value of M at t_i+1 as M|_i+1, the values of M|_i and dM/dt|_i are required in addition to the values of M_an|_i+1, dM_an/dt|_i+1, etc., which have been collected from previous computations. An overall computing process is demonstrated in Figure 1(b). It should be noted that the values of M_an, dM/dt, and M should be calculated subsequently from t₁ to t_n.

Figure 1. The solving process of the proposed numerical method. (a) Required variables to solve for dM/dt and M; (b) an overall process of the proposed numerical solving method.

DownLoad: Full-Size Img PowerPoint

2.3. Computation performance of the numerical method using the example of Terfenol-D

The frequency-dependent Jiles-Atherton model is related on both the frequency f and amplitude of the applied magnetic field H_amp. Here, we take the Terfenol-D material ^[18] as the calculated example to demonstrate the computational performance of the above numerical methods. The parameter values are reached by use of a crude search ^[58] from the test data as α = 0.018, c = 0.3, M_S = 700 kA/m, a = 12.2 kA/m, k = 1.85 kA/m, K_edd = 1.50 ×10^–6 s, and K_exc = 0.60 ×10^–3 (A·s/m)^1/2. To guarantee high computational precisions, the number of sampling points in one time period is 1000 (the sampling frequency is 1000 times as high as the frequency of the applied magnetic field). Figure 2 shows the loop curves under different frequencies with the field amplitude of 5 kA/m and Figure 3 shows the curves under various amplitudes with the frequency of 200 Hz.

Figure 2. Calculated magnetization-magnetic field loops under different conditions: (a) frequencies from 5 Hz to 1 kHz; (b) field amplitudes from 1.0 kA/m to 10 kA/m.

DownLoad: Full-Size Img PowerPoint

Figure 3. The changes of the maximum value of the magnetization and loop area with respect to the frequency under different field amplitudes: (a) maximum value; (b) loop area.

DownLoad: Full-Size Img PowerPoint

According to the proposed numerical method, the variations of the magnetization-magnetic field loops (M-H loops) with the frequency or field amplitude changing are clearly displayed. By use of the counting functions of "tic" and "toc" in MATLAB to monitor the computation time, it is verified that the numerical method has fast computing speed, as the computing time from the initial magnetizing curve to the stable hysteresis loop is always lower than 0.53 s. Under most commonly used conditions far from the boundary of the feasible region which will be shown in Section 3.4, the computation time is less than 0.03 s.

Figure 3 summarizes the changes of the maximum magnetization and loop area with the change of the frequency under different field amplitudes. In Figure 3, the ratio values are calculated taking the low-frequency result as the baseline value, and the points in the arbitrary specified curve have the same field amplitude. From the numerical results, the maximum magnetization is increasing while the loop area is decreasing with the frequency increasing under a specified field amplitude. The variation rules are simple, in that the influences of the frequency on the maximum value and loop area may be predicted by some polynomial functions within the second order. These numerical results can provide useful information for the simplification of the frequency-dependent Jiles-Atherton model in engineering applications.

The iteration method to solve M_an costs most of the computation time. Though Eq (13) introduces a new iteration process, the initial values can be set easily (using the value of the previous point) and it can be executed in quite a short time. As the differential data are not predetermined, Newton's method is not friendly to use, and the secant method is employed here to save computation time.

Compared to the fixed-point method ^[36,49,50] with or without acceleration, the selected secant method improves the computation speed effectively. The computation time is collected by use of the "tic" and "toc" functions in MATLAB. As M_an is solved separately from the other expressions, the data of M_an can be first stored and then called to remove the following computation time. Calculating on 500 points per period, Table 1 shows the required numbers of iterations and computation times of the three solution methods. Compared to the other two methods, the proposed numerical method has the fastest computation speed, as the required time is approximately 64.7% of the time spent by the fixed-point method with Aitken acceleration. When M_an must be resolved in every cycle under some conditions, the saved time is more obvious. Taking the time-series data at 90 Hz as an example, the proposed method can calculate all the points in 41.420 s, which is the lowest among the three methods.

Table 1. Computation speed of the three solution methods.

Solution method to solve M_an	Number of iterations (storage)	Computation time [s] (storage)	Number of iterations (recomputing)	Computation time [s] (recomputing)
Fixed-point without acceleration	8 206	1.038	740 052	94.532
Fixed-point with Aitken acceleration	5 498	0.695	489 762	63.968
Proposed numerical method	3 520	0.450	318 623	41.420

| Show Table

DownLoad: CSV

Regarding the process of solving the magnetization, the implicit one-step trapezoidal rule shown in Eqs (11)–(13) is also carefully presented. Besides the trapezoidal rule, the Euler method or the Runge-Kutta 4^th order (or higher) method has also been widely used to solve the initial value problem. As the (implicit) backward Euler method must be inconvenient and have a lower precision than the trapezoidal rule shown in Eq (11), it is not necessary to list here. The (explicit) forward Euler method is the simplest method and the iterative process shown in Eq (13) can be removed. The computational process built on this method is written as

$\left\{ \begin{aligned} {\left. M \right|_{i + 1}} & = {\left. M \right|_i} + \Delta t{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|_i}, \\ {\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|_{i + 1}} & = {f_M}\left\{ {{{\left. t \right|}_{i + 1}}, {{\left. M \right|}_i} + \Delta t{{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i}, {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i}, \left\langle {{{\left. H \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}}, {{\left. {{M_{an}}} \right|}_{i + 1}}, {{\left. {\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}}} \right|}_{i + 1}}} \right\rangle } \right\} \\ & = \frac{{\left( {1 - c} \right){\delta _{{{\left. M \right|}_{i + 1}}}}}}{{\delta k}}\left[ {{{\left. {{M_{an}}} \right|}_{i + 1}} - \left( {{{\left. M \right|}_i} + \Delta t{{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i}} \right)} \right]\left( {{{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}} + \alpha {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i}} \right) + c{\left. {\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}}} \right|_{i + 1}} \\ &- \frac{{\left( {1 - c} \right){K_{edd}}}}{{\delta k}}{\left( {{{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}} + {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i}} \right)^2} - \frac{{\left( {1 - c} \right){K_{exc}}}}{{\delta k}}{\left| {\left( {{{\left. {\frac{{{\text{d}}H}}{{{\text{d}}t}}} \right|}_{i + 1}} + {{\left. {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|}_i}} \right)} \right|^{\frac{3}{2}}}. \\ \end{aligned} \right.$

(14)

Compared to Eqs (11) and (13), the forward Euler method severely reduces the solving difficulty. However, the forward Euler method requires more sampling points per period to reach the same computational accuracy as some other methods. Regarding the Runge-Kutta 4^th order (or higher) method, the value of M or dM/dt at the middle point (between the i^th and i+1^th one) is not given such that four unknown quantities, dM/dt|_i+1, M|_i+1, dM/dt|_i+1/2, and M|_i+1/2, should be solved at the same time, where *|_i+1/2 means the value of the point at the middle of t_i and t_i+1. Therefore, the standard Runge-Kutta 4^th order method is not friendly to use. In addition, the multistep method will further increase the number of unknown quantities. To avoid the implicit system of equations, the approximation shown in Eq (15) can also be employed in the one-step Runge-Kutta method and then the value at the middle point can be obtained from the cubic spline interpolation.

The comparisons of the computation performance between the three models are tabulated in Table 2, where the magnetic field is with the amplitude 60 kA/m and frequency 100 Hz. The step size should be set low enough to reach high-precision solutions. For the forward Euler method, at least 1430 points per period should be calculated such that the computation time is really long. The simplified Runge-Kutta 4^th order method with interpolation requires the least number of points as the accumulated error is the smallest. However, the computation time is not the shortest because M_an at the middle points should also be solved from the iterations. Overall, the implicit one-step trapezoidal rule employed in this manuscript is a simple expression and has fast computation speed.

Table 2. Computation performances of the forward Euler method, simplified RK4 method, and the proposed model.

Solution method	Required number of sampling points	Computation time [s]
Forward Euler method	1430	0.761
Runge-Kutta 4^th order with interpolation	263	0.316
Proposed numerical method	441	0.228

| Show Table

DownLoad: CSV

3. Numerical analysis of the frequency-dependent Jiles-Atherton model

3.1. Feasible region

It is clearly shown in Figure 3 that some points are unavailable under some conditions; mainly both the field amplitude H_amp and the frequency f are high. This is caused by the expression of the Jiles-Atherton model, while not the case with the numerical method. From the expressions shown in Eqs (4) and (10), the last two terms, representing the eddy-current and excess loss, respectively, are higher-order functions of dH/dt than that of the other terms. A too-high value of H_amp or f will lead to nonconvergence of the solution of the differential equation. To put it another way, the values of K_edd and K_exc cannot be increased unlimitedly when the values of H_amp and f are high.

The infeasible region where the convergence solutions are unavailable is shown as the white space in Figure 4. With specified parameters of K_edd and K_exc, the frequency-dependent Jiles-Atherton model is suitable for the conditions falling into the region below the provided boundary. The boundary of the feasible and infeasible regions can be approximated by a function as H_amp·f = Const, where the value of Const is determined by the material property and shape while independent on the magnetic field. Taking the Terfenol-D material as the example shown in Figure 4, the boundary function is H_amp·f = 6300 Hz·kA/m. According to this approximation function, when the value of H_amp·f is higher than this specified value, the frequency-dependent Jiles-Atherton model is nonconvergent.

Figure 4. Infeasible region of the frequency-dependent Jiles-Atherton model.

DownLoad: Full-Size Img PowerPoint

From the physical point of view, the infeasible region means that the frequency-dependent energy loss is higher than the total energy. That is, the values of K_edd and K_exc are too high under this condition. The calculation results provide a revision idea for the Jiles-Atherton model such that the values of K_edd and K_exc are considered as the decreasing functions of H_amp and f while not just related to the material or structural style, etc. On the other hand, the conclusion provides an effective searching range for the parameter values when we do the parameter identification.

3.2. Applicability of the commonly used approximation

In Eq (5), dH/dt + dM/dt in the last two terms is generally approximated by dM/dt when the material has high magnetic permeability, which is built on the assumption of B = μ₀(H+M) ≈ μ₀M. While for the magnetic material with relative permeability around 10, similar to Terfenol-D or smaller, the applicability of this commonly used simplification should be discussed carefully.

Built on this assumption, the energy conservation equation in differential form is written as ^[56,64]

$\frac{{{\text{d}}M}}{{{\text{d}}t}} = \frac{{\left( {1 - c} \right){\delta _M}}}{{\delta k}}\left( {{M_{an}} - M} \right)\left( {\frac{{{\text{d}}H}}{{{\text{d}}t}} + \alpha \frac{{{\text{d}}M}}{{{\text{d}}t}}} \right) + c\frac{{{\text{d}}{M_{an}}}}{{{\text{d}}t}} - \frac{{\left( {1 - c} \right){K_{edd}}}}{{\delta k}}{\left( {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right)^2} - \frac{{\left( {1 - c} \right){K_{exc}}}}{{\delta k}}{\left| {\frac{{{\text{d}}M}}{{{\text{d}}t}}} \right|^{\frac{3}{2}}}.$

(15)

Through solving Eq (15) similar to solving Eq (10), the computational deviations between the results of the frequency-dependent Jiles-Atherton model before and after the approximation are shown in Figure 5. In Figure 5, the subfigures (a)–(c) are calculated at f = 10 Hz with a field amplitude, respectively, of 10, 40, and 80 kA/m, and (d)–(f) are reached from f = 500 Hz with the field amplitude, respectively, of 2.0, 4.0, and 8.0 kA/m. The relative errors under various conditions are calculated built on treating the results before the approximation as the "exact" results.

Figure 5. Deviations between the calculated results before and after the approximation: (a) H_amp = 10 kA/m under 10 Hz; (b) H_amp = 40 kA/m under 10 Hz; (c) H_amp = 80 kA/m under 10 Hz; (d) H_amp = 2.0 kA/m under 500 Hz; (e) H_amp = 4.0 kA/m under 500 Hz; (f) H_amp = 8.0 kA/m under 500 Hz.

DownLoad: Full-Size Img PowerPoint

From the relative errors, with the frequency or field amplitude increasing, the computational deviation between the Jiles-Atherton models before and after the approximation will be increased roughly. In addition, the length of the interval with high deviations at higher frequency is higher than the low-frequency one, as the high-deviation interval is about [–H_amp/4, H_amp/4] at f = 10 Hz while changing to [–H_amp/2, H_amp/2] at f = 500 Hz. The deviations mainly occur around M ≈ 0 and the approximation has little influence on the shape of the M-H loop or the magnetization points on the interval of [H_amp/2, H_amp]. Roughly speaking, it is easily concluded that the approximation B ≈ μ₀M is acceptable for Terfenol-D material or similar from the viewpoints of amplitude and curve shape under most conditions. Only one condition should be considered: when the output of the material should be controlled continuously, as in employing the material to actuate a servo motor or valve. The maximum relative error of the calculated magnetization is higher than 10% on some interval such that the description precision of the approximated Jiles-Atherton model will be quite low.

On the other hand, this approximation provides little improvement on the computations as the above iterations or subsequent solving process cannot be removed. The computation time has hardly changed compared to the time spent on solving the equation before approximation, which may be caused by the term dH/dt not being totally removed from the initial equation.

3.3. Required numbers of sampling points per period

The step size of the magnetic field has great influence on the computation precision ^[36]. A smaller step size provides higher precision but longer computing time, compared to the higher one. Generally, the sampling length of the magnetic field data is unequal as the time is spaced equally while the variation of the magnetic field is nonlinear with respect to time. The computation precision of the numerical method in solving the static Jiles-Atherton model is influenced by the value of dM/dH while not influenced by the value of dH/dt. In contrast, the precision in solving the frequency-dependent model is influenced by both dM/dH and dH/dt, which can be easily reached from the expression shown in Eq (5). That is to say, the increment of H and dH/dt should be set small enough to guarantee a high-precision solution.

It is quite difficult and unnecessary to analyze the sizes of the two increments from the perspective of error transmission and then determine the sampling frequency. The numerical results under various numbers of sampling points per period, and also the times of the sampling frequency compared to the signal frequency, are calculated and compared directly to determine the size of the sampling frequency. Supposing N_p is the number of sampling points per period, Figure 6 shows the computation performance under different values of N_p when the field amplitude takes 5.0 kA/m, 20 kA/m, and 60 kA/m, respectively, at 50 Hz. From the computations, when N_p = 500,500, and 1000, respectively, the M-H loops change little with N_p increasing such that these three curves can be treated as the exact solutions. Then the computational precision under other values of N_p can be evaluated through comparing the calculated results with these exact solutions to determine the required minimum value of N_p. The increments of the magnetic fields under various values of N_p are also provided to take a look at the contrast.

Figure 6. Computational performances of the proposed numerical method with different values of N_p at 50 Hz: (a) M-H loop under H_amp = 5.0 kA/m; (b) increment of H under H_amp = 5.0 kA/m; (c) M-H loop under H_amp = 20 kA/m; (d) increment of H under H_amp = 20 kA/m; (e) M-H loop under H_amp = 60 kA/m; (f) increment of H under H_amp = 60 kA/m.

DownLoad: Full-Size Img PowerPoint

From the calculation results, a small N_p means a high sampling step size of the magnetic field and the magnetic field curve is not so similar to a sinusoid wave. As shown in Figure 6, when N_p takes the minimum value, the high deviations between the loop curve calculated from these conditions and the exact solutions are quite big such that the computation error is unacceptable. The low precision cannot be solved by use of the cubic spline interpolation to replace the linear interpolation shown in Figure 6, as the deviations are global. The calculated M-H curves completely deviate from a standard loop under some conditions, for example, N_p = 28 and H_amp = 20 kA/m as shown in Figure 6(c). Even worse, the numerical method is unavailable when N_p takes smaller values than the values shown in Figure 6.

Under H_amp not lower than 20 kA/m, the value of N_p is better to be not lower than 40, as at least 40 points are better to be collected in a period in order to predict the magnetization with high precision. With higher field amplitude, the proposed numerical method requires a higher value of N_p. When the field amplitude is 60 kA/m, the required N_p value is increased to 160, or the hysteresis width cannot be effectively predicted.

From the increment curves shown in Figure 6(b), (d), and (f), the biggest increment of the magnetic field always occurs around H = 0, which can be easily concluded from the derivative property of the magnetic field function. That is, the computation errors caused from the increments of the magnetic field around H = 0 are higher than the ones at other positions. When H is close to its amplitude, the relative errors are quite small such that the amplitude of the magnetization can be predicted effectively. In fact, the maximum magnetization can be calculated with high precision under most conditions as long as N_p meets the requirement of normal execution of the numerical methods. Therefore, if the maximum magnetization is the only considered characteristic, taking a quite small value of N_p is also acceptable as long as the numerical method can be executed.

Besides H_amp, the value of f has some influence on the value of N_p, just as is shown in Figure 7. Generally, under the same H_amp, a higher f value requires higher N_p for equal computation precision. The influence of the frequency is slight as the required value of N_p is increased from 20 to 40 with f changing from 20 Hz to 600 Hz, compared with the influence of the field amplitude. Therefore, the minimum value of N_p can be determined first referring to H_amp and then supplemented with further increasement according to f.

Figure 7. Influence of the frequency on the required number of sampling points per period N_p: (a) f = 20 Hz; (b) f = 200 Hz; (c) f = 400 Hz; (d) f = 600 Hz.

DownLoad: Full-Size Img PowerPoint

Recommended values of N_p under various H_amp are shown in Figure 8. The linear function reached from a simple data fitting is N_p = 7H_amp [kA/m] + 40, where the function value is always higher than the required value of N_p. The fitting function is also suitable to a high-frequency condition as long as the Jiles-Atherton model is convergent, that is, satisfying Section 3.3.

Figure 8. Recommended values of N_p suitable to a high-frequency condition.

DownLoad: Full-Size Img PowerPoint

4. Conclusions

This paper proposes an effective numerical solving method for the frequency-dependent Jiles-Atherton hysteresis model. In the numerical method, the anhysteretic magnetization is calculated by the secant method and its derivative is solved from the analytical expression. Then the trapezoidal rule is utilized to remove the M|_i+1 and form the implicit function just dependent on dM/dt and M|_i. Furthermore, the fixed-point iteration is used to solve dM/dt and then M is calculated from the previous trapezoidal rule. Compared to the other numerical methods, the proposed one is friendly to use and fast convergent.

To guarantee the solutions available, the feasible region of the Jiles-Atherton model is H_amp·f < 6300 Hz·kA/m. This conclusion is quite helpful for determining the searching range of the parameter values. In addition, the commonly used approximation that B ≈ μ₀M is acceptable under most conditions, while it provides little improvement on the numerical solving process as the iterations or subsequent solving process cannot be removed. The computation precision of the numerical method is greatly influenced by the number of sampling points per period N_p. A recommended value for calculating Terfenol-D material is N_p = 7H_amp [kA/m] + 40, which is suitable to various frequencies as long as the model is convergent.

To show the numerical results, this manuscript takes Terfenol-D material as the example, while the numerical method is suitable to various types of hysteresis through adjusting the parameter values in the Jiles-Atherton model. In addition, the conclusions from the numerical analysis are also valid, as the feasible region meets H_amp·f < Const approximately, B ≈ μ₀M is acceptable under most conditions, and a certain number of sampling points is required to form a small enough step size.

Author contributions

Cheng Zhang and Guangming Xue: Conceptualization, Methodology, Validation, Writing-original draft, Writing-review & editing. Both authors contributed equally to this work.

Acknowledgments

This work was supported by the Young and Middle-aged Teachers Education and Research Project (Science and Technology) of Fujian Province (No. JAT220016), Fuzhou University Research Project (No. XRC-23052), and Fuzhou University Qishan Scholar Project (XRC-24010).

Conflict of interest

The authors declare no conflict of interest.

References

[1]	A. G. Maslovskaya, L. I. Moroz, A. Y. Chebotarev, A. E. Kovtanyuk, Theoretical and numerical analysis of the Landau-Khalatnikov model of ferroelectric hysteresis, Commun. Nonlinear Sci., 93 (2021), 105524. https://doi.org/10.1016/j.cnsns.2020.105524 doi: 10.1016/j.cnsns.2020.105524
[2]	A. Chandra, B. Daniels, M. Curti, K. Tiels, E. A. Lomonova, D. M. Tartakovsky, Discovery of sparse hysteresis models for piezoelectric materials, Appl. Phys. Lett., 122 (2023), 214101. https://doi.org/10.1063/5.0146134 doi: 10.1063/5.0146134
[3]	L. Chen, Y. Feng, R. Li, X. Chen, H. Jiang, Jiles-Atherton based hysteresis identification of shape memory alloy-actuating compliant mechanism via modified particle swarm optimization algorithm, Complexity, 2019 (2019), 7465461. https://doi.org/10.1155/2019/7465461 doi: 10.1155/2019/7465461
[4]	E. Abreu, A. Bustos, P. Ferraz, W. Lambert, A relaxation projection analytical-numerical approach in hysteretic two-phase flows in porous media, J. Sci. Comput., 79 (2019), 1936–1980. https://doi.org/10.1007/s10915-019-00923-4 doi: 10.1007/s10915-019-00923-4
[5]	G. Quaranta, W. Lacarbonara, S. F. Masri, A review on computational intelligence for identification of nonlinear dynamical systems, Nonlinear Dyn., 99 (2020), 1709–1761. https://doi.org/10.1007/s11071-019-05430-7 doi: 10.1007/s11071-019-05430-7
[6]	P. Folhento, M. Braz-César, R. Barros, Cyclic response of a reinforced concrete frame: Comparison of experimental results with different hysteretic models, AIMS Mater. Sci., 8 (2021), 917–931. https://doi.org/10.3934/matersci.2021056 doi: 10.3934/matersci.2021056
[7]	V. D. Santis, A. D. Francesco, A. G. D'Aloia, A numerical comparison between Preisach, J-A and D-D-D hysteresis models in computational electromagnetics, Appl. Sci., 13 (2023), 5181. https://doi.org/10.3390/app13085181 doi: 10.3390/app13085181
[8]	D. C. Jiles, D. L. Atherton, Theory of ferromagnetic hysteresis, J. Magn. Magn. Mater., 61 (1986), 48–60. https://doi.org/10.1016/0304-8853(86)90066-1 doi: 10.1016/0304-8853(86)90066-1
[9]	B. Upadhaya, P. Rasilo, L. Perkki, P. Handgruber, A. Benabou, A. Belahcen, et al., Alternating and rotational loss prediction accuracy of vector Jiles-Atherton model, J. Magn. Magn. Mater., 527 (2021), 167690. https://doi.org/10.1016/j.jmmm.2020.167690 doi: 10.1016/j.jmmm.2020.167690
[10]	M. Brokate, On the moving Preisach model, Math. Method. Appl. Sci., 15 (1992), 145–157. https://doi.org/10.1002/mma.1670150302 doi: 10.1002/mma.1670150302
[11]	M. X. Tian, H. C. Li, H. Y. Zhang, Neural network model for magnetization characteristics of ferromagnetic materials, IEEE Access, 9 (2021), 71236–71243. https://doi.org/10.1109/access.2021.3078554 doi: 10.1109/access.2021.3078554
[12]	Y. Yang, S. Wang, B. Zhu, R. Wang, Y. Lu, L. Jiang, et al., A method to study the influence of background magnetic field on magnetic cores: measurement, parameter identification and discussion, Measurement, 220 (2023), 113329. https://doi.org/10.1016/j.measurement.2023.113329 doi: 10.1016/j.measurement.2023.113329
[13]	D. C. Jiles, D. L. Atherton, Theory of ferromagnetic hysteresis, J. Appl. Phys., 55 (1984), 2115–2120. https://doi.org/10.1063/1.333582 doi: 10.1063/1.333582
[14]	D. C. Jiles, D. L. Atherton, Ferromagnetic hysteresis, IEEE Trans. Magn., 19 (1983), 2183–2185. https://doi.org/10.1109/TMAG.1983.1062594 doi: 10.1109/TMAG.1983.1062594
[15]	D. C. Jiles, Modelling the effects of eddy current losses on frequency dependent hysteresis in electrically conducting media, IEEE Trans. Magn., 30 (1994), 4326–4328. https://doi.org/10.1109/20.334076 doi: 10.1109/20.334076
[16]	B. Upadhaya, P. Rasilo, L. Perkkiö, P. Handgruber, A. Belahcen, A. Arkkio, Comparison of anisotropic energy-based and Jiles-Atherton models of ferromagnetic hysteresis, IEEE Trans. Magn., 56 (2020), 7300307. https://doi.org/10.1109/tmag.2020.2964745 doi: 10.1109/tmag.2020.2964745
[17]	X. Hu, Y. Bu, J. Zhang, A nonlinear magneto-elastoplastic coupling model based on Jiles-Atherton theory of ferromagnetic materials, J. Phys. D: Appl. Phys., 55 (2022), 165005. https://doi.org/10.1088/1361-6463/ac42f9 doi: 10.1088/1361-6463/ac42f9
[18]	J. Ji, Z. Zhao, Hysteresis characteristics prediction method of amorphous materials based on static Jiles-Atherton hysteresis model and Maxwell's equation, J. Magn. Magn. Mater., 588 (2023), 171460. https://doi.org/10.1016/j.jmmm.2023.171460 doi: 10.1016/j.jmmm.2023.171460
[19]	Y. Zhan, C. Lin, A constitutive model of coupled magneto-thermo-mechanical hysteresis behavior for giant magnetostrictive materials, Mech. Mater., 148 (2020), 103477. https://doi.org/10.1016/j.mechmat.2020.103477 doi: 10.1016/j.mechmat.2020.103477
[20]	X. J. Zheng, X. E. Liu, A nonlinear constitutive model for Terfenol-D rods, J. Appl. Phys., 97 (2005), 053901. https://doi.org/10.1063/1.1850618 doi: 10.1063/1.1850618
[21]	B. Zidaric, M. Zagirnyak, K. Lenasi, D. Miljavec, Hysteresis losses in soft magnetic composite materials, COMPEL, 25 (2006), 157–168. https://doi.org/10.1108/03321640610634416 doi: 10.1108/03321640610634416
[22]	B. Upadhaya, P. Rasilo, P. Handgruber, A. Belahcen, A. Arkkio, Finite element level validation of an anisotropic hysteresis model for non-oriented electrical steel sheets, J. Magn. Magn. Mater., 564 (2022), 169978. https://doi.org/10.1016/j.jmmm.2022.169978 doi: 10.1016/j.jmmm.2022.169978
[23]	R. Szewczyk, Application of Jiles-Atherton model for modelling magnetization characteristics of textured electrical steel magnetized in easy or hard axis, In: Progress in automation, robotics and measuring techniques, Cham: Springer, 2015,293–302.https://doi.org/10.1007/978-3-319-15796-2_30
[24]	A. H. S. Atyia, A. M. Ghanim, Limitations of Jiles-Atherton models to study the effect of hysteresis in electrical steels under different excitation regimes, COMPEL, 43 (2024), 66–79. https://doi.org/10.1108/compel-02-2023-0061 doi: 10.1108/compel-02-2023-0061
[25]	Y. Z. Ren, Y. H. Wang, C. C. Liu, Low-frequency electromagnetic transient modeling of shell-type transformers based on dynamic Jiles-Atherton hysteresis model, IEEE Trans. Magn., 60 (2024), 7300905. https://doi.org/10.1109/tmag.2024.3417021 doi: 10.1109/tmag.2024.3417021
[26]	R. A. Naghizadeh, B. Vahidi, S. H. Hosseinian, An adaptive approach for simulation of inrush current in three-phase transformers considering hysteresis effects, Electr. Pow. Compo. Syst., 44 (2016), 673–682. https://doi.org/10.1080/15325008.2015.1122102 doi: 10.1080/15325008.2015.1122102
[27]	M. Birsan, Simulation of a ship's deperming process using the Jiles-Atherton model, IEEE Trans. Magn., 57 (2021), 7300407. https://doi.org/10.1109/tmag.2021.3068555 doi: 10.1109/tmag.2021.3068555
[28]	J. Q. Chen, H. D. Shang, D. Xia, S. Wang, T. Peng, C. Y. Zang, A modified vector Jiles-Atherton hysteresis model for the design of hysteresis devices, IEEE Trans. Energy Conver., 38 (2023), 1827–1835. https://doi.org/10.1109/tec.2023.3243101 doi: 10.1109/tec.2023.3243101
[29]	U. Rupnik, A. Alic, D. Miljavec, Harmonization and validation of Jiles-Atherton static hysteresis models, Energies, 15 (2022), 6760. https://doi.org/10.3390/en15186760 doi: 10.3390/en15186760
[30]	H. Singh, S. D. Sudhoff, Reconsideration of energy balance in Jiles-Atherton model for accurate prediction of B-H trajectories in ferrites, IEEE Trans. Magn., 56 (2020), 7300608. https://doi.org/10.1109/tmag.2020.2994022 doi: 10.1109/tmag.2020.2994022
[31]	K. Chwastek, Modelling of dynamic hysteresis loops using the Jiles-Atherton approach, Math. Comp. Model. Dyn., 15 (2009), 95–105. https://doi.org/10.1080/13873950802432016 doi: 10.1080/13873950802432016
[32]	I. Belgasmi, M. Hamimid, Accurate hysteresis loops calculation under the frequency effect using the inverse Jiles-Atherton model, Adv. Electromagn., 9 (2020), 93–98. https://doi.org/10.7716/aem.v9i2.1515 doi: 10.7716/aem.v9i2.1515
[33]	H. Wu, G. Xue, H. Bai, Z. Ren, A new modeling methodology for frequency-dependent hysteresis from the perspective of phase lag and amplitude attenuation, Nonlinear Dyn., in press. https://doi.org/10.1007/s11071-024-10531-z
[34]	R. Szewczyk, Progress in development of Jiles-Atherton model of magnetic hysteresis, AIP Conf. Proc., 2131 (2019), 020045. https://doi.org/10.1063/1.5119498 doi: 10.1063/1.5119498
[35]	R. Malczyk, J. Izydorczyk, The frequency-dependent Jiles-Atherton hysteresis model, Physica B, 463 (2015), 68–75. https://doi.org/10.1016/j.physb.2015.01.034 doi: 10.1016/j.physb.2015.01.034
[36]	M. Nowicki, R. Szewczyk, T. Charubin, A. Marusenkov, A. Nosenko, V. Kyrylchuk, Modeling the hysteresis loop of ultra-high permeability amorphous alloy for space applications, Materials, 11 (2018), 2079. https://doi.org/10.3390/ma11112079 doi: 10.3390/ma11112079
[37]	Y. Li, P. Zhang, Z. He, G. Xue, D. Wu, S. Li, et al., A simple magnetization model for giant magnetostrictive actuator used on an electronic controlled injector, J. Magn. Magn. Mater., 472 (2019), 59–65. https://doi.org/10.1016/j.jmmm.2018.09.126 doi: 10.1016/j.jmmm.2018.09.126
[38]	G. Xue, H. Bai, T. Li, Z. Ren, Z. Wu, A new hysteresis model based on Weibull cumulative distribution function and Jiles-Atherton hysteresis model, Nonlinear Dyn., 112 (2024), 6403–6420. https://doi.org/10.1007/s11071-024-09394-1 doi: 10.1007/s11071-024-09394-1
[39]	G. Xue, H. Bai, T. Li, Z. Ren, X. Liu, C. Lu, Numerical solving method for Jiles-Atherton model and influence analysis of the initial magnetic field on hysteresis, Mathematics, 10 (2022), 4431. https://doi.org/doi:10.3390/math10234431 doi: 10.3390/math10234431
[40]	G. Xue, P. Zhang, Z. He, D. Li, Z. Yang, Z. Zhao, Modification and numerical method for the Jiles-Atherton hysteresis model, Commun. Comput. Phys., 21 (2017), 763–781. https://doi.org/10.4208/cicp.050615.300816a doi: 10.4208/cicp.050615.300816a
[41]	S. Azzaoui, K. Srairi, M. E. H. Benbouzid, Non linear magnetic hysteresis modelling by finite volume method for Jiles-Atherton model optimizing by a genetic algorithm, Journal of Electromagnetic Analysis and Applications, 3 (2011), 5351. https://doi.org/10.4236/jemaa.2011.36032 doi: 10.4236/jemaa.2011.36032
[42]	L. Perkkiö, B. Upadhaya, A. Hannukainen, P. Rasilo, Stable adaptive method to solve FEM coupled with Jiles-Atherton hysteresis model, IEEE Trans. Magn., 54 (2018), 7400208. https://doi.org/10.1109/TMAG.2017.2782214 doi: 10.1109/TMAG.2017.2782214
[43]	M. d'Aquino, G. Rubinacci, A. Tamburrino, S. Ventre, Three-dimensional computation of magnetic fields in hysteretic media with time-periodic sources, IEEE Trans. Magn., 50 (2014), 7001104. https://doi.org/10.1109/TMAG.2013.2284339 doi: 10.1109/TMAG.2013.2284339
[44]	B. Ducharne, J. Juuti, Y. Bai, A simulation model for narrow band gap ferroelectric materials, Adv. Theor. Simul., 3 (2020). https://doi.org/10.1002/adts.202000052 doi: 10.1002/adts.202000052
[45]	J. Chen, H. Zhang, T. Zhu, S. Pan, Trajectory tracking control of a manipulator based on an immune algorithm-optimized neural network in the presence of unknown backlash-like hysteresis, Appl. Math. Comput., 470 (2024), 128552. https://doi.org/10.1016/j.amc.2024.128552 doi: 10.1016/j.amc.2024.128552
[46]	X. Zhang, Y. Tan, M. Su, Modeling of hysteresis in piezoelectric actuators using neural networks, Mech. Syst. Signal Proc., 23 (2009), 2699–2711. https://doi.org/10.1016/j.ymssp.2009.05.002 doi: 10.1016/j.ymssp.2009.05.002
[47]	M. R. Zakerzadeh, S. Naseri, P. Naseri, Modelling hysteresis in shape memory alloys using LSTM recurrent neural network, J. Appl. Math., 2024 (2024), 1174438. https://doi.org/10.1155/2024/1174438 doi: 10.1155/2024/1174438
[48]	M. Chiampi, D. Chiarabaglio, M. Repetto, A Jiles-Atherton and fixed-point combined technique for time periodic magnetic field problems with hysteresis, IEEE Trans. Magn., 31 (1995), 4306–4311. https://doi.org/10.1109/20.488295 doi: 10.1109/20.488295
[49]	M. E. Mathekga, R. A. McMahon, A. M. Knight, Application of the fixed point method for solution in time stepping finite element analysis using the inverse vector Jiles-Atherton model, IEEE Trans. Magn., 47 (2011), 3048–3051. https://doi.org/10.1109/tmag.2011.2141655 doi: 10.1109/tmag.2011.2141655
[50]	L. Coelho, V. C. Mariani, J. V. Leite, Solution of Jiles-Atherton vector hysteresis parameters estimation by modified differential evolution approaches, Expert Syst. Appl., 39 (2012), 2021–2025. https://doi.org/10.1016/j.eswa.2011.08.035 doi: 10.1016/j.eswa.2011.08.035
[51]	E. Kokornaczyk, M. W. Gutowski, Anhysteretic functions for the Jiles-Atherton model, IEEE Trans. Magn., 51 (2015), 7300305. https://doi.org/10.1109/TMAG.2014.2354315 doi: 10.1109/TMAG.2014.2354315
[52]	A. Grunwald, A. G. Olabi, Design of a magnetostrictive (MS) actuator, Sensor. Actuat. A-Phys., 144 (2008), 161–175. https://doi.org/10.1016/j.sna.2007.12.034 doi: 10.1016/j.sna.2007.12.034
[53]	F. Braghin, S. Cinquemani, F. Resta, A low frequency magnetostrictive inertial actuator for vibration control, Sensor. Actuat. A-Phys., 180 (2012), 67–74. https://doi.org/10.1016/j.sna.2012.03.015 doi: 10.1016/j.sna.2012.03.015
[54]	M. Hamel, A. Nait Ouslimane, F. Hocini, A study of Jiles-Atherton and the modified arctangent models for the description of dynamic hysteresis curves, Physica B, 638 (2022), 413930. https://doi.org/10.1016/j.physb.2022.413930 doi: 10.1016/j.physb.2022.413930
[55]	S. Gans, J. Molnár, D. Kovác, Estimation of Jiles-Atherton parameters of toroid cores using Matlab/simulink, Acta Phys. Pol. A, 143 (2023), 389–399. https://doi.org/10.12693/APhysPolA.143.389 doi: 10.12693/APhysPolA.143.389
[56]	D. C. Jiles, Frequency dependence of hysteresis curves in conducting magnetic materials, J. Appl. Phys., 76 (1994), 5849–5855. https://doi.org/10.1063/1.358399 doi: 10.1063/1.358399
[57]	K. Chwastek, Frequency behaviour of the modified Jiles-Atherton model, Physica B, 403 (2008), 2484–2487. https://doi.org/10.1016/j.physb.2008.01.010 doi: 10.1016/j.physb.2008.01.010
[58]	Y. Li, J. G. Zhu, L. H. Zhu, Y. J. Li, G. Lei, A dynamic magnetostriction model of grain-oriented sheet steels based on Becker-Doring crystal magnetization model and Jiles-Atherton theory of magnetic hysteresis, IEEE Trans. Magn., 56 (2020), 7511405. https://doi.org/10.1109/tmag.2019.2953887 doi: 10.1109/tmag.2019.2953887
[59]	Y. Liu, X. Gao, Y. Li, Giant magnetostrictive actuator nonlinear dynamic Jiles-Atherton model, Sensor. Actuat. A-Phys., 250 (2016), 7–14. https://doi.org/10.1016/j.sna.2016.09.009 doi: 10.1016/j.sna.2016.09.009
[60]	P. Shi, Magneto-elastoplastic coupling model of ferromagnetic material with plastic deformation under applied stress and magnetic fields, J. Magn. Magn. Mater., 512 (2020), 166980. https://doi.org/10.1016/j.jmmm.2020.166980 doi: 10.1016/j.jmmm.2020.166980
[61]	Z. Jia, H. Liu, F. Wang, C. Ge, Research on a novel force sensor based on giant magnetostrictive material and its model, J. Alloy. Compd., 509 (2011), 1760–1767. https://doi.org/10.1016/j.jallcom.2010.10.035 doi: 10.1016/j.jallcom.2010.10.035
[62]	K. Chwastek, J. Szczyglowski, M. Najgebauer, A direct search algorithm for estimation of Jiles-Atherton hysteresis model parameters, Mat. Sci. Eng. B, 131 (2006), 22–26. https://doi.org/10.1016/j.mseb.2005.11.030 doi: 10.1016/j.mseb.2005.11.030
[63]	V. Recupero, Sobolev and strict continuity of general hysteresis operators, Math. Method. Appl. Sci., 32 (2009), 2003–2018. https://doi.org/10.1002/mma.1124 doi: 10.1002/mma.1124
[64]	S. Hussain, D. A. Lowther, Prediction of iron losses using Jiles-Atherton model with interpolated parameters under the conditions of frequency and compressible stress, IEEE Trans. Magn., 52 (2016), 7300404. https://doi.org/10.1109/TMAG.2015.2487975 doi: 10.1109/TMAG.2015.2487975

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(708) PDF downloads(70) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(8) / Tables(2)

AIMS Mathematics

Numerical analysis of the frequency-dependent Jiles-Atherton hysteresis model using the example of Terfenol-D material

Related Papers:

Abstract

1. Introduction

2. Numerical method to solve the Jiles-Atherton model

2.1. Expression of the frequency-dependent Jiles-Atherton model

2.2. Numerical method to solve the Jiles-Atherton model

2.2.1. Solving the anhysteretic magnetization and its derivative

2.2.2. Solving the magnetization

2.3. Computation performance of the numerical method using the example of Terfenol-D

3. Numerical analysis of the frequency-dependent Jiles-Atherton model

3.1. Feasible region

3.2. Applicability of the commonly used approximation

3.3. Required numbers of sampling points per period

4. Conclusions

Author contributions

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Numerical analysis of the frequency-dependent Jiles-Atherton hysteresis model using the example of Terfenol-D material

Related Papers:

Abstract

1. Introduction

2. Numerical method to solve the Jiles-Atherton model

2.1. Expression of the frequency-dependent Jiles-Atherton model

2.2. Numerical method to solve the Jiles-Atherton model

2.2.1. Solving the anhysteretic magnetization and its derivative

2.2.2. Solving the magnetization

2.3. Computation performance of the numerical method using the example of Terfenol-D

3. Numerical analysis of the frequency-dependent Jiles-Atherton model

3.1. Feasible region

3.2. Applicability of the commonly used approximation

3.3. Required numbers of sampling points per period

4. Conclusions

Author contributions

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog