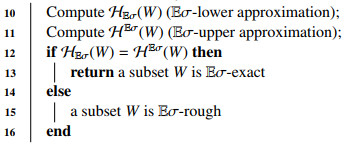Cardinality rough neighborhoods with applications

1.   Introduction

As a fundamental framework for analyzing information systems containing imperfect or ambiguous data, Pawlak ^[33] introduced traditional rough set theory (TRST). This theory begins with an equivalence relation defined over the universe, forming the basis of granules (or blocks). These granules are referred to as equivalence classes. To ascertain the nature of information derived from rough datasets, TRST introduces the pivotal concepts of lower and upper approximations. To provide further insight into the structure and comprehensiveness of knowledge derived, the concepts of boundary regions and accuracy degrees have been proposed. These concepts inform us about the quantity of uncertainty data and the nature of their structure.

We often encounter numerous practical challenges across various disciplines where an equivalence relation does not accurately describe the relationship between the objects involved. This means that we should relax the condition of TRST to successfully address these issues. Therefore, several authors endeavored to set up novel rough set models that were defined via a nonequivalence relation such as dominance ^[36], similarity ^[2,43], and quasi-order ^[40]. In 1996, Yao ^[47] presented two kinds of neighborhood systems, namely, right neighborhood and left neighborhood, and exploited them as granules or blocks to construct new rough approximation operators. This paved the way for authors and scholars to offer novel paradigms of rough set theory through different sorts of relations that are not necessarily an equivalence relation. To look over some of these paradigms, Abu-Donia ^[4] produced some rough set models by defining the previous neighborhoods by deal with a finite number of relations rather than a single relation. Mareay ^[30] proposed four neighborhoods based on the equality between the original neighborhoods and offered new rough approximation operators. He scrutinized their main properties and elucidated their pros. Atef et al. ^[19] completed Mareay's work by introducing other paradigms following the same technique. Dai et al. ^[20] defined the maximal right neighborhood over a similarity relation and put forward some rough set models. Newly, Al-shami with co-authors have established novel paradigms generated from new forms of neighborhoods such as intersection neighborhoods ^[14], containment neighborhoods ^[8], subset neighborhoods ^[12], and maximal neighborhoods ^[11]. They have revealed their main characterizations and the interrelations between them; also, they have illustrated how these paradigms are applied to prevent the spread of COVID-19 and reduce the pressure on health facilities. Al-shami and Mhemdi ^[17] and Demiralp ^[21] proposed a novel technique to study rough neighborhoods and their generalized approximation spaces generated by the hybridization of the right and left neighborhoods as well as minimal right and minimal left neighborhoods. Additionally, this theory has served as a valuable mechanism for characterizing information content across various models and applications in numerous diverse fields; see ^[1,25,26].

Due to the similarities in the behaviors of topological and rough set concepts, rough set models can be studied from a topological perspective. This matter was first noted by Skowron ^[44] who set up its fundamentals. This approach has attracted many topologists who are interested in rough set theory. To name a few, Lashin et al. ^[28] considered the original neighborhoods as a subbase for topology and then linked between the concepts of topology and rough set theory. Zhang et al. ^[49] discussed some topological concepts such as compactness and connectedness when the topology is structured by a reflexive relation. Salama ^[37] provided a topological solution for the problem of missing attribute values. Al-shami ^[9,10] made use of two generalizations of open sets to describe information systems. Al-shami and Mhemdi ^[16] employed subset rough neighborhoods to initiate topological spaces of rough set models. Güler et al. ^[24] and Mustafa et al. ^[32] introduced various topological spaces of rough set models using containment rough neighborhoods. Moreover, some authors employed supra topology ^[13], infra topology ^[15], nano-topology ^[27], and bitopology ^[38], which are extensions of topology, to study generalized rough approximation spaces. Almarri and Azzam ^[7] and El-Sharkasy ^[23] discussed these spaces via the minimal structures. Further studies can be found in ^{[29,42,45,48]}.

For several reasons this manuscript was prepared. First, to present a novel technique, free from an equivalence relation requirement, for addressing situations that focus on the cardinality number of $\mathcal{N}\sigma$-neighborhoods, such as those encountered in social media or in categorizing applicants based on the number of their qualities. Second, to retain most characteristics of the traditional rough set model outlined in Proposition 2.3. Third, to address certain shortcomings in the properties of $\mathcal{N}\sigma$-neighborhoods, which may necessitate updates to the formula used for calculating accuracy measures or the imposition of additional condition(s) on the applied relations; refer to ^[22]. Fourth, to propose an abstract method inspired by topology as an equivalent alternative for the proposed rough set models.

This manuscript is designed as follows. Following this introduction, we summon the definitions and findings that are essential for understanding the content in Section 2. Then, in Section 3, we suggest new forms of neighborhoods called cardinality rough neighborhoods and look at their primary features with the assistance of several examples. In Section 4, we utilize these neighborhoods to introduce various rough set paradigms and elucidate the fundamental features of their lower and upper approximations. We devote Section 5 to building topological paradigms that are equivalent to the forgoing ones in the cases of $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$, which helps a wide range of users to choose the suitable methods with their expertise. We structure a practical example to clarify how the current paradigms are applied and analyze the advantages and limitations of this work in Sections 6 and 7, respectively. Finally, a summary of this manuscript and suggestions for future work are provided in Section 8.

2.   Preliminaries

This section is devoted to reviewing several key definitions and results. Also, the necessity to introduce the idea of cardinal neighborhoods ($\mathbb{E}_\sigma$-neighborhoods) will be justified.

2.1.   Traditional approximation space (TAS)

Definition 2.1. ^[33] Let $\mathcal{B}$ denote a universe, defined as a nonempty finite set. A binary relation $\Psi$ on $\mathcal{B}$ is characterized as a subcollection of $\mathcal{B}\times \mathcal{B}$. The pairing $(\alpha, \beta)\in \Psi$ is commonly expressed as $\alpha \Psi \beta$. A relation $\Psi$ on $\mathcal{B}$ is termed reflexive (resp., symmetric, transitive) if $\alpha \Psi \alpha$ for any $\alpha\in \mathcal{B}$ (resp., $\alpha \Psi \beta\Longleftrightarrow \beta \Psi \alpha$, $\alpha \Psi \delta$ when $\alpha \Psi \beta$ and $\beta \Psi \delta$). An equivalence relation is defined as one that is reflexive, symmetric, and transitive. Furthermore, a comparable relation, denoted by $\Psi$, satisfies $\alpha\Psi\beta$ or $\beta\Psi\alpha$ for all $\alpha, \beta\in \mathcal{B}$.

Definition 2.2. ^[33] Let $\Psi$ be an equivalence relation on $\mathcal{B}$. Suppose $W\subseteq \mathcal{B}$, so the lower, upper approximations of $W$ will be represented, respectively, as:

The notation $\mathcal{B}/ \Psi$ symbolizes the family comprising all equivalence classes induced by the relation $\Psi$.

The pair $(\mathcal{B}, \Psi)$ is henceforth referred to as an approximation space. $W$ is characterized as rough if $\overline{\Psi}(W)$ and $\underline{\Psi}(W)$ are not equal. Conversely, if the upper and lower approximations coincide, the set is termed definable or exact.

The core features of the traditional rough set model are enumerated in the subsequent proposition.

Proposition 2.3. ^[33,34,35] Consider an equivalence relation $\Psi$ defined on $\mathcal{B}$. For sets $S, W$, the next characteristics hold:

Traditional theory ^[33] has been generalized through diverse methodologies, with comprehensive verification of the validity of these properties. Unfortunately, certain properties have been found to be uncertain. Nevertheless, the acquisition of as many of these properties as feasible is regarded as advantageous within these methodologies.

Also, rough sets can be described numerically by using the next two measures:

Definition 2.4. ^[34,35] Consider an equivalence relation $\Psi$ on $\mathcal{B}$, the $\mathbf{A}$-accuracy and $\mathbf{R}$-roughness criteria of $W$ are determined as:

In many positions, the equivalence relations are not attainable. Consequently, the classical approach has been extended by employing weaker relations than full equivalence.

2.2.   $\sigma$-Neighborhood space

Definition 2.5. ^{[3,5,6,46,47]} Consider an arbitrary relation $\Psi$ on $\mathcal{B}$. If $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle, u, \langle u\rangle\}$, then the $\sigma$-neighborhoods of $\kappa\in \mathcal{B}$, symbolized by $\mathcal{N}_\sigma (\kappa)$, are identified as:

(ⅰ) $\mathcal{N}_r(\kappa) = \{o\in \mathcal{B} : \kappa$ $\Psi$ $o\}$.

(ⅱ) $\mathcal{N}_l(\kappa) = \{o\in \mathcal{B} : o$ $\Psi$ $\kappa\}$.

(ⅲ)

(ⅳ)

(ⅴ) $\mathcal{N}_i(\kappa) = \mathcal{N}_r(\kappa)\bigcap \mathcal{N}_l(\kappa)$.

(ⅵ) $\mathcal{N}_u(\kappa) = \mathcal{N}_r(\kappa)\bigcup \mathcal{N}_l(\kappa)$.

(ⅶ) $\mathcal{N}_{\langle i\rangle}(\kappa) = \mathcal{N}_{\langle r\rangle}(\kappa)\bigcap \mathcal{N}_{\langle l\rangle}(\kappa)$.

(ⅷ) $\mathcal{N}_{\langle u\rangle}(\kappa) = \mathcal{N}_{\langle r\rangle}(\kappa)\bigcup \mathcal{N}_{\langle l\rangle}(\kappa)$.

Henceforward, unless otherwise specified, we will consider $\sigma$ to belong to the set $\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle, u, \langle u\rangle\}$.

Definition 2.6. ^[39] Consider a relation $\Psi$ on $\mathcal{B}$ and let $\zeta_\sigma$ denote a mapping from $\mathcal{B}$ to $2^\mathcal{B}$, associating each member $\kappa\in \mathcal{B}$ with its $\sigma$-neighborhood in $2^\mathcal{B}$. Consequently, the triple $(\mathcal{B}, \Psi, \zeta_\sigma)$ is termed a $\sigma$-neighborhood space, abbreviated as $\mathcal{N}_\sigma$S.

The aforementioned types of neighborhoods were utilized to introduce novel variations of lower and upper approximations, as well as accuracy (roughness) criteria. In the desire of enhancing the quality of approximations and maximizing accuracy criteria, numerous comparisons among the preceding types of neighborhoods were conducted.

Definition 2.7. ^{[3,5,6,46,47]} Given a relation $\Psi$ on $\mathcal{B}$, the lower and upper approximations of each subset $W$ regarding to the various kinds of neighborhoods are introduced as:

Definition 2.8. ^[3,5,6,47] Consider a relation $\Psi$ on $\mathcal{B}$. The $\mathbf{A}_{\mathcal{N}\sigma}$-accuracy and $\mathcal{R}_{\mathcal{N}\sigma}$-roughness criteria of a nonempty set $W$ in regard to $\Psi$ are represented by :

Definition 2.9. ^[34,35] Consider two relations $\Psi_1$ and $\Psi_2$ on $\mathcal{B}$ such that $\Psi_1\subseteq \Psi_2$. The approximations derived from $\mathcal{N}$-neighborhoods show the property of monotonicity in both accuracy and roughness of any set if $\mathbf{A}_{\mathcal{N}\sigma_1}(W)\geq \mathbf{A}_{\mathcal{N}\sigma_2}(W)$ and, respectively, $\mathcal{R}_{\mathcal{N}\sigma_1}(W)\leq \mathcal{R}_{\mathcal{N}\sigma_2}(W)$.

Definition 2.10. ^[18,30] Consider a relation $\Psi$ on $\mathcal{B}$. For each $\sigma$, the $\mho$-neighborhoods of an element $\kappa$ of $\mathcal{B}$ is represented as:

(ⅰ) $\mho_r(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_r(\kappa) = \mathcal{N}_r(o)\}$.

(ⅱ) $\mho_l(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_l(\kappa) = \mathcal{N}_l(o)\}$.

(ⅲ) $\mho_i(\kappa) = \mho_r(\kappa)\cap \mho_l(\kappa)$.

(ⅳ) $\mho_u(\kappa) = \mho_r(\kappa)\cup \mho_l(\kappa)$.

(ⅴ) $\mho_{\langle r\rangle}(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_{\langle r\rangle}(\kappa) = \mathcal{N}_{\langle r\rangle}(o)\}$.

(ⅵ) $\mho_{\langle l\rangle}(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_{\langle l\rangle}(\kappa) = \mathcal{N}_{\langle l\rangle}(o)\}$.

(ⅶ) $\mho_{\langle i\rangle}(\kappa) = \mho_{\langle r\rangle}(\kappa) \cap \mho_{\langle l\rangle}(\kappa)$.

(ⅷ) $\mho_{\langle u\rangle}(\kappa) = \mho_{\langle r\rangle}(\kappa) \cup \mho_{\langle l\rangle}(\kappa)$.

Definition 2.11. ^[8] Consider a relation $\Psi$ on $\mathcal{B}$. For each $\sigma$, the $\mathbb{C}$-neighborhoods of a member $\kappa$ of $\mathcal{B}$ is represented as:

(ⅰ) $\mathbb{C}_r(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_r(o)\subseteq \mathcal{N}_r(\kappa)\}$.

(ⅱ) $\mathbb{C}_l(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_l(o)\subseteq \mathcal{N}_l(\kappa)\}$.

(ⅲ) $\mathbb{C}_i(\kappa) = \mathbb{C}_r(\kappa)\cap \mathbb{C}_l(\kappa)$.

(ⅳ) $\mathbb{C}_u(\kappa) = \mathbb{C}_r(\kappa)\cup \mathbb{C}_l(\kappa)$.

(ⅴ) $\mathbb{C}_{\langle r\rangle}(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_{\langle r\rangle}(o)\subseteq \mathcal{N}_{\langle r\rangle}(\kappa)\}$.

(ⅵ) $\mathbb{C}_{\langle l\rangle}(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_{\langle l\rangle}(o)\subseteq \mathcal{N}_{\langle l\rangle}(\kappa)\}$.

(ⅶ) $\mathbb{C}_{\langle i\rangle}(\kappa) = \mathbb{C}_{\langle r\rangle}(\kappa)\cap \mathbb{C}_{\langle l\rangle}(\kappa)$.

(ⅷ) $\mathbb{C}_{\langle u\rangle}(\kappa) = \mathbb{C}_{\langle r\rangle}(\kappa)\cup \mathbb{C}_{\langle l\rangle}(\kappa)$.

Definition 2.12. ^[12] Consider a relation $\Psi$ on $\mathcal{B}$. For each $\sigma$, the $\mathbb{S}$-neighborhoods of a member $\kappa$ of $\mathcal{B}$ is represented as:

(ⅰ) $\mathbb{S}_r(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_r(\kappa)\subseteq \mathcal{N}_r(o)\}$.

(ⅱ) $\mathbb{S}_l(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_l(\kappa)\subseteq \mathcal{N}_l(o)\}$.

(ⅲ) $\mathbb{S}_i(\kappa) = \mathbb{S}_r(\kappa)\cap \mathbb{S}_l(\kappa)$.

(ⅳ) $\mathbb{S}_u(\kappa) = \mathbb{S}_r(\kappa)\cup \mathbb{S}_l(\kappa)$.

(ⅴ) $\mathbb{S}_{\langle r\rangle}(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_{\langle r\rangle}(\kappa)\subseteq \mathcal{N}_{\langle r\rangle}(o)\}$.

(ⅵ) $\mathbb{S}_{\langle l\rangle}(\kappa) = \{o\in \mathcal{B} : \mathcal{N}_{\langle l\rangle}(\kappa)\subseteq \mathcal{N}_{\langle l\rangle}(o)\}$.

(ⅶ) $\mathbb{S}_{\langle i\rangle}(\kappa) = \mathbb{S}_{\langle r\rangle}(\kappa)\cap \mathbb{S}_{\langle l\rangle}(\kappa)$.

(ⅷ) $\mathbb{S}_{\langle u\rangle}(\kappa) = \mathbb{S}_{\langle r\rangle}(\kappa)\cup \mathbb{S}_{\langle l\rangle}(\kappa)$.

3.   Cardinality neighborhood systems

According to any binary relation, this section is consecrated to introduce the notion of cardinality neighborhoods for any element in the universe. Their main properties will be explored and the conditions under which some of them are identical will be determined. To support the gained results and relationships, illustrative examples are included. The study of cardinality neighborhoods aspires to improve the accuracy of approximations.

For any $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle, u, \langle u\rangle\}$, $|\mathcal{N}_\sigma(.)|$ denotes the cardinality of $\mathcal{N}_\sigma(.)$.

Definition 3.1. Consider a relation $\Psi$ on $\mathcal{B}$. For each $\sigma$, the cardinality neighborhoods of an element $\kappa$ of $\mathcal{B}$ (briefly, $\mathbb{E}_\sigma(\kappa)$) are defined as:

(ⅰ) $\mathbb{E}_r(\kappa) = \{o\in \mathcal{B} : |\mathcal{N}_r(\kappa)| = |\mathcal{N}_r(o)|\}$.

(ⅱ) $\mathbb{E}_l(\kappa) = \{o\in \mathcal{B} : |\mathcal{N}_l(\kappa)| = |\mathcal{N}_l(o)|\}$.

(ⅲ) $\mathbb{E}_i(\kappa) = \mathbb{E}_r(\kappa)\cap \mathbb{E}_l(\kappa)$.

(ⅳ) $\mathbb{E}_u(\kappa) = \mathbb{E}_r(\kappa)\cup \mathbb{E}_l(\kappa)$.

(ⅴ) $\mathbb{E}_{\langle r\rangle}(\kappa) = \{o\in \mathcal{B} : |\mathcal{N}_{\langle r\rangle}(\kappa)| = |\mathcal{N}_{\langle r\rangle}(o)|\}$.

(ⅵ) $\mathbb{E}_{\langle l\rangle}(\kappa) = \{o\in \mathcal{B} : |\mathcal{N}_{\langle l\rangle}(\kappa)| = |\mathcal{N}_{\langle l\rangle}(o)|\}$.

(ⅶ) $\mathbb{E}_{\langle i\rangle}(\kappa) = \mathbb{E}_{\langle r\rangle}(\kappa) \cap \mathbb{E}_{\langle l\rangle}(\kappa)$.

(ⅷ) $\mathbb{E}_{\langle u\rangle}(\kappa) = \mathbb{E}_{\langle r\rangle}(\kappa) \cup \mathbb{E}_{\langle l\rangle}(\kappa)$.

The next example will demonstrate the conduct of cardinal neighborhoods, assist us in displaying the dealings amongst them, and bring to light the method of computing cardinal neighborhoods.

Example 3.2. Let's consider $\Psi = \{(\beta, \beta), (\alpha, \beta), (\beta, \delta), (\delta, \kappa)\}$ as a relation on $\mathcal{B} = \{\alpha, \beta, \delta, \kappa\}$. Subsequently, the cardinality neighborhoods for all members of $\mathcal{B}$ will be calculated and presented in Table 1.

Proposition 3.3. (ⅰ) $\kappa\in\mathbb{E}_i(\alpha)$ iff $|\mathcal{N}_r(\kappa)| = |\mathcal{N}_r(\alpha)|$ and $|\mathcal{N}_l(\kappa)| = |\mathcal{N}_l(\alpha)|$.

(ⅱ) $\kappa\in\mathbb{E}_u(\alpha)$ iff $|\mathcal{N}_r(\kappa)| = |\mathcal{N}_r(\alpha)|$ or $|\mathcal{N}_l(\kappa)| = |\mathcal{N}_l(\alpha)|$.

(ⅲ) $\kappa\in\mathbb{E}_{\langle i\rangle}(\alpha)$ iff $|\mathcal{N}_{\langle r\rangle}(\kappa)| = |\mathcal{N}_{\langle r\rangle}(\alpha)|$ and $|\mathcal{N}_{\langle l\rangle}(\kappa)| = |\mathcal{N}_{\langle l\rangle}(\alpha)|$.

(ⅳ) $\kappa\in\mathbb{E}_{\langle u\rangle}(\alpha)$ iff $|\mathcal{N}_{\langle r\rangle}(\kappa)| = |\mathcal{N}_{\langle r\rangle}(\alpha)|$ or $|\mathcal{N}_{\langle l\rangle}(\kappa)| = |\mathcal{N}_{\langle l\rangle}(\alpha)|$.

Proof. Follows from Definition 3.1. □

Corollary 3.4. If $\Psi$ is a symmetric relation, then:

(ⅰ) $\mathbb{E}_i(\alpha) = \{o\in \mathcal{B} : |\mathcal{N}_i(\alpha)| = |\mathcal{N}_i(o)|\}$.

(ⅱ) $\mathbb{E}_{\langle i\rangle}(\alpha) = \{o\in \mathcal{B} : |\mathcal{N}_{\langle i\rangle}(\alpha)| = |\mathcal{N}_{\langle i\rangle}(o)|\}$.

(ⅲ) $\mathbb{E}_u(\alpha) = \{o\in \mathcal{B} : |\mathcal{N}_u(\alpha)| = |\mathcal{N}_u(o)|\}$.

(ⅳ) $\mathbb{E}_{\langle u\rangle}(\alpha) = \{o\in \mathcal{B} : |\mathcal{N}_{\langle u\rangle}(\alpha)| = |\mathcal{N}_{\langle u\rangle}(o)|\}$.

In Example 3.2, one can remark that $\mathbb{E}_i(\alpha) = \mathbb{E}_{\langle i\rangle}(\alpha) = \{\alpha\}$, whereas $\{o\in \mathcal{B}: |\mathcal{N}_i(\alpha)| = |\mathcal{N}_i(o)|\} = \{\alpha, \delta, \kappa\}$ and $\{o\in \mathcal{B}: |\mathcal{N}_{\langle i\rangle}(\alpha)| = |\mathcal{N}_{\langle i\rangle}(o)|\} = \{\alpha, \kappa\}$. This confirms the necessity of a symmetric condition of the above corollary. That is, we cannot replace the condition $|\mathcal{N}_r(\alpha)| = |\mathcal{N}_r(o)|$ and $|\mathcal{N}_l(\alpha)| = |\mathcal{N}_l(o)|$ with $|\mathcal{N}_i(\alpha)| = |\mathcal{N}_i(o)|$ in general.

Proposition 3.5. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$. If $\kappa\in\mathcal{B}$, then $\mathbb{E}_\sigma(\kappa)\neq\emptyset$ for each $\sigma$.

Proof. Follows from the fact that $\kappa\in\mathbb{E}_\sigma(\kappa)$ for each $\sigma$. □

The above result will be beneficial in the next section to provide a formulation of an accuracy measure similar to the original one given by Pawlak without additional condition(s). That is, we guarantee that the lower approximation of every set is always a subset of its upper approximation.

Proposition 3.6. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$ and $\kappa\in\mathcal{B}$. Then, $\kappa\in\mathbb{E}_\sigma(\alpha)$ iff $\alpha\in\mathbb{E}_\sigma(\kappa)$, for each $\sigma$.

Proof. In the instances where $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle\}$, we obtain $\kappa\in\mathbb{E}_\sigma(\alpha)$ $\Longleftrightarrow$ $|\mathcal{N}_\sigma(\kappa)| = |\mathcal{N}_\sigma(\alpha)|$ $\Longleftrightarrow$ $\alpha\in\mathbb{E}_\sigma(\kappa)$. The other cases of $\sigma\in\{i, \langle i\rangle, u, \langle u\rangle\}$ follow directly from this fact. □

Proposition 3.7. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$. If $\kappa\in\mathbb{E}_\sigma(\alpha)$, $\alpha\in\mathbb{E}_\sigma(\beta)$, then $\kappa\in\mathbb{E}_\sigma(\beta)$, for any $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$.

Proof. In the instances where $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle\}$, we obtain $\kappa\in\mathbb{E}_\sigma(\alpha)$, $\alpha\in\mathbb{E}_\sigma(\beta)$ iff $|\mathcal{N}_\sigma(\kappa)| = |\mathcal{N}_\sigma(\alpha)|$, $|\mathcal{N}_\sigma(\alpha)| = |\mathcal{N}_\sigma(\beta)|$. This means that $|\mathcal{N}_\sigma(\kappa)| = |\mathcal{N}_\sigma(\beta)|$. Hence, $\kappa\in\mathbb{E}_\sigma(\beta)$. The cases of $\sigma\in\{i, \langle i\rangle\}$ follow directly from this fact. □

From the above propositions, the next corollaries are understandable.

Corollary 3.8. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$ and $\kappa\in\mathcal{B}$. Then, $\kappa\in\mathbb{E}_\sigma(\alpha)$ iff $\mathbb{E}_\sigma(\kappa) = \mathbb{E}_\sigma(\alpha)$, for any $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$.

Corollary 3.9. For every $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$, the cardinality neighborhood of elements of $\mathcal{B}$ constitute a partition of $\mathcal{B}$, that is, the relation $\Psi$ defined by

is an equivalence relation for all $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$.

Remark 3.10. If $\sigma\in\{u, \langle u\rangle\}$, then Proposition 3.7 and Corollaries 3.21, 3.9 need not to be valid as both Example 3.2 and Table 1 illustrate.

The subsequent proposition indicates the relations between the various sorts of $\mathbb{E}_\sigma$-neighborhoods.

Proposition 3.11. (ⅰ) $\mathbb{E}_{i}\subseteq$ $\mathbb{E}_{r}\cap\mathbb{E}_{l}$ $\subseteq$ $\mathbb{E}_{r}\cup\mathbb{E}_{l}\subseteq$ $\mathbb{E}_{u}$.

(ⅱ) $\mathbb{E}_{\langle i\rangle}\subseteq$ $\mathbb{E}_{\langle r\rangle}\cap\mathbb{E}_{\langle l\rangle}$ $\subseteq$ $\mathbb{E}_{\langle r\rangle}\cup\mathbb{E}_{\langle l\rangle}\subseteq\mathbb{E}_{\langle u\rangle}$.

(ⅲ) $\mathbb{E}_{r} = \mathbb{E}_{l}$ = $\mathbb{E}_{i} = \mathbb{E}_{u} = \mathbb{E}_{\langle r\rangle}$ = $\mathbb{E}_{\langle l\rangle} = \mathbb{E}_{\langle i\rangle}$ = $\mathbb{E}_{\langle u\rangle}$, if $\Psi$ is a symmetric relation on $\mathcal{B}.$

Proof. Sentences (ⅰ), (ⅱ) are directly proved. To prove (ⅲ), one notes that $\mathcal{N}_r = \mathcal{N}_l$ when $\Psi$ is symmetric, so $\mathbb{E}_{r}$ = $\mathbb{E}_{l}$ = $\mathbb{E}_{i}$ = $\mathbb{E}_{u}$ and $\mathbb{E}_{\langle r\rangle}$ = $\mathbb{E}_{\langle l\rangle}$ = $\mathbb{E}_{\langle i\rangle}$ = $\mathbb{E}_{\langle u\rangle}$. It remains to show that $\mathbb{E}_{\sigma} = \mathbb{E}_{\langle \sigma\rangle}$ for one case of $\sigma\in\{r, l, i, u\}$. To do this, we proved that $\mathbb{E}_{r}$ represents a partition for $\mathcal{B}$, which means that $\mathbb{E}_{r} = \mathbb{E}_{\langle r\rangle}$. Thus, the desired outcome has been achieved. □

Corollary 3.12. If $\Psi$ is a symmetric relation, then the cardinality neighborhood of elements of $\mathcal{B}$ constitute a partition of $\mathcal{B}$ for each $\sigma\in\{u, \langle u\rangle\}$.

Example 3.2 illustrates that the converse of $(i), (ii)$ of Proposition 3.11 is generally incorrect. Additionally, it emphasizes the necessity of a symmetric relation in condition $(iii)$.

Proposition 3.13. $\mathcal{N}_{\sigma} = \mathcal{N}_{\langle \sigma\rangle}$ for $\sigma\in\{r, l\}$, if $\Psi$ is a reflexive and transitive relation on $\mathcal{B}$.

Proof. Let $\sigma = r$ and $\Psi$ be reflexive. Then, $\mathcal{N}_{\langle r\rangle}(\gamma)\subseteq \mathcal{N}_{r}(\gamma)$ for each $\gamma$. Conversely, let $\alpha\in \mathcal{N}_{r}(\gamma)$; that is, $\gamma\Psi \alpha$. Now, for each $\beta\in\mathcal{B}$ with $\gamma\in \mathcal{N}_{r}(\beta)$, we have, by the condition of transitive, $\beta\Psi \alpha$, which means that $\alpha\in \mathcal{N}_{r}(\beta)$. Thus, $\mathcal{N}_{r}(\gamma)\subseteq \mathcal{N}_{\langle r\rangle}(\gamma)$. Hence, the proof is complete. By following a similar argument, the proof of $\sigma = l$ follows. □

Corollary 3.14. $\mathcal{N}_{\sigma} = \mathcal{N}_{\langle \sigma\rangle}$ for $\sigma\in\{i, u\}$, if $\Psi$ is a reflexive and transitive relation on $\mathcal{B}.$

Proposition 3.15. $\mathbb{E}_{\sigma} = \mathbb{E}_{\langle \sigma\rangle}$ for $\sigma\in\{r, l, i, u\}$, if $\Psi$ is a reflexive and transitive relation on $\mathcal{B}$.

Proof. It immediately follows by Proposition 3.13 and Corollary 3.14. □

The next example shows that $\mathbb{E}_{\sigma}\neq\mathbb{E}_{\langle \sigma\rangle}$, $\sigma\in\{r, l, i, u\}$ despite $\Psi$ being a reflexive relation on $\mathcal{B}$.

Example 3.16. Consider $\Psi = \blacktriangle \cup \{(\delta, \alpha), (\delta, \beta), (\delta, \kappa), (\kappa, \alpha), (\kappa, \delta)\}$ is a reflexive relation on $\mathcal{B} = \{\alpha, \beta, \delta, \kappa\}$. Then,

$\mathcal{N}_r(\alpha) = \{\alpha\}$, $\mathcal{N}_r(\beta) = \{ \beta\}$, $\mathcal{N}_r(\delta) = \mathcal{B}$, $\mathcal{N}_r(\kappa) = \{\alpha, \delta, \kappa\}$.

$\mathcal{N}_l(\alpha) = \{\alpha, \delta, \kappa\}$, $\mathcal{N}_l(\beta) = \{ \beta, \delta\}$, $\mathcal{N}_l(\delta) = \{\delta, \kappa\}$, $\mathcal{N}_l(\kappa) = \{\delta, \kappa\}$.

$\mathcal{N}_{\langle r\rangle}(\alpha) = \{\alpha\}$, $\mathcal{N}_{\langle r\rangle}(\beta) = \{ \beta\}$, $\mathcal{N}_{\langle r\rangle}(\delta) = \{\alpha, \delta, \kappa\}$, $\mathcal{N}_{\langle r\rangle}(\kappa) = \{\alpha, \delta, \kappa\}$.

$\mathcal{N}_{\langle l\rangle}(\alpha) = \{\alpha, \delta, \kappa\}$, $\mathcal{N}_{\langle l\rangle}(\beta) = \{ \beta, \delta\}$, $\mathcal{N}_{\langle l\rangle}(\delta) = \{\delta\}$, $\mathcal{N}_{\langle l\rangle}(\kappa) = \{\delta, \kappa\}$.

$\mathcal{\mathbb{E}}_r(\alpha) = \{\alpha, \beta\}$, $\mathcal{\mathbb{E}}_r(\beta) = \{\alpha, \beta\}$, $\mathcal{\mathbb{E}}_r(\delta) = \{\delta\}$, $\mathcal{\mathbb{E}}_r(\kappa) = \{\kappa\}$.

$\mathcal{\mathbb{E}}_l(\alpha) = \{\alpha\}$, $\mathcal{\mathbb{E}}_l(\beta) = \{ \beta, \delta, \kappa\}$, $\mathcal{\mathbb{E}}_l(\delta) = \{ \beta, \delta, \kappa\}$, $\mathcal{\mathbb{E}}_l(\kappa) = \{ \beta, \delta, \kappa\}$.

$\mathcal{\mathbb{E}}_i(\alpha) = \{\alpha\}$, $\mathcal{\mathbb{E}}_i(\beta) = \{ \beta\}$, $\mathcal{\mathbb{E}}_i(\delta) = \{\delta\}$, $\mathcal{\mathbb{E}}_i(\kappa) = \{\kappa\}$.

$\mathcal{\mathbb{E}}_u(\alpha) = \{\alpha, \beta\}$, $\mathcal{\mathbb{E}}_u(\beta) = \mathcal{B}$, $\mathcal{\mathbb{E}}_u(\delta) = \{ \beta, \delta, \kappa\}$, $\mathcal{\mathbb{E}}_u(\kappa) = \{ \beta, \delta, \kappa\}$.

$\mathcal{\mathbb{E}}_{\langle r\rangle}(\alpha) = \{\alpha, \beta\}$, $\mathcal{\mathbb{E}}_{\langle r\rangle}(\beta) = \{\alpha, \beta\}$, $\mathcal{\mathbb{E}}_{\langle r\rangle}(\delta) = \{\delta, \kappa\}$, $\mathcal{\mathbb{E}}_{\langle r\rangle}(\kappa) = \{\delta, \kappa\}$.

$\mathcal{\mathbb{E}}_{\langle l\rangle}(\alpha) = \{\alpha\}$, $\mathcal{\mathbb{E}}_{\langle l\rangle}(\beta) = \{ \beta, \kappa\}$, $\mathcal{\mathbb{E}}_{\langle l\rangle}(\delta) = \{\delta\}$, $\mathcal{\mathbb{E}}_{\langle l\rangle}(\kappa) = \{ \beta, \kappa\}$.

$\mathcal{\mathbb{E}}_{\langle i\rangle}(\alpha) = \{\alpha\}$, $\mathcal{\mathbb{E}}_{\langle i\rangle}(\beta) = \{ \beta\}$, $\mathcal{\mathbb{E}}_{\langle i\rangle}(\delta) = \{\delta\}$, $\mathcal{\mathbb{E}}_{\langle i\rangle}(\kappa) = \{\kappa\}$.

$\mathcal{\mathbb{E}}_{\langle u\rangle}(\alpha) = \{\alpha, \beta\}$, $\mathcal{\mathbb{E}}_{\langle u\rangle}(\beta) = \{\alpha, \beta, \kappa\}$, $\mathcal{\mathbb{E}}_{\langle u\rangle}(\delta) = \{\delta, \kappa\}$, $\mathcal{\mathbb{E}}_{\langle u\rangle}(\kappa) = \{ \beta, \delta, \kappa\}$.

The following example demonstrates that $\mathbb{E}{\sigma}\neq\mathbb{E}{\langle \sigma\rangle}$, for $\sigma\in\{r, l, i, u\}$, even when $\Psi$ is a transitive relation on $\mathcal{B}$.

Example 3.17. Consider $\Psi = \{(\alpha, \alpha), (\alpha, \beta), (\alpha, \delta), (\alpha, \kappa), (\beta, \beta), (\beta, \kappa), (\delta, \delta)\}$ is a transitive relation on $\mathcal{B} = \{\alpha, \beta, \delta, \kappa\}$. So, the cardinality neighborhoods of all members of $\mathcal{B}$ will be computed in Table 2.

Proposition 3.18. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$. If $\kappa\in\mathcal{B}$, then $\mho_\sigma(\kappa)\subseteq \mathbb{E}_\sigma(\kappa)$, for each $\sigma$.

Proof. Assume that $\alpha\in \mho_\sigma(\kappa)$. Hence, $\mathcal{N}_\sigma(\kappa) = \mathcal{N}_\sigma(\alpha)$, so $|\mathcal{N}_\sigma(\kappa)| = |\mathcal{N}_\sigma(\alpha)|$, which means that $\alpha\in \mathbb{E}_\sigma(\kappa)$. □

As depicted in Table 1, it is evident that $\mho_\sigma(\kappa) = {\kappa}$ holds true for every $\sigma$. This observation highlights the failure of the converse statement in the preceding proposition.

Proposition 3.19. Assume that $\alpha\in\mathbb{E}_\sigma(\kappa)$. Hence, $\alpha\in \mho_\sigma(\kappa)$ iff $\alpha\in \mathbb{C}_\sigma(\kappa)$ iff $\alpha\in \mathbb{S}_\sigma(\kappa)$, for every $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$.

Proof. Let $\sigma = r$ and $\alpha\in\mathbb{E}_\sigma(\kappa)$. Then,

If $\alpha\in \mathbb{C}_\sigma(\kappa)$ or $\alpha\in \mathbb{S}_\sigma(\kappa)$, then $\mathcal{N}_r(\alpha)\subseteq \mathcal{N}_r(\kappa)$ or $\mathcal{N}_r(\alpha)\supseteq \mathcal{N}_r(\kappa)$. From (3.1), it follows that $\mathcal{N}_r(\alpha) = \mathcal{N}_r(\kappa)$, implying that $\alpha\in \mho(\kappa)$, as required. □

Remark 3.20. We call the reader's attention to that the preceding kinds of neighborhoods, i.e., $\mho$-neighborhoods ^[18,30], intersection neighborhoods ^[14], subset neighborhoods ^[12], and containment neighborhoods ^[8], are equivalent to their counterparts of $\sigma$-neighborhoods when the relation is equivalent. On the other hand, this characteristic is not satisfied for the current neighborhoods.

Remark 3.21. Consider a relation $\Psi$ on $\mathcal{B}$. Then, for each $\sigma$, there is no relationships between $\mathbb{E}_\sigma$-neighborhoods and $\mathcal{N}_\sigma$-neighborhoods.

4.   New kinds of rough set models founded upon $\mathbb{E}_\sigma$-neighborhoods

In this portion, novel approximations known as $\mathcal{H}_{\mathbb{E}\sigma}$-lower and $\mathcal{H}^{\mathbb{E}\sigma}$-upper approximations will be presented. These approximations will be utilized to designate new regions and accuracy criteria for any set.

Definition 4.1. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$. Based on cardinality neighborhoods, the pair $(\mathcal{H}_{\mathbb{E}\sigma}(W), \mathcal{H}^{\mathbb{E}\sigma}(W))$ represents the lower and upper approximations of a set $W$, respectively, assigned as:

Definition 4.2. The $\mathbb{E}_\sigma$-boundary, $\mathbb{E}_\sigma$-positive, and $\mathbb{E}_\sigma$-negative regions of a subset $W$ within a $\sigma$-NS $(\mathcal{B}, \Psi, \zeta_\sigma)$ are identified, respectively, as:

Further, rough sets by cardinality neighborhoods can be characterized numerically by utilizing the following two criterions:

Definition 4.3. The $\mathbb{E}_\sigma$-accuracy and $\mathbb{E}_\sigma$-roughness criteria of $W\neq \emptyset$ of a $\sigma$-NS $(\mathcal{B}, \Psi, \zeta_\sigma)$ are, respectively, endowed by:

To illustrate the computation of the defined approximations, boundary regions, and accuracy criteria for all $\sigma$, the following example will be offered.

Example 4.4. Continued from Example 3.2. Suppose $W = \{\alpha, \delta\}$ as a subset of a $\sigma$-NS $(\mathcal{B}, \Psi, \zeta_\sigma)$. Then,

(ⅰ) if $\sigma\in\{r, \langle r\rangle, i, \langle i\rangle\}$, then $\mathcal{H}_{\mathbb{E}\sigma}(W) = \{\alpha, \delta\}$, $\mathcal{H}^{\mathbb{E}\sigma}(W) = \{\alpha, \delta\}$, $\mathcal{B}_{\mathbb{E}\sigma} = \emptyset$, and $\mathbf{A}_{\mathbb{E}\sigma}(W) = 1$.

(ⅱ) if $\sigma\in\{l, u\}$, then $\mathcal{H}_{\mathbb{E}\sigma}(W) = \{\alpha\}$, $\mathcal{H}^{\mathbb{E}\sigma}(W) = \{\alpha, \delta, \kappa\}$, $\mathcal{B}_{\mathbb{E}\sigma} = \{\delta, \kappa\}$, and $\mathbf{A}_{\mathbb{E}\sigma}(W) = \frac{1}{3}$.

(ⅲ) if $\sigma\in\{\langle l\rangle, \langle u\rangle\}$, then $\mathcal{H}_{\mathbb{E}\sigma}(W) = \{\alpha\}$, $\mathcal{H}^{\mathbb{E}\sigma}(W) = \{\alpha, \beta, \delta\}$, $\mathcal{B}_{\mathbb{E}\sigma} = \{\beta, \delta\}$, and $\mathbf{A}_{\mathbb{E}\sigma}(W) = \frac{1}{3}$.

The forthcoming results will investigate which of Pawlak's properties are maintained by $\mathbb{E}_\sigma$-lower and $\mathbb{E}^\sigma$-upper approximations.

Theorem 4.5. For each $\sigma$, consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$. If $S, W\subseteq \mathcal{B}$, then the next statements hold true.

(ⅰ) $\mathcal{H}_{\mathbb{E}\sigma}(W)\subseteq W$.

(ⅱ) $\mathcal{H}_{\mathbb{E}\sigma}(\emptyset) = \emptyset$.

(ⅲ) $\mathcal{H}_{\mathbb{E}\sigma}(\mathcal{B}) = \mathcal{B}$.

(ⅳ) If $S\subseteq W$, then $\mathcal{H}_{\mathbb{E}\sigma}(S)\subseteq \mathcal{H}_{\mathbb{E}\sigma}(W)$.

(ⅴ) $\mathcal{H}_{\mathbb{E}\sigma}(S\cap W) = \mathcal{H}_{\mathbb{E}\sigma}(S)\cap \mathcal{H}_{\mathbb{E}\sigma}(W)$.

(ⅵ) $\mathcal{H}_{\mathbb{E}\sigma}(W^c) = (\mathcal{H}^{\mathbb{E}\sigma}(W))^c$.

(ⅶ) $\mathcal{H}_{\mathbb{E}\sigma}(\mathcal{H}_{\mathbb{E}\sigma}(W)) = \mathcal{H}_{\mathbb{E}\sigma}(W)$ for each $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$.

(ⅸ) $\mathcal{H}_{\mathbb{E}\sigma}(\mathcal{H}_{\mathbb{E}\sigma}(W))\subseteq \mathcal{H}_{\mathbb{E}\sigma}(W)$ for each $\sigma\in\{u, \langle u\rangle\}$.

(ⅹ) Let $z\in \mathcal{B}$. Then, $\mathcal{H}_{\mathbb{E}\sigma}(\mathcal{\mathbb{E}}_\sigma(z)) = \mathcal{\mathbb{E}}_\sigma(z)$, for each $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$.

(xi) Let $z\in \mathcal{B}$. Hence, $\mathcal{H}_{\mathbb{E}\sigma}(\mathcal{\mathbb{E}}_\sigma(z)) \subseteq \mathcal{\mathbb{E}}_\sigma(z)$, for each $\sigma\in\{u, \langle u\rangle\}$.

Proof. (ⅰ) From the fact $\alpha\in\mathbb{E}_\sigma(\alpha)$ for each $\alpha\in$$\mathcal{B}$, we obtain $\mathcal{H}_{\mathbb{E}\sigma}(W)\subseteq W$.

(ⅱ) Obvious.

(ⅲ) Given that $\alpha\in\mathbb{E}_{\sigma}(\alpha)\subseteq \mathcal{B}$ for every $\alpha\in \mathcal{B}$, it follows that $\mathcal{H}_{\mathbb{E}\sigma}(\mathcal{B}) = \mathcal{B}$.

(ⅳ) If $S\subseteq W$, then $\mathcal{H}_{\mathbb{E}\sigma}(S) = \{\alpha\in \mathcal{B}: \mathbb{E}_{\sigma}(\alpha)\subseteq S\}\subseteq\{\alpha\in \mathcal{B}: \mathbb{E}_{\sigma}(\alpha)\subseteq W\} = \mathcal{H}_{\mathbb{E}\sigma}(W)$.

(ⅴ) This can be inferred from (iv) that $\mathcal{H}_{\mathbb{E}\sigma}(S\cap W)\subseteq \mathcal{H}_{\mathbb{E}\sigma}(S)\cap \mathcal{H}_{\mathbb{E}\sigma}(W)$. Conversely, let $\alpha\in \mathcal{H}_{\mathbb{E}\sigma}(S)\cap \mathcal{H}_{\mathbb{E}\sigma}(W)$. Then, $\alpha\in \mathcal{H}_{\mathbb{E}\sigma}(S)$ and $\alpha\in \mathcal{H}_{\mathbb{E}\sigma}(W)$. This implies that $\mathbb{E}_{\sigma}(\alpha)\subseteq S$ and $\mathbb{E}_{\sigma}(\alpha)\subseteq W$. Consequently, $\mathbb{E}_{\sigma}(\alpha)\subseteq S\cap W$. Thus, $\alpha\in\mathcal{H}_{\mathbb{E}\sigma}(S\cap W)$, and so $\mathcal{H}_{\mathbb{E}\sigma}(S)\cap \mathcal{H}_{\mathbb{E}\sigma}(W)\subseteq \mathcal{H}_{\mathbb{E}\sigma}(S\cap W)$.

(ⅵ) $\alpha\in\mathcal{H}_{\mathbb{E}\sigma}(W^c)\Longleftrightarrow \mathbb{E}_{\sigma}(\alpha)\subseteq W^c$

$\quad \quad\quad \quad\quad \quad \quad \quad \quad\Longleftrightarrow \mathbb{E}_{\sigma}(\alpha)\cap W = \emptyset$

$\quad \quad\quad \quad\quad \quad \quad \quad \quad\Longleftrightarrow \alpha\not\in\mathcal{H}^{\mathbb{E}\sigma}(W)$

$\quad \quad\quad \quad\quad \quad \quad \quad \quad\Longleftrightarrow \alpha\in(\mathcal{H}^{\mathbb{E}\sigma}(W))^c$.

(ⅶ) It follows from (ⅰ) and (ⅳ) that $\mathcal{H}_{\mathbb{E}\sigma}(\mathcal{H}_{\mathbb{E}\sigma}(W))\subseteq \mathcal{H}_{\mathbb{E}\sigma}(W)$. For the other side, let $\alpha\in \mathcal{H}_{\mathbb{E}\sigma}(W)$, which implies that $\mathbb{E}_{\sigma}(\alpha)\subseteq W$. Let $\kappa\in\mathbb{E}_{\sigma}(\alpha)$, hence $|\mathbb{E}_{\sigma}(\kappa)| = |\mathbb{E}_{\sigma}(\alpha)|$, for each $\kappa\in\mathbb{E}_{\sigma}(\alpha)$. Therefore, $\mathbb{E}_{\sigma}(\kappa)\subseteq W$, for each $\kappa\in\mathbb{E}_{\sigma}(\alpha)$. Then, $\kappa\in\mathcal{H}_{\mathbb{E}\sigma}(W)$, for each $\kappa\in\mathbb{E}_{\sigma}(\alpha)$, and so $\alpha\in\mathcal{H}_{\mathbb{E}\sigma}(\mathcal{H}_{\mathbb{E}\sigma}(W))$. Consequently, $\mathcal{H}_{\mathbb{E}\sigma}(W)\subseteq$$\mathcal{H}_{\mathbb{E}\sigma}(\mathcal{H}_{\mathbb{E}\sigma}(W))$. So, $\mathcal{H}_{\mathbb{E}\sigma}(\mathcal{H}_{\mathbb{E}\sigma}(W)) = \mathcal{H}_{\mathbb{E}\sigma}(W)$.

(ⅸ) Obvious.

(ⅹ) Obvious.

(xi) Obvious.

□

Corollary 4.6. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$. Then $\mathcal{H}_{\mathbb{E}\sigma}(S)\cup \mathcal{H}_{\mathbb{E}\sigma}(W)\subseteq \mathcal{H}_{\mathbb{E}\sigma}(S\cup W)$ for any $S, W\subseteq \mathcal{B}$.

Theorem 4.7. For each $\sigma$, consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$. Let $S, W\subseteq \mathcal{B}$, then the next statements hold true.

(ⅰ) $W\subseteq \mathcal{H}^{\mathbb{E}\sigma}(W)$.

(ⅱ) $\mathcal{H}^{\mathbb{E}\sigma}(\emptyset) = \emptyset$.

(ⅲ) $\mathcal{H}^{\mathbb{E}\sigma}(\mathcal{B}) = \mathcal{B}$.

(ⅳ) If $S\subseteq W$, then $\mathcal{H}^{\mathbb{E}\sigma}(S)\subseteq \mathcal{H}^{\mathbb{E}\sigma}(W)$.

(ⅴ) $\mathcal{H}^{\mathbb{E}\sigma}(S\cup W) = \mathcal{H}^{\mathbb{E}\sigma}(S)\cup \mathcal{H}^{\mathbb{E}\sigma}(W)$.

(ⅵ) $\mathcal{H}^{\mathbb{E}\sigma}(W^c) = (\mathcal{H}_{\mathbb{E}\sigma}(W))^c$.

(ⅶ) $\mathcal{H}^{\mathbb{E}\sigma}(\mathcal{H}^{\mathbb{E}\sigma}(W)) = \mathcal{H}^{\mathbb{E}\sigma}(W)$ for each $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$.

(ⅸ) $\mathcal{H}^{\mathbb{E}\sigma}(\mathcal{H}^{\mathbb{E}\sigma}(W))\supseteq \mathcal{H}^{\mathbb{E}\sigma}(W)$ for each $\sigma\in\{u, \langle u\rangle\}$.

Proof. The proof closely resembles that of Theorem 4.5. □

Corollary 4.8. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$. Then, $\mathcal{H}^{\mathbb{E}\sigma}(S\cap W)\subseteq\mathcal{H}^{\mathbb{E}\sigma}(S)\cap \mathcal{H}^{\mathbb{E}\sigma}(W)$ for every $S, W\subseteq \mathcal{B}$.

The converses of items (ⅳ) and (ⅸ) of Theorem 4.5, as well as items (ⅳ) and (ⅸ) of Theorem 4.7 and Corollaries 4.6, 4.8, are determined to be invalid, as demonstrated by the following example.

Example 4.9. Consider a $\sigma$-NS $(\mathcal{B}, \Psi, \zeta_\sigma)$ as described in Example 3.2.

(ⅰ) Consider $S = \{\alpha, \delta\}$ and $W = \{\beta, \kappa\}$. Hence, $\mathcal{H}_{\mathbb{E}u}(S) = \{\alpha\}$ and $\mathcal{H}^{\mathbb{E}u}(W) = \{\beta, \delta, \kappa\}$, but $\mathcal{H}_{\mathbb{E}u}(\mathcal{H}_{\mathbb{E}u}(S)) = \emptyset$ and $\mathcal{H}^{\mathbb{E}u}(\mathcal{H}^{\mathbb{E}u}(W)) = \mathcal{B}$.

So, $\mathcal{H}_{\mathbb{E}u}(\mathcal{H}_{\mathbb{E}u}(W))\neq \mathcal{H}_{\mathbb{E}u}(W)$ and $\mathcal{H}^{\mathbb{E}u}(\mathcal{H}^{\mathbb{E}u}(W))\neq \mathcal{H}^{\mathbb{E}u}(W)$.

(ⅱ) Consider $S = \{\alpha\}$ and $W = \{\delta\}$. Hence, $\mathcal{H}_{\mathbb{E}u}(S\cup W) = \{\alpha\}\supset \emptyset = \mathcal{H}_{\mathbb{E}u}(S)\cup \mathcal{H}_{\mathbb{E}u}(W)$. Also, $\mathcal{H}^{\mathbb{E}u}(S\cap W) = \emptyset\subset \{\alpha, \delta\} = \mathcal{H}^{\mathbb{E}u}(S)\cap \mathcal{H}^{\mathbb{E}u}(W)$.

So, $\mathcal{H}_{\mathbb{E}\sigma}(S\cup W)\nsubseteq \mathcal{H}_{\mathbb{E}\sigma}(S)\cup \mathcal{H}_{\mathbb{E}\sigma}(W)$, and $\mathcal{H}^{\mathbb{E}\sigma}(S)\cap \mathcal{H}^{\mathbb{E}\sigma}(W) \nsubseteq \mathcal{H}^{\mathbb{E}\sigma}(S\cap W)$.

(ⅲ) Consider $S = \{\alpha, \beta\}$ and $W = \{\beta, \kappa\}$. Hence, $\mathcal{H}_{\mathbb{E}{u}}(S) = \mathcal{H}_{\mathbb{E}{u}}(W) = \{\beta\}$. Also, $\mathcal{H}^{\mathbb{E}u}(S) = \mathcal{H}^{\mathbb{E}u}(W) = \{\alpha, \delta, \kappa\}$. However, neither $S\not\subseteq W$ nor $W\not\subseteq S$.

Proposition 4.10. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$. If $W\subseteq \mathcal{B}$, then

(ⅰ) $\mathcal{H}_{\mathbb{E}u}(W)\subseteq\mathcal{H}_{\mathbb{E}r}(W)\cap \mathcal{H}_{\mathbb{E}l}(W)\subseteq \mathcal{H}_{\mathbb{E}r}(W)\cup \mathcal{H}_{\mathbb{E}l}(W)\subseteq\mathcal{H}_{\mathbb{E}i}(W)$.

(ⅱ) $\mathcal{H}^{\mathbb{E}i}(W)\subseteq\mathcal{H}^{\mathbb{E}r}(W)\cap \mathcal{H}^{\mathbb{E}l}(W)\subseteq \mathcal{H}^{\mathbb{E}r}(W)\cup \mathcal{H}^{\mathbb{E}l}(W)\subseteq \mathcal{H}^{\mathbb{E}u}(W)$.

(ⅲ) $\mathcal{H}_{\mathbb{E}\langle u\rangle}(W)\subseteq\mathcal{H}_{\mathbb{E}\langle r\rangle}(W)\cap \mathcal{H}_{\mathbb{E}\langle l\rangle}(W)\subseteq \mathcal{H}_{\mathbb{E}\langle r\rangle}(W)\cup \mathcal{H}_{\mathbb{E}\langle l\rangle}(W)\subseteq\mathcal{H}_{\mathbb{E}\langle i\rangle}(W)$.

(ⅳ) $\mathcal{H}^{\mathbb{E}\langle i\rangle}(W)\subseteq\mathcal{H}^{\mathbb{E}\langle r\rangle}(W)\cap \mathcal{H}^{\mathbb{E}\langle l\rangle}(W)\subseteq \mathcal{H}^{\mathbb{E}\langle r\rangle}(W)\cup \mathcal{H}^{\mathbb{E}\langle l\rangle}(W)\subseteq \mathcal{H}^{\mathbb{E}\langle u\rangle}(W)$.

Proof. Following from Proposition 3.11 and Definition 4.1. □

Corollary 4.11. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-$NS$. If $W\subseteq \mathcal{B}$, then

(ⅰ) $\mathbf{A}_{\mathbb{E}u}(W)\leq \mathbf{A}_{\mathbb{E}r}(W)\leq \mathbf{A}_{\mathbb{E}i}(W)$.

(ⅱ) $\mathbf{A}_{\mathbb{E}u}(W)\leq \mathbf{A}_{\mathbb{E}l}(W)\leq \mathbf{A}_{\mathbb{E}i}(W)$.

(ⅲ) $\mathbf{A}_{\mathbb{E}\langle u\rangle}(W)\leq \mathbf{A}_{\mathbb{E}\langle r\rangle}(W)\leq \mathbf{A}_{\mathbb{E}\langle i\rangle}(W)$.

(ⅳ) $\mathbf{A}_{\mathbb{E}\langle u\rangle}(W)\leq \mathbf{A}_{\mathbb{E}\langle l\rangle}(W)\leq \mathbf{A}_{\mathbb{E}\langle i\rangle}(W)$.

Proof. Only result (ⅰ) will be demonstrated, and the remaining results can be proven using a similar approach. Since $\mathcal{H}_{\mathbb{E}u}(W)\subseteq\mathcal{H}_{\mathbb{E}r}(W)\subseteq \mathcal{H}_{\mathbb{E}i}(W)$,

Considering $\mathcal{H}^{\mathbb{E}i}(W)\subseteq\mathcal{H}^{\mathbb{E}r}(W)\subseteq \mathcal{H}^{\mathbb{E}u}(W)$, $\mid\mathcal{H}^{\mathbb{E}i}(W)\mid\leq \mid\mathcal{H}^{\mathbb{E}r}(W)\mid\leq \mid\mathcal{H}^{\mathbb{E}u}(W)\mid$. Given the assumption that $W$ is nonempty, it follows that $\mid\mathcal{H}^{\mathbb{E}\sigma}(W)\mid > 0$ for all $\sigma$. Therefore,

In view of (4.1) and (4.2),

Thus, the desired results are attained. □

To demonstrate the failure of the converse aspect of Proposition 4.10 and Corollary 4.11, we compute the approximation operators and accuracy criteria for all subsets utilizing the data provided in Example 3.2. The results are presented in Tables 3 and 4.

Remark 4.12. It is worth noting that if $(\mathcal{B}, \Psi_{1}, \zeta_\sigma)$, $(\mathcal{B}, \Psi_{2}, \zeta_\sigma)$ are $\sigma$-$NS$ with $\Psi_{1}\subseteq\Psi_{2}$, then the concepts of $\mathbb{E}_1\sigma(\kappa)$ and $\mathbb{E}_2\sigma(\kappa)$ are independent of each other for some $\kappa\in\mathcal{B}$ and each $\sigma$, that is, the cardinality neighborhoods lose the property of monotonicity.

The following two propositions are obvious and, hence, their proofs are omitted.

Proposition 4.13. If $W$ is a nonempty subset of $\mathcal{B}$, $0\leq\mathbf{A}_{\mathbb{E}\sigma}(W)\leq 1$ for any $\sigma$.

Proposition 4.14. $\mathbf{A}_{\mathbb{E}\sigma}(\mathcal{B}) = 1$ for each $\sigma$-NS $(\mathcal{B}, \Psi, \zeta_\sigma)$.

We call a subset $W$ $\mathbb{E\sigma}$-exact if $\mathbf{A}_{\mathbb{E}\sigma}(W) = 1$. Otherwise, $W$ is called $\mathbb{E\sigma}$-rough.

Ultimately, Algorithm 1 is built to determine whether a set is $\mathbb{E\sigma}$-exact or $\mathbb{E\sigma}$-rough.

The next example shows how one applies Algorithm 1 to determine whether a subset is $\mathbb{E\sigma}$-exact or $\mathbb{E\sigma}$-rough in the case of $\sigma = l$.

Example 4.15. Take an $\sigma$-$NS$ $(\mathcal{B}, \Psi, \zeta_l)$ introduced in Example 3.2. To examine subsets $W_1 = \{\beta, \kappa\}$ and $W_2 = \{\delta, \kappa\}$ of $\mathcal{B}$ in terms of $\mathbb{E\sigma}$-exactness and $\mathbb{E\sigma}$-roughness, we first remark that step 1 of Algorithm 1 is given in Example 3.2. Then, we choose $\sigma = l$. The computations of $\mathcal{N}_{l}$ and $\mathbb{E}_{l}$, for each element of $\mathcal{B}$, are made in Example 3.2. Now, we calculate $\mathbb{E}l$-lower and $\mathbb{E}l$-upper approximations for subsets $W_1$ and $W_2$:

Accordingly, $\mathcal{H}_{\mathbb{E}l}(W_2) = \mathcal{H}^{\mathbb{E}l}(W_2)$, so $W_2$ is an $\mathbb{E}l$-exact subset whereas $\mathcal{H}_{\mathbb{E}l}(W_1)\neq\mathcal{H}^{\mathbb{E}l}(W_1)$, so $W_1$ is an $\mathbb{E}l$-rough subset.

5.   Topologies generated by cardinality neighborhoods

Via cardinal neighborhoods, one can originate different topologies. The next theorem will explain that.

Theorem 5.1. Let $(\mathcal{B}, \Psi, \zeta_\sigma)$ be a $\sigma$-NS. For each $\sigma$, the family $\top_{\mathbb{E\sigma}}$ = $\{W \subseteq\mathcal{B}$ : $\mathbb{E}_\sigma(\kappa)\subseteq W, \forall$ $\kappa$$\in$$W\}$ constitutes a topology on $\mathcal{B}$.

Proof. At the beginning, suppose $W_{\iota}$$\in$$\top_{\mathbb{E\sigma}}$, for each $\iota$$\in$$\Delta$. Let $\kappa$$\in$$\cup_{\iota\in\Delta}W_{\iota}$, then there is an $\iota_{0}$$\in$$\Delta$ s.t., $\kappa$$\in$$W_{\iota_{0}}$ and $\mathbb{E}_\sigma(\kappa)\subseteq W_{\iota_{0}}\subseteq\cup_{\iota\in\Delta}W_{\iota}$. Therefore, $\cup_{\iota\in\Delta}W_{\iota}$$\in$$\top_{\mathbb{E\sigma}}$.

Second, let $W_{1}, W_{2}$ be members of $\top_{\mathbb{E\sigma}}$ and $\kappa$ belongs to the intersection of $W_{1}$ and $W_{2}$. Then, $\mathbb{E}_\sigma(\kappa)\subseteq W_{1}$ and $\mathbb{E}_\sigma(\kappa)\subseteq W_{2}$. Hence, $\mathbb{E}_\sigma(\kappa)\subseteq W_{1}\cap W_{2}$. This means that $W_{1}$$\cap$$W_{2}$$\in$$\top_{\mathbb{E\sigma}}$.

Finally, it is easy to see that $\emptyset, \mathcal{B}$$\in$$\top_{\mathbb{E\sigma}}$, for each $\sigma$. Consequently, $\top_{\mathbb{E\sigma}}$ is a topology on $\mathcal{B}$. □

A subset $W$ is named a $\top_{\mathbb{E\sigma}}$-open set, if $W$$\in$$\top_{\mathbb{E\sigma}}$, and its complement is named a $\bot_{\mathbb{E\sigma}}$-closed set, where $\bot_{\mathbb{E\sigma}} = \{F : F^{c} \in \top_{\mathbb{E\sigma}}\}$.

Example 5.2. Continuing from Example 3.2.

$\top_{\mathcal{N}r} = \{\emptyset, \mathcal{B}, \{\kappa\}, \{\delta, \kappa\}, \{ \beta, \delta, \kappa\} \}$.

$\top_{\mathcal{N}l} = \{\emptyset, \mathcal{B}, \{\alpha\}, \{\alpha, \beta\}, \{\alpha, \beta, \delta\} \}$.

$\top_{\mathcal{N}\langle r\rangle} = \{\emptyset, \mathcal{B}, \{\alpha\}, \{ \beta\}, \{\kappa\}, \{ \beta, \kappa\}, \{\alpha, \kappa\}, \{\alpha, \beta\}, \{ \beta, \delta\}, \{\alpha, \beta, \delta\}, \{\alpha, \beta, \kappa\}, \{ \beta, \delta, \kappa\} \}$.

$\top_{\mathcal{N}\langle l\rangle} = \{\emptyset, \mathcal{B}, \{\delta\}, \{ \beta\}, \{\kappa\}, \{ \beta, \kappa\}, \{\alpha, \beta\}, \{\delta, \kappa\}, \{ \beta, \delta\}, \{\alpha, \beta, \delta\}, \{\alpha, \beta, \kappa\}, \{ \beta, \delta, \kappa\} \}$.

$\top_{\mathbb{E}r} = \{\emptyset, \mathcal{B}, \{ \beta\}, \{\kappa\}, \{ \beta, \kappa\}, \{\alpha, \delta\}, \{\alpha, \beta, \delta\}, \{\alpha, \delta, \kappa\} \} = \bot_{\mathbb{E}r}$.

$\top_{\mathbb{E}l} = \{\emptyset, \mathcal{B}, \{ \beta\}, \{\alpha\}, \{\delta, \kappa\}, \{\alpha, \beta\}, \{ \beta, \delta, \kappa\}, \{\alpha, \delta, \kappa\} \} = \bot_{\mathbb{E}l}$.

$\top_{\mathbb{E}i} = 2^{\mathcal{B}} = \bot_{\mathbb{E}i}$.

$\top_{\mathbb{E}u} = \{\emptyset, \mathcal{B}, \{ \beta\}, \{\alpha, \delta, \kappa\} \} = \bot_{\mathbb{E}u}$.

$\top_{\mathbb{E}\langle r\rangle} = \{\emptyset, \mathcal{B}, \{\alpha\}, \{\delta\}, \{ \beta, \kappa\}, \{\alpha, \delta\}, \{\alpha, \beta, \kappa\}, \{ \beta, \delta, \kappa\} \} = \bot_{\mathbb{E}\langle r\rangle}$.

$\top_{\mathbb{E}\langle l\rangle} = \{\emptyset, \mathcal{B}, \{\alpha\}, \{\kappa\}, \{\alpha, \kappa\}, \{ \beta, \delta\}, \{\alpha, \beta, \delta\}, \{ \beta, \delta, \kappa\} \} = \bot_{\mathbb{E}\langle l\rangle}$.

$\top_{\mathbb{E}\langle i\rangle} = 2^{\mathcal{B}} = \bot_{\mathbb{E}\langle i\rangle}$.

$\top_{\mathbb{E}\langle u\rangle} = \{\emptyset, \mathcal{B}, \{\alpha\}, \{ \beta, \delta, \kappa\} \} = \bot_{\mathbb{E}\langle u\rangle}$.

Theorem 5.3. The following properties hold for the topologies generated by cardinality neighborhoods:

(ⅰ) $\top_{\mathbb{E}u}\subseteq\top_{\mathbb{E}r}\cap \top_{\mathbb{E}l}\subseteq \top_{\mathbb{E}r}\cup \top_{\mathbb{E}l}\subseteq\top_{\mathbb{E}i}$.

(ⅱ) $\top_{\mathbb{E}\langle u\rangle}\subseteq\top_{\mathbb{E}\langle r\rangle}\cap \top_{\mathbb{E}\langle l\rangle}\subseteq \top_{\mathbb{E}\langle r\rangle}\cup \top_{\mathbb{E}\langle l\rangle}\subseteq\top_{\mathbb{E}\langle i\rangle}$.

Proof. Obvious, by using Proposition 3.11. □

Example 5.2 displays that $\top_{\mathbb{E}i}\neq\top_{\mathbb{E}r}$, $\top_{\mathbb{E}i}\neq\top_{\mathbb{E}l}$, $\top_{\mathbb{E}u}\neq\top_{\mathbb{E}r}$, $\top_{\mathbb{E}u}\neq\top_{\mathbb{E}l}$, and $\top_{\mathbb{E}i}\neq\top_{\mathbb{E}u}$.

$\top_{\mathbb{E}\langle i\rangle}\neq\top_{\mathbb{E}\langle r\rangle}$, $\top_{\mathbb{E}\langle i\rangle}\neq\top_{\mathbb{E}\langle l\rangle}$, $\top_{\mathbb{E}\langle u\rangle}\neq\top_{\mathbb{E}\langle r\rangle}$, $\top_{\mathbb{E}\langle u\rangle}\neq\top_{\mathbb{E}\langle l\rangle}$, and $\top_{\mathbb{E}\langle i\rangle}\neq\top_{\mathbb{E}\langle u\rangle}$.

Definition 5.4. Let $\top_{\mathbb{E\sigma}}$ denote the topology generated by cardinality neighborhoods. The lower and upper approximations, as well as the accuracy criteria, of any set $W$ in $\mathcal{B}$, are endowed by: $\underline{\mathbf{T\sigma}}(W) = int_{\mathbb{E\sigma}}(W)$, $\overline{\mathbf{T\sigma}}(W) = cl_{\mathbb{E\sigma}}(W)$, and $\mathbf{A}_{\mathbf{T\sigma}}(W) = \frac{\mid\underline{\mathbf{T\sigma}}(W) \mid}{\mid\overline{\mathbf{T\sigma}}(W)\mid}$, $\mid\overline{\mathbf{T\sigma}}(W)\mid\neq 0$.

It is clear that $0 \leq \mathbf{A}_{\mathbf{T\sigma}} \leq 1$. If $\mathbf{A}_{\mathbf{T\sigma}}(W) = 1$, hence $W$ is referred to as an $\mathbb{E\sigma}$-exact set. Elsewise, $W$ is termed an $\mathbb{E\sigma}$-rough set.

Referring to Definition 5.4, one can prove the following results utilizing the characteristics of interior and closure topological operators. It is worth noting that some properties that are missing for $\mathcal{H}_{\mathbb{E}\sigma}$-approximation and $\mathcal{H}^{\mathbb{E}\sigma}$-approximation are still valid for the $\underline{\mathbf{T\sigma}}$-approximation and $\overline{\mathbf{T\sigma}}$-approximation, such as item (ix) of Theorems 4.5 and 4.7.

Theorem 5.5. For each $\sigma$, consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-NS. If $S, W\subseteq \mathcal{B}$, then the next statements are valid:

(ⅰ) $\underline{\mathbf{T\sigma}}(W)\subseteq W$.

(ⅱ) $\underline{\mathbf{T\sigma}}(\emptyset) = \emptyset$.

(ⅲ) $\underline{\mathbf{T\sigma}}(\mathcal{B}) = \mathcal{B}$.

(ⅳ) If $S\subseteq W$, then $\underline{\mathbf{T\sigma}}(S)\subseteq \underline{\mathbf{T\sigma}}(W)$.

(ⅴ) $\underline{\mathbf{T\sigma}}(S\cap W) = \underline{\mathbf{T\sigma}}(S)\cap \underline{\mathbf{T\sigma}}(W)$.

(ⅵ) $\underline{\mathbf{T\sigma}}(W^c) = (\overline{\mathbf{T\sigma}}(W))^c$.

(ⅶ) $\underline{\mathbf{T\sigma}}(\underline{\mathbf{T\sigma}}(W)) = \underline{\mathbf{T\sigma}}(W)$ for each $\sigma$.

Corollary 5.6. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-NS. Then, $\underline{\mathbf{T\sigma}}(S)\cup \underline{\mathbf{T\sigma}}(W)\subseteq \underline{\mathbf{T\sigma}}(S\cup W)$ for any $S, W\subseteq \mathcal{B}$.

Theorem 5.7. For each $\sigma$, consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-NS. If $S, W\subseteq \mathcal{B}$, then the next statements are valid:

(ⅰ) $W\subseteq \overline{\mathbf{T\sigma}}(W)$.

(ⅱ) $\overline{\mathbf{T\sigma}}(\emptyset) = \emptyset$.

(ⅲ) $\overline{\mathbf{T\sigma}}(\mathcal{B}) = \mathcal{B}$.

(ⅳ) If $S\subseteq W$, then $\overline{\mathbf{T\sigma}}(S)\subseteq \overline{\mathbf{T\sigma}}(W)$.

(ⅴ) $\overline{\mathbf{T\sigma}}(S\cup W) = \overline{\mathbf{T\sigma}}(S)\cup \overline{\mathbf{T\sigma}}(W)$.

(ⅵ) $\overline{\mathbf{T\sigma}}(W^c) = (\underline{\mathbf{T\sigma}}(W))^c$.

(ⅶ) $\overline{\mathbf{T\sigma}}(\overline{\mathbf{T\sigma}}(W)) = \overline{\mathbf{T\sigma}}(W)$ for each $\sigma$.

Corollary 5.8. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-NS. Then, $\overline{\mathbf{T\sigma}}(S\cap W)\subseteq\overline{\mathbf{T\sigma}}(S)\cap \overline{\mathbf{T\sigma}}(W)$ for any $S, W\subseteq \mathcal{B}$.

Proposition 5.9. If $W$ is a nonempty subset of $\mathcal{B}$, $0\leq\mathbf{A}_{\mathbf{T}\sigma}(W)\leq 1$ for any $\sigma$.

Proposition 5.10. For each $\sigma$-NS $(\mathcal{B}, \Psi, \zeta_\sigma)$, $\mathbf{A}_{\mathbf{T}\sigma}(\mathcal{B}) = 1$.

Proposition 5.11. Consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-NS. If $W\subseteq \mathcal{B}$, then

(ⅰ) $\underline{\mathbf{Tu}}(W)\subseteq\underline{\mathbf{Tr}}(W)\cap \underline{\mathbf{Tl}}(W)\subseteq \underline{\mathbf{Tr}}(W)\cup \underline{\mathbf{Tl}}(W)\subseteq \underline{\mathbf{Ti}}(W)$.

(ⅱ) $\overline{\mathbf{Ti}}(W)\subseteq \overline{\mathbf{Tr}}(W)\cap \overline{\mathbf{Tl}}(W)\subseteq \overline{\mathbf{Tr}}(W)\cup \overline{\mathbf{Tl}}(W)\subseteq \overline{\mathbf{Tu}}(W)$.

(ⅲ) $\underline{\mathbf{T\langle u\rangle}}(W)\subseteq \underline{\mathbf{T\langle r\rangle}}(W)\cap \underline{\mathbf{T\langle l\rangle}}\subseteq \underline{\mathbf{T\langle r\rangle}}(W)\cup \underline{\mathbf{T\langle l\rangle}}(W)\subseteq\underline{\mathbf{T\langle i\rangle}}(W)$.

(ⅳ) $\overline{\mathbf{T\langle i\rangle}}(W)\subseteq\overline{\mathbf{T\langle r\rangle}}(W)\cap \overline{\mathbf{T\langle l\rangle}}(W)\subseteq \overline{\mathbf{T\langle r\rangle}}(W)\cup \overline{\mathbf{T\langle l\rangle}}(W)\subseteq \overline{\mathbf{T\langle u\rangle}}(W)$.

Corollary 5.12. Let $(\mathcal{B}, \Psi, \zeta_\sigma)$ be a $\sigma$-NS. If $W$ is a nonempty subset of $\mathcal{B}$, then

(ⅰ) $\mathbf{A}_{\mathbf{T}u}(W)\leq \mathbf{A}_{\mathbf{T}r}(W)\leq \mathbf{A}_{\mathbf{T}i}(W)$.

(ⅱ) $\mathbf{A}_{\mathbf{T}u}(W)\leq \mathbf{A}_{\mathbf{T}l}(W)\leq \mathbf{A}_{\mathbf{T}i}(W)$.

(ⅲ) $\mathbf{A}_{\mathbf{T}\langle u\rangle}(W)\leq \mathbf{A}_{\mathbf{T}\langle r\rangle}(W)\leq \mathbf{A}_{\mathbf{T}\langle i\rangle}(W)$.

(ⅳ) $\mathbf{A}_{\mathbf{T}\langle u\rangle}(W)\leq \mathbf{A}_{\mathbf{T}\langle l\rangle}(W)\leq \mathbf{A}_{\mathbf{T}\langle i\rangle}(W)$.

Now, we will compare the approximations and accuracy criteria presented here based on topological structures with their analogues introduced in the preceding section. To facilitate this comparison, we begin by the following lemma.

Lemma 5.13. Let $(\mathcal{B}, \Psi, \zeta_\sigma)$ be a $\sigma$-NS. Then, $\mathcal{\mathbb{E}}_\sigma(\kappa)$ is a member of $\top_{\mathbb{E\sigma}}$ for all $\kappa\in \mathcal{B}$ and $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$.

Proof. Let $\alpha\in \mathcal{\mathbb{E}}_\sigma(\kappa)$ and $\sigma$ be as given. Then, by Corollary 3.8, we have $\mathcal{\mathbb{E}}_\sigma(\alpha) = \mathcal{\mathbb{E}}_\sigma(\kappa)$. This means, according to Definition 5.1, that $\mathcal{\mathbb{E}}_\sigma(\kappa)\in\top_{\mathbb{E\sigma}}$, as required. □

Proposition 5.14. For $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$, consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-NS. If $W\subseteq \mathcal{B}$, then

(ⅰ) $\underline{\mathbf{T\sigma}}(W) = \mathcal{H}_{\mathbb{E}\sigma}(W)$, and

(ⅱ) $\overline{\mathbf{T\sigma}}(W) = \mathcal{H}^{\mathbb{E}\sigma}(W)$.

Proof. To prove (ⅰ), let $\alpha\in \underline{\mathbf{T\sigma}}(W)$. There exists a subset $V\in \top_\sigma$ such that $\alpha\in V\subseteq W$. This implies that $\alpha\in \mathcal{\mathbb{E}}_\sigma(\alpha)\subseteq V\subseteq W$. Thus, $\alpha\in \mathcal{H}_{\mathbb{E}\sigma}(W)$; hence, $\underline{\mathbf{T\sigma}}(W)\subseteq \mathcal{H}_{\mathbb{E}\sigma}(W)$. Conversely, let $\alpha\in \mathcal{H}_{\mathbb{E}\sigma}(W)$. Then, $\alpha\in \mathcal{\mathbb{E}}_\sigma(\alpha)\subseteq W$. By Lemma 5.13, $\mathcal{\mathbb{E}}_\sigma(\alpha)\in \top_\sigma$, so $\alpha\in \mathcal{\mathbb{E}}_\sigma(\alpha)\subseteq int_{\mathbb{E\sigma}}(W) = \underline{\mathbf{T\sigma}}(W)$. Thus, $\mathcal{H}_{\mathbb{E}\sigma}(W)\subseteq \underline{\mathbf{T\sigma}}(W)$. Thus, the proof is concluded.

Using a similar approach, one can establish (ⅱ). □

Corollary 5.15. For $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$, consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-NS. If $W\subseteq \mathcal{B}$, then

Based on the aforementioned results, it is evident that the topological approximations and measures coincide with their counterparts introduced in the preceding section for $\sigma\in{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle}$. However, differences arise for $\sigma\in{u, \langle u\rangle}$, as elucidated in the subsequent results and examples.

Proposition 5.16. For $\sigma\in\{u, \langle u\rangle\}$, consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-NS. If $W\subseteq \mathcal{B}$, then

(ⅰ) $\underline{\mathbf{T\sigma}}(W)\subseteq \mathcal{H}_{\mathbb{E}\sigma}(W)$, and

(ⅱ) $\mathcal{H}^{\mathbb{E}\sigma}(W)\subseteq \overline{\mathbf{T\sigma}}(W)$.

Proof. (ⅰ) Similar to the proof of necessary part of (ⅰ) of Proposition 5.14.

(ⅱ) Suppose $\alpha\not\in \overline{\mathbf{T\sigma}}(W)$. Then, there is a subset $S\in \top_\sigma$ containing $\alpha$ s.t. $S\cap W = \emptyset$. Since $\alpha\in \mathcal{\mathbb{E}}\sigma(\alpha)\subseteq S$, it follows that $\mathcal{\mathbb{E}}\sigma(\alpha)\cap W = \emptyset$. Consequently, $\alpha\not\in \mathcal{H}^{\mathbb{E}\sigma}(W)$, thus establishing the desired result. □

Corollary 5.17. For $\sigma\in\{u, \langle u\rangle\}$, consider $(\mathcal{B}, \Psi, \zeta_\sigma)$ as a $\sigma$-NS. If $W\subseteq \mathcal{B}$, then

The converse of Proposition 5.16 and Corollary 5.17 may not hold true, as demonstrated in the following counterexample

Example 5.18. Continuing from Examples 3.2 and 5.2, consider $W = \{\beta, \delta, \kappa\}$ and $S = \{\alpha, \kappa\}$. The following observations can be made

(ⅰ) $\underline{\mathbf{Tu}}(W) = \{\beta\}$, $\overline{\mathbf{Tu}}(W) = \mathcal{B}$ and $\mathbf{A}_{\mathbf{T}u}(W) = \frac{1}{4}$ whereas $\mathcal{H}_{\mathbb{E}u}(W) = \{\beta, \kappa\}$, $\mathcal{H}^{\mathbb{E}u}(W) = \mathcal{B}$, and $\mathbf{A}_{\mathbb{E}u}(W) = \frac{1}{2}$.

(ⅱ) $\underline{\mathbf{T\langle u\rangle}}(S) = \{\alpha\}$, $\overline{\mathbf{T\langle u\rangle}}(S) = \mathcal{B}$ and $\mathbf{A}_{\mathbf{T}\langle u\rangle}(S) = \frac{1}{4}$ whereas $\mathcal{H}_{\mathbb{E}\langle u\rangle}(S) = \{\alpha\}$, $\mathcal{H}^{\mathbb{E}\langle u\rangle}(S) = \{\alpha, \beta, \kappa\}$, and $\mathbf{A}_{\mathbb{E}\langle u\rangle}(S) = \frac{1}{3}$.

6.   Practical example

Here, we provide a practical example of how we can apply the present neighborhoods to describe a real situation and extract its unapparent information. Let $X = \{a_1, a_2, a_3, a_4, a_5, a_6\}$ be a set of authors who authored some books or participate in the authority of them; and let the set of books be $Y = \{b_1, b_2, b_3, b_4, b_5, b_6, b_7, b_8, b_9\}$. In Table 5, we associate each author with the books who authored them or participated in their authority using the mapping $F$ of $X$ into the power set of $Y$ defined by $F(a) =$ the books authored by the author "a" partially or completely.

Now, we determine the relation between the authors by the following formula:

Accordingly, we have $\Psi = \{(a_1, a_1), (a_2, a_2), (a_3, a_3)$, $(a_4, a_4), (a_5, a_5), (a_6, a_6)$, $(a_7, a_7), (a_1, a_3)$, $(a_1, a_7)$, $(a_7, a_1)$, $(a_4, a_2), (a_6, a_5), (a_7, a_3)\}$. It is evident that $\Psi$ is reflexive and transitive, so by Proposition 3.15, $\mathbb{E}_{\sigma} = \mathbb{E}_{\langle \sigma\rangle}$ for $\sigma\in\{r, l, i, u\}$. But it is not symmetry, so we cannot utilize the traditional rough set model to deal with this system. In Table 6, we build the systems of $\mathcal{N}_\sigma$-neighborhoods and $\mathbb{E}_\sigma$-neighborhoods of each element in $X$.

Take subsets $W = \{a_1, a_2, a_3, a_7\}$ and $V = \{a_1, a_2, a_3, a_5\}$ of $X$. Then, the information that can be extracted from this subset is outlined in the following:

● In cases of $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$, the approximations and accuracy criteria computed with respect to both rough set models of Sections 4 and 5 are identified as we proved in Proposition 5.14 and Corollary 5.15. For the sake of brevity, we compute them for $\sigma = r$:

(ⅰ) $\underline{\mathbf{Tr}}(W) = \mathcal{H}_{\mathbb{E}r}(W) = \{a_1, a_7\}$.

(ⅱ) $\overline{\mathbf{Tr}}(W) = \mathcal{H}^{\mathbb{E}r}(W) = X\setminus \{a_4, a_6\}$.

(ⅲ) $\mathbf{A}_{\mathbf{T}r}(W) = \mathbf{A}_{\mathbb{E}r}(W) = \frac{2}{5}$.

● In cases of $\sigma = u$, the approximations and accuracy computed with respect to both rough set models of Sections 4 and 5 are, respectively, calculated in the following:

(ⅰ) $\underline{\mathbf{Tu}}(V) = \emptyset$, $\overline{\mathbf{Tu}}(V) = X\setminus \{a_4, a_6\}$, and $\mathbf{A}_{\mathbf{T}u}(V) = 0$.

(ⅱ) $\mathcal{H}_{\mathbb{E}u}(V) = \{a_3\}$, $\mathcal{H}^{\mathbb{E}u}(V) = X\setminus \{a_4, a_6\}$, and $\mathbf{A}_{\mathbb{E}u}(V) = \frac{1}{5}$.

It can be seen that the computations given above are in agreement with the obtained results in Proposition 5.14, Corollary 5.15, Proposition 5.16, and Corollary 5.17. That is, the lower and upper approximations and accuracy measures of subsets obtained from rough set models founded upon $\mathbb{E}_\sigma$-neighborhoods (in Section 4) are better than their topological counterparts (in Section 5) in the cases of $\sigma\in\{u, \langle u\rangle\}$. Also, these approximations and accuracy measures are equal in cases of $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$.

7.   Discussions: Strengths and limitations

In this part, we discuss, in detail, the pros and cons of the proposed rough set models.

● Strengths

(ⅰ) There is no condition on the binary relation used to establish $\mathbb{E}_\sigma$-neighborhoods and their approximation operators. In Pawlak model, it was imposed as an equivalence relation, also, some other rough neighborhoods and their paradigms were introduced under specific types of relations such as reflexive and similarity relations; see, ^[2,3,20,43].

(ⅱ) Every $\mathbb{E}_\sigma$-neighborhood presented herein is not empty for any element in the universal set, whereas some existing neighborhoods in literature are empty for some elements. This matter gives rise to deficiencies in the properties of these neighborhoods, which require some updates for the formula used to calculate the accuracy measures or impose further condition(s) of the applied relations; see, ^[22].

(ⅲ) Most characteristics of the original rough set model given in Proposition 2.3 are still valid for the present rough set models as investigated in Propositions 4.5 and 4.7.

(ⅳ) The neighborhood systems and rough set models suggested in this work provide an efficient instrument to address some real situations and they focus on the cardinality number of $\mathcal{N}_\sigma$-neighborhoods, such as those are applied in the social media or used to categorize the applicants according to the number of their qualities.

(ⅴ) The topological rough set models debated in the previous section are equivalent to their counterparts introduced in Section 4 in the cases of $\sigma\in\{r, \langle r\rangle, l, \langle l\rangle, i, \langle i\rangle\}$, which helps a wide range of users to choose the suitable methods with their expertise. That is, users with abstract backgrounds prefer to deal with the topological approach because of the ease of computing the approximation operators from their corresponding interior and closure topological operators.

● Limitations

(ⅰ) The efficiency of the present rough set models is less than the rough paradigms produced by $\mho$-neighborhoods ^[30] in terms of enlarging the upper approximation and shrinking the lower approximation.

(ⅱ) The current topological models produce less accuracy measures than their counterparts induced by $\mathbb{E}_\sigma$-neighborhoods in cases of $\sigma\in\{u, \langle u\rangle\}$.

8.   Conclusions

One of the effective methods for extracting information from incomplete systems is a rough set introduced in 1983 by Pawlak. Since its appearance, it has been developed in several ways, one of them being neighborhood systems inspired by specific or arbitrary relations.

In this manuscript, we have offered the notion of cardinality rough neighborhoods, which is utilized to originate novel kinds of generalized approximation spaces. We have searched the major properties of these neighborhoods and spaces and provided some examples to clarify their relationships among each other, as well as their connections with the preceding ones. In this regard, we have demonstrated that all $\mathbb{E}_{\sigma}$-neighborhoods are equivalent under a symmetric relation, and $\mathbb{E}_{\sigma} = \mathbb{E}_{\langle \sigma\rangle}$ for $\sigma\in\{r, l, i, u\}$ under a reflexive and transitive relation. We have proved that all characteristics of Pawlak that are given in Proposition 2.3 have been acquired for the approximations $\mathcal{H}^{\mathbb{E}\sigma}, \mathcal{H}_{\mathbb{E}\sigma}$, except properties $L8$ and $U_8$ are partially losing whenever $\sigma = u$ or $\langle u\rangle$. Also, we have discussed a topological approach to study the given paradigms and demonstrated that this approach produces approximation operators similar to the given paradigms in six cases, which helps to deal with information systems in most cases by different ways. A practical example concerning manuscripts and the authors who authored them or participated in their authorship have been given.

There are some merits of the proposed types of neighborhoods and rough paradigms such as working without the rigorous condition of an equivalence relation, overcoming the shortcomings of some previous neighborhoods concerning the way of calculating the accuracy measures, and some subsets are not contained by its lower approximation; also, we simulate the original model of Pawlak by keeping its basic properties. On the other hand, we face a limitation regarding the size of approximation operators of some subsets compared to $\mho$-neighborhoods.

In the next points, we suggest some ideas that can be researched as possible forthcoming works.

● hybridize the system of $\mathbb{E}_\sigma$-neighborhoods with ideal structures to minimize the upper approximation and maximize the lower approximation;

● investigate the characteristics of rough set models that are defined by the following types of neighborhoods.

(ⅰ) $\mathbb{E}^\star_i(\kappa) = \{o\in \mathcal{B}: |\mathcal{N}_i(\kappa)| = |\mathcal{N}_i(o)|\}$.

(ⅱ) $\mathbb{E}^\star_u(\kappa) = \{o\in \mathcal{B}: |\mathcal{N}_u(\kappa)| = |\mathcal{N}_u(o)|\}$.

(ⅴ) $\mathbb{E}^\star_{\langle i\rangle}(\kappa) = \{o\in \mathcal{B}: |\mathcal{N}_{\langle i\rangle}(\kappa)| = |\mathcal{N}_{\langle i\rangle}(o)|\}$.

(ⅵ) $\mathbb{E}^\star_{\langle u\rangle}(\kappa) = \{o\in \mathcal{B}: |\mathcal{N}_{\langle u\rangle}(\kappa)| = |\mathcal{N}_{\langle u\rangle}(o)|\}$.

It should be observed that the aforementioned neighborhoods and $\mathbb{E}_\sigma$-neighborhoods ($\sigma\in\{i, u, \langle i\rangle, \langle u\rangle\}$) are independent of each other.

● explore the notions presented herein in the frames of fuzzy and soft settings ^[26,31,41].

Author contributions

Tareq M. Al-shami: Conceptualization, Methodology, Validation, Formal analysis, Investigation, Writing-original draft, Writing-review and editing, Supervision. Rodyna A. Hosny: Validation, Formal analysis, Investigation, Writing-original draft. Abdelwaheb Mhemdi: Formal analysis, Investigation, Writing-review and editing. M. Hosny: Formal analysis, Investigation, Funding acquisition. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The fourth author extends her appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through a research groups program under grant RGP2/398/45.

Conflict of interest

The authors declare that they have no competing interest.