A study of fixed point sets based on Z-soft rough covering models

1.   Introduction

Microgrids are small-scale electrical grids that link localized loads to distributed electricity sources, contributing to increased power stability and resiliency. With the global need for energy increasing, microgrids are gaining popularity for their ability to provide reliable, efficient power ^[1,2,3]. The market share for microgrids is expected to grow due to the increasing availability of large-scale renewable power production options and the demand for a more robust and reliable energy supply. Governments are sponsoring microgrid efforts, and the market share for grid-connected connections is expected to grow the most in the coming year. The market share for microgrids is expected to grow due to their efficiency, cost-effectiveness, and potential for growth ^[4].

Parallel to this growth, the inclusion of microgrids into traditional power grids is gaining traction. Microgrids are essential for widely incorporating distributed energy sources (DES) into the current utility power grid ^[5]. Microgrids, on the other hand, provide both alternating current (AC) and direct current (DC) power through independent power connections. Another variable is the rate at which distinct species become dominant ^[6]. The interface between microgrids is where coupling occurs. To ensure reliable operation, each system's protective mechanisms are customized based on a distinct set of characteristics and guiding principles ^[7]. Voltage, frequency, and power quality are monitored and managed by sophisticated control systems and techniques. Therefore, AC/DC and DC/AC converters are essential electrical system components ^[8]. Microgrids are compatible with renewable and nonrenewable distributed generation technologies, such as solar thermal, photovoltaic (PV), wind, fuel cell, and biomass. Particularly, solar and wind power generation technologies have witnessed tremendous expansion and now account for a significant fraction of many microgrids' overall energy production ^[9]. The stability, dependability, and performance of microgrids are significantly affected by the presence of a storage system. The authors of ^[10] examined some of the most significant energy storage technologies now employed in microgrids. A microgrid system's load exists in various ways (AC, DC). The classification of loads is critical from an operational aspect when managing a microgrid.

The global microgrid market is expected to grow significantly between 2021 and 2028, contributing to the growth of the power supply industry. Key contributors include technological breakthroughs, infrastructure upgrades, and the desire for a stable global power supply. Asia Pacific accounts for 41.3% of microgrid revenue, while North America accounts for 32.5%. The market share is expected to grow due to the need for reliable and secure electricity supply, renewable energy storage, and government efforts to reduce carbon emissions ^{[1,2,5,11,12]}.

Long-term energy management system (EMS) algorithms seek to optimize the equilibrium between total power production and demand ^[13]. Due to their emphasis on influencing current operating conditions to enhance desired characteristics, microgrid interfaces, and power converter control can benefit from short-term approaches ^[9]. A microgrid energy management technique is presented to reduce overall system costs and enhance the grid power profile. A load scheduling system that considers energy costs and customer satisfaction is provided using dependable appliance intervals. It is proposed to solve a multi-objective optimization problem for a community of residences equipped with electric vehicles, photovoltaics, air conditioners, and water heaters to increase consumer satisfaction while decreasing energy costs and the load peak-to-average ratio ^[14].

Using dependable battery management systems and accurate prediction algorithms can alleviate these restrictions. These issues can be resolved by employing optimization techniques, such as the punctual scheduling of alternative energy sources or energy storage and the more efficient dispatch of generated electricity for economic advantage ^[15].

Modern microgrids may utilize AC, DC or a hybrid alternating and direct current (HACDC) microgrid. AC microgrids utilize power electronic interfaces to directly couple AC generators, whereas DC generators such as solar panels and fuel cells require DC/AC converters to generate AC power. However, there are costs connected with these multiple modifications ^[16]. The worth of electrical power and the system's dependability are bracketed among hybrid systems' many unique and crucial characteristics. A well-considered selection of hardware allows for the most effective and dependable system architecture. Therefore, an intelligent and cost-effective HACDC microgrid system proposal must include an acceptable sizing strategy ^[17].

Microgrids can be divided into three basic kinds based on whether they employ AC, DC, or a combination. It is essential to thoroughly analyze the benefits and negatives of each option because they are all distinct ^[18]. The author ^[19] compares the control, safeguards, and power losses of each microgrid type. Obtaining power for the AC microgrid from the broader power grid is a distinct advantage. Every power source in an AC microgrid (such as a wind turbine) is connected to the AC bus via an AC/AC power converter. To link devices with DC output (such as solar panels) to the AC bus, DC/AC converters are required. To import and export electricity while keeping the system stable and reliable, an AC microgrid needs a very complicated controller. DC microgrids only link DC-output sources directly to the bus, whereas AC-output sources connect via AC/DC converters. Hence, DC microgrids offer investment and operating cost advantages over AC microgrids due to their greater system efficiency and smaller size. In a DC system, fewer power converters are required. Therefore, size and efficiency can be increased without compromising performance. However, unlike the AC system, the protection infrastructure for DC distribution must still be fully completed ^[20].

Distributed, autonomous microgrids with low/medium voltage rely primarily on renewable energy system (RES), such as solar/wind plants, batteries, and hybrid vehicles. Microgrid operators need robust controllers to adjust voltage, frequency, stability, accuracy, and perceived power effectively. Energy management for AC/DC microgrids has been investigated in depth. Management of microgrid energy was given using model predictive control ^[5]. Considering PVs and electric vehicles (EVs), an effective scheduling model for a DC microgrid with multiple purposes was devised. A decentralized power-sharing technique was developed to share the load between the AC and DC power suppliers. In a previous study, the author in ^[18] examined the difficulty of managing the DC bus voltage of a microgrid in the presence of highly variable renewable energy.

This article aims to explore and understand power grid management benefits, limitations and challenges by optimizing the power supply and demand, reducing costs, enhancing grid power profiles, integrating renewable energy sources, and improving microgrids' efficiency, reliability and sustainability. The study investigates various technologies and control systems, such as EMS, distributed energy resource management systems (DERMS), internet of things (IoT), big data analytics, blockchain technology, artificial intelligence (AI), digital twin technology, cloud computing, and augmented reality (AR), to enhance the performance of microgrids. The studies also focus on different microgrids, including AC/DC microgrids, and their advantages and disadvantages. Overall, the research aims to contribute to the understanding, developing, and implementation of microgrids in the power supply industry.

However, the contribution spans various topics, highlighting the need for more studies of AC/DC microgrid energy management systems. Second, it highlights the value of thoroughly analyzing the current microgrid energy management systems and optimization methodologies. It also highlights the significance of AC/DC power grid management and optimization and incorporating various digital technologies into microgrids. Finally, the article recognizes the value of researching and assessing new programming methods for microgrid energy management systems. These contributions are made to fill a knowledge gap, enhance the effectiveness, dependability, and cost-effectiveness of microgrid systems, and offer helpful viewpoints and approaches to their efficient deployment and management.

This paper presents a unified EMS model for AC/DC microgrids, addressing protection, control mechanisms, reactive power compensation, and frequency regulation. The study focuses on the application of EMS in intelligent microgrids, highlighting significant advancements in managing electrical energy generation, transmission, and distribution. It proposes a load scheduling strategy that considers energy cost and satisfaction function and a multi-objective optimization problem that considers preferences, energy costs, and peak-to-average load ratio. EMS suppliers are essential for designing, developing, installing, and maintaining EMS in electric power conversion (ECC), with features such as network model construction, security analysis, autonomous generation control, and dispatch. The transition from analog to digital infrastructure is also discussed, highlighting the complexity of the electric grid and its impact on the next generation of power systems.

This paper will adhere to the following outline. Section two describes power management in a microgrid. In section three, the digitalization of microgrids is presented, and in section four, the AC/DC power grid management system. Section five contains the strategic microgrid energy management system, and finally, section six concludes the study overview.

2.   Power management in a microgrid

The EMS plays a significant role in smart microgrid control, as long-term energy management algorithms seek to match total power supply to demand optimally ^[21]. Controlling voltage, current, power, and frequency in the present is the primary objective of solutions for short-term power management. A microgrid energy management technique is presented to reduce overall system costs and enhance the grid power profile ^[22].

For communities with EVs, PV, and heating, ventilating, and air conditioning (HVAC), an optimization problem with multiple objectives can be provided, such as maximizing customer satisfaction while minimizing energy costs and load the peak-to-average ratio. Using an evolutionary method based on Pareto tribes, the solution set is established ^[23]. Unpredictability and instability induced by renewable energy production's intermittent or unpredicted nature are the primary obstacles to RES incorporation into smart networks. Using dependable battery management systems and accurate prediction algorithms can alleviate these restrictions. Optimization methods include improved scheduling of alternative energy sources or storage and a more efficient distribution of generated electricity for optimum economic benefit ^[24]. Energy management is distinguished among the numerous overused idioms in electrical engineering. Considering there are now so many distinct energy management strategies and optimization approaches, it was determined that a comprehensive evaluation of the available possibilities was required ^[25].

Microgrids can attach to the main utility grid or operate independently. Microgrids can incorporate renewable energy sources, such as solar panels or wind turbines, to provide more reliable, localized fallback power. Microgrid loads may be variable or constant depending on whether or not the distributed generations (DGs) can be dispatched. The microgrid can enter islanding mode and become disconnected from the larger grid by toggling the point of common coupling (PCC) switch. Microgrids provide essential grid services to consumers and utilities, such as power supply stabilization, reduction of carbon emissions, economic expansion, and energy efficiency enhancement. A microgrid consists primarily of DG, DS, and a PCC. In the past five years, microgrid research has expanded significantly ^[26,27,28].

The three most common varieties are AC, DC, and hybrid microgrids. Equipment for AC microgrids operates following specified voltage and frequency parameters. DC microgrids, hybrid configurations that combine AC and DC systems, offer integration, synchronization, voltage transformation, economic viability, protection, and dependability ^[29]. Virtual microgrids offer the most benefits to multiple energy consumers. Microgrids provide the military with safe and dependable power. At the core of industrial microgrids are energy-efficiency measures. Microgrids that power single-family residences are an environmentally friendly and cost-effective option for remote areas. Multiple microgrids can communicate via a network. Although integration problems involve numerous factors and constraints, delays and voltage fluctuations can be mitigated using variable renewable sources ^[30].

Processing, gas extraction, gas purification, and pre-treatment are just a few obstacles to biomass power generation. The biomass-producing region is typically far from the electricity-generating facilities, reducing energy supply costs. The ability of biomass to absorb and discharge water influences biomass's energy production ^[31,32]. Complex control methods are required to ensure microgrids' safe operation and productive interconnection. They require a dependable communication system and access to numerous DG. Control systems for microgrids evaluate dispatchable quantities and resources. The following obstacles must be overcome: Bidirectional power flows, stability concerns, modeling, minimal inertia, and uncertainty. The primary objectives of the control architecture are line voltage control, frequency regulation, repair cost minimization, and microgrid and grid integration optimization ^[33,34].

The decentralized control of microgrids emphasized peer-to-peer techniques through a hierarchical structure and autonomously operating local controllers. This method enables the connection of multiple distributed generation units (DGUs) to the microgrid without modifying the controller's parameters. In a hierarchical structure, there are three levels of control: Primary, secondary and tertiary. Primary control regulates voltage and frequency, while secondary control collects data on microgrid management from DG devices ^[35,36]. Information sent from the tertiary control level to the secondary control level is used to administer the microgrid's subsystems and its basic control level. Two or more microgrids can share electricity through conventional coupling in a networked microgrid. They are complex systems that can be managed either centrally or decentrally. Solar photovoltaic power microgrids require accurate modeling of PV arrays, a boost converter with maximum power point tracker capabilities, accurate modeling of DC-link capacitors and inductor-capacitor-inductor (LCL) filter design ^[37,38].

Photovoltaic systems need controllers to regulate the microgrid's voltage, current, and power distribution. Linear or nonlinear controller systems can be used with direct and nonlinear controllers for inverter control. Wind energy is generated in windswept regions by wind turbines, and a solution integrating two distinct energy storage technologies was investigated to reduce costs and maximized output ^[27]. Batteries, flywheels, supercapacitors and supermagnetic energy storage are significant energy storage technologies. Three primary energy storage system configurations are utilized in island mode: Aggregated, distributed and hybrid. Active and reactive power (PQ) control, voltage and frequency (V/f) control and droop control are three distinct techniques for regulating ESSs. Microgrid operators must choose the most suitable ESS for accomplishing microgrid stability and ongoing management, operation and maintenance. If they are to be successful in the future, microgrids will need to adapt to new technologies and continue to develop ^[28,39].

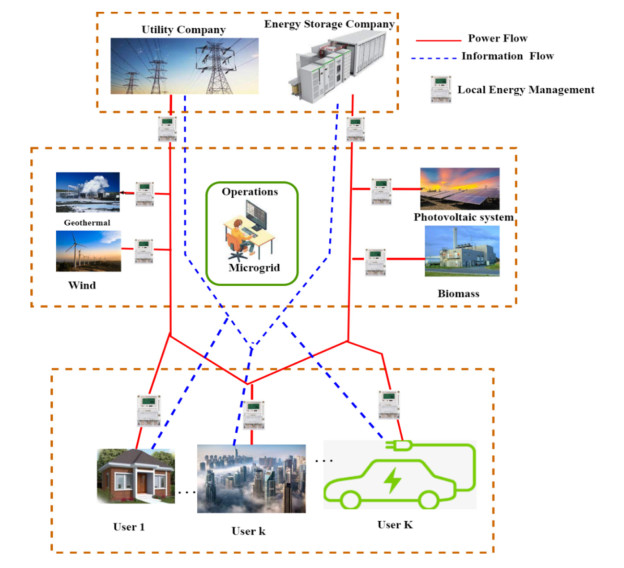
Figure 1 depicts a simplified notion of a microgrid with multiple renewable energy generators, loads, and EMSs ^{[40,41,42,43]}. This article examines how several optimization solutions have been employed to resolve microgrids EMS problem. Understanding microgrid models and the optimization strategy used by the EMS in microgrids is one of the most significant contributions of the review noted in this overview study. The intended goal of the EMS scheme, the citation score, the power mode, the operational mode, and the type of supervisory control were all considered in a thorough examination ^[44,45,46]. In this summary, this article classifies the objectives of the EMS scheme as anticipatory, economic/environmental, unit commitment, or demand management. The objective of a unit commitment is to allow energy providers to collaborate toward a common objective and in this case, it is satisfying demand at a lower cost and enhancing income returns, even if fossil fuel-based producing sources are also utilized. Demand management's major objective is to boost profitability through improved scheduling of loads and consumption patterns ^[7,8,47,48].

Figure 1 depicts the utility business, the energy storage company, the consumers, and the numerous renewable energy sources that comprise a typical microgrid energy management system. This study refers to the conventional energy generator as the utility and the renewable energy storage provider as the storage provider without limiting the system's applicability. The utility company and the storage firm are considered energy suppliers to supply the microgrid's electric power demand and ensure power system stability. To implement efficient energy management, the microgrid should be responsible for energy dispatch and satisfying customers' electricity demands based on renewable energy generation forecasts. Due to the unpredictability, fluctuation, and intermittent nature of renewables, the microgrid may need help to meet the electrical demand of consumers. It may have to purchase electricity from utility and storage companies.

Microgrid is a novel tool that enhances the efficiency of power systems by enhancing dependability, resiliency and power quality. It aids in designing, developing, and controlling microgrids optimizing their performance. Applications include health monitoring, forecasting, fault detection, control management, decision-making, and cybersecurity. Health monitoring captures system degradation, performance and aging data, while forecasting helps maintain the supply-demand balance. Microgrid also aids in fault detection, reducing system response time and associated implications. Its use in electricity networks ensures reliable and secure operation ^[33,49].

Microgrids are a key component in improving the reliability and resilience of the energy system. They distribute energy generation and storage across multiple sources, reducing the risk of a single point of failure. This is particularly useful in critical infrastructure facilities like hospitals and military bases ^[26,50]. Microgrids can operate in "island mode" during emergencies or when disconnected from the main grid, ensuring uninterrupted power supply. Islanding allows microgrids to operate autonomously, optimizing energy management based on local demand, renewable energy generation, and storage capacity. This flexibility reduces reliance on fossil fuels and promotes a more resilient energy infrastructure. Microgrids also enable a rapid response to changes in demand and supply conditions, ensuring redundancy and minimizing the risk of cascading failures. These features make microgrids ideal for critical infrastructure, remote areas, and environments prone to disruptions, ensuring a reliable and robust energy supply ^[51,52].

Microgrids offer numerous cost savings and economic benefits, making them an attractive energy solution for businesses, communities, and governments. They enable energy efficiency by generating electricity locally and avoiding transmission and distribution losses associated with long-distance power delivery in centralized grids. Microgrids can leverage RESs like solar and wind, which have lower operating and fuel costs than conventional fossil-fuel-based generations ^[32,53,54]. They facilitate demand response programs, allowing customers to adjust their energy consumption patterns based on price signals or grid conditions. Microgrids can also participate in energy trading or sell surplus energy back to the main grid, generating additional revenue streams. Microgrids also participate in electricity markets and earn revenue by selling energy and grid services. They contribute to local economic development by stimulating job growth and generating income for the community. However, challenges in implementing microgrids include optimal power flow, stability and protection, resynchronization after fault, integration of renewable energy resources (RER), harmonics, and data security. The adoption of microgrid and blockchain technologies in Saudi Arabia faces legal and regulatory barriers, public perception and adoption challenges, technical challenges related to interoperability and data security, and challenges related to integrating renewable energy sources into the grid ^[55,56].

The adoption of microgrid technology faces challenges such as lack of technical expertise, interoperability issues, high costs, regulatory barriers, public perception and adoption, harsh environmental conditions, and long distances between inhabited locations. These challenges can limit the efficiency and control of the system, leading to system failures. Cybersecurity concerns also pose a threat, as smart microgrids collect, transmit, and process data to govern system functioning. Common cyber threats include distributed denial of service (DDoS), malware attacks, ransomware attacks, social engineering attacks, insider threats, physical attacks, supply chain attacks, advanced persistent threat (APT) attacks, credential stuffing attacks, and zero-day attacks. These attacks compromise availability, integrity, and confidentiality, leading to system failures and disruptions. Therefore, it is crucial to address these challenges to ensure the successful implementation of microgrid technology ^[57,58].

Microgrid control structures are digital networks that manage vital services and applications to keep power facilities and distribution grids operational. These systems ensure adequate energy supply security at the lowest cost possible by communicating optimal decisions to each generating, storing, and loading unit. Microgrid stability must be maintained through control mechanisms to account for variations in weather and energy use. Modern methods, such as intelligent and adaptive approaches, and more conventional methods, such as hierarchical control systems, attain and maintain voltage and frequency stability. These techniques enhance system performance dependability and ensure seamless transitions and automation in the event of an unanticipated disconnection ^[35,59].

Microgrid energy generation requires centralized control mechanisms to facilitate real-time monitoring and administration. There are hierarchical, decentralized, distributed and intelligent control strategies. While a single central processing unit (CPU) makes all decisions in a decentralized system, it is readily expandable. In distributed control architecture, local controllers communicate with a master controller to improve system monitoring and control ^[29]. Intelligent techniques like fuzzy logic and neural network controllers can increase control systems' efficiency and dependability on power sources. Optimization, regulation, and identification of system parameters are typical applications for artificial neural network controllers such as neural networks. Nonlinear data approaches do not match these controllers as they assure fault tolerance, stability systems, prediction, parametric optimization, self-learning, and load sharing in large-scale systems ^[38].

New technologies, such as fuzzy logic controllers, adaptive control techniques, and microgrid monitoring systems, have significantly improved the dependability and stability of microgrids. Distributed control systems have implemented fuzzy logic to maximize microgrid performance characteristics, which divides logical problems into more manageable chunks. Adaptive control strategies are required in microgrid applications to maintain system stability and robustness ^[60]. The IoT facilitates data creation, collection, and dissemination by connecting disparate devices, systems, and people to the web. Smart meters (SMG) have become popular due to the enhanced efficacy and dependability of IoT technologies. By implementing IoT technology in areas such as smart residences, energy storage systems, electric vehicles, charging stations, and fluctuating loads, the adaptability and dependability of SMG can be enhanced ^[50,52].

Smart infrastructures, microgrids, intelligent buildings, and control devices are some of the many applications resulting from the development of IoT technologies. Microgrids implement IoT solutions for energy management and system monitoring to decrease operational costs and improve security procedures ^[49]. Digital instrumentation, communication networks, software, and databases are technologies that develop energy monitoring systems for residences and businesses. Cloud computing, which has proved to be a practical and scalable solution for managing IoT services and delivering data analysis tools, has also been utilized for microgrid monitoring. Microgrids utilize low-cost IoT-based communication technologies such as Thingspeak Middleware for efficient energy management. Communication and microgrid monitoring rely heavily on the performance of sensors ^[61,62].

IoT and smart meters, which can facilitate quicker and more reliable communication between consumers and operators, must be integrated into the creation of intelligent distribution networks. Smart meter technology enables more flexible billing and information management based on electronic integrated circuits embedded in meters. Introducing smart grid components, such as AC, DC and hybrid AC/DC microgrids, can alleviate stability, control, and power management issues ^[31,55]. Using renewable energy sources in microgrids can reduce the total inertia of DC microgrids, and large-scale decentralized resources can be tailored to satisfy specific microgrid requirements. Future MGs may become more adept at defect detection and self-repair if the IoT enables real-time platforms for integrating decentralized and transactional energy markets. Deep learning and blockchain technology can safeguard energy transactions and distributed energy resources (DER) operations ^[58,62,63].

2.1.   Subheading function of EMS

Numerous software providers for the EMS are included in ECCs for utility companies. EMS providers are in high demand for power system architects with solid software development skills ^[10]. Between 1970 and 2000, most EMS software applications were developed for installation on control center computers. The application service provider model, in which the software is hosted by the vendor and accessed via the internet by control center personnel, is currently an attractive alternative ^[64].

Network model construction, security analysis, autonomous generation control, and dispatch are the main features of the EMS. Energy management involves monitoring and regulating electricity production, transmission, and consumption ^[18,65]. It is necessary to manage the physical infrastructure, which includes generating facilities, transmission lines, substations, and load centers. Substations are the terminals of transmission lines where switching, voltage transformation, measuring and controlling are performed ^[15,43].

Load management, or demand-side management, is the remote monitoring and controlling of electrical consumption at multiple levels from sub-transmission to distribution ^[9,66]. The EMS system can perform the following functions: System load forecasting, unit commitment, economic dispatch, hydro-thermal scheduling, megawatts (MW) exchange evaluation, transmission loss minimization, security-constrained dispatch, maintenance scheduling, and production cost calculation ^[20,67]. Additionally, it ensures efficient maintenance and dispatch for neighboring systems.

Most EMS used in industry and commerce does not require dispatch from the grid due to their simplicity. In addition, EMS equipment integration management, centralized control, millisecond-level rapid responses, operational safety, and battery balance management are also supported. The energy storage power station that the power grid must dispatch imposes stringent requirements on the EMS system, including the management and monitoring of energy in applications such as energy transfer, microgrids and power frequency regulation ^[12,68]. Figure 2 presents the functionalities of the energy management system.

2.2.   Optimization strategies for microgrid EMS

Microgrid energy management systems, called nano-grids because of their diminutive size, are designed to serve a single structure or an entire neighborhood ^[10]. In microgrid electrical topologies, the power converters of a decentralized energy system are connected to the grid via a main bus. The protection, dependability, and power quality of hybrid AC-DC microgrids are enhanced. In the domain of EMS modeling, simple rule-based strategies coexist with more complex machine learning and data-driven approaches ^[69,70].

Various algorithms, including heuristic, stochastic, and soft computing-based models, have been investigated in academic literature. However, benchmark evaluations, EMS reference solution evaluation, and energy system sizing are all areas where optimization techniques can be applied directly and easily ^[71,72]. Rolling time horizon (RTH) strategies, which combine optimization and energy system prediction algorithms, are frequently employed to resolve this problem. However, due to their reliance on forecast accuracy and the absence of interpretability, RTH techniques are black-box models ^[73,74,75].

Typically, RTH strategies are deployed utilizing machine learning models such as neural networks (NNs) and fuzzy systems. Recent research have focused on NN models such as long short term memory (LSTM), Echo State Networks (ESNs), Fuzzy Inference Systems (FISs), and adaptive neuro-fuzzy inference systems (ANFISs) ^[19,76]. Rules-based systems, such as FISs, can be a viable alternative due to their increased interpretability and simplicity of implementation ^[77].

This article suggests employing an FIS-based EMS to manage the real-time energy fluxes of a grid-connected MG with an ESS. An EMS can be synthesized with the help of a hierarchical genetic algorithm (GA)-FIS paradigm by defining the FIS consequent component of each rule, adjusting the membership functions (MFs), setting rule weights, and removing inefficient input MFs. The RTH reference and benchmark solutions are utilized to assess the outcomes ^[78,79].

Microgrid EMS optimization strategies can be classified as AI-based, game theory-based, multi-agent-based, NN-based, reinforcement learning-based, and conventional. The primary objective of traditional EMS, EMS based on NNs, EMS based on reinforcement learning, EMS based on game theory, and EMS based on multiple agents is battery schedule optimization ^[24,80,81].

As demonstrated by ant colonies, bird flocks, animal herds, hawk hunts and fish schools, swarm intelligence-based EMS is adaptable, fast to respond to fluctuations and effective in achieving economic and environmental objectives. Unique EMS methods include adaptive partitioned contextual learning, a bi-level decision analysis framework, and an adaptive direct search algorithm for a mesh ^[15,65,82].

2.3.   Virtual power management

Proliferate, difficulties in sustaining grid resiliency are arising. Electric vehicles, solar photovoltaic panels installed on rooftops, and residential energy storage systems are examples of the numerous resources added to the power grid ^[21]. Given that the existing infrastructure still needs to be updated to accommodate bidirectional electricity flows, these developments present new problems and opportunities for grid modernization. The software provided by virtual power plants (VPPs) is crucial for addressing these concerns and sustaining stable, consistent electric infrastructures. North American utilities and grid operators are just some of the ones interested in modernizing their demand response (DR) programs to take advantage of the numerous benefits DERs provide ^[83,84].

Studies of utilities and grid operators highlighted shared concerns in an era of accelerated global change. Utilities and grid administrators are interested in managing diverse DERs, such as loads and generation, energy storage and EVs. The VPP industry has shifted toward the mixed-asset subsegment due to machine learning, scalability and computational speed developments. Approximately one-fourth of respondents already utilize a VPP or DERMS system to monitor and manage their DER ^[21,44].

All VPP initiatives are implemented to provide grid services, including the California demand response market. By installing solar panels and batteries on-site, VPP fleets provide homeowners with a clean, continuous energy source that can be relied upon in the event of a utility failure. Electric vehicles are one example of a new form of DER being incorporated into VPPs via vehicle-grid integration (VGI), which enables EVs to participate in grid balancing schemes as generating or demand assets for grid operators ^[44,85]. Electric vehicles are well-suited for balancing reactive power and voltage, modulating frequency and optimizing DR firming and flexible capacity when coupled with energy storage. VPPs and DERMS are converging due to regulatory frameworks, proposal requests, and software technology advancements ^[86].

VPPs' primary objectives are collective energy demand management and addressing the prospect of network outages. The remote software that comprises these systems is responsible for connecting, coordinating, and monitoring distributed storage and controlled-charge energy sources. VPPs provide consumers with flexibility, accurate forecasts, and enhanced judgment. They provide affordable energy production, reduce our ecological footprint, and reduce network outages ^[85,87]. Australia's renewable energy financing agency is commissioning Australian gas light (AGL) energy to conduct a feasibility study on the viability of a VPP implementation method, and European programs are investigating methods to increase distributed network supply capacity.

3.   Digitalization of microgrid

DERMS, microgrid energy management systems (MEMS), IoT devices, big data analytics, blockchain technology, AI, digital twin technology, cloud computing and AR are among the digital technologies that have been incorporated into microgrids as a result of their digitalization ^[80]. By providing a centralized platform for managing DERs in a microgrid, DERMSs facilitate real-time control and optimization. Microelectromechanical systems are essential to microgrids' efficient and dependable operation by monitoring and controlling energy production, consumption, storage, and management ^[69].

Open-source technology is of tremendous benefit to the microgrid community because it promotes cooperation and the exchange of information. Within a microgrid, distributed energy resources such as PV systems, wind turbines, energy storage systems, EVs, and DR systems can be managed by a software platform known as a DERMS ^[39,50,52]. Connectivity and interoperability of data, large-scale investments in infrastructure and technology, and the protection of critical energy infrastructure are just a few of the obstacles that must be surmounted to implement DERMS for microgrids. Maximum utilization of distributed energy resources is the objective of DERMSs, which emphasize efficient administration, control, and optimization of a diverse range of distributed energy resources ^[4,88].

Due to the IoT, microgrids are becoming an increasingly vital component of the energy industry. IoT devices that collect real-time energy consumption, production, and distribution data can improve energy efficiency and optimize microgrid operations ^[34]. Integrating renewable energy sources enables the management of variable output and optimizes resource consumption. By identifying system malfunctions or anomalies, IoT technology in microgrids can improve their reliability and resilience, making them less susceptible to outages and downtime. In a power outage, IoT-enabled microgrids can utilize energy storage devices as a fallback. Implementing IoT in microgrids presents challenges, including data privacy and security, interoperability, and regulatory obstacles ^[69,89].

Microgrids must be digitized by collecting, processing, and analyzing massive amounts of data produced by distinct microgrid components. Energy consumption trends and probable defects can be detected in advance using smart instruments, sensors and big data analysis. Despite these obstacles, big data analytics can improve efficiency, dependability, cost-effectiveness, sustainability, predictability, decision-making and scalability in energy use, infrastructure, and operating expenses. By implementing practices such as data collection and integration processes, data quality assurance techniques, data security measures and cloud computing, among others, microgrid operators can maximize the benefits of microgrids in enhancing energy sustainability and resilience ^[29,90].

Blockchain technology, a decentralized distributed ledger system, could revolutionize the energy industry by facilitating verifiable, auditable transactions. When increased efficiency, security, and transparency are incorporated into microgrids, their ability to meet the energy needs of communities is enhanced. Network, consensus, and application layers are the three fundamental components of blockchain technology ^[36,58]. The consensus layer validates and adds transactions to the blockchain, while the network layer communicates between nodes; on top of the application layer, which also functions as the user interface, decentralized applications like smart contracts that automate tasks like payments, asset transfers, and identity verification can be built. By integrating blockchain technology with MGs, we can reduce energy costs, increase the use of renewable energy sources, and enhance security and transparency ^[36,57]. AI algorithms such as machine learning (ML) and deep learning (DL) can improve the efficiency of electrical infrastructures and decision-making processes. The ability to precisely estimate energy consumption and generation allows them to optimize charging and discharging schedules and power generation. The ability of AI algorithms to regulate power fluxes among energy sources allows a dependable and cost-effective power supply to be maintained with less reliance on traditional sources ^[50].

AI has considerable potential in microgrids, particularly in defect identification and diagnosis. AI algorithms can monitor the system and detect problems before they cause significant disruption. The combination of blockchain and microgrids has the potential to profoundly alter the energy industry by fostering greater efficiency, security, and transparency, increasing the use of renewable energy sources, and fostering a more environmentally conscious culture ^[36,39,55]. The potential of AI to improve microgrids' efficiency, dependability, and sustainability needs to be improved by data availability and quality constraints, the complexity of microgrid systems, and cybersecurity concerns. Creating a digital twin of a physical asset or system, which enables operators to model and optimize its performance in real time, is a prominent energy industry tool acquiring traction in microgrids ^[57,91].

By enabling the digitalization of microgrids, cloud computing is revolutionizing the energy sector. It comprises infrastructure for cloud computing, cloud platform, cloud software, cloud storage, and cloud security. With the assistance of cloud computing applications such as energy management systems, demand response platforms, energy trading platforms, and predictive analytics, it is possible to optimize energy production, storage, and consumption, reduce costs, enhance dependability, and promote sustainability. However, the potential of cloud computing in microgrids is hindered by obstacles that must be surmounted ^[57]. AR technology can superimpose digital information on real-world environments, enabling remote monitoring, maintenance, training, defect identification, and optimization for microgrids. However, AR confronts obstacles, including cost, complexity, and accessibility. AR in microgrids could increase as technology advances, benefiting users, technicians, and businesses ^[57].

The digital twinning architecture consists of three components: Physical systems, virtual systems, and data transmission between the two. By integrating high-fidelity models with data from multiple sources, such as sensor data, historical data, technical information, and maintenance history, accurate physical system models are developed and kept up-to-date for various operating conditions ^[92]. A higher degree of accuracy in representing the actual system, the ability to use ML and AI to enhance the model and compatibility with Industry 4.0 environments are all advantages of data-driven simulation modeling ^[24,93].

Digital twins (DTs) must employ accurate simulations of physical systems and processes to imitate a real sibling's behavior. Modeling techniques can be derived from physics, data, or a combination. Combining the two methodologies is an effective digital twin modeling strategy ^[24,93].

Field measurements, IoT devices, and smart instruments all contribute to the necessary data collection for twinning. Complex data analysis techniques are necessary to preprocess chaotic raw data and improve data quality ^[24,92].

The significance of DT applications in microgrids has increased as a global concern for diminishing natural resources and environmental degradation has increased. Utilizing DT, which provides a high-fidelity simulation platform for developing, testing, and evaluating microgrids, enables more efficient planning of system equipment and renewable energy sources. Effective forecasters improve prediction accuracy, increasing system reliability and reducing the need for large reservoirs and oversized system components ^[22,69,85]. The autonomy of the power system forecasting model requires efficient data management systems. DT technology can improve the autonomy and efficiency of microgrid forecasting techniques by providing a cutting-edge data management system, a high-fidelity simulation platform, and a dynamic and interactive platform for modeling consumer responses to stimuli and predicting power consumption under various conditions. DT enables the precise modeling of market dynamics and the interaction of numerous market participants, enabling more accurate energy price forecasts ^[94,95,96].

DT can be a powerful instrument in a DT-driven decision support system (DSS) for microgrid control and operation management by assisting operators with transients and steady-state evaluation, identifying crucial operating situations, analyzing system performance and making prompt decisions in response to changes. This method can investigate the effects of system operation management strategies on system lifetime and degradation trends, thereby bolstering the growing interest in the circular economy ^[24,95,97].

An accurate and dynamic model of the physical system is beneficial for designing effective EMS for remote control systems. DT-driven power generation and consumption forecasting algorithms reduce uncertainty in available power and power consumption, making EMSs more efficient. The controller can be executed in real time using a field-programmable gate array (FPGA) to account for dynamic changes ^[68].

Condition and state of health (SoH) monitoring of systems and equipment can be enhanced by DT, allowing for more effective operation management even in challenging environments. DT has been implemented in various contexts, including data-driven DT and the evaluation of battery pack degradation, in addition to automotive braking systems ^[70,98].

System awareness (SA) is vital to microgrids' security and resilience for preventing fault propagation and mitigating its effects on their area of responsibility and adjacent interconnected networks. Improved SA, a cutting-edge asset management system, a lifelike simulation platform, highly trained DSSs, automatic event model updates via DT modeling engines, and the adaptation of preventative, corrective, and restorative actions by training the DSS for future events using cutting-edge ML techniques all contribute to DT's enhanced operational flexibility ^[70,84,94].

In summary, DTs provide a robust and cost-effective infrastructure for simulating the microgrid ecosystem over time and determining the optimal time and strategy for growth planning. The new policy must be consistent with policymakers' objectives, and DTs provide a useful testing ground for predicting how the system will react to future events over various time horizons.

4.   AC/DC power grid management system

A single hybrid AC/DC MG can be made by linking the required sources and loads to the AC and DC subgrids. In an AC subgrid, the AC bus connects DGs and AC loads, while the DC bus connects PV generators, energy storage devices, and DC loads. Bidirectional linking converters (BICs) connect AC and DC distribution networks ^[8,99,100]. AC bus is utilized for power transmission in the utility grid (UG). To form a networked MG, the DC buses of many microgrids are interconnected. The DC network is adjustable according to the interconnection relationship of many microgrids, making it both scalable and expandable for usage in large-scale systems. The following factors influence the layout of this building: In AC/DC hybrid versions, the benefits of both AC and DC motor generators are kept ^[40,44]. They are grid-compatible, reduce the number of power conversion stages, and make it easier to incorporate a wide range of power sources and loads. DC networks considerably facilitate system analysis and power distribution consolidation (no reactive power sharing issues, frequency synchronization). Because electricity is shared across the network, several microgrids are more dependable, efficient, and cost-effective than a single microgrid ^[7,101]. Tn following Table 1 shows the DC and AC microgrids applicative strategies.

This paper refers to a microgrid incorporating AC and DC components as a "hybrid system". A microgrid's voltage is always a tradeoff between safety, economics, and effectiveness. The construction of a hybrid microgrid is determined by the configurations of AC or DC buses and the connection of distributed generation sources (DGS) and loads. Interface converters connect DGS and storage devices to a DC bus in a DC microgrid. Interface converters connect distributed generation sources and energy storage devices to an AC bus in an AC microgrid. In addition, the utility grid is connected to both buses via the required interface devices ^{[8,65,102,103,104]}. As seen in Figure 3, a hybrid microgrid utilizes appropriate coupling converters to link AC and DC buses.

DGS attached to the relevant AC/DC buses provides electricity to the loads on those buses when everything functions correctly. When there is a surplus of energy, the storage component is charged, and the excess is transmitted to the grid. The coupling converter provides a two-way energy flow in the event of a power imbalance, and the storage mechanism ensures the system's continuing stability. In this hybrid system, potential DGS include PV, the wind energy conversion system (WECS), fuel cells, a micro-turbine, and a reciprocating engine ^[105]. Figure 4 presents an AC/DC microgrid with multi-grid schemes.

When renewable energy sources are integrated into the power grid, the hybrid AC/DC microgrid offers a reliable and flexible option. Figure 4 depicts the various subgrids that go into making up the hybrid microgrid. Several AC/DC subgrids, each operating at their own rated frequency and voltage, are integrated into this system. The AC and DC subgrids can access the necessary bus voltage thanks to bidirectional AC/DC converters (BADCs) and bidirectional DC/DC converters (BDDCs) ^{[65,104,106,107]}.

The system's storage is organized into a storage subgrid that regulates the bus' DC voltage. The authors establish and investigate the multi-time scale concept in ^[47] to achieve stable control and optimal operation of the hybrid microgrid. ^[45,108,109] there are modeled microgrids that function on synchronized time scales and energy kinds. The most crucial features are presented in the optimization algorithm and case studies. Unlike standard hierarchical control, the suggested coordination technique considers the coupling of time scales, which can be advantageous for decentralized microgrids. By splitting the system into a stable region, a precautionary region, and an emergency region, it is possible to apply a hierarchical frequency control method across multiple time scales. The following Table 2 presents advantages of AC/DC microgrids.

The authors of ^[47,65] proposed a reduced-order multi-scale model to simplify the system's model without sacrificing the most crucial information at the largest time scales. Since multi-time scale coordinated systems are centralized and rely on a single point of failure, they are susceptible to reliability difficulties. The hybrid microgrid can only function if power is managed (or controlled) on a shorter timescale that considers the underlying technology ^[110]. Table 3 presents the limitations of AC/DC microgrids.

This study describes a safe and decentralized EMS for managing networks of microgrids. Each microgrid works to keep its operational costs as low as feasible in light of the energy and power capacity limits imposed by the UG, DGs, ESSs, and BICs. To lower the operational expenses of individual MGs, it is proposed to plan power outputs from the UG, DGs, ESSs, BICs, and microgrids, as well as participation factors from the UG, DGs, and ESSs. If a microgrid has more power than it needs, it will send the extra juice to the DC grid, and vice versa if it is low on juice ^[40,113]. Power is transmitted through the DC grid using microgrids. An optimization model of the networked microgrid system has been devised to reduce microgrid running expenses and transmission losses. Microgrids are wary about merging their data because it is spread out over many sources (such as the dispatched power output of DGs and ESSs). The safeguard distributed approach is used to solve the optimisation model ^[16,100,104].

4.1.   AC microgrid energy

Many forms of RES have profited from the widespread usage of DG units on electrical networks, including microturbines, fuel cells, PV systems, and wind energy systems. DG units can cause voltage and voltage oscillation variations in a distribution network. To address these concerns, many DG units are interconnected to form a microgrid ^{[9,64,101,114]}. Figure 5 depicts the fundamental design of an AC microgrid unit. PV systems and ESSs connect to the AC bus via DC/DC/AC converters, while wind turbines connect via AC/DC/AC converters. The AC supply to loads is controlled when RESs are set up in an island configuration. Power is transmitted from the microgrid to the grid through a tie line physically connected to the upstream grid at the synchronization point during grid-connected operation ^[100,109].

Optimal circumstances in a smart microgrid need attention to the precision and dynamic stability of active power sharing. To fine-tune the power-dynamic sharing's performance without reducing the static droop gain, the study provides a decentralized adaptive droop-based control strategy that strengthens active power-dynamic sharing ^[23,115].

Moreover, ^[14,116] provides algorithmic active power regulation and management approaches. Active power-sharing under complicated load situations is made possible by the methods presented in ^[14,116], including an algorithm-based active power regulation approach and a hierarchical active power management strategy. Improved PV and Q/f droop management algorithms are provided in ^[18] to facilitate active power-sharing in resistive/unknown feeder impedance settings, with the added benefit of superior voltage disturbance rejection performance. Numerous droop control methods have been developed for exact reactive power distribution, including adaptive voltage droop control, enhanced control approach, and a hierarchical control strategy.

While alternative strategies can improve active power sharing, signal injection decreases power quality and makes the system unstable. Adaptive inverse control with a modified droop control approach can regulate unbalanced and reactive power by modifying the weight coefficients of digital filters in real time ^[12,16]. Therefore, reactive power would not be distributed efficiently in disconnected microgrids under nonlinear and unstable loads. Techniques have been described for separating the active and reactive powers, and they are not restricted to enhanced droop control. Its utility reduces when the microgrid system stabilizes with the feeder or load ^[88]. Using the proposed hierarchical control method, the microgrid's active and reactive powers may be shared while preserving stable and dynamic performance, the microgrid's redundancy can be reinforced and the microgrid's frequency and voltage amplitude may be restored to rated values ^[87,116,117]. Figure 5 depicts the three-level hierarchical structure of microgrid control systems.

The AC-coupled system's control strategy and power management scheme maintain voltage and frequency stability on the AC subgrid by balancing power generation and consumption. Due to its ease of construction, maintenance, and operation, the AC-coupled microgrid has been the system of choice for some time. In AC-coupled microgrids, multiple-port converters that combine numerous power sources into a single power converter reduce the need for individual interfacing converters (IFCs) for each DG or ESS ^[12,101].

4.2.   DC microgrid energy

The microgrid and EMS-based systems simultaneously address technological, economic and environmental challenges. Each of the two basic EMS operation modes—grid-connected and island—require a unique strategy for operation, energy scheduling, and system resilience. A DC microgrid is a sophisticated multi-target control system that can operate alone or connect to a larger power grid. The control hierarchy of a DC microgrid consists of a primary controller, a secondary controller, and a tertiary controller ^[2,105,118]. Figure 6 illustrates the constituents of a DC microgrid. This includes micro sources, ESS, electronic coupling (EC) devices and machinery for load control. Several studies have examined ways to improve the implementation of droop control, which is commonly employed in primary control. The current sharing divergence between microgrid units can be eliminated using a nonlinear droop technique, such as a high-order polynomial. Nevertheless, sensor problems and mismatched line impedance restrict the technology's precision ^[47,65,114].

Direct current-coupled microgrids offer a simple architecture that eliminate the need for frequency and phase angle synchronization between many DGs. Alternating current terminal voltage synchronization may make parallel microgrid IFCs difficult to control and operate. DC and AC voltage regulations are necessary for a DC-coupled system and subsystem power management. With DC-coupled hybrid microgrids, converters are unnecessary because the ESSs are connected directly to the DC bus ^[41,101]. Several input power sources can be coupled to a common DC connection with the help of multiple-port power converters used in AC-coupled and DC-coupled hybrid microgrids ^[41,47,103].

The nonlinear droop formula can be modified to improve the DC microgrid's current sharing effectiveness. Nonetheless, a compromise between voltage regulation and precision current distribution is still possible. The DC microgrid's secondary control can resolve the primary controller's voltage deviation and current-sharing precision issues ^[1,44,80]. The traditional technique employs a centralized control strategy, but this has several downsides, including limited flexibility in plug-and-play components, increased computing and communication requirements and reliance on a few controllers microgrid central controller (MGCC). The control architecture of distributed multi-agent system (MAS) allows for the development of an innovative secondary compensating control technique. To further reduce the load variance and guarantee that the system is controlled with low voltage, digital average current sharing (DACS) management can be used ^[20,80,81].

IFCs will be required to connect the AC supply and loads to the DC bus. DC-coupled microgrids primarily rely on PV and battery technologies. The DC bus is connected to every DG and ESS in this design. The DC bus in this microgrid is coupled to variable frequency AC demands, such as variable speed motors, via a DC/AC converter ^[103,117]. Improved control, power quality, and efficiency are the results of doing away with the conventional AC/DC grid-side rectifier used for AC bus connection. The DC/AC IFCs in this configuration allow power to flow in both directions between the microgrid's DC bus and AC bus. Often, parallel IFCs with greater ratings and dependability are utilized for energy transfer between DC and AC buses ^[1,12,17].

Microgrids are decentralized, electrically contained networks of inputs and energy-generating units. They can operate independently or on a global grid system. Both microgrids powered by AC and DC have advantages and disadvantages, as seen in Table 4.

5.   Strategic microgrid energy management system

Conventional energy management methods for DC microgrids have only been examined in a few studies. Previous research ^[100,114] has mostly focused on reducing the physical footprint of standalone PV-wind turbine (WT) and hybrid energy system (HES) systems. However, they may be useful plans for homemade EMS. This article reviews various microgrid EMS programming techniques, such as iterative programming, linear programming, mixed integer linear programming, stochastic programming, and predictive model control ^[7,8,65].

5.1.   Iterative algorithms

In the literature, iterative algorithms are employed for many diverse purposes. It has been implemented to minimize the footprint of standalone systems, including single objective optimization (SOO) components. The authors of ^[107,119] used the loss of energy expectation (LOEE) and loss of load expectation (LOLE) to evaluate the stability of the HES. This study's premise was that the LOLE parameter value should be less than 2% for the system's reliability ^{[107,119,120]}. Without the fuel cell (FC) system, the PV-WT-BS HES was more cost-effective and reliable. An enumeration-based iterative technique for microgrid energy management was presented by ^{[14,43,74,121]} to optimize the size of microgrid components. It had solar panels, wind turbines, and a battery. It comprised solar panels, wind turbines, a battery bank, and some tiny generators dispersed around the countryside. This study examined the batteries' state-of-charge (SOC) to determine the system's dependability ^[122]. In addition, the study determined that the PV-WT-DG HES system is technically and economically viable for distributing electricity to users in remote places ^{[123,124,125]}.

The conventional alternating iteration approach for solving AC-DC power flow computations is based on the coupling relationship between AC and DC power flows. The AC bus voltage causes the AC system to influence the DC system, while the AC injection power at the converter station causes the DC system to influence the AC system. This research departs from the norm by analyzing how the DC system influences the AC system and how the converter station injects DC power. DC power infrastructure state variables consist of only DC and DC voltage ^[126]. Figure 7 illustrates the enhanced alternating iterative method, in which data is read for DC grid power-flow calculations and the AC-side augmented matrix is obtained if the DC grid does not exceed the limit.

5.2.   Linear programming

In standalone HESs equipped with PV and WTs, linear programming (LP) has recently been implemented. To minimize the overall cost of the system and maximize its dependability based on a measure of the probability of a power outage. This was made possible by inventing a reliable mechanism for managing power delivery ^[114,127]. Providing continuous power to DC loads did not influence the injected grid current's total harmonic distortion (THD). ^[62] created a prototype to predict the effect of vehicle-to-grid (V2G) networks on the electricity market. An optimization model based on linear programming was added to the EMS to examine how microgrids interact with the larger electrical grid ^[74,128]. Figure 8 is a flowchart illustrating the relationship between LP and stochastic simulation technology.

The unknowns related to renewable energy generation and vehicle aggregation were addressed using stochastic programming and robust optimization, two distinct methods. ^[64] used a PV panel, FC system, battery, and supercapacitor to create a basic but effective EMS. Electricity distribution planners accounted for sixteen combinations of day and night. PV and FC systems had maximum power point trackers (MPPTs) and compensators to boost peak power production ^[73,129]. Using a combination of solar panels, a wind turbine, and a battery in addition to the traditional grid connection, ^[80,81,102] looked at the feasibility of installing an EMS in a residential microgrid. The primary goal was to minimize fluctuations in energy production across the system. This result was attained by implementing a unified control rule considering all three factors: Renewable generation, load forecasts, and battery state of charge.

The LP method used here considers model uncertainty. LP, which can locate the optimal solution within a given range, was used to solve the model using this information ^[130].

5.3.   LP using mixed-integers

Since mixed-integers LP employs integer and binary variables to identify the active system, it is ideally suited for modeling energy management issues. Many authors have altered MILP techniques for microgrid EMS by modifying the causes and objectives ^[127,131]. Using the mix-mode microgrid EMS developed by ^[131], power sharing, continuous operation, and on/off operation are possible. Modeling and solving the on/off mode with the MILP technique optimizes microgrid operation based on the connection status of the FC system ^[99,131]. ^[66] presented EMSs for residential microgrids utilizing the MILP energy trade profit model, in which LP was utilized to represent and avoid the problems associated with the other two modes. The predicted PV power was computed using a fundamental NN technique. With careful load balancing, using thermal storage and batteries was a success ^[119]. Due to their high purchase price and maintenance requirements, these batteries were deemed unsuitable for residential use. To effectively regulate energy usage in a residential microgrid, ^[127,131] described a MILP-based operating cost reduction strategy. Also discussed were the costs associated with modifying load shedding or engaging in energy trading. Throughout the optimization phase, energy consumption and battery drain were considered.

A new two-level approach was introduced to simplify optimization challenges and increase precision over time series aggregation alone ^[120]. This technique for solving optimization problems employs the framework for integrated energy (FINE) model to solve problems in two phases, as shown in Figure 9. At the first level, optimization specifications for microgrid energy system models are created using time series data, demand profiles and techno-economic factors. The second level outlines parameters for time series aggregation (TSA) using typical periods and the cluster approach. The superposition of system states enables the storage of data between periodic reviews ^[98]. The study concludes that using a smaller sample of typical days increases computing performance, whereas using a smaller sample of typical days decreases the accuracy of the optimization results. In Figure 9, the workflow of the linear program using mixed-integers is presented.

5.4.   Uncertain and dependable programming

Stochastic and resilient programming is a two-step procedure for dealing with constrained optimization under uncertainty. A growing number of intermittent power plants complicates the energy management of microgrids ^[132]. Reference ^[67] recommends employing stochastic and robust optimization strategies to address some challenges. The best cost-effective approach to operate a hybrid AC/DC microgrid one day in advance was determined using probabilistic scenarios ^[133,134]. Operating costs can be reduced by estimating future energy prices, solar power output, wind power output, AC load and DC demand. Reference ^[68] details a two-stage stochastic programming approach to optimize microgrid operations when RERs and fluctuating load demand are present. The system energy consumption is controlled in the former while optimizing the original microgrid investment ^[135]. Figure 10 depicts the primary design choices addressed by the investigation.

Where in the accompanying diagram, the options are divided into five distinct categories, including modeling considerations and robust design elements. Each design decision affects the others. For instance, multi-objective and single-objective formulations are approached differently ^[136].

5.5.   Control and predictive modeling

Daily emissions and generating costs can be reduced in microgrid systems using model predictive control (MPC) to keep within technological constraints ^[22,137]. The writers emphasize the need for intelligent loads for productive work. Using a supervised NN, the modifiable residential load was forecasted. To minimize energy trading costs with the main grid and maximize battery use during peak demand, another study ^[70] created an MPC-based EMS for a grid-connected microgrid. In addition, it ensured that wind energy was utilized to its maximum capacity. In the event of unanticipated losses of WTs or power outages, the authors have designed a fault-tolerant technique to maintain the regular operation of the microgrid ^[23,137]. ^{[3,79,89,104]} presented the hierarchical resource-sharing approach among residential users. Each home in a residential microgrid connected to a larger power grid is likewise equipped with an EMS controller, allowing for centralized data collecting and analysis. The objective was to reduce the initial investment by promoting decentralized electricity generation and distribution among private residences. The researchers discovered that a shorter payback period was related to greater power sharing across households ^{[3,23,79,89,104,137]}.

The microgrid-HVAC building control architecture employs a central MPC controller for optimal energy savings and indoor comfort. However, this architecture has drawbacks, such as its incapacity to scale, an increase in the cost of computing, and the possibility of errors. Studies have proposed hierarchical control frameworks in which a master controller creates set points for subordinate controllers and permits information exchange to solve these issues. Cooperation between controllers sharing time-sensitive information can be both cost- and energy-efficient ^[68]. Figure 11 shows Schematic diagram of model predictive control in hierarchical agglomerative clustering algorithm.

6.   Conclusions

The majority of microgrids are diverse DERs, EMSs, loads, and communication devices. Microgrids are required for both the implementation of smart grids and the inclusion of RES in off-grid locations. Much research has been devoted to EMSs in microgrids' history, function, stability, dependability, cost, and application. This study offered a comprehensive investigation of different EMSs of AC/DC microgrids. The DC type of microgrid offers substantial advantages over the more prevalent AC type and the hybrid AC/DC type. However, many features, such as its protection system, architectural design, control systems, and stabilizing mechanisms, demand in-depth examination. This study has mainly addressed several crucial problems with AC/DC microgrids and the application of AC/DC microgrids in the global residential environment, such as their architectural design, communication technologies, control structure, and EMS classifications. Future microgrids may employ several AC/DC voltage standards to reduce power conversion steps and boost system efficiency. The challenges with EMS at the tertiary level have received significant attention for residential applications. In addition to the predictive capabilities on future energy generation, low demand, and energy market instability added to EMSs in recent publications, EMSs are generally more flexible and efficient when addressing complex optimization problems.

The article highlighted the necessity for long-term energy management algorithms and reliable EMS to overcome the constraints and challenges of power management in microgrids. It also details the pros and cons of the AC/DC microgrid. However, it needs more specific details and empirical evidence. The potential advantages of digital technologies in microgrids are also discussed but need more empirical data or real-world case studies. In order to better manage energy in microgrids and investigate their interactions, the report suggests that more study is required. Recommendations for future study include expanding the understanding of AC/DC microgrids' EMSs, developing optimization strategies, integrating digital technologies, examining the advantages and disadvantages of AC/DC microgrids, and developing programming techniques to optimize microgrid components and address uncertainties.

In conclusion, EMS models are essential for monitoring microgrids' energy transfers and connections. By learning more about the practical implications of these algorithms in MGs, researchers can enhance the energy management of these machines. To ensure the efficient and dependable functioning of AC/DC microgrids, researching the interaction between EMSs could be a fascinating research direction.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in creating this article.

Acknowledgments

I would like to thank my PhD supervisor Prof. MTE Kahn at Cape Peninsula University of Technology, PO Box 1906, Bellville, 7535, Cape Town, South Africa. His exceptional leadership and unwavering support, invaluable guidance, and constant encouragement have been instrumental in shaping my research journey and establishing me as a researcher in this field, may he have the privilege to witness the tangible results of his mentorship in the achievements of his students within this research and throughout their future academic pursuits. I also wish to acknowledge the valuable feedback provided by the editor and reviewers during the submission process to this journal.

Conflict of interest

The authors declare no conflict of interest.