Figure 1.
Local supply system with associated load.
Citation: Ahsan Iqbal, Ayesha Ayoub, Asad Waqar, Azhar Ul-Haq, Muhammad Zahid, Syed Haider. Voltage stability enhancement in grid-connected microgrid using enhanced dynamic voltage restorer (EDVR)[J]. AIMS Energy, 2021, 9(1): 150-177. doi: 10.3934/energy.2021009
| [1] | Ahmed Eldessouky, Hossam Gabbar . SVC control enhancement applying self-learning fuzzy algorithm for islanded microgrid. AIMS Energy, 2016, 4(2): 363-378. doi: 10.3934/energy.2016.2.363 |
| [2] | K. M. S. Y. Konara, M. L. Kolhe, Arvind Sharma . Power dispatching techniques as a finite state machine for a standalone photovoltaic system with a hybrid energy storage. AIMS Energy, 2020, 8(2): 214-230. doi: 10.3934/energy.2020.2.214 |
| [3] | Pascal Hategekimana, Adrià Junyent-Ferré, Etienne Ntagwirumugara, Joan Marc Rodriguez Bernuz . Improved methods for controlling interconnected DC microgrids in rural villages. AIMS Energy, 2024, 12(1): 214-234. doi: 10.3934/energy.2024010 |
| [4] | Abdulrahman J. Babqi, NasimUllah, Ahmed Althobaiti, Hend I. Alkhammash, Asier Ibeas . Current model predictive fault-tolerant control for grid-connected photovoltaic system. AIMS Energy, 2022, 10(2): 273-291. doi: 10.3934/energy.2022015 |
| [5] | Abdollah Kavousi-Fard, Amin Khodaei . Multi-objective optimal operation of smart reconfigurable distribution grids. AIMS Energy, 2016, 4(2): 206-221. doi: 10.3934/energy.2016.2.206 |
| [6] | Gul Ahmad Ludin, Mohammad Amin Amin, Ahmad Shah Irshad, Soichiro Ueda, Zakirhussain Farhad, M. H. Elkholy, Tomonobu Senjyu . Power transmission in Afghanistan: Challenges, opportunities and proposals. AIMS Energy, 2024, 12(4): 840-871. doi: 10.3934/energy.2024040 |
| [7] | H. H. H. De Silva, D. K. J. S. Jayamaha, N. W. A. Lidula . Review on design and control of solid state transformer based microgrids. AIMS Energy, 2019, 7(6): 901-923. doi: 10.3934/energy.2019.6.901 |
| [8] | Santosh Kumar Sharma, D. K. Palwalia, Vivek Shrivastava . Distributed generation integration optimization using fuzzy logic controller. AIMS Energy, 2019, 7(3): 337-348. doi: 10.3934/energy.2019.3.337 |
| [9] | Hari Charan Nannam, Atanu Banerjee . A novel control technique for a single-phase grid-tied inverter to extract peak power from PV-Based home energy systems. AIMS Energy, 2021, 9(3): 414-445. doi: 10.3934/energy.2021021 |
| [10] | Habibullah Fedayi, Mikaeel Ahmadi, Abdul Basir Faiq, Naomitsu Urasaki, Tomonobu Senjyu . BESS based voltage stability improvement enhancing the optimal control of real and reactive power compensation. AIMS Energy, 2022, 10(3): 535-552. doi: 10.3934/energy.2022027 |
The electrical power distribution system is undergoing major power reliability issues in different parts of the world. This is due to increasing demand of electricity versus less generation of electricity in power stations, limited resources of natural fuels (like coal, and gas) that run power stations, complete power failure (blackout) and partial power failure (brownout), infeasible nature of distribution system to directly integrate renewable energy resources (RES) like solar photovoltaic (PV) and wind generation [1,2]. Study about microgrid is being conducted as it is considered as reliable structure to overcome the shortcomings of typical distribution system that are discussed above [3]. Microgrid structure is consists of distributed generation (DG) units that may have renewable energy resources (including solar PV, wind generation, fuel cell, and electric vehicles EVs) or non-renewable energy resources (including diesel generator, gas turbine) or combination of both. Energy storage system (ESS) and necessary power electronics interface (PEI) are also basic elements of microgrid. Microgrid works in two mode of operation in grid-connected mode (GCM) and islanded mode (IM), in grid-connected mode of operation the microgrid works together with local grid to supply loads whereas, in islanded mode of operation the microgrid works independently to provide power to associated loads. The islanding mode operation of microgrid has more complex PEI mechanism when compare to grid-connected mode operation as overall tasks strength are more in it to resolve on-line working challenges [4,5].
In addition to power supply reliability issues in the local distribution system the most concerning problem is the quality of power which is being delivered to loads simply it is called power quality of electrical supply [6]. Power quality is explanation of the term that how much standardized waveforms of voltage and current are being delivered to electrical loads, bad power quality leads to number of problems in local distribution system. These are heating of power lines, heating of power transformers, bad efficiency of electrical loads, less life of electrical equipment, loss of data and loss of production, etc. There are number of power quality problems that disrupt electrical loads those common power quality problems are voltage sag and voltage swell, voltage transients, voltage unbalance, current harmonics, and current unbalance [7,8]. Among these power quality issues voltage sag and voltage swell are those that affect electrical equipment and electrical loads in extreme manner. Voltage sag can be explained as sudden decrease in amplitude of line voltages in comparison with nominal voltage level whereas; voltage swell can be explained as sudden increase in amplitude of line voltages in comparison with nominal voltage level. The distribution system facing the problem of voltage sag due to number of factors like single line-to-ground faults, switching of heavy loads, large motors starting, and partial power failure [9]. On the other side, the main reasons of voltage swell are abrupt reduction in large loads, malfunctioning of transformers and power electronics interfaces, and common faults in power lines. The impact of voltage sag/swell problem in practical distribution system is adverse, sensitive loads are majorly affected due to these problems [10]. The main effects are damage of essential electrical equipment and loads, malfunctioning of electrical equipment, loss of production data and corruption of data, underperformance of electrical systems [11].
Nowadays, microgrid is a need of distribution system as the microgrid structure provides necessary medium to integrate renewable energy resources with distribution system. Power electronics interface of microgrid acts as power transferring midway between microgrid's DGs/ESS and distribution system. Reliability pattern of local distribution system will be increased if it links with microgrid, microgrid structure will not only acts as backup supply but also stores its surplus power in its energy storage unit. Typically, microgrid structure is lack of any additional strategy with the help of which the power quality concern can be addressed. For satisfactory performance of electrical distribution system in terms of loads' requirement the electrical distribution system at a same time needs microgrid facility and power quality compensation technique. In this case, microgrid will be responsible for power supply reliability enhancement and power quality compensation technique will oversee standardization of power supply. The literature survey has discussed different approaches in which microgrid and power quality compensation technique worked together to enhance distribution system performance. Multiple distributed generation (DG) units working together with distributed control mechanism in power park microgrid in [12], each DG unit produces standardized power quality and controlled by superior central control unit as a result the power quality of whole system is good in terms of loads. Hybrid AC/DC microgrid concept is now widely use to combine the features of both AC and DC microgrid as the resulting system is big and more complicated therefore, inertia control technique is introduced in [13] to efficiently regulate the power quality of individual DG. Two-level control is proposed for interfacing converter (IC) to mitigate DG level and system level power quality problems in which, primary level is responsible for compensation of DG based power quality problems whereas, secondary level is responsible for compensation of hybrid microgrid system level power quality problems in [14]. Distributed generation units are deployed in a manner to enhance microgrid system power quality including voltage fluctuation and voltage imbalance in [15]. Instead of typical microgrid design an enhanced battery energy storage system is introduced and successfully linked with distribution system to reduce the power quality issues that would produce in microgrid [16]. Grid connected microgrid structure produces many complex challenges in terms of power quality concerns, for analyzing these complex variables a scheme based on advanced mathematics is proposed and practically apply in [17]. To compensate power quality problems in islanded microgrid a unique control mechanism is introduced for power quality compensator in [18]. Power quality compensation in microgrid with two separate compensation devices in [19], both are installed to mitigate source side and load side power quality problems. Solar PV (photovoltaic) based power quality compensator is presented to enhance the overall capacity of compensator to mitigate power quality problems in grid connected microgrid in [20]. Severe power quality problems associated with microgrid structure are mitigated using different FACTS devices in [21,22].
Voltage sag and swell have been identified as the major power quality problems not only in power distribution system but also in microgrid arrangement, both problems are relatively alike in opposite manner and have severe consequences on the electrical power system. Microgrid design is non-stiff and its inertia is less than that of distribution power system this is due to the intermittent nature DGs that are present in microgrid design. For this reason, voltage sag and swell problems are frequent in microgrid than in distribution system. Dynamic voltage restorer (DVR) is a prominent FACTS device and it is considered as an excellent compensator to resolve voltage sag and swell related problems. Conducted literature covers different scenarios in which DVR resolves voltage sag and swell in distribution system and microgrid, different orientations of DVR are applied. A new scheme of DVR named dual-dc-port dynamic voltage restorer (DDP-DVR) is presented to mitigate different level of voltage sag in distribution system moreover special technique has been introduced to reduce the power rating of (DDP-DVR) [23]. For optimal performance of DVR and related FACTS devices new alignment approaches have been used to compensate voltage related problems [24,25]. A new design model of DVR is proposed and used as custom power device in secondary distribution system to reshape distorted voltage profile according to distribution-level voltage standards [26,27,28]. Many advanced operating mechanisms with general DVR components are being used to enhance the performance of DVR in presence of DGs within distribution system [29,30]. Photovoltaic based microgrid secured with in-phase voltage injection scheme of DVR in [31], controlling voltage variabilities of medium scale microgrid in [32,33] where specific DGs are more of intermittent nature than other. Due to the success in the field of power electronics more and more electrical equipment are being made to cope the challenge of fast processing in the electrical industry, one major disadvantage of this competition is the power quality problems that arises due to these efficient power electronics equipment especially voltage related problems meanwhile, it is important to make custom power devices CPDs (one like DVR) more effective to balance the development [34,35].
Topology or scheme of DVR and related FACTS devices are one of many factors that play important role in success of their operation, out of these factors the most important one is control strategy which is being associated with the power quality compensation device. This is the control strategy which differentiates the performance of one device unit to others as control strategy gives logical and rational power to device. A comprehensive survey is also conducted on different updated control mechanisms that run these devices. A controller consists of hysteresis design and SRF philosophy is presented and used against repetitive power quality problems in [36]. New control algorithm based on catastrophe theory and particle swarm optimization theory is proposed in [37] the robustness of presented control is worthy under variating conditions whereas, online tuning method for PI controller gains is presented in [38] this method is automatic in terms of response. Modified synchronous reference frame (MSRF) introduced and used in high power rating power quality compensation devices in [39]. A unique control link is developed to track two power quality compensation devices simultaneously in [40] the power rating of both devices is decreased with proposed control scheme. An optimal control method with selective compensation characteristics is presented for fast response, optimal performance, and less cost in [41] whereas, dual vector control (DVC) based power quality compensation equipment is proposed for grid side voltage related problems in [42]. Comparison of different real time control procedures has been conducted in terms of advanced FACTS devices and the major factors of concern are processing time and accuracy [43,44]. An ordinary direct-quadrature axis algorithm centered power quality compensation device has less capacity to deal with power quality problems that arise in microgrid system therefore, some modifications have been introduced in device's control to efficiently mitigate those problems [45]. Sliding mode control (SMC) for power quality compensation device in [46] resolved specific order power quality distortion issues. Maximum Loading margins can be effectively calculated and use as input in SRF based control algorithm to mitigate voltage distortions [47]. Different approaches have been used to redesign direct-quadrature axis control for power quality compensation equipment to resolve power system voltage quality problems [48,49,50].
Although, DVR is considered as most versatile FACTS device to resolve voltage sag/swell problems however, efficacy of DVR is depending on its coupling topology with power line and control unit. Literature survey, mainly [23,26,27,29,30,33,35,55,56] have designed complex filter combination for DVR and used overall measured design therefore, power quality problems are not optimally compensated and DVRs injected unwanted signals at the time of compensation, and performance of DVRs in [29,30] is marginally affected due to compound structure of microgrid. Moreover, the control algorithms in [38,40,42,46,48,49,50,54,57] are especially shape for those DVR structures that working in tough conditions and however, there are giving slow response and imprecise compensation voltage injection in sudden variation conditions of voltage waveform. In this paper,
1.An enhanced dynamic voltage restorer (EDVR) is presented for efficient compensation of voltage sag and swell in grid connected microgrid scheme. New control strategy is developed for fast and precise working of EDVR, the proposed control strategy involves two sub control units an enhanced synchronous reference frame (ESRF) control unit and fuzzy technique control system.
2.ESRF control unit is responsible for smartly regulation of voltage sag/swell and fuzzy technique control unit is responsible for fast perception of voltage sag/swell in line voltage. DC link voltage of EDVR is perfectly controlled at the time of sag/swell compensation, the stability analysis of ESRF control is also presented with the help of modeling of VSC of DVR.
3.The associated loads are secure in terms of complete/partial power failure and severe voltage sag/swell under presented overall scheme. The performance of EDVR is good in presence of microgrid structure.
The remaining paper is structured as following, section 2 will discuss EDVR based microgrid system description, section 3 will explain overall control philosophy of EDVR, section 4 will discuss results verification, and section 5 contains final conclusion.
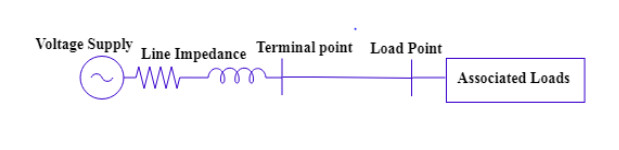
Power distribution system is a last part of power supply system and it is considered as least secure part of power supply system, generally it gets supply by central supplier. However, the local distribution system faces reliability issues in terms of power supply. Figure 1 shows a typical power distribution supply system in which loads are being fed by local voltage supply. Associated loads are consisting of sensitive and normal operating loads like medical supply loads, household loads, etc. Supply system in Figure 1 is non-secure as there is no other source of power exists if the local voltage supply system fails due to faults and natural disasters. Figure 2 shows another power supply system in which microgrid is also exists in addition to local voltage supply overall, this supply system is more secure in terms of power reliability and loads' expectation of power availability. In this system, if the local voltage supply fails to provide power to loads then there is a reliable backup power supply in form of microgrid exists to fulfill power demand of loads.
Figure 3 shows a typical design structure of microgrid [51], different possible components of microgrid are shown in the figure. Microgrid can be powered by renewable and non-renewable energy resources, different categories of loads can be a part of microgrid, and microgrid can work together with local utility grid to supply power to loads. As already discussed, the typical microgrid is not capable to deal with power quality problems that disturb loads as it works only to provide necessary reliability to loads. Therefore, special approach will be needed for power supply system represented in Figure 2 to make it protected from adverse effects of voltage sag/swell as without this approach the system will only deal with power availability challenge and will be exposed to power quality problems. Figure 4 shows the modified design of power supply system in which a power quality compensation technique exists together with microgrid and local utility grid, shown technique is positioned at appropriate place in power supply system for effective mitigation of voltage sag/swell.
Dynamic voltage restorer (DVR) is the preeminent choice to mitigate the voltage sag/swell issues in the load bus or power line. The typical design structure of (DVR) is shown in Figure 5, it consists of a control unit, power electronics-based voltage source converter (VSC), necessary filter design, and series coupling transformer or injection transformer. The DVR connects with power line in series and injects the anti-sag/swell voltage to mitigate the effects of voltage sag/swell. The control unit of DVR has principle authority and it drives VSC to produce anti-sag/swell, later the anti-sag/swell passes through filter combination of DVR to filter out unwanted noise signals in injection voltage. The coupling transformer injects anti-sag/swell in power line smoothly. The performance of DVR in power supply system is mostly depends on the selection of its control method and design of its filter combination.
Figure 6 shows the block diagram of the proposed microgrid system design with DVR to enhance electrical power reliability for loads and mitigate voltage sag/swell in power line. The proposed design consists of microgrid's distributed generation (DG) (solar PV) & ESS coupled with local utility grid through point of common coupling (PCC) whereas, PCC is supplying power to associated loads. The associated loads are secured with DVR to mitigate voltage sag/swell related problems. Figure 7(a) shows the three-line diagram of whole system, it is comprehensive representation of the system in which utility grid and microgrid is coupled at PCC, loads are attached with load bus which is being fed from PCC. A detailed depiction of proposed DVR is also shown in which CT is coupling/injection transformer, the combination of (Rf, Cf, & Lf) is proposed filter design for DVR. Rf is filter's resistance, Cfis filter's capacitor, and Lf is filter's inductor. VSC of DVR is power electronics based voltage source converter, and CDCL is DC link capacitor of VSC of DVR. Eqs 1 and 2 show the calculation to find the values of Lf and Cf, fs is switching frequency of VSC of DVR, and f is fundamental frequency.
| Cf=12π(fs2)Rf | (1) |
| Lf=1(2πf)2Cf | (2) |
Figure 7(b) shows the single line diagram of proposed power supply system, microgrid and enhanced dynamic voltage restorer (EDVR) is also shown in this diagram. Figure 8 displays the basic components of DG unit that used for the operation of DG in microgrid for this, first the output voltage of PV array regulated through DC boost converter then this regulated DC voltage converted into standardized AC voltage using grid-tied inverter. The performance of DG unit in the microgrid depends on internal design of DG especially, design of inverter. Figure 9 shows the comprehensive diagram of proposed power supply system with control block, the working of this system is as follows:
Associated loads get power from utility grid in the normal working condition the power supply mode changes from utility grid to microgrid if the utility grid faces black out or partial power failure due to any reason. The DVR structure comes in operation if the voltage across the loads faces dip or increase in line voltage.
The performance of DVR is completely depending on the control strategy which is built in its control unit, the control unit differentiates the power quality problem mitigation approach of two DVRs that have same VSC design. The main purpose of using any power quality compensation device is to first perceive power quality problems in power line secondly, mitigate that problem in a minimum interval of time. To achieve this purpose, an efficient control methodology is designed for DVR to first perceive and then mitigate voltage sag/swell in the line voltage, Figure 10 shows this methodology. The proposed control approach consists of two-stage control a fuzzy logic-based technique system and enhances synchronous reference frame ESRF based control, fuzzy logic-based technique system capably detects voltage sag/swell related issues in a power line or across load whereas, ESRF based control efficiently mitigate that voltage sag/swell and secure loads from their adverse effects.
Fuzzy inference system (FIS) is an exceptional logic control mechanism which gives us fast and precise results when compare to typical logic controllers. Major components of fuzzy inference system are fuzzification unit, defuzzification unit, knowledge base and decision-making unit. Knowledge base unit is further divided into rule base and database. Database depends on membership functions that we make according to our data whereas, rule base depends on if-then rules that we define according to our database [52]. Decision making unit is one which performs operation on rules. Fuzzification unit converts the normal input values/quantities into fuzzy quantities to perform operation. On the other side, defuzzification unit converts fuzzy quantities into normal values/quantities that can be used as output of fuzzy inference system. Figure 11 shows the block diagram of fuzzy logic system. Figure 12(a, b) shows the surface viewer in two-axis system whereas, Figure 13(a–c) shows the surface viewer in FIS control in three-axis system. Figure 13(d) shows the quiver view of FIS control. Table 1 shows the defined rules in FIS control.
| Rule No. | Sag Disturbance | Swell Disturbance | EDVR Output |
| 1 | no | no | off |
| 2 | yes | no | on |
| 3 | no | yes | on |
DownLoad:
CSV
Synchronous reference frame SRF is one of the flexible & adaptable control techniques; there are many factors that make this control technique superior than others. Other related control techniques like instantaneous reactive power (IRP) theory and Adaline-based control have basic problems like complexity, computational speed limitation, and flexibility [53,54]. In this paper, an enhanced SRF based control is designed for effectual mitigation of voltage sag/swell. Multiple loops of error reduction and speed increment have been added in the SRF based control to firstly, reduce the error between the nominal voltage & line voltage during voltage sag/swell and secondly, increase the speed of overall control during controlling operation. Figure 14 shows the fundamental flow of the SRF based control, which is adopted for DVR to make it distinctive, first the line voltage which is affected due to voltage sag/swell converts into park transformation. The park transformation also called dq0 transformation as it converts three-phase abc signals into dq0 reference frame, the proposed enhanced control methodology then applied on dq0 reference frame components. After applying control approach the resultant components again converts into abc signals by using inverse park transformation also called inverse dq0 transformation.
Figure 15 shows the detailed diagram of enhanced SRF based control which is proposed for DVR to mitigate voltage sag/swell, first the three-phase line voltage VLabc converts into dq0 reference frame through park transformation, ɵref* is reference angle. The resulted VLd and VLq pass through low pass filter (LPF) to filter out higher order components that present in line voltage. The output of LPFs then compared to respected reference signals (reference voltage) in d and q components. Error signals Vd1 and Vq1 then added to DC link capacitor voltage feedback signal VDCLcon. To further enhance the accuracy of this control an additional accuracy loop (VLdref2 + Vd22) added in q-axis of the control, Vd2 and Vq2 passes through PI controller for necessary control action. Error of output of PI controllers in d & q axis is taken out and passes through PI to regulate zero axis of dq0 control. At end, Vdq0sol is again converted into abc signal using inverse park transformation. The resulted signal then converted into sine pulse width modulation (SPWM) to apply to VSC of DVR as switching signal. Eqs 3 and 4 show the calculation for park and inverse park transformation respectively.
| [vdvqv0]=[cos(θ)cos(θ−2π3)cos(θ+2π3)−sin(θ)−sin(θ−2π3)−sin(θ+2π3)121212][vavbvc] | (3) |
| [VaVbVc]=[cos(θ)−sin(θ)1cos(θ−2π3)−sin(θ−2π3)1cos(θ+2π3)−sin(θ+2π3)1][VdVqV0] | (4) |
The model of VSC of DVR is presented in this section of paper; development of efficient linear control will be result of this section [58]. The average ac side voltages, voltages (terminal), and line current is shown using E*, VL, and IL* respectively. The DVR's power electronics components linked with load side are represented using Rf, Cf, and Lf. However, VDC and IDC* are voltage and current at dc side of VSC. The abc and Park transformation coordinates are represented in Eqs 5 and 6 respectively. Eqs 7 and 8 show the important relation between dc and ac side of VSC. While, m* = ma* mb* mc* & M* = Md* Mq* show the modulation signals for VSC of DVR in abc and Park transformation coordinates.
| ∗E=∗Ea∗Eb∗Ec∗IL=∗ILa∗ILb∗ILcVL=VLaVLbVLc | (5) |
| ∗E=∗Ed∗Eq∗IL=∗ILd∗ILqVL=VLdVLq | (6) |
| ∗IL=∗m∗IDCVDC=∗mVL | (7) |
| ∗IL=∗M∗IDCVDC=∗MVL | (8) |
Equations 9 and 10 show the association for VSC in Park transformation components when Kirchhoff's laws (KCL/KVL) applied, where is used as ac side's angular frequency. For this case, the Pac (active power) is given in Eq 11. Equation 12 shows the modified form of input and state variables for calculation of state space equations (linear). Equations 13 and 14 will be used as reference to calculate transfer function for VSC of DVR. Equation 15 shows the transfer function of ESRF based closed-loop system in which vout is output voltage of EDVR and d is VSC's duty cycle. This is calculated using stability criteria of linear closed-loop system (A-Bk). The stability analysis of enhanced SRF based controller has been done using eigenvalues stability analysis, according to eigenvalues stability analysis any given closed-loop system is stable if its eigenvalues are map on the left half of s-plane. Table 2 displays the eigenvalues of proposed controller in closed-loop system, it is verified both the eigenvalues are in left half of s-plane therefore, DVR's closed-loop system with proposed controller is asymptotically stable. Kp and ki are the values of gains of PI controller that used in the control system, these gains are proportional and integral respectively.
| ddt∗ILd=−RfLf∗ILd+ω∗ILq−1LfVLd+1Lf∗Edddt∗ILq=−ω∗ILd−RfLf∗ILq−1LfVLq+1Lf∗Eq | (9) |
| ddtVLd=1Cf∗ILd+ωVLq−1Cf∗Md∗IDCddtVLq=1Cf∗ILd−ωVLd−1Cf∗Mq∗IDC | (10) |
| Pac=32∗Ed∗ILd+32∗Eq∗ILq | (11) |
| ∗Ud=∗Ed−VLd∗Uq=∗Eq−VLq | (12) |
| ddt∗ILd=−RfLf∗ILd+ω∗ILq+1Lf∗Udddt∗ILq=−ω∗ILd−RfLf∗ILq+1Lf∗Uq | (13) |
| ddt∗Ud=−1Cf∗ILd+ω∗Uq+1Cse∗ILdddt∗Uq=−1Cf∗ILq−ω∗Ud+1Cf∗ILq | (14) |
| voutd=a3s3+a2s2+a1s+a0b3s3+b2s2+b1s+b0 | (15) |
where,
| a3=−LfCfkp,a2=−(LfCfki+RfCfkp),a1=−(RfCfki+kp−1),a0=−kib3=LfCf,b2=RfCf+b1=1,b0=0 |
| Value | |
| Eigen values of Control System | －0.0011 + 1.0127i －0.0011 − 1.0127i |
| kp | 15 |
| ki | 25 |
DownLoad:
CSV
To assess the performance of whole system the simulation analysis is carried out, and whole system with microgrid and EDVR is simulated in MATLAB/Simulink environment. The parameters of system are given in Table 3, the main purpose of microgrid design is to maintain electrical power during utility grid problems whereas, EDVR should ensure the voltage sag/swell free power supply across loads. To validate this, three distinct cases have been made. The simulation results verified the performance of microgrid design and EDVR under proposed control methodology.
| Parameters | Values |
| Nominal per phase voltage Line Frequency | 190 V50 Hz |
| Line Impedance | R = 0.23 Ω, L = 2.75 mH |
| Load | 2.1k + j1.45k |
| DC link Capacitor of EDVR | 6980 uF |
| Rf | 0.07 Ω |
| Cf | 3 uF |
| Lf | 3.25 mH |
| Turn ration of CT | 1:1 |
DownLoad:
CSV
In this case, the performance of microgrid design under utility grid is assessed. The nominal voltage across the loads is 190 V and fundamental frequency is 50 Hz, Figure 16(a) shows the case when the utility grid experiences complete black out at 0.1 s due to fault in the grid side in this case, if no back up supply present then loads will suffer power outage. Figure 16(b) displays the RMS value of this case. Figure 16(c) shows the recovery of load voltage at 0.1 s when the utility grid supported with microgrid structure the load voltage immediately restores and power delivery to loads continue, Figure 16(d) shows the RMS value in this case. Figure 16(e, f) shows the output voltage of PV array (microgrid's DG) and its VI characteristic curve respectively.
This is the case in which the performance of EDVR has been assessed under voltage sag condition. The nominal voltage across the loads is 190 V and fundamental frequency is 50 Hz, Figure 17(a) shows the case when the line voltage experiences voltage sag at 0.1 s due to sudden load change, if no protection device present then this sag pass through load bus and damage electrical loads and power equipment. Figure 17(b) shows RMS value of this condition. Figure 17(c) shows the recovery from voltage sag when EDVR detects sag at 0.1 s and mitigate it in minimum time interval (approx. 5 ms) the RMS value in this case is shown in Figure 17(d). Figure 17(e) shows the regulated DC link voltage during voltage sag compensation. The proposed control approach enables EDVR to detect and resolve this voltage sag.
The nominal voltage across the loads is 190 V and fundamental frequency is 50 Hz, Figure 18(a) shows the case when the line voltage experiences voltage swell at 0.1 s due to single line to ground fault if no protection device present then this swell will pass through load bus and damage electrical loads and power equipment. Figure 18(b) shows RMS value of this condition. This is the case in which the performance of EDVR has been assessed under voltage swell condition. Figure 18(c) shows the recovery from voltage swell when EDVR detects sag at 0.1 s and mitigate it in minimum time interval (approx. 5 ms) the RMS value in this case is shown in Figure 18(d). Figure 18(e) shows the regulated DC link voltage during voltage swell compensation. The proposed control approach enables EDVR to detect and resolve this voltage swell.
In this paper, a microgrid and EDVR based power supply system is presented to increase utility grid reliability in terms of availability of power supply and voltage sag/swell free load supply, a comprehensive design approach is used to complete both tasks successfully. An efficient and stable control technique is proposed for DVR, presented control of DVR is composed of two separate control stages a fuzzy technique system-based control and enhanced synchronous reference frame EDVR based control. Fuzzy technique system-based control ensures detecting skills of DVR to detect voltage sag/swell whereas; EDVR ensures effectual mitigation of voltage sag/swell. Both sub-controls made DVR an enhanced DVR as it resolves voltage sag/swell with accuracy and speed. Presented results verified the performance of microgrid and EDVR based power supply system, modeling of VSC of DVR is conducted to perform its stability analysis. In the presence of this combined system the loads are completely secure from utility grid related faults as well as voltage sag/swell related power quality problems.
In future, different techniques can be used on the controller such as Sliding mode control, Fractional order sliding mode control and limitation of proposed control on the capacitor size will be removed in future work. Moreover, implementation of hardware and present EDVR as a market product. Other power quality problems can be resolved such as Harmonics, Frequency deviation, transients with the same control of EDVR.
All authors declare no conflicts of interest in this paper.
| [1] |
Zia MF, Benbouzid M, Elbouchikhi E, et al. (2020) Microgrid transactive energy: Review, architectures, distributed ledger technologies, and market analysis. IEEE Access 8: 19410–19432. doi: 10.1109/ACCESS.2020.2968402
|
| [2] |
Han Y, Ning X, Yang P, et al. (2019) Review of power sharing, voltage restoration and stabilization techniques in hierarchical controlled DC microgrids. IEEE Access 7: 149202–149223. doi: 10.1109/ACCESS.2019.2946706
|
| [3] | Wu X, Xu Y, He J, et al. (2019) Pinning-based hierarchical and distributed cooperative control for AC microgrid clusters. DIEEE Trans Power Elect, 1–20. |
| [4] | Natesan C, Kumar AS, Palani P, et al. (2014) Survey on microgrid: power quality improvement techniques. ISRN Otolaryngology. Available from: https://www.oalib.com/paper/3089465. |
| [5] |
Rocabert J, Luna A, Blaabjerg F, et al. (2012) Control of power converters in AC microgrids. IEEE Trans Power Electron 27: 4734–4749. doi: 10.1109/TPEL.2012.2199334
|
| [6] |
Frolov V, Thakurta PG, Backhaus S, et al. (2019) Operations and uncertainty-aware installation of FACTS devices in a large transmission system. IEEE Trans contral Network Syst 6: 961–970. doi: 10.1109/TCNS.2019.2899104
|
| [7] |
Nascimentoa S, Gouvêa M (2016) Voltage stability enhancement in power systems with automatic facts device allocation. Energy Procedia 107: 60–67. doi: 10.1016/j.egypro.2016.12.129
|
| [8] |
Wvong D, Mihirig AM (1986) Catastrophe theory applied to transient stability assessment of power systems. IEE Proceed 133: 314–318. doi: 10.1049/ip-d.1986.0052
|
| [9] |
Yorino N, Priyadi A, Kakui H, et al. (2010) A new method for obtaining critical clearing time for transient stability. IEEE Trans Power Syst 25: 1620–1626. doi: 10.1109/TPWRS.2009.2040003
|
| [10] |
Pradhan M, Mishra MK (2019) Dual P-Q theory based energy-optimized dynamic voltage restorer for power quality improvement in a distribution system. IEEE Trans Ind Elect 66: 2946–2955. doi: 10.1109/TIE.2018.2850009
|
| [11] | Ghahremani E, Kamwa I (2012) Optimal placement of multiple-type FACTS devices to maximize power system loadability using a generic graphical user interface. IEEE Trans Power Syst, 1–15. |
| [12] |
Prodanovixc M, Green TC (2006) High-quality power generation through distributed control of a power park microgrid. IEEE Trans Ind Elect 53: 1471–1482. doi: 10.1109/TIE.2006.882019
|
| [13] |
He L, Li Y, Guerrero JM, et al. (2020) A comprehensive inertial control strategy for hybrid AC/DC microgrid with distributed generations. IEEE Trans Smart Grid 11: 1737–1747. doi: 10.1109/TSG.2019.2942736
|
| [14] |
Nejabatkhah F, Li YW, Tian H (2019) Power quality control of smart hybrid AC/DC microgrids: An overview. IEEE Access 7: 52295–52318. doi: 10.1109/ACCESS.2019.2912376
|
| [15] | Shalukho AV, Lipuzhin IA, Voroshilov AA (2019) Power quality in microgrids with distributed generation. 2019 International ural conference on electrical power engineering (UralCon), 54–58. |
| [16] | Ovaskainen M, Rni J, Leinonen A (2019) Superposed control strategies of a BESS for power exchange and microgrid power quality improvement. IEEE International Conference on Environment and Electrical Engineering; IEEE Industrial and Commercial Power Systems Europe. Merus Power Dynamics Oy, Nokia, Finland. |
| [17] |
Baimel D, Belikov J, Guerrero JM, et al. (2017) Dynamic modeling of networks, microgrids, and renewable sources in the dq0 reference frame: A survey. IEEE Access 5: 21323–21335. doi: 10.1109/ACCESS.2017.2758523
|
| [18] |
Srivatchana NS, Rangarajanb P, Rajalakshmib S (2015) Control scheme for power quality improvement in Islanded. Procedia Technol 21: 212–215. doi: 10.1016/j.protcy.2015.10.090
|
| [19] | Dong T, Li L, Key ZM (2013) A combined system of APF and SVC for power quality improvement in microgrid. Power Engineering and Automation Conference (PEAM). Available from: https: //ieeexplore.ieee.org/document/6612554. |
| [20] |
Priyavarthini S, Kathiresan AC, Nagamani C, et al. (2018) PV-fed DVR for simultaneous real power injection and sag/swell mitigation in a wind farm. IET Power Electron 11: 2385–2395. doi: 10.1049/iet-pel.2018.5123
|
| [21] |
Nikoobakht A, Aghaei J, Parvania M, et al. (2018) Contribution of FACTS devices in power systems security using MILP-based OPF. IET Gener, Transm Distrib 12: 3744–3755. doi: 10.1049/iet-gtd.2018.0376
|
| [22] |
Roldan-Pxerez J, Garcxıa-Cerrada A, Ochoa-Gimenez M, et al. (2019) Delayed-signal-ancellation-based sag detector for a dynamic voltage restorer in distorted grids. IEEE Trans Sus Energy 10: 2015–2027. doi: 10.1109/TSTE.2018.2877505
|
| [23] |
Wang J, Xing Y, Wu H, et al. (2019) A novel dual-DC-port dynamic voltage restorer with reduced-rating integrated DC–DC converter for wide-range voltage sag compensation. IEEE Trans Power Electron 34: 7437–7449. doi: 10.1109/TPEL.2018.2882534
|
| [24] |
Li P, Xie L, Han J, et al. (2018) A new voltage compensation philosophy for dynamic voltage restorer to mitigate voltage sags using three-phase voltage ellipse parameters. IEEE Trans Power Electron 33: 1154–1166. doi: 10.1109/TPEL.2017.2676681
|
| [25] | Rawat MS, Vadhera S (2016) Comparison of FACTS devices for transient stability enhancement of multi machine power system. 2016 International Conference on Microelectronics, Computing and Communications. Available from: https://ieeexplore.ieee.org/document/7522419. |
| [26] | Ogunboyo PT, Tiako R, Davidson IE (2018) Effectiveness of dynamic voltage restorer for unbalance voltage mitigation and voltage profile improvement in secondary distribution system. Can J Elect Comput Eng 41: 105–114. |
| [27] | Maharashtra S (2013) Enhancement of voltage profile using dynamic voltage restorer. Int J Adv Res Elect, Elect Instrum Eng (IJAREEIE) 2: 5871–5876. |
| [28] | Ramasamy AK, Iyer RK, Chandaramuthy VK, et al. (2005) Dynamic voltage restorer for voltage sag compensation. IEEE PEDS, 1289–1294. |
| [29] |
Hagha MT, Shakera A, Sohrabia F, et al. (2017) Fuzzy-based controller for DVR in the presence of DG. Procedia Comput Sci 120: 684–690. doi: 10.1016/j.procs.2017.11.296
|
| [30] |
Razak HNA, Said DM, Ahmad N (2018) Improved analysis of DVR performance for voltage sag mitigation. ELEKTRIKA-J Elect Eng 17: 36–40. doi: 10.11113/elektrika.v17n3.110
|
| [31] | Rao SS, Krishna PSR, Babu S (2017) Mitigation of voltage sag, swell and THD using dynamic voltage restorer with photovoltaic system. International Conference on Algorithms, Methodology, Models and Applications in Emerging Technologies (ICAMMAET), 1–7. |
| [32] | Ma H, Du C (2015) Multi-objective coordinated design of TCSC and SVC for improving transient stability fifth. International Conference on Instrumentation and Measurement, Computer, Communication and Control, 246–250. |
| [33] |
Zheng ZX, Xiao XY, Chen XY, et al. (2018) Performance evaluation of a MW-class SMES-BES DVR system for mitigation of voltage quality disturbances. IEEE Trans Ind Appl 54: 3090–3099. doi: 10.1109/TIA.2018.2823259
|
| [34] |
Remya VK, Parthiban P, Ansal V, et al. (2018) Dynamic voltage restorer (DVR)–A review. J Green Eng 8: 519–572. doi: 10.13052/jge1904-4720.844
|
| [35] | Riddhi FB (2018) Study on compensation of voltage sag and voltage swell by using DVR (Dynamic Voltage Restorer). IEEE International Conference on Current Trends toward Converging Technologies, Coimbatore, 1–12. |
| [36] | Tiwari SP, Sharma PK (2017) Synchronous reference frame theory for active power filter. Int J Eng Sci Comput 7. Available from: https://www.researchgate.net/publication/335602113_synchronous_reference_frame_theory_for_active_power_filter. |
| [37] |
EIAdany M, EIDesouky A, Sallam A (2018) Power system transient stability: An algorithm for assessment and enhancement based on catastrophe theory and FACTS devices. IEEE Access 6: 26424–26437. doi: 10.1109/ACCESS.2018.2834906
|
| [38] |
Dash SK, Ray PK (2018) Power quality improvement utilizing PV fed unified power quality conditioner based on UV-PI and PR-R controller. CPSS Trans Power Electron Appl 3: 243–253. doi: 10.24295/CPSSTPEA.2018.00024
|
| [39] | Bhushan S, Rakhonde A, Bobade CM (2017) Harmonic mitigation using modified synchronous reference frame theory. IRJET 4: 2340–2345. |
| [40] | Zheng Z, Xia X, Huang C, et al. (2019) Enhancing transient voltage quality in a distribution power system with SMES-based DVR and SFCL. IEEE Trans Appl Supercond 29: 1–5. |
| [41] |
Zhai H, Zhuo F, Zhu C, et al. (2020) An optimal compensation method of shunt active power filters for system-wide voltage quality improvement. IEEE Trans Power Electron 67: 1270–1281. doi: 10.1109/TED.2020.2967242
|
| [42] | Karthikeyan A, Gururaj D, Krishna A, et al. (2010) Dual role CDSC-based dual vector control for effective operation of DVR with harmonic mitigation. IEEE Trans Power Electron 66: 4–13. |
| [43] | Singh B, Solanki J (2009) A comparison of control algorithms for dstatcom. IEEE Trans Power Electron 56: 2738–2745. |
| [44] | Choudante SD, Bhole AA (2018) A review: Voltage stability and power flow improvement by using UPFC controller. 2018 International conference on computation of power, energy, information and communication (ICCPEIC), 462–465. |
| [45] | Upadhyay P, Singh N, Yadav S (2018) Voltage quality compensation of DFIG with series DVR (SDVR) under three phase fault. International Conference on Electronics, Materials Engineering and Nano-Technology. Available from: https://ieeexplore.ieee.org/document/8465397. |
| [46] | Biricik S, Komurcugil H, Tuyen ND, et al. (2019) Protection of sensitive loads using sliding mode controlled three-phase DVR with adaptive notch filter. IEEE Trans Power Electron 66: 5465–5475. |
| [47] | Kamarposhti MA, Lesani H (2010) Comparison between parallels and series FACTS devices on static voltage stability using MLP index. International symposium on power electronics, electrical drives, automation and motion, 257–261. |
| [48] | Prakash Y, Sankar S (2014) Power quality improvement using DVR in power system. Power and energy systems: Towards sustainable energy (PESTSE), 1–6. |
| [49] |
Zong S, Fan G, Yang X (2019) Double voltage rectification modulation for bidirectional DC/DC resonant converters for wide voltage range operation. IEEE Trans Power Electron 34: 6510–6521. doi: 10.1109/TPEL.2018.2875816
|
| [50] |
Zia MF, Benbouzid M, Elbouchikhi E, et al. (2020) Microgrid transactive energy: Review, architectures, distributed ledger technologies, and market analysis. IEEE Access 8: 19410–19432. doi: 10.1109/ACCESS.2020.2968402
|
| [51] |
Lu Y (2018) Adaptive-fuzzy control compensation design for direct adaptive fuzzy control. IEEE Trans Fuzzy Syst 26: 3222–3231. doi: 10.1109/TFUZZ.2018.2815552
|
| [52] | Meng L, Guerrero JM (2017) Optimal power quality service in multi-bus microgrid systems. 2017 IEEE Power & Energy Society General Meeting. Available from: https://ieeexplore.ieee.org/document/8274169. |
| [53] | Zhong Q, Yao W, Lin L, et al. (2018) Data analysis and applications of the power quality monitoring. International Conference on Power System Technology (POWERCON), 6–8. |
| [54] |
Omar AI, Shady HE, Aleem A, et al. (2019) An improved approach for robust control of dynamic voltage restorer and power quality enhancement using grasshopper optimization algorithm. ISA Trans 95: 110–129. doi: 10.1016/j.isatra.2019.05.001
|
| [55] |
Talwariya A, Singh P, Kolhe ML, et al. (2020) Fuzzy logic controller and game theory based distributed energy resources allocation. AIMS Energy 8: 474–492. doi: 10.3934/energy.2020.3.474
|
| [56] |
Poullikkas A, Papadouris S, Kourtis G, et al. (2014) Storage solutions for power quality problems in cyprus' electricity distribution network. AIMS Energy 2: 1–17. doi: 10.3934/energy.2014.1.1
|
| [57] |
Ahmed eldessouky and hossam gabbar (2016) SVC control enhancement applying self-learning fuzzy algorithm for islanded microgrid. AIMS Energy 4: 363–378. doi: 10.3934/energy.2016.2.363
|
| [58] | Patnaik RK, Mishra SP, Patra JP (2015) Active and reactive power based feedback linearization control technique for grid-connected voltage source converter. Power Communication and Information Technology Conference (PCITC), 290–296. |
| 1. | Ahsan Iqbal, Asad Waqar, Rajvikram Madurai Elavarasan, Manoharan Premkumar, Toqeer Ahmed, Umashankar Subramaniam, Saad Mekhilef, Stability assessment and performance analysis of new controller for power quality conditioning in microgrids, 2021, 2050-7038, 10.1002/2050-7038.12891 | |
| 2. | Md. Fatin Ishraque, Akhlaqur Rahman, Sk. A. Shezan, S. M. Muyeen, Grid Connected Microgrid Optimization and Control for a Coastal Island in the Indian Ocean, 2022, 14, 2071-1050, 16697, 10.3390/su142416697 | |
| 3. | Adib Aktab Arnab, Md. Tahmid Jamil, Rafsan Huda, Mosiur Rahman, Ata E Rabbi, Tareq Aziz, 2022, A Study of Enhancing PV Hosting Capacity in an Industrial Microgrid, 978-1-6654-5577-0, 1, 10.1109/ICEPE56629.2022.10044897 | |
| 4. | Essam A. Al-Ammar, Azhar Ul Haq, Ahsan Iqbal, Wonsuk Ko, Marium Jalal, Muhammad Almas Anjum, Hyeong-Jin Choi, Hyun-Koo Kang, Synchronous Reference Frame Theory Based Intelligent Controller for Current THD Reduction, 2021, 16, 1975-0102, 2917, 10.1007/s42835-021-00824-3 | |
| 5. | Salman Ahmed Khan, Prof. Sanjeev Jarariya, AI Based system Performance Enhancement Fed by BESS with grid Integration, 2021, 2582-4600, 44, 10.24113/ijoscience.v7i8.403 | |
| 6. | Md. Fatin Ishraque, Akhlaqur Rahman, Sk. A. Shezan, GM Shafiullah, Operation and Assessment of a Microgrid for Maldives: Islanded and Grid-Tied Mode, 2022, 14, 2071-1050, 15504, 10.3390/su142315504 | |
| 7. | Anna Ostrowska, Łukasz Michalec, Marek Skarupski, Michał Jasiński, Tomasz Sikorski, Paweł Kostyła, Robert Lis, Grzegorz Mudrak, Tomasz Rodziewicz, Power Quality Assessment in a Real Microgrid-Statistical Assessment of Different Long-Term Working Conditions, 2022, 15, 1996-1073, 8089, 10.3390/en15218089 | |
| 8. | Vladimir Z. Kovalev, Alexander G. Shcherbakov, Rustam N. Khamitov, Development of a method for analysis and forecast of the quality of electric power microgrid in the Far North, 2022, 18, 2078-9114, 67, 10.18822/byusu20220167-78 | |
| 9. | Shaila Arif, Ata E Rabbi, Shams Uddin Ahmed, Molla Shahadat Hossain Lipu, Taskin Jamal, Tareq Aziz, Mahidur R. Sarker, Amna Riaz, Talal Alharbi, Muhammad Majid Hussain, Enhancement of Solar PV Hosting Capacity in a Remote Industrial Microgrid: A Methodical Techno-Economic Approach, 2022, 14, 2071-1050, 8921, 10.3390/su14148921 | |
| 10. | Tanmoy Parida, Anshuman Satpathy, Niranjan Nayak, Arun Kumar Sahoo, 2022, An Artificial Intelligence Based Robust Controller for Power Quality Improvement in AC Micro Grid, 978-1-6654-7839-7, 1, 10.1109/ODICON54453.2022.10010312 | |
| 11. | Abhishek Kumar, Yan Deng, Xiangning He, Arvind R. Singh, Praveen Kumar, R.C. Bansal, M. Bettayeb, C. Ghenai, R.M. Naidoo, Impact of demand side management approaches for the enhancement of voltage stability loadability and customer satisfaction index, 2023, 339, 03062619, 120949, 10.1016/j.apenergy.2023.120949 | |
| 12. | Franz Teske, Jano Schubert, Adrian Fehrle, Felix Funk, Jörg Franke, Techno-economic analysis of battery storage systems and hydrogen-based storage systems as an alternative to grid expansion in the medium voltage grid in Germany, 2023, 11, 2333-8334, 358, 10.3934/energy.2023019 | |
| 13. | Viktor Denysov, Tatiana Eutukhova, Dynamic models for developing reference scenarios of energy system in the low-carbon transition, 2024, 2024, 27867633, 17, 10.15407/srenergy2024.01.017 | |
| 14. | G. Indira Rani, V.Sunil Kumar, R. Rishith, M. Abhishek, 2024, Improving Voltage Stability in Fixed Speed Wind Energy Conversion System using FACTS Controller (STATCOM), 979-8-3503-6115-5, 1, 10.1109/INCET61516.2024.10593593 | |
| 15. | Poornima Aldi, Shilpa Shrigiri, K Smita, 2023, Study of Topologies, Power Converters, and Control Techniques for the Dynamic Voltage Restorer (DVR), 979-8-3503-1545-5, 1, 10.1109/ICIICS59993.2023.10421409 | |
| 16. | Essamudin Ali Ebrahim, Maged N. F. Nashed, Mona N. Eskander, Hardware in the Loop-Based Testing of Three Schemes for Mitigation the Effect of Unsymmetrical Grid Faults on DFIG, 2023, 18, 2224-350X, 203, 10.37394/232016.2023.18.22 | |
| 17. | Peng Cao, Daowang Wang, Xingyang Jiang, Optimization of emission scheduling in microgrids with electric vehicle integration, 2024, 11, 2731-9237, 10.1186/s40807-024-00134-y |
Figures(36) / Tables(3)
Ahsan Iqbal, Ayesha Ayoub, Asad Waqar, Azhar Ul-Haq, Muhammad Zahid, Syed Haider. Voltage stability enhancement in grid-connected microgrid using enhanced dynamic voltage restorer (EDVR)[J]. AIMS Energy, 2021, 9(1): 150-177. doi: 10.3934/energy.2021009
| Rule No. | Sag Disturbance | Swell Disturbance | EDVR Output |
| 1 | no | no | off |
| 2 | yes | no | on |
| 3 | no | yes | on |
DownLoad:
CSV
| Value | |
| Eigen values of Control System | －0.0011 + 1.0127i －0.0011 − 1.0127i |
| kp | 15 |
| ki | 25 |
DownLoad:
CSV
| Parameters | Values |
| Nominal per phase voltage Line Frequency | 190 V50 Hz |
| Line Impedance | R = 0.23 Ω, L = 2.75 mH |
| Load | 2.1k + j1.45k |
| DC link Capacitor of EDVR | 6980 uF |
| Rf | 0.07 Ω |
| Cf | 3 uF |
| Lf | 3.25 mH |
| Turn ration of CT | 1:1 |
DownLoad:
CSV
| Rule No. | Sag Disturbance | Swell Disturbance | EDVR Output |
| 1 | no | no | off |
| 2 | yes | no | on |
| 3 | no | yes | on |
| Value | |
| Eigen values of Control System | －0.0011 + 1.0127i －0.0011 − 1.0127i |
| kp | 15 |
| ki | 25 |
| Parameters | Values |
| Nominal per phase voltage Line Frequency | 190 V50 Hz |
| Line Impedance | R = 0.23 Ω, L = 2.75 mH |
| Load | 2.1k + j1.45k |
| DC link Capacitor of EDVR | 6980 uF |
| Rf | 0.07 Ω |
| Cf | 3 uF |
| Lf | 3.25 mH |
| Turn ration of CT | 1:1 |
