Strongly-coupled and predator-prey subelliptic system on the Heisenberg group

1.   Introduction

This article investigates the stability of the nonlinear magnetic diffusion equation and its fully implicit discrete scheme for the following equation system in ^[1]:

where $B$ is the magnetic field, $e$ is the internal energy density (that is, internal energy per volume), $\mu_0$ is the vacuum permeability constant $({\mu _0} = 4\pi \times {10^{ - 7}}$N/A$^2)$, and $\eta(e)$ is the resistivity in the material. The relationship between $\eta(e)$ and $e$ results in nonlinearity of the diffusion term $\frac{\partial}{\partial x}(\frac{\eta(e)}{\mu_{0}}\frac{\partial}{\partial x}B(x, t))$ in (1.1).

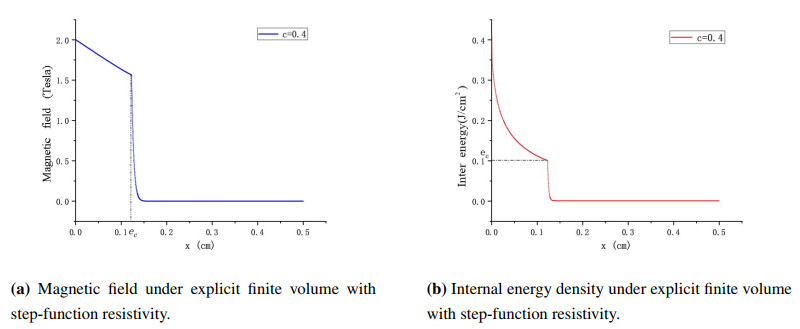
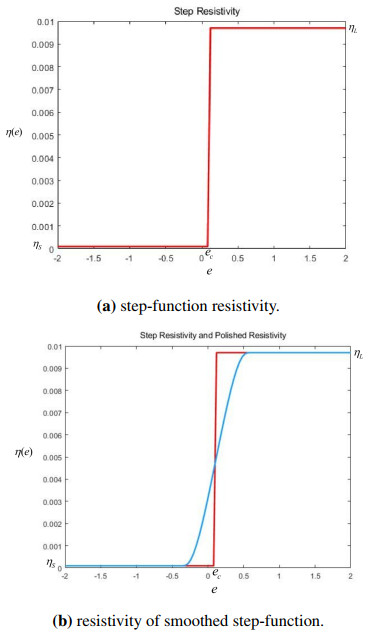
The resistivity $\eta(e)$ in the equation system (1.1) is a step-function, as shown in Figure 1a:

$e_c = 0.11084958$, representing the critical value of internal energy density.

In electromagnetic loading experiments^[2], when the magnetic field outside the metal wall is relatively small (below 10 T), the driving current is also very small, the heating in the metal is weak, the temperature rise is slow, and the change in metal resistivity is not significant. At this point, the diffusion of the magnetic field exhibits behavioral characteristics similar to common diffusion phenomena such as thermal diffusion and concentration diffusion. When the magnetic field outside the metal wall reaches a strong magnetic field level of 100 T, the diffusion of the magnetic field in the metal will exhibit a nonlinear magnetic diffusion wave phenomenon. Compared to ordinary magnetic diffusion in metals, nonlinear magnetic diffusion waves have higher penetration rates and velocities, which can cause rapid magnetic flux leakage and device load erosion in high-energy-density physical experiments. Although nonlinear magnetic diffusion waves in metals with strong magnetic fields were proposed as early as 1970, it was not until after 2000 that phenomena related to nonlinear magnetic diffusion waves gradually attracted people's attention with the widespread development of electromagnetic driven high-energy-density physics experiments. The fundamental reason for the formation of nonlinear magnetic diffusion waves is that during the process of metal temperature rise caused by magnetic diffusion, the metal resistivity also changes accordingly^[3]. Before the metal forms a highly conductive plasma, the overall resistivity shows an upward trend. After metal gasification, as the temperature increases, the degree of metal vapor ionization increases, and the resistivity gradually decreases. In ^[4,5], authors such as B. Xiao assume that the electrical resistivity of metals undergoes a sudden change of several orders of magnitude after reaching a critical temperature, while the electrical resistivity before and after the sudden change is independent of temperature. They consider an approximate theoretical analytical solution for one-dimensional steep-gradient surface magnetic diffusion waves under the step-function resistivity model. In ^[1], C. H. Yan et al. designed an explicit finite volume discretization scheme for one-dimensional magnetic field diffusion problems based on the step resistivity model. By relaxing the time step, the formulas for excessive magnetic flux transport and total internal energy transport were truncated when solving strong magnetic diffusion problems. On the basis of using the truncated magnetic flux transport capacity and total internal energy transport capacity, the program can allow for larger time steps without causing oscillation dispersion. In addition, there are also some studies on magnetic diffusion problems, such as ^[6,7,8].

The stability of solutions is an important issue in the study of differential equations. Stability generally refers to the behavior of the solution remaining unchanged or tending to a certain equilibrium state when there is a small disturbance in the initial or boundary conditions of the equation. In ^[9], Y. L. Zhou et al. studied a class of parallel nature difference schemes for the initial boundary value problem of quasi-linear parabolic systems, and proved the unconditional stability of the constructed parallel nature difference scheme solutions under the discrete $W_{2}^{(2, 1)}$ norm. In ^[10], author G. W. Yuan proved the uniqueness and stability of the obtained difference solution under the general non-uniform grid difference scheme. In ^[11,12], based on the non-uniform grid difference scheme, the authors constructed and developed an implicit discrete scheme that maintains the conservation of the implicit scheme while maintaining the required accuracy and unconditional stability for parallel computing through various methods such as estimation correction, to meet the needs of large-scale numerical solutions to radiation fluid dynamics problems.

The magnetic diffusion problem studied in this article is also based on the step-function resistivity model. We first reproduced the results of equation system (1.1) in ^[1] (under explicit finite volume discretization scheme):

Next, in the magnetic diffusion equation system (1.1), the smoothed step-function resistivity $\eta_\delta(e)$ is used, where $\delta$ is used to describe the distance from the smooth curve inflection point to $e_c$, as shown in Figure 1b. The experimental results of the implicit finite volume method are as follows:

The above experiment indicates that by replacing the step-function resistivity $\eta(e)$ in equation system (1.1) and using the smoothed step-function resistivity model $\eta_\delta(e)$, the experimental results in ^[1] can be well reproduced. Can the modified resistivity maintain the stability of the solution to the magnetic diffusion equation? What are the advantages of the corrected resistivity compared to the step-function resistivity? These are the starting points of this study and will be answered one by one in the following text. Below, we will first theoretically prove that the solution of the one-dimensional nonlinear magnetic diffusion equation and its fully implicit scheme under the smoothed step-function resistivity are stable with initial values. Then, the correctness and stability of the magnetic diffusion model under the smoothed step-function resistivity in the implicit finite volume discrete scheme are further verified through comparative experiments of explicit and implicit schemes^[13].

2.   Mathematical preliminaries

A measurable function $u[0, T] \rightarrow X$ that satisfies the following conditions:

forms the $L^p(0, T; X)$ space.

The polishing function $J(x)$ satisfies

and the conclusions are as follows.

Lemma 1 (^[14]). For any $\epsilon > 0$, when taking $J_{\epsilon}(x) = \frac{1}{\epsilon} J\left(\frac{x}{\epsilon}\right)$, $J\left(x\right)$ and $J_{\epsilon}(x)$ satisfy the following properties:

(1) $J\left(x\right) \in C^{\infty}\left(\mathbb{R}\right)$, and when $\left|x\right| \geq 1, k \in \mathbb{N}$, $J^{\left(k\right)}\left(x\right) = 0$;

(2) ${\int}_\mathbb{R} J\left(x\right) \, \mathrm{d}x = {\int}_\mathbb{R} J_{\epsilon}\left(x\right) \, \mathrm{d}x = 1$.

Then, the step-function resistivity (1.2) can be smoothed to the following continuous differentiable function:

where,

According to ^[14], it is easy to know that the resistivity (2.3) after the effect of the polishing function (2.1) satisfies the following properties:

Thereby, $\eta_\delta(e)$ in (2.2) is continuously differentiable across all real number fields. Further, $\eta_{\delta}(e)$ converges to $\eta(e)$: $\eta(e)$ is integrable on ${I_\epsilon} = [e_c-\epsilon, e_c+\epsilon]$. By the Lemma 1, for each $x\in {I_\epsilon} = [e_c-\epsilon, e_c+\epsilon]$, there is ${\int}_{\mathbb{R}} J_{\epsilon}\left(x - y\right) \, \mathrm{d}y = 1$, and for any $\epsilon > 0$, it is easily available that

where $C = max{|J_\epsilon(x-y)|}$, and $\eta_S, \eta_L$ are the minimum and maximum values of $\eta(e)$. Thus, it can be concluded that $lim_{\epsilon\rightarrow0}\eta_\delta(x) = \eta(x)$.

Remark: This provides us with a theoretical basis for a stability proof by replacing the step-function resistivity $\eta(e)$ in equation system (1.1) with the smoothed resistivity $\eta_\delta(e)$ (continuous, differentiable).

Lemma 2. (Young's inequality) If $p > 1, q > 1,$ such that $\frac1p+\frac1q = 1$, then $\forall a, b\geq0$, the following inequality holds:

and specifically, when $a = \sqrt{\varepsilon }u, b = \frac{v}{2\sqrt{\varepsilon}}$, Young's inequality can be expressed as

Lemma 3. (Continuous Gronwall' inequality) Let $g(t)$ and $h(t)$ be non negative integrable functions, and satisfy $f'(t)\leq f(t)g(t)+h(t)$. The following inequality holds:

Lemma 4. (Discrete Gronwall' inequality)^[15] Let $\{f^n\}$, $\{g^n\}$, and $\{h^n\}$ be sequences of non-negative functions satisfying, $\frac{f^{n+1}-f^{n}}{\Delta t} \leq f^{n+1}g^{n+1} +h^{n+1}$, for $\forall \alpha > 1$, such that

where $\Delta t > 0$. Then, the following inequality holds:

where $C$ and $\tau$ are constants that depend on the initial conditions.

Lemma 5. (Abel's identity) Let $\{a_n\}$ and $\{b_n\}$ be sequences of real or complex functions. If $Q_n = \sum_{i = 1}^nb_i$, the following identity holds:

Lemma 6. (Embedding inequality)

derived from the Poincaré inequality, $w(\cdot, t) \in H_0^1(0, l)$. Then, the inequality $\|w(\cdot, t)\|_{2} \lesssim \|w_x(\cdot, t)\|_{2}$ holds. Substituting this inequality into (2.9) yields $\|w(\cdot, t)\|_{\infty}^2 \lesssim \|w_x(\cdot, t)\|_{2}^2$.

Lemma 7. (Discrete embedding inequality) (space direction)

and similar to Lemma 6, it is easy to derive $\|w_{h}^{k}(\cdot, t)\|_{\infty}^2 \lesssim \|\delta w{_{h}^{k}}(\cdot, t)\|_{2}^2$.

Remark: The conclusions of Lemmas 6 and 7 hold only in one dimension.

Lemma 8. (Discrete embedding inequality) (time direction)

3.   Stability proof of one-dimensional magnetic diffusion equation

3.1.   Homogeneous boundary conditions

This section proves that the equation is stable with initial values. Now, we will transform the non-zero boundary value problem into a non-zero initial value problem.

Let $B({x}, t) = u({x}, t)+v({x}, t)$, and $v({x}, t)$ satisfies the boundary conditions in (3.1), that is,

Construct auxiliary functions $v({x}, t) = 0.2-\dfrac{2}{5}{x}$, $x\in [0, 0.5]$, based on boundary conditions. Then, the equation satisfying the definite solution condition in (3.1) with respect to $u({x}, t)$ is

Remark: The equation to be proved below indicates the stability with respect to initial values, which also implies the stability of the original equation with respect to boundary values.

3.2.   The proof of stability

Consider the one-dimensional magnetic diffusion equation with Dirichlet boundary as follows:

where, $B$ and $\widetilde{B}$ are the magnetic field, and $e$ and $\widetilde{e}$ are the internal energy density ($e = e(B), \; \widetilde{e} = e(\widetilde{B})$).

The solutions of Eqs (3.3) and (3.4) belong to $L^{\infty}(0, T;H_0^1(0, l))\cap L^{2}(0, T;H^2(0, l))$, and the following is an inequality for energy estimation:

On the premise of not causing misunderstandings, for the convenience of labeling and calculation, in this section, we still use $\eta(e)$ to represent the step-function resistivity after polishing. Let $w(x, t) = B(x, t)-\widetilde{B}(x, t)$, and based on the differentiability of the smoothed resistivity $\eta(e)$, it can be assumed that the derivatives of $\eta$ and $e$ satisfy the following relationship:

Remark: The $c_1$ in (3.6) depends on the value of $\epsilon$ in (2.3).

Subtract the first equation in (3.3) from the first equation in (3.4) to obtain

The above equation can be changed to

According to the Lagrange mean value theorem, $\eta(e(B))-\eta(e(\widetilde{B}))$ in (3.8) can be resolved as

where, $\eta_e(\zeta)$ represents the first derivative of $\eta$ with respect to $e$, $\zeta$ is the value between $e(B)$ and $e(\widetilde{B})$, $e^\prime{(\xi)}$ represents the first derivative of $e$ with respect to $B$ and $\widetilde{B}$, and $\xi$ is the value between $B$ and $\widetilde{B}$.

Substituting (3.9) into (3.8) yields

Multiply $w_{xx}$ on both sides of (3.10) and integrate on $x\in(0, l)$ to obtain

The first term at the left end of the above equation can be written by the partial integration method as follows:

By combining (1.2) $\eta(e)\geq \eta_S > 0$ with (3.12), the left end of (3.11) can be simplified as

that is,

Take absolute values on both sides of (3.13) and obtain from (3.11)

On the basis of the assumption (3.6), (3.14) can be resolved as

and according to the Lemma 2 (Young's inequality), (3.15) can be transformed into

where $c_3 = c_1\varepsilon_1+2c_1\varepsilon_2+c_1c_2\varepsilon_3$.

By the Lemma 6 (embedding inequality)

Remark: The conclusion of (3.17) only holds for one-dimensional cases.

Substitute (3.17) into (3.16), and from the energy estimation inequality (3.5), obtain

where $c_9 = c_5C\|B_x(\cdot, 0)\|_2^2$.

According to (3.18)

so

Remark: $c_3 = c_1\varepsilon_1+2c_1\varepsilon_2+c_1c_2\varepsilon_3$ can ensure that $\eta_S-c_{3} > 0$.

Substitute (3.20) into the right-hand end of (3.18), and organize it to obtain

In (3.21), on the one hand

In (3.22), take $f^\prime(t) = \dfrac{d}{dt}\|w_{x} \|_2^2$, $f(t) = \|w_{x} \|_2^2$, $g(t) = c_{10}(1+\|\widetilde{B}_{xx}\|_2^2)$, $h(t) = c_{11}$, by using the Lemma 3 (continuous Gronwall' inequality), it can be concluded that

On the other hand, as can be seen from (3.21).

Integrate the two sides of Eq (3.24) in the time direction on $[0, T]$ and obtain from (3.23)

From (3.23) and (3.25), it can be concluded that

Thus, the stability of the magnetic diffusion equation is proven.

3.3.   Stability of fully implicit scheme for magnetic diffusion equation

The following proves the stability of the fully implicit scheme corresponding to Eq (3.3) or (3.4):

taking

The energy estimation in the discrete scheme is

Let $w_j^{n+1} = B_j^{n+1}- {\widetilde{B}}_j^{n+1}$, and subtract the first equation in (3.27) from the first equation in (3.28) to obtain:

After applying the Lagrange mean value theorem to the above equation, the following is obtained:

where $\delta\eta(\zeta_{j}^{n+1})$ represents the first derivative of $\eta$ with respect to $e$, $\zeta_{j}^{n+1}$ is the value between $e(B_{j}^{n+1})$ and $e(\widetilde{B}_{j}^{n+1})$, $\delta e{(\xi_{j}^{n+1})}$ represents the first derivative of $e$ with respect to $B_{j}^{n+1}$ or $\widetilde{B}_{j}^{n+1}$, and $\xi_{j}^{n+1}$ is the value between $B_{j}^{n+1}$ and $\widetilde{B}_{j}^{n+1}$.

Multiply $\delta^{2}w_j^{n+1}$ on both sides of (3.30), and sum $j = 1, 2, \ldots, J-1$ to obtain

We can consider the first term in equation (3.31)

Let

Using Lemma 5 (Abel's identity), it can be obtained that

According to the inequality

Let $u = \frac{w_{j}^{n+1}-w_{j-1}^{n+1}}{h}$, $v = \frac{w_{j}^{n}-w_{j-1}^{n}}{h}$, and from (3.34), (3.33) can be changed to

that is

From $\eta > \eta_S$ and substituting (3.36) into (3.31), it can be concluded that

By the assumption (3.6)

Applying Lemma 2 (Young's inequality) to Eq (3.38) yields

From the energy estimation inequality (3.29) and Lemma 7 (discrete embedding inequality, space direction), (3.39) can be expressed as

Let $a = \frac{2 \eta_S}{\mu_0}$, and according to (3.40)

so

Substituting (3.42) into the right-hand side of (3.40) yields

Summing the two sides of (3.43) with respect to $n$, from inequality (3.29), it can be concluded that:

According to Lemma 7, the right-hand side of the (3.44) inequality can be written as

From (3.45),

and then,

Substituting (3.47) into the right-hand of (3.45) yields

On the basis of Lemma 8 (discrete embedding inequality, time direction), $\|w_h^{k+1}\|_2^2$ on the right hand of (3.48) can be expressed as

Using the bootstrapping and fully utilizing the properties of the format itself, it can be concluded from (3.30) that

Substitute the above equation into (3.49), use the energy estimation inequality (3.29) and the assumption condition (3.6), and repeat the above steps to obtain

that is,

For the $\|w_h^{m}\|_2^2$ in the above equation, the embedding theorem is applied to obtain: $\| w_h^{m}\|_2^2\leq\| w_h^{m}\|_\infty^2 \leq \|\delta w_h^{m}\|_2^2$. Thus(3.51) can be simplified as

Substituting (3.52) into (3.48) yields

Similarly, by

it can be inferred that

Thereby it can be deduced that

Substituting (3.56) into the right end of (3.53) yields

By Lemma 2.7 (discrete Gronwall inequality), we have

and from (3.57),

Then, take $f^n = \sum_{k = 0}^{n}\|\delta w_h^{k+1}\|_2^2\Delta t$, $g^{n+1} = c_{25}$, $h^{n+1} = c_{26}(\|w_{h}^{0}\|_2^{2}+\|\delta w_h^{0}\|_2^2)$, and we can obtain

Substituting (3.60) into (3.57) yields

Thus the stability of the discrete scheme is demonstrated.

4.   Numerical verification

4.1.   Verification of correctness of discrete scheme

Next, we will verify the correctness of the implicit finite volume discretization scheme for the magnetic diffusion equation with constant resistivity, and consider the following magnetic diffusion equation:

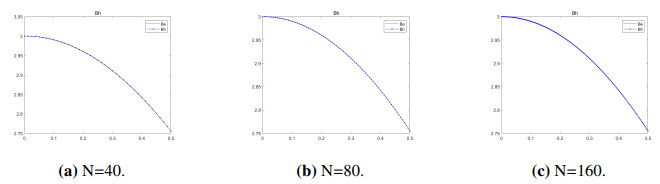
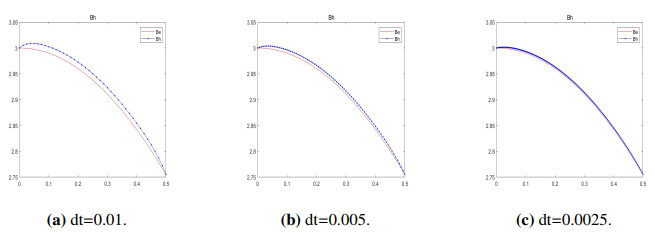
The solution interval is $(x, t)\in[0, 0.5]\times[0, 1]$. Take $\mu_0 = 4\pi$. The number of mesh segments is, respectively $N = 40, 80,160$, and the number of nodes is, respectively, $N_1 = 41, 81,161$. The resistivity $\eta = 9.7\times10-3$. The length of the line segment $L = 0.5$, the average length of the grid $dx = L/N$, $T = 1$, and the time step $dt = dx\ast dx$. It is easy to know that the true solution to this problem is $B(x, t) = 2cos(x)+t^2$. The error used in the experiment is $L_2$, that is, $Error_{L_2} = \sqrt{\frac{\Sigma_{n = 1}^{N_1}(B-B_{exact})^2}{N_1}}$.

Conclusions: From the above comparative experiments, it can be seen that when the grid size increases by 2 times with a fixed time scale, the error ratio between the experimental results and the true solution is close to 4. When the grid size is fixed, and the time scale increases by 2 times, the error ratio between the experimental results and the true solution is equal to 2, which conforms to the expected experimental errors of $o(h^2)$ and $o(t)$, thus verifying the correctness of the implicit finite volume discretization scheme in this experiment.

4.2.   Stability experiments with different resistivities

In this experiment, the true solution is denoted as $B$, and the perturbation solution is denoted as $B_\varepsilon$. $B^{100}$ represents the true solution at time step $dt = 0.01$, and $B_\varepsilon^{100}$ represents the perturbation solution at time step $dt = 0.01$. The error ratio still uses $L_2$.

Experiment (1): Step-function resistivity

Conclusions: Under the same time step $dt$, when there is a small disturbance in the initial value, the error ratio changes significantly, indicating that the solution of the magnetic diffusion equation under step-function resistivity cannot be stable based on the initial value.

Experiment (2): Constant resistivity $\eta(e) = 9.7e-3$.

Experiment (3): Linear resistivity $\eta(e) = 9.7e-3$.

where, $e_c = 0.11084958$.

Experiment (4): The step-function resistivity after polishing.

Conclusion: From experiments (2), (3), and (4), it can be seen that under the same time step $dt$, when there is a small disturbance in the initial value, the error ratio does not change much. Especially, the solution of the magnetic diffusion equation under the smoothed step-function resistivity model has good stability. This is also the advantage of smoothed step-function resistivity $\eta_\delta(e)$ compared to step-function resistivity $\eta(e)$.

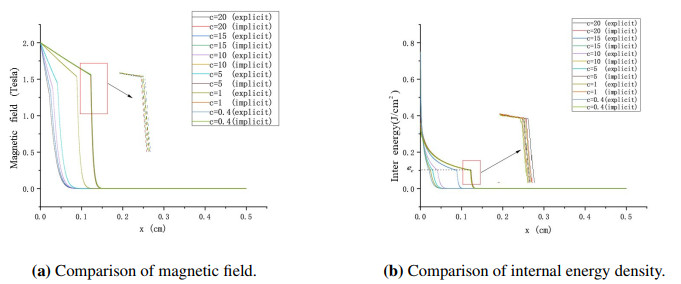
4.3.   Comparison experiment of explicit and implicit schemes under step-function resistivity

In the comparison experiment between explicit and implicit schemes, we take $dt = \frac{c\mu_0*(dx)^2}{\eta_L}$, where, $\mu_0 = 4\pi$, $dx = L/N$, $\eta_L = 100\times9.7\times 10-3$. Therefore, $c$ is the factor that affects $dt$, and the larger $c$ is, the larger the time step $dt$.

Conclusions: From the comparison experiment in the figure above, it is evident that when we use the curve at $c = 0.4$ as the true solution graph, as the value of $c$ increases (that is, as the time step increases), the explicit solution gradually diverges from the true solution. In contrast, the implicit solutions remain nearly identical to the true solution, with differences only noticeable upon close inspection. This observation further demonstrates the strong stability and weak time step constraints of the fully implicit method. These characteristics particularly underscore the superiority of the fully implicit method, especially when dealing with models exhibiting strong nonlinearity.

Author contributions

Gao Chang: Conceptualization, Writing–original draft, Data curation, Software, Investigation; Chunsheng Feng: Conceptualization, Software, Writing–review and editing, Methodology; Jianmeng He: Conceptualization, Writing–review and editing, Validation, Investigation; Shi Shu: Conceptualization, Supervision, Formal analysis, Methodology, Writing–review and editing. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to express their gratitude to Professor Guangwei Yuan and Associate researcher Bo Xiao for their valuable contributions and support during the course of this research. This work was partially supported by the National Science Foundation of China (Grant No. 12371373), the National Key Research and Development Program of China (Grant No. 2023YFB3001604), the Hunan innovative province construction special project (Grant No. 2022XK2301), and the Postgraduate Scientific Research Innovation Project of Hunan Province.

Conflict of interest

The authors declare that they have no conflicts of interest.