New hybrid model for nonlinear systems via Takagi-Sugeno fuzzy approach

1.   Introduction and literature review

Most physical systems and processes can be modeled mathematically as complex nonlinear systems. As some parts of nonlinear systems are always coupled or correlated, and influence each other, it is generally difficult to analyze and synthesize these systems. Therefore, establishing an effective and suitable control model to address this issue in nonlinear systems is crucial. In recent years, the Takagi-Sugeno (TS) fuzzy model ^[37] has become an effective method to analyze and synthesize nonlinear systems due to its ability to transform a complex nonlinear system into several simple linear systems with membership functions, approximating the nonlinear function smoothly with arbitrary precision in the closed set space; this has applications in chemical processes, robotics systems, and automatic systems. In ^[32], for example, some systems for hydraulic turbines were modeled by nonlinear systems with time delays, where the TS fuzzy approach was applied for modeling and control with Lyapunov stability.

To control or model a phenomenon via fuzzy controllers or models, we always apply the so-called fuzzy rules, which are composed of some linguistic statements "if-then", and involve the concepts of fuzzy logic, such as fuzzy sets, fuzzy inference, and so on. The most known fuzzy rules are those of Mamdani (MAM) and Takagi-Sugeno. They allow controllers and modelers to understand and represent the knowledge, experience, and link between the input and output variables.

Recently, fuzzy control has been applied to many industrial applications. From its various applications, fuzzy control offers many advantages, such as the realization of multi-objective control, expert control, and robust control. On the other hand, one of the disadvantages of fuzzy control is the lack of analytical tools for fuzzy control systems. In other words, we need a fuzzy systems theory similar to linear systems theory. In this context, important concepts concerning the establishment of a fuzzy systems theory need to be considered, such as the connection problems of fuzzy block diagrams, the stability analysis of fuzzy control systems, and the new design technique of a fuzzy controller. In the linear case, block diagrams, which are represented by transfer functions, are utilized in the analysis of linear control systems. Similarly, we can analyze fuzzy control systems with the concepts of fuzzy block diagrams, which represent the diagrams of fuzzy control systems. The stability analysis of fuzzy control systems is one of the most important concepts in the analysis of control systems. We can theoretically design a model-based fuzzy controller if we have a useful stability criterion for fuzzy control systems.

However, fuzzy models are not effective in many cases, such as non-stationary signals, nonlinear or singular systems, and volatile or fluctuated data ^[13]. In these cases, the choice of the modeler and controller is not known in advance. This motivates the application of advanced tools and techniques to accurately describe or fit the hidden behavior or structure of the case study. Wavelets are advanced mathematical tools that have shown great success in describing the dynamics, fluctuations, volatility, fractality, and hidden structures in analyzed data. We know that wavelets are the most capable functional bases to precisely follow the fluctuations (high oscillations and dynamics) of the function or signal to be modeled. These fluctuations are essentially due to the nonlinearities of the original problem, as in our case. We have two nonlinearities, one convex superlinear, and another concave, singular sub-linear or non-Lipchitzian (rather only Holderian). We know that these facts lead to problems such as bifurcation, singularities, chaotic and fractal solutions, and also possible blow-ups.

The TS fuzzy model, which will be used here, has been applied in several fields such as supply chain management. In such a case, supply chains are considered piecewise linear dynamic systems (hence, nonlinear over the entire domain). In ^[1], a TS fuzzy model was developed for supply chain management with lead times. Asymptotic stability and smooth transitions within the subsystems were discussed via suitable membership functions, resulting in reduced fluctuations in the system's variables. Zhang et al. ^[42] proposed a TS fuzzy nonlinear supply chain system control approach with lead times. The approach considered submodels' switching actions as well as customers' stochastic demands. Stability and fluctuation of the system variables were investigated via the proposed model. These studies support our study in many points. One link is the approximation with piecewise linear approximators. Furthermore, the volatility and uncertainty are also common points. We recall that one of the most important problems in these chains is mainly due to transport problems, which may cause breaks in the chain due to several factors such as wars, pandemics, etc. These breaking points can be modeled by extreme values or singularities in our case.

In the same line of supply chain fuzzy modeling, Ahmadi and Ghasemi ^[3] presented a Mamdani fuzzy mathematical model for pricing strategies for online hotel searches via optimal sequencing of hotels with minimal searching. The model was based on the involvement of government intervention in hotel revenues via incentives and tariffs, energy savings, environmental impacts on hotel pricing, and the Stockholm game model for hotel pricing, considering the government as the leader and the hotel as the follower. Based on a concrete case study, the fuzzy inference system was proven to be an efficient forecaster. In ^[35], a fuzzy inference system was developed for management control in small and medium enterprises, especially in developing and growing economies. The approach used the well-known Mamdani fuzzy inference system as a decision-making technique and showed that the influence of management control tools on the organizational performance of these enterprises may be explored via fuzzy systems.

In ^[36], a nonlinear TS fuzzy system identification technique was proposed and proved for uncertain nonlinear dynamic systems investigation. The proposed approach used an entropy-like measure to avoid over-fitting, to minimize complexity while maximizing rediction accuracy.

One of the control concepts of stability in the study of dynamical systems is the concept of the Lyapunov exponent. Relative to the present work, this concept is already linked to wavelet theory. The estimation of the Lyapunov exponent and, consequently, the stability of dynamic systems by wavelets was initiated by Ghez and Vaienti in ^[21,22] and by Lamarque and Malasoma ^[30]. Bentez et al. ^[11] developed a hybrid method combining wavelets and the Lyapunov exponent to study the non-periodicity in signals. These studies claim that the concept of scale is strongly related to the Lyapunov exponent. In ^[27], a hybrid method combining wavelets and Lyapunov exponent was applied to forecast river water quality. The wavelet decomposition was applied to eliminate noise from the water quality time series. The denoised signal was used for the reconstruction of phase space and trajectory dynamics, and finally, a correlation dimension was constructed to identify chaos using a wavelet-based largest Lyapunov exponent estimation.

Similarly to the present work, Awrejcewicz et al. ^[5] applied a hybrid wavelet Lyapunov exponent approach for the control of plates and shells via nonlinear dynamical systems of PDEs. In ^[6], wavelets and Lyapunov exponent concepts were applied to study the chaotic behavior of nonlinear PDEs arising in vibrations of infinitely long flexible panels subject to longitudinal sign-changeable external load actions. The approach showed that the involvement of wavelets allowed the understanding of transition scenarios from regular to chaotic dynamics. Xu and Liu ^[39] involved wavelets in a neural network approach to study the chaotic behavior of the system via the wavelet function disturbance and the estimation of the maximum Lyapunov exponent.

Cozar et al. ^[17] studied a large-scale, high-dimensional adapted fuzzy regression tree. As a tree concept, it acts as a directed graph, in which each node or level is assumed to be a test and input for the next node or level. This concept aligns with our idea on wavelet decomposition, which, with the aid of wavelet algorithms (decomposition/reconstruction), also acts as a tree where each level is used as an input for the next and vice versa. Regarding the investigation of high-dimensional problems, the authors in ^[4] used an ensemble fuzzy regression tree to identify multi-output systems. The method used a local estimation model according to the data space split, which is, in turn, based on a threshold process. On each sub-space, a fuzzy linear regression is acted. This idea joins the wavelet processing and our present idea regarding the splitting of the data into sub-parts according to the wavelet decomposition. One of the well-known methods to eliminate noise from the data is the wavelet threshold. A useful reference on high-dimensional fuzzy systems may be found in ^[34], where a comparison with Gaussian processes was developed, which in turn may be a starting step to develop a general comparison with wavelets.

Our approach may also be expected to handle high-dimensional problems. Such problems have always been a challenge for fuzzy systems, such as hierarchical fuzzy systems. In ^[33], the authors developed a gradient boosting scheme for the design of a Takagi-Sugeno-Kang (TSK) fuzzy model using a hierarchical fuzzy regression tree to get an ensemble system. The main idea splits the rule space into subspaces in each round by adapting a novel membership division method. This approach aligns with the present one naturally. Indeed, using wavelets, we also project the signal onto the subspaces due to the multiresolution analysis, which guarantees more flexibility by being orthogonal, and by the fact that the parameters will be estimated according to these subspaces. Moreover, we estimate that the approach in ^[33] may be improved and/or combined with wavelets by considering the concept of wavelet gradient scheme, which is a well-known concept. It was referred in ^[33] that the TSK fuzzy system may achieve a highly nonlinear description of the input-output space by partitioning the input space into several subspaces and applying a local function to each subspace to describe the input-output relationship. This joins the wavelet processing, as wavelets are also powerful in describing the local behavior and split the signal into sub-signals.

In ^[29], a hierarchical TS fuzzy system architecture was developed to reduce the number and complexity of the fuzzy rules in the process. The approach follows also the one in ^[33] and the wavelet processing by possessing a cascading topology in which the predicted result computed at the previous layer is considered in the output part of the fuzzy rules. This process is the basic rule in wavelet decomposition and wavelet multiresolution analysis. In these cited studies, we may apply the wavelet cascading process to yield the level approximations recursively from each other. Moreover, wavelets may outperform the models in ^[29,33] by their ability to conduct a backward process. We may fix, for example, an objective (which may be an error, cost function, maximum level, and so on), and go back to the preceding rules by using the wavelet algorithms (see ^[24,31]).

Besides, it is also convenient to recall that the theory of wavelets in higher dimensions has several forms that may be used. Indeed, one form is the definition of multidimensional wavelets through the tensor product of several one-dimensional wavelets, which makes it possible to separate the variables and consequently obtain one-dimensional systems. The other form consists of considering multi-wavelets, which also provide a functional basis allowing the signal to be separated or projected onto orthogonal subspaces and to separate variables (see ^[28,41]).

This literature and its related studies motivated us to develop, in the present paper, a hybrid model that combines fuzzy logic, essentially the TS fuzzy model, and wavelet decomposition to obtain a robust, effective, and efficient model for nonlinear dynamical systems. The idea consists of applying the TS fuzzy model in the piecewise solution of the dynamical system, where these sub-solutions correspond to the wavelet decomposition components of the whole solution. The issue is somewhat similar to a control unit that repairs the direction or the behavior of the approximation solution whenever it moves away from the real one, by adopting wavelet decomposition.

The present paper will be structured as follows. Section 2 is devoted to a brief presentation of the wavelet toolkit. Section 3 is concerned with our new hybrid wavelet TS fuzzy approach. Section 4 is devoted to the development of a concrete application to a nonlinear Schrödinger dynamical system characterized by the presence of mixed nonlinearities, one of these being singular. Numerical simulations as well as error estimates are provided. Section 5 is devoted to discussions and interpretations of the numerical simulations and results. Section 6 is a conclusion.

2.   The wavelet processing toolkit

The wavelet analysis of time series or signals is based essentially on

● an efficient representation of the processed objects,

● a robustness in front of models' specification,

● a reduced computation time,

● and a time-frequency or time-space localization.

These special properties may be obtained simultaneously via an analysis based on a special function called the mother wavelet, a function that is the source of the functional basis applied to analyze the signal in hand. To own the name of a mother wavelet, a function $\psi\in L^2(\mathbb{R})$ has to satisfy some motherhood conditions such as

● the admissibility resumed in the condition

● the possession of enough vanishing moments (enough oscillations), in the sense that, there exists $m\in\mathbb{N}$ such that

● and the localization in time, in the sense that, precisely,

To conduct a wavelet processing of a signal, we start with its wavelet transform, a way of representing the signal in a time-frequency form. According to the type of processed signal, there is an adapted or adequate wavelet transform: the continuous wavelet transform (CWT) and the discrete wavelet transform (DWT).

Let $\psi$ be a wavelet (satisfying (2.1)–(2.3), $p\in\mathbb{R}$, and $s > 0$. Let also $f\in L^(\mathbb{R})$. The CWT of $f$ at the position $p$ and scale $s$ is defined by the convolution product

Using this transform, we know, in wavelet theory, that the analyzed signal $f$ may be reconstructed via its CWT. Indeed, denote $D_f:(s, p)\longmapsto d_{s, p}(f)$, and $\widetilde{\psi}:(s, p)\longmapsto \frac{1}{s^2}\psi\left(\frac{-p}{s}\right)$. We get

To process discrete signals, the convolutions (2.4) and (2.5) above have to be converted to discrete analogs. We thus get the DWT. On the dyadic grid, for example, $s = 2^{-j}$ and $p = k2^{-j}$, $j, k\in\mathbb{Z}$, we adopt the notations $\psi_{j, k}$ for the translated-dilated copy of $\psi$ and $d_{j, k}$ for the DWT. More precisely, we write

It holds, in wavelet theory ^[2,18], that $\left(\psi_{j, k}\right)_{j, k\in\mathbb{Z}}$ constitutes an orthonormal basis of $L^2(\mathbb{R})$, in which any element $f$ may be reconstructed as

called the wavelet series decomposition of $f$ (which replaces (2.5)). Notice that, if we split the sum (2.7) according to a level $J\in\mathbb{Z}$, we get

Denote next

Using (2.9), the decomposition (2.8) takes the form

Therefore, if for $j\in\mathbb{Z}$, we denote $W_j = spann(\psi_{j, k}, \, k)$ and $V_j = \underset{j\leq j-1}{\oplus}W_j$, we deduce that the sum $A_J(f)\in V_J$, and the sum $D_j(f)\in W_j$. It holds, in wavelet theory, that as the spaces $W_j$, there is also a function $\varphi\in L^2(\mathbb{R})$ such that $V_j = spann(\varphi_{j, k}, \, k)$, where the $\varphi_{j, k}$ is the analog of $\psi_{j, k}$ in (2.6), and that the sum $A_J(f)$ may therefore be decomposed as

The new coefficients $a_{J, k}(f)$ in (2.11) are known as the approximation coefficients of $f$ at the scale $J$ and the position $k$, and may be deduced from a convolution product by replacing $\psi$ with $\varphi$, and $(j, k)$ with $(J, k)$ in the $d_{j, k}(f)$'s equation (2.6). The component $A_J(f)$ is called the approximation of $f$ at the level $J$, and is designated to describe the global shape of $f$, while the component $D_j(f)$ is known as the detail component of $f$ at the level $j$ and reflects all the hidden structures of $f$, such as fluctuations, nonlinearity, non-stationarity, volatile behavior, and high dynamics of $f$. Accordingly, $V_J$ is the approximation space at the level $J$, and $W_j$ is the detail space at the level $j$. The pair $(\varphi, \psi)$ is the (father, mother) wavelet, and the sequence $(V_j)_j$ is called the multiresolution analysis. Details about all these concepts may be found in ^[2,18,24].

3.   The wavelet TS fuzzy hybrid model

The TS fuzzy model was originally developed in ^[37]. This model is based on describing local nonlinear input-output relations via the fuzzy rule "IF-THEN" to explore an accurate description of the local behavior (dynamics, volatility, fluctuation) of a fuzzy rule by a possible linear (linearized) system. The TS fuzzy model was shown to be a good estimator for many nonlinear dynamical systems, meanwhile also being accurate only in highly regular cases ^[7,19].

Mathematically speaking, the TS model is based on functional fuzzy rules, where output variables are functions instead of fuzzy sets. Therefore, a TS fuzzy control model will be of the form

where $X = (x_1, x_2, \dots, x_N)$ is the output vector, $M = M_1\times M_2\times\dots\times M_N$ is a fuzzy set, $Y = (y_1, y_2, \dots, y_N)$ is the output vector, $N\geq1$ is an integer, and $F:\mathbb{R}^N\longrightarrow\mathbb{R}^n$ is a function eventually nonlinear. Besides, the TS fuzzy modeling uses a fuzzy rule of the form

where, in this case, $Y_n = (y_k, y_{k+1}, \dots, y_{n-2}, y_{n-1}, y_n)$ ($1\leq k\leq n$ fixed) is a part of the output of the system that we search to model at the time interval $[k, n]$, $U_n$ represents the system input (at the time interval $[l, n]$), and $Y_{n+1}$ is the next-time ($n+1$) output. Notice here, that if we look at the system as a forecasting form, the part $Y_n$ looks like the past of the variable $Y$, with some auto-regression order $k$. Finally, $F:\mathbb{R}^{n-k}\times\mathbb{R}^{n-l}\longrightarrow\mathbb{R}^n$ is any arbitrary function eventually nonlinear.

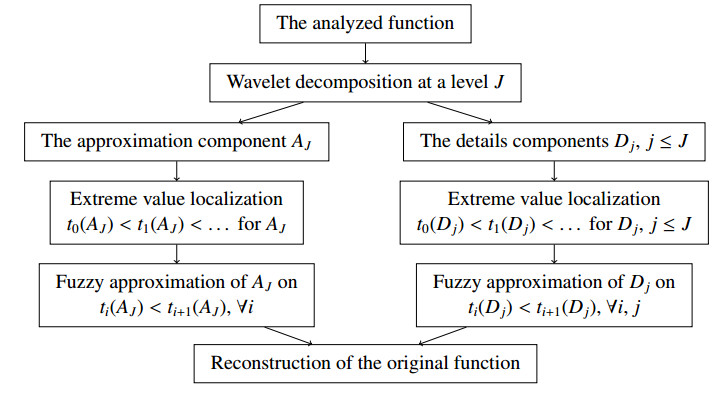
Our main idea consists of constructing a hybrid model by combining the TS fuzzy model with wavelets. More precisely, the TS fuzzy modeling rules (3.1) and (3.2) will be applied to the wavelet representation to get a prediction and then using the wavelet bases, lifting to the source or the wanted function $Y$ or $Y_{n+1}$ is deduced. More precisely, write for a level $J$, $\mathcal{V}_{J}(f) = (A_{J}(f), D_{J}(f), , D_{J-1}(f), \dots)$ as in (2.10). We introduce a $J$-level wavelet TS fuzzy control model as

and a $J$-level wavelet TS fuzzy modeling rule as

The functioning of this hybrid model is illustrated in Figure 1 and the Algorithm 1 below.

4.   Application to a nonlinear dynamical system

In this section, we apply the wavelet TS fuzzy model to the following mixed nonlinear convex-concave, upper-sublinear dynamical system:

where $\phi''$ is the second derivative of $\phi$, and $a$, $\alpha$, and $\beta$ are fixed real number parameters with $0 < \beta < 1 < \alpha$.

The problem (4.1) has applications in many fields such as physics, and applied mathematics. The solutions may be seen as steady-state solutions of general time-dependent Schrödinger, heat, and wave systems, or also a mixed system of these equations. It is well-known that the solutions of the system (4.1) possess many behaviors depending on the range of the initial values $a$ as well as the powers $\alpha$ and $\beta$, and the steady state parameter $\omega$ (see for instance ^[14,15]). Before developing the experimental part, we must mention that the numerical simulations that will be conducted in this work are done with Matlab R2018a Simulink on a Dell Latitude 5530, Windows 10, 64-bit Operating System, x64-based processor, 12th Gen Intel(R) Core(TM) i7-1255U 1.70 GHz, 16.0 GB RAM.

The first simulation in Figure 2 shows the phase space representation of the solution due to the problem (4.1).

Figure 2 clearly shows two equilibrium points or two focal points, which are the positive and negative zeros of the nonlinear part $|z|^{\alpha-1}+|z|^{\beta-1}-\omega$, with a possible singular behavior near the zeros of the solution. However, the linearization of the system around the focal points yields a different behavior.

The main approach uses the concept of sector nonlinearity, which may be summarized in the fact that the pair (input, output) should remain in a specific domain under suitable assumptions and rules. We propose, in this section, to apply the TS modeling process based on the domain of these parameters. To do this, denote $\Theta = [\phi\; \phi']^T = [z_1\; z_2]^T$, where the upper-script $^T$ is the transpose. The dynamical system (4.1) is equivalent to

which may be written in the matrix-vector form

where $A = A(z_1)$ is the matrix

and where $f$ is the real-valued function defined by

Now, we develop the TS model results. We will conduct a comparison between the wavelet-free TS modeling and the wavelet TS one. The latter consists of transforming the system above to a discrete system depending on the wavelet coefficients of the solution. Denote by $z_{\alpha, \beta}$ the positive real number, such that

We know (from ^[8,9,10]) that the solution $\phi$ of (4.1) oscillates infinitely around 0, with its limit being equal to 0 whenever $a\in(-z_{\alpha, \beta}, z_{\alpha, \beta})\setminus\{0\}$.

4.1.   The TS modeling

In this subsection, we fix first the domain $z_1\in(-z_{\alpha, \beta}, z_{\alpha, \beta})$. Using (4.2) or (4.3), we deduce the domain $z_2\in(-t_{\alpha, \beta}, t_{\alpha, \beta})$, where $t_{\alpha, \beta} = \frac{\alpha-\beta}{\alpha-1}z_{\alpha, \beta}$. To get a TS fuzzy model, we introduce a membership function system as

where $K_1$, $K_2$, $L_1$, and $L_2$ are the membership functions. More precisely, $K_1$ increasingly transforms $[-z_{\alpha, \beta}, z_{\alpha, \beta}]$ to $[0, 1]$, $L_1$ increasingly transforms $[-t_{\alpha, \beta}, t_{\alpha, \beta}]$ to $[0, 1]$, and $K_1+K_2 = L_1+L_2 = 1$. To fix the TS fuzzy rules, we write

● $A_1 = \{K_1\geq K_2\}$ and $A_2 = \{K_1\leq K_2\}$,

● $B_1 = \{L_1\geq L_2\}$ and $B_2 = \{L_1\leq L_2\}$.

We thus define the TS fuzzy rules as

● Rule 1: IF $z_1\in A_1$ and $z_2\in B_1$, THEN $\Theta' = M_1\Theta$,

● Rule 2: IF $z_1\in A_1$ and $z_2\in B_2$, THEN $\Theta' = M_2\Theta$,

● Rule 3: IF $z_1\in A_2$ and $z_2\in B_1$, THEN $\Theta' = M_3\Theta$,

● Rule 4: IF $z_1\in A_2$ and $z_2\in B_2$, THEN $\Theta' = M_4\Theta$,

where

Consider now the cross-products

In the present work, we propose a modified TS fuzzy model, in which we consider the matrix nonlinear functions

We obtain the following defuzzification model:

4.2.   Numerical estimations and efficiency measurements

In this section, we provide concrete estimations based on exact values of the problem (4.1) to show the accuracy, efficiency, and performance of the models presented previously. For this, we will define $\alpha = \frac{5}{4}\; \; \hbox{and}\; \; \beta = \frac{1}{4}.$ In this case, we get from (4.4) that $z_{\alpha, \beta} = 3$ and $t_{\alpha, \beta} = 12$. The matrices of each rule become

These matrices have the respective spectra

This allows to get approximations of the solution of the problem (4.1) or, equivalently, (4.2) via the TS fuzzy approach (4.5) and (4.6). Nevertheless, to compare with the classical or older fuzzy model, and thus to show the superiority of the present TS-based one, we provide in a first step the result of applying the fuzzy logic method due to Mamdani ^{[7,12,13,16,38]}.

The application of this model results in two bounds, an upper approximation and a lower one, both being linear and resulting from a linear optimization (fuzzy regression) program. Notice that the major problem with this model is that it leads to approximations, which become increasingly inefficient as shown in Figure 3, where the approximations move away linearly from the real solution.

Next, we apply the advanced fuzzy logic model due to TS. It is clear that the application of this model generates more precise envelopes (Figure 4). Besides, these approximations reflect somehow the effect of the TS fuzzy model, as they appear as a superposition of exponential modes due to the matrices $M_i$, $i = 1, 2, 3, 4$ and their spectra, which by applying the defuzzification technique, induces a mixture of exponentials $\exp(\lambda x)$, where $\lambda$ lies in the union of the matrices' spectra. Meanwhile, these envelopes do not efficiently take into account the high oscillations or nonlinearities of the solution. We see that the approximations are not oscillating highly as the approximated function.

As the major problem in modeling and controlling nonlinear systems is the precise description of the oscillating or nonlinear behavior of the solution, the findings above bring to mind a modification in the TS fuzzy model, consisting of applying it piecewise instead of the global way applied previously. More precisely, the solution to be modeled is split into pieces according to its extrema. Each piece is approximated via the TS fuzzy model. We then proceed with two approximations, one linear and another quadratic, to better describe the solution to the problem via the TS model. The result is illustrated by Figure 5, which shows a better fitting.

A first easy remark is the good fit of the peacewise monotonicity of the analyzed function on the sub-intervals, which confirms our idea about applying wavelets to obtain the hybrid model that combines both fuzzy models and wavelets. We know that wavelets are the most capable functional bases or modelers to precisely follow the fluctuations (high oscillations, dynamics) of the function or the signal to be modeled. These fluctuations are essentially due to the nonlinearities existing in the original problem, as in our case: We have two nonlinearities, one convex super-linear and one concave, singular sublinear or non-Lipchitzian (rather only Holderian). We know that these facts lead to problems such as bifurcation, singularities, chaotic and fractal solutions, and also blow-ups. For this reason, we need advanced tools and models to properly analyze the case. In our work, the idea is to apply a step-by-step hybrid TS-wavelet model,

● Step 1: Apply the wavelet decomposition to the dynamical system, which leads to a system of equations according to the wavelet decomposition components.

● Step 2: Evaluate or compute the extrema of the wavelet components and their positions.

● Step 3: On each interval of successive positions, apply the TS fuzzy model.

We then proceed, as previously, with two techniques, one linear and another quadratic, to better describe the solution to the problem via the TS fuzzy wavelet model. The result is illustrated by Figure 6, which shows a better appearance (good fitting). Nevertheless, we also provid the result of the combination of wavelets with the classical Mamdani fuzzy method (Figure 7) for comparing with existing methods, and to show the superiority of the new hybrid TS wavelet fuzzy approach proposed here.

To reinforce the graphical illustrations, we provide estimates of model errors. For this, we introduce the error

where $z_{app}$ is the approximation due to the model applied. The error estimates are summarized in Table 1. We recall that the wavelet decomposition level is fixed to $J = 4$ as in the graphical illustrations above.

As a final and eventual step to investigate the efficiency of the proposed model, we provide the results of the Lyapunov exponent for stability. Figure 8 illustrates the Lyapunov exponents due to the classical Mamdani fuzzy model. Figure 9 illustrates the Lyapunov exponents due to the linear TS fuzzy model. Figure 10 illustrates the Lyapunov exponents due to the quadratic TS fuzzy model. Figure 11 illustrates the Lyapunov exponents due to the pure wavelet model. Figure 12 illustrates the Lyapunov exponents due to the hybrid Mamdani wavelet fuzzy model. Figure 13 illustrates the Lyapunov exponents due to the hybrid linear TS wavelet fuzzy model. Finally, Figure 14 illustrates the Lyapunov exponents due to the quadratic TS wavelet fuzzy model.

Figures 8–14 represent the Lyapunov exponent relating to the different models. A first remark is that the largest Lyapunov exponent decreases according to the order of figures, with a divergence range that is well controlled and very reduced. However, this maximum exponent is positive, indicating that a chaotic aspect can occur in the studies problem. By further analyzing these figures, we note that the first model–Mamdani fuzzy model–does not show a good fit, especially at the beginning and end of the interval. This fitting becomes increasingly effective with the other models. The last hybrid wavelet TS fuzzy model is the most precise.

5.   Further discussions

Unlike existing fuzzy systems, the hybrid system presented here is composed of several subsystems, which are not necessarily linear. On the other hand, each subsystem evolves independently of the others, either by the inputs/outputs or by its region. To tackle a complex system, it is necessary to establish a set of equations both faithful to the actual behavior of the system and mathematically viable through assumptions and approximations. In the majority of existing cases, the models operate through simultaneous equations, unlike the present model where the inputs/outputs resulting from the wavelet decomposition are independent. We do not need to linearize the characteristic phenomena of the system around the extreme points. In this context, time/frequency or space/frequency wavelet methods constitute the most efficient tools for analysis and synthesis. We know that overall, no physical system such as the present problem is strictly linear. Furthermore, linearization is always local and therefore cannot describe the global behavior. Nonlinear effects are neglected disturbers, which may contradict the fact that the dynamics due to these nonlinear effects are richer than linear systems. It should also be noted that the number of equilibrium points between the initial nonlinear system and the linearized version may differ.

From a theoretical point of view, the developed approach can be useful in the case of nonlinear dynamic systems having non-integer, non-Lipschitzian, and/or singular nonlinearities. Other systems with fuzzy initial data or fuzzy boundary conditions can also be considered, namely PDEs and EDS applied in finance and environment, where fuzzy factors exist. In the present case, the system has a mixed nonlinearity composed by a super-linear convex part and a sublinear concave part. It may be seen as a perturbation of the super-linear problem

In this last case, classical theories make it possible to study the system from the point of view of existence, uniqueness, stability, regularity, and control. Indeed, we even know the general form of the solution of (5.1) as

modulo a translation. The present case is thus a singular disturbance, where we lose the general form of the solution, depending on the variation of the sublinear exponent. In cases like these, the classical theories of existence, especially of uniqueness, convergence, and stability, cease to be applicable. Furthermore, a well-known problem in the study of dynamic systems of the present type is the appearance of extreme values or singularities of the solutions. In wavelet theory itself, we resort to the estimation of the wavelet coefficient near the singular or extreme point, which can imply a redundancy of the solutions around this point. In our approach, these points will be considered as initial or boundary data, which reduces their effects on the solution.

Another implication that can be at the same time linked to the numerical framework more than the theoretical one is that, in general, we convert the dynamical system to an iterative equation to estimate the solution in a certain number of iterations (linked to an error predicted, for example). These iterative schemes require specific conditioning such as contractility and fixed-point theorems, which may not be satisfied. In our case, we did not need to resort to such circumstances.

Additionally, the mixed nonlinearities, particulary the singular components, contribute to the class of fluctuating, volatile, and non-stationary signals commonly encountered in fields such as finance, economics, and climate change. Analyzing these signals and/or functions requires accurate localization of extreme and singular points, where the majority of the signal's information or energy is located. The pure fuzzy tool is insufficient to properly describe the strange behaviors of the series and functions analyzed.

To further exploit the results from the numerical simulations, we recall that, in general, it is not easy to predict the approximation error of fuzzy models, as these models depend on the structure of the data to be modeled (uncertainty, non-stationarity, chaoticity, and so on). The advantage of using wavelets is their ability to estimate this error in advance, depending on the level of wavelet approximation or decomposition. Indeed, given a function $F$ and its wavelet decomposition $F_J$ at a level $J$, we have

Moreover, we may obtain a finer estimate using the regularity of the function $F$ (measured via its Hölder exponent, for example). Given a Hölder exponent value $\gamma$ of $F$ at a point $x$, we have

Using wavelets, we thus estimate the function or signal locally and uniformly by a regular function of order $\gamma$ at any point of the support. This immediately leads to the fact that the Lyapunov exponent of the wavelet estimator approaches the real Lyapunov exponent of the function or signal; see ^{[21,22,25,26]}.

Looking at Eq (5.2), we note that the intervention of wavelets induces an error of at least $2^{-2J}\sim10^{-4}$, which is clearly reflected in Table 1. We also note that increasing the level of nonlinearity (linear = polynomial of degree 1, quadratic = polynomial of degree 2) induces an improvement in approximation, which is expected given that the solution, even in the unperturbed case (5.1), is no longer linear but infinitely regular, which expresses its polynomial approximation. We know that it can be expanded into a Taylor series of any order. Polynomial fuzzy approaches have been applied in studies such as ^[20,23,40], where control and stability of nonlinear systems were investigated using polynomial fuzzy controllers and Lyapunov functions.

As mentioned above, to avoid estimating the analyzed function around singular and extreme points, which in turn can lead to redundancies, these points are considered as endpoints of the subintervals linked to the approximation subspaces. In other words, these points are treated as initial or boundary data, thus eliminating the need to find an approximator for the function around these points. The application of the TS model over the entire interval induced, as shown in Table 1, a higher error. Figure 4 shows that the application of the TS model to the entire interval does not capture the oscillatory behavior of the function, whereas the piecewise version, depicted in Figure 5, gives a better description and a smaller error as indicated in Table 1. On the other hand, by examining the control of the method through the Lyapunov exponent, we see that the hybrid approximators reflect greater stability and adequacy, as shown in Figures 12–14.

Finally, we recall that the wavelet decomposition results in signal components that are more stable in terms of stationarity, fluctuation, volatility, and noise. This process can be seen as zooming in on an image: at each zoom level, the observer or the modeler makes the necessary adjustments based on the observations provided by the machine. The process stops when a certain desired shape is achieved, or when the process no longer provides improvements, which is expressed here by the piecewise, linear, quadratic, polynomial process, and by the level of wavelet decomposition.

6.   Conclusions

In the present paper, a hybrid model based on a combination of wavelet decomposition and Takagi-Sugeno fuzzy model was developed as an effective method for analyzing nonlinear systems. The hybrid model is applied to a nonlinear Schrödinger dynamical system characterized by mixed nonlinearities. The first nonlinearity is convex super-linear, and the second one is concave sub-linear, and singular. In this type of problems, many difficulties arise, and strange behaviors of the solution may appear such as blow-up, which makes the approximation or control of the solution difficult. In our present work, we showed that combining wavelets with fuzzy models may yield good control and/or description of the solution. Wavelets are indeed capable of localizing the strange or change points in the function such as singularities, extreme points, dynamics, and fluctuations. The TS fuzzy model is the applied to model the solution piecewisely relative to the wavelet change point behavior. The theoretical results are provided with numerical simulations and comparisons with existing models via tests based on linear and polynomial TS approximators. The present model is shown to be effective. The present work openes several future research directions, such as the combination of fuzzy logic with wavelets in fields where non-stationary, chaotic, noisy, and strange behaviors are present in the data, such as time series from climate, finance, and so on.

Here, the approach proposed uses the variation of patterns in the wavelet components of the signal, while forgetting about the wavelet coefficients. Therefore, it may be better to consider the wavelet coefficients to better describe the hidden behavior of the signal. This idea is expected to yield better results, especially for signals issued from other fields, where more strange structures are contained in the data.

Additionally, the majority of works applying or combining wavelets and fuzzy logic or wavelets and the Lyapunov exponent intersect at a common point by considering only the approximation component $A_J$ (which reflects the trend of the time series). The detail components are added in the final reconstruction phase. This influences the entire process, as the strange behavior (non-stationarity, volatility, noise, fluctuations, etc.) is carried by the detail components $D_j$ themselves and no longer by the approximation component $A_J$.

Besides, although the new approach showed an improvement compared with some existing methods, some limitations, linked essentially to the degrees of the polynomials considered in the approximation, may be noticed. Theoretically, these degrees can be estimated through the regularity exponent of the function, which in turn can be estimated through the wavelet coefficients at the desired location. This characterization was originally done by ^[25,26], which reinforces our idea of considering, for an eventual improvement, the vector of wavelet coefficients instead of whole components.

We expect the present model to induce better results in other fields with more complexity such as non-stationarity, chaos, noise, etc. Wavelets have already been proven effective in removing noise from noisy data. For PDEs, such as the present case, the singular, extreme, and/or stochastic behavior can be predicted in advance from the PDE itself (coefficients, nonlinearities, initial data, boundary or boundary conditions, and existence of stochastic terms or parameters such as noise, etc.). For financial, economic, and environmental data, the behavior and structure of the data itself are inherently subjects of investigation and are always unknown and uncertain.

Author contributions

Anouar Ben Mabrouk, Abdulaziz Alanazi: Supervision; Anouar Ben Mabrouk, Abdulaziz Alanazi, Dalal Alanazi: Methodology, Writing-original draft, Visualization; Anouar Ben Mabrouk, Abdulaziz Alanazi, Zaid Bassfar, Dalal Alanazi: Conceptualization, Formal analysis, Investigation, Writing-review & editing; Anouar Ben Mabrouk: Funding acquisition. All authors have read and agreed to the published version of the manuscript.

Funding resources

The present work is funded by the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia through the project number (0135-1443-S).

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors express their gratitude to the editor(s) and the anonymous reviewers for their kind collaboration. Their comments and suggestions were very helpful and improved the paper well.

The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (0135-1443-S).

Conflict of interest

The authors declare no conflicts of interest in this paper.