Real-time detection of small objects in transverse electric polarization: Evaluations on synthetic and experimental datasets

1.   Introduction

We consider the limited-aperture inverse scattering problem for fast identification of the existence and location of a set of two-dimensional (2D) small objects from measured scattered field data. Previous researchers have developed various imaging techniques, including the bifocusing method for identifying small objects in inverse scattering problem [1], in microwave imaging [2], and damage detection of concrete void [3], the direct sampling method to localize 2D small inhomogeneities with multi- [4] and mono- [5] measurement environments, and perfectly conducting cracks [6], the MUltiple SIgnal Classification (MUSIC) algorithm for localizing small objects buried in a half-space [7], microwave imaging [8], and limited-aperture inverse scattering problem [9], Kirchhoff and subspace migration techniques to retrieve small cracks with measurements placed on a line [10], curve-like perfectly conducting cracks [11], and small anomalies from limited-aperture measurements in real-world microwave imaging [12], topological derivatives for inversion of Fresnel databases [13], multi-frequency limited data [14], and shape reconstruction of thin, curve-like inhomogeneities [15], the linear sampling method for identifying unknown scatterers from limited-aperture measurement data [16] and experimental dataset [17], and breast cancer detection [18], and the orthogonality sampling method for localizing unknown objects from experimental dataset [19], 3D far-field pattern data [20], and scattering parameter data [21]. We also refer to several references [22,23,24,25,26,27] about fast imaging techniques.

Although these techniques are fast, effective, and robust, they are typically designed for the detection of objects with dielectric permittivities that differ from the background value; the detection of objects with different magnetic permeabilities from the background permeability has been comparatively neglected. We refer to [28,29,30,31,32] for related studies. These studies report that rings with large magnitudes centered at the location of small objects appear in the imaging results. However, unlike the previous studies, peaks of large magnitude appear at the location of small objects with the Fresnel dataset. Thus, it is possible to recognize the existence and approximate locations of small objects. However, the theoretical reason for this phenomenon has not been explored.

Motivated by the above problem, we apply KM with a limited-aperture experimental measurement configuration [33] for a fast identification of small objects with different magnetic permeabilities from the background value. To validate object detection, we show that the imaging function of the KM can be expressed in terms of the size and permeability of the objects, squared zero-order and first-order Bessel functions, and an infinite series of Bessel functions of integer order greater than two. This is based on the fact that measured scattered field can be modeled as a 2D scalar Helmholtz equation and represented by an asymptotic expansion formula. The identified structure reveals some properties of the KM and explains some phenomena, such as object detectability.

The remainder of this study is structured as follows: Section 2 briefly introduces the 2D forward problem in the presence of small objects and the asymptotic expansion formula of the scattered field. Section 3 introduces and analyzes the imaging function, and explains some properties of the imaging results. Section 4 exhibits numerical simulation results with synthetic and Fresnel experimental data to support the theoretical results. Section 5 briefly concludes the paper and proposes future research.

2.   Forward problem and the asymptotic expansion formula

Here, we briefly introduce the forward problem and the asymptotic expansion formula of the scattered field when a set of small circular objects is completely embedded in a homogeneous region $\Omega\subset\mathbb{R}^2$. These objects with radii of $\alpha_s$ at locations $\mathbf{r}_s$ are denoted as $D_s$, $s = 1, 2, \cdots, S$, and all $D_s$ are assumed to be well separated. Let $D$ be the collection of $D_s$ and based on the simulation configuration in [33], the values of the background conductivity, magnetic permeability, and dielectric permittivity are $\sigma_{\mathrm{b}}\approx0$, $\mu_{\mathrm{b}} = 4\pi\times 10^{−7}\;{\rm{H/m}}$, and $\varepsilon_{\mathrm{b}} = 8.854 \times 10^{−12}\;{\rm{F/m}}$, respectively, at a given angular frequency $\omega$. Additionally, we denote $k_{\mathrm{b}} = \omega\sqrt{ \varepsilon_{\mathrm{b}} \mu_{\mathrm{b}}}$ as the background wavenumber.

In this paper, we assume that every material is characterized by its value of permeability at $\omega$. Denoting $\mu_s$ as the permeability of $D_s$, we introduce the piecewise constant of magnetic permeability

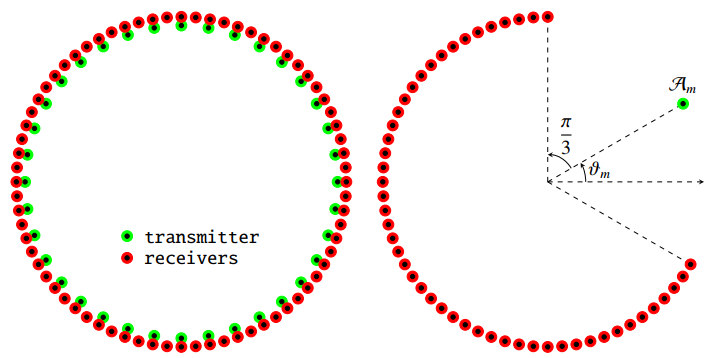
Let $\mathcal{A}_m$, $m = 1, 2, \ldots, M$, and $\mathcal{B}_n$, $n = 1, 2, \ldots, N$, be the $m$th transmitter and $n$th receiver located at $\mathbf{a}_m$ and $\mathbf{b}_n$, respectively. Based on [33], antennas $\mathcal{A}_m$ and $\mathcal{B}_n$ are placed on the circles with radii of 0.72 m and 0.76 m, respectively. The transmitters $\mathcal{A}_m$ are uniformly distributed with step sizes of $\triangle\vartheta = \pi/18$ from $0$ to $35\pi/18$, and at each location of $\mathcal{A}_m$, the receivers $\mathcal{B}_n$ are uniformly distributed with step sizes of $\triangle\theta = \pi/36$ from $\pi/3$ to $5\pi/3$. For an illustration of the simulation configuration, we refer to Figure 1. Then, the locations of $\mathbf{a}_m$ and $\mathbf{b}_n$ are given by

and

respectively.

With this setting, the incident field generated at $\mathcal{A}_m$ is given by

where $H_0^{(1)}$ denotes the zero-order Hankel function of the first kind. Assuming a time dependence of $e^{-i\omega t}$, the time-harmonic total field $u(\mathbf{b}_n, \mathbf{r})$ measured at $\mathcal{B}_n$ satisfies

Let $u_{\rm{scat}}(\mathbf{r}, \mathbf{a}_m) = u(\mathbf{r}, \mathbf{a}_m)-u_{\rm{inc}}(\mathbf{r}, \mathbf{a}_m)$ be the measured scattered field data at $\mathbf{r}$ in the presence of $D$ that satisfies the outgoing wave condition (or Sommerfeld radiation condition)

uniformly in all directions $\frac{ \mathbf{r}}{| \mathbf{r}|}$ as $r\longrightarrow\infty$. Based on [34], $u_{\rm{scat}}(\mathbf{b}_n, \mathbf{a}_m)$ can be expressed as the double-layer potential

where $\psi$ is an unknown density function. We emphasize that, as the complete form of $\psi$ is unknown, it must be replaced with an alternative expression to design an imaging function. Due to this reason, we consider the following asymptotic expansion formula (see [35]) to introduce and analyze the imaging function.

Lemma 2.1 (Asymptotic formula). If $\alpha_s$, $s = 1, 2, \ldots, S$ is small, the scattered field $u_{\rm{scat}}(\mathbf{b}_n, \mathbf{a}_m)$ can be represented as

3.   Introduction and analysis of the imaging function

This section introduces the imaging function for $D_s$ identification and analyzes its structure to elucidate its various properties. To this end, assume that we can handle the following multi-static response (MSR) matrix:

Using (2.1), $\mathbb{K}$ can be represented as

Following previous work [11,28,29], we extract $\mathbf{r}_s\in D_s$ using two test vectors for each $\mathbf{r}\in\Omega$:

and introduce the corresponding normalized imaging function:

Then, on the basis of [28], rings with large magnitudes centered at $\mathbf{r}_s$ will be included in the map of $\mathfrak{F}(\mathbf{r})$.

It is worth emphasizing that complete entries of $\mathbb{K}$ cannot be collected in a limited-aperture measurement configuration; specifically, for a fixed transmitter number $m$, only $N' = 49$ elements of scattered field data $u_{\rm{scat}}(\mathbf{b}_n, \mathbf{a}_m)$, $n\in \mathfrak{I}_m = \left\{{2m+p\; (\text{mod}\; 72):p = 11, 12, \ldots, 59}\right\}$ are measurable. In order to treat unmeasurable scattered field data, motivated by several studies [17,21,36,37], we convert the $N-\#(\mathfrak{I}_m) = N-N' = 23$ unknown data to zero and use the corresponding MSR matrix $\mathbb{M}$ with entries $\varphi_{nm}$, where

Fortunately, contrary to the previous research, it is possible to recognize the existence and location of $D_s$ by using the following normalized imaging function.

In order to explain the applicability of detection, we derive the following result:

Theorem 3.1. For each $\mathbf{r}\in\Omega$, let $\mathbf{r}- \mathbf{r}_s = | \mathbf{r}- \mathbf{r}_s|(\cos\phi_s, \sin\phi_s)$ and assume that $k_{\mathrm{b}}| \mathbf{r}- \mathbf{a}_m|\gg0.25$ and $k_{\mathrm{b}}| \mathbf{r}- \mathbf{b}_n|\gg0.25$ for all $m = 1, 2, \ldots, M$ and $n = 1, 2, \ldots, N$. Then, $\mathfrak{F}(\mathbf{r})$ can be represented as

where

and

Here, $J_p$ denotes the Bessel function of the first kind of order $p$.

Proof. Since $k_{\mathrm{b}}| \mathbf{r}- \mathbf{a}_m|\gg0.25$ and $4 k_{\mathrm{b}}| \mathbf{r}- \mathbf{b}_n|\gg1$ for $n = 1, 2, \cdots, N$, the following asymptotic forms hold (see [1,34] for instance)

Thus, we can write

and correspondingly, we can evaluate

Since the following relations hold uniformly (e.g., see [11]):

and

it is possible to derive that

where

Thus,

Reapplying (3.6), we have

Furthermore, since

and

we can obtain

and correspondingly (3.3) can be derived. □

Based on the result of Theorem 3.1, we can explore some undiscovered properties of the imaging function.

Remark 3.1 (Detectability of objects). Following the previous studies, the main component of the imaging function in TE polarization is $J_1(k_{\mathrm{b}}| \mathbf{r}- \mathbf{r}_s|)^2$. Therefore, rings of large magnitude appeared in the imaging results. Contrary to the previous studies, the imaging function $\mathfrak{F}(\mathbf{r})$ is composed of $J_0(k_{\mathrm{b}}| \mathbf{r}- \mathbf{r}_s|)^2$, $J_1(k_{\mathrm{b}}| \mathbf{r}- \mathbf{r}_s|)^2$, and $\mathcal{E}(k_{\mathrm{b}}| \mathbf{r}- \mathbf{r}_s|)$. Hence, the local maxima of $\mathfrak{F}(\mathbf{r})$ will appear at the location of the object because $J_0(0) = 1$ and $J_p(0) = 0$ for nonzero $p$. This is the theoretical reason that, unlike the previous studies, the existence and outline shape of objects can be identified through the map $\mathfrak{F}(\mathbf{r})$.

Remark 3.2 (Material properties). Since

the value of $\mathfrak{F}(\mathbf{r})$ should depend on the size and permeability of objects. For example, if the sizes of the objects are the same and $\mu_s > \mu_{s'}$, then $\mathfrak{F}(\mathbf{r}_s) < \mathfrak{F}(\mathbf{r}_{s'})$. Correspondingly, if the size or permeability of an object $D_s$ is extremely smaller or greater than the one of another object $D_{s'}$, the existence of $D_s$ cannot be recognized through the map of $\mathfrak{F}(\mathbf{r})$ because $\mathfrak{F}(\mathbf{r}_s)\ll\mathfrak{F}(\mathbf{r}_{s'})$.

Remark 3.3 (Applied frequencies and image resolution). The resolution of $\mathfrak{F}(\mathbf{r})$ is highly dependent on the value of $k_{\mathrm{b}}$. Based on the property of the $J_0$, an image with high resolution can be obtained if one applies a high frequency, but several artifacts are also included. If one applies a low frequency, an image with low resolution will be obtained. We refer to Figure 2 for 1D plots of $J_0(k_{\mathrm{b}}|x|)$ with several frequencies.

Notice that as $J_1(x)$ is maximized at $x\approx3.8317$, the two large-magnitude peaks appear at

That is, two peaks will converge to the location of $D$ at sufficiently high frequency, and correspondingly, it will be possible to recognize not only the existence but also the outline shape of objects. We refer to Figure 3 and Example 2.

4.   Numerical simulation results using synthetic and experimental data

In this section, we support Theorem 3.1 through numerical simulations on synthetic and experimental data. For the synthetic data experiment, we set three small circles $D_s$, $s = 1, 2, 3$, with radius $\alpha_s$, permittivity $\varepsilon_{\mathrm{b}}$, permeability $\mu_s$, and locations $\mathbf{r}_1 = ({0.07}\;{\rm{m}}, {0.05}\;{\rm{m}})$, $\mathbf{r}_2 = (-{0.07}\;{\rm{m}}, {0.00}\;{\rm{m}})$, and $\mathbf{r}_3 = ({0.04}\;{\rm{m}}, -{0.06}\;{\rm{m}})$. Table 1 lists the parameter values of the four experimental cases. The antenna arrangements and other simulation configurations are those specified in [33], and the search domain $\Omega$ was chosen as a square region $[{-0.1}\;{\rm{m}}, {0.1}\;{\rm{m}}]\times[{-0.1}\;{\rm{m}}, {0.1}\;{\rm{m}}]$. Within this setting, maps of $\mathfrak{F}(\mathbf{r})$ were obtained at frequencies of $f = 4, 8, {12}\;{\rm{GHz}}$.

Example 4.1 (Results of the synthetic data). Figure 4 shows maps of $\mathfrak{F}(\mathbf{r})$ in Case $1$. Although the existence and locations of $D_s$ can be identified in the imaging results, the outline shapes are indistinguishable. Similarly, the existence and locations of $D_s$ in the imaging results of Case $2$ with different $\mu_s$ values are discernible, but the outline shapes are obscured (see Figure 5).

Figure 6 shows the imaging results of Case $3$. Here, $D_3$ cannot be recognized because it is much smaller than $D_1$ (i.e., $\alpha_1^2\gg\alpha_3^2$). Therefore, $\mathfrak{F}(\mathbf{r})$ in the neighborhood of $D_3$ is very much smaller than $\mathfrak{F}(\mathbf{r})$ in the neighborhood of $D_1$.

Figure 7 shows maps of $\mathfrak{F}(\mathbf{r})$ in Case $4$. Since

$\mathfrak{F}(\mathbf{r})$ in the neighborhood of $D_1$ is considerably larger than $\mathfrak{F}(\mathbf{r})$ in the neighborhoods of $D_2$ and $D_3$. Correspondingly, $D_3$ cannot be recognized, and $D_2$ is barely recognizable.

Example 4.2 (Results of the experimental data). Figure 8 shows the $\mathfrak{F}(\mathbf{r})$ maps of a metallic rectangle $D$ from the dataset '$\mathtt{rectTE\_8f.exp}$' from [33]. At $f = {4}\;{\rm{GHz}}$ and $f = {8}\;{\rm{GHz}}$, the imaging results display a large-magnitude peak at the location of $D$ and two large-magnitude peaks in the normal direction of $D$. Notice that, as we discussed in Remark 3, we can recognize not only the existence but also the outline shape of object $D$ through the map of $\mathfrak{F}(\mathbf{r})$ with high frequency $f = {12}\;{\rm{GHz}}$.

5.   Conclusions

We applied KM for fast identification of the existence and locations of small objects in transverse electric polarization. By considering the relationship between the imaging function and the squared zero-order and first-order Bessel functions and an infinite series of Bessel functions of order greater than two, we also explored various properties (including the possibility of object detection) of the KM. From the simulation results of synthetic and Fresnel experimental data, we concluded that the KM algorithm effectively detects small objects in transverse electric polarization scenarios.

Although the existence and approximate locations of objects can be retrieved, the locations and outline shapes of objects are not satisfactorily resolved. An improved imaging technique will be developed in forthcoming work. The current study focused on the retrieval of small 2D objects. Extension to the three-dimensional problem on a dataset [38] will be an interesting research topic.

Author contributions

Junyong Eom: Formal analysis, Methodology, Writing - original draft, Writing - review & editing, Funding acquisition; Won-Kwang Park: Conceptualization, Formal analysis, Investigation, Software, Validation, Writing - original draft, Writing - review & editing, Funding acquisition. All authors have read and agreed to the published version of the manuscript.

Use of AI tools declaration

The authors declare that no Artificial Intelligence (AI) tools were used in the creation of this article.

Acknowledgements

This study was supported by the JSPS KAKENHI (Grant Number 23K19002) and National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (NRF-2020R1A2C1A01005221).

Conflict of interest

The authors declare no conflicts of interest regarding the publication of this paper.