Predicting the optimal heating function for uniform exit temperature in a pipe flow

1.   Introduction

As global warming becomes increasingly severe, the importance of energy conservation is also correspondingly heightened. For instance, building energy efficiency has become a primary goal in regional, national and even international energy policies. Among various building services, the energy consumption of heating, ventilation and air conditioning (HVAC) systems has shown particularly significant growth. In a typical HVAC system, fluids such as air are heated or cooled and brought to a predetermined temperature before being distributed to different areas of the building through a network of pipes. In this process, ensuring an even temperature distribution within the pipes is crucial, as it directly affects the comfort levels in different areas and the overall system performance ^[1,2].

On the other hand, various facilities within power plants, such as steam boilers and cooling towers, also require heat transfer through pipelines. In these processes, whether the fluid is water, steam or other cooling agents, its temperature distribution within the pipes is of utmost importance. Optimal heating control strategies that ensure a uniform distribution of steam temperature within the pipes can enhance heat transfer efficiency, reduce thermal stress due to uneven temperatures and consequently extend the boiler's lifespan ^[3,4,5].

In addition, with the continuous development of the semiconductor industry, temperature control plays an increasingly prominent role in processing and measurement technologies. Techniques such as chemical vapor deposition (CVD), thermal oxidation and isothermal closed space sublimation (ICSS) heavily rely on precise temperature control. Specifically, ICSS is employed in the production of thin films for semiconductor and optoelectronic devices, involving a sublimation reaction between two parallel substrates under isothermal conditions to form the thin film ^[6,7].

In numerous technological research, industrial production and laboratory applications, thermostatic baths have played crucial roles due to their ability to provide precise and stable temperature control. However, in the abovementioned cases where the object to be heated is excessively long or of large volume, the applicability of thermostatic baths in these specific environments is limited. To address these issues, this study proposes a strategy for optimization control using a gradient-based algorithm, with the aim of achieving isothermal control of the fluid at the exit of a circular pipe. This strategy achieves the desired isothermal state of the exit fluid temperature by precisely controlling the heat flux distribution on the outer pipe wall.

The gradient-based optimization algorithm ^[8], due to its self-regularized characteristic, is popular in many areas, including heat flow management. This method uses the mathematical concept of the gradient to find the minimum or maximum of partial differential equations. In addition, it does not require a priori information of the functional form of the unknown quantities, and reliable estimations can always be obtained. Therefore, it provides an effective way to find the optimal solution.

For instance, Chen and Ozisik applied a gradient-based algorithm to address a nonlinear optimal control problem, wherein they determined the optimal heating sources for both a slab ^[9,10] and a cylinder ^[11]. Huang ^[12] employed an iterative regularization approach within a non-linear optimal control problem, aiming to forecast the magnitudes of optimal boundary heat fluxes.

The CFD-ACE+ software ^[13] is utilized for numerical computations in this work since it boasts exceptional computational performance and precise simulation capabilities. The present optimal heating problem is transformed into two sub-problems, namely, sensitivity and adjoint problems. We integrate the CFD-ACE+ software with our core optimization program, where the gradient-based algorithm is used for determining the optimal heating function required for various specified temperature distributions on the inner wall, thereby controlling the desired uniform fluid outlet temperature.

Finally, the optimal heating function is estimated for various inner wall specified temperature distributions to verify the validity of using the gradient-based algorithm to solve the considered optimal heating problem.

2.   Materials and methods

2.1.   Problem formulation

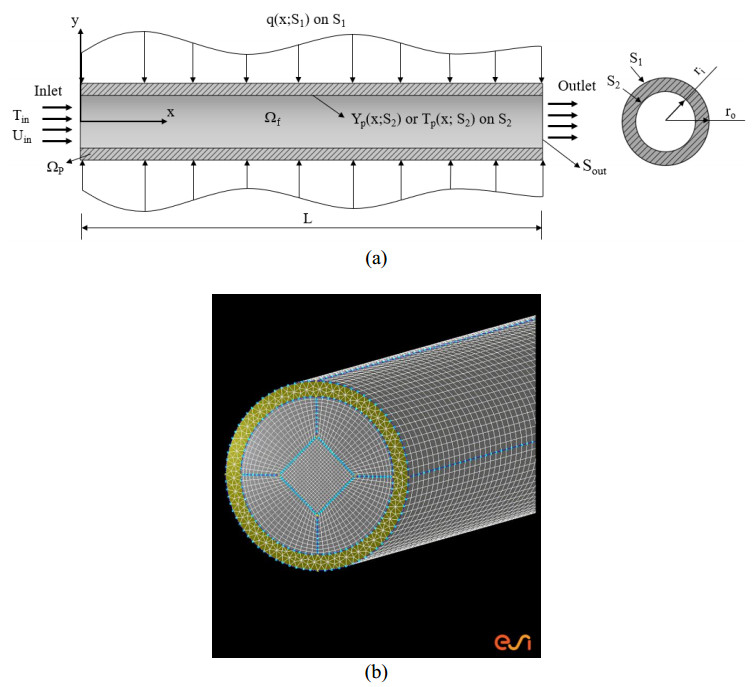
A thin wall circular pipe is considered as the demonstration model of this optimal heating problem. The computational domain Ω consists of two sub-domains, i.e., the pipe and fluid domains, Ω_p and Ω_f, respectively. The computational domain and grid system of the present work are illustrated in Figure 1(a), (b), respectively.

An incompressible laminar flow fluid with constant properties and neglected viscous heating term enters into the pipe with a velocity ${\mathrm{U}}_{\mathrm{i}\mathrm{n}} = {\mathrm{u}}_{\mathrm{i}\mathrm{n}}$ and an ambient temperature ${\mathrm{T}}_{\mathrm{f}, \mathrm{i}\mathrm{n}} = {\mathrm{T}}_{\mathrm{\infty }}$. An unknown heat flux is applied on the outer surface of pipe S₁ to increase the temperature of the fluid to yield the desired uniform temperature at the outlet of the pipe. For practical consideration, the heating function is assumed not to be a function of radial direction; therefore, it is only a function of axial direction, q(x; S₁).

The goal of this study is to predict the optimal heating function to achieve the desired uniform temperature of the fluid at the pipe outlet. The interfacial surfaces of Ω_p and Ω_f, i.e., S₂, are subjected to the perfect thermal contact condition, i.e., the temperatures and heat fluxes of the pipe are identical to those of the fluid on S₂.

The differential equations for this optimal control problem can be expressed as follows:

(I) Pipe domain (Ω_p)

where k_p and T_p are the thermal conductivity and temperature of the pipe, respectively, and the outer surface S₁ is subjected to an unknown optimal heating function q(x; S₁).

(II) Fluid domain (Ω_f)

The continuity, momentum and energy equations for the fluid domain are given below:

where the velocity vector, thermal conductivity and fluid temperature are presented as U, k_f and T_f, respectively. Here, the inlet fluid has a velocity ${\mathrm{U}}_{\mathrm{i}\mathrm{n}} = {\mathrm{u}}_{\mathrm{i}\mathrm{n}}$ and a temperature $\rm {{\text{T}}_{f, in}} = {{\text{T}}_\infty }$.

(III) Pipe-fluid interface (${\mathrm{S}}_{{\mathrm{\Omega }}_{\mathrm{p}}\cap {\mathrm{\Omega }}_{\mathrm{f}}}$ = S₂)

The perfect thermal contact condition is utilized with S₂:

If the heating function q(x) is known, the temperature solutions to the above hydro-thermal conjugated problem can be solved using CFD-ACE+, and the outlet temperature of the pipe can be calculated.

2.2.   The optimal heating problem

From a theoretical perspective, if the outer surface of the pipe is designated to possess a constant temperature Y_p(x; S₁), the fluid's temperature upon entering the pipe with an initial temperature ${T}_{\infty }$ will ultimately align with Y_p(x; S₁) at the pipe outlet, provided the pipe length is sufficiently extensive. However, it is impractical to employ an exceedingly elongated pipe to achieve uniform fluid temperature at the outlet. Furthermore, the task of sustaining a consistent temperature on the outer pipe surface poses considerable challenges.

Hence, in this investigation, the designated temperatures Y_p(x; S₂) are assigned to the inner surface of the pipe, S₂. Subsequently, the corresponding optimal heating function q(x; S₁) for achieving these Y_p(x; S₂) values is determined. Additionally, if the specified temperature on S₂ surpasses the desired uniform temperature at the outlet, Y_f(L; S_out), it becomes plausible to shorten the pipe length.

Designate the specified temperatures on S₂ as Y_p(x; S₂), and the resolution of the optimal heating problem involves employing Y_p(x; S₂) to estimate the optimal heat flux q(x; S₁).

The following cost function must be minimized for obtaining q(x; S₁):

where T_p(x; S₂) are the estimated temperatures on S₂, and α is a given weighting coefficient.

The first term on the right hand side in Eq (7) is the integration of the square of the difference between the estimated and specified temperature over S₂. The second term denotes the integration of the square of the optimal heating function q(x; S₁) over x, multiplied by a weighting coefficient α. The weighting coefficient α is a design parameter that control the closeness of T_p(x; S₂) to Y_p(x; S₂). As an illustration, when α = 0, T_p(x; S₂) closely aligns with Y_p(x; S₂), yet the estimated q(x; S₁) might exhibit oscillatory behavior. Therefore, to mitigate such oscillations and achieve a smoother q(x; S₁), it becomes essential to introduce a finite value for the weighting coefficient α.

2.3.   Gradient-based method for minimization

The following gradient-based iterative equation ^[8] is utilized to compute the optimal heating function q(x; S₁) by minimizing the cost function J[q(x; S₁)]:

where n represents the iteration index, βⁿ and $\mathrm{J}^{'\mathrm{n}}\left(\mathrm{x}; \mathrm{S}_1\right)$ denote the values of search step size and gradient of cost function, and they must be computed before Eq (8) can be applied. The solutions to the sensitivity and adjoint functions can be derived below and utilized to compute the values of βⁿ and $\mathrm{J}^{'\mathrm{n}}\left(\mathrm{x}; \mathrm{S}_1\right)$.

2.3.1.   The sensitivity functions

The sensitivity functions pertaining to the sensitivity problem can be obtained by perturbing the unknown optimal heat flux within the original problem, following the procedure outlined below. We assume that q(x; S₁) experiences a minor perturbation, denoted as Δq, consequently leading to perturbations in T_p and T_f, represented as ΔT_p and ΔT_f, respectively. Substituting q, T_p and T_f with q+Δq, T_p+ΔT_p and T_f+ΔT_f, respectively, in Eqs (1) to (6), and subsequently subtracting the resulting equations from Eqs (1) to (6) while retaining only the first-order terms, yields the following equations for the sensitivity functions within the context of the linear problem considered here.

(I) Pipe domain (Ω_p)

where the base surface S₁ is subjected to a heat flux Δq,

(II) Fluid domain (Ω_f)

The continuity and momentum equations for Ω₂ are given by Eqs (3) and (4), and the corresponding energy equation is given below.

The inlet conditions for the sensitivity functions are obtained as U_in = u_in and ΔT_{a, in} = 0.

(III) Pipe-fluid interface (S₂)

The perfect thermal contact condition is derived for the interface surface S₂ and obtained as

The above sensitivity functions can be solved by CFD-ACE+.

By using a Taylor expansion of the cost function $\mathrm{J}\left[\mathrm{q}\left(\mathrm{x}; \mathrm{S}_1\right)\right]$, the following new form of the cost function can be derived:

The sensitivity functions $\rm \Delta {T_p}({J^{'}}^n)$ are the solutions of the sensitivity problem given by Eqs (9) to (12) on S₂ using $\rm \Delta q = {J^{'}}^{\text{n}}$.

Equation (13) is minimized with respect to βⁿ to obtain the expression for determining the value of βⁿ:

2.3.2.   The adjoint functions

The derivation of the adjoint functions for the adjoint problems proceeds as follows: The energy equations for the pipe and fluid domains are multiplied by λ_p and λ_f, respectively. The resulting equations are then integrated over their respective domains, denoted as Ω_p and Ω_f. Subsequently, these two integrations are added to the right-hand side of Eq (7), leading to the following expression:

The change in the cost function ΔJ can be derived by perturbing q, T_p and T_f by Δq, ΔT_p and ΔT_f, respectively, in Eq (15). This involves subtracting the original Eq (15) from the perturbed equation and retaining only the terms of the first order. Consequently, the ensuing adjoint functions for the adjoint problems can be determined as follows.

Green's second identity is utilized to reformulate two domain integration terms in Eq (16), Eqs (10) and (12) are utilized, and ΔJ is assumed to approach zero. Finally, the equations of the adjoint functions λ_p and λ_f can be obtained.

(I) Pipe domain (Ω_p)

where the base surface S₁ is subjected to the insulation condition given below.

(II) Fluid domain (Ω_f)

The inlet conditions for λ_p and λ_f are U_in = u_in and λ_{f, in} = 0. Here, U can be determined from Eqs (3) and (4).

(III) Pipe-fluid interface (S₂)

The boundary condition for the interface surfaces on S₂ are given below:

It is important to highlight that a perfect thermal contact condition is absent on S₂, and further heat sources are present on S₂ for the adjoint functions. The solutions for the aforementioned adjoint functions are computed using CFD-ACE+.

Finally, the following integration term is left.

The increment in the cost function was obtained as ^[8]

From Eqs (21) and (22), the gradient of the cost function ${\text{J'}}\left({\text{q}} \right)$ is determined as

Once βⁿ and $\rm {J^{'}}^n(x; {S_1}) = {J^{'}}^n(q)$ are obtained, Eq (8) can be iterated to compute the optimal heating function q(x; S₁). The stopping criterion for Eq (8) is given below:

where $\rm \overline {{T_f}} {{\text{(L; }}{{\text{S}}_{out}})^{n{\text{ + 1}}}}$ and $\rm \overline {{T_f}} {{\text{(L; }}{{\text{S}}_{out}})^n}$ denote the average outlet fluid temperatures at the iteration indices n+1 and n.

2.4.   Computational procedure

The computational methodology employed to address the optimal heating problem through a gradient-based algorithm is outlined as follows:

Assume that ${\mathrm{q}}^{\mathrm{n}}\left(\mathrm{x}; {\mathrm{S}}_{1}\right)$ is known at the iteration index n.

Step 1. Solve Eqs (1) to (6) for T_p and T_f.

Step 2. Check the stopping criterion Eq (24). Continue to Step 3 if the stopping criterion is not satisfied.

Step 3. Solve Eqs (17) to (20) for λ_p and λ_f.

Step 4. Compute ${\mathrm{J}}^{\mathrm{{'}}}\left[\mathrm{q}\right({\mathrm{S}}_{1}\left)\right]$ from Eq (23).

Step 5. Set $\mathrm{\Delta }\mathrm{q} = {{\mathrm{J}}^{\mathrm{{'}}}}^{\mathrm{n}}$, and solve Eqs (9) to (12) for ΔT_p and ΔT_f.

Step 7. Compute β_n from Eq (14).

Step 8. Compute the new estimate for ${\mathrm{q}}^{\text{n+1}}\left(\text{x; }{\text{S}}_{1}\right)$ from Eq (8) and return to Step 1.

3.   Results

The objective of this study is to employ a gradient-based algorithm to determine the optimal heating function q(x; S₁) within a pipe, aiming to achieve the desired uniform outlet fluid temperature. Given the absence of prior knowledge regarding the functional form of the unknown optimal heating function, this task can be categorized as function estimation within an optimal control problem.

An aluminum alloy material with k = 190 W/(m·K) is considered for the pipe module, and the inlet fluid is considered as water with inlet temperature ${\mathrm{T}}_{\mathrm{\infty }}$ = 300 K. The outer surface S₁ of the pipe is subjected to an unknown heating function q(x; S₁), and the perfect thermal contact condition is utilized on the inner surfaces S₂ between the pipe and water.

Two pipe models will be investigated in this work, i.e., Case A (L = 6 m, u_in = 0.4 m/s, r_o = 3.5 mm and r_i = 2.5 mm) and Case B (L = 6 m, u_in = 0.2 m/s, r_o = 6 mm and r_i = 5 mm). The grid-independent tests for the pipes of Cases A and B will be studied first using q(x; S₁) = 1000 W/m² and T_∞ = 300 K, and the outlet average temperature of the water $\overline{{\mathrm{T}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ will be computed.

For Case A, three grid numbers of 114, 000, 228, 000 and 380, 000 are used, and $\overline{{\mathrm{T}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ is computed as 303.248 K, 304.322 K and 304.321 K, respectively. The relative error in $\overline{{\mathrm{T}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ between the grid numbers 228, 000 and 380, 000 is only 0.00033%; therefore, grid number 228, 000 will be utilized for subsequent computations. Similarly, three grid numbers of 121, 050, 242, 100 and 403, 500 are used for Case B, and $\overline{{\mathrm{T}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ is calculated as 304.559 K, 305.257 K and 305.256 K, respectively. The relative error in $\overline{{\mathrm{T}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ between the grid numbers 242, 100 and 403, 500 is only 0.00033%; therefore, grid number 242, 100 will be considered for further calculations.

The forthcoming numerical experiments will be examined to validate the utilization of the current gradient-based algorithm in estimating the optimal heating function q(x; S₁), contingent upon the desired uniform outlet water temperature of the pipe flow, set at $\overline{{\mathrm{Y}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ = 323 K.

The benefit of employing the gradient-based algorithm for predicting the optimal heating function lies in the flexibility of selecting initial guesses. Consequently, for all the numerical experiments conducted in this study, the initial guess for the optimal heating function is arbitrarily set to q(x; S₁)⁰ = 100 W/m². We explore two numerical test cases, denoted as Cases A and B, encompassing distinct pipe diameters and inlet velocities while maintaining the same pipe length. These cases involve different specified temperature distributions on S₂.

(A) Case A

Within Case A, three distinct temperature distributions will be designated along the inner wall S₂ of the front part of the pipe, ranging from 0 m to 3.2 m. In the subsequent section, spanning from 3.2 m to 6 m, a constant temperature of 323 K will be specified to ensure compliance with the requirement of achieving $\overline{{\mathrm{Y}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ = 323 K. This specification is applied to Cases A1−A3, leading to the estimation of corresponding optimal heating functions on S₁.

Case A1:

The specified temperature distribution Y_p(x; S₂) on S₂ is given as

Figure 2(a) displays the graph of the Y_p(x; S₂) function. Employing the gradient-based algorithm with α = 0, the optimization analysis resulted in a reduction of the cost function to 20 after 104 iterations. Figure 3 illustrates the change in the cost function over the course of iterations. This graphical representation highlights a rapid decline in the value of the cost function, exhibiting a consistently decreasing trend.

The estimated optimal heating function q(x; S₁) and the computed temperature T_p(x; S₂) are given in Figure 2(a), and it shows that the values of Y_p(x; S₂) and T_p(x; S₂) are almost identical. This implies that the optimal control algorithm used in this study is indeed effective, since the estimated q(x; S₁) can produce T_p(x; S₂) to match with Y_p(x; S₂). The temperature distributions of the water along the x-axis and at the cross-section of the outlet are given in Figure 2(b), (c), respectively. Evidently, the water within the pipe undergoes heating from T_p(x; S₂), a process regulated by q(x; S₁), resulting in the attainment of the desired fluid exit temperature.

The calculated average outlet temperature of the water was found to be $\overline{{\mathrm{T}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ = 326.2 K, in contrast to the specified requirement of $\overline{{\mathrm{Y}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ = 323 K. This discrepancy suggests an excessive infusion of energy into the fluid, indicating the need for energy extraction from the front segment of the pipe in the subsequent cases under investigation. Moreover, $\overline{{\mathrm{T}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ represents an average value of exit temperatures, making it inadequate for assessing the uniformity of these temperatures. Consequently, an additional index must be formulated to accurately evaluate the exit temperature uniformity.

The uniformity of exit temperatures is then defined as follows:

Here, ${\mathrm{T}}_{\mathrm{f}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ signifies the temperatures at the outlet of the flow. In the context of Case A1, the uniformity of exit temperatures is quantified as ΔT(L; S_out) = 7.1 K. Observing Figure 2(c), it becomes evident that the uniformity of exit temperatures is not optimal, as discernible color variations within the outlet fluid are noticeable.

An abrupt surge in heat flux is observable at the initial section of the pipe, while a discontinuity in heat flux is present at x = 3.2 m. These abrupt alterations in heat flux pose challenges for practical control. To address this limitation, a corrective measure has been implemented by introducing a weighting coefficient α into the cost function, as depicted in Eq (7).

When employing a weighting coefficient α = 1×10^-6, the optimal solution converged after 31 iterations, as depicted in Figure 4. It is notable that the fluctuations in heat flux have become smoother and more refined, although the values of Y_p(x; S₂) and T_p(x; S₂) are not as optimal as those attained with α = 0. In this case, $\overline{{\mathrm{T}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ reached 327.7 K, and ΔT(L; S_out) decreased from 7.1 K to 4.7 K. This underscores the efficacy of the weighting coefficient in effectively smoothing the optimal heating function.

Case A2:

For Case A1, the specified temperature Y_p(x; S₂) within the range of 0 to 3.2 m was established at 363 K, revealing an excess of energy input. Consequently, in Case A2, the temperature distribution within the same range was modified to exhibit a linear decrease from 363 K to 323 K.

This approach proves effective in curbing excessive energy infusion into the fluid. With α = 0, the optimal solution converged after 102 iterations, leading to a reduction in the cost function to 35. The outcomes of this estimation are showcased in Figure 5, and the convergence pattern is illustrated in Figure 6. It is evident from Figure 5(a) that the values of Y_p(x; S₂) and T_p(x; S₂) exhibit a near-identical correspondence.

This suggests that the estimated heat flux serves as an accurate representation of the optimal heating function, reinforcing the validity of the optimization algorithm. Figure 5(b), (c) depicts the temperature distributions along the x-axis and at the outlet, respectively. The calculated values for $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ and ΔT(L; S_out) are 322.7 K and 1.2 K, respectively. These results indicate a close proximity of $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ to 323 K and a further reduction of ΔT(L; S_out) to 1.2 K. This signifies a notable improvement in the uniformity of exit temperatures, as evidenced by the absence of color variation in the water outlet temperature seen in Figure 5(c).

By utilizing Eq (27), the discontinuity in heat flux at x = 3.2 m is eliminated. However, a distinct surge in heat flux persists at the outset of the pipe. Consequently, to mitigate this issue, a weighting coefficient α = 1×10^-6 is incorporated to enhance the smoothness of the estimated heat flux. After 31 iterations, the optimal heating function converges, and the outcomes are illustrated in Figure 7. Figure 7(a) distinctly displays the amelioration of the abrupt increase in heat flux, yet the alignment between the values of Y_p(x; S₂) and T_p(x; S₂) is not as precise with α = 1×10^-6. However, $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ attains a value of 327.7 K, on par with the result achieved with α = 0. Nonetheless, ΔT(L; S_out) escalates from 1.2 K to 2.2 K, introducing a discernible color variation in the outlet temperature seen in Figure 7(c). Despite this change, the uniformity of exit temperatures remains notably satisfactory even with α = 1×10^-6.

Case A3:

While the average exit temperature $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ in Case A2 achieved through linearly decreasing heating closely approximates the target temperature $\rm \overline {{{\text{Y}}_f}} {\text{(L; }}{{\text{S}}_{out}})$, the uniformity of the exit temperature ΔT(L; S_out) remains at 1.2 K. Consequently, Case A3 introduces a more intricate temperature distribution characterized by a floor function (step-like) profile. This is done to investigate whether such complexity can yield further enhancements in the uniformity of the exit temperature.

A floor function, $\left\lfloor \bullet \right\rfloor$, temperature distribution is specified from 0 to 3.2 m as follows:

With α = 0, the optimal solution converges after 100 iterations, resulting in the estimated outcomes showcased in Figure 8. The cost function value diminishes to 62, with the convergence pattern portrayed in Figure 9. From Figure 8(a), a noticeable alignment between the values of Y_p(x; S₂) and T_p(x; S₂) becomes apparent, signifying that the estimated q(x; S₁) indeed functions as the optimal heating function. Nevertheless, the estimated q(x; S₁) demonstrates minor jumps owing to the step-like nature of the floor function. Addressing these jumps can be achieved by introducing a weighting coefficient, as will be explored later.

Figure 8(b), (c) elucidates the temperature distributions of water along the x-axis and at the outlet (S_out), respectively. The calculated values for $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ and ΔT(L; S_out) are 323.0 K and 0.3 K, respectively. In comparison to Case A2, the design of Case A3 showcases superior exit temperature uniformity, with a remarkably reduced ΔT(L; S_out) of only 0.3 K. This is evident, as there is no noticeable color variation in the water outlet temperature at S_out, as depicted in Figure 8(c).

In order to mitigate the abrupt spikes and discontinuous behaviors of q(x; S₁), we introduced weighting coefficients α = 1×10^-6 and 1×10^-5 to facilitate a smoother profile for q(x; S₁). The values of q(x; S₁) converged after 30 and 22 iterations for α = 1×10^-6 and 1×10^-5, respectively. The outcomes for α = 1×10^-6 and 1×10^-5 are illustrated in Figures 10 and 11, respectively. Figures 10(a) and 11(a) clearly demonstrate the enhancement in alleviating the abrupt spikes and discontinuities in q(x; S₁) with α = 1×10^-6 and 1×10^-5. However, the alignment between the values of Y_p(x; S₂) and T_p(x; S₂) is not as precise with these weighting coefficients. The values of $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ and ΔT(L; S_out) reach 323.3 K and 1.7 K, respectively, when α = 1×10^-6. These values are comparable to those obtained with α = 0. However, with α = 1×10^-5, the values of $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ and ΔT(L; S_out) are 316.0 K and 11.5 K, respectively. As depicted in Figure 11(c), the uniformity of the exit temperature deteriorates significantly.

In conclusion, opting for α = 1×10^-6 facilitates the smoothing of the estimated heat flux while upholding desirable temperature uniformity. Nonetheless, when the weighting coefficient becomes too large, such as α = 1×10^-5, the estimated heat flux undergoes excessive damping, consequently impacting the uniformity of exit temperatures. This underscores the significance of meticulously selecting an appropriate weighting coefficient for tackling the optimal heating problem. The estimated results for Case A are summarized in Table 1.

(B) Case B

For Case B, an investigation is conducted involving a larger pipe radius (r_o = 6 mm and r_i = 5 mm) at a flow velocity of u_in = 0.2 m/s. Given the effectiveness of the specified floor function temperature distribution, it will be employed in Case B as the heating function on S₂ to ensure the satisfaction of $\overline{{\mathrm{Y}}_{\mathrm{f}}}\left(\text{L; }{\text{S}}_{\mathrm{o}\mathrm{u}\mathrm{t}}\right)$ = 323 K.

The specified temperature distribution Y_p(x; S₂) on S₂ is expressed as follows:

The Y_p(x; S₂) function is depicted in Figure 12(a). Employing α = 0 for the optimization analysis, the cost function diminishes to 10 after 101 iterations.

The estimated q(x; S₁) and the computed T_p(x; S₂) are illustrated in Figure 12(a), unveiling a near-identical correspondence between Y_p(x; S₂) and T_p(x; S₂). This once again underscores the efficacy of the gradient-based algorithm employed in this study, as q(x; S₁) successfully aligns T_p(x; S₂) with Y_p(x; S₂). The temperature distributions that vary along the x-axis and the cross-sectional perspective at the outlet are presented in Figure 12(b), (c), respectively.

The calculated average outlet temperature of the water stands at $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ = 323.2 K, signifying adherence to the stipulated requirement of $\rm \overline {{{\text{Y}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ = 323 K. Nevertheless, the uniformity of the exit temperature ΔT(L; S_out) is determined to be 7.6 K, contributing to the discernible color shift in Figure 12(c). This observation highlights the potential necessity for a longer tube length when dealing with larger pipe diameters in order to ensure sufficient heating for achieving temperature uniformity conditions at the pipe exit. The convergence pattern is illustrated in Figure 13, which demonstrates a rapid convergence rate.

To address the abrupt spikes and discontinuities in q(x; S₁), a weighting coefficient α = 1×10^-6 is introduced. After 36 iterations, the convergence of q(x; S₁) is achieved, and the results are depicted in Figure 14. Analysis of Figure 14 indicates an amelioration in the sudden rise and discontinuity behaviors of q(x; S₁), although the alignment between the values of Y_p(x; S₂) and T_p(x; S₂) is not optimal. $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ and ΔT(L; S_out) reach 323.4 K and 9.1 K, respectively, which can be deemed acceptable in accordance with the desired conditions. The estimated results for Case B are summarized in Table 1.

4.   Conclusions

The current study delves into a novel approach to address the optimal heating problem. This method involves prescribing a temperature function along the inner surface of the pipe to facilitate fluid heating, complemented by the utilization of a gradient-based algorithm. This algorithm is applied to ascertain the optimal heating function along the outer surface of the pipe, aligning with the specified temperature function and resulting in uniform fluid exit temperatures. Numerical experiments affirm that the application of the estimated optimal heat function consistently achieves the desired uniform fluid exit temperatures to a satisfactory degree.

In the context of Case A, characterized by a smaller pipe diameter, the utilization of the specified floor function temperature distribution, as observed in Case A3, yielded the most favorable outcomes for $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ and ΔT(L; S_out) at the pipe exit. However, the estimated q(x; S₁) exhibited abrupt surges and discontinuities. These behaviors can be alleviated by introducing a weighting coefficient into the cost function, leading to maintained accuracy in $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ and ΔT(L; S_out). In the scenario of Case B, featuring a larger pipe diameter and the same floor function temperature specification, the estimated $\rm \overline {{{\text{T}}_f}} {\text{(L; }}{{\text{S}}_{out}})$ remains precise, though ΔT(L; S_out) achieves a satisfactory level. This suggests that a larger pipe diameter might necessitate an elongated tube length to enhance the uniformity of exit temperatures.

Use of AI tools declaration

The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

The research was funded by the National Science and Technology Council of Taiwan, under Grant NSTC-112-2221-E-006-140-MY3.

Conflict of interest

The authors declare that they have no conflicts of interest.