Hopf bifurcation exploration and control technique in a predator-prey system incorporating delay

1.   Introduction

As is known to us, predator-prey models play a vital role in describing the interaction between predator population and prey population in real natural world. In order to expose the internal change process and development law of predator population and prey population, a great deal of predator-prey models have been established. Through the discussion on predator-prey models, we can find the impact of parameters on the biological population densities in some specific environment. During the past decades, a lot of work on predator-prey models has been carried out and abundant fruits have been resulted. For example, Balc ^[1] explored the stability, well-posedness, and bifurcation issue of a fractional prey-predator model. Pandey et al. ^[2] explored the rich dynamics (e.g., transcritical, saddle-node, Hopf-bifurcation, etc.) of a delayed predator-prey model. Rao and Kang ^[3] established the conditions for the existence of a unique ergodic stationary distribution and the extinction conditions of predator species and prey species for a stochastic predator-prey model. Sarkar and Khajanchi ^[4] dealt with the spatiotemporal dynamical trait of a prey-predator model involving the fear effect. For more concrete examples, one can see ^[5,6,7,8].

In 2020, Sen et al. ^[9] formulated the following predator-prey system:

where $u_1(t)$ stands for the density of prey at time $t$ and $u_2(t)$ stands for the density of predator at time $t$, $h_1$ is the intrinsic growth rate of prey and $h_2$ is the intrinsic growth rate of predator, $a_1$ denotes the intra-species competition of prey and $a_2$ denotes the intra-species competition of predator, $b$ denotes the handling parameter, which is the product of the handling time and the searching efficiency, $d > 0$ is the conversion efficiency and $d_1$ represents the searching efficiency by an individual predator per unit time. All other parameters are positive real numbers. In details, one can see ^[9,10,11,12].

In many cases, the densities of prey and predator are affected due to the time delay of population development, then it is necessary to introduce the delay into the predator-prey models. Based on this viewpoint, we can establish more suitable delayed predator-prey models. Assume that the density of prey is affected by the self feedback time from $u_1$ to $u_1$, then we can modify model (1.1) as follows:

where $\delta > 0$ is a time delay. All other parameters are positive real numbers. Assume that the density of prey is affected by the self feedback time from $u_1$ to $u_1$ and the density of predator is affected by the self feedback time from $u_2$ to $u_2$, then we can modify model (1.1) as follows:

where $\delta > 0$ is a time delay. All other parameters are positive real numbers.

Many studies show that delay is often a vital factor that affects the dynamical behavior of the delayed dynamical model. In many instances, delay will make the system lose its stability, produce periodic vibration, generate chaotic behavior and so on ^{[13,14,15,16,17,18,19,20,21,22]}. In particular, delay-induced Hopf bifurcation is an important dynamical peculiarity. Biologically, delay-induced Hopf bifurcation plays a vital role in describing the balanced relationship among the concentrations of numerous biological populations. In the light of this viewpoint, we argue that exploring the delay-induced Hopf bifurcation in abundant predator-prey models has very important theoretical significance. Inspired by the above idea, we are going to investigate the delay-induced Hopf bifurcation and control of bifurcation for models (1.2) and (1.3). Specifically, we are to deal with the following three core points: (1) Study the well-posedness (e.g., non-negativeness, boundedness, existence and uniqueness) of solution to models (1.2) and (1.3). (2) Explore the emergence of Hopf bifurcation and stability of models (1.2) and (1.3). (3) Construct two different controllers to control the region of stability and the time of generation of bifurcation behavior of models (1.2) and (1.3).

The key highlights of this study are stated as follows: (Ⅰ) Depending on the previous studies, a new bifurcation and stability criterion without relying on time delay for model (1.2) is built. (Ⅱ) By virtue of two different controllers, the domain of stability and the time of generation of Hopf bifurcation of models (1.2) and (1.3) are effectively under control. (Ⅲ) The impact of time delay on dominating Hopf bifurcation phenomenon and stabilizing the densities of predators and preys of models (1.2) and (1.3) is presented.

This structure of this article is presented as follows: The well-posedness involving existence and uniqueness, non-negativeness and boundedness of the solution of system (1.2) is discussed in Section 2. Section 3 explores the bifurcation phenomenon and stability nature of system (1.2). Section 4 focuses on the control problem of bifurcation phenomenon for system (1.2) by virtue of a reasonable hybrid controller incorporating state feedback and parameter perturbation involving delay. Section 5 handles the control problem of bifurcation phenomenon and stability for system (1.3). Section 6 handles the control problem of bifurcation phenomenon for system (1.3) by virtue of a reasonable hybrid controller incorporating state feedback and parameter perturbation involving delay. Section 7 carries out numerical experiments to verify the rationality of the acquired key outcomes. A brief conclusion is included to finish this work in Section 8.

2.   Well-posedness

In this part, we are going to explore the well-posedness of solutions to model (1.2) and model (1.3) (include boundedness, existence and uniqueness, non-negativeness) via making use of fixed point theory, inequality technique and construction of a reasonable function.

Theorem 2.1. Denote $\Psi = \{u_1, u_2\in R^2: \max\{|u_1|, |u_2|\}\leq {\mathcal{U}}\}$, where ${\mathcal{U}} > 0$ denotes a constant. For each $(u_{10}, u_{20})\in \Psi$, system (1.2) under the initial state $(u_{10}, u_{20})$ owns a unique solution $U = (u_1, u_2)\in \Psi.$

Proof. Define the following mapping:

where

For every $U, \bar{U} \in \Psi,$ we can get

where

Thus $f(U)$ obeys the Lipschitz condition for $U$. Using fixed point theorem, one can conclude that Theorem 2.1 is right.

Theorem 2.2. Every solution of system (1.2) starting with $R_{+}^2$ is non-negative.

Proof. In view of the first equation of system (1.2), we can get

then

which leads to

and then one gets

Thus,

In a same way, we know

Thus, Theorem 2.2 is correct.

Theorem 2.3. The solutions of system (1.2) are uniformly bounded.

Proof. We consider two cases: $d > 1$ and $0 < d < 1$.

Case 1. If $d > 1$, let $W(t) = u_1(t)+u_2(t).$ Then

where

Let

Then,

According to the differential inequality theorem, we get

then

Case 2. If $0 < d < 1,$ let $W(t) = u_1(t)+u_2(t).$ Then,

where

Let

so

According to the differential inequality theorem, one gets

which results in

Based on these two cases, we can conclude that Theorem 2.3 is correct.

3.   Exploration of bifurcation of model (1.2)

In this section, we are going to explore the bifurcation and stability issue of model (1.2). Firstly, we assume that $E(u_{1\star}, u_{2\star})$ is the equilibrium point of model (1.2), then $u_{1\star}, u_{2\star}$ obey the following condition:

Let

Substitute system (3.2) into system (1.2), we gain the linear system of model (1.2) at $E(u_{1\star}, u_{2\star})$:

where

The characteristic equation of system (3.3) owns the following expression:

which leads to

If $\delta = 0,$ then Eq (3.6) becomes

If

is fulfilled, then the two roots $\lambda_1, \lambda_2$ of Eq (3.7) have negative real parts. Thus the equilibrium point $E(u_{1\star}, u_{2\star})$ of system (1.2) with $\delta = 0$ is locally asymptotically stable.

Assume that $\lambda = i\varepsilon$ is the root of Eq (3.6), then Eq (3.6) becomes

It follows from (3.9) that

Then

Let

Assume that

By virtue of $({\mathcal{A}}_2)$, we know $\Pi_1(0) = (b_1b_4+b_2b_3)^2-(b_1b_5)^2 < 0$, since $\lim_{\varepsilon \to \infty}\Pi_1(\varepsilon) > 0$, then we will know Eq (3.11) has at least one positive real root. Therefore Eq (3.6) has at least one pair of purely imaginary roots. Without loss of generality, we can assume that Eq (3.11) has four positive real roots (say $\varepsilon _j, j = 1, 2, 3, 4$). Relying on (3.10), we know

where $j = 1, 2, 3, 4; n = 0, 1, 2, \cdots$. Assume $\delta _0 = \min_{\{j = 1, 2, 3, 4; n = 0, 1, 2, \cdots\}}\{\delta _{j}^{(n)}\}$ and suppose that when $\delta = \delta_0$, Eq (3.6) has a pair of imaginary roots $\pm i\varepsilon _0$.

Next we present the following assumption:

where

Lemma 3.1. Suppose that $\lambda(\theta) = \epsilon_1(\delta)+i\epsilon_2(\delta)$ is the root of Eq (3.6) at $\delta = \delta_0$ such that $\epsilon_1(\delta_0) = 0$, $\epsilon_2(\delta_0) = \varepsilon_0$, then $Re\left(\frac{d\lambda}{d\delta}\right)\Big|_{\delta = \delta_0, \varepsilon = \varepsilon_0} > 0.$

Proof. By Eq (3.6), we can get

It means that

where

Hence

By the assumption $({\mathcal{A}}_3)$, we get

which ends the proof. According to the above discussion, the following outcome is easily derived.

Theorem 3.1. Suppose that $({\mathcal{A}}_1)$–$({\mathcal{A}}_3)$ hold, then the equilibrium point $E(u_{1\star}, u_{2\star})$ of model (1.2) holds a locally asymptotically stable state if $\delta \in [0, \delta _{0})$ and model (1.2) generates a cluster of Hopf bifurcations around the equilibrium point $E(u_{1\star}, u_{2\star})$ when $\delta = \delta _{0}.$

4.   Control of bifurcation for model (1.2) using hybrid controller

In this section, we are to study the Hopf bifurcation issue of system (1.2) by using a reasonable hybrid controller consisting of parameter perturbation with delay and state feedback. By virtue of the idea in ^[19,20], we formulate the following controlled predator-prey model:

System (4.1) owns the same equilibrium point $E(u_{1\star}, u_{2\star})$ as that in system (1.2). Let

The linear system of system (4.1) near $E(u_{1\star}, u_{2\star})$ can be expressed as follows:

where

The characteristic equation of system (4.3) owns the following expression:

which leads to

If $\delta = 0,$ then Eq (4.6) reads as:

If

is fulfilled, there are two roots $\lambda_1$ and $\lambda_2$ of Eq (4.6) that have negative real parts. Thus the equilibrium point $E(u_{1\star}, u_{2\star})$ of system (4.1) with $\delta = 0$ holds a locally asymptotically stable state. Suppose that $\lambda = i\varepsilon^*$ is the root of Eq (4.6), then Eq (4.6) becomes:

It follows from (4.9) that

By (4.10), we can get

where

So there is

Because of $\cos^2\varepsilon^\ast \delta +\sin^2\varepsilon ^\ast \delta = 1$, we can get

So

According to Eq (4.12), one gets

where

Using (4.15) and (4.16), we know

therefore, the results can be obtained as follows:

where

Let

We can make the following assumption:

If $({\mathcal{A}}_5)$ holds, then $\Pi_2 \left (0 \right) = -D_6 < 0$. Since $\lim_{\varepsilon^\ast\to \infty}\Pi_2 \left (\varepsilon^\ast\right) = +\infty > 0$, then Eq (4.19) has at least one pair of positive real roots, and Eq (4.6) has at least one pair of pure roots. So we can assume that Eq (4.19) has 12 positive solid roots (say $\varepsilon_j^{*}, j = 1, 2, 3, ..., 12$). It is available according to Eq (4.11),

where $j = 1, 2, 3, \cdots, 12$; $k = 0, 1, 2, \cdots$. Let $\delta _\ast = \min_{\{j = 1, 2, 3, \cdots, 12; k = 0, 1, 2, \cdots\}}\{\delta _{j}^{(k)}\}$, and assume that when $\delta = \delta _\ast$, Eq (4.6) has at least one pair of pure real roots $\pm i\varepsilon _{0}^{\ast}$.

Next the following assumption is given:

where

Lemma 4.1. Suppose that $\lambda(\theta) = \bar{\epsilon}_1(\delta)+i\bar{\epsilon}_2(\delta)$ is the root of Eq (4.6) at $\delta = \delta_{*}$ such that $\bar{\epsilon}_1(\delta_{*}) = 0$, $\bar{\epsilon}_2(\delta_{*}) = \varepsilon_0^{\ast}$, then $Re\left(\frac{d\lambda}{d\delta}\right)\Big|_{\delta = \delta_{*}, \varepsilon = \varepsilon_0^{\ast}} > 0.$

Proof. By Eq (4.6), one gets

which implies

where

Hence

According to $({\mathcal{A}}_6)$, one gets

which completes the proof.

Depending on the analysis above, the following conclusion is acquired:

Theorem 4.1. Suppose that $({\mathcal{A}}_4)$–$({\mathcal{A}}_6)$ hold, then the equilibrium point $E(u_{1\star}, u_{2\star})$ of model (4.1) is locally asymptotically stable if $\delta \in [0, \delta _{\ast })$ and model (4.1) generates a cluster of Hopf bifurcations near the equilibrium point $E(u_{1\star}, u_{2\star})$ when $\delta = \delta_{\ast }.$

5.   Exploration of bifurcation for model (1.3)

In this section, we are going to explore the Hopf bifurcation phenomenon of system (1.3). System (1.3) owns the same equilibrium point $E(u_{1\star}, u_{2\star})$ as that in system (1.2). Let

The linear system of system (1.3) near $E(u_{1\star}, u_{2\star})$ can be expressed as follows:

where

The characteristic equation of system (5.2) owns the following expression:

which leads to:

that is,

If $\delta = 0,$ then Eq (5.6) reads as:

If

is fulfilled, there are two roots $\lambda_1, \lambda_2$ of Eq (5.7) that have negative real parts. Thus the equilibrium point $E(u_{1\star}, u_{2\star})$ of system (1.3) with $\delta = 0$ is locally asymptotically stable.

Suppose that $\lambda = i\varepsilon^\tau$ is the root of Eq (5.6), then Eq (5.6) becomes:

By (5.9), we have

which means

where

So, we can get

Because of $\cos^2\varepsilon^\tau \delta +\sin^2\varepsilon ^\tau\delta = 1$, then

It follows from (5.14) that

By (5.12), one gets

where

Using (5.15) and (5.16), we know

Therefore, the results can be obtained as follows

where

Let

We can make the following assumptions:

If $({\mathcal{A}}_8)$ holds, then $\Pi_3 \left (0 \right) = -N_6 < 0$, since $\lim_{\varepsilon^\tau\to\infty}\Pi_3\left(\varepsilon^\tau\right) = +\infty > 0$, then Eq (5.19) has at least one pair of positive real roots, and Eq (5.6) has at least one pair of pure roots. So we can assume that Eq (5.19) has 12 positive real roots (say $\varepsilon^\tau_j, j = 1, 2, 3, ..., 12$).

By Eq (5.11), one gets

where $j = 1, 2, 3, \cdots, 12; m = 0, 1, 2, \cdots.$

Let $\delta _\star = \min_{\{j = 1, 2, 3, \cdots, 12; m = 0, 1, 2, \cdots.\}}\{\delta _{j}^{(m)}\}$, and assume that when $\delta = \delta _\star$, Eq (5.6) has at least one pair of pure of real roots $\pm i\varepsilon _{0}^{\tau}$.

Next the following assumption is needed:

where

Lemma 5.1. Suppose that $\lambda(\theta) = \xi_1(\theta)+i\xi_2(\theta)$ is the root of Eq (5.6) at $\delta = \delta _{\star}$, such that $\xi_1(\delta _\star) = 0$, $\xi_2(\delta _\star) = \varepsilon ^\tau _0$, then $Re\left(\frac{d\lambda}{d\delta }\right)\Big|_{\delta = \delta _{\star}, \varepsilon = \varepsilon^\tau_{0}} > 0.$

Proof. By Eq (5.6), one gets

which implies

where

Hence

By $({\mathcal{A}}_9)$, we have

which ends the proof.

Depending on the discussion above, the following results is obtained:

Theorem 5.1. Suppose that $({\mathcal{A}}_7)$–$({\mathcal{A}}_9)$ are fulfilled, then the equilibrium point $E(u_{1\star}, u_{2\star})$ of model (5.1) is locally asymptotically stable if $\delta \in [0, \delta _{\star})$ and model (5.1) generates a cluster of Hopf bifurcations near the equilibrium point $E(u_{1\star}, u_{2\star})$ when $\delta = \delta_{\star}.$

Remark 5.1. In model (1.3), there is only one delay. If there are two different delays in model (1.3), we can deal with the effect of two delays on the stability and bifurcation. We leave it for future work.

6.   Control of bifurcation for model (1.3) using extended delayed feedback controller

In this section, we are to study the Hopf bifurcation issue of system (1.3) by using a reasonable extended delayed feedback controller consisting of parameter perturbation with delay. By virtue of the idea in ^[23,24,25], we formulate the following controlled predator-prey model:

System (6.1) owns the same equilibrium point $E(u_{1\star}, u_{2\star})$ as that of system (1.3). Let

The linear system of system (6.1) around $E(u_{1\star}, u_{2\star})$ takes the following expression:

where

The characteristic equation of system (6.3) owns the following expression:

which leads to:

that is

If $\delta = 0,$ then Eq (6.7) reads as:

If

is fulfilled, then the two roots $\lambda_1, \lambda_2$ of Eq (6.7) have negative real parts. Thus the equilibrium point $E(u_{1\star}, u_{2\star})$ of system (6.1) with $\delta = 0$ is locally asymptotically stable.

Suppose that $\lambda = i\varepsilon ^\mu$ is the root of Eq (6.7), then Eq (6.7) becomes:

By (6.10), we have

which means

where

So, we can get

Because of $\cos^2\varepsilon^\mu\delta +\sin^2\varepsilon ^\mu\delta = 1$,

It follows from (6.15) that

By (6.13), one gets

where

Using (6.16) and (6.17), we know

therefore, the results can be obtained as follows:

where

Let

We can make the following assumption:

If $({\mathcal{A}}_{11})$ holds, then $\Pi_4\left (0 \right) = -X_6 < 0$. Notice that $\lim_{\varepsilon^\mu \to \infty}\Pi_4 \left (\varepsilon ^\mu\right) = +\infty > 0$, then Eq (6.20) has at least one pair of positive real roots, and Eq (6.7) has at least one pair of purely real roots. So we can assume that Eq (6.20) has 12 positive real roots (say $\varepsilon^\mu_j, j = 1, 2, 3, \cdots, 12$).

By Eq (6.14), one gets

where $j = 1, 2, 3, \cdots, 12; \theta = 0, 1, 2, \cdots$.

Let $\delta_{0\ast} = \min_{\{j = 1, 2, 3, \cdots, 12; \theta = 0, 1, 2, \cdots\}}\{\delta_{j}^{(\theta)}\}$, and assume that when $\delta = \delta_{0\ast}$, Eq (6.7) has at least one pair of pure real roots $\pm\varepsilon_{0}^{\mu}$.

Next the following assumption is needed:

where

Lemma 6.1. Suppose that $\lambda(\theta) = \bar{\xi}_1(\theta)+i\bar{\xi}_2(\theta)$ is the root of Eq (6.7) at $\delta = \delta _{0\ast}$ such that $\bar{\xi}_1(\delta _{0\ast}) = 0$, $\bar{\xi}_2(\delta _{0\ast}) = \varepsilon ^\mu_0$, then $Re\left(\frac{d\lambda}{d\delta }\right)\Big|_{\delta = \delta _{0\ast}, \varepsilon = \varepsilon^\mu_{0}} > 0.$

Proof. By Eq (6.7), one gets

which implies

where

Hence

By $({\mathcal{A}}_{12})$, we have

which completes the proof.

Depending on the study above, the following conclusion is acquired:

Theorem 6.1. Suppose that $({\mathcal{A}}_{10})$–$({\mathcal{A}}_{12})$ hold, then the equilibrium point $E(u_{1\star}, u_{2\star})$ of model (6.1) is locally asymptotically stable if $\delta \in [0, \delta _{0\ast})$ and model (6.1) generates a cluster of Hopf bifurcations at the equilibrium point $E(u_{1\star}, u_{2\star})$ when $\delta = \delta_{0\ast}.$

Remark 6.1. In this paper, some mathematical formulas and assumptions are very complicated (for example, $({\mathcal{A}}_{6}), ({\mathcal{A}}_{12}),$ etc.), but we can check their correctness using computerized calculations.

Remark 6.2. The control methods in this paper can be applied to control the bifurcation or chaos of fractional-order dynamical system.

7.   Simulation outcomes

In this section, to verify the obtained key outcomes of this paper, we give some computer simulations.

Example 7.1. Consider the following predator-prey system incorporating delay:

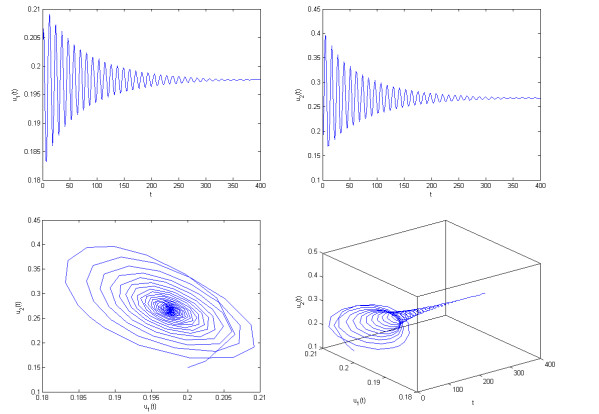
where $h_1 = 0.5, h_2 = 0.5, a_1 = 2, a_2 = 2, d_1 = 0.4, b = 0.1, d = 0.45.$ Clearly, model (7.1) admits a unique positive equilibrium point $E(0.1975, 0.2674)$. One can easily derive that the conditions $({\mathcal{A}}_1)$–$({\mathcal{A}}_3)$ of Theorem 3.1 hold. Making use of computer software, one can obtain that $\delta_{0}\approx2.9$. To verify the correctness of the gained outcomes of Theorem 3.1, we choose two nonidentical values of delay. One is $\delta = 2.8$ and the other is $\delta = 2.97.$ If $\delta = 2.8 < \delta_{0}\approx2.9$, we gain computer simulation diagrams that are given in Figure 1. From Figure 1, we can easily understand that $u_1\rightarrow0.1975, u_2\rightarrow0.2674$ when $t\rightarrow +\infty.$ Namely, unique positive equilibrium point $E(0.1975, 0.2674)$ of model (7.1) maintains locally asymptotically stable status. If $\delta = 2.97 > \delta_{0}\approx2.9$, we gain computer simulation diagrams that are given in Figure 2. From Figure 2, we are able to see that $u_1$ is to keep a periodic quavering level around the value $0.1975$, $u_2$ is to keep a periodic quavering level around the value $0.2674$. In other words, a cluster of periodic solutions (namely, Hopf bifurcations) arise near the positive equilibrium point $E(0.1975, 0.2674)$.

Example 7.2. Consider the following controlled predator-prey system incorporating delay:

where $h_1 = 0.5, h_2 = 0.5, a_1 = 2, a_2 = 2, d_1 = 0.4, b = 0.1, d = 0.45.$ Let $\alpha_1 = 0.6, k = 0.5$. Clearly, model (7.2) admits a unique positive equilibrium point $E(0.1975, 0.2674)$. One can easily derive that the conditions $({\mathcal{A}}_5)$–$({\mathcal{A}}_7)$ of Theorem 4.1 hold. Making use of computer software, one can obtain that $\delta_{\star}\approx2.85$. To verify the correctness of the gained outcomes of Theorem 4.1, we choose two nonidentical values of delay. One is $\delta = 2.83$ and the other is $\delta = 3.0.$ If $\delta = 2.83 < \delta_{\ast}\approx2.85$, we gain computer simulation diagrams that are given in Figure 3. From Figure 3, we can easily understand that $u_1\rightarrow0.1975, u_2\rightarrow0.2674$ when $t\rightarrow +\infty.$ Namely, unique positive equilibrium point $E(0.1975, 0.2674)$ of model (7.2) maintains locally asymptotically stable status. If $\delta = 3.0 > \delta_{\ast}\approx2.85$, we gain computer simulation diagrams that are given in Figure 4. From Figure 4, we are able to see that $u_1$ is to keep a periodic quavering level around the value $0.1975$, $u_2$ is to keep a periodic quavering level around the value $0.2674$. In other words, a cluster of periodic solutions (namely, Hopf bifurcations) arise near the positive equilibrium point $E(0.1975, 0.2674)$.

Example 7.3. Consider the following predator-prey system incorporating delay:

where $h_1 = 0.5, h_2 = 0.5, a_1 = 2, a_2 = 2, d_1 = 0.4, b = 0.1, d = 0.45.$ Clearly, model (7.3) admits a unique positive equilibrium point $E(0.1975, 0.2674)$. One can easily derive that the conditions $({\mathcal{A}}_8)$–$({\mathcal{A}}_{10})$ of Theorem 5.1 hold. Making use of computer software, one can obtain that $\delta_{\star}\approx2.8$. To verify the correctness of the gained outcomes of Theorem 5.1, we choose two nonidentical values of delay. One is $\delta = 2.7$ and the other is $\delta = 2.88.$ If $\delta = 2.7 < \delta_{\star}\approx2.8$, we gain computer simulation diagrams that are given in Figure 5. From Figure 5, we can easily understand that $u_1\rightarrow0.1975, u_2\rightarrow0.2674$ when $t\rightarrow +\infty.$ Namely, unique positive equilibrium point $E(0.1975, 0.2674)$ of model (7.3) maintains locally asymptotically stable status. If $\delta = 2.88 > \delta_{\star}\approx2.8$, we gain computer simulation diagrams that are given in Figure 6. From Figure 6, we are able to see that $u_1$ is to keep a periodic quavering level around the value $0.1975$, $u_2$ is to keep a periodic quavering level around the value $0.2674$. In other words, a cluster of periodic solutions (namely, Hopf bifurcations) arise near the positive equilibrium point $E(0.1975, 0.2674)$.

Example 7.4. Consider the following controlled predator-prey system incorporating delay:

where $h_1 = 0.5, h_2 = 0.5, a_1 = 2, a_2 = 2, d_1 = 0.4, b = 0.1, d = 0.45.$ Let $k_1 = 0.3, k_2 = 0.1$. Clearly, model (7.4) admits a unique positive equilibrium point $E(0.1975, 0.2674)$. One can easily derive that the conditions $({\mathcal{A}}_8)$–$({\mathcal{A}}_{10})$ of Theorem 6.1 hold. Making use of computer software, one can obtain that $\delta_{0\ast}\approx4.1$. To verify the correctness of the gained outcomes of Theorem 6.1, we choose two nonidentical values of delay. One is $\delta = 3.8$ and the other is $\delta = 4.4.$ If $\delta = 3.8 < \delta_{0\ast}\approx4.1$, we gain computer simulation diagrams that are given in Figure 7. From Figure 7, we can easily understand that $u_1\rightarrow0.1975, u_2\rightarrow0.2674$ when $t\rightarrow +\infty.$ Namely, unique positive equilibrium point $E(0.1975, 0.2674)$ of model (7.4) maintains locally asymptotically stable status. If $\delta = 4.4 > \delta_{0\ast}\approx4.1$, we gain computer simulation diagrams that are given in Figure 8. From Figure 8, we are able to see that $u_1$ is to keep a periodic quavering level around the value $0.1975$, $u_2$ is to keep a periodic quavering level around the value $0.2674$. In other words, a cluster of periodic solutions (namely, Hopf bifurcations) arise near the positive equilibrium point $E(0.1975, 0.2674)$.

Remark 7.1. Based on the computer simulation figures in Examples 7.1 and 7.2, one can easily know that the bifurcation values of model (7.1) and model (7.2) are $\delta_0\approx2.9$ and $\delta_{\ast}\approx2.85$, which implies that we can reduce the domain of stability and shorten the time of emergence of bifurcation of model (7.1) via the designed hybrid controller. Based on the computer simulation figures in Examples 7.3 and 7.4, one can easily know that the bifurcation values of model (7.3) and model (7.3) are $\delta_{\star}\approx2.8$ and $\delta_{0\ast}\approx4.1$, which implies that we can enlarge the domain of stability and delay the time of emergence of bifurcation of model (7.3) via the designed extended delayed feedback controller.

8.   Conclusions

Nowadays, the investigation of predator-prey models has attracted much interest from mathematical and biological circles. From a mathematical point of view, revealing the effect of time delay on the many dynamical peculiarities of predator-prey models is a very significant topic. In this article, two new delayed predator-prey models are formulated. The non-negativeness, existence and uniqueness, and boundedness of solution of the established delayed predator-prey models are detailedly analyzed. By regarding the delay as the parameter of bifurcation, we gain two delay-independent criteria to guarantee the emergence of bifurcation and stability of the established two delayed predator-prey models. Making use of two different controllers, we have availably adjusted the region of stability and the time of onset of the bifurcation phenomenon of the two delayed predator-prey models. The fruits of this article have immense theoretical significance in taking control of the balance of the concentrations of predator and prey. Furthermore, the exploration idea can be applied to explore the control problem of bifurcation in many other differential models. In the near future, we will adopt other controllers to deal with the bifurcation control of these two delayed predator-prey models. Recently, there have many studies on Hopf bifurcation of fractional-order dynamical models ^{[26,27,28,29,30,31]}. We will also focus on Hopf bifurcation of fractional-order predator-prey models in the near future.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by National Natural Science Foundation of China (No.12261015, No. 62062018), Project of High-level Innovative Talents of Guizhou Province ([2016]5651), University Science and Technology Top Talents Project of Guizhou Province (KY[2018]047), Foundation of Science and Technology of Guizhou Province ([2019]1051), Guizhou University of Finance and Economics (2018XZD01). The authors would like to thank the referees and the editor for helpful suggestions incorporated into this paper.

Conflict of interest

The authors declare that they have no conflict of interest.