Asymmetric integral barrier function-based tracking control of constrained robots

Abbreviations: BTC: Bitcoin futures prices; DCC: dynamic conditional correlations

1.   Introduction

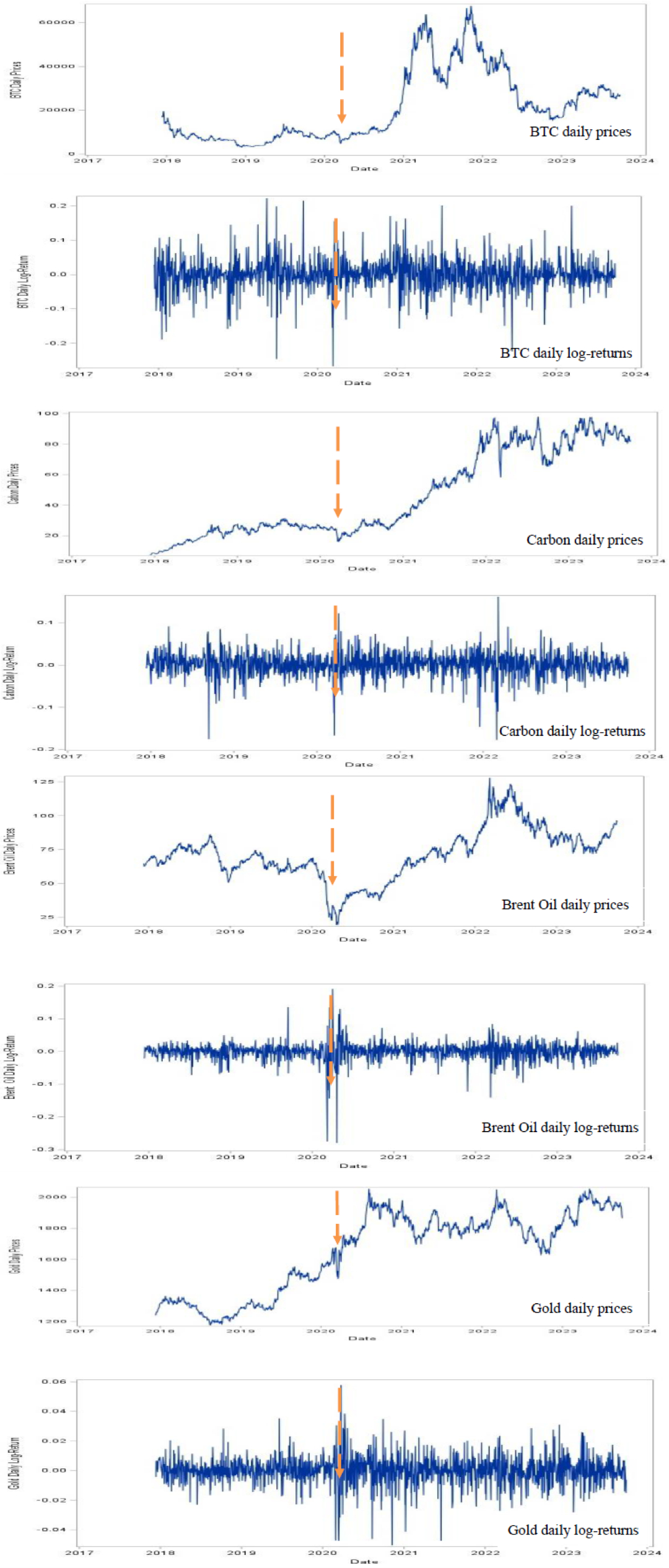
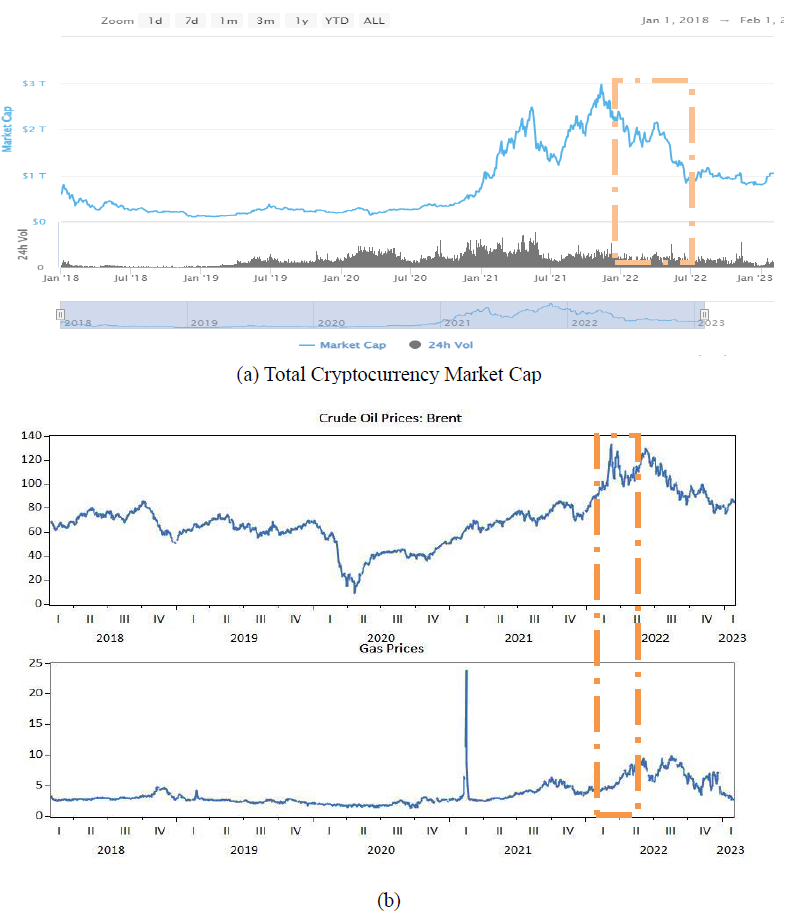
Crude oil, carbon dioxide emissions and Bitcoin are prevalent issues that have significant impacts on the global economy as well as the environment and also attracted extensive interest from market participants, policymakers and researchers ^[1,2], among many others. These issues are complicated interlinkages in terms of profound implications for economy and environmental policy including extreme weather phenomena. Undoubtedly, engagement in crypto mining is regarded as highly energy-intensive with significant carbon emissions ^[3]. Accordingly, spillover and linkage between crypto and energy markets is of major concern. Regarding this issue, the returns of Bitcoin fluctuation are essentially linked to carbon and energy investments in nature. Thus, the considerable number of studies have documented to examine the volatility transmission mechanism between Bitcoin and energy markets, inclusive of technology firms and fossil fuel prices e.g., ^[4,5,6]. These research findings suggest the time-varying spillovers between Bitcoin and oil assets and conclude the potential role of Bitcoin as a hedger and diversifier for conventional energy assets. Nevertheless, the existing studies highlight the spillover of cryptocurrencies, environmentally sustainable assets, with other assets e.g., ^[1,7,8,9]. There exists a scant article on the linkage between sustainable assets and Bitcoin that incorporates carbon futures into portfolios and may attract new investors to carbon markets for double goals of risk diversification. After mid-November 2021, the total market cap of the cryptocurrencies has also dropped considerably (as depicted in Figure 1a). The public cryptocurrency environmental attention in the market could be attributed to these price fluctuations, which might have spillover effects on other markets, where environmental aspects of cryptocurrency mining exist.

Subsequently, with insights from the considered markets, Figure 1 visualizes the universe of cryptocurrency and energy assets. While the impact of the unprecedented coronavirus pandemic on global economic growth fell by 3.5% in 2020, afterward, the Russia-Ukraine conflict came up on February 24, 2022. As shown in Figure 1b, European Brent crude oil price was trading at ＄90.24 per barrel on 1 February 2022 just before the Russia-Ukraine war. As of 8 March 2022, the peak price was selling at ＄133.18 per barrel, about ＄43 higher than the pre-war level. The ongoing geopolitical risk leading to crude prices has raised global oil marketing to gradually increase fuel prices to minimize their possible losses. Commodities are exposed to ongoing inflationary pressure. The global stocks and commodity market turmoil linked to the Russia-Ukraine war have more exposed to the regulatory risks of the low-carbon energy transitions performed better and to mitigate carbon dioxide (CO₂) emissions ^[10,11]. However, in response to the COVID-19 pandemic and geopolitical risk, hedging derivatives on cryptocurrency and carbon emission markets have been underexplored. In this study, we aim to fill this research gap, and the portfolio hedges including crypto and gold might be considered against the energy crisis attributing to market turbulence. In post COVID-19 pandemic era, Bitcoin and Gold are regarded as popular safe havens when geopolitical risk arises. These cryptocurrencies and various mainstream financial assets (e.g., oil, gold and futures) are better options to recognize the capability/role of Bitcoin: A hedging instrument, a diversifier or a safe haven e.g., ^[5,12,13,14].

More recently, there is extensive empirical evidence that cryptocurrency, energy and major commodity markets are closely connected. We are motivated by the growing number of studies investigating the interconnectedness between cryptocurrencies and various futures classes. Crucially, an in-depth analysis of the interrelatedness between Bitcoin and carbon emission or oil and gold futures markets. It can play a significant role in conducting adequate investment strategies that enable market participants to effectively manage their portfolios. This study could be crucial for investors applying Bitcoin to conduct safe haven, portfolio diversification and hedge against inflation or trading strategies during market crash periods. Theoretically, knowledge regarding economic uncertainty or inflation risk will allow market actors to obtain excess returns by allocating hedging assets ^[15,16]. Thus, the price of hedging assets may be regarded as a leading indicator of inflation risk, and act as an instrument to hedge against future risk or inflation ^[5]. The recent and rapidly growing of these hedging instruments include Bitcoin futures and options, as well as carbon emission, oil and gold futures prices that are related to Bitcoin futures prices. Accordingly, two subjects naturally appear:

(1) How much the asset weights should be in investors' portfolios?

(2) What potential role matters that adding Bitcoin or other asset classes to one's portfolio might positively impact his/her final wealth?

Theoretically, to discover the dynamic correlations among asset classes, we introduce DCC-GJR-GARCH (1, 1) model and copula-DCC-GJR-GARCH model to capture the prevailing dependence structure between Bitcoin and several financial assets. In this study, we emphasize three competitive models of the fitting Elliptical (Student-t) and Archimedean (Clayton and Gumbel) copulas and their implications on Bitcoin and other financial assets. Since copulas have become flexible and effective methodologies to measure dependence structure between two or more considered variables ^[17]. In particular, they have been gradually introduced to uncover the nonlinear dependence structure between financial markets and to solve many asset-allocation and portfolio risk-assessment problems ^[15,16,18].

Our investigation of the dynamic correlations across the considered assets contributes to the existing research along the two fundamental folds. First, the significance of this study is that the Gumbel copula leads to the best-fit copula and provides the most suitable model for capturing the dependence structure between Bitcoin and other financial assets, followed by the testing of log-likelihood values. Copulas offer useful time-varying information about the dynamic correlations between Bitcoin and other financial markets. Second, unlike prior literature, we draw attention to providing empirically informed insights regarding the hedging capacity of risk exposures in futures linked to pricing discovering mechanisms and then suggest that Bitcoin is not suitable for hedging against coal. Since the Bitcoin mining activities of energy consumption have access to linkages of fossil fuel which is a hydrocarbon-containing material such as coal.

To the best of our knowledge, this is the pioneering article to examine the Bitcoin futures volatility linkages across carbon emission, oil and gold futures and analyze whether the hedging strategies involving Bitcoin and these futures reduce considerably the portfolio's risk. From a practical viewpoint and financial perspective, our finding uncovers that Bitcoin or carbon emission futures may offer more hedging capacity and diversification benefits than other commodity futures for investors.

2.   Related literature review

Most of the existing studies concentrate on the dynamic dependence between cryptocurrencies (e.g., Bitcoin) and the other asset classes (i.e., commodity, crude oil and gold), while the information interdependence between the commodity and crypto assets has become a prominent research topic ^{[12,19,20,21]}. Many market participants are attracted to the cryptocurrency market to earn speculative profit from its high volatility and leverage. In contrast, gold is recognized safe-haven asset and considered a hedging product against cryptocurrency, stocks and bonds, in that it is considered to be used as an instrument to lighten portfolio risk ^[22]. Their empirical interpretation document that during crisis periods, gold acts as a store of value generating minimal intermediary costs.

In the related literature, carbon emission trading markets are often considered to be the most cost-effective emission reduction tool, particularly in fighting climate change (see ^{[23,24,25,26,27]}). From a carbon risk management financial perspective, the interlinkages between carbon emission trading and energy assets and price discovery are crucial to better identify the hedging and potential diversification features between carbon emission and energy commodities (see ^[28,29]).

Differently from several studies that focus on the interconnectedness of cryptocurrency and stock or gold markets ^[30,31], our work allows us to examine the role played by carbon emission futures in crypto markets going beyond the influence associated with Bitcoin futures. To restrict the scope of our investigation, we empirically analyze the most important cryptocurrency (Bitcoin) and other major commodities. Evidently, cryptocurrencies and traditional commodities (oil, gold) or carbon emission assets can be integrated into portfolios for investors who seek hedging effectiveness and also for optimal portfolio weights against market turmoil or the COVID-19 pandemic outbreak, see also ^{[12,14,19,32,33,34,35]}.

The explosive growth of the crypto ecosystem is fueling demand for Bitcoin futures markets. Very few studies have investigated how much the position of commodity/Bitcoin should be in an investor's portfolio. For this purpose, we attempt to fill this gap and make use of GJR news' impact curve of the asymmetric DCC models to describe the asymmetric response to news on volatility effects. Similarly, Guesmi et al. ^[36] also show that VARMA (1, 1)-DCC-GJR-GARCH performs the best-fit model for modeling the dynamics of various financial assets.

The multivariate GARCH models are regarded as the most popular classes of MGARCH specifications and are often used to forecast financial time series (see, e.g., ^[37]). We uncover the interconnections of volatilities between Bitcoin and commodity futures. In the existing literature, a copula-DCC-GARCH model is an alternative approach and offers significant advantages to modeling the dependence structure of variable pairs ^[38,39,40]. Using copula functions allows capturing the separate marginal behavior of the considered assets from the examination of joint extreme co-movements, which is critical to make optimal asset-allocation decisions and to constructing risk management strategies ^[17,41].

The article is laid out in four sections. Section 2 outlines a related literature review. Section 3 interprets our empirical design and econometric model. Section 4 performs the empirical findings and analyzes estimation results. Section 5 shows economic implications and Section 6 concludes the study.

3.   Methodology and econometric model

3.1.   The DCC-GJR-GARCH model

Numerous studies suggest that the dynamic conditional correlation (DCC) GARCH model is appropriate for examining time-varying correlations and optimal portfolio construction between multiple assets ^{[36,42,43,44]}, among others. To capture the volatility dynamics and correlations of the Bitcoin and commodity, we extend the analysis to include the asymmetric dynamic conditional correlation (A-DCC) approach developed by Cappiello et al. ^[45]. Such an A-DCC GARCH model can capture asymmetric responses in conditional volatility and interconnectedness between assets during periods of shocks. This method is also popular and widely used in applications, and can be stated as in the following equation:

where $\boldsymbol{R}_{\boldsymbol{t}}$ indicates a 2×1 vector of Bitcoin and commodities' returns including Bitcoin (BTC), Carbon Emission, Oil and Gold Futures. ${\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\bf{t - 1}}}}$ represents the information set at time t-1, and $\varepsilon_{i, t}$ refers to conditionally heteroskedastic random errors for different commodities and Bitcoin futures' returns. $\xi_{i, t+1}$ denotes a sequence of i, i, d error terms. $\boldsymbol{H}_t$ specifies the variance-covariance matrix. Let us suppose that $h_{i, t}$ follows a bivariate GJR-GARCH process ^[46] and can be expressed as

where i = Bitcoin, commodities, $I_{t-1} = \left\{\begin{array}{l}1, \text { if } \varepsilon_{i, t-1} < 0 \\ 0, \text { if } \varepsilon_{i, t-1}>0\end{array}\right.$,

where $\alpha_{i, i}$ is the short-run persistence of shocks to changes, or ARCH effect, $\beta_{i, i}$ denotes the GARCH effect and $\alpha_{i, i}+\beta_{i, i}$ is the long-run persistence of shocks to changes.

To empirically analyze dynamic conditional correlations among Bitcoin and commodity futures, the dynamic relationship of volatility is analyzed with the use of a DCC-GARCH approach proposed by Engle (2002) ^[47]. Hereafter, the conditional covariance matrix can be estimated by applying the residuals $z_{i, t}$ with a DCC- GARCH model. As our primary goal is to investigate the one-to-one correlation between the pair assets' returns, we apply a bivariate model, accordingly. The bivariate GARCH model with the specification of the dynamic conditional correlation estimators is specified by:

where $\boldsymbol{D}_t = {diag}\left(v_t\right), v_t = \left(h_{B T C, t}^{1 / 2}, h_{\text {commodities }, t}^{1 / 2}\right)$, commodities = Carbon Emission, Oil and Gold Futures.

where is the square matrix of order i referring to symmetric

where $\mathit{\boldsymbol{\overline{Q}}}$ denotes the i × i (2×2)matrix composed by the unconditional covariance of residual ${\mathit{\boldsymbol{z}}_{\mathit{\boldsymbol{t}}}}$ and $z_{i, t} = \left[z_{B T C}, z_{\text {commodity }}\right]^{\prime}$ represents a vector of i, i, d random noises defined as $z_{i, t} = \varepsilon_{i, t} / \sqrt{h_{i, t}}$; a and b denote the estimated parameters with non-negative coefficients satisfy a+b < 1. The conditional correlation coefficient is expressed as

The estimates of the model parameters can be computed using Quasi-Maximum Likelihood (QML) method and the log-likelihood function is given as below

where the definition of residuals ${\mathit{\boldsymbol{z}}_\mathit{\boldsymbol{t}}}$ also expands the joint distribution of traditional DCC proposed by Engle ^[47].

3.2.   Copula DCC-GARCH model

An n-dimensional copula $C\left(u_1, \ldots, u_n\right)$ and its marginal function $F_1, \ldots, F_d$ in the unit hypercube $[0, 1]^n$ is a continuous function, then we can find the unique Copula. In addition, the Sklar (1959) ^[48] proposes that the joint distribution, F, of a random vector, $X = \left(x_1, \ldots, x_n\right)$, with marginals, $F_1\left(x_1\right), \ldots, F_n\left(x_n\right)$, can be interpreted as follows:

where C is the copula, which is distinctively established in the interval [0, 1]ⁿ for F under continuous marginals:

The density function can be expressed as:

where f_i and C depict the marginal densities and density function of the copula, respectively. Further, the density functions of f_i and C are given by:

where ${F_i^{ - 1}}$ stands for the functional quantile margins.

3.2.1.   Elliptical copulas

In the case of elliptical copulas, we consider ${t_{v, R}}$ as the standard multivariate t distribution along correlation matrix R, then the Student-t copula is expressed analogously as follows

where ν and ${t_v^{ - 1}}$ denote degrees of freedom and the inverse cumulative distribution (ICD) of Student's t function, respectively.

3.2.2.   Archimedean copulas

In the case of Archimedean copulas, the parameter θ can be estimated as follows:

where ψ denotes the generator of the Archimedean copula and ψ-1 depicts the inverse of the generator. As shown in Table A1, two types of Archimedean copulas are used in the study.

3.2.3.   Maximum likelihood estimation

A multiple integral in $u_j \in[0, 1]$ for $\forall j$, can be interpreted as follows:

Because the copula in Eq (10) belongs to a distribution function, the copula density in the interior $\left(u_1, \ldots, u_n\right)^T \in[0, 1]^n$ is given by

In conjunction with the copula parameter given as the generic vector Ω, then the multivariate distribution function Eq (10) can be defined as:

By differentiating the copula and the density function is given by

The above Eqs (18) and (19) on differentiation and using Sklar's theorem in terms of density functions and yields:

Where f_i denotes the derivative of the distribution function F_j with respect to z_j; i.e., f_j depicts the jth density function. According to Sklar's theorem in terms of density functions Eq (20) the log-likelihood function is obtained as:

3.3.   Optimal portfolio analysis

The accuracy estimation of the time-varying covariance matrix is necessary to hedging, portfolio management, forecasting risk and asset pricing. To demonstrate the importance of the covariance matrix to a variety type of financial assets, we used the preceding results to two subjects. First, consider the subject of computing the optimal fully allocated portfolio weights subject to investment constraints including no-short-selling. This application is illustrative that portfolio managers face these kinds of problems when deriving their optimal portfolio weights without reducing their expected returns. Therefore, making the subject equivalent to estimating the risk-minimizing portfolio holdings can be written as follows.

Taking into account a portfolio that consists of Bitcoin and stablecoins and expected utility (EU) that the mean-variance utility function assumed, the optimal portfolio weights of the Bitcoin are constructed as following constraints

where w_{12, t} denotes the portfolio weight for the first position- Bitcoin relative to the second position- commodity at time t, h_{11, t} is the conditional variance of the first position- Bitcoin, h_{22, t} refers to the conditional variance of the second position- commodity and h_{12, t} is the conditional covariance between the first (Bitcoin) and the second (commodities) position.

Second, we consider an econometric approach to estimate a dynamic risk-minimizing hedge ratio by applying DCC-GJR- GARCH model. To minimize the risk of a portfolio including a short position ＄δ in a commodity futures portfolio can hedge a long position ＄1 in a Bitcoin portfolio, where the "risk -minimizing hedge ratio" takes the following form

see, for example ^[49,50].

3.4.   Performance on portfolios of maximize expected utility

Based on the mean-variance portfolio optimization theory developed by ^[51], investors should select an optimal trade-off between the expectation and variance of portfolio payoffs. In addition, Markowitz ^[52] also proposes that more than a half-century study in the mean-variance analysis has been generally supported. To conduct research on this model, we proceed by computing the vector of portfolio weights (w), by applying the utility function maximization in regard to w as follows:

where m is the sample mean and Σ is the covariance matrix, the parameter γ denotes the relative risk aversion of investors. We also apply no-short selling constraints $\left(w_i \geq 0, \forall i\right)$ and the normalized portfolio weights $\left(\sum_{i = 1}^N w_i = 1\right)$. Therefore, the following optimization problem can be defined:

s.t. $w_i \geq 0, \forall i, \quad \sum_{i = 1}^N w_i = 1$.

Next, we introduce the preceding mean-variance optimal portfolio by maximizing the expected utility function, which is expressed by employing the Arrow-Pratt risk aversion index to balance risk and return. Using the forecasted volatility-covariance $\widehat{H}$ estimated from the preceding DCC-GJR model in the portfolio optimization and then compare this trading strategy (max U) with three benchmark trading strategies: Holding Bitcoin (BTC) only, holding commodities only (carbon emission…) and the well-known equal-weight portfolio (EQ, half- Bitcoin and commodities). For the mean-variance optimal portfolio (MVO) rule, at each time t, the investor chooses the optimal weights (w) to maximize the expected utility function. The mean-variance term and in the objective function can be represented by:

where r is the momentum factor ^[53], γ is the risk aversion coefficient and $\widehat{H}$ is the estimated variance-covariance matrix obtained from the preceding DCC-GJR model.

4.   Empirical application and portfolio analysis

The study is based on daily data for the leading cryptocurrency of Bitcoin futures as well as commodity futures including carbon emission, Brent oil and gold futures that are obtained from December 11, 2017 to September 29, 2023. The datasets used are collected from https://www.investing.com/commodities/ which is the trading platform that is most popular among investors and Bitcoin enthusiasts. Crucially, we consider the data synchronization on the (daily) frequency trading and the process of establishing consistency and consolidation of data between various futures. The natural logarithm of closing prices change for return series are expressed as follows:

where $R_{i, t}$ refers to the return series of futures assets i at time t. $P_{i, t}$ denotes the price series of futures assets i at time t, and ${P_{i, t-1}}$ denotes the lagged price of futures i. The sample data of the futures profile consists of 5,960 observations. The descriptive statistics and second moment are depicted in Table 1. Statistically, the estimated volatility can be measured by the standard deviation of the log-return for all futures. As evidenced in Table 1, we observe that Bitcoin shows the most volatile shock equal to 4.5%, whereas the commodities' volatilities range from 0.28% (carbon) to 2.69% (oil). Thus, the average volatility of BTC is substantially greater than the average of commodities' volatilities. The light orange (dotted) lines in Figure 2 also display the significant volatility jump and indicate that all assets' returns are significantly impacted by shocks from the first wave of the COVID-19 pandemic. As shown in the Table 1, the skewness of the four assets is equal to -0.2083, -0.5614, -1.4143 and -0.1609, respectively, while the kurtosis is equal to 4.4961, 4.6101, 19.7804 and 4.7797, respectively, implying the same features with the common financial time series. All series of daily futures returns exhibit the distribution of negative skewness (skewness smaller than 0) and all series present leptokurtic distribution (kurtosis greater than 3). A goodness-of-fit test of the Jarque-Bera statistics with extremely small p-values suggests that the four series deviate from the normal distribution.

4.2.   Evidence of volatility spillovers

The DCC-GARCH results indicate the significance of $\alpha_{11}, \alpha_{22}, \beta_{11}$ and $\beta_{22}$, which implies that the current conditional volatility in the Bitcoin-commodity market responds to lagged conditional volatility and shock dependence in its own market. As shown in Table 2, regarding own-shock $\left(\alpha_{11}, \alpha_{22}\right)$ and own volatility spillovers $\left(\beta_{11}, \beta_{22}\right)$ estimations provide the volatility spillover among Bitcoin and commodity futures. The findings demonstrate that the lagged shocks and volatility have a positive and significant impact on current conditional volatility in Bitcoin and commodity futures at the 1% level. These findings are in line with the results of ^[54].

Unsurprisingly, a more thorough exploration of estimations of ARCH and GARCH coefficients, reflects volatility persistence and shock dependence in the conditional variance equations. The results document that patterns can also be very commonly observed between Bitcoin and other assets. Exactly, these highly significant coefficients appear in most cases.

The values of parameters $\left(\beta_{11}, \beta_{22}\right)$ for Bitcoin and carbon emission futures return are 0.874 and 0.8132, respectively, other 0.8744, 0.8561 for the BTC/oil and 0.880, 0.931 for the BTC/gold. The volatility sensitivity to past own conditional volatility (GARCH terms) shows statistically significant for all Bitcoin vs. commodity volatility series at the 1% level.

4.3.   Dynamic conditional correlations

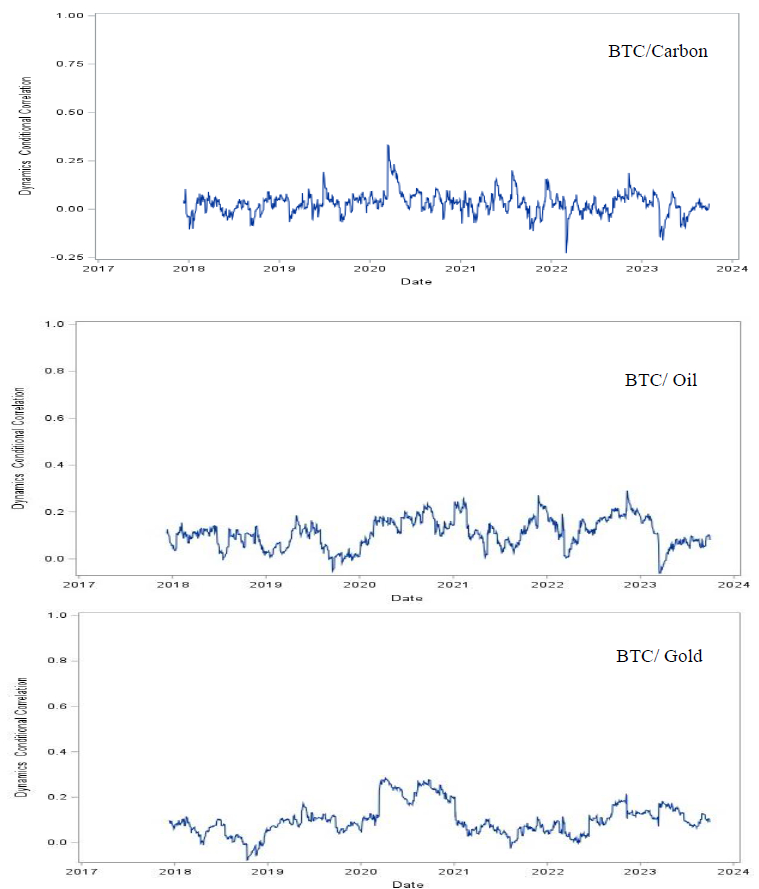
The findings of time-varying correlations are depicted in Figure 3 for the pairs of BTC/commodity futures. The dynamic conditional correlations (DCC) that varied over time are significantly positive for all pairs futures (except for dcc a of Bitcoin-carbon emission) analogous to the evidence of ^[19,55]. For each pair of correlations, the dynamic conditional correlations (DCC) produced from Bitcoin asset correlate weak with those produced from the carbon, oil and gold assets in all cases, as shown in Figure 3. The dynamic dependence relationship between the Bitcoin and oil assets has fluctuated from 0.05 to 0.2 in the pre-and post-COVID-19 phase. Similarly, the weak relationship between Bitcoin and gold assets has exhibited time-varying at (0, 0.2) for the sample period under study. Overall, as evidenced in Figure 3, Bitcoin is found weakly linked to carbon, crude oil and gold. Thus, incorporating Bitcoin with asset classes is a crucial consideration to achieve diversification benefits. The result is supported by Reboredo and Ugolini ^[23], suggesting that Bitcoin is weakly connected with carbon, green bond and energy markets.

In the same way, the DCC-GARCH model is employed (Table 2), and the estimates of the DCC parameters (a and b) are meaningful as mass coefficients and found to be statistically significant in most of the cases. The short-term persistence of the shocks on the DCC exhibits the highest for BTC/gold at 0.009, while the largest long-run shock persistence to the DCC is 0.98 for BTC/gold.

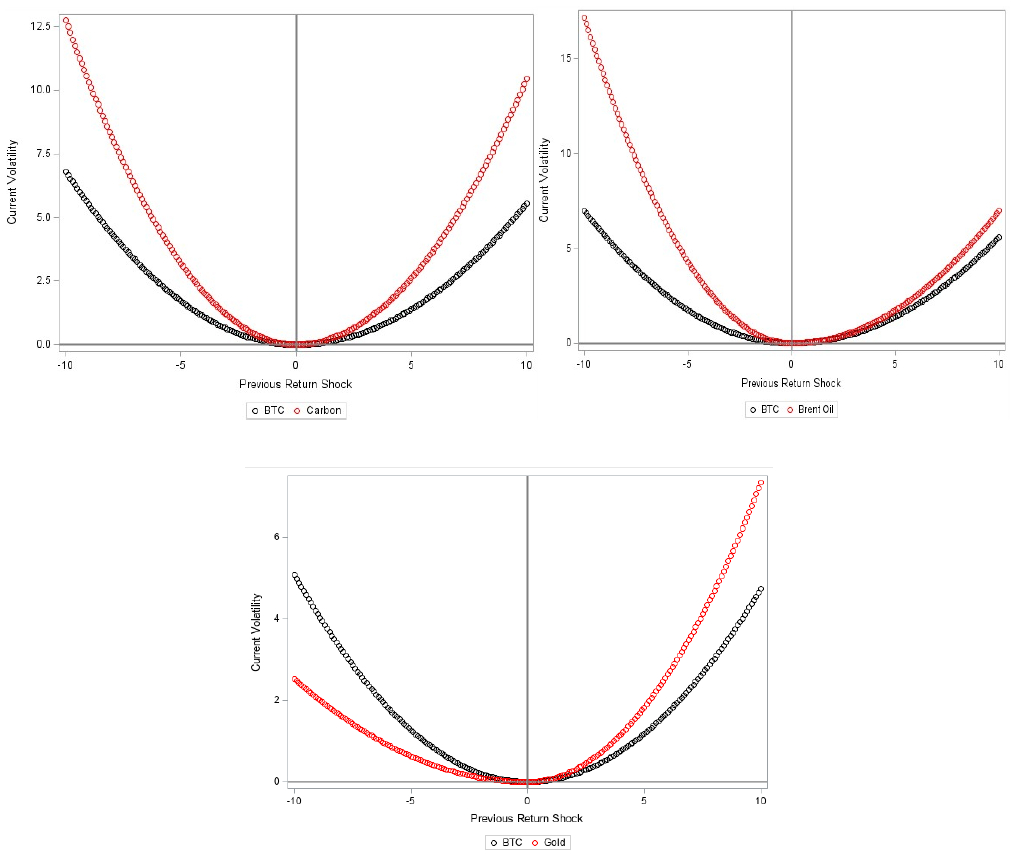
To determine the impact of the significant asymmetries matter, we examine the asymmetric response of correlation to cryptocurrency market shocks and Table 2 reports the coefficient $\gamma_{i, i}$, and most futures confirm the asymmetry phenomenon, except for Bitcoin and carbon emission. In addition, to visualize the news impact curve analysis for the DCC-GJR -GARCH model its graph is generalized to the "news impact curve" ^[56]. As observed in Figure 4, the news impact curve reports that the nexus between previous returns and news presents qualitative similarity for all four assets with an increase in the news, either positive or negative, and a corresponding increase in previous returns. Nonetheless, the shocks of similar magnitude have an apparent influence on previous returns in carbon than the other Bitcoin markets suggesting evidence for greater risk aversion linked to Bitcoin.

Summarizing all, the above news impact curves can capture adequately the asymmetric or leverage effect by accessing either the center of the news impact curve.

The three charts exhibit near similar news impact curves for commodity futures, implying that when modeling the variances of futures, these patterns act similarly and depict the U shape. However, remark also that the Bitcoin news impact curve by conducting the DCC models. Further, we found that DCC-GJR-GARCH (1, 1) may be representative of the asymmetric dynamic conditional volatility process for the futures portfolios.

4.4.   Illustration of economic importance

After investigating the existence of asymmetry and spillover, the usage of the conditional variance and covariance series computed from DCC-GJR-multivariate GARCH models has useful implications. Subsequently, we employ the methodology introduced by Kroner and Ng ^[57] to count the optimal portfolio weights subject to a no shorting constraint and the hedging ratios (portfolio risk), respectively. The portfolio weight (average) suggests the optimal weights of stablecoins and Bitcoin assets to minimize the risk-hedging strategies without slashing the expected returns. Additionally, the hedge ratio on average implies the investors to allocate either a short or long position for these assets.

Regarding risk-hedging strategies of portfolio implications, Table 3 exhibits the average optimal weights and hedge ratios for the pairs of BTC/commodities futures during the sample periods, respectively. Consistent results are computed from these futures portfolios, the average optimal weights are 0.8582, 0.7629 and 0.9769 for BTC/carbon emission, BTC/oil and BTC/gold futures portfolios, respectively. The observed findings depict that the optimal weight exhibits 0.8582 for the pair of BTC/carbon emission, suggesting that for a ＄100 portfolio of BTC-carbon emission, investors should invest ＄85.82 in Bitcoin then remain ＄14.18 in carbon emission futures. Other weights are illustrated as follows. For a 100 portfolio of BTC-oil, on average ＄76.29 should be allocated in Bitcoin, and investors should remain ＄23.71 for oil futures.

Last, for ＄100 dollars of the BTC- gold portfolio, investors should allocate ＄96.94 in Bitcoin and the remainder of ＄3.06 invested in gold futures. Considering non-short selling constraints, these optimal weights are found to be low positions of commodity, implying that investors should lower their asset allocation in commodity futures for all BTC/commodity portfolios. Overall, Katsiampa ^[58] also documents that the leading Bitcoin should outweigh the top 2 Ethereum based on portfolio weight optimization.

For a robustness perspective, we also empirically evaluate the hedging strategies of the optimal hedge ratio estimates obtained via the DCC-GARCH model. As depicted in Table 3, the average hedge ratio for the BTC/carbon emission portfolio is 0.04 which reveals that a ＄1 long position in Bitcoin futures could be hedged by a short position of 4 cents in carbon emission futures. Similarly, for the other cases, a ＄1 long position in Bitcoin futures requires with the mean of the hedge ratio 0.21, that can be hedged with a short position of ＄21 cents in oil futures. Moreover, a ＄1 long position in Bitcoin futures requires the mean of the hedge ratio of 0.42, which can be hedged with a short position of 42 cents in gold futures. Overall, these commodity portfolios have above-zero hedge ratios, A closer review of these dynamic hedge ratios from Table 3 suggests that in general, indicating that more Bitcoin futures is necessary to minimize the risk of commodity futures. Parallel results are confirmed by Haffar et al. ^[59], who found that Bitcoin can play an important role in stabilizing portfolio performance, for time -varying levels of risk exposure.

4.5.   Robustness checks the performance of asset allocation

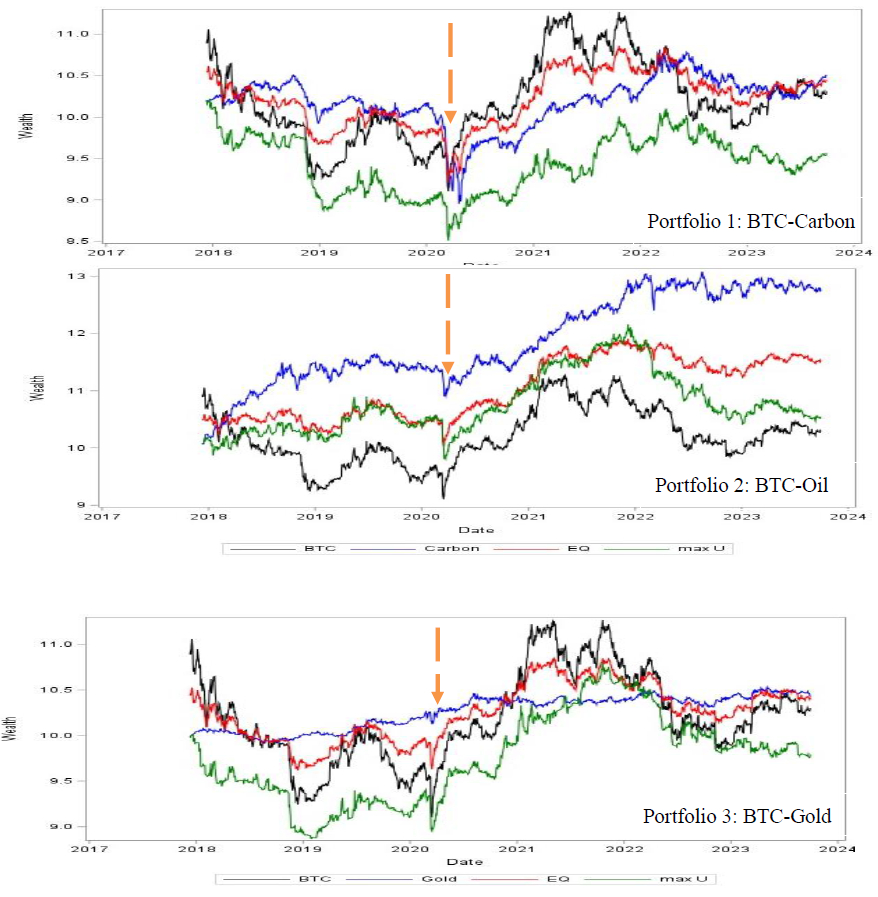
To illustrate the potential importance of constructing the optimal futures-asset allocation, we empirically evaluate the performance of the investment strategy depending on the conditional variances and covariances estimates of the DCC-GARCH (1, 1) model. As shown in Table 4 portfolio performance is reported, the naïve strategy has both the better average return and annual percentage yield (APY) than max U strategy (simulation results from Eq (25)). In addition, according to the Sharpe ratio (an indicator of risk-adjusted return), the performance of equal weighs (EQ) outperforms those obtained from max U strategy. Over 5 years, the final wealth that simulation results from using the naïve strategy is about 2.48% more than the final wealth that performance from using the max U strategy. Figure 5 depicts the wealth curve (or portfolio value) of each trading strategy against time. On the whole, based on the DCC-GJR-GARCH model, the result indicated that Bitcoin is a successful hedge against the other futures and a weak safe haven during COVID-19 Pandemic era. More importantly, we can obtain the Sharpe ratio values produced by the mean-variance (positive) strategy. The portfolio (#1) performance of the carbon emission futures mostly outperform other futures portfolio, and the values are 0.03, 12.74 and 18.48 for Sharpe Ratio, Final Wealth and APY (%), respectively. To evaluate the wealth path and portfolio performance of trading strategies, we find that carbon emission alone depicted as the blue trajectories (highest solid lines) in top Panel of Figure 5, outperforms overwhelmingly than other strategies, especially during the pre-COVID-19 Pandemic era. Accordingly, carbon emission futures offer more diversification benefits than other futures during the COVID-19 Pandemic era. In addition, the final wealth path and performance of the reference strategies has plunged significantly (as highlighted in Figure 5) by the COVID-19 shock amidst the pandemic outbreak in February 2020. However, all strategies broadly achieve better performances post- COVID-19 era.

4.6.   Copulas and the optimal problem

Copulas have become flexible and effective methodologies to measure the dependence structure between two or more random variables. As it can be observed, Table 5 shows the Copula DCC-GARCH model estimation results for Bitcoin and the financial assets series. According to the results for the Bitcoin and financial assets series, there was a positive dependence structure correlation between (each paired market) Bitcoin and other financial assets of 5% significance, except for the Bitcoin- coal series. Additionally, we observed that most Bitcoin and the financial assets series indicated shock dependence with a significance level of 1%. This result is also parallel to the result from the DCC-GARCH model (Table 4), indicating a significant volatility spillover (dcc1_2) between Bitcoin and other assets classes.

Besides, to verify the reliability of the outcomes of the families of DCC copula model, we compared its performance with that of three competitively used models, namely Student-t DCC copula, Clayton DCC copula and Gumbel DCC copula, employing log-likelihood (LL). According to the lowest value of the log-likelihood, the Gumbel copula gives the best fitting among the three copulas tested and produces the best fit, the Clayton copula the second best and the Student-t model the worst fit. However, Clayton appears to be the best copula fit for capturing the prevailing dependence structures between the Bitcoin and Brent oil prices. Notably, the outcomes in Table 5 suggest that Gumbel copula leads to the best fit of the copula-DCC-GARCH. This result corroborates with prior research, like ^[60,61] among others, who have concluded that the fit of Gumbel copula provides superior performance to those from other copulas in financial data.

Interestingly, we also briefly depict some major indicators of copula families and the dependence structure in measure of Kendall's τ. All the Kendall coefficients between Bitcoin and the other asset classes are significantly positive and tend neither to infinity nor to zero.

As depicted in the bottom of Table 5, the Bitcoin-carbon dependence is positive with Kendall's τ at 0.036. Moreover, the Bitcoin-Oil dependence is positive with a fairly small Kendall coefficient of 0.053, which implies that the fall or rise in Bitcoin returns co-occurs with a comparatively slight depreciation or appreciation of the Oil prices. The Bitcoin-Gold dependence is positive with a fairly small Kendall coefficient of 0.065, which indicates that the fall or rise in Bitcoin returns is only followed by a comparatively slight depreciation or appreciation of the gold prices. In addition, the Kendall dependence is positive, suggesting that the constructed Student-t, Clayton and Gumbel copulas are more effective in modelling dynamic positive dependence for Bitcoin and other assets. The Kendall dependence, although weak in general, our findings further expand the works of ^[62,63,39], who document the potential diversifying role of ESG stocks during the COVID-19 Pandemic.

Furthermore, in order to give additional test to the coal market, we apply Copula-DCC-GARCH model to examine the dynamic correlations between the Bitcoin market and the coal market, as represented by coking coal futures retrieved from Investing.com (https://www.investing.com/). Concerning the dependence structure between Bitcoin and coal prices, the copula function reveals positive dependence with Kendall's τ at 0. 015 (shown in Table 5), demonstrating that Bitcoin cannot hedge against coal prices. Empirically, concerning the case of the coal market, our results are in line with those of ^[64], suggesting that the time-varying linkages is an important property in detecting dependence structure between Bitcoin and coal futures prices. More specifically, the Bitcoin mining activities of energy consumption have access to linkages of fossil fuel which is a hydrocarbon-containing material such as coal. In light of these results, Bitcoin is not suitable for hedging against coal.

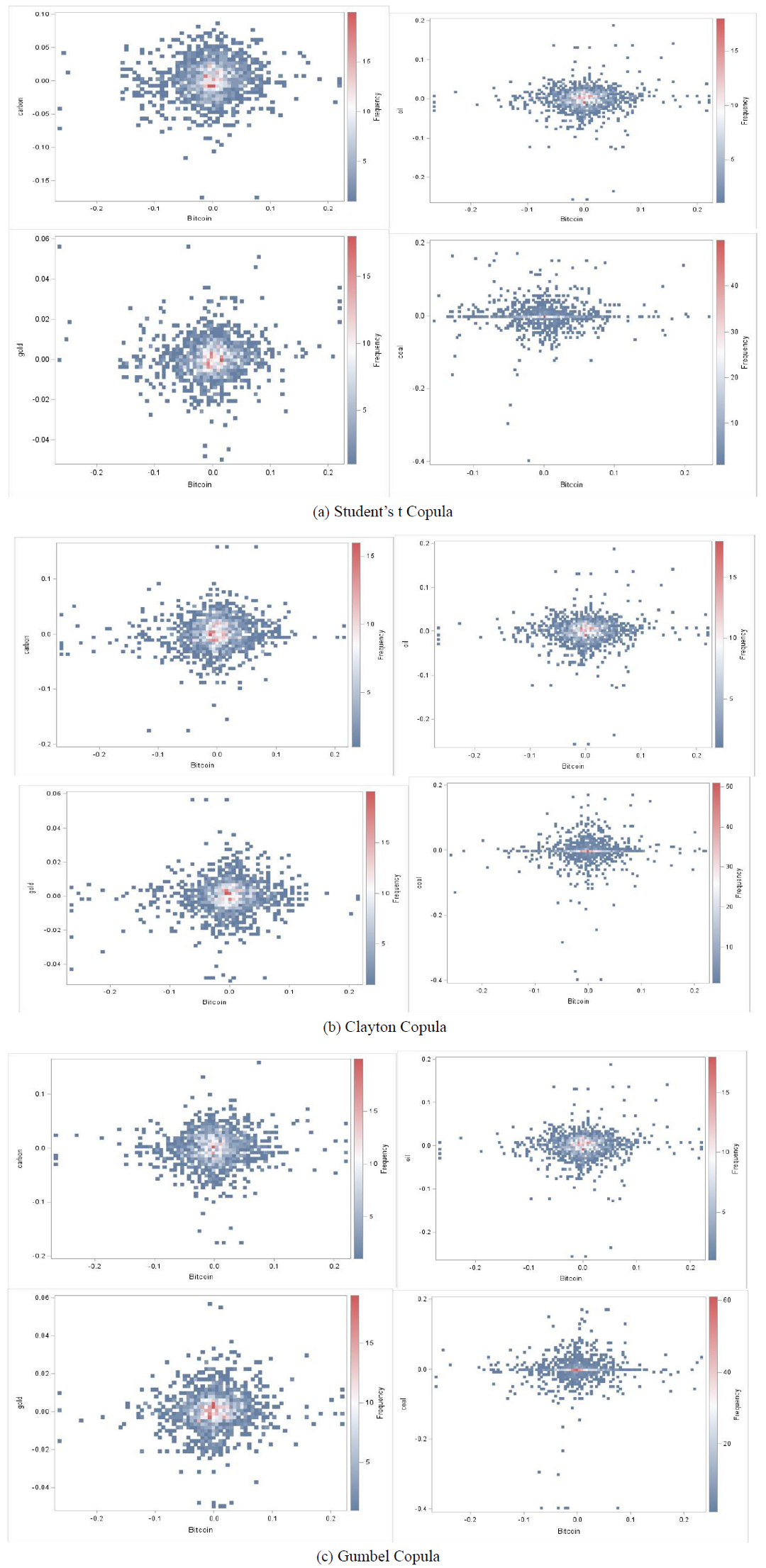
As displayed in Figure 6, it is to be noted that the heatmap of the fitting copula families on dependence structure is observed. Because the red blocks are more concentrated at the central quadrant of the X and Y axes and show significant concentration dependence. The non-parametric density estimates facilitate in offering graphical evidence of positive dependence not only between Bitcoin and other assets' prices but also between Bitcoin and coal prices, also underlines a good fit to the data and captures the dependence structure in each of the four portfolios (cases).

Figure 7 depicts the graphical illustration of DCC based on three competitive copulas models among Bitcoin, carbon, crude oil, gold and coal assets in a pairwise pattern. Graphical representations of DCC exhibit that pairwise correlation between two return series that varies with time and fluctuates between positive and negative values. Accordingly, it indicates evidence of asymmetry and move in clustering structures that suggest better opportunities for portfolio diversification. In addition, the dynamic association between any pair assets could be discovered to display substantial fluctuations between the negative and positive values as evident from Figure 7. The negligible and negative correlations indicate a good timing for hedging portfolio. For instance, the negative interdependence between Bitcoin and crude oil at a given time frame symbolizes that the Bitcoin price tends to fall in a bear market when the crude oil market resides in a bullish state. Such insights could potently be applied for risk light as it prevails clear hedging opportunities. Overall, the DCC value between Bitcoin and gold is maximum, and the DCC values range from (-)0.50 to 0.85, which exhibits that the DCC signifies a high volatile feature in these assets. In contrast, the DCC values between Bitcoin and coal are minimum. We also observe that both the time-varying correlations and dynamic low correlations fluctuate significantly amidst times of economic turbulence.

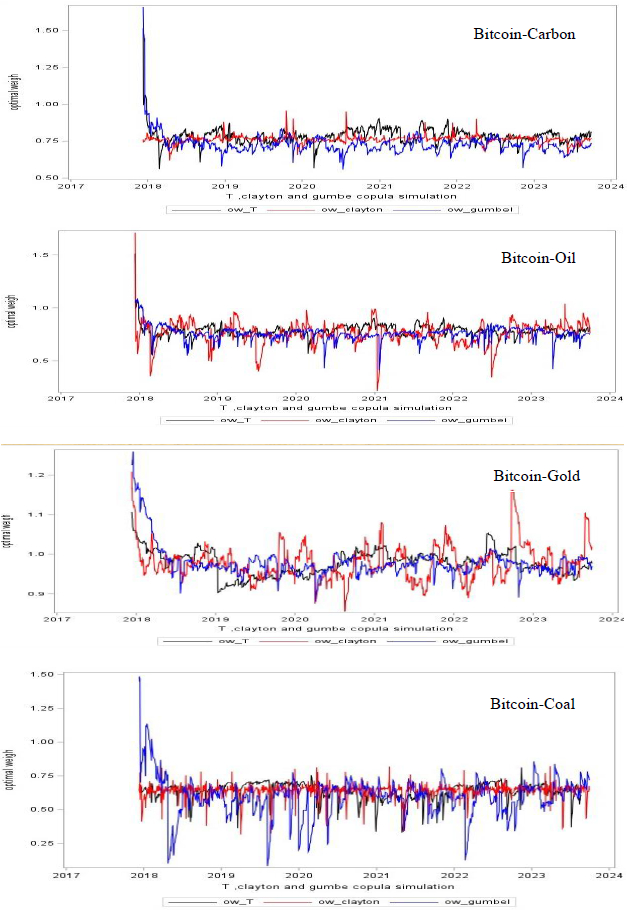
In contrast, in Figure 8, we can observe that the optimal weights produced from three competitive copulas models for most asset portfolios also fluctuate over time, particularly with peaks in specific time frames. For instance, Bitcoin hit a peak of unprecedented boom in December 2017 and the COVID-19 pandemic.

4.7.   Policy implications and what golden rule can learn from futures lessons

In summary, we synthesize the above results. On the whole, our empirical results provide crucial information to investors, crypto traders and portfolio managers regarding optimal allocation, hedging strategy, diversification and risk management. In particular, this study provides the following guidelines and implications for market participants in the construction of their crypto portfolios that include commodities.

First, we present fresh evidence that Bitcoin is not suitable for hedging against coal. Since the Bitcoin mining activities of energy consumption have access to linkages of fossil fuel which is a hydrocarbon-containing material such as coal. Second, empirically, carbon futures offer more diversification benefits than other futures, especially during the COVID-19 Pandemic era.

5.   Conclusions

This study is particularly important because it is crucial for futures investors to construct risk-hedging strategies in the various futures assets. Our results highlight some empirical insights, and it is evidenced that dynamic conditional correction between the largest cryptocurrency BTC and major commodity futures. Crucially, we demonstrate that a multivariate GARCH model can describe the dynamic conditional correlations among the active futures and then in their application that involves a novel approach in dynamic covariance matrices forecasting (e.g., computing the risk-minimizing portfolio or measuring the optimal hedge ratio).

Additionally, using the DCC-GJR-GARCH model and Copula DCC-GJR-GARCH model, we show that the diversification benefits of final wealth on Bitcoin futures compared to emerging futures portfolios are observed to be larger during the COVID-19 era than the pre-COVID-19 era. The asymmetric DCC approach is introduced to examine the dynamic volatility interlinkage between Bitcoin futures return and futures from the carbon emission, oil and gold returns.

Generally, our results are not valuable for only recognizing the dynamic relationships between the futures markets, but they are also of major attraction to future enthusiasts, investors and portfolio managers who are actively trading in Bitcoin and commodity futures. Perhaps the most prominent application of our findings has crucial implications for practical futures investments. How much futures should be in an investor's portfolio ultimately relies on the investor's risk tolerance and beliefs about futures assets. Based on optimal weights, investors are recommended to decrease their funds in carbon emission, oil and gold for all portfolios of Bitcoin/commodity Futures. Indeed, for investors, portfolio strategies involving optimal weights and hedge ratios have important economic implications for constructing a futures portfolio while potentially limiting risk exposure during pro- and pre- COVID-19 Pandemic periods. In particular, we construct the golden rule of crypto portfolios suggested from the evidence of hedging, diversifier and safe haven capabilities between Bitcoin and commodity futures. This highlights an opportunity for investors between Bitcoin and commodities assets.

Regarding future study, a crucial question is left: What should the future trading via a decentralized financial system for commodities? After the unprecedented COVID-19 Pandemic, the tokenization of commodities through blockchain also enables direct transactions, effectively dismissing the requirement for middlemen who have historically made undue profits. This ensures that farmers and producers obtain their fair share. Also, further research is needed to discuss the potential of tokenized commodities illustrating the blockchain offers huge opportunities in introducing new revenue streams, reducing external debt and boosting the overall economy. Thus, this work will be left to further research.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors greatly appreciate the three anonymous reviewers for their constructive comments and suggestions to help us improve the manuscript.

Conflict of interest

All authors declare no conflicts of interest in this paper.