Practical stability for nonlinear systems with generalized conformable derivative

1.   Introduction

As the effectiveness of data systems continues to improve, more and more mathematical approaches are being applied to real-world applications to yield exceptional outcomes. Fractional approaches, such as fractional calculus, fractional Fourier analysis, and the linear canonical transform, are gaining importance in the field of mathematics and among applied mathematicians. The theory and method of fractional domain analysis may further define the dynamic process of signal translation from the time domain to the frequency domain, thereby creating a new avenue for non-stationary signal analysis and treatment studies. In technical domains, such as radar, communications, and sonar, fractional approaches are preferred over traditional integral methods because they bring novel concepts, procedures, and ideas ^{[1,2,3,28,29,30,31,33]}. Due to the unpredictability of signals in actual engineering systems and the effects of different disturbances and noises on the transmission process, despite the numerous benefits of these new fractional approaches, there are still critical issues that need to be resolved. Additionally, fractional theory is confronted with several practical limitations in engineering, such as sampling and filtering in the sphere of multidimensional signals.

Lyapunov stability is a fundamental concept in control theory and plays a significant role in the analysis of fractional order systems. Lyapunov stability analysis of fractional order systems aims to establish the stability of a system by determining whether its trajectory remains within a certain region of the state space. Unlike integer-order systems, fractional order systems exhibit complex behaviors, such as memory effects, non-locality, and infinite-dimensional dynamics, which make their stability analysis more challenging. In the past few decades, several Lyapunov stability criteria have been proposed for fractional order systems, including algebraic, geometric, and analytical methods. These criteria have been used to establish practical stability, asymptotic stability, uniform stability, and robust stability for fractional order systems. Despite the progress made in the field, the Lyapunov stability analysis of fractional order systems remains an active area of research with significant potential for future advancements ^[38,39]. However, Khalil et al. ^[4,20] presented a new derivative called the conformable Fractional Derivative (FD), which goes beyond the conventional limit definitions of derivatives. Some theorems of classical calculus require alternate expansions for fractional differential models, and this idea makes that possible. Academics find the conformable derivative intriguing since it appears to possess all the features of the conventional derivative ^[5], and it makes computations easier with FD formulas. There are now several applications of this novel idea. In fact, a new exact solution was presented for Burgers-type equations with conformable derivatives in ^[6], and ^[7] investigates the time scales method of dealing with conformable derivatives. Additionally, parameter variation was investigated in this work ^[8]. The Fractional Fourier series is also addressed in the publication ^[9], and new conformable derivative properties are described in study ^[10]. Conversely, ^[11] looks at a generalization of the classical conformable fractional derivative and establishes the Generalized Fractional Derivative (GCD) as a new class of fractional derivatives. Several examples in research show that the solution to the diffusion equation is unique (see ^[12]). Multi-agent systems with impulsive control protocols ^[13], numerical methods ^[14], the time power-based grey model ^[15], the multivariate grey system model ^[16], controllability and observability ^[17], the Barbalat Lemma ^[18], H infinite observers ^[19], exponential quasi-synchronization ^[21], partial practical stability ^[22], stability analysis depending on a parameter ^[23] are just a few examples of recent research that have expanded on the GCD. Numerous recent research articles highlight the significance of the conformable derivative in tackling a wide range of issues in science and engineering, demonstrating its widespread applicability ^[32,34,35]. However, the conformable derivative has not yet been fully investigated, and there are still unanswered questions about it.

On the other hand, the definition of practical stability for nonlinear systems is widely utilized to demonstrate the stability of such systems, where the state converges towards an arbitrarily small neighborhood of the origin. Various authors have developed the concept of practical stability, as shown in references ^[36,37]. This notion is especially significant in engineering applications when there are unpredictable, time-varying, or unbounded external inputs or disturbances that might create instability and oscillations. If the system's trajectories wobble around an unstable route in this case, the best course of action is to guarantee that the system's performance is still acceptable in a practical sense. This means that if the starting values of the external disturbances are constrained, the deviations of the system's motion from equilibrium should remain within specified boundaries given by the physical circumstances, resulting in the system being stable. The concept of practical stability has been extended to fractional order systems, and has been shown to be an effective tool for analyzing the stability of such systems, particularly when traditional methods may be insufficient, see for example ^[24,25]. In fact, work ^[25] explores the notion of practical stability for a class of general conformable nonlinear systems. For a certain class of fractional-order nonlinear systems, Makhlouf in ^[22] has developed a stability analysis that guarantees convergence of certain solutions towards a ball.

In this study, we have conducted a theoretical investigation of the practical stability analysis for a class of nonlinear systems with a generalized conformable derivative, a topic that has not been previously addressed in the literature. Our main contribution is providing detailed descriptions of practical uniform stability and practical global uniform asymptotic stability results for the proposed system. To demonstrate the validity of our theoretical findings, we have applied the approach to a specific nonlinear system with generalized conformable derivative. Additionally, we have provided a numerical simulation to show the effectiveness of the proposed approach in practice. Overall, our study offers a novel and comprehensive approach to practical stability analysis for nonlinear systems with generalized conformable derivative.

Driven by the foregoing interpretations, our study is summarized by the following key points:

● To the best of our knowledge, there are no published papers that address the fundamental and theoretical analysis of practical stability of nonlinear systems with a generalized conformable derivative.

● We provide a detailed description of practical uniform stability and practical global uniform asymptotic stability results.

● An application of the practically globally uniformly asymptotically stable result is presented to illustrate the validity of the theoretical findings.

● We also provide two numerical examples with simulation results to demonstrate the effectiveness of the proposed results.

2.   Preliminaries

We begin by giving some definitions and preliminary results (see ^[4,7,11,12]).

Definition 2.1. Let $h$ be a function defined on $[z_1, z_2)$ so, the GCD of $h$ is defined by

for all $s > {z_1}$, where $\beta \in (0, 1]$ and $\phi_{z_1}(s, \beta)$ is a positive function and satisfies

where $\beta_1\neq \beta_2$ and $\beta_1, \ \beta_2 \in (0, 1], \ \phi_{z_1}(s, 1) = 1.$

If $T^{\beta, \phi_{z_1}}_{{z_1}}h(s)$ exists, for every $s\in({z_1}, z)$, for some $z > z_1$ and $\lim\limits_{s \longrightarrow {z_1}^+}T^{\beta, \phi_{z_1}}_{{z_1}}h(s)$ exists, then, by definition

Remark 2.1. As a further analysis of GCD's properties, we assume that $\phi_{z_1}(s, \beta) > 0$, for all $s > z_1$, $\frac{1}{\phi_{z_1}}(., \beta)$ is locally integrable and

where g is a positive function with

Definition 2.2. For $0 < \beta < 1$, the general Conformable Integral (CI) of a continuous function $h$ is given by

Lemma 2.1. Let $h$ be a continuous function on $[z_1, z_2]$. Therefore

for every $s\geq {z_1}$.

Definition 2.3. It is said that a function $\varpi \in C(\mathbb{R}_+, \mathbb{R}_+)$ belongs to class $\mathcal{K}$ if $\varpi(0) = 0$ and it is strictly increasing. It will belong to class $\mathcal{K}_\infty$ if it in addition $\lim\limits_{z\longrightarrow +\infty} \varpi(z) = +\infty$.

Lemma 2.2. ^[27] If $\varpi\in \mathcal{K}$, then for every $d_1, d_2\in \mathbb{R}_+$, we have

Lemma 2.3. ^[26] For every $d_1, d_2 \geq 0$ and $q \geq 1$, we have

and

3.   Stability analysis

In this section, the following parameterized differential equations with GCD derivatives are considered:

where $r_0 \in \mathbb{R}_+$, $\iota\in \mathbb{R}^*_+$ and $f(., ., \iota) \in C\big(\mathbb{R}_+ \times \mathbb{R}^n, \mathbb{R}^n\big)$. We denote by $x_\iota(t; r_0, x_0)$ the solution of the system (3.1). For $m > 0$, we write $x = (y, z), \ z\in \mathbb{R}^p, \ y\in \mathbb{R}^m.$

Definition 3.1. The system (3.1) is called $\iota^*$-$y$-practically uniformly stable ($\iota^*$-$y$-PUS), if for each $l_2 > 0$ there is $l_1 > 0$ and $\hat{\iota} \in (0, \iota^*]$ such that for every $r_0\in \mathbb{R}_+$, for every $x_0\in \mathbb{R}^n$ with $\|x_0\| < l_1$ and for every $\iota \in (0, \hat{\iota}]$, $\|y_\iota(t; r_0, x_0)\| < l_2$ for every $t\geq r_0$.

Definition 3.2. The system (3.1) is called $\iota^*$-$y$-practically uniformly bounded ($\iota^*$-$y$-PUB), if for each $l_1 > 0$, there is $l_2 > 0$ and $\hat{\iota} \in (0, \iota^*]$ such that for every $r_0\in \mathbb{R}_+$, for every $x_0\in \mathbb{R}^n$ with $\|x_0\| < l_1$ and for each $\iota \in (0, \hat{\iota}]$, $\|y_\iota(t; r_0, x_0)\| < l_2$ for every $t\geq r_0$.

Definition 3.3. The system (3.1) is called $\iota^*$-$y$-globally uniformly practically attractive ($\iota^*$-$y$-GUPA), if for each $l_1 > 0$, $l_2 > 0$ there is $T > 0$ and $\hat{\iota} \in (0, \iota^*]$ such that for every $r_0\in \mathbb{R}_+$, for every $x_0\in \mathbb{R}^n$ with $\|x_0\| < l_1$ and for every $\iota \in (0, \hat{\iota}]$, $\|y_\iota(t; r_0, x_0)\| < l_2$ for every $t\geq r_0+T$.

Definition 3.4. The system (3.1) is called $\iota^*$-$y$-practically globally uniformly asymptotically stable ($\iota^*$-$y$-PGUAS), if it is $\iota^*$-$y$-PUS, $\iota^*$-$y$-PUB and $\iota^*$-$y$-GUPA.

Definition 3.5. The system (3.1) is called $\iota^*$-$y$-practically uniformly exponentially stable ($\iota^*$-$y$-PUES), if for every $0 < \iota \leq \iota^*$ there is positive scalars $C(\iota)$, $\delta(\iota)$ and $\varrho(\iota)$ such that:

where

with $\varrho(\iota)\longrightarrow 0$ as $\iota \longrightarrow 0^+$ and there is $C, \ \delta_1, \ \delta_2 > 0$, such that $\delta_1\leq \delta(\iota)\leq \delta_2$ and $0 < C(\iota)\leq C$ for every $\iota \in (0, \iota^*]$.

Theorem 3.1. Let $\iota^* > 0$. Suppose that for every $0 < \iota \leq \iota^*$, there is a $C^1$ function $V_{\iota}$: $\mathbb{R}_+ \times \mathbb{R}^n\longrightarrow \mathbb{R}$, class $\mathcal{K}$ functions $\varpi_j$, $(j = 1, 2)$, $\theta\in C \big(\mathbb{R}_+, \mathbb{R}_+\big)$ and constants $\varsigma_1(\iota) > 0$, $\varsigma_2(\iota) > 0$, $r_1(\iota) > 0$ and $r_2(\iota) > 0$ such that

$(1)$

$(2)$

where $\gamma = (x_1, x_2, ..., x_k)$, $m \leq k \leq n$, with

● $\forall \iota \in (0, \iota^*]$, $0 < \frac{\varsigma_2(\iota)}{\varsigma_1(\iota)} \leq K$, where $K > 0$.

● There is $M > 0$, such that

● $d(\iota)\longrightarrow 0$ as $\iota \longrightarrow 0^+$, where

Then, the system (3.1) is $\iota^*$-$y$-PUS. Moreover, if $\varpi_j\in \mathcal{K}_\infty, \, (j = 1, 2)$, therefore, the system (3.1) is $\iota^*$-$y$-PUB.

Proof. Let $l_2 > 0$. We consider $l_1 > 0$ and $\hat{\iota}\in (0, \iota^*]$, such that

and

It follows from (3.3) and (3.4) that

For $x_0 \in \mathbb{R}^n$, with $\|x_0\| < l_1$, we get Then,

Thus,

Therefore, the system (3.1) is $\iota^*$-$y$-PUS. We now consider the case where $\varpi_j\in \mathcal{K}_\infty, \, (j = 1, 2)$.

Let $l_1 > 0$. Take $\hat{\iota}_1\in (0, \iota^*]$ such that

In this case (3.6) becames:

Then,

Hence, the system (3.1) is $\iota^*$-$y$-PUB. □

Remark 3.1. In Theorem 3.1, if $\gamma = y = x$, we get the practical uniform stability and the practical uniform boundedness of the solutions of the system (3.1).

Theorem 3.2. Let $\iota^* > 0$. Suppose that for every $0 < \iota \leq \iota^*$, there is a $C^1$ function $V_{\iota}$: $\mathbb{R}_+ \times \mathbb{R}^n\longrightarrow \mathbb{R}$, class $\mathcal{K}_\infty$ functions $\varpi_j$, $(j = 1, 2)$, $\theta\in C \big(\mathbb{R}_+, \mathbb{R}_+\big)$ and constants $\varsigma_1(\iota) > 0$, $\varsigma_2(\iota) > 0$, $\varsigma_3(\iota) > 0$, $r_1(\iota) > 0$ and $r_2(\iota) > 0$ such that

$(1)$

$(2)$

where $\gamma = (x_1, x_2, ..., x_k)$, $m \leq k \leq n$, with

● $\forall \iota \in (0, \iota^*]$, $\frac{\varsigma_3(\iota)}{\varsigma_2(\iota)} \geq c$ and $0 < \frac{\varsigma_2(\iota)}{\varsigma_1(\iota)} \leq \Psi$, with $c$, $\Psi > 0$.

● There is $M_1 > 0$, such that

● $d(\iota)\longrightarrow 0$ as $\iota \longrightarrow 0^+$, where

with $M = M_1+\frac{1}{c}$.

Therefore, the system (3.1) is $\iota^*$-$y$-PGUAS.

Proof. From Eqs (3.7) and (3.8) we give:

where

and

Using Lemma $1$ in ^[25], we get

By (3.7), we get

Then,

Using Lemma 2.2, we get

Let $l_2 > 0$. From (3.12), we get

We have

and

then, there is $l_1 > 0$ and $\hat{\iota} \in (0, \iota^*]$, such that

Therefore, the system (3.1) is $\iota^*$-$y$-PUS.

Let $d_1 > 0$, we have

then, there exists $\hat{\iota}_1 > 0$, such that

Therefore, the system (3.1) is $\iota^*$-$y$-PUB.

Let $\delta_1 > 0$, $\delta_2 > 0$. Let $x_0\in \mathbb{R}^n$ such that $\|x_0\| < \delta_1$. It follows from (3.12) that

We have

then there exist $T > 0$ and $\hat{\iota}_2 > 0$ such that

Therefore, the system (3.1) is $\iota^*$-$y$-GUPA. Thus, the system (3.1) is $\iota^*$-$y$-PGUAS. □

Remark 3.2. In Theorem 3.2, if $\gamma = y = x$, we get the practical global uniform asymptotic stability of the system (3.1).

Remark 3.3. In Theorem 3.2, if we have

and

with $p_1, p_2 > 0$ and $q \geq 1$, then the system (3.1) is $\iota^*$-$y$-PUES.

4.   Application

In this section, we examine a class of system that can be modelled by the following system:

where $A\in \mathbb{R}^{n\times n}, \; C\in \mathbb{R}^{p\times n}$ and $\xi$: $\mathbb{R}_+ \times \mathbb{R}^n\longrightarrow \mathbb{R}^n$.

We now focus on the most important assumptions made in the observer stability proof, with respect to the system described by (4.1).

$(H_1)$ Suppose that $(A, C)$ is observable, Consequently, there exists a matrix $L$ of dimension $n\times p$ for which the eigenvalues of the matrix $A_0 = A-LC$ are in the open-left-half plane.

$(H_2)$ There exists a $p\times 1$ function $w(t, x)$ that verify:

where $P\in \mathbb{R}^n \times \mathbb{R}^n$ and $P^T = P$, such that

with $Q^T = Q > 0.$

$(H_3)$ There exist a positive scalar function $\alpha(t, y)$ such that

$(H_4)$ There is $M_1 > 0$ such that

To recap, our goal is to create an observer that can make estimates of the states $x(t; r_0, x_0)$ described in (4.1). Our proposed observer for this purpose is as follows:

where $\hat{x}\in \mathbb{R}^{n}$ is the estimated vector of $x$ and the control $u\in \mathbb{R}^{n}$ is defined as

with $\iota > 0$, $\theta(t)$ is a positive continuous function and $e = x-\hat{x}$ denote the vector error.

Before establishing the stability result for the suggested observer, we initially develop the dynamics of the observation error. We get:

The following stability theorem is now stated.

Theorem 4.1. Under assumptions $(H_1)$–$(H_4)$ the observation error (4.8) is $\iota^*$-$e$-PGUAS.

Proof. Let the Lyapunov function $V$ be

We obtain by considering the time derivative of $V$ along the trajectory of the specified observation error system:

Substituting (4.2) and (4.7) into (4.10) yields

Then, the following upper bound on $T^{\beta, \phi_{r_0}}_{r_0}V(t)$ is obtained:

where $c = \lambda_{min}(Q).$

By getting a common denominator for the final two components in Eq (4.12), the upper bound on $T^{\beta, \phi_{r_0}}_{r_0}V$ is reduced to be as follows:

Therefore,

It follows from Theorem 3.2 that the system (4.8) is $\iota^*$-$e$-PGUAS. □

Remark 4.1. The above theorem discusses the application of an observer design for a class of generalized conformable fractional-order nonlinear systems with a practical stability result.

5.   Numerical examples

Example 5.1. Let us consider the following system

where $x = \big(x_1, x_2, x_3\big) \in \mathbb{R}^3$.

Let

We get

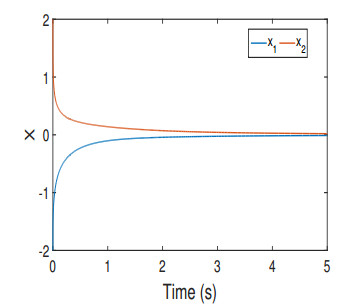
According to Theorem 3.2 the system (5.1) is $\iota^*$-$(x_1, x_2)$-PGUAS.

In Figure 1, there is a representation of the computed numerical solutions for the state $x_1$ and $x_2$ of a particular system described by Eq (5.1). The graph in Figure $1$ illustrates how the state $x_1$ and $x_2$ of the system changes over time, providing the result of Theorem 3.2.

Example 5.2. Let us consider the system (4.1) for

and

One choose

and by solving the Lyapunov equation, one gets

and

Thus, $(H_2)$ is verified with $w(t, x) = \cos(x_2) x_1$. Also, $(H_3)$ is verified with $\alpha(t, y) = |x_1|$.

Our proposed observer for this purpose is as follows:

where

and $u$ is defined as

where $e_1 = x_1-\hat{x}_1$ and $\theta(t) = 1$.

According to Theorem 4.1 the error system is $\iota^*$-$e$-PGUAS. The numerical solutions of the error system are illustrated in Figures 2 and 3. In this case, according to Figures 2 and 3, we can see the convergence of the solution towards a small ball centered at the origin.

6.   Conclusions

In this paper, we analyze the stability of a class of nonlinear systems with a generalized conformable derivative, which ensures that their solutions converge to a ball centered at the origin. In this paper, the theoretical underpinnings of practical stability are addressed. In addition, the notion is illustrated by an application. Finally, the presented theoretical insights are demonstrated by a numerical example that corresponds to the selected application.

Conflict of interest

The authors declare that there are no conflicts of interest.