Two classes of two-weight linear codes over finite fields

1.   Introduction

Epidemic dynamics is a crucial method for the quantitative study of infectious diseases, developing mathematical models that represent the process of disease progression and the principles of transmission. Mathematical research has achieved significant advances in both theory and application, leading to several well-known models of infectious disease dynamics ^[1,2,3,4].

Numerous researchers have explored mathematical models concerning population-level transmission dynamics, such as SIR model that susceptible-infected-recovered-infectious disease model and SIRS model is based on the SIR model with the addition of the process of loss of immunity, among others^[1]. These models have been studied and analyzed from various perspectives, including incidence, treatment functions, and age structure. Many reliable conclusions have emerged, contributing to the advancement of infectious disease dynamics ^[3,4,5,6]. For example, Li et al. ^[5] investigated epidemic models of the SIR and SIRS types with a general contact rate and constant immigration, particularly emphasizing the impact of the influx of infectious individuals. The model complexity and greater stochastic volatility of multiparameter stochastic perturbations have resulted in relatively little relevant research. The purpose of this study is to investigate the extinction and persistence of stochastic SIRSW model solutions under multiparameter stochastic perturbations, the propagation laws of infectious disease dynamics, and the effects of different parameters on disease spread. Among these, the SIRSW model is based on the SIRS model, adding the environmental pathogen infection process.

In recent years, due to environmental degradation and varying degrees of contamination of water and food, people have faced numerous infectious diseases stemming from environmental issues^[7]. Infectious diseases such as cholera, tuberculosis, and COVID-19 exhibit spatial-temporal and multi-scale characteristics, including direct transmission between humans at the macroscale population level and indirect transmission between humans and environmental pathogens at the microscale ^[8,9,10,11]. In the environmental transmission of certain infectious diseases, the excretion of pathogens and their transmission are two major processes. Additionally, between-host disease transmission and within-host viral load are interdependent^[12]. To investigate the effects of individual movement and pathogen dispersal in space on disease transmission, Xiao et al.^[13] developed a coupled model that considers direct infection resulting from random human movements and indirect infection following pathogen shedding in the environment, which took the following form

where $N$ denotes the total population, $S, I, R$ are the number of susceptible, infected, and recovered individuals, $W(t)$ is the pathogen concentration in the environment at time t, respectively, $\beta$ is the direct transmission rate, $\nu$ is the indirect transmission rate, $\eta$ is the environmental virus shedding rate, $\mu$ is the natural mortality rate, and $\gamma$ is the rate of recovery of infected individuals. Xiao et al. performed a numerical simulation analysis from a data-driven perspective and reached many interesting conclusions, but no theoretical analysis was performed. In the following section, refining the theoretical analyses of the corresponding models is also an important research objective of this paper.

Deterministic modeling of viral infections has been studied by some researchers^[14,15,16]. Edoardo^[14] proposes a mathematical model of the marine bacteriophage infection and analyzes its basic mathematical features. Ivo et al.^[15] extended the Beretta-Kuang model to allow the estimation of virus growth parameters under model-specific parameterizations. Depending on the characteristics of the infection, the recovering person loses immunity after a period of time and becomes susceptible to infection again, which is called SIRS infection^[17]. On this basis, by considering birth and death rates, the following deterministic model is obtained:

where $\Lambda$ is the input rate of susceptible individuals, $\zeta$ denotes the rate of immune loss, and $c$ denotes the rate of viral failure. The environmental pathogen concentration level is denoted by $W.$ Denote

By calculation, model (1.2) has a disease-free equilibrium

and exists an endemic equilibrium

The basic reproduction number

is obtained by using the next generation matrix method. Further, if $R_0 < 1$, $E_0$ is globally asymptotically stable in D (in Remark 1). If $R_0 > 1$, $E^*$ is globally asymptotically stable in D.

In the realm of infectious diseases transmission, the coefficients governing this process are frequently affected by stochastic environmental disturbances ^[18,19]. This environmental interference can be mathematically characterized as standard Brownian motion. Relying solely on deterministic models to describe and predict the evolution of disease dynamics and transmission mechanisms is often inadequate. Hence, there is an increasing recognition of the practical significance of investigating infectious disease models that incorporate stochastic factors, leading to a growing scholarly focus on these stochastic frameworks in recent years ^[20,21,22]. For instance, Ji et al.^[23,24] explored the threshold behavior of the SIR infection model in the presence of stochastic noise perturbations, examining both the persistence and extinction dynamics of the SIR model under various stochastic perturbation patterns. They derived threshold conditions for disease extinction and persistence utilizing Itô's formula and the stochastic comparison theorem. In another study, Zhao et al. ^[25] investigated a class of stochastic SIRS models characterized by saturated incidence, taking into account the dynamics of recovered individuals who lose immunity and revert to susceptibility after a period. They established conditions for disease extinction and persistence through the stochastic comparison theorem, supported by numerical simulations that corroborated their theoretical findings. Yang et al. ^[26] developed a stochastic multi-scale COVID-19 model that integrates both within-host and between-host dynamics, employing interval parameters. This model was derived through fast-slow decoupling via singular perturbation theory, distinguishing between a rapid within-host model and a slower between-host stochastic model. Rihan et al.^[27,28] developed a stochastic epidemiological SIRC model to study the transmission of COVID-19 with cross-immunity classes and time-delayed transmission terms. Which the SIRC model is a new partition added to the SIR model, cross immunity (C). Echoing the insights of Mao et al. ^[29], this paper posits that fluctuations in the environment predominantly manifest as variations in the transmission coefficient

where $B_i(t)$ is a standard Brownian motion and $\sigma_i > 0$ indicates the white noise intensity, $i = 1, 2$. Then we have

Our model considers the loss of immunity rate and the effects of random disturbances based on Xiao et al.^[13], investigating a stochastic SIRSW model that accounts for environmentally driven infection and incorporates multiparameter perturbations. It innovatively examines the impacts of both direct and indirect transmission rates on the spread of the disease through multiparameter perturbations. This model is more comprehensive and aligns more closely with real-world situations. However, as a multi-scale model that integrates macro and micro perspectives, it is challenging to unify the data across temporal and spatial scales. The numerical simulation remains relatively idealized, and there is still a significant gap between the results and the actual inter-evolutionary outcomes. It considers environmental pathogen infections with stochastic perturbations in two key parameters: direct and indirect transmission rates. We conclude that, compared to perturbations in the indirect infection rate, changes in noise intensity affecting the direct infection rate have a more significant impact on disease transmission. Additionally, we find that the direct transmission rate notably influences the threshold of $R_0^s$. These parameters are crucial for analyzing the impact of environmental fluctuations on disease dynamics.

The structure of the paper is delineated as follows: In Sections 1 and 2, we present the foundational concepts, along with relevant notations and lemmas essential for our analysis. Section 3 is devoted to establishing the existence and uniqueness of global positive solutions for the SIRS infectious disease system under consideration. In Sections 4 and 5, we explore the sufficient conditions that govern the persistence and extinction of the stochastic SIRS infectious disease model. Section 6 focuses on analyzing the asymptotic stability of the disease-free equilibrium, as well as the endemic equilibrium of the deterministic counterpart to the stochastic model. To conclude, we provide a series of numerical simulations accompanied by a summary of our principal findings, aimed at elucidating the theoretical results presented throughout the paper.

2.   Preliminaries

In this paper, unless otherwise stated, let $(\Omega, \mathscr{F}, \{\mathscr{F_t}\}_{t \geq 0}, \mathbb{P})$ denote the complete probability space of the filtration $\mathscr{F_t}_{t \geq 0}$ that satisfies the regularity condition. Let $B_i(t)(i = 1, 2)$ denote the independent standard Brownian motions defined on this complete probability space. For any $a, b \in R$, note that

For convenience, the following symbols have been introduced,

Lemma 1. ^[30] (Strong law of large number) Let

be a real-valued continuous local martingale, and

Then,

and

Lemma 2. ^[23] Suppose $f \in \mathbb{C}\left[ \Omega \times[0, +\infty), \mathbb{R}_{+}\right]$ if there exists a positive ordinal $\lambda, \lambda_0$, such that

Then, for any $t \geq 0$, there are $F \in \mathbb{C}\left[\Omega \times[0, +\infty), (-\infty, +\infty)\right]$ and

a.s., such that

Lemma 3. Suppose $f \in \mathbb{C}\left[ \Omega \times[0, +\infty), \mathbb{R}_{+}\right]$ if there exists a positive ordinal $\lambda, \lambda_0$, such that

Then, for any $t \geq 0$, there are $F \in \mathbb{C}\left[\Omega \times[0, +\infty), (-\infty, +\infty)\right]$ and

a.s., such that

Remark 1. For the model (1.3), we have

and we assume the initial values $(S_{0}, I_{0}, R_{0}, W_{0})\in \mathrm{\; D}$, which shows that the positive invariant set of the model is

3.   Existence and uniqueness of the global positive solution

The following theorem will show the existence and uniqueness of global positive solutions of system ($1.3$).

Theorem 1. For any initial value $(S(0), I(0), R(0), W(0)) \in \mathbb{R}_{+}^4$, there exists a positive salutation $(S(t), I(t), R(t), W(t))$ of the stochastic model (1.3) for $t \geq 0$, and the solution will hold in $\mathbb{R}_{+}^4$ with probability one.

Proof. Since the coefficients of the model (1.3) satisfy the local Lipschits condition, for any $S(0), I(0), R(0), W(0))\in \mathbb{R}_{+}^4$, there exists a locally unique solution $(S(t), I(t), R(t), \; W(t))$ on $t \in\left[0, \tau_{\varepsilon}\right)$, where $\tau_{\mathrm{e}}$ denotes the moment of explosion. It is sufficient to show that

Let $k_0 \geq 1$ denote a sufficiently large constant, and we have that $S(0), I(0), R(0), W(0)$ are all in the interval $\left[\frac{1}{k_0}, k_0\right]$. For any constant $k > k_0$, define the stopping time,

or

Let

usually, $\infty$ denotes the empty set. Clearly, $\left\{\tau_k\right\}_{k \geq k_0}$ is a monotonically increasing function. If

then $\tau_{\infty} \leq \tau_e$ a.s. If

then for any $t \geq 0, \tau_e = \infty$, and $(S(t), I(t), R(t), W(t)) \in \mathbb{R}_{+}^4 \; \text{a.s.}$ Assuming that $\tau_{\infty} \neq \infty$, there exist a constant $T \geq 0$ and $\varepsilon \in(0, 1)$ such that

where, for any $k \geq k_0$, there exists a constant $k_{1} \geq k_{0}$ such that, when all the $k \geq k_{1}$, there is

Define a $C^2$-equation $V$: $\mathbb{R}_{+}^4 \rightarrow \mathbb{R}_{+}$ as follows:

Apply the It$\hat{o}$'s formula

where,

Because of the mean value theorem, we can obtain

where,

$H$ is a positive constant which is independent of $S(t), I(t), R(t), W(t), t$. Integrate both sides of the Eq ($3.2$) from 0 to

and then take the expectation as follows:

By using Gronwall inequality ^[31], we have

Let

and by the inequality (3.1), it is known that

For any $\omega \in \Omega_k$, $S\left(\tau_k, \omega\right), I\left(\tau_k, \omega\right), R\left(\tau_k, \omega\right), W\left(\tau_k, \omega\right)$, at least one of them equals $\frac{1}{k}$ or $k$, therefore,

Combined with the above Eqs ($3.2$) and ($3.8$), we can get

Here $I_{\Omega_k}(\omega)$ is the indicator function for $\Omega_k$. When $k \rightarrow +\infty$, there are

This is a clear contradiction, and it is proved that

a.s. Thus, the theorem can be proved. □

4.   Extinction of disease

As a stochastic infectious disease model, when diseases become extinct it is a major concern. In this section, we study the conditions for disease extinction and give a better condition for when a phenomenon like disease extinction will occur. Denote

Theorem 2. Let $(S(t), I(t), R(t), W(t))$ be the solution of the model (1.3) with initial values $(S(0), I(0), R(0), W(0)) \in \mathbb{R}_{+}^4$. If

or

then we have

It can be shown that the $I(\mathrm{t})$ index tends to 0, the disease will become die out with probability one, and there are

Proof. Integration of the model (1.3) is obtained,

According to Eq (4.4), it can be obtained that

From Eqs ($4.4$) and ($4.5$), we can get

where

Obviously,

Applying Itô's formula to the second equation of model (1.3) and integrating from 0 to $t$ leads to

where

Note that $M_1(t)$ and $M_2(t)$ are a real-valued continuous local martingale vanishing at time zero and

then by Lemma $1$, it leads to

Bringing Eq (4.6) into the above Eq (4.9), we have

where

From Eqs ($4.8$) and ($4.11$), we obtain

Case 1. Assume that $R_0^s < 1$ and $R_s \leq 0,$ then the above Eq (4.12) gets

and combining ($4.14$), it can be obtained that

Case 2. Assume that

since

Therefore, from Eqs ($4.12$) and ($4.17$), we have

and combining ($4.14$), it can be obtained that

From the proofs of Cases 1 and 2, it can be shown that the $I(\mathrm{t})$ index tends to 0 and the disease will become die out with probability one, then we have

Let

Accroding to (4.20), we have

For any $\theta > 0$ and $\omega \in \Omega_i$, there exists

such that for any $t \geq T_i$, there exists

Substituting it into the third equation of model (1.3), and according to the comparison theorem for stochastic differential equations, we obtain

For all $\omega \in \Omega_i$ and $t > 0$, such that $R(t, \omega)$, since the arbitrariness of $\theta$, we can get

It follows from

that, consequently,

Similarly, we have

Through model (1.3), we can obtain

therefore,

which, together with Eqs (4.20) and (4.23), yields

This completes the proof. □

5.   Persistence of disease

Disease persistence is an important characteristic of infectious disease dynamics, meaning that the disease persists in the population. Theorem 3 will show the persistence of disease.

Theorem 3. If $R_0^S > 1, R_s \leq 0,$ let $(S(t), I(t), R(t), W(t))$ be the solution of the model (1.3) with initial values $(S(0), I(0), R(0), W(0)) \in \Omega$. It has the following properties:

Proof. From the above Eq (4.12), we get:

Therefore,

By Eq (4.14) and Lemma 3, we have

Bring Eq (4.24) to Eq (4.9), and by Remark 1, we have

Bringing Eq (4.6) into the above Eq (5.3), we have

Therefore, it is possible to get

where

From Eqs ($4.8$) and ($4.11$), we can get

By Lemma 2 and Eq ($5.5$), one obtains

The proof is complete. □

6.   Asymptotic

In epidemiology, stability is of high practical importance. This section discusses the asymptotical stability of the disease-free equilibrium and the endemic equilibrium of the deterministic model corresponding to the stochastic model.

6.1.   Asymptotic property for the disease-free equilibrium of the deterministic model

The basic reproduction number plays an important role in the study of infectious disease dynamics and determines whether a disease becomes extinct or not. We know that the basic reproduction number of a deterministic system

and the disease-free equilibrium of the deterministic model is $E_{0}(\frac{\Lambda}{\mu}, 0, 0)$.

Theorem 4. Let $(S(t), I(t), R(t), W(t))$ be the solution of the model (1.3) with initial values $(S(0), I(0), R(0), W(0)) \in \Omega$. If $R_{0} < 1$ and $\sigma_{1}, \sigma_{2}$ are small enough, then

Proof. Define a Lyapunov function $V$: $\mathbb{R}_{+}^4 \rightarrow \mathbb{R}_{+}$ as follows:

Applying It$\hat{o}$'s formula, we have

Therefore,

Due to

integrating both sides of the above Eq (6.2) from 0 to $t$, and then taking the expectation as follows:

Therefore,

The proof is complete. □

6.2.   Asymptotic properties around endemic equilibrium

In studying epidemic dynamics, the stochastic infectious disease model has no endemic equilibrium, but it is obtained from a deterministic model in which the infectious rate is subjected to a random perturbation. Therefore, the asymptotic behavior of the solution of the stochastic model in the region around $E^{*}(S^*, I^*, R^*, W^*)$ is studied. The expressions $E^{*}$ is as follows:

Theorem 5. Let $(S(t), I(t), R(t), W(t))$ be the solution of the model (1.3) with initial values $(S(0), I(0), R(0), W(0)) \in \Omega$. If $R_{0} > 1$,

Then,

Proof. The deterministic system obeys the following relationship at the endemic equilibrium:

Define a Lyapunov function $V$: $\mathbb{R}_{+}^4 \rightarrow \mathbb{R}_{+}$ as follows:

Applying It$\hat{o}$'s formula, we have

Therefore,

and because $a \leq |a|$, we can get

Take a positive number $\epsilon$, such that

and from Remark 1, we have

Due to

integrating both sides of the above Eq (6.6) from 0 to $t$, and then taking the expectation as follows,

Because of

we obtain

The proof is complete. □

7.   Simulations

Numerical simulations are presented below to illustrate the theoretical results of this chapter. We provide some numerical examples to support our results. The numerical simulations of epidemic dynamics are carried out for academic purposes, using arbitrary parameter values that do not correspond to any specific epidemic and only demonstrate the theoretical properties of the numerical solutions of the models considered. We present our results using the Milstein's higher order method developed in ^[32]. The discrete form of the model ($1.3$) is as follows:

where $\xi_{j, i} j = 1, 2$ are Gaussian random variables following the standard normal distribution $N(0, 1)$ and the time increment

Let

In different examples, parameters $\beta, \nu, \sigma_{1}$, and $\sigma_{2}$ will take different values.

Example 1. To start, we choose

such that

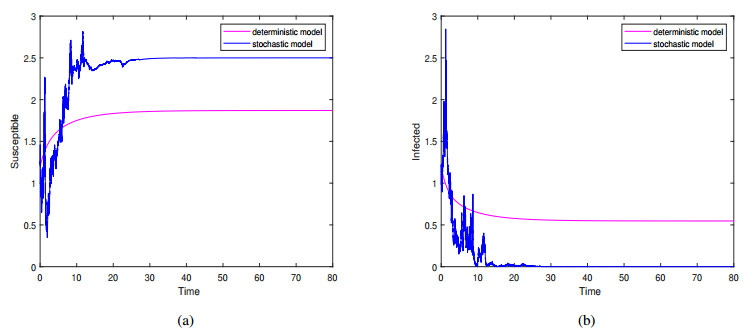
then from Theorem 2, the disease of model ($1.3$) will become extinct; see Figure 1.

Let

and the other parameters are shown in $(7.2)$ such that

and

According to Theorem 2, the disease of model ($1.3$) will be extinct; see Figure 2.

In order to verify Theorem 2, numerical simulations were carried out with the parameters selected above. The results are shown in Figures 1 and 2. From the Figures 1b and 2b, it can be concluded that the disease $I(t)$ in stochastic model ($1.3$) will die out with probability one, and compared to deterministic model (1.2), white noise accelerates disease extinction and inhibits disease transmission.

Example 2. To begin, we choose

and the other parameters are shown in $(7.2)$ such that

and

According to Theorem 3, the disease of model ($1.3$) will be persist. Figure 3 supports the result.

In order to verify Theorem 3, numerical simulations were carried out with the parameters selected above. The results are shown in Figure 3. From the Figure 3b, it can be concluded that the disease $I(t)$ in stochastic model ($1.3$) will be permanent in the time mean. This suggests that the disease will persist.

Example 3. Take

and the other parameters are shown in $(7.2)$ such that

and

According to Theorem 5, solutions of stochastic model ($1.3$) fluctuate in time average around endemic equilibrium $E^{*}$ of the deterministic model, which can be verified by using Figure 4, and the oscillation amplitude increases with white noise intensity.

Example 4. Take

and the other parameters are shown in $(7.2)$ such that

Figure 5 shows that $\sigma_{1}$ and $\sigma_{2}$ have a significant impact on both extinction and persistence of disease. With the intensity of $\sigma_{1}, \sigma_{2}$, the disease of model ($1.3$) will accelerate extinction.

The results show that large amounts of white noise can lead to disease extinction, while even small amounts of white noise were found to inhibit disease outbreaks. We conclude that changes in noise intensity affecting direct transmission rates have a more pronounced effect on disease spread than perturbations in indirect infection rates. This tells us that in the prevention and control of infectious diseases, as well as in public health practice, cutting off direct sources of infection and reducing the rate of direct infection are very useful measures.

Example 5. Take $\sigma_1 = 0.25$, $\sigma_2 = 0.1$, and the other parameters are shown in $(7.2)$. Figure 6a shows how threshold $R_0^s$ varies with $\beta$ and $\nu$, as well as shows the positive correlation. Figure 6b shows how threshold $R_0^s$ varies with white noise intensity $\sigma_1$ and $\sigma_2$, and as the noise intensity increases, $R_0^s$ becomes smaller and smaller.

8.   Conclusions and discussion

In this paper, we investigate a stochastic SIRS epidemic model that incorporates environmentally driven transmission dynamics alongside multiparameter perturbations. The purpose of this study is to investigate the extinction and persistence of stochastic SIRW model solutions under multiparameter stochastic perturbations, the propagation laws of infectious disease dynamics, and the effects of different parameters on disease spread. We commence our study by establishing the existence and uniqueness of the global positive solution for the model presented in Eq ($1.3$). Subsequently, we derive the threshold conditions necessary for disease extinction and persistence, employing the comparison theorem in conjunction with It$\hat{o}$'s formula for stochastic differential equations. The theoretical findings are substantiated through a series of numerical simulations, as depicted in Figures 1–3. These simulations show that large amounts of white noise can lead to disease extinction, whereas even small amounts of white noise can suppress disease outbreaks, with the dynamics transitioning from persistence to extinction as the noise intensity increases. Furthermore, we analyze the asymptotic stability of both the disease-free equilibrium and the endemic equilibrium of the deterministic model corresponding to our stochastic framework, utilizing principles from stochastic stability theory. Our results demonstrate that the solutions of the stochastic model ($1.3$) exhibit fluctuations around the endemic equilibrium $E^{*}$ of the deterministic counterpart, with the oscillation amplitude increasing in response to higher levels of white noise intensity, as shown in Figure 4. Additionally, we observe that variations in noise intensity affecting the direct transmission rate exert a more pronounced influence on disease transmission compared to perturbations in the indirect infection rate, as illustrated in Figure 5. Finally, we find that the direct transmission rate plays a critical role in determining the threshold $R_0^s$, as highlighted in Figure 6. This suggests that disruption of direct source links and isolation controls to reduce the rate of direct infection are very useful measures in the prevention and control of infectious diseases and in public health practice.

In the future, we will consider the dynamics of infectious disease processes across different temporal scales. It is also interesting to incorporate the immunological processes occurring within the host into system (1.2), and we will leave this for future research.

Author contributions

Zhengwen Yin: responsible for mathematical modelling and analysis, paper writing, numerical simulations; Yuanshun Tan: responsible for mathematical modelling, model analysis, paper framework construction. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

This work was supported by the National Natural Scicnce Foundation of China (No. 12271068), the Rescarch and Innovation Project for Graduate Research in Chongqing Jiaotong University (No. 2024S0138).

Conflict of interest

The authors declare that they have no conflicts of interest concerning this article.