A linearly convergent self-adaptive gradient projection algorithm for sparse signal reconstruction in compressive sensing

1.   Introduction

Sparse signal reconstruction (SSR), i.e., using the least entries from a complete dictionary to represent the signal of interest, is a popular technique for recovering a sparse signal or an image from an under-determined linear system ^[1,2], which can be formulated as the following non-smooth minimization problem

where $A\in R^{m\times n}$ ($m\ll n$) is the design matrix, $b\in R^{n}$ is the observation vector and $\|x\|_0$ denotes the number of nonzero elements of vector $x\in R^n$ to be estimated. Since the problem (1.1) is NP hard ^[3,4], it cannot be solved approximately within a fixed ratio unless $P = NP$. In addition, as for $Ax = b$, it is often the case that is ill-posed due to possible ill-conditionedness of $A$. To deal with the ill-posed case, and take into consideration sparse structure of (1.1), the $\ell_1$-norm regularization techniques have successfully been used for inducing sparsity of solutions ^[5]. Thus, the problem (1.1) is transformed into the following Lagrangian form or penalty form, which is usually written as the following form

where $\rho$ is a positive parameter and $\|x\|_1 = \sum\limits^{n}_{j = 1}|x_j|$ denotes the $\ell_1$-norm of $x$.

Based on the convex relaxation form (1.2), many researchers have developed various algorithms for solving this problem, including interior-point methods ^[6], projected gradient methods ^[7], spectral gradient methods ^[8], spectral residual methods ^[9], conjugate gradient projection methods ^[10], alternating direction algorithms ^[11], and iterative thresholding ^[12] and so on.

A large class of the first order $\ell_1$-minimization algorithms (abbreviated as the first order algorithms) for problem (1.2) is based on the iterative shrinkage/thresholding (IST) method or on variants of IST ^[12,13]. Recently, many extensions and modifications of these basic algorithms have been introduced and investigated. For instance, Hale et al. ^[14] present a fixed-point continuation method by shrinkage operator. Beck and Teboulle ^[15] propose a fast iterative shrinkage-thresholding algorithm (FISTA), which has virtually the same complexity as IST, but has better convergence properties. Bioucas-Dias and Figueiredo ^[16] present a two-step IST method, which has exhibited much faster convergence rate than IST. Another closely related method to IST is the proximal thresholding algorithm by Combettes et al. ^[17]. A gradient based algorithm is especially one of the most popular methods for solving (1.2). One of the earliest gradient projection method for sparse reconstruction was developed by Figueiredo et al. ^[7]. Another method, SPGL1, was proposed by van den Berg and Friedlander ^[18]. Other gradient based methods include Nesterov's algorithm (NESTA) ^[19] and Sparse Reconstruction by Separable Approximation method (SpaRSA) ^[20] all have good performance. A large class of the second order information of the underlying function based algorithms (abbreviated as the second order algorithms) is also popular for solving problem (1.2), which include Orthant-Based adaptive method (OBA) ^[21], FBS-Newton ^[22], Semismooth Newton method with multidimensional filter globalization (SNF) ^[23], Inexact successive quadratic approximation (SQA) method ^[24] and so on. Although the second order algorithms often outperform the first order algorithms in seeking high-precision solutions, the computational cost of each step is usually much higher than that of the first order algorithms.

In recent years, a lot of numerical algorithms about the equivalent forms of (1.2) have been extensively developed. For instance, Xiao and Zhu ^[25] transformed (1.2) into convex constrained monotone equations, and presented a conjugate gradient method for this equivalent form. Sun and Tian ^[26] gave a class of derivative-free conjugate gradient projection method for the equivalent form of (1.2). Sun et al. ^[27] reformulated (1.2) as variational inequality problem, and proposed a novelly inverse matrix-free proximal point algorithm for the equivalent form of (1.2). Based on the same transformation, Feng and Wang ^[28] also proposed a projection-type algorithm without any backtracking line search. Xiao et al. ^[29] proposed a spectral gradient method for solving an equivalent non-smooth equation of (1.2). Liu et al. ^[30,31] presented a projection method to solve monotone nonlinear equations with convex constraints, and applied it to solve an equivalent non-smooth equation of (1.2). In ^[32], Wang et al. proposed a smooth and convex Lagrange-dual reformulation of (1.2), and many state of the art gradient-type algorithms can be used to solve the reformulation. Landi ^[33] considers the nonnegative constrained quadratic program reformulation of (1.2), and proposes modified Newton projection method to solve it. On the other hand, since (1.2) can be equivalently converted into a separable convex programming by introducing an auxiliary variable, the numerical methods which can solve the separable convex programming are applicable to solving (1.2), such as the alternating direction method of multipliers and its linearized version ^[11,34], the Peaceman-Rachford splitting method (PRSM) or Douglas-Rachford splitting method (DRSM) of multipliers ^[35,36], the symmetric alternating direction method of multipliers ^[37], etc. Certainly, problem (1.1) can be formulated as a splitting feasible problem (SFP) ^[38], and the numerical methods which are designed for SFP are also applicable to solve (1.1) ^[38,39].

As can be seen from this brief review, existing methods are able to solve (1.2). However, the solving speed and accuracy are adversely affected when the dimension increases greatly. In the paper, we will establish a new self-adaptive gradient projection method for solving (1.2), which have closed-form solutions, the motivation for this approach is to achieve better numerical performance, especially for large-scale problem (1.1). From theoretical perspectives, the global linear rate convergence result for new algorithms is established without any assumptions, which is a new result for constrained convex (rather than strictly convex) quadratic programming problem. In addition, an approximate optimal solution is obtained in a finite number of iterations, and these stronger convergence results are one of the most important motivations for this work.

The remainder of this paper is organized as follows. In Section 2, we use the separating technique to transform (1.2) into a differentiable problem and present some related properties, which are the basis of our analysis. In Section 3, we propose a new self-adaptive gradient projection method, in which line search step is different from that in Qu ^[39]. The global convergence of the proposed method is discussed in detail. We establish a global $R$-linear rate convergence theorem without any assumptions, which is weaker than the condition in Theorem 3.3 in ^[34]. Furthermore, we can obtain an approximate optimal solution in a finite number of iterations. In Section 4, some numerical experiments on sparse signal reconstruction or image restoration are given, and compare the CPU time and the mean of squared error among the Algorithm 2.1 in ^[30], the CQ algorithm in ^[39], FISTA ^[15], the primal alternating direction method ^[11] and our proposed algorithm, and show that our algorithm is much faster than other algorithms, and also have higher accuracy. Finally, some remarks and conclusions are presented in Section 5 and Section 6, respectively.

To end this section, some notations used in this paper are in order. We use $R_+^n$ to denote the nonnegative quadrant in $R^n$, and the $x_{+}$ denotes the orthogonal projection of vector $x\in R^n$ onto $R^n_{+}$, that is, $(x_{i})_{+}: = \max\{x_{i}, 0\}, \; 1\leq i \leq n$; the norm $\|\cdot\|$ and $\|\cdot\|_{1}$ denote the Euclidean 2-norm and 1-norm, respectively. For $x, y\in R^n,$ use $(x; y)$ to denote the column vector $(x^\top, y^\top)^\top$. We denote by $det(M)$ the determinant of a matrix $M$ and, by $I_n$ the identity matrix of order $n$.

2.   Preliminaries

In this section, a smooth equivalence transformation of the problem (1.2) is established.

Firstly, we briefly review the process for constructing a convex quadratic program problem of Figueiredo et al. ^[7]. For any vector $x\in R^n$, it can be formulated for $x = \mu-\nu$, $\mu\geq0$, $\nu\geq0$, where $\mu\in R^n$, $\nu\in R^n$, and $\mu_i = (x_{i})_{+}$, $\nu_i = (-x_{i})_{+}$ for all $i = 1, 2, \cdots, n$. Subsequently, the $\ell_1$-norm of the vector can be represented as $\|x\|_1 = (e^\top, e^\top)(\mu; \nu)$, where $e\in R^n$ denotes the vector composed by elements $1$, i.e., $e = (1, 1, \cdots, 1)^\top$. Thus, we can reformulate (1.2) into

In order to make the description more concise, we let $\omega = (\mu; \nu)$. Thus, the problem (2.1) can be further written as

where $M = \left(\begin{array}{rr}A^\top A & -A^\top A\\-A^\top A&A^\top A\end{array}\right), p = \left(\begin{array}{r}A^\top\\-A^\top\end{array}\right) b-\rho\left(\begin{array}{r}e\\e\end{array}\right)$. We assume the solution of the problem is nonempty and denote it by $\Omega^*$.

Although the dimension of (2.2) is twice of the original problems, it is shown that this increases only slightly the impact of computation. In addition, the computation of the function values or the gradient requires two matrix-vector multiplications involving $A$ and $A^\top$ ^[7].

Obviously, the problem (2.2) is a convex optimization problem, then the stationary set of (2.2) coincides with its solution set which also coincides with the solution set of the following problem: find $\omega^*\in R_+^{2n}$ such that

where $\nabla f(\omega) = M\omega-p$.

Secondly, we will give the definition of projection operator and some related properties ^[40], which are the basis of our analysis.

For a nonempty closed convex set $K\subset R^{n}$ and vector $z\in R^{n}$, the orthogonal projection of $z$ onto $K$, i.e., $\arg\min\left\{\|z-y\|\; |\; y\in K\right\}$, is denoted by $P_{K}(z)$.

Proposition 2.1. Let $K$ be a closed convex subset of $R^{n}$, then $\|P_{K}(z_1)-P_{K}(z_2)\|\leq \|z_1-z_2\|, \; \forall z_1, z_2\in R^{n}.$

For (2.3) and $\omega\in R^{2n}$, define the projection residue

where $\hat{\rho} > 0$ is some constant. The projection residue is intimately related to the solution of (2.3) as shown by the following well-known result, which is due to Noor ^[41].

Proposition 2.2. The vector $\omega^*$ is a solution of (2.3) if and only if $r(\omega^*, \hat{\rho}) = 0$ with some $\hat{\rho} > 0$.

Finally, we recall the following lemma, which is the well-known fundamental property for a smooth function in the class $C^{1, 1}$.

Lemma 2.1. (Lemma 3.2 ^[42]) Let $F : R^{n}\rightarrow R$ be a continuously differentiable function with Lipschitz continuous gradient and Lipschitz constant $L_F$.Then, for any $L \geq L_F$, one has

For any $\omega, \bar{\omega}\in R^{2n}$ and the function $f$ defined in (2.2), one has $\|\nabla f(\omega)-\nabla f(\bar{\omega})\|\leq \|M\|\|\omega-\bar{\omega}\|,$ i.e., the gradient function $\nabla f(\omega)$ be Lipschitz continuous and Lipschitz constant $\|M\|$. Applying Lemma 2.1, it follows that

where

and

From (2.7) and (2.8), it is easy to calculate that

3.   Algorithm and global convergence

In this section, we will propose a new algorithm for solving the model (2.3), and prove global convergence and $R$-linear convergence rate of the new algorithm in detail.

Now, we formally state our algorithm.

Algorithm 3.1

Step 0. Select $\beta > 0, \eta > 1, \epsilon \geq 0, \gamma \in (0, 1), \omega^{0}\in R^{2n}$, and let $k: = 0$.

Step 1. For the current iterate points $\omega^{k-1}$, compute

where $L_{k} = \eta^{m_k}\beta$, and $m_k$ is the smallest nonnegative integer $m$ such that

and

Step 2. If $\|\omega^{k} - \omega^{k-1}\|\leq \epsilon$, stop. Then, $\omega^{k}$ is an approximate solution of (2.3). Otherwise, go to Step1 with $k : = k+1$.

From (3.2) and (3.3), one has

If $L_{k}\ge \left\|M\right\|$, using (3.4) and (2.6), we get

Furthermore,

Thus, the sequence $\{f(\omega^{k})\}$ produced by Algorithm 3.1 is nonincreasing.

The termination criteria in step 2 of Algorithm 3.1 is reasonable, which can be proved by (3.20) and Theorem 3.2 below. It can make Algorithm 3.1 terminate in a finite step, which can be proved in Theorem 3.1 below.

Remark 3.1. By (3.2) and (3.3), we assure the existence of upper and lower bounds of the parameter $L_k$, see details from Lemma 3.1 below. Furthermore, we adopted Armijo-like technique in a new way, such that the iteration stepsize $\frac{1}{L_k}$ can be self-adaptive updated in Algorithm 3.1.

Lemma 3.1. Assume parameters $\beta > 0, \eta > 1$ defined as in Algorithm 3.1, then $\beta \leq L_{k} < \eta \left\|M\right\|, \forall k\ge\; 1.$

Proof. By $L_{k} = \eta^{m_k}\beta$ and $\eta > 1$, one has $L_{k}\geq \beta, \forall k\ge 1$. Since (3.2) and (3.3) are satisfied for some $\eta^{m}\beta \ge \left\|M\right\|$, combining this with the definition of $m_k$, we ensure that $L_{k}/\eta = \eta^{m_k-1}\beta$ must violate (3.2) or (3.3), it follows that (3.4) does not holds. Combining this with Lemma 2.1, we obtain that $L_{k}/\eta < \left\|M\right\|$ for every $k\ge 1$. Hence, the desired result follows. □

Lemma 3.2. For any $\omega\in R^{2n}_+$, we have

Proof. By (3.5), one has

By (2.7) with $\omega = \omega^{k}, \bar{\omega} = \omega^{k-1}, L = L_k$, then

Since $f$ is convex, one has

Combining (3.8) and (3.10) with (3.9), one has

Applying the first-order optimality condition of (3.1), one has

i.e., $\left \langle \omega-\omega^{k}, \nabla f(\omega^{k-1})\right \rangle\ge L_{k}\left \langle \omega-\omega^{k}, \omega^{k-1}-\omega^{k}\right \rangle, \quad\forall \omega\in R^{2n}_+.$

Combining this with (3.11), one has

We next prove that the sequence $\{\omega^{k}\}$ terminates in a finite number of steps at an approximate optimal solution of (2.2).

Theorem 3.1. Assume that $\omega^{*}$ is a solution of (2.3), and the sequence $\{\omega^{k}\}$ generated by Algorithm 3.1. Then, for any $k \ge1$, one has

Proof. In order to make the description more concise. In (3.7), let $\omega = \omega^{*}$, and replace $\omega^k$ with $\omega^m$, we obtain

Since $\omega^{*}$ be a solution of (2.3), then it be also a solution of (2.2), and one has $f(\omega^{*})-f(\omega^{m})\leq0$. Combining this with Lemma 3.1, we obtain

Summing (3.15) over $m = 1, 2, \cdots, k$ gives

We note that Lemma 3.2 holds for any $\omega\in R_+^{2n}$. Hence, we take $\omega = \omega^{m-1}$, and replace $\omega^k$ with $\omega^m$ in (3.7), we get

Since $L_{m}\ge \beta$ and $f(\omega^{m-1})-f(\omega^{m})\ge 0$, it follows that

i.e., $2\beta^{-1}[(m-1)f(\omega^{m-1})-mf(\omega^{m})+f(\omega^{m})]\geq (m-1)\|\omega^{m}-\omega^{m-1}\|^2.$ Multiplying both sides of the above inequality by $\frac{\beta}{\eta\|M\|}$ and summing over $m = 1, 2, \cdots, k$, we have

Adding (3.16) and (3.19), we have

Combining this with $f(\omega^{*})-f(\omega^{k})\leq0$, the desired result follows. □

Remark 3.2. Theorem 3.1 above means that we can obtain an $\epsilon$-optimal solution, denoted by $\hat{\omega}$, requires the number of iterations at most $[c/\epsilon]+1$, such that $f(\hat{\omega})-f(\omega^{*})\leq \epsilon$, where $c: = \frac{1}{2}\eta \|M\|\|\omega^{0}-\omega^{*}\|^2.$ In fact, using (3.13), and set $f(\omega^{k})-f(\omega^{*})\leq \frac{\eta \|M\|}{2k}\|\omega^{*}- \omega^{0}\|^2\leq \epsilon$, then one has $k\geq c/\epsilon$, i.e., requiring the number of iterations at most $[c/\epsilon]+1$.

In the following convergence analysis, we assume that Algorithm 3.1 generates an infinite sequence, and first prove the global convergence of the proposed algorithm.

Theorem 3.2. Suppose that the solution set of (2.3) is bounded. Then, the sequence ${\omega^{k}}$ generated by Algorithm 3.1 converges globally to a solution of (2.3).

Proof. By (3.6) and $f(\omega)\geq 0$, we know that the nonnegative sequence ${f(\omega^{k})}$ is monotonically decreasing, so it converges. Combining this with (3.18), one has

Applying (3.14) and the fact $f(\omega^{*})-f(\omega^{k})\leq0$, we have

i.e., the nonnegative sequence $\{\|\omega^{k}-\omega^{*}\|\}$ is monotonically decreasing, so it converges. Thus, the sequence $\{\omega^k\}$ is bounded, and there exits a convergent subsequence $\{\omega^{k_i}\}$ of $\{\omega^k\}$, we assume that $\lim_{k\rightarrow \infty}\omega^{k_i} = \bar{\omega}$. Combining this with (3.20), we have

From the second equality of (3.1), we obtain $\langle \omega-\omega^{k_i}, \nabla f(\omega^{k_i-1})+L_{k_i}(\omega^{k_i}-\omega^{k_i-1})\rangle\geq0, \; \forall \omega \in R_+^{2n}.$ Combining this with (3.20) and (3.22), we have $\langle \omega-\bar{\omega}, \nabla f(\bar{\omega})\rangle\geq0, \; \forall \omega \in R_+^{2n},$ i.e., $\bar{\omega}$ is a solution of (2.3). So, the $\bar \omega$ can be used as $\omega^{*}$ to discuss in Theorem 3.1 above, we obtain that the sequence $\{\|\omega^{k}-\bar{\omega}\|\}$ is also convergent, combining this with $\lim_{k\rightarrow \infty}\|\omega^{k_i}-\bar{\omega}\| = 0$, one has $\lim_{k\rightarrow \infty}\|\omega^{k}-\bar{\omega}\| = 0$. Thus, the desired result follows. □

Theorem 3.3. The sequence$\{x^{k}\}$ converges globally to a solution of (1.2), where $x^k = \mu^k-\nu^k, (\mu^k; \nu^k) = \omega^k$.

Proof. From Theorem 3.2, we know that ${\omega^{k}}$ converges globally to a solution of (2.3), say $\omega^{*}$, and assume $\omega^{*} = (\mu^{*}; \nu^{*})$, $x^{*} = \mu^{*}-\nu^{*}$. A direct computation yields that

as $k\rightarrow \infty$. Thus, the desired result follows. □

In the end of this section, we discuss the convergence rate of Algorithm 3.1. To this end, the following lemmas are needed.

Lemma 3.3. For the sequence $\{\omega^k\}$ generated by Algorithm 3.1. Then, there exists a positive constant $\tau$ such that

where $dist(\omega^k, \Omega^*)$ denotes the distance from point $\omega^k$ to the solution set $\Omega^*$.

Proof. By Theorem 3.2, we obtain that the sequence $\{\omega^k\}$ is bounded, i.e., there exists a constant $c_0 > 0$ such that $\|\omega^k\|\leq c_0$. The following proof uses a similar technique to that of Corollary 3.2 in ^[43]. □

Lemma 3.4. For the sequence $\{\omega^k\}$ generated by Algorithm 3.1, it holds that

where positive constant $\tau$ defined in Lemma 3.3.

Proof. By (3.1), one has

Then, by (2.4), one has

where the second equality follow from (3.26), the second inequality follows from Proposition 2.1. Combining (3.27) with Lemma 3.3 yields (3.25). □

Lemma 3.5. For the sequence $\{\omega^k\}$ generated by Algorithm 3.1, it holds that

where $\sigma$ is a positive constant, $\bar{\omega}^k\in \Omega^*$ is the point closest to $\omega^k$.

Proof. By (2.2), and using the Mean Value Theorem with some $n$-vector $z^k$ lying on the line segment joining $\bar{\omega}^k$ with $\omega^k$, we have

where the first inequality follows from (3.12) with $\bar{\omega}^k\in R^{2n}_+$, and the second inequality is by the Cauchy-Schwartz inequality, the third inequality follows from the fact that $\|z^k-\bar{\omega}^k\|\leq\|\omega^k-\bar{\omega}^k\|$ and Lemma 3.1, the last inequality is by (3.25), let $\sigma = 2\|M\|[\tau(1+\frac{\|M\|}{\beta})]^2+(\eta+1)\|M\|[\tau(1+\frac{\|M\|}{\beta})]$, and thus, the desired result follows. □

Theorem 3.4. The generated sequence $\{\omega^k\}$ by Algorithm 3.1 converges global linearly to an element of $\Omega^*$.

Proof. For $\omega^*, \bar{\omega}^{k}\in \Omega^*$, by (2.2), one has $f(\omega^*) = f(\bar{\omega}^k)$. Combining this with (3.28) and (3.18), we obtain

i.e.,

where $0 < \varrho: = \frac{\frac{2\sigma}{\beta}}{1+\frac{2\sigma}{\beta}} < 1$. Since $f(\omega^{k})-f(\omega^*) > 0, f(\omega^{k+1})-f(\omega^*) > 0$, so (3.30) implies that $\{f(\omega^k)\}$ converges global linearly to $f(\omega^*)$.

By (3.18) and (3.30), we obtain

Combining this with (3.25), we obtain

where $0 < \sqrt{\varrho} < 1$. Thus, the sequence $\{\omega^k\}$ converges global linearly an element of $\Omega^*$. □

Remark 3.3. Riahi et al.(Theorem 2 ^[44]) give a linear rate of convergence of the Fletcher-Reeves' nonlinear conjugate gradient method (NCG), satisfying strong Wolfe conditions when the Hessian matrix of the cost function is positive definite and continuous and has bounded eigenvalues, which is the first result with a linear rate of convergence reported for such NCG in a general framework. In this paper, we propose a gradient projection method with global $R$-linear rate convergence. Our method is very different because first, the iterative method and line search step of the proposed algorithm are different from that in ^[44], and second because the Hessian matrix of objective function in (2.2) is semi-positive definite instead of positive definite. In fact, since $m\ll n$ in (1.1), we know that the rank of the sensing matrix $A$ is less than $m$, then the matrix $A^\top A$ is semi-positive definite instead of positive definite, and according to (2.2), one has

it follows that $det(M) = 0$. Hence, the desired result follows. Finally because the proof method of linear convergence in this paper is different from that of Theorem 2 in ^[44].

Thus, the global $R$-linear rate convergence of the proposed Algorithm 3.1 is a new result for constrained convex (rather than strictly convex) quadratic programming problem.

4.   Numerical experiments

In this section, some numerical experiments on sparse signal recovery were provided to prove the efficiency of the proposed method. All codes are written by version of Matlab 9.20.538062 and performed on a Windows 10 PC with Intel(R) Core(TM) i3-10105F CPU @ 3.70GHz 3.70 GHz and 16GB of memory. For experiments below, we set the matrix $A$ is generated by Matlab scripts:

The original signal $\bar{x}$ is generated by

Then, the observed signal is $y = A\bar{x}+\bar{n}$, where $\bar{n}$ is generated by a standard Gaussian distribution $N(0, 1)$ and then it is normalized. The initial points $\omega^{0} = (\mu^0;\nu^0),$ where $\mu^0 = \max\{0, A^\top y\}$, $\nu^0 = \max\{0, -A^\top y\}$.

The stop criterion is

where $f_k$ denotes the objective value of (2.2) at iteration $\omega^k$.

In our experiment, we assess the quality of restoration by mean of squared error (MSE) to the original signal $\bar{x}$, i.e.,

where $x^{*}$ denotes the recovery signal.

We compare the proposed Algorithm 3.1 with several state-of-the-art algorithms, all of which were the most popular in iterative algorithms for solving the $\ell_1-$ norm regularization problem arising from compressive sensing. In Section 4.1 and 4.2, we compare the proposed Algorithm 3.1 with PCG ^[30]$-$ a projection conjugate gradient algorithm for monotone nonlinear equations with convex constraints, and GCQ ^[39]$-$ a CQ algorithm for splitting feasible problems. In Section 4.3, we compare the proposed Algorithm 3.1 with FISTA ^[15]$-$ a fast iterative shrinkage-thresholding algorithm for linear inverse problems, and PADM ^[11]$-$ a primal alternating direction method for $\ell_1-$ problems in compressive sensing. In Section 4.4, we compare the proposed Algorithm 3.1 with PCG for debluring image. In Section 4.5, we present convergence curve of the proposed Algorithm 3.1.

4.1.   Test on additive Gaussian white noise

In this subsection, we will illustrate the feasibility and effectiveness of the proposed Algorithm 3.1 by recovering sparse signal of which observation data is corrupted by additive Gaussian white noise, and give some comparisons with PCG and GCQ.

We set $n = 2^{13}, m = 2^{11}, k = 2^{9}$, and the parameters in the three tested algorithms are listed as follows:

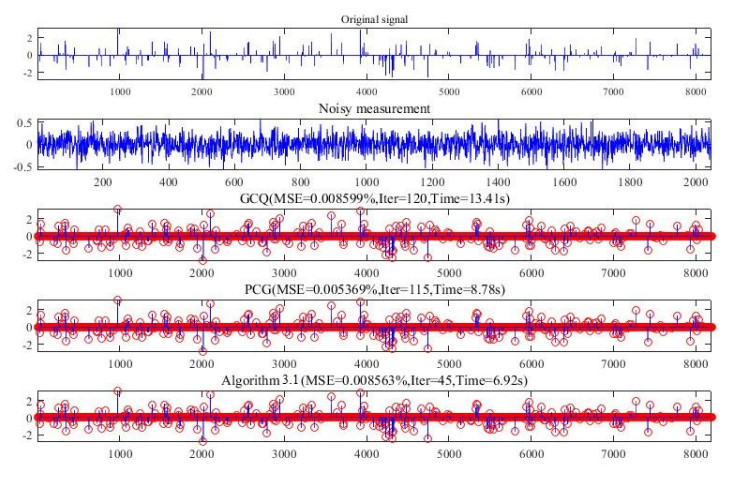
The original signal, the measurement and the reconstructed signal (marked by red point) by Algorithm 3.1, GCQ and PCG are given in Figure 1.

Comparing the first, third, fourth and the last plots in Figure 1, all elements in the original signal are circled by the red points, which indicates that the three methods can recover the original signal quite well. Furthermore, we record the number of iterations (abbreviated as Iter), the CPU time in seconds (abbreviated as CPUTime) and MSE of three methods. Figure 1 indicates that Algorithm 3.1 is always faster than GCQ and PCG methods, and also have higher accuracy. Thus, Algorithm 3.1 is an efficient method for sparse signal recovery.

4.2.   Comparison with GCQ and PCG in different dimension

In this subsection, we compare MSE, CPUTime and Iter among Algorithm 3.1, GCQ and PCG in different dimension $n$, where some parameters in the tested algorithms are given above. We set $m = \frac{n}{4}, k = \frac{m}{8}$. The following experiments is divided into two cases: adding noise and not adding noise.

The numerical results are listed in Table 1. From Table 1, whether it is Free noise or Gaussian noise, we can see that the CPU time of Algorithm 3.1 are always less than that of both GCQ and PCG in different dimensions except for $n = 1024$, which shows that Algorithm 3.1 converges faster than both GCQ and PCG. In the not noise case, the MSE of Algorithm 3.1 is almost smaller than that of GCQ. In other cases, although the MSE of Algorithm 3.1 is occasionally bigger than that of GCQ or PCG, the difference between them is very small. Specially, as the dimensionality of the recovered signal increases, the recovery speed advantage of Algorithm 3.1 becomes more obvious.

4.3.   Comparison with FISTA and PADM in different dimension

In this subsection, we present comparison results of the proposed Algorithm 3.1 and FISTA ^[15], PADM ^[11] on Gaussian noise, where some parameters in FISTA and PADM are listed as follows:

some parameters in the proposed Algorithm 3.1 are given Subsection 4.1. Comparison with Subsection 4.2, The sparse signal is double that of Subsection 4.2, i.e., $m = \frac{n}{4}, k = \frac{m}{4}$.

The numerical results are listed in Table 2. From Table 2, we obtain that the CPU time of Algorithm 3.1 are obviously less than that of FISTA and PADM in different k-Sparse signal, which shows that the recovery speed of Algorithm 3.1 is faster than that of FISTA and PADM, respectively. The MSE of Algorithm 3.1 is smaller than that of FISTA. Although the MSE of algorithm 3.1 is larger than that of PADM, the difference between the two is only slightly. Especially, the recovery speed advantage of Algorithm 3.1 becomes more obvious with the increase of dimension. All of these indicate that Algorithm 3.1 is an efficient method for different k-Sparse signal recovery.

4.4.   Noisy image restoration

In this subsection, we will use the proposed Algorithm 3.1 and PCG to deblur image with salt-and-pepper noise. Some parameters in tested algorithms are given above. We choose Lena ($512\times512$), Barbara ($512\times512$) and Baboon ($512\times512$) as the test images, and assess the restoration performance by applying the peak signal to noise ratio (PSNR), that is

For three different test images, we use different noise levels for numerical comparison to verify the resilience of the Algorithm 3.1 and PCG, and calculate numerical result for each noise sample of each image for each noise level. The detailed numerical results are listed in Table 3, where $r$ denotes the noise level, where $r = 1$ means that the picture is all noise. Iter, CPUTime and PSNR denote numerical results for the proposed Algorithm 3.1 denoising, Iter$\_$PCG, CPUTime$\_$PCG and PSNR$\_$PCG denote numerical results for PCG denoising, PSNR$\_$Noise denotes peak signal to noise ratio with noise.

From Table 3, using different salt-and-pepper noise level $r = 0.1, 0.3, 0.5, 0.7$, we can see that the Algorithm 3.1 and PCG could restore the image very well. Compared with PCG, the Algorithm 3.1 not only has a faster denoising speed, but also a higher PSNR, which means the effective of Algorithm 3.1 to remove salt and pepper noise.

Figure 2 shows the restoration results obtained by using the tested methods to the test images corrupted with 30%. From Figure 2, we could obtain that the Algorithm 3.1 and PCG could restore the image with salt-and-pepper noise very well.

4.5.   Convergence curve with different dimension

In this subsection, we respective draw convergence curve of the proposed Algorithm 3.1 for $n = 4096, 6144, 8192$, where $m = \frac{n}{4}, k = \frac{m}{4}$. The experiments divided into two cases: adding Gaussian noise and not adding Gaussian noise. The numerical results are drawn in Figure 3. As can be seen from Figure 3, $\|x^k-x^*\|$ is approximately an exponential function of the number of iterations $k$ whether it is free noise or Gaussian noise, i.e., $\|x^k-x^*\|\approx c_0 a^k$ where $c_0$ and $a$ are two positive constants, and $0 < a < 1$, which means $R-$ linearly convergence behavior of proposed algorithm.

5.   Discussion

This work has possible extensions. First, the parameters $\beta = 0.6, \gamma = 0.5$ of Algorithm 3.1 is adjusted dynamically to further enhance the efficiency of the corresponding method. Second, Riahi ^[45] present a new steepest-descent type algorithm for the optimization of a positive definite quadratic form, which can effectively handle ill-conditioned quadratic programming problem. Motivated by this technique, we will investigate the feasibility of applying the algorithm presented by Riahi to (2.2) with ill-conditioned the matrix $A$ and the semi-positive definite Hessian matrix. Finally, since the regularized nuclear norm minimization (RNNM) model defined in ^[46,47] is a convex program, we explore the possibility of the proposed algorithm developed for (1.2) model to solve the RNNM model from theoretical results and numerical experiments. These will be our further research directions.

6.   Conclusions

In this paper, we propose a new self-adaptive gradient projection algorithm for solving sparse signal reconstruction problem in compressive sensing. Its global convergence is established in detail. Without any assumptions, we establish global $R$-linear convergence rate, which is a new result for constrained convex (rather than strictly convex) quadratic programming problem, and also obtain an approximate optimal solution in a finite number of iterations. Thus, it has fast solving speed and pinpoint accuracy when the dimension increases. It makes the proposed algorithm very attractive for solving large-scale problems. We present numerical a comparison of five tested methods on sparse signal recovery. The proposed method is competitive with other existing ones in terms of recovery speed and computational efficiency.

Acknowledgments

This study was funded by the Natural Science Foundation of China (Nos. 12071250, 11801309), and Shandong Provincial Natural Science Foundation (ZR2021MA088).

Conflict of interest

The authors declare no conflict of interest.