Two discrete Mittag-Leffler extensions of the Cayley-exponential function

1.   Introduction

In the last decade of the last century, the time scale calculus appeared as a unification tool for the discrete, quantum and ordinary calculi ^[10]. Since then, it has affected the development of both the ordinary and fractional calculus. Many researchers have started to study fractional calculus benefiting from the time scales tools ^[3,9,20]. Exponential functions are considered to be the main set of functions to study linear dynamic equations. Due to this vitality, they occupied a considerable place in the time scale theory. Different version of exponential functions have appeared in this sequel. The author in ^[11] formulated a new type of exponential functions on time scales called Cayley-exponential function. Indeed, instead of assuming that the exponential function should satisfy the dynamic equation $\Delta \chi(t) = \lambda \chi(t), \; \chi(0) = 1$, for example, he requested it to satisfy the dynamic equation

where $\Delta$ is the forward type derivative on time scales and $\sigma(t)$ is the forward jumping operator. Notice that when the time scale is $\mathbb{R}$, then $\sigma(l) = l$ and, hence, Eq (1.1) will be reduced to the ordinary linear equation $\frac{d}{dt} \chi(t) = \lambda \chi(t), \; \chi(0) = 1$ whose solution, then becomes the exponential function $e^{\lambda t}$ and hence this new exponential function has a sense. The author in ^[11] used a bijection that relates the delta exponential function to Cayley-exponential function by replacing $\chi(\sigma(t))$ by $\Delta \chi(t)+\chi(t)$. In fractional calculus the ML functions play the role of or extended exponential functions ^[14,15,17]. On the other hand, researchers extended the delta and nabla discrete (on the time scale $\bf{Z}$) exponential functions to nabla and delta discrete ML functions either in delta ot nabla senses ^[2,4,7,19]. For some recent developments in discrete fractional calculus and its importance in short memory, we refer to ^[18,20]. In this work, we define nabla discrete ML extensions to discrete Cayley-exponential functions. We obtain two types of extensions: one by using the bijection through replacing $\chi(t-1)$ by $\chi(t)-\nabla \chi(t)$ and then allowing the nabla Caputo fractional difference to act in place of $\nabla \chi(t)$. The first type, the one through the bijection, is easy to obtain by making use of the already defined nabla discrete ML function in literature mentioned above. However, the second looks harder and its compact formula consists of double summations instead of one summation. For that reason, we may call nabla discrete ML functions as first level extensions and the one with double summation a second level one. The two newly defined nabla discrete ML functions in this article have the advantage that they relax the interval of convergence of the parameter $\lambda$.

This article is organized as follows: Section 2 includes preliminaries about discrete fractional sums and differences in the nabla sense, where the nabla discrete exponential and ML functions are recalled, and provides some nabla discrete Laplace transforms tools. In Section 3, we give a discrete ML function extending the nabla exponential function of Cayley type via a bijection. Section 4 is about the Cayley ML extension without the use of the bijection. Section 5 is devoted to the discrete Laplace transforms of the obtained discrete ML extensions. Finally, in Section 6 we summarize our conclusions.

2.   Preliminaries

In this section, we review some basics about nabla discrete fractional calculus on a time scale $\mathbb{N}_0 = \{0, 1, 2, ...\}$. For more details and more generally on a time scale $\mathbb{N}_{0, h} = \{0, h, 2h, 3h, ..\}, \; \; h > 0$, we refer the reader to ^[6]. The book ^[12] is a recommended reference as well.

2.1.   Nabla fractional differences and sums

In this section we set some essential terminology to proceed on.

Definition 2.1. ^[9] (The rising factorial)

(i) Let $\varsigma$ be a natural number; then the $\varsigma$ rising factorial of $t$ has the form

(ii) For any real number, the $\gamma$ rising function becomes

In addition, we have

hence $t^{\overline{\gamma}}$ is increasing on $\mathbb{N}_0$.

The backward difference operator on $\mathbb{Z}$ is given by $\nabla \chi(t) = \chi(t)-\chi(t-1)$, while the jumping operator is $\rho(n) = n-1$.

Consider the dynamic equation

where $1- \omega(t)\neq 0$ on $\mathbb{N}_{a} = \{a, a+1, a+2, ...\}$.

Then, the nabla exponential function $\widehat{e}_{p}(t, a)$ satisfies (2.4) and if $\omega$ is a positive constant with $1- \omega \neq 0$ then it has the form:

Definition 2.2. (Discrete ML function in nabla sense) (^[4,5]) For $\lambda \in \mathbb{R}, \; \; |\lambda| < 1$ and $\gamma, z \in \mathbb{C}$ with $Re(\gamma) > 0$, the nabla discrete ML function is

To know more details about the properties and the use of ML functions in fractional calculus, we refer to ^[14,15,17].

Definition 2.3. ^[6] For a function $\chi:\mathbb{N}_{a} = \{a, a+1, a+2\ldots\}\rightarrow \mathbb{R}$, the nabla left fractional sum of order $\gamma > 0$ is given by

Definition 2.4. ^[6] (The Caputo fractional differences) Let $\gamma \in (0, 1]$, then, the left Caputo fractional difference of order $\gamma$ starting at $a$ is defined by

Lemma 2.1. ^[6] Let $\gamma > 0, \; \mu > 0$. Then,

2.2.   Nabla discrete Laplace transforms

The Laplace transform on time scales was studied in ^[10,13,21]. The $Z-$transform can be found in ^[10] as well. As a special isolated time scale, we can consider the Laplace transform for the discrete fractional calculus. Following the nabla time scale book ^[10], the discrete Laplace transform on $\mathbb{N}_{a} = \{a, a+1, a+2, ...\}$ is given as follows.

Definition 2.5. The nabla discrete Laplace transform of a discrete function $\chi(t)$ defined on $\mathbb{N}_{a} = \{a, a+1, a+2, ...\}$ has the form

In case $a = 0$ and we write

Definition 2.6. ^[5] Let $s \in \mathbb{R}$, and $\chi_1, \chi_2:\mathbb{N}_{a}\rightarrow \mathbb{R}$ be a functions. The discrete convolution of $\chi_1$ with $\chi_2$ within nabla is defined by

If $a = 0$, then

Theorem 2.2. ^[6] $\textrm{(The discrete convolution theorem in nabla sense)}$ For any $\gamma \in \mathbb{R}\setminus\{\ldots, -2, -1, 0\}$, $s \in \mathbb{R}$ and $\chi_1, \chi_2$ defined on $\mathbb{N}_{a}$, we have

Lemma 2.3. ^[5,6] Let $\chi$ be defined on $\mathbb{N}_{a}$. Then,

Lemma 2.4. (For a = 0 see ^[6]) For any $\gamma \in \mathbb{R}\ \{\ldots, -2, -1, 0\}$ and $|1-s| < 1$, we have

Lemma 2.5. ^[6] For $\gamma, \lambda \in \mathbb{C}$ ($Re(\beta) > 0$), and $s \in \mathbb{C}$ with $Re(s) > 0, \; \; |\lambda s^{-\gamma}| < 1$, we have

The following discrete Laplace lemma is useful in what follows.

Lemma 2.6. Assume $\chi(t)$ is a real valued function defined on the set of integers $\mathbb{Z}$. Then, we have

where $\mathcal{N}\{\chi(t)\}(s) = X(s)$, and the empty sum leads to $0$.

Proof. By Definition 2.5, we have

Of particular interest of Lemma 2.6 above are the following two cases:

and

where $P(t) = t^{\overline{\gamma}}, \; \gamma > 0$. The latter case is due to the fact that dividing by poles of Gamma function leads to $0$.

3.   A nabla discrete ML extension via a bijection

In this section, we study the bijection between Anderson etal-exponential function and the nabla Cayley-exponential function, and define a nabla discrete ML extension. Consider the equation

Using that $\chi(t-1) = \chi(t)-\nabla \chi(t)$, then (3.1) becomes

Notice that $\frac{2\lambda}{2+\lambda}\neq 1$ implies that $\lambda\neq 2$.

Definition 3.1. (The nabla Cayley exponential function) The solution of the Eq (3.1), is called the nabla discrete Cayley function. It is given by

or

If we replace $\nabla \chi(t)$ in (3.2) with the Caputo fractional difference $(\; ^{C}\nabla^\gamma \chi)(t)$ of order $0 < \gamma\leq 1$, and make use of Example 48 in ^[4], then the solution of (3.2) will be of the form:

Notice that the convergence condition $|\omega| < 1$ in (3.5) implies that $\lambda \in (-\frac{2}{3}, 2)$.

On the light of (3.5), we can define the following discrete ML extension of the Cayley-exponential (C-exponential) function obtained by making use of the bijection $\omega = \frac{2\lambda}{2+\lambda}$.

Definition 3.2. The nabla discrete ML function in the sense of Cayley via the bijection $\omega$ is defined by

at least.

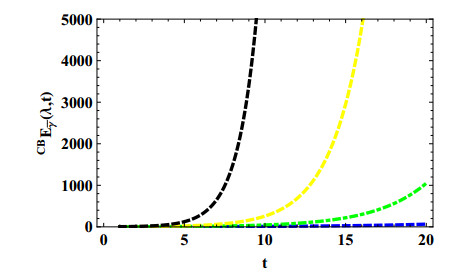
Remark 3.1. Notice that while the nabla discrete ML function $E_{\overline{\gamma}}(\lambda, t)$ extending the discrete Anderson etal-exponential function converges for $\lambda \in (-1, 1)$, the ML extension $\; ^{CB}E_{\overline{\gamma}}(\lambda, t)$ converges for $\lambda \in (-\frac{2}{3}, 2)$.

Below Figure 1 explains the graphs of the $\; ^{CB}E_{\overline{\gamma}}(\lambda, t)$ function and its convergence behavior for $\gamma = \frac{1}{2}$ and different values of $\lambda$ ($0.5, 0.7, 0.9, 1.2$).

4.   The discrete ML in the sense of Cayley without the use of the bijection $\omega$

In general, it is not true that

where $f:\mathbb{Z}\rightarrow \mathbb{R}$ is a discrete function defined on the integers. However, for the power functions we have the following assertion.

Lemma 4.1. Assume $\gamma > 0$ and $\eta > -1$. Then, for any $k = 0, 1, 2, ...$ and $t \in \mathbb{N}_0$, we have

Proof. We follow the proof by induction on $k$. For $k = 1$, we have

Now, by (4.3) we have

Hence, by replacing $t$ by $t-1$ we obtain the case $k = 1$. In fact, the assertion for any $k = 2, 3, ...$ can be proved by following similar to above and by using the fact that $(-j)^{\overline{\eta}} = 0$ for any $j = 0, 1, 2, 3, ...$, which is due to that division by a pole of the Gamma function results in $0$.

Remark 4.1. ● If in Lemma 4.1, the step in the discrete time scale is any positive $h$, then we can have

● From above it can be seen that (4.1) is in general true for discrete functions $f:\mathbb{Z}\rightarrow \mathbb{R}$ satisfying $f(-j) = 0$ for all $j, 0, -1, -2, -3, ...$.

Consider the equation

By applying the nabla fractional sum $\; _{0}\nabla^{-\gamma}$ of order $\gamma$ on the left hand side of (4.9) and making use of Proposition 28 in ^[4], we get the solution representation:

To proceed by the successive approximation (the existence and uniqueness theorem is straight forward), we set

For $s = 1$, and by the help of the identity (see for example Proposition 22 in ^[4])

or by Lemma 2.1, with $a = 0$, we have

For $s = 2$, we have

Lemma 4.1 with $k = 1$, then implies that

Similarly for $s = 3$, Lemma 4.1 with $k = 1, 2$ implies

If we proceed in this way, then we claim the following form:

where an empty sum is understood to be nil and $C_{i}^{j} = \frac{i!}{j! (i-j)!}$. To prove that (4.14) is true we proceed inductively. Assume (4.14) is true for $s = n$, and we need to show that it is true for $s = n+1$. That is

To this end, we have

That is,

Which completes the proof.

Upon (4.14), we set the following definition.

Definition 4.1. The nabla discrete ML function in the sense of Cayley without bijection use, of order $\gamma$, is given by:

Remark 4.2. By making use of Definition 9, the solution of (4.9) is given by

Notice that it converges for $|\lambda| < 2$.

Below Figure 2 explains the graph of the discrete function $\; ^{CA}E_{\overline{\gamma}}(\lambda, t)$ and its convergence behavior for $\gamma = \frac{1}{2}$ and $\lambda = 0.7$.

5.   Laplace transforms for the discrete ML type extensions

From Lemma 2.5, we recall that for $|\lambda s^{-\gamma}| < 1$, we have

Hence, we have

If we substitute $\omega = \frac{2 \lambda}{2+\lambda}$, then for $|\omega s^{-\gamma}| < 1$, we have

To calculate the discrete Laplace transform of $\; ^{CA}E_{\overline{\gamma}} (\lambda, t)$, we shall follow an indirect way. Namely, we shall solve the fractional difference initial value problem (4.9) by using the nabla discrete Laplace transform. Firstly, by writing $(\; ^{C}_{0}\nabla^\gamma \chi)(t) = \frac{t^{\overline{-\gamma}}}{\Gamma(1-\gamma)}*(\nabla \chi)(t)$, and by the help Theorem 2.2, Lemma 2.3 and Lemma 2.4, we have

where $\mathcal{N} \{\chi(t)\}(s) = X(s).$ On the other hand, by (2.16) with $\chi(0) = 1$, we conclude that

Hence,

Finally, upon Remark 4.2, we conclude that

On the other hand, it seems complicated to calculate the nabla discrete Laplace of $\mathcal{N}\{ \; ^{CA}E_{\overline{\gamma}} (\lambda, t) \}(s)$ by directly applying the $\mathcal{N}$ to the formula stated in Definition 4.1. Indeed, by making use of (2.17) or Lemma 2.6, we have

Therefore, we conclude that

where the left hand side of (5.7) is at least complicated to be evaluated. But if we set $\Lambda(s) = [\frac{\lambda s+2 s^{\gamma}}{4 s^{\gamma}+ 2\lambda(s-2)}-\frac{1}{2}]$ and $D_i(s) = \sum_{j = 0}^{i-1} C_{i-1}^j (1-s)^j$, then under the condition that $|\frac{\lambda D_i(s)^{1/i}}{2s^\gamma}| < 1$, we can come to the conclusion that

6.   Conclusions

We have defined two discrete ML functions $\; ^{CB}E_{\overline{\gamma}} (\lambda, t)$ and $\; ^{CA}E_{\overline{\gamma}} (\lambda, t)$ that extended the nabla discrete exponential functions in the sense Cayley. In fact, using the fractional order gives the chance to get the double series discrete ML extension $\; ^{CA}E_{\overline{\gamma}} (\lambda, t)$, whereas the Cayley exponential function is only related to the classical one by a bijection. Both of the obtained discrete ML functions obtained will result in a discrete Cayley exponential function when $\gamma = 1$.

We have noticed that, while the discrete ML function $E_{\overline{\gamma}} (\lambda, t)$ converges for $|\lambda| < 1$, $\; ^{CB}E_{\overline{\gamma}} (\lambda, t)$ and $\; ^{CA}E_{\overline{\gamma}} (\lambda, t)$ converge for $\lambda \in (\frac{-2}{3}, 2)$ and $|\lambda| < 2$, respectively. Further, we have calculated the nabla discrete Laplace transforms of both of the defined discrete ML functions. The newly defined discrete Mittag-Leffler functions are allowed to express the solutions of linear fractional difference equations when we average the solution and its one step backward in the right hand side of the linear equation. Due to this averaging, the formula is expressed by means of double summation seeking for better representations. Hence, we believe that the second level extension $\; ^{CA}E_{\overline{\gamma}} (\lambda, t)$ will play a central role in developing a new branch of discrete fractional calculus with better convergence criteria.

In this article, we have considered the nabla approach. Although, we can always construct dual identities between nabla and delta fractional difference operators, it is unclear to find direct dual identities that relate nabla and delta discrete exponential functions and more generally Mittag-Leffler functions. Hence, it will be of interest to consider the delta case in future works. For the classical delta discrete Mittag-Leffler case, we may refer to ^[22]. Also, it is of interest to consider the $q-$fractional case to study several theoretical aspects, such as in ^[1] and proceed in applications, such as in ^[8,16].

Acknowledgments

The author would like to thank Prince sultan University for paying the APC and for the support through the TAS research lab. The author would like to thank Prof. Hamid Boulares for the help in obtaining the compact formula (4.14).

Conflict of interest

The authors declare no conflicts of interest.