Results on monochromatic vertex disconnection of graphs

1.   Introduction

Connectivity is perhaps the most fundamental graph theoretic subject, in both the combinatorial and network science senses. To expand its application area, connectivity is strengthened through tasks such as requiring graph coloring, Hamiltonicity ^[13] and conditional connectivity ^[11].

In 2008, Chartrand et al. ^[5,6] introduced an interesting way, i.e., the rainbow $k$-connection, to strengthen conventional connectivity. An edge-colored graph $G$ is called rainbow $k$-connected if any pair of vertices are connected by $k$ internally vertex-disjoint rainbow paths, where a rainbow path is a path with edges that all carry different colors. This concept comes from the communication of information between agencies of the government, and it is also applied to communication networks. More developments for variants of rainbow $k$-connectivity of different graph families can be found, e.g., in the survey ^[18].

Moving away from deterministic graphs, similar results have also been investigated for random graph models (see ^[7,22]). In particular, a multiplex approach to cope with rainbow-related concepts has recently attracted increasing research attention in random settings. For example, Shang ^[23] approached rainbow $k$-connectivity by considering an alternative random network with multiple layers. Meanwhile, many colored versions of connectivity parameters have been introduced in recent years. For example, the monochromatic connection introduced by Caro and Yuster ^[3] in 2011 is defined from the monochromatic version; the monochromatic vertex connection introduced by Cai, Li and Wu ^[4] in 2018 is defined from the vertex version. For more results, we refer the reader to ^{[10,14,19,23]}.

There are two ways to study the connectivity, one using paths and the other using vertex cuts. These concepts mentioned above use paths, so it is natural to consider monochromatic vertex cuts. Let $G$ be a vertex-colored graph. A vertex cut $S$ is called a monochromatic vertex cut if the vertices of $S$ are colored with the same color, and a monochromatic $x$-$y$ vertex cut is a monochromatic vertex cut that separates $x$ and $y$. Obviously, if $x$ is adjacent to $y$, there is no $x$-$y$ vertex cut, so we only need to consider nonadjacent vertices in the sequel. Then, $G$ is called monochromatically vertex-disconnected if any two nonadjacent vertices of $G$ have a monochromatic vertex cut separating them; the corresponding coloring is called monochromatic vertex-disconnection coloring ($MVD$-coloring for short). The monochromatic vertex disconnection number of $G$, denoted by $mvd(G)$, is the maximum number of colors that are used to make $G$ monochromatically vertex-disconnected. An $MVD$-coloring with $mvd(G)$ colors is called an $mvd$-coloring of $G$.

In addition to being a natural combinatorial measure, our parameter can also be applied to communication networks. Suppose that $G$ represents a network (e.g., a cellular network) where messages can be transmitted between any two vertices. To intercept messages (e.g., to prevent the transmission of error messages), each vertex is equipped with an interceptor that requires a fixed password (color) to be turned on. There is a fixed interception passphrase between any two different vertices. Entering this passphrase at the vertex cut where the password matches will turn on these interceptors and intercept the message between the two vertices. To enhance system security, the number of passwords should be as large as possible. This number is precisely $mvd(G)$.

In this paper, the connection between graph parameters are studied: $mvd(G)$ and connectivity $\kappa(G)$. We obtain the following results in Section 2:

Theorem 1.1. If $G$ is a connected non-complete graph, then $1\leq mvd(G)\leq n-\kappa^{+}(G)+1 \leq n-\kappa(G)+1$. The upper bound is tight.

Further, for the minimally $2$-connected graph of order $n\geq 4$, we give a new upper bound:

Theorem 1.2. If $G$ is a minimally $2$-connected graph of order $n\geq 4$, then $mvd(G)\leq \left\lfloor {\frac{n}{2}}\right\rfloor$. The bound is tight.

For the graph $G$ with $\kappa(G) = 1$, $mvd$-coloring, a global property of $G$, is transformed into a local property of each block, which greatly simplifies the original problem:

Theorem 1.3. If $\kappa(G) = 1$ and $G$ has $r$ blocks $B_{1},$ $\ldots, B_{r}$, then $mvd(G) = (\sum\limits_{i = 1}^{r} mvd(B_{i}))-r+1$.

In Section 3, we focus on the value of $mvd(G)$ for some well-known graphs with $\kappa(G)\geq2$ and obtain several classes of graphs with $mvd(G) = k$, where $k\in \{1, 2, n\}$. Moreover, we completely characterize $G$ when $n-5\leq mvd(G)\leq n$ and all blocks of $G$ are minimally 2-connected triangle-free graphs.

The Erdős-Gallai theorem ^[8] originated in 1959 and is an interesting problem in extremal graph theory, where the Erdős-Gallai-type result aims at determining the maximum or minimum value of a graph parameter with some given properties. For a graph parameter, it is always interesting and challenging to get the Erdős-Gallai-type results; see ^{[1,9,15,16,20]} for more such results on various kinds of graph parameters. In Section 4, we study two kinds of Erdős-Gallai-type problems for our parameter $mvd(G)$.

Problem Ⅰ. Given two positive integers $n$ and $k$ with $1\leq k\leq n$, compute the minimum integer $f_v(n, k)$ such that, for any graph $G$ of order $n$, if $|E(G)|\geq f_v(n, k)$, then $mvd(G)\geq k$.

Problem Ⅱ. Given two positive integers $n$ and $k$ with $1\leq k\leq n$, compute the maximum integer $g_v(n, k)$ such that, for any graph $G$ of order $n$, if $|E(G)|\leq g_v(n, k)$, then $mvd(G)\leq k$.

By Theorem 1.3, for any tree $G$ of order $n$, we have $mvd(G) = n$, so $g_v(n, k)$ does not exist for $1\leq k\leq n-1$. Since $mvd(K_n) = n$, where $K_n$ is a complete graph, $g_v(n, n) = \frac{n(n-1)}{2}$. The result of Problem Ⅰ is shown below.

Theorem 1.4. Given two positive integers $n$ and $k$ with $n\geq5$ and $1\leq k\leq n$,

Moreover, we obtain the maximum size of $G$ with $mvd(G) = k$ for any $k$.

Theorem 1.5. Given two positive integers $n$ and $k$ with $n > 4$ and $1\leq k\leq n$, the maximum size of a connected graph $G$ of order $n$ with $mvd(G) = k$ is

2.   Some basic results

All graphs considered in this paper are simple, connected, finite and undirected. We follow the terminology and notation of Bondy and Murty ^[2]. Let $n = |G|$ be the order of $G$, and let $|E(G)|$ be the size of $G$. For $D\subseteq E(G)$, $G-D$ is the graph obtained by removing $D$ from $G$. For $S\subseteq V(G)$, $G-S$ is the graph obtained by removing $S$ and the edges incident to the vertices of $S$ from $G$. We use $[r]$ to denote the set $\{1, 2, \dots, r\}$. For a vertex-coloring $\tau$ of $G$, $\tau(v)$ is the color of vertex $v$, $\tau(G)$ is the set of colors used in $G$ and $|\tau(G)|$ is the number of colors in $\tau(G)$. If $H$ is a subgraph of $G$, then the part of the coloring of $\tau$ on $H$ is called $\tau$-$restricted$ on $H$. To show the connection between $mvd(G)$ and connectivity $\kappa(G)$, we need the following lemma:

Lemma 2.1. If $\tau$ is an $MVD$-coloring of $G$, then $\tau$ restricted on $G[S]$ is also an $MVD$-coloring of $G[S]$.

Proof. Let the coloring of $\tau$ restricted on $G[S]$ be denoted as $\tau'$, and let $x$ and $y$ be two nonadjacent vertices of $G[S]$. If $D$ is a monochromatic $x$-$y$ vertex cut of $G$, then $D' = D\cap V(G[S])$ is a monochromatic $x$-$y$ vertex cut in $G[S]$. Otherwise, if there is an $x, y$-path $P$ in $G[S]-D'$, then $P$ is also in $G-D$, which is a contradiction. Thus, $\tau'$ is an $MVD$-coloring of $G[S]$.

Proof of Theorem 1.1. $G$ is a non-complete graph and $x$ and $y$ are two nonadjacent vertices of $G$. Let $\kappa(x, y)$ be the minimum size of an $x$-$y$ vertex cut, and let $\kappa^{+}(G)$ be the upper bound of the function $\kappa(x, y)$. Obviously, $mvd(G)\geq 1$. For the upper bound, assume that $S$ is a monochromatic $x$-$y$ vertex cut. Therefore, $mvd(G)\leq 1+(n-|S|)\leq n-\kappa(x, y)+1$. Thus, $mvd(G)\leq n-\kappa^{+}(G)+1\leq n-\kappa(G)+1$.

$\textbf{Tight example 1:}$ Let $G$ be a graph obtained by adding $k$ edges to $K_{n-1}$ from a vertex $v$ outside $K_{n-1}$, where $k\in [n-2]$. Clearly, $\kappa(G) = k$. Define a vertex-coloring $\tau$ of $G$: $V(G)\rightarrow [n-k+1]$ such that $\tau(G-N(v))\rightarrow [n-k]$ and $\tau(N(v)) = n-k+1$. If $x$ and $y$ are two nonadjacent vertices in $G$, then either $x$ or $y$ is $v$, i.e., $v = x$. Since $\tau(N(v)) = n-k+1$, $N(v)$ is a monochromatic $v$-$y$ vertex cut and $\tau$ is a $MVD$-coloring of $G$. So, $mvd(G)\geq n-k+1$. It follows that $mvd(G) = n-\kappa(G)+1$. The upper bound is tight.

A graph $G$ is $minimally$ 2-$connected$ ($minimal\ block$) if $G$ is 2-connected but $G-\{e\}$ is not 2-connected for every $e\in E(G)$. Before proving Theorem 1.2, we need more preparation: a nest sequence of graphs is a sequence $G_0, G_1, \ldots, G_t$ of graphs such that $G_i\subset G_{i+1}, 0\leq i < t$; an $ear\ decomposition$ of a $2$-connected graph $G$ is a nest sequence $G_0, G_1, \ldots, G_t$ of 2-connected subgraphs of $G$ satisfying the following conditions: (ⅰ) $G_0$ is a cycle of $G$; (ⅱ) $G_{i+1} = G_{i}\cup P_{i}$, where $P_i$ is an ear of $G_i$, $0\leq i < t$; (ⅲ) $G_{t} = G$.

Lemma 2.2. ^[17] Let $G$ be a minimally $2$-connected graph, and $G$ is not a cycle. Then, $G$ has an ear decomposition $G_0, G_1, \ldots, G_{t}\ (t\geq 1)$ satisfying the following conditions:

(i) $G_{i+1} = G_{i}\cup P_{i}\ (0\leq i < t)$, where $P_{i}$ is an ear of $G_{i}$ in $G$ and at least one vertex of $P_{i}$ has degree two in $G$;

(ii) each of the two internally disjoint paths in $G_0$ between the endpoints of $P_0$ has at least one vertex with degree two in $G$.

Lemma 2.3. ^[21] If $G$ is a minimally $2$-connected graph of order $n\geq 4$, then $G$ contains no triangles.

Lemma 2.4. If $G$ is a cycle of order $n\geq 4$, then $mvd(G) = \left\lfloor {\frac{n}{2}}\right\rfloor$.

Proof. Let $G = v_1e_1\ldots v_ne_nv_1$. Define a vertex-coloring $\tau: V(G)\rightarrow \big[\left\lfloor {\frac{n}{2}}\right\rfloor\big]$ such that, if $j\equiv i$ $(mod$ $\left\lfloor {\frac{n}{2}}\right\rfloor)$, then $\tau(v_j) = i$, where $i\in\big[\left\lfloor {\frac{n}{2}}\right\rfloor\big]$ and $j\in[n]$. It can be shown that, for any two nonadjacent vertices $x$ and $y$, there is a monochromatic $x$-$y$ vertex cut. So, $\tau$ is an $MVD$-coloring and $mvd(G)\geq \left\lfloor {\frac{n}{2}}\right\rfloor$.

If, on the contrary, for $n\geq 4$, $mvd(G)\geq \left\lfloor {\frac{n}{2}}\right\rfloor+1$ and $\tau$ is an $mvd$-coloring of $G$ with $|\tau(G)| = mvd(G)\geq \left\lfloor {\frac{n}{2}}\right\rfloor+1$, then there must be a color that colors only one vertex $v_i$; otherwise, we have $V(G)\geq 2|\tau(G)| \geq 2\left(\left\lfloor {\frac{n}{2}}\right\rfloor+1\right) \geq n+1$. Since $\kappa(G) = 2$, the monochromatic $v_{i-1}$-$v_{i+1}$ vertex cut must contain $v_i$ and some vertex $v_j$ in $G-\{v_{i-1}, v_i, v_{i+1}\}$. However, $\tau(v_i)\neq\tau(v_j)$, which contradicts the fact that $\tau$ is an $mvd$-coloring. Thus, $mvd(G) = \left\lfloor {\frac{n}{2}}\right\rfloor$.

Proof of Theorem 1.2. We make the following claim:

Claim 1: If $G$ is a 2-connected triangle-free graph and every ear $P_{i}$ $(0\leq i < t)$ has internal vertices, then $mvd(G)\leq \left\lfloor {\frac{n}{2}}\right\rfloor$.

Let $F = \{G_0, G_1, \ldots, G_t\}$ be an ear decomposition of $G$. We use induction on $|F|$. By Lemma 2.4, the claim holds for $|F| = 1$. If $|F| = t+1 > 1$, let $\tau$ be an $mvd$-coloring of $G$. Since $|P_{t-1}|\geq 3$, $G_{t-1}$ is a connected vertex-induced subgraph of $G$. By Lemma 2.1, $\tau$ restricted on $G_{t-1}$ is an $MVD$-coloring of $G_{t-1}$. By induction, we have

Suppose that the endpoints of $P_{t-1}$ are $a$ and $b$ and $L$ is the shortest $a, b$-path in $G_{t-1}$. Since $P_{t-1}$ is the last ear, cycle $C = L\cup P_{t-1}$ is a connected vertex-induced subgraph of $G$ and $\tau$ restricted on $C$ is an $MVD$-coloring of $C$. Then, there are at most $|P_{t-1}|-2$ vertices that are assigned colors in $\tau(G)-\tau(G_{t-1})$. Since $|C|\geq 4$, each color in $\tau(G)-\tau(G_{t-1})$ colors at least two internal vertices of $P_{t-1}$. Otherwise, if $j\in \tau(G)-\tau(G_{t-1})$ and only colors one internal vertex of $P_{t-1}$, say $x_{j}$, then $x_{j-1}$ and $x_{j+1}$ are two nonadjacent vertices of $G$ and the monochromatic $x_{j-1}$-$x_{j+1}$ vertex cut must contain $x_{j}$ and another vertex, which is a contradiction. Then, $|\tau(G)-\tau(G_{t-1})|\leq \left\lfloor {\frac{|P_{t-1}|-2}{2}}\right\rfloor$. So,

Above all, $mvd(G)\leq \left\lfloor {\frac{n}{2}}\right\rfloor$.

By Lemmas 2.2 and 2.3, if $G$ is not a cycle, then there is an ear decomposition satisfying the conditions in Claim 1. Thus, $mvd(G)\leq \left\lfloor {\frac{n}{2}}\right\rfloor$.

$\textbf{Tight example 2:}$ If $G$ is a cycle, then, according to Lemma 2.4, we have $mvd(G) = \left\lfloor {\frac{n}{2}}\right\rfloor$. The bound is tight.

A $block$ is a maximal connected subgraph of $G$ that has no cut-vertex. Every block of a nontrivial connected graph is either $K_2$ or a 2-connected subgraph, called $trivial$ and $nontrivial$, respectively. To show the connection between $mvd(G)$ and block decomposition, we need the following result:

Theorem 2.1. Let $G$ be a connected graph with $r$ blocks. Then, $\tau$ is an $mvd$-coloring of $G$ if and only if $\tau$ restricted on each block is an $mvd$-coloring of each block and the colors of different blocks are different except at the cut vertices.

Proof. Let $\{ B_1, \ldots, B_r \}$ be the block decomposition of $G$. Let $\tau$ be a vertex-coloring of $G$, and let $\tau_i$ be the coloring of $\tau$ restricted on $B_i$, $i\in [r]$. If $G$ has no cut vertex, then $G = B_1$ and the result follows. Now, we assume that $G$ has at least one cut vertex:

Claim 1: $\tau$ is an $MVD$-coloring of $G$ if and only if $\tau$ restricted on each block is an $MVD$-coloring of each block.

Since each block is a vertex-induced subgraph of $G$, the necessity is obvious by Lemma 2.1. Now, let $\tau_i$ be an $MVD$-coloring of $B_i$, where $i\in [r]$. For any two nonadjacent vertices $x$ and $y$ in $G$, if there is a block, say $B_1$, which contains both $x$ and $y$, then any monochromatic $x$-$y$ vertex cut in $B_1$ is also a monochromatic $x$-$y$ vertex cut in $G$. If $x$ and $y$ are in different blocks, then there is exactly one internally disjoint $x, y$-path containing at least one cut vertex $v$. The vertex $v$ is a monochromatic $x$-$y$ vertex cut in $G$. Thus, $\tau$ is an $MVD$-coloring of $G$.

Next, let $\tau_i$ be an $mvd$-coloring of $B_i$ satisfying that, if $B_i\cap B_j = v$, then $\tau_i(B_i)\cap \tau_j(B_j) = \tau_i(v) = \tau_j(v)$, and if $B_i\cap B_j = \varnothing$, then $\tau_i(B_i)\cap \tau_j(B_j) = \varnothing$, where $i, j\in[r]$ and $i\neq j$. Then, $\tau$ is an $MVD$-coloring of $G$ by Claim 1. We claim that $\tau$ is an $mvd$-coloring of $G$. Otherwise, there is an $mvd$-coloring $\tau'$ of $G$ satisfying $|\tau'(G)| > |\tau(G)|$. Let the coloring of $\tau'$ restricted on $B_i$ be $\tau'_i$, which is an $MVD$-coloring of $B_{i}$ by Claim 1. Then, for any $i\in [r]$, $|\tau'_i(B_i)|\leq |\tau_i(B_i)|$, which contradicts $|\tau'(G)| > |\tau(G)|$. Thus, $\tau$ is an $mvd$-coloring of $G$.

Now, we prove the necessity of the theorem. Let $\tau$ be an $mvd$-coloring of $G$. According to Claim 1, $\tau_i$ is an $MVD$-coloring of $B_i$, $i\in[r]$. Similar to the proof of Claim 1, it can be shown that, if $B_i\cap B_j = v$, then $\tau_i(B_i)\cap \tau_j(B_j) = \tau_i(v) = \tau_j(v)$, and if $B_i\cap B_j = \varnothing$, then $\tau_i(B_i)\cap \tau_j(B_j) = \varnothing$, where $i, j\in[r]$ and $i\neq j$. We only need to prove that $\tau_{i}$ is an $mvd$-coloring of $B_{i}$, $i\in[r]$. If $\tau_1$ is not an $mvd$-coloring of $B_1$, then there must be an $mvd$-coloring $\tau'_1$ of $B_1$ satisfying that all colors in $\tau'_1(B_1)$ are unused colors, except for those owned by cut vertices. It follows that $|\tau'_1(B_1)| > |\tau_1(B_1)|$ and $|\tau'(G)| > |\tau(G)|$. According to the sufficiency of Claim 1, $\tau'$ is an $MVD$-coloring of $G$, which contradicts the maximality of $\tau$.

Proof of Theorem 1.3. Let $G$ be a connected graph with blocks $B_1, B_2, \ldots, B_r$, and let $\tau$ be an $mvd$-coloring of $G$. We use induction on $r$. The result holds for $r = 1$. If $r > 1$, then $G$ is not 2-connected; we know that there is a block, say $B_r$, containing only one cut vertex, say $v$. Let $G' = G-(V(B_r)-\{v\})$. Then, $G'$ is a connected graph with blocks $B_1, B_2, \ldots, B_{r-1}$. By Theorem 2.1, $\tau$ restricted on $G'$ is an $mvd$-coloring of $G'$, and, combined with the induction hypothesis, we have $|\tau(G')| = mvd(G') = (\sum_{i = 1}^{r-1} mvd(B_i))-(r-1)+1$. According to Theorem 2.1, $\tau$ restricted on $B_r$ is an $mvd$-coloring of $B_r$ and $\tau(B_r)\cap \tau(G') = \tau(v)$. So, we deleted $|mvd(B_r)|-1$ colors from $\tau(G)$ to obtain $\tau(G')$; $mvd(G)$ is as desired.

3.   Results for special graphs

If $G$ and $H$ are vertex-disjoint, then let $G\vee H$ denote the $join$ of $G$ and $H$, which is obtained from $G$ and $H$ by adding edges $\{xy:x\in V(G), y\in V(H)\}$. If $C_{n-1}$ is a cycle of order $n-1$, then $W_{n} = C_{n-1}\vee K_1$ is called a $wheel\ graph$. We first show several classes of graphs with $mvd(G) = k$, where $k\in \{1, 2, n\}$.

Theorem 3.1. If $G$ is one of the following graphs, then $mvd(G) = 1$.

(i) $G$ is a wheel graph other than $W_4$;

(ii) $G = K_{n_1, \ldots, n_k}$ is a complete $k$-partite graph with $n_k$, $n_{k-1}\geq 2$ and $k > 2$.

(1) Let $G = W_n = C_{n-1}\vee K_1$, where cycle $C_{n-1} = v_1v_2\ldots v_{n-1}v_1$ and $K_1 = v$. It is known that $mvd(W_4) = mvd(K_4) = 4$. We claim that $mvd(W_n) = 1$ for $n > 4$.

Let $\tau$ be an $mvd$-coloring of $W_{n}$, say $\tau(v) = 1$. Since $n > 4$, $v_1$ and $v_3$ are two nonadjacent vertices with three internally disjoint $v_1, v_3$-paths, namely, $v_1v_2v_3$, $v_1vv_3$ and $v_1v_{n-1}v_{n-2}\cdots v_4v_3$. Since $\kappa(W_n) = 3$, any monochromatic $v_1$-$v_3$ vertex cut must contain the vertex set $\{v_2, v, v_i\}$, where $v_i\in\{v_{n-1}, v_{n-2}, \ldots, v_{4}\}$, so $\tau(v_2) = 1$. Similarly, $v_2$ and $v_4$ are two nonadjacent vertices, and we get $\tau(v_3) = 1$. Repeat operations above until all vertices of $C_{n-1}$ are colored, and we get $\tau(v) = \tau(v_1) = \tau(v_2) = \cdots = \tau(v_{n-1}) = 1$. Therefore, $mvd(W_n) = 1$ for $n > 4$.

(2) Let $G = K_{n_1, n_2, \ldots, n_k}$ be a complete $k$-partite graph of order $n$, where $k\geq2$ and $1\leq n_1\leq n_2\leq\cdots\leq n_k$. Let $V_1, V_2, \ldots, V_k$ be the vertex-partition sets of $G$ with $|V_i| = n_i$, where $i\in[k]$. There are four cases below.

Case 1. $n_i = 1$ for $i\in[k]$; then, $mvd(G) = mvd(K_n) = n$.

Case 2. $n_i = 1$ for $i\in[k-1]$, and $n_k\geq2$:

Define a vertex-coloring $\tau:V(G)\rightarrow [n-k+2]$ such that $\tau(V_k)\rightarrow [n-k+1]$ and $\tau(V_i) = n-k+2$ for $i\in [k-1]$. If $x$ and $y$ are two nonadjacent vertices in $G$, then $x, \ y\in V_k$ and $V(G)-V_k$ is a monochromatic $x$-$y$ vertex cut in $G$. Thus, $\tau$ is an $MVD$-coloring of $G$ and $mvd(G)\geq n-k+2$. On the other hand, since any two vertices in $V_k$ have $k-1$ internally disjoint paths, according to Theorem 1.1, $mvd(G)\leq n-\kappa^{+}(G)+1 = n-k+2$.

Case 3. $k > 2$ and $n_k\geq n_{k-1}\geq2$:

$x$ and $y$ are nonadjacent. If $x, \ y\in V_{k-1}$, then any $x$-$y$ vertex cut must contain $V(G)-V_{k-1}$. So, $V(G)-V_{k-1}$ are assigned the same color. Similarly, if $x, \ y\in V_k$, then $V(G)-V_k$ are assigned the same color. Since $k > 2$, the sets $V(G)-V_{k-1}$ and $V(G)-V_{k-1}$ intersect. Then, $mvd(G) = 1$.

Case 4. $k = 2$, $n_2\geq n_1\geq 2$:

Similarly, since $k = 2$, the sets $V(G)-V_1$ and $V(G)-V_2$ are disjoint; then, $mvd(K_{n_1, n_2}) = 2$.

The $Cartesian\ product$ of $G$ and $H$, written as $G\Box H$, is the graph with the vertex set $V(G)\times V (H)$, specified by putting $(u, v)$ adjacent to $(u', v')$ if and only if either $u = u'$ and $vv'\in E(H)$, or $v = v'$ and $uu'\in E(G)$. If $P_n$ is a path with order $n$, then $P_{m}\Box P_{n}$ is called the $m$-by-$n$ $grid$.

Theorem 3.2. If $G$ is one of the following graphs, then $mvd(G) = 2$.

(i) $G = P_m\Box P_n$ is a nontrivial grid other than $P_1\Box P_n$ with $n > 2$;

(ii) $G$ is a Petersen graph.

Proof. (1) Let $G = P_m\Box P_n$ and define $x_{i, j}$ to be the vertex in the $i$-th row and $j$-th column, where $i\in [m]$ and $j\in [n]$. It is known that $mvd(P_1\Box P_n) = mvd(P_n) = n$. Then, $mvd(P_1\Box P_2) = 2$ and $mvd(P_1\Box P_n) > 2$ for $n > 2$. We claim that $mvd(P_m\Box P_n) = 2$ for $m, n\geq2$.

Define a vertex-coloring $\tau$ of $G$: $V(G)\rightarrow [2]$ such that $\tau(x_{i, j}) = 1$ if $i+j$ is even and $\tau(x_{i, j}) = 2$ if $i+j$ is odd. For any vertex $x$ in $G$, the set $N(x)$ is monochromatic. Thus, for any two nonadjacent vertices $x$ and $y$ in $G$, $N(x)$ is a monochromatic $x$-$y$ vertex cut. So, $mvd(G)\geq 2$.

Now, we prove that $mvd(G) = 2$. Any $MVD$-coloring of a 4-cycle can have only two cases, where one is trivial and the other is to assign colors 1 and 2 to the four vertices of the 4-cycle alternately. Suppose that $mvd(G) > 2$ and $\tau$ is an $mvd$-coloring of $G$. By Lemma 2.1, $\tau$ restricted on each $4$-cycle $G[x_{i, j}, x_{i, j+1},$ $x_{i+1, j+1}, x_{i+1, j}]$ is an $MVD$-coloring, given $1\leq i < m, 1\leq j < n$, which contradicts that $mvd(G) > 2$. Therefore, $mvd(P_m\Box P_n) = 2$ for $m, n\geq 2$.

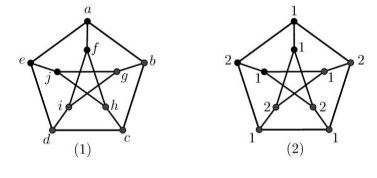
(2) Define a vertex-coloring $\tau$ of $G$: $V(G)\rightarrow [2]$ as shown in Figure 1(2). For any two nonadjacent vertices $x$ and $y$, there is only one common neighbor, say $z$. Suppose that $\tau(z) = t$; it can be shown that the set of all vertices colored by $t$, except $x$ and $y$, is a monochromatic $x$-$y$ vertex cut. Thus, $\tau$ is an $MVD$-coloring of $G$ and $mvd(G)\geq 2$. We prove that $mvd(G) = 2$ below.

Any $MVD$-coloring of $C_5$ can only be two cases, where one is trivial and the other is to assign colors 1 and 2 to the five vertices of $C_5$ alternately. At least two adjacent vertices in $C_5$ have the same color. Suppose that $mvd(G) > 2$ and $\tau$ is an $mvd$-coloring of $G$. Let the four 5-cycles of $G$ be $G_1 = G[a, b, c, d, e], G_2 = G[c, d, i, f, h], G_3 = G[a, b, c, h, f]$ and $G_4 = G[f, h, j, g, i]$. Since $\tau$ restricted on $G_1$ is an $MVD$-coloring, there are two cases.

Case 1. $G_1$ is colored nontrivially.

Suppose that $\tau(a) = \tau(c) = \tau(d) = 1$ and $\tau(b) = \tau(e) = 2$. Then, $\tau$ restricted on $G_2$ is an $MVD$-coloring. If $G_2$ is colored trivially, i.e., $\tau(f) = \tau(h) = \tau(i) = 1$, it is obvious that $\tau$ is not an $MVD$-coloring restricted on $G_3$. By Lemma 2.1, $\tau$ is not an $MVD$-coloring of $G$, which contradicts that $\tau$ is an $mvd$-coloring of $G$. If $G_2$ is colored nontrivially, i.e., $\tau(f) = 1$ and $\tau(h) = \tau(i) = 2$, then $\tau$ is a nontrivial $MVD$-coloring restricted on $G_4$ with $\tau(g) = \tau(j) = 1$, which contradicts that $mvd(G) > 2$.

Case 2. $G_1$ is colored trivially.

Suppose that $\tau(a) = \tau(b) = \tau(c) = \tau(d) = \tau(e) = 1$. Then, $\tau$ is a trivial $MVD$-coloring restricted on $G_3$ with $\tau(f) = \tau(h) = 1$. Since $\tau$ is an $MVD$-coloring restricted on $G_4$, $|\tau(G_4)|\leq 2$, which contradicts that $mvd(G) > 2$.

Above all, $mvd(G) = 2$.

Theorem 3.3. Let $G$ be a connected graph of order $n$. Then, $mvd(G) = n$ if and only if each block of $G$ is complete.

Proof. Let $\{ B_1, B_2, \ldots, B_r \}$ be a block decomposition of $G$. If $B_i\ (i\in [r])$ is complete, we define a coloring $\tau: V(G)\rightarrow [n]$ such that all vertices of $G$ have different colors. By Theorem 2.1, $\tau$ is an $mvd$-coloring of $G$ and $mvd(G) = n$. On the contrary, if $mvd(G) = n$, we define a coloring $\tau: V(G)\rightarrow [n]$ such that all vertices of $G$ have different colors. By Theorem 2.1, $\tau(B_i)$ is an $mvd$-coloring of $B_i$. Then, $B_i$ is complete. Otherwise, since $B_i$ is $2$-connected, by Theorem 1.1, $mvd(B_i)\leq |B_i|-\kappa(B_i)+1\leq |B_i|-1$, which is a contradiction.

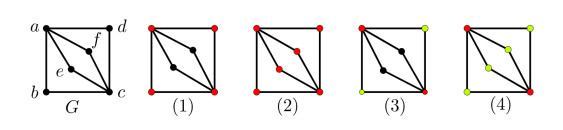
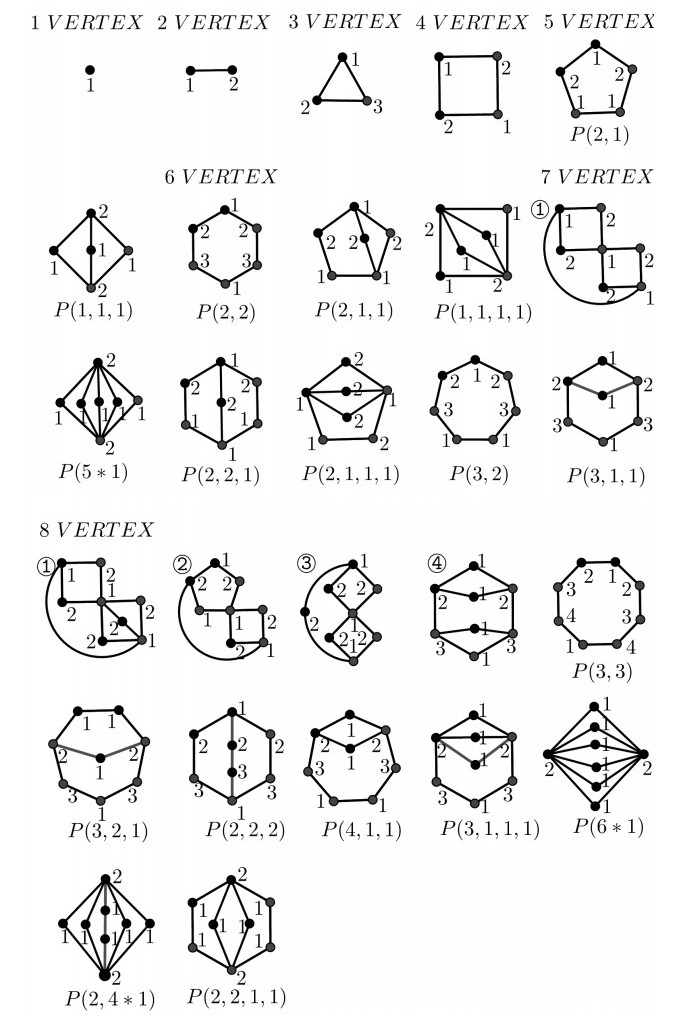
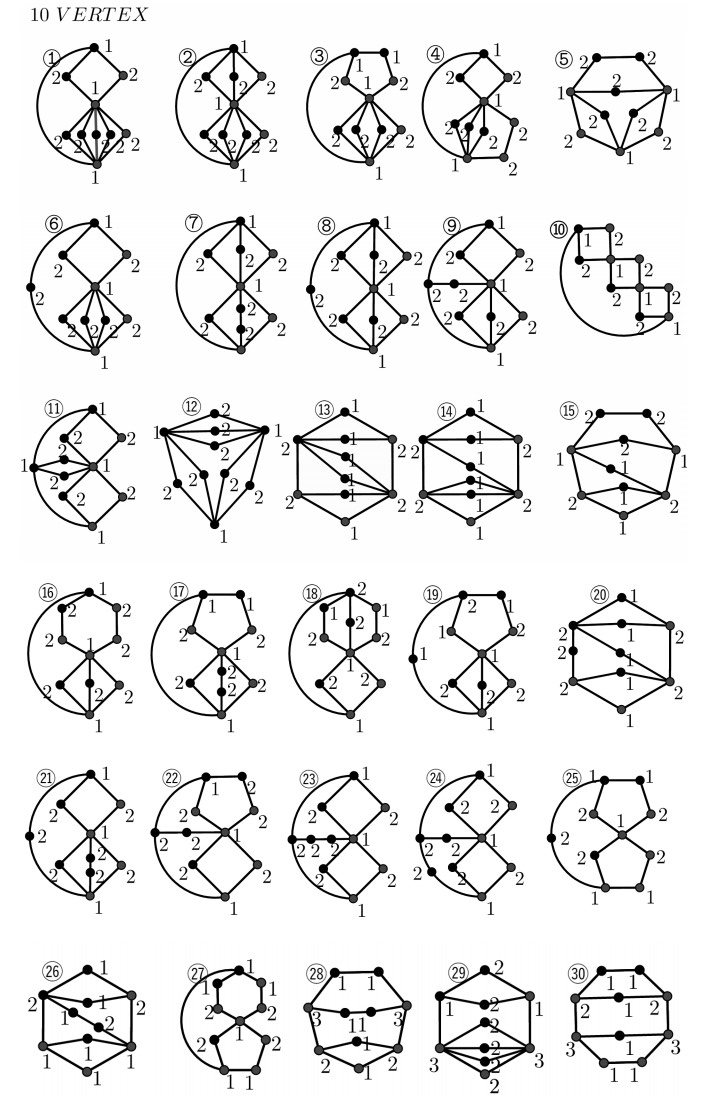
Now, we focus on minimally $2$-connected graphs ^[12] of order 10 or less. As an example, see Figure 2; let the three 4-cycles of $G$ be $G_1 = G[a, b, c, d], G_2 = G[a, b, c, e]$ and $G_3 = G[a, f, c, d]$. According to Lemma 2.1, if $\tau$ is an $mvd$-coloring of $G$, then $\tau(G_1)$ may be (1) or (3), i.e., an $MVD$-coloring of $G_1$. For Case (1), $\tau(G_2)$ and $\tau(G_3)$ must be (2). For Case (3), $\tau(G_2)$ and $\tau(G_3)$ must be (4). It can be shown that both (2) and (4) are $MVD$-colorings of $G$ and (4) is an $mvd$-coloring of $G$. Using the same method, after tedious calculations, the $mvd(G)$ of minimally 2-connected graph $G$ is shown in ^*Table 1, and the $mvd$-coloring of $G$ is shown in Appendix $A$ (In fact, this method is applicable to many graphs with small order).

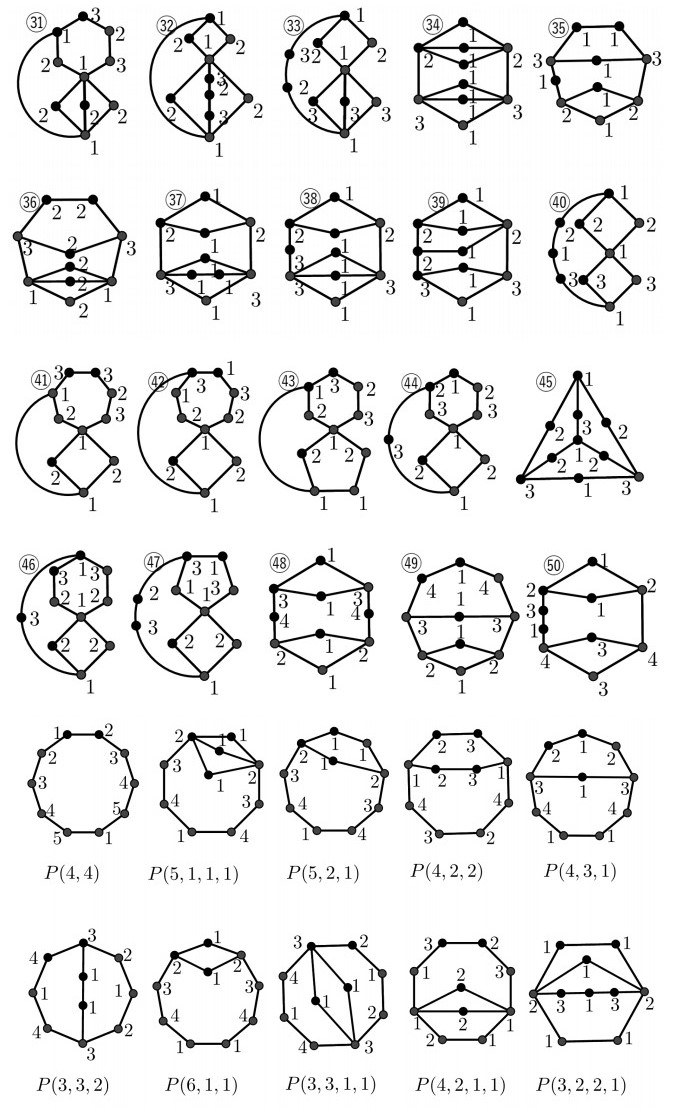
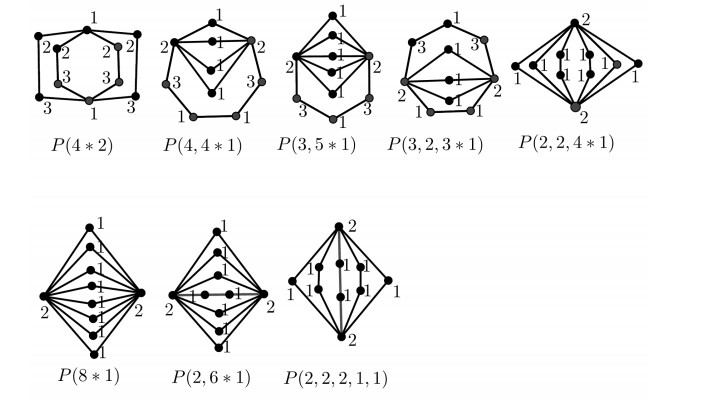
^*$P_{n_1}, \ldots, P_{n_k}$ are $k$ disjoint paths with $|P_{n_i}| = n_i$. The first and the last vertices of $p_{i}$ are denoted by $f(P_{n_i})$ and $l(P_{n_i})$. $P(n_1, \ldots, n_k)$ is the graph with the vertex set $\{\cup_{i\in[k]} V(P_{n_i})\} \cup \{u, \ v\}$ and edge set $\cup_{i\in[k]} \big[E(P_{n_i}) \cup \{f(P_{n_i})u, l(P_{n_i})v\}\big]$, where $u, v\notin \cup_{i\in[k]}$ $V(P_{n_i})$. If $n_{i+1} = \cdots = n_{i+j}$, then $P(n_1, \ldots, n_k) = P(n_1, \ldots, n_i, j*n_{i+1}, n_{i+j+1}, \ldots, n_k)$.

Finally, when $n-5\leq mvd(G)\leq n$ and all blocks of the graph $G$ are minimally 2-connected triangle-free graphs, we characterize $G$. We need the following lemma:

Lemma 3.1. $G$ is a connected graph of order $n$ with $r$ blocks, where $t$ blocks are trivial. If all blocks are minimally $2$-connected triangle-free graphs, then $mvd(G)\leq \left\lfloor {\frac{n+2t-r+1}{2}}\right\rfloor$.

Proof. Let $\{ B_1, B_2, \ldots, B_r \}$ be the block decomposition of $G$. We claim that

The proof proceeds by induction on $r$. The result holds for $r = 1$. If $r > 1$, then $G$ is not $2$-connected, we know that there is a block, say $B_r$, containing only one cut vertex, say $v$. Let $G' = G-(V(B_r)-\{v\})$. Then, $G'$ is a connected graph with blocks $B_1, B_2, \ldots, B_{r-1}$. By the induction hypothesis, $|G'| = (\sum_{i = 1}^{r-1} |B_i|)-(r-1)+1$. Since we deleted $|B_r|-1$ vertices from $G$ to obtain $G'$, the number of vertices in $G$ is as desired.

Without loss of generality, let the trivial blocks be $B_1, \ldots, B_t$, and let the nontrivial blocks be $B_{t+1}, \ldots, B_{r}$. By Theorems 1.2 and 1.3, we have

Combined with Eq (3.1), we have

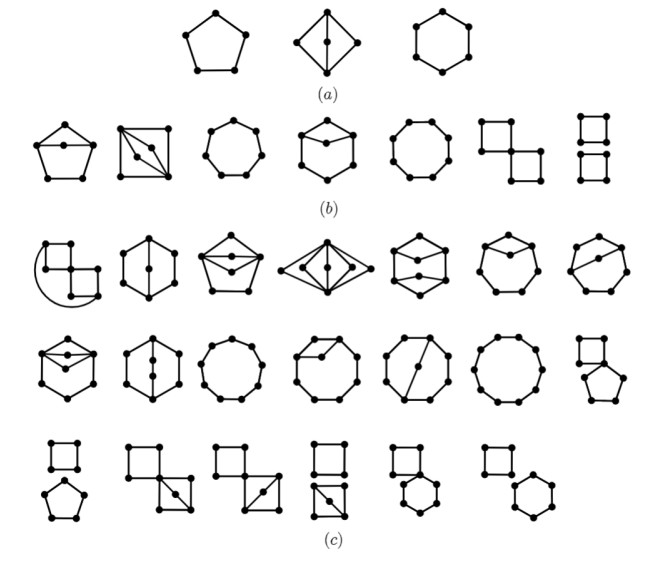
The nontrivial block-induced subgraph of $G$ is the subgraph induced by all nontrivial blocks of $G$. Let $\mathcal{A}$ be a set of connected graphs whose nontrivial block-induced graph is exactly one of the graphs shown in Figure 3$(a)$. Similarly, we define $\mathcal{B}$ and $\mathcal{C}$ according to Figure 3$(b)$ and 3$(c)$, respectively.

Theorem 3.4. For a connected graph $G$, if blocks in $G$ are all minimally $2$-connected triangle-free graphs, then

Proof. By Table 1 and Theorems 1.3 and 2.1, it is easy to verify the sufficiency. Now, we prove the necessity. If $mvd(G) = n$, then $B_i$ is complete by Theorem 3.3. Since $G$ is triangle-free, $G$ is a tree.

Now, suppose that $mvd(G)\geq n-5$ and $G$ has $r$ blocks, of which $t$ are trivial. By Lemma 5, $n-5\leq mvd(G)\leq \left\lfloor {\frac{n+2t-r+1}{2}}\right\rfloor$. There are two cases below.

Case 1. $n-r$ is even.

So, $2t\geq n+r-10$. Since $t\leq r$, $r\geq n-10$, then $r$ may be $n-2, \ n-4, \ n-6, \ n-8$ or $n-10$. We discuss them below.

(Ⅰ) For $r = n-2$, combined with $2t\geq n+r-10$ and the fact that $r = t$ if and only if $G$ is a tree (i.e., $r = n-1$), we have that $n-6\leq t\leq n-3$. Since $G$ is triangle-free, when $t = n-3, n-4, n-5$ or $n-6$, respectively, we have $\sum_{i = 1}^{r} |B_{i}|\geq 4+2(n-3), 8+2(n-4), 12+2(n-5)$ or $16+2(n-6)$, contradicting Eq (3.1). Note that, in other cases, we first use this method to determine the number of nontrivial blocks in $G$.

(Ⅱ) For $r = n-4$, similarly, we have that $n-7\leq t\leq n-5$, and there is only one nontrivial block in $G$. By Eq (3.1), this nontrivial block is of order $5$, i.e., $P(2, 1)$ or $P(1, 1, 1)$ (see Appendix A. 5 VERTEX). According to Table 1 and Theorems 1.3 and 2.1, $mvd(G) = n-3$ in both cases.

(Ⅲ) For $r = n-6$, similarly, we have that $n-8\leq t\leq n-7$. Since $G$ is triangle-free, combined with Eq (3.1), we obtain the following.

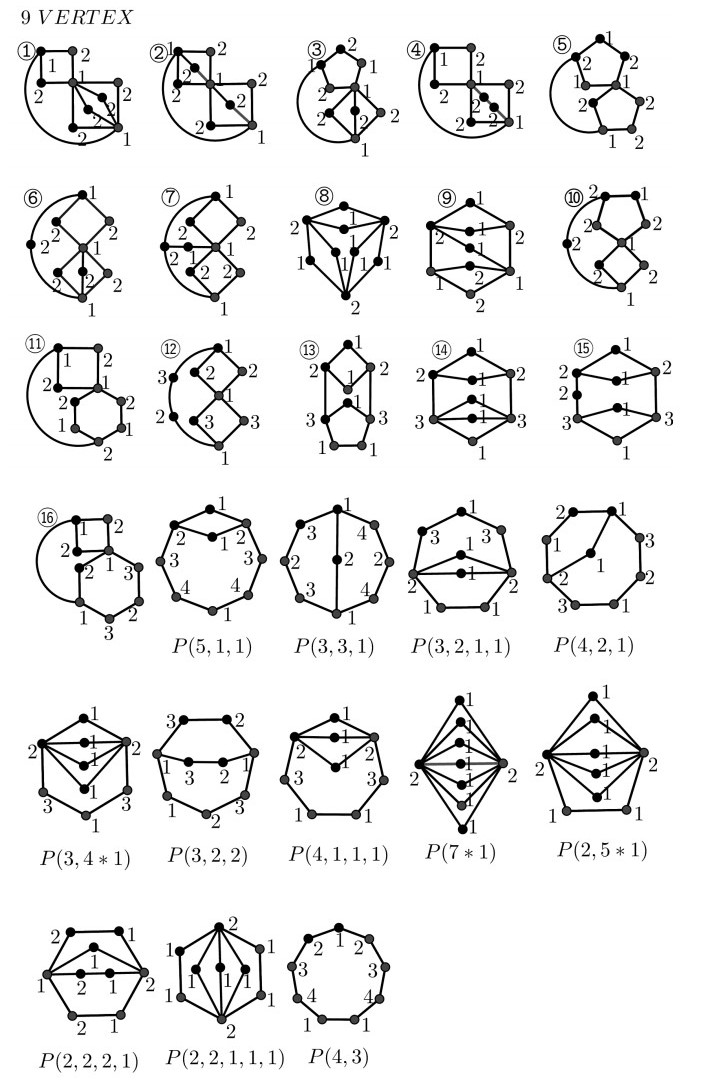
If $t = n-7$, then the order of this nontrivial block is $7$, i.e., one of the graphs in Appendix A. $7$ VERTEX.

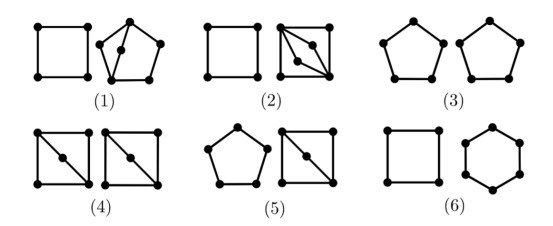
If $t = n-8$, then there are two nontrivial blocks $B_{i}$ and $B_{j}$ with $|B_{i}|+|B_{j}| = 9$, and the nontrivial block-induced subgraph of $G$ is one of the graphs in Figure 4. Note that $B_i$ and $B_j$ may or may not be adjacent, and the figure only shows the case when $B_i$ and $B_j$ are not adjacent.

According to Table 1 and Theorems 1.3 and 2.1, $mvd(G) = n-4$ when the nontrivial block-induced subgraph of $G$ is $P(3, 2)$ or $P(3, 1, 1)$, and $mvd(G) = n-5$ for the remaining cases.

(Ⅳ) For $r = n-8$, similarly, we have that $t = n-9$. By Eq (3.1), this nontrivial block is of order $9$, i.e., one of the graphs in Appendix A. $9$ VERTEX. According to Table 1 and Theorems 1.3 and 2.1, $mvd(G) = n-5$ when the nontrivial block-induced subgraph of $G$ is one among $\{P(4, 3), P(5, 1, 1), P(3, 3, 1)\}$, and $mvd(G) < n-5$ for the remaining cases.

(Ⅴ) For $r = n-10$, similarly, we have that $n-10\leq t\leq n-11$, which is a contradiction.

Case 2. $n-r$ is odd.

So, $2t\geq n+r-11$. Since $t\leq r$, $r\geq n-11$, then $r$ may be $n-1, \ n-3, \ n-5, \ n-7, \ n-9$ or $n-11$. We discuss them below.

(Ⅰ) For $r = n-1$, $G$ is a tree and $mvd(G) = n$.

(Ⅱ) For $r = n-3$, combined with $2t\geq n+r-11$ and the fact that $r = t$ if and only if $G$ is a tree (i.e., $r = n-1$), we have that $n-7\leq t\leq n-4$. Since $G$ is triangle-free, when $t = n-5, n-6$ or $n-7$, respectively, we have that $\sum_{i = 1}^{r} |B_{i}|\geq 8+2(n-5), 12+2(n-6)$ or $16+2(n-7)$, contradicting Eq (3.1). Then, $G$ has exactly one nontrivial block. Note that, in other cases, we first use this method to determine the number of nontrivial blocks in $G$. By Eq (3.1), this nontrivial block is of order $4$, i.e., $C_{4}$. According to Table 1 and Theorems 1.3 and 2.1, $mvd(G) = n-2$.

(Ⅲ) For $r = n-5$, similarly, we have that $n-8\leq t\leq n-6$, and there are at most two nontrivial blocks in $G$. Since $G$ is triangle-free, combined with Eq (3.1), we obtain the following.

If $t = n-6$, then the order of this nontrivial block is $6$, i.e., one of the graphs in Appendix A. 6 VERTEX.

If $t = n-7$, then there are two nontrivial blocks $B_{i}$ and $B_{j}$ with $|B_{i}|+|B_{j}| = 8$, i.e., both $B_{i}$ and $B_{j}$ are $C_{4}$.

According to Table 1 and Theorems 1.3 and 2.1, $mvd(G) = n-3$ when the nontrivial block-induced subgraph of $G$ is $P(2, 2)$, and $mvd(G) = n-4$ for the remaining cases.

(Ⅳ) For $r = n-7$, similarly, we have that $n-9\leq t\leq n-8$. Since $G$ is triangle-free, combined with Eq (3.1), we obtain the following.

If $t = n-8$, then the order of this nontrivial block is $8$, i.e., one of the graphs in Appendix A. 8 VERTEX.

If $t = n-9$, then there are two nontrivial blocks $B_{i}$ and $B_{j}$ with $|B_{i}|+|B_{j}| = 10$, and the nontrivial block-induced subgraph of $G$ is one of the graphs in Figure 5. Note that $B_i$ and $B_j$ may or may not be adjacent, and the figure only shows the case when $B_i$ and $B_j$ are not adjacent.

According to Table 1 and Theorems 1.3 and 2.1, $mvd(G) = n-4$ when the nontrivial block-induced subgraph of $G$ is $P(3, 3)$, $mvd(G) = n-5$ when it is one among $\{P(4, 1, 1), P(3, 2, 1), P(3, 1, 1, 1),$ $P(2, 2, 2)$, Appendix A. 8VERTEX④ , Figure 5(6)$\}$ and $mvd(G) = n-6$ for the remaining cases.

(Ⅴ) For $r = n-9$, similarly, we have that $t = n-10$. By Eq (3.1), this nontrivial block is of order $10$, i.e., one of the graphs in Appendix A. $10$ VERTEX. According to Table 1 and Theorems 1.3 and 2.1, $mvd(G) = n-5$ when the nontrivial block-induced subgraph of $G$ is $P(4, 4)$, and $mvd(G) < n-5$ for the remaining cases.

(Ⅵ) For $r = n-11$, similarly, we have that $n-11\leq t\leq n-12$, which is a contradiction.

For easy reading, when $mvd(G) = n-3, n-4$ or $n-5$, the possible configurations of the nontrivial block-induced subgraph of $G$ are as summarized in Figure 3. The theorem is proved.

4.   Erdős-Gallai-type problems

In this section, we first study the following extremal problem and obtain Theorem 1.5. To solve this problem, we show some lemmas.

For integers $k$ and $n$ with $1\leq k\leq n$, what is the maximum possible size of a connected graph $G$ of order $n$ with $mvd(G) = k$?

Lemma 4.1. If $G$ is obtained by removing any edge $e$ from $K_{n}$, where $n\geq3$, then $mvd(G) = 3$; if $G$ is obtained by removing any two edges $e_1$ and $e_2$ from $K_{n}$, where $n\geq4$, then $mvd(G)\leq 4$.

Proof. Let $v$ be one of the endpoints of $e$; then, $G$ is obtained by adding $n-2$ edges from $v$ to $K_{n-1}$. From (1), $mvd(G) = 3$. If $e_1$ and $e_2$ are adjacent edges incident with a vertex $v$ of $G$, then $G$ is obtained by adding $n-3$ edges from $v$ to $K_{n-1}$. So, $mvd(G) = 4$. If $e_1$ and $e_2$ are nonadjacent, then $G = K_{2, 2}$ when $n = 4$, or $G = K_{2, 2, 1, \ldots, 1}$ when $n > 4$. According to Theorem 3.1(2), $mvd(G) = 2$ or $mvd(G) = 1$.

Lemma 4.2. Let $G$ be a connected graph of order $n\geq 2$. Then, the maximum size of $G$ with $mvd(G) = 2$ is

Proof. Since $mvd(K_n) = n$, the maximum size of $G$ with $mvd(G) = n = 2$ is $1$. There is no graph $G$ with $n = 3$ and $mvd(G) = 2$. According to Lemma 6, if $n\geq 4$ and $mvd(G) = 2$, then $|E(G)|\leq |E(K_{n})|-2$ and the equation holds only when $n = 4$. Now, let $n\geq 5$.

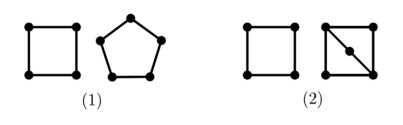
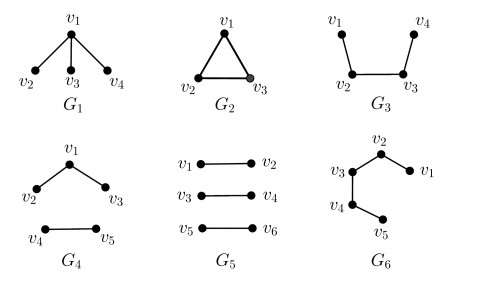
Claim 1: If $G$ is a graph of order $n$ that is obtained by removing any three edges from $K_{n}$, where $n\geq5$, then $mvd(G) = 2$ if and only if $n = 5$, and the three removed edges are shown as $G_4$ in Figure 6.

There are five cases to consider for the three removed edges (see $G_i, i\in [5]$ in Figure 6), and if $n = 5$, $G_5$ is excluded. Note that, for the case $G_i$, $i\in [4]$, $G$ is connected since $n\geq5$, and for the case $G_5$, $G$ is connected only when $n > 5$. For the case $G_1$, $G$ is obtained by adding $n-4$ edges from $v_1$ to $K_{n-1}$. It follows by Tight example 1 that $mvd(G) = 5$. For the case of $G_2$, define a vertex-coloring $\tau: V(G)\rightarrow [4]$ such that $\tau(N(v_1)) = \tau(N(v_2)) = \tau(N(v_3)) = 1$, $\tau(v_1) = 2$, $\tau(v_2) = 3$ and $\tau(v_3) = 4$. For any two nonadjacent vertices $x$ and $y$, $N(v_1)$ is a monochromatic $x$-$y$ vertex cut since $N(v_1) = N(v_2) = N(v_3)$. Then, $mvd(G)\geq4$. For the case of $G_3$, define a vertex-coloring $\tau: V(G)\rightarrow [3]$ such that $\tau(N(v_2)) = \tau(N(v_3)) = 1$, $\tau(v_2) = 2$ and $\tau(v_3) = 3$. For any two nonadjacent vertices $x$ and $y$, $N(v_2)$ or $N(v_3)$ is a monochromatic $x$-$y$ vertex cut; then, $mvd(G)\geq3$.

For the case of $G_4$, we claim that, if $n = 5$, then $mvd(G) = 2$; if $n\geq6$, then $mvd(G) = 1$. If $n = 5$, define a vertex-coloring $\tau: V(G)\rightarrow [2]$ such that $\tau(v_1) = \tau(v_2) = \tau(v_3) = 1$ and $\tau(v_4) = \tau(v_5) = 2$. For any two nonadjacent vertices $x$ and $y$, if $\{x, y\} = \{v_4, v_5\}$, then $\{v_1, v_2, v_3\}$ is a monochromatic $x$-$y$ vertex cut; otherwise, $\{v_4, v_5\}$ is a monochromatic $x$-$y$ vertex cut. Then, $mvd(G)\geq2$. Suppose that $mvd(G) > 2$ and $\tau'$ is an $mvd$-coloring of $G$. For nonadjacent vertices $v_4$ and $v_5$, it must be that $\tau'(v_1) = \tau'(v_2) = \tau'(v_3)$ since $N(v_4) = N(v_5) = \{v_1, v_2, v_3\}$. Thus, $\tau'(v_4)\neq \tau'(v_5)$, and both are different from $\tau'(v_1)$, which contradicts the existence of a monochromatic $v_1$-$v_2$ vertex cut since $N(v_1)\cap N(v_2) = \{v_4, v_5\}$. If $n\geq 6$ and $\tau'$ is an $mvd$-coloring of $G$, then $\tau'(V(G)-\{v_4, v_5\})$ is monochromatic since $N(v_4) = N(v_5) = V(G)-\{v_4, v_5\}$. For nonadjacent vertices $v_1$ and $v_2$, since $N(v_1)\cap N(v_2) = N(v_1) = V(G)-\{v_1, v_2, v_3\}$ and $(V(G)-\{v_4, v_5\}) \cap(V(G)-\{v_1, v_2, v_3\}) \neq \varnothing$ for $n\geq 6$, $\tau'(V(G)-\{v_1, v_2, v_3\}) = \tau'(V(G)-\{v_4, v_5\})$. Therefore, $mvd(G) = 1$. At last, $G = K_{2, 2, 2, 1, \ldots, 1}$ for the case of $G_5$; then, it follows by Theorem 3.1(2) that $mvd(G) = 1$.

Therefore, the maximum size of $G$ with $n = 5$ and $mvd(G) = 2$ is $7$. Furthermore, if $n\geq 6$ and $mvd(G) = 2$, then $|E(G)|\leq |E(K_{n})|-4$. Thus, we only need to prove the following claim to complete the proof of Lemma 4.2.

Claim 2: $G$ is a graph of order $n$, $n\geq 6$, and if $G$ is obtained by removing any four edges from $K_{n}$, where the four removed edges are shown as $G_6$ in Figure 6, then $mvd(G) = 2$.

$G$ is connected since $n\geq 6$. Define a vertex-coloring $\tau: V(G)\rightarrow [2]$ such that $\tau(V(G)-\{v_3\}) = 1$ and $\tau (v_3) = 2$. For any two nonadjacent vertices $x$ and $y$, $V(G)-\{x, y, v_3\}$ is a monochromatic $x$-$y$ vertex cut. Then, $mvd(G)\geq 2$. Let $\tau'$ be an $mvd$-coloring of $G$. For nonadjacent vertices $v_4$ and $v_5$, $\tau'(V(G)-\{v_3, v_4, v_5\})$ is monochromatic since $N(v_4)\cap N(v_5) = N(v_4) = V(G)-\{v_3, v_4, v_5\}$. For nonadjacent vertices $v_1$ and $v_2$, since $N(v_1)\cap N(v_2) = N(v_2) = V(G)-\{v_1, v_2, v_3\}$ and $(V(G)-\{v_3, v_4, v_5\}) \cap (V(G)-\{v_1, v_2, v_3\}) \neq \varnothing$ for $n\geq 6$, $\tau'(V(G)-\{v_1, v_2, v_3\}) = 1$. Uncolored vertex $v_3$ adds a new color at most. Therefore, $mvd(G) = 2$.

Proof of Theorem 1.5. If $mvd(G) = n$, then the size is maximum when $G = K_n$. By Lemma 4.1, if $G$ is a graph of order $n$ that is obtained by removing any edge from $K_{n}$, where $n\geq3$, then $mvd(G) = 3$. So, if $mvd(G) = 3$ and $n\geq 4$, then the maximum size of $G$ of order $n$ is $\frac{n(n-1)}{2}-1$. There is no graph $G$ with $1 < n\leq 4$ and $mvd(G) = 1$. By Lemma 4.1, if $mvd(G) = 1$ and $n\geq5$, then the maximum size of $G$ is $\frac{n(n-1)}{2}-2$. If $mvd(G) = 2$, we refer to Lemma 4.2. Now, we consider the case that $4\leq k\leq n-1$. Let $t$ denote the number of vertices with degree $n-1$. We first claim that, if the size of a connected graph $G$ of order $n$ is at least $\frac{n(n-1)}{2}-k+3$, then $mvd(G)\leq k-1$.

Case 1. $n-k+2\leq t\leq n-1$.

For any two nonadjacent vertices $x$ and $y$ in $G$, since $x$ and $y$ are adjacent to each vertex of degree $n-1$ in $G$, $|N(x)\cap N(y)|\geq n-k+2$. Therefore, $mvd(G)\leq k-1$ by Theorem 1.1.

Case 2. $0\leq t\leq n-k+2$.

Claim 1: There is at least one vertex with degree $n-2$.

Otherwise, with the exception of $t$ vertices with degree $n-1$, the maximum degree of the remaining vertices in $G$ is $n-3$ at most. Then, the size is

which is a contradiction. Thus, $G$ has at least one vertex with degree $n-2$.

Claim 2: $\delta(G)\geq n-k+2$.

Otherwise, there is a vertex with degree at most $n-k+1$; then, the size is

which is a contradiction. Thus, $\delta(G)\geq n-k+2$.

Let $x$ be a vertex of $G$ with degree $n-2$. There is a vertex $y$ in $G$ which is nonadjacent to $x$. By Claim 2, $d(y)\geq n-k+2$; then, $|N(x)\cap N(y)|\geq n-k+2$. In other words, there are at least $n-k+2$ internal disjoint $x, y$-paths. Therefore, $mvd(G)\leq k-1$ by Theorem 1.1.

Above all, if $mvd(G)\geq k$, then the size of $G$ of order $n$ is at most $\frac{n(n-1)}{2}-k+2$. It remains to show that, for any integers $k$ and $n$, where $4\leq k\leq n-1$, there must be a connected graph $G$ of order $n$ and size $\frac{n(n-1)}{2}-k+2$ such that $mvd(G) = k$. Suppose that $G$ is a graph of order $n$ and size $\frac{n(n-1)}{2}-k+2$ that is obtained by adding $n-k+1$ edges to $K_{n-1}$ from a vertex $v$ outside $K_{n-1}$. By Tight example 1, $mvd(G) = k$.

Proof of Theorem 1.4. It is worth mentioning that the parameter $f_v(n, k)$ is equivalent to another parameter. Let $s_v(n, k) = max\{|E(G)|:|G| = n, mvd(G)\leq k\}$. It is easy to see that $f_v(n, k) = s_v(n, k-1)+1$. Let $n\geq5$. There are three cases, as follows.

Case 1. $k = 1$.

Since $mvd(G)\geq1$ holds for any graph $G$ and the tree has minimum size, $f_v(n, 1) = n-1$.

Case 2. $2\leq k\leq3$.

According to Theorem 1.5, $|E(G)|_{max} = \frac{n(n-1)}{2}-2$ if $mvd(G) = 1$, $|E(G)|_{max} = \frac{n(n-1)}{2}-3$ if $mvd(G) = 2$ and $n = 5$ and $|E(G)|_{max} = \frac{n(n-1)}{2}-4$ if $mvd(G) = 2$ and $n\geq6$. So, we have that $s_v(n, 1) = s_v(n, 2) = \frac{n(n-1)}{2}-2$. Since $f_v(n, k) = s_v(n, k-1)+1$, $f_v(n, 2) = f_v(n, 3) = \frac{n(n-1)}{2}-1$.

Case 3. $4\leq k\leq n$.

According to Theorem 1.5, $|E(G)|_{max} = \frac{n(n-1)}{2}-1$ if $mvd(G) = 3$, and $|E(G)|_{max} < \frac{n(n-1)}{2}-1$ if $3 < mvd(G)\leq n-1$. So, we have that $s_v(n, 3) = s_v(n, 4) = \cdots = s_v(n, n-1) = \frac{n(n-1)}{2}-1$. Since $f_v(n, k) = s_v(n, k-1)+1$, $f_v(n, 4) = f_v(n, 5) = \cdots = f_v(n, n) = \frac{n(n-1)}{2}$.

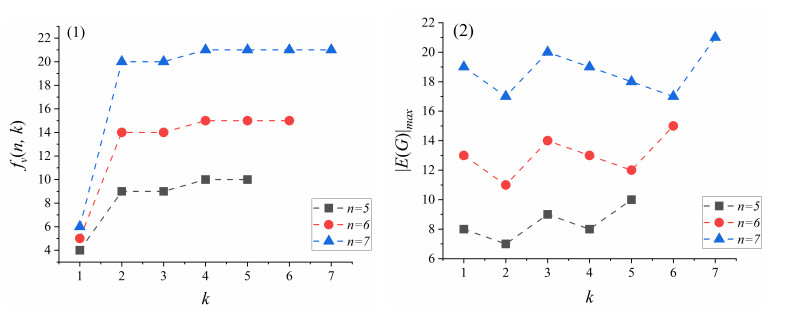
Remark 1. For positive integers $n$ and $k$ with $1\leq k\leq n\leq 4$, the results are shown in Table 2. Moreover, to further understand Theorems 1.4 and 1.5, when $n = 5, 6, 7$, the evolution between $k$ and $f_v(n, k)$ are shown in Figure 7(1), and the evolution between $k$ and $|E(G)|_{max}$ are shown in Figure 7(2).

Acknowledgments

This work was supported by the National Natural Science Foundation of China (NSFC11801410 and NSFC11971346) and the China Scholarship Council.

Conflict of interest

The authors declare no conflict of interest.

A.   Appendix

$mvd$-colorings of minimal blocks with small order.