Parameter estimation for discretely observed Cox–Ingersoll–Ross model driven by fractional Lévy processes

1.   Introduction

There are many life-threatening diseases, out of which Malaria is one of them that is produced through the parasite known as Plasmodium that transmits to humans with the infected anopheles mosquito bite ^[1,2,3]. People with malaria are infected by the Protozoan parasite, which grows within the cells of red blood and spreads the illness. There are four Plasmodia species that can become the reason of infection, known as oval, falciparum, malaria, and vivax, while the two other most widespread Plasmodium species are falciparum and vivax ^[4]. Malaria affects lots of people each year, mainly in South Asia, Africa, and South America. It becomes the major reason of death and illness in various developing regions, specifically young children, and pregnant women. The main symptoms of malaria are fever, muscle pain, and headache. Malaria can progress promptly, possibly severe anemia, lung problems, and even cause death. There are various effective tactics that proposed the World Health Organization (WHO) to treat and prevent this dangerous disease. Some of them are indoor spraying, pesticide-treated bed nets, and some antimalarial medications. The vector control systems can be applied to lessen the poisoned mosquito population. In general, malaria is a substantial global health task, which needs a comprehensive approach for its cure by using the strategies of vector control and early identification for its treatment.

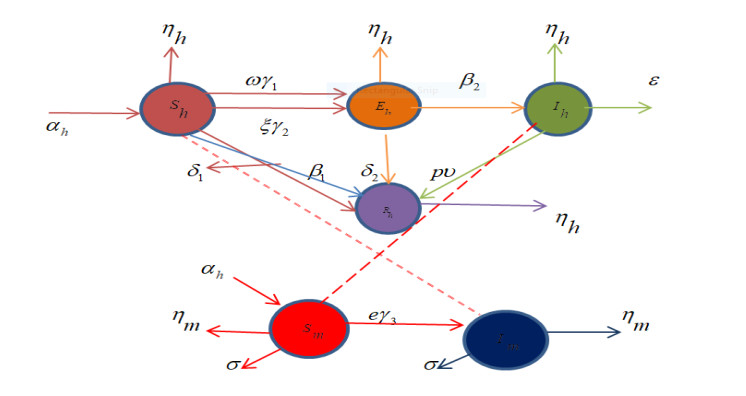
Malaria is a dynamic and complicated disease, which is considered difficult to present its model mathematically. The malaria parasite's life cycle is complex due to numerous phases of development both in mosquito vector and human host. These points are prompted by numerous features, e.g., mosquito actions, host immunity, and environmental environments that is used to make difficult the disease dynamics to predict and understand. The intricacy of the virus's spread dynamics is one of the main problems with malaria modelling. Malaria spread is influenced by numerous interrelated influences, e.g., the mosquito vector density, the host immunity degree, and the accessibility of efficient mediations. The relations between these aspects indicate the nonlinearity and hard to capture using the mathematical systems ^[5]. However, the mathematical malaria disease model based on the pesticides and medication (MDMPM) is presented, which is categorized in four human (susceptible, exposed, infected, recovered) and two vector (susceptible, infected) classes. The pathogen infects the population of host then the individuals are categorized into groups based on the parasites number and virus types. Kermack-McKendrick ^[6] proposed the mathematical SEIRSI model based on the population of human/vector groups. The nonlinear dynamics of the SEIRSI model is presented as ^[7]:

The compartmental illustration of the SEIRSI model based on the MDMPM is shown in Figure 1, while the description of each parameter is given in Table 1.

Figure 1.  Graphical representations of the MDMPM.

DownLoad: Full-Size Img PowerPoint

Table 1.  Parameter details of the MDMPM.

Parameters	Details
${\beta _1}$	Susceptible form of recovered individuals
${\alpha _m}$	Newborn mosquitoes transfer rate into ${S_m}$
${\alpha _h}$	Newborns ratio to enter in ${S_h}$
${\gamma _1}$	Transfer ratio of illness from one affected to susceptible people
$\psi$	Transfusions rate of average blood with stable time in ${I_h}$ and ${S_h}$
${\beta _2}$	Exposed to infected infection rate in people
$\xi$	Infected mosquito susceptible bites using fixed time
${\gamma _3}$	Rate of Mosquitos infection
${\gamma _2}$	Disease transfer through infected (mosquito) to susceptible (individual)
${\eta _h}$	People natural rate of death
${\delta _2}$	Exposed recovered population
${\delta _1}$	Susceptible recovered population
$p$	Rate of humans heal
$\varepsilon$	Infected human death due to disease
${\eta _m}$	Mosquitos' natural death
$\upsilon$	Anti-malarial prescriptions
$e$	Bites ${S_m}$ using the infected humans
$\sigma$	Expires sections using spraying for ${S_m}$ and ${I_m}$
$x$	Time

---

 | Show Table

DownLoad: CSV

There are various deterministic and conventional numerical schemes that have been presented to solve the biological models, including the wavelet Bernstein scheme that has been presented to solve the epidemic SIR fractional kind of infectious disease model ^[8], Laplace method is applied for the fractional epidemic system of born vector disease ^[9], q-homotopy transform technique is proposed to solve the fractional Schistosomiasis disease model ^[10,11], a theoretic investigation is presented based on the impacts of vector-virus transmission mechanism ^[12], a collocation technique with shifted Chebyshev polynomials is applied to solve the fractional order diseased model of Rubella ailment ^[13], an analytical computational approach is provided for the inflammatory atherosclerosis disease system ^[14], the differential stomach and coronavirus models have been discussed numerically by applying the Adam method ^[15,16] and the design of a numerical method is presented for the maturing communication in population and epidemic models ^[17]. Some more deterministic procedures that have been applied to solve different dynamical models are presented in ^{[18,19,20,21,22]}.

All mentioned schemes have their individual strength, and demerits, however the stochastic solvers have never been tested before for the nonlinear dynamics of the MDMPM. The current study is related to the numerical solutions of the MDMPM through the stochastic procedures using the scale conjugate gradient neural networks (SCJGNNs). In recent years, the stochastic computing paradigms have been proposed in various applications, e.g., eye surgery differential systems ^[23,24], food chain systems ^[25,26], smoking dynamical systems ^[27], models arising in biological applications, ^[28,29], thermal explosion singular systems ^[30,31], and many more ^{[32,33,34,35,36,37,38,39,40,41,42,43]}. Based on these noteworthy applications of neuro-computing paradigm, the authors are motivated to present the numerical solutions of the malaria disease model of pesticides and medication (MDMPM) with stochastic framework of scale conjugate gradient neural networks (SCJGNNs). The purpose of this work is to provide a stochastic framework based on the SCJGNNs for solving the mathematical model representing MDMPM dynamics.

The contributions, insights and innovative aspects of the current scheme is portrayed in terms of salient features as follows:

• A novel design of the stochastic framework via SCJGNNs is introduced/presented to get the numerical results/outcomes of the nonlinear dynamics of governing mathematical model of MDMPM.

• The capability and knacks of Runge-Kutta solver is exploited/developed to formulate the target datasets for different scenario of MDMPM system that are used for the testing, and training procedure of the networks via SCJGNNs.

• The exactness of the stochastic SCJGNNs is attained/verified/validated through the overlapping of the results with standard counterparts having very small magnitude of absolute error (AE).

• The reliable matching of the numerical results, a strong arrangement using the benchmark outputs along with consistent statistical performance indices further prove the importance/significance/role of the SCJGNNs to solve the variant of MDMPM models.

The remaining paper is presented as: Proposed SCJGNNs design is shown in Section 2, Sect 3 presents the numerical results, and the conclusions are discussed in the final section.

2.   Proposed SCJGNNs scheme

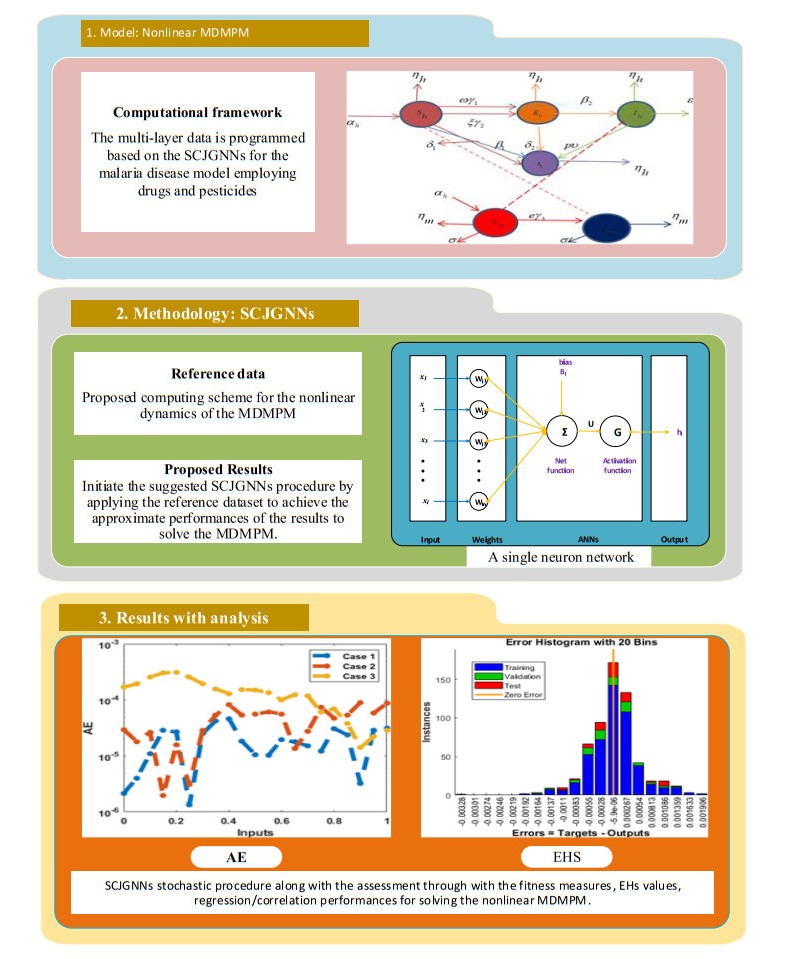
The current section is used to design the computing SCJGNNs structure to solve the MDMPM in two steps, including the detail of designed SCJGNNs performances along with its execution. The designed SCJGNNs is presented in Figure 2. In the 1^st phase of Figure 2, the nonlinear mathematical system is illustrated, the stochastic methodology using the SCJGNNs is provided in the 2nd phase of Figure 2, while some results are presented in the last phase of Figure 2. The performances using the multi-layers network based on the structure of single neuron is illustrated in Figure 3.

Figure 2.  Illustration of proposed SCJGNNs performances to solve the MDMPM.

DownLoad: Full-Size Img PowerPoint

Figure 3.  Single layer neural network.

DownLoad: Full-Size Img PowerPoint

The computing SCJGNNs approach for solving the MDMPM is executed using the command 'nftool' in software 'MATLAB', n-folded cross authentication, layers (output/hidden/input) structure, epochs are taken maximum 1000, fifteen hidden neurons, transfer function log-sigmoid, stopping standards, SCJG algorithm, tolerances, and step size. The label statics and input/target training are achieved using the basic outputs by taking the statics of validation (12%), testing (10%), and training (78%) for the MDMPM.

The designed computing SCJGNNs for the solutions of the MDMPM is performed by using 15 neurons, which have been validated through the best values of underfitting and overfitting based on the authorization and training at epochs 100, 86 and 69. For small neurons, the premature convergence (under fitting) problem is faced, while similar precision by using higher intricacy (overfitting issue) is noticed by taking higher neurons. The trials have been taken for the validation (12%), testing (10%), and training (78%) to solve the MDMPM. By taking a smaller data training, like 40% to 60%, the MSE values for testing 30% to 40% increase and generally poor presentations have been observed. On the other hand, if the training statics is almost designated > 90% and 5% for both testing and certification, the procedure's correctness improves marginally by choosing the label static, which presents the bias and targets input, but stochastic procedure's strength is not severely established for unbiased statics exclusive based targets information. The proposed values are performed on the input [0, 1] by applying the stochastic SCJGNNs procedure for the numerical performances of the MDMPM. The neuron structure using the input, output and hidden layers is shown in Figure 4.

Figure 4.  Different layers structure for the MDMPM.

DownLoad: Full-Size Img PowerPoint

3.   Results and analysis

The numerical solution for three different cases of the MDMPM by applying the computing procedures based on the SCJGNNs is presented in this section.

Case 1: Consider the values $\psi = 0.038$, ${\alpha _h} = 0.027,$ ${\gamma _1} = 0.020,$ $\xi = 0.13$, ${\beta _1} = \frac{1}{{730}}$, ${\gamma _2} = 0.010$, ${\delta _1} = 0.001$, ${\eta _h} = 0.0004$, ${\delta _2} = 0.001$, $p = 0.611$, ${\beta _2} = 0.001$, $\varepsilon = 0.05$, $\upsilon = 0.01$, $e = 0.022$, ${\alpha _m} = 0.13$, ${\gamma _3} = 0.072$, ${S_h}(0) = 0.01,$ ${E_h}(0) = 0.02,$ ${I_h}(0) = 0.03,$ ${R_h}(0) = 0.04,$ ${S_m}(0) = 0.05,$ and ${I_m}(0) = 0.06$ in system (1), which is shown as:

Case 2: Consider the parameter values $\psi = 0.038$, ${\alpha _h} = 0.027,$ ${\gamma _1} = 0.020,$ $\xi = 0.13$, ${\beta _1} = \frac{1}{{730}}$, ${\gamma _2} = 0.010$, ${\delta _1} = 0.001$, ${\eta _h} = 0.0004$, ${\delta _2} = 0.001$, $p = 0.611$, ${\beta _2} = 0.001$, $\varepsilon = 0.05$, $\upsilon = 0.01$, $e = 0.022$, ${\alpha _m} = 0.13$, ${\gamma _3} = 0.072$, ${S_h}(0) = 0.02,$ ${E_h}(0) = 0.03,$ ${I_h}(0) = 0.04,$ ${R_h}(0) = 0.05,$ ${S_m}(0) = 0.06,$ and ${I_m}(0) = 0.07$ in system (1) that is given as:

Case 3: Consider $\psi = 0.038$, ${\alpha _h} = 0.027,$ ${\gamma _1} = 0.020,$ $\xi = 0.13$, ${\beta _1} = \frac{1}{{730}}$, ${\gamma _2} = 0.010$, ${\delta _1} = 0.001$, ${\eta _h} = 0.0004$, ${\delta _2} = 0.001$, $p = 0.611$, ${\beta _2} = 0.001$, $\varepsilon = 0.05$, $\upsilon = 0.01$, $e = 0.022$, ${\alpha _m} = 0.13$, ${\gamma _3} = 0.072$, ${S_h}(0) = 0.03,$ ${E_h}(0) = 0.04,$ ${I_h}(0) = 0.05,$ ${R_h}(0) = 0.06,$ ${S_m}(0) = 0.07,$ and ${I_m}(0) = 0.08$ in system (1), given as:

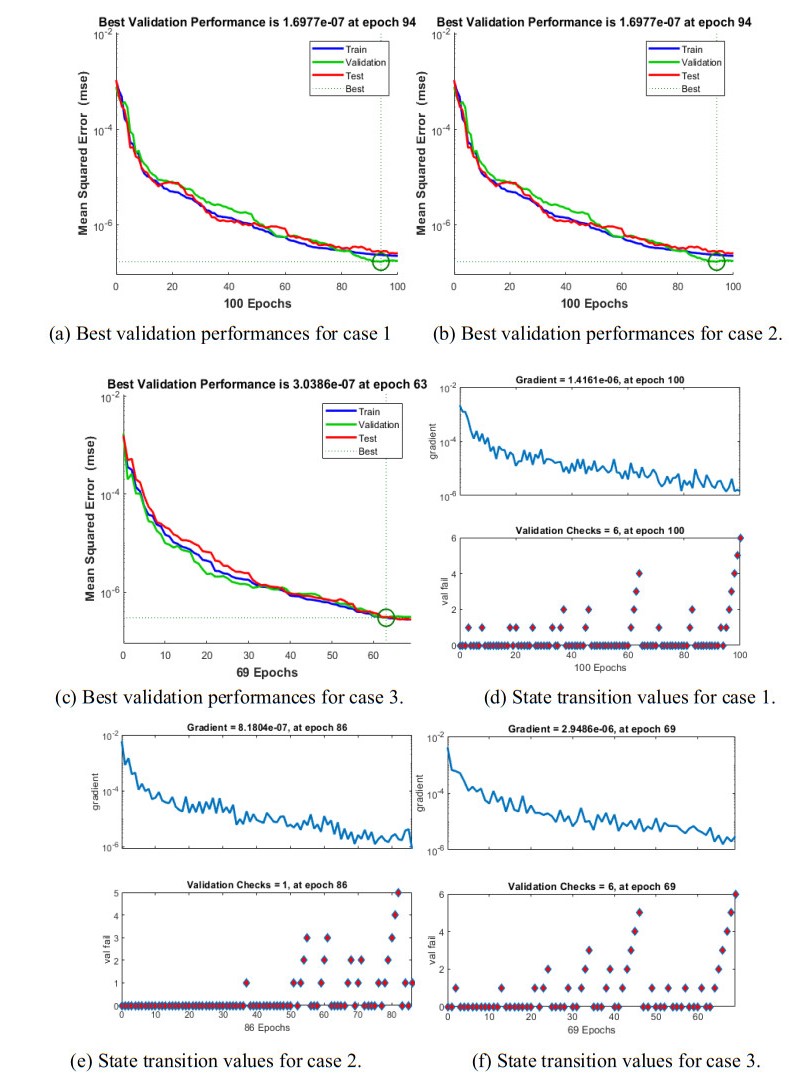
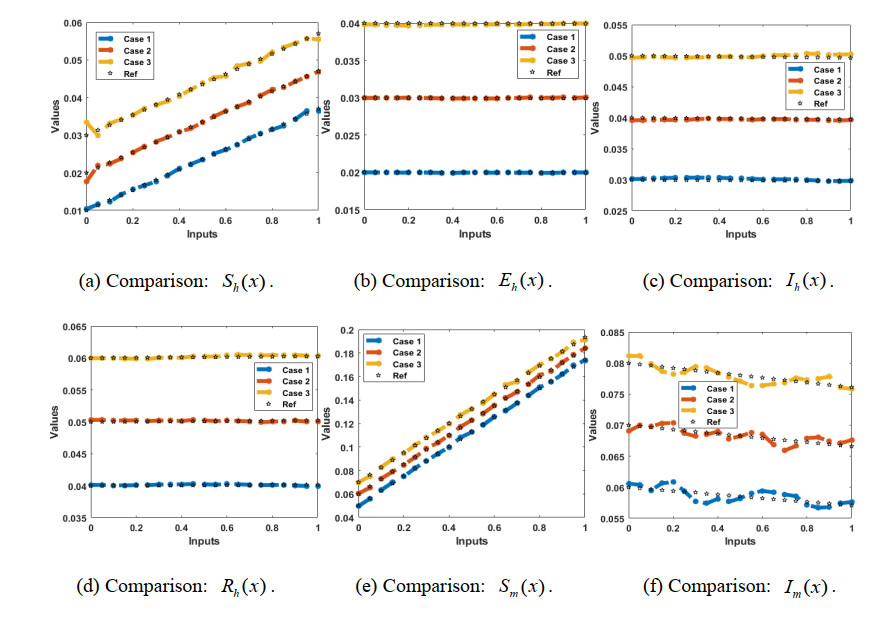
The plots of the estimated results based on the numerical SCJGNNs procedure for solving the MDMPM are shown in Figures 5 to 9. Figure 5 presents the best validation measures and state transitions for the nonlinear dynamics of the MDMPM through the stochastic computing SCJGNNs scheme. The values of the mean square error (MSE) and the state of transition values are depicted in Figure 5. The computed performances of MSE using the best curves plots, certification, and training are provided in Figure 5(a-c) and the SoT measures are portrayed in Figure 5(d-f). The best solution performances of the MDMPM are shown at epochs 100, 86 and 69, which are found around 1.69774 ×10⁻⁰⁷, 1.4324 × 10⁻⁰⁷ and 3.5876 × 10⁻⁰⁷. It indicates that convergence through the MSE is observed based on dataset of training, testing and certification. It is also observed that by updating the epochs, the authentications, training, and testing graphs lead to steady-state position up to 10^-07. The gradient curves by applying the process of SCJGNNs to solve the MDMPM are calculated as 1.4161×10^-06, 8.1804 × 10⁻⁰⁷ and 2.9486 × 10⁻⁰⁶. These graphic curves indicate the precision, exactness, and convergence by using the SCJGNNs procedure for the MDMPM. An error gradient presents the direction and magnitude that is calculated by the designed neural network for updating the weights in the proper amount/direction. In neural network fitting, the process of backpropagation is used to compute the loss function gradient. Mu is the used for the network's training for the momentum parameter, which includes the updated weight expressions to avoid the local minimum issues. It is observed that the network can stuck sometimes to the local minimum, which does not perform the convergence. In addition, Mu shows the control parameter based on that scheme that is used in the neural network's training.

Figure 5.  Best validation measures and state transitions for the nonlinear dynamics of the MDMPM by applying the stochastic computing SCJGNNs procedure.

DownLoad: Full-Size Img PowerPoint

Figure 6.  Function fitness values and error histogram performances to solve the MDMPM by applying the SCJGNNs.

DownLoad: Full-Size Img PowerPoint

Figure 7.  Values of regression for the MDMPM (1).

DownLoad: Full-Size Img PowerPoint

Figure 8.  Values of regression for the MDMPM (2).

DownLoad: Full-Size Img PowerPoint

Figure 9.  Values of regression for the MDMPM (3).

DownLoad: Full-Size Img PowerPoint

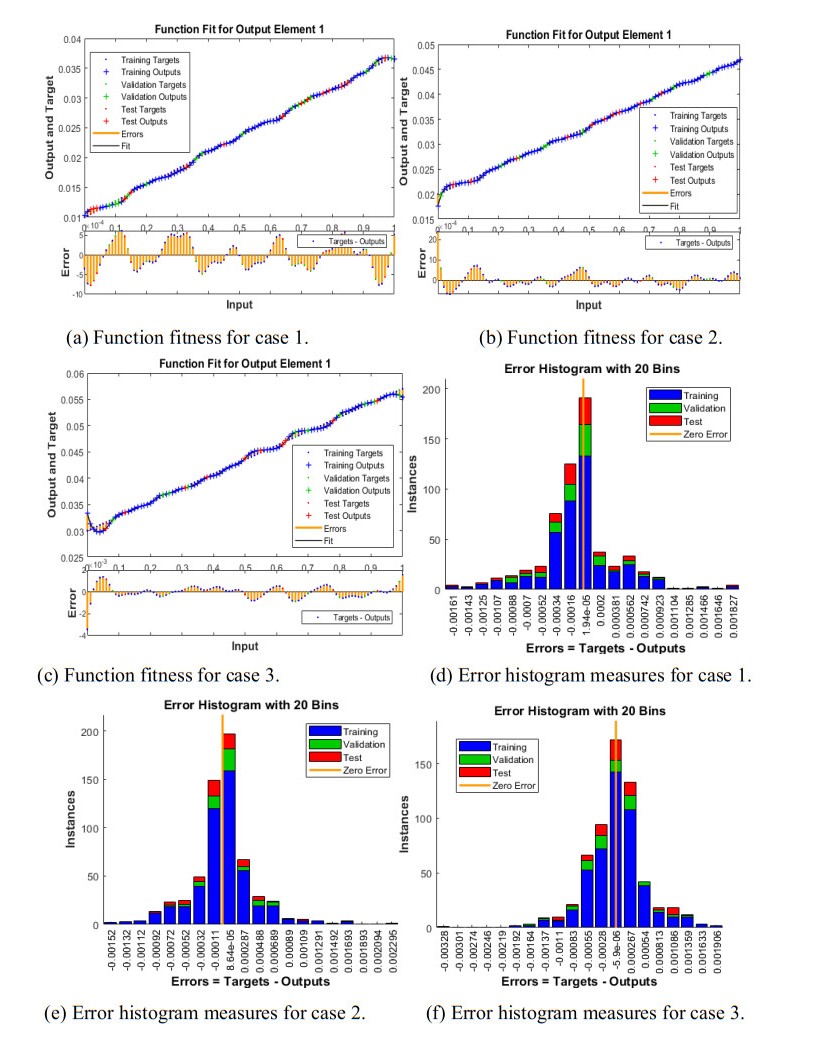
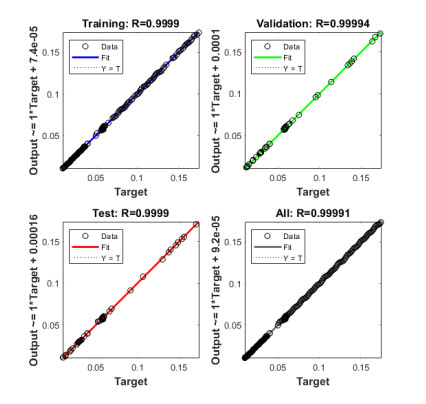
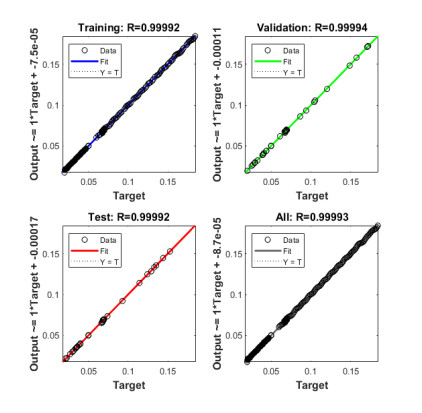
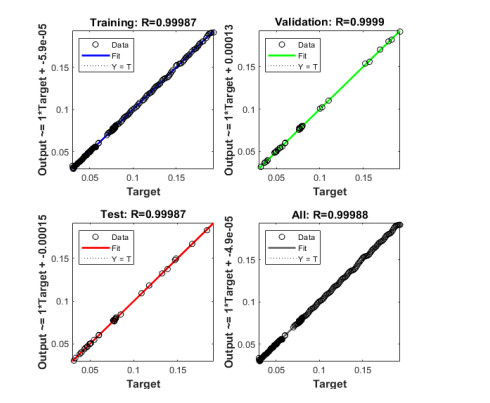
Figure 6(a to c) presents the curves of fitting for the nonlinear MDMPM, which certifies the comparison of the results. Figure 6(d-f) signifies the error histogram (EH) values for the MDMPM by applying the computing SCJGNNs. The construction of EH is used to test the errors of the targeted and predicted values after the designed artificial neural network training. These errors present that how predicted measures contrast from the targeted values. These values based on the EH are obtained as 1.95 × 10⁻⁰⁵, 8.64 × 10⁻⁰⁵ and −5.90 × 10⁻⁰⁶ for respective dynamics of the MDMPM. Figures 7 to 9 present the correlation values for the MDMPM using the SCJGNNs. These measures based on the determination coefficient R² are found as 1 for each case of the MDMPM. The graphs of substantiation, testing, and training verify the correctness of the MDMPM using the numerical stochastic SCJGNNs procedure. The values of MSE convergence using the train, epochs, certification, backpropagation, test, and intricacy are tabulated in Table 2. The complexity measures using the SCJGNNs for the MDMPM are performed to authenticate the intricacy based on the network's training, i.e., epoch execution.

Table 2.  MSE performances for solving the MDMPM.

Case	MSE for instances of sampling			Gradient	Performance	Epoch	Time
	Test	validation	Train
I	2.745×10−07	1.697 ×10−07	2.366×10−07	1.42×10−06	2.26×10−07	100	2 Sec
II	1.795×10−07	1.432×10−07	1.920×10−07	8.18×10−07	1.91×10−07	86	2 Sec
III	5.112×10−07	3.038×10−07	3.678×10−07	2.94×10−06	2.09×10−07	69	2 Sec

---

 | Show Table

DownLoad: CSV

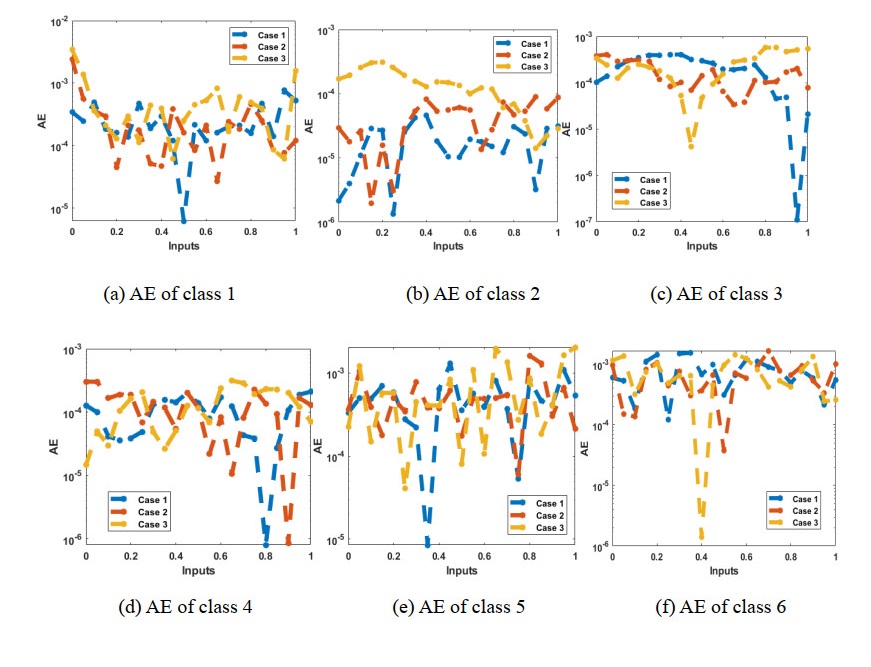
Figures 10 and 11 present the comparison graphs and AE using the obtained and source statics for the MDMPM. It is demonstrated that the source and calculated outcomes of the MDMPM precisely coincided. Figure 10 represents the AE graphs for each category of the MDMPM. For the first class, the AE lies as 10⁻⁰³ to 10⁻⁰⁵ for case I and III and 10⁻⁰² to 10⁻⁰⁴ for case II. These values for the 2^nd category of the MDMPM are found around 10⁻⁰⁵ to 10⁻⁰⁶, 10⁻⁰⁴ to 10⁻⁰⁶ and 10⁻⁰³ to 10⁻⁰⁵ for cases I, II and III. The AE measures for the 3^rd dynamics of the MDMPM lie as 10⁻⁰⁴ to 10⁻⁰⁷, 10⁻⁰³ to 10⁻⁰⁵ and 10⁻⁰³ to 10⁻⁰⁶ for respective cases. These values for the 4^th class of the MDMPM are calculated as 10⁻⁰³ to 10⁻⁰⁵ for case I and for case II and III, these AE are found as 10⁻⁰³ to 10⁻⁰⁴. The AE values for the 5^th and 6^th dynamics are found as 10⁻⁰³ to 10⁻⁰⁵ for each case of the model. These reduceable AE measures provides the accuracy of the scheme for the MDMPM.

Figure 10.  Achieved and reference results of the nonlinear MDMPM.

DownLoad: Full-Size Img PowerPoint

Figure 11.  The values of the AE for the nonlinear MDMPM.

DownLoad: Full-Size Img PowerPoint

5.   Conclusions

The stochastic numerical performances of the malaria disease using the pesticides and medication have been presented in this study. The populations-based host and vector are divided in the mathematical classification of the malaria using the pesticides and medication. Some conclusions of this work are reported as:

• The stochastic scale conjugate gradient neural network framework has been designed successfully for the numerical malaria disease model.

• The neural network procedure is presented by using fifteen neurons along with the log-sigmoid transfer function in the hidden layers to solve the model.

• The supervised neural networks process using the data as for validation 12%, testing 10%, and training 78% is presented for the numerical solutions of the system.

• The accuracy of the proposed stochastic scheme is examined through the overlapping of the achieved obtained and Runge-Kutta source solutions.

• The negligible performances of AE indicate the exactness of the computing stochastic approach.

• The consistency and trustworthiness of the designed procedure are assessed through the correlation, histogram curves, regression, and functional fitness process to solve the MDMPM.

• The perks/advantages of the proposed stochastic SCJGNNs procedure includes simplicity of the concept and understanding, straightforwardness in implementations and execution, provision of outcome on continuous domain, expandability and applicability.

The limitation/disadvantage of the stochastic SCJGNNs paradigm is the issue of trapping in local minima for scale conjugate gradient methodology while training of the weights of the networks, however, the said limitation is rectified by exploited heuristic global search methodologies in future by the interested readers. Additionally, in future, the designed SCJGNNs procedure can be explored/implemented for different applications of the nonlinear mathematical models arising in the field of computational fluid mechanics.

Conflict of interest

The authors declare that they have no conflict of interest

Authors' contributions

Manal Alqhtani: Conceptualization, methodology, validation, Writing-original draft preparation, writing-review; J.F. Gómez-Aguilar: Conceptualization, methodology, validation, investigation, Writing-original draft preparation, writing-review; Khaled M. Saad: Conceptualization, methodology, validation, writing-review and editing; Zulqurnain Sabir: Validation, investigation, Writing-original draft preparation, writing-review; Eduardo Pérez-Careta: Validation, formal analysis, investigation. All authors have read and agreed to the published version of the manuscript.

Acknowledgement

The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work under the General Research Funding program grant code (NU/RG/SERC/12/22).

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.