Entropy formation analysis for magnetized UCM fluid over an exponentially stretching surface with PST and PSHF wall conditions

Abbreviations: $\alpha$ : Stretching ratio; $\lambda$ : Relaxation time; L: Reference length; Pr: Prandtl number; ${Re}$ : Reynolds number; β: Deborah number; ν: Kinematic viscosity; $Br$ : Brinkman number; $\varPsi$ : Viscous dissipation; µ: Dynamic viscosity; k: Thermal conductivity; Rn: Radiation parameter; σ∗: Stefan-Boltzmann constant; A, B: Temperature exponents; ${E_G}$ : Entropy generation number; k∗: Mean absorption coefficient; $\xi$ : Finite temperature difference; c_p: Specific heat at constant pressure; θ: Dimensionless temperature in PST; $\phi$ : Dimensionless temperature in PSHF; $\gamma$ Temperature-dependent thermal conductivity

1.   Introduction

The primary issue that is emerging in any industry these days is the effective transport of energy. In this modern era of science and technology, almost all mechanical machines that work with thermo-fluidic systems face this energy loss. Basically, all thermo-fluidic structures bring in irreversibilities, resulting in an energy drop. This loss of thermal energy reduces the system's capacity for thermal competence. In 1850, the German physicist Rudolf Clausius initially introduced his theory of this energy/efficiency loss as "entropy." Clausius' concept of entropy was like a candle in a dark room for the scientists of the 19th century. The second law mechanism is a splendid and productive guideline to figure out the entropy of any engineering machine. Actually, entropy is linked to several energy-related fields, including geothermal power generation, the cooling of cutting-edge electronics, and solar energy generation. Initially, Bejan ^[1] presented entropy as a philosophical concept. Bejan analyzed the effects of heat transfer and viscous dissipation on entropy formation. Rashidi et al. ^[2] investigated the entropy production that occurs due to fluid friction and the irreversibility of Joule dissipation when it passes through a porous duct. Aksoy ^[3] studied entropy formation due to fully developed flow in a rectangular porous duct. In their paper, Abrar et al. ^[4] explore the entropy production that occurs as a result of heat transport, viscosity, and magnetic irreversibility. Kamran et al. ^[5] numerically studied the entropy formation of Casson fluid flow over a slip boundary. Rashid and Mustafa's ^[6] study focused on the flow of a Reiner-Rivlin fluid across a stretchable, rotating surface, as well as its effects on viscous heating. Recently, Abrar et al. ^{[7,8,9,10,11]} conducted many studies related to entropy with multiple physical constraints of interest.

There have been remarkable advancements in scientific research and technological development due to an approach known as boundary layer flow over moving surfaces with heat transfer. Various applications, such as crystal growth, glass fiber production, paper-making, continuous casting, metallurgical operations, the cooling of metallic sheets in cooling baths, and plastic film design, have benefited from this approach. The pioneering study on stretching surfaces was initially proposed by Sakiadis ^[12]. After this fundamental approach, many researchers have contributed to demonstrating two-dimensional flows over a stretching surface with different aspects due to their demanding applications. However, three-dimensional flows for such cases have not been extensively examined yet due to their complex mathematical nature. A few recent studies for three-dimensional flows via different flow assumptions include the following: Singh ^[13] analytically solved the double-diffusive boundary layer analysis for Newtonian fluids, Razzaq et al. ^[14] presented the flow of a magnetized nanofluid over a stretching plate by using a non-similar approach, Razzaq and Farooq ^[15] investigated convection analysis for the Oldroyd-B model past a stretching surface, Cui et al. ^[16] studied the consequences of magnetic dissipation, viscous dissipation, and chemical reaction in the flow, temperature, and concentration fields, Umer et al. ^[17] and Farooq et al. ^[18] separately discussed computational analyses for forced and mixed convection, and Talat et al. ^[19] explored the flow over a rotating porous disk. Qaiser et al. ^[20] numerically addressed the mixed convection flow of a nanofluid across a stretched surface, Khan et al. ^[21] explored the properties of a Maxwell bio-nanofluid in the presence of solar radiation, Cui et al. ^[22,23,24] discussed heat transport analysis in a biconvection model with different body forces, Khan et al. ^[25] discussed the Marangoni convection flow due to a rotating disk, Guo et al. ^[26] examined entropy analysis for a radiative nanofluid, Ali et al. ^[27,28] examined heat and mass transport for three-dimensional nanofluids over a stretching sheet, Khattak et al. ^[29] numerically examined the heat flux model past a nonlinear stretching surface, and Khan et al. ^[30] analyzed the entropy generation for micro-rotating Casson fluid flow.

Motivated by the above-cited literature review, this study was purposed to examine the entropy formation due to temperature-dependent thermal conductivity for a three-dimensional flow of a Maxwell fluid past an exponentially stretching sheet. Furthermore, a heat transport investigation was performed under two different heat circumstances, i.e., a prescribed surface temperature (PST) and prescribed surface heat flux (PSHF). Series solutions were produced for velocity and temperature profiles by using a semi-analytical approach called the homotopy analysis method (HAM). In the forthcoming section, the authors disclose the problem formulation. Section 3 formulates the formula for the entropy formation in the presence of a PST and PSHF. In Section 4, the authors address the series solution of the governed mathematical model. Section 5 presents to present the physical importance of the governed model through plots and tables. The last section reflects the concluding remarks of the study.

2.   Problem formulation

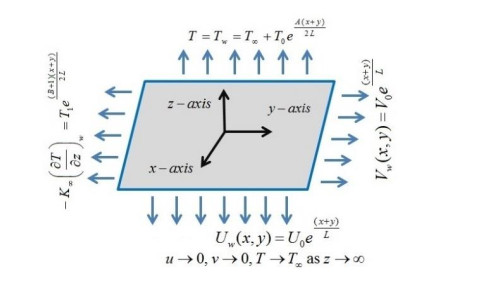
In this study, consideration has been given to the three-dimensional flow of a Maxwell fluid bounded past an exponentially stretching sheet. Using the Cartesian coordinate system, $x$ and $y$ axes were selected to be parallel to the direction of motion along the sheet, whereas the z- axis was chosen to be perpendicular to the axis of motion. The driving force for the fluid is the stretching sheet at $z = 0$, and represents the fluid stretching velocities in the $x$ and $y$ directions, respectively. Figure 1 reflects the systematic view of the physical model.

The flow is governed by the following relations:

and the supported boundary conditions for the assumed physical situation are as follows:

Let us introduce the convenient variables:

As a result, (2) and (3) simplify to (1), and (1) is satisfied automatically.

where the appropriate boundary conditions are as follows:

here $\beta =\frac{\lambda {­­}{U}_{m}}{2L}$ represents the Deborah number, where ${U}_{m}$ is of $O\left({U}_{0}{e}^{\raise0.7ex\hbox{${x + y}$} \!\mathord{\left/ {\vphantom {{x + y} L}}\right.} \!\lower0.7ex\hbox{$L$}}\right)$ and $\alpha =\left(\frac{{V}_{0}}{{U}_{0}}\right)$ represents the stretching ratio parameter. Note that, for $\alpha =0$, the three-dimensional flow becomes two-dimensional flow (i.e., $g=0$) which is:

also, when we set $\alpha =1,$ one can reach the axisymmetric flow (i.e., $f=g$) with similar boundary conditions as (10).

2.1.   Heat transfer mechanism

The heat transport equation with the thermal radiation phenomenon has the following form:

and the wall conditions for the PST and PSHF circumstances are as follows:

It may be shown that the thermal conductivity (k) is a function of temperature in the following way:

PST case:

PSHF case:

a similarity transformation is introduced as

Equation (11) reduces to the following forms after using (14):

The reduced boundary conditions are as follows:

where the Prandtl number and the radiation parameter are given as $\left({Pr}={\raise0.7ex\hbox{${\mu {c_p}}$} \!\mathord{\left/ {\vphantom {{\mu {c_p}} {{k_\infty }}}}\right. } \!\lower0.7ex\hbox{${{k_\infty }}$}}\right)$ and $\left(Rn={\raise0.7ex\hbox{${16\sigma *{T_\infty }^3}$} \!\mathord{\left/ {\vphantom {{16\sigma *{T_\infty }^3} {3{k_\infty }k*}}}\right. } \!\lower0.7ex\hbox{${3{k_\infty }k*}$}}\right)$ respectively.

3.   Second law analysis with a PST and PSHF

The philosophy of the second law of thermodynamics offers a computational way by which one can compute the irreversibilities in any system. The volumetric entropy generation rate $\; \left({{S_{Gen}}} \right)$ and viscous dissipation $\left(\varPsi \right)$ are a result of the following calculations ^[10]:

where $\; \left({{S_{gen}}} \right)$ is the rate at which characteristic entropy is generated

3.1.   Incorporating the PST

The dimensionless local generation entropy $\left({E}_{G}\right)$ is defined in the following way:

Equation (22) clearly discloses the involvement of three diverse roots of entropy generation (i.e., entropy generation due to the PST $\left({E}_{PST}\right)$, thermal radiation $\left({E}_{Rn}\right)$ and viscous dissipation $\left({E}_{\varPsi }\right)$.

3.2.   For the case of PSHF

The dimensionless locally generated entropy $\left({E}_{G}\right)$ is defined in the following way:

In the above equations, ${Re}$ is the local Reynolds number, $Br$ is the Brinkman number, and $\xi$ is the finite temperature difference.

To calculate the irreversibility distribution (for the PST and PSHF cases), the Bejan number (Be) is given as:

4.   Series solution

To establish the series solutions, we considered a very efficient technique, particularly, the HAM (see ^[31,32,33]). When (6), (7), (15) and (16) are subject to boundary conditions (8) and (9), the HAM is applied to obtain the corresponding analytical solutions (17). You may quickly and simply get at your initial guesses and the linear operator by doing the following:

A MATHEMATICA code has been constructed for the defined problem in which we endorse $({\hslash }_{f}, {\hslash }_{g}, {\hslash }_{\theta } ~~{\hslash }_{\varphi })$ as the auxiliary parameters for the unknown function $\left(f, g, \theta ~~{and}~~\varphi \right)$, which gives the convergence region. To find the admissible values of $({\hslash }_{f}$, ${\hslash }_{g, }{\hslash }_{\theta }~~and~~{\hslash }_{\varphi })~~\mathrm{a}\mathrm{n}\mathrm{d}$ the so called $\hslash -$ curves were developed as displayed for the 15^th order of approximation in Figures 2 and 3. These figures show that the admissible values are $-0.7\le {\hslash }_{f}\le -0.2, -0.6\le {\hslash }_{g}\le -0.2, -0.6\le {\hslash }_{\theta }\le -0.2$ and $-0.8\le {\hslash }_{\varphi }\le -0.1$. It is further noticed that the range of admissible values of $\hslash$ increases by increasing the order of approximations. Figures 2 and 3 depict the values of $(\hslash {{­}}_{f}, {\hslash }_{g}, {\hslash }_{\theta } ~~{and}~~{\hslash }_{\varphi })$.

Table 1 gives knowledge about the approximation order, which helps us in making a judgment about the orders of approximations that is sufficient for the convergence. It is noticed that convergent solutions up to the fifth decimal place are acquired at just the 16th and 20th order of estimation.

5.   Results and discussion

In this section, several graphical illustrations and numerical tables are presented to show the rheology of various parameters. Figures 4 and 5 were developed to visualize the behavior of the viscoelastic fluid parameter (Deborah number) on $f$ and ${f}^{{'}}$, respectively. By analyzing these numbers, we conclude that raising the Deborah number slows down the flow of the fluid. Physically, ($\beta < 1$) relates to fluids for which the relaxation time is less than the characteristic deformation time. This is the case for fluids with low viscosities. Thus, the non-Newtonian fluid behaves as a purely viscous fluid. On the other hand, when ($\beta < 1$), the fluid behaves as if it were an elastically solid substance. Figures 6 and 7 visualize the response of the stretching ratio parameter on $g\left(\eta \right)$ and ${g}^{{'}}\left(\eta \right)$, respectively. It is observed in these figures that the fluid velocity significantly increases with an enhancement in the stretching parameter. Physically, we can conclude that for $\alpha =0$, the flow reduces to two-dimensional, whereas $\alpha > 0$ corresponds to three-dimensional flow as is evident from Figure 6. Moreover, it is also observed that the flow is axisymmetric when $1.0$. Figure 8 demonstrates the consequences of temperature-dependent thermal conductivity. A significant increase in the fluid energy is observed when is increased. The thermal boundary layer thickness accelerates fruitfully when is increased. Figure 9 shows the impact of $\gamma$ on $\varphi$. It is observed that as $\varphi$ increases, the temperature of the fluid decreases.

Figures 10 and 11 illustrate the different values of the radiation parameter (Rn) throughout time. It is perceived that, with the increase of radiation there is an increase in both temperature profiles (i.e., PST and PSHF), which is obvious. The influence of the stretching ratio parameter for (Pr = 0.7 and 0.02) on the temperature profile is plotted in Figures 12 and 13, respectively. The temperature fields (PST and PSHF) demonstrate purposeful overshoots for a low Pr (liquid metal = 0.02), whereas, for a high Pr (air=0.02) the temperature variation was not that crucial. From a physical perspective, we can conclude that the reaction of the stretching ratio parameter is very impressive in the case of liquid metals because of a low viscosity, whereas for higher Pr values, the overshoot does not exist because a high Pr indicates a more viscous fluid.

Figures 14-19 were sketched to illustrate the behavior of the entropy generation $\left({{E_G}} \right)\;$ under the influence of various physical parameters, i.e., the Brinkman number $\left({Br} \right), \;$ Prandtl number $\left({\Pr } \right)$ and thermal radiation $\left(Rn\right)$ as function of the PST and PSHF wall conditions. Figures 14 and 15 show the influence of ${E_G}$ with increasing values of $Br$ for the PST and PSHF wall conditions, respectively. It can be seen that ${E}_{G}$ is the increasing function of $Br$ for both (PST and PSHF) situations. Physically, an increase in ${E}_{G}$ is due to the fact that as $Br$ increases, the fluid friction increases near the surface, which consequently increases the entropy of the system. The influence of increasing $\Pr \;$ on the entropy number is represented in Figure 16 (PST) and Figure 17 (PSHF). In these figures, we have plotted different ranges of $\Pr$ (i.e., liquid metal, air, sea water and engine oil). It can be seen that the entropy of the system is frequently increasing for increasing values of the Prandtl number. Impact of $Rn\;$ is observed in Figures 18 and 19 as a function of the entropy generation for the PST and PSHF conditions, respectively. It is noticed that an increase in the radiation parameter leads to a decrease in the entropy production. Physically, an increase in $Rn$ means a decrease in the buoyancy force, which subsequently decreases the entropy production.

Figures 20-23 illustrate the physical sense of the Bejan number $\left(Be\right)$ for increasing values of the Brinkman number $\left(Br\right)$ and radiation parameter $\left(Rn\right).$ It is observed that $Be$ continuously decreases with increasing values of $Br,$ which is due to the fact that heat transfer irreversibility is small as compared to the total irreversibility: see Figures 20 and 21. On the other hand, $Be$ increases effectively with an enhancement in Rn for both the PST and PSHF wall conditions (see Figures 22 and 23).

Table 2 gives the comparison of velocity profiles. Consistency is found between the numerical and HAM results. Table 2 gives the numerical temperature dependent thermal conductivity for multiple values of $\alpha$ and $Rn.$ Table 3 gives the numerical PST and PSHF wall conditions with respect to entropy for various values of the Brinkman number while other parameters remain fixed. It is noted that, as we increase the domain, i.e., $(\eta \to \infty)$, both wall conditions are becoming fully matured.

Figures 24 and 25 show the streamline behavior for two and three-dimensional Maxwell fluid models. It was found that the streamline for two and three-dimensional flows are quite interesting.

6.   Conclusions

The main ideas of the analysis are as follows:

• The Deborah number retards the fluid velocity.

• Three-dimensional flow reduces to two-dimensional flow for $\alpha =0.$

• The non-Newtonian fluid behaves as a purely viscous fluid when the Deborah number exceeds 1.

• Temperature-dependent thermal conductivity has quite different effects in the PST and PSHF cases.

• The stretching ratio parameter has a greater over shoot for liquid metals (low Prandtl number).

• It is noted from Table 3 that as the domain increases, the solution settles down for both PST and PSHF wall conditions.

• In the case of the Bejan number, the magnitude of the PSHF is greater than the PST.

• The Bejan number is directly proportional to the radiation parameter and inversely proportional to the Brinkman number.

• It is noted from Table 3 that, as the domain increases, the solution settles down for both the PST and PSHF wall conditions.

Acknowledgments

The authors Aziz Khan and Thabet Abdeljawad would like to thank Prince Sultan University for paying the APC and the support through the TAS research lab.

Conflict of interest

The authors declare that they have no competing interests.