1.
Introduction
Nowadays, the subject of fixed point theory is one of the most beautiful and attractive subjects in science because this subject has many applications in all aspects of science. Many authors have extracted many fixed point results, and applied their results to give a set of conditions for such integral equations, and ordinary differential equations to guarantee existence solutions to such equations, see [1,2,3,4] and the references cited there. Ameer et al. [5] employed the directed graph to introduce new mappings, called "hybrid Ćirić type graphic Υ,Λ-contraction mappings", and then applied their new results to study some applications to electric circuit and fractional differential equations.
The thought of metric spaces has been extended in many directions, such as G-metric spaces, cone metric spaces and b-metric spaces in order to expand Banach's contraction [6] to more beneficial forms. Recently, Kamran et al. [7] expanded the thought of b-metric spaces in the sense introduced by Baktain [8] and Czerwik [9] into a new concept called "extended b-metric spaces". The benefit of extending metric spaces to new spaces is to enrich the sciences with new findings relevant to fixed points for mappings that satisfy a set of suitable conditions to ensure the existence of fixed points for some findings in b-metric and extended b-spaces, see [10,11,12,13,14,15,16,17].
Abdeljawad et al. [18] extended some results in fixed points to partial b-metric spaces. Shatanawi et al. [19] utilized the ordered relation to present a new extension of Banach's contraction theorem. Roshan et al. [20] presented some common fixed points in ordered b-metric spaces for functions that satisfy contraction condition based on two different functions. Recently, Mlaiki et al. [21] launched a new space, called "controlled metric type space", and they gave a new version of the Banach contraction theorem. Then, some authors obtained good results on this new topic, see [22,23,24,25]. Farhan et al. [26] studied some results of Reich-type and (α,F)-contractions in partially ordered, double-controlled metric-type spaces. Then, they applied their results to obtain some applications to non-linear fractional differential equations.
Henceforth, Q stands for a non-empty set.
Definition 1.1. [7] For a set Q, let θ : Q×Q→[1,∞) be a function. Then, the function ν : Q×Q→[0,∞) is called an extended b-metric, if ∀ζ,φ,ϱ∈Q, we have
(1) ν(ζ,φ)=0⟺ζ=φ,
(2) ν(ζ,φ)=ν(φ,ζ),
(3) ν(ζ,φ)≤θ(ζ,φ)[ν(ζ,ϱ)+ν(ϱ,φ)].
The pair (Q,ν) is referred to as an extended b-metric space.
Some examples for (Q,ν) are stated here:
Example 1.1. For Q=[0,∞), set θ : Q×Q→[1,∞) and ν : Q×Q→[1,∞) via θ(ζ1,ζ2)=1+ζ1+ζ2, ∀ζ1,ζ2∈Q, and
Example 1.2. For Q=[0,∞), set θ : Q×Q→[1,∞) and ν : Q×Q→[0,∞) via θ(ζ,v)=3+ζ+v2, for all ζ,v∈Q, and
(1)ν(ζ,v)=0, for all ζ,v∈Q, ζ=v,
(2)ν(ζ,v)=ν(v,ζ)=5, for all ζ,v∈Q−{0}, ζ≠v,
(3)ν(ζ,0)=ν(0,ζ)=2, for all ζ∈Q−{0}.
In this paper, we take advantage of the notion of extended b-metric to present new contraction conditions, and we make use of our new contractions to formulate new results related to a fixed point of a mapping that satisfies a set of conditions. More precisely, we will prove six new fixed point theorems in the context of extended b-metric spaces. Also, we construct two examples to show the validity and usefulness of our findings. Furthermore, we add an application to an integral equation to support our results.
2.
Mains results
From now on, FP stands for a fixed point.
Theorem 2.1. Suppose (Q,ν) is complete. Assume there exist r∈(0,1] and h∈[0,1), such that T:Q→Q satisfies
for all s,v∈Q. Assume that for any m∈N,
where si=Tis0 for s0∈Q. Also, suppose that for any v,s∈Q, we have
Then, T has a FP in Q.
Proof. Let s0∈Q. Then, set up a sequence (st) in Q by putting st=Qts0. For t∈N, condition (2.1) gives
Simplifying inequality (2.3) to have
For t∈N, inequality (2.4) yields
For t,m∈N with m>t, we choose k∈N with m=t+k. The triangular inequality of the definition ν produces
In light of the values of θ greater than or equal to 1, the above inequalities imply
By using inequalities (2.5) and (2.6), it becomes
Define
Then,
The ratio test makes certain
is Cauchy, accordingly the sequence (st) is Cauchy in (Q,ν). So, ∃s′∈Q as an output of the completeness of (Q,ν), such that
Our mission is to verify Ts′=s′. Before that, we need to verify
The triangular inequality with addition to inequality (2.2) emphasize
Thus, (2.10) has been achieved. Again, the triangular inequality and (2.1) yield
On letting t→+∞ in (2.12) and benefiting from (2.9) and (2.10), we arrive at ν(s′,Ts′)=0. Accordingly, Ts′=s′.
In the following result, we assume that θ is continuous in its variables.
Theorem 2.2. Suppose (Q,ν) is complete. Assume there exist r∈(0,∞) and h∈[0,1), such that T:Q→Q satisfies
for all s,v∈Q. Assume that for any m∈N,
where si=Tis0 for s0∈Q. If θ is continuous in its variables, then T has a FP in Q.
Proof. We proceed in the same way as in proof of Theorem 2.1, to generate a sequence (st=Tts0) in Q, such that st→s′∈Q and
Also, the continuity of θ in its variables implies that
Now,
Allow t→+∞ in the above inequalities, and make use of (2.13) and (2.14) to obtain
This means that Ts′=s′. Thus, the desired result is obtained.
The uniqueness of the FP in Theorem 2.1 or Theorem 2.2 can be obtained if an appropriate condition is added.
Theorem 2.3. Suppose (Q,ν) is complete. Assume there exist r∈(0,1] and h∈[0,1), such that T:Q→Q satisfies
for all s,v∈Q. Assume that for any m∈N,
where si=Tis0 for s0∈Q. Moreover, assume that for any v,s0∈Q,
Also, suppose that ∀v,s∈Q, we have
Then, T has only one FP in Q.
Proof. If for any v,s0∈Q, we have lim supi→+∞θ(v,Tis0) exists and less than 1−hr, then Theorem 2.1 ensures that ∃s′∈Q, such that Ts′=s′.
If θ is continuous in its variables, then Theorem 2.2 ensures that ∃s′∈Q, such that Ts′=s′.
To verify that T achieves only one FP, let v′∈Q, such that Tv′=v′. Now,
On taking the limit of supremum as t→+∞ in the above inequality, we reach to
a contradiction. Thus, v′=s′ and we conclude that T has only one FP.
Corollary 2.1. Suppose (Q,ν) is complete. Assume there exists r∈(0,1], such that T:Q→Q satisfies
for all s,v∈Q. For s0∈Q, let sn=Tns0. Assume for any m∈N,
Also, suppose that for any v,s∈Q, we have
Then, T has a FP in Q.
Proof. By choosing h=0 in Theorem 2.1, we obtain the result as desired.
Corollary 2.2. Suppose (Q,ν) is complete. Assume there exists r∈(0,1], such that T:Q→Q satisfies
for all s,v∈Q. For s0∈Q, let sn=Tns0. Assume that for any m∈N,
If θ is continuous in its variables, then, T has a FP in Q.
Proof. By choosing h=0 in Theorem 2.2, we obtain the result as desired.
Corollary 2.3. Suppose (Q,ν) is complete. Assume there exists r∈(0,1], such that T:Q→Q satisfies
for all s,v∈Q. For s0∈Q, let sn=Tns0. Assume that for any m∈N,
Moreover, assume that for any v,s0∈Q,
Suppose for any v,s∈Q, we have
Then, T has only one FP in Q.
Proof. By taking h=0 in Theorem 2.3, we get the desired result.
Corollary 2.4. Suppose (Q,ν) is a complete b-metric space with constant b≥1. Assume there exist r∈(0,1] and h∈[0,1) with b2r+h<1, such that T:Q→Q satisfies
for all s,v∈Q. Then, T has only one FP in Q.
Proof. Define θ:Q×Q→[0,+∞) via θ(s,p)=b,∀s,v∈Q. Now, for s0∈Q, we have
Also, from br≤b2r+h<1, we arrive at
So, all conditions of Theorem 2.3 are met. So, the result also follows.
Corollary 2.5. Suppose (Q,ν) is complete. Assume there exists r∈(0,1], such that T:Q→Q satisfies
for all s,v∈Q. Assume that for any m∈N,
where si=Tis0 for s0∈Q. Suppose that for all v,s∈Q, we have
Then, T has only one FP in Q.
Proof. Let (st+1=Tst) be a sequence in Q constructed as in the proof of Theorem 2.1. So,
Thus,
has been obtained. Take m∈N, as in the proof of Theorem 2.1, we obtain
and, hence, (st) is Cauchy in Q. Then, one can show that T has a FP, say t∈Q. Since r<1, then the uniqueness of t follows from inequality 2.16.
Theorem 2.4. Suppose (Q,ν) is complete. Assume there exist r∈(0,1] and h∈[0,1), such that T:Q→Q satisfies
for all s,v∈Q. Also, suppose that for any m∈N,
where si=Tis0 for s0∈Q. Moreover, assume that for any v∈Q, we have lim supi→+∞ν(v,si) exists and is finite. Then, T has a FP in Q.
Proof. Presume s0∈Q. Then, set up a sequence (st) in Q, such that st=Qts0 owns condition (2.18). For t∈N, condition (2.17) gives
Simplifying inequality (2.19) to have
For n∈N, inequality (2.20) yields
Choose t,m∈N in such a way that m>t. Select k∈N, such that m=t+k. By helping with triangular inequality of the definition ν and imitation of the procedure in the proof of Theorem 2.1, at the end of the day, we obtain
By employing inequality (2.21), inequality (2.22) can be written as
Define
Then,
Ratio test implies that
By moving towards infinity in (2.23), the following will be achieved:
and, hence, (st) is Cauchy in (Q,ν). As an output of the completeness of (Q,ν), we find s′∈Q, such that st→s′; that is,
Our task is to verify Ts′=s′. Now, (2.25) and (2.17) lead us to
By using the triangular inequality, and then moving towards infinity to obtain
and, hence, ν(s′,Ts′)=0. Accordingly, Ts′=s′.
In our next result, we assume that θ is continuous in its variables.
Theorem 2.5. Suppose (Q,ν) is complete. Assume there exist r∈(0,1] and h∈[0,1), such that T:Q→Q satisfies
for all s,v∈Q. Also, suppose that for any m∈N,
where sj=Tjs0 for s0∈Q. If T is continuous, then T has a FP in Q.
Proof. By starting with s0∈Q, we launch a sequence (st) as in the proof of Theorem 2.4, such that there exists s′∈Q with
Now, we show that Ts′=s′. The triangular inequality and inequality 2.27 imply that
By permitting t→+∞ in the above inequalities, we have ν(s′,Ts′)=0 and, hence, s′=Ts′.
The uniqueness of the FP can be achieved in Theorem 2.4 or Theorem 2.5 if a suitable condition is added.
Theorem 2.6. Suppose (Q,ν) is complete. Assume there exist r∈(0,1] and h∈[0,1), such that T:Q→Q satisfies
for all s,v∈Q. Also, suppose that for any m∈N,
where sj=Tjs0 for s0∈Q. Moreover, assume that for any v∈Q, we have lim supt→+∞θ(v,st) exists and is finite. Also, suppose for any v,s∈Q, lim supt→+∞θ(Ttv,Tts) exists and less than 1−hr. Then, T has only one FP in Q.
Proof. Theorem 2.4 ensures that there exists s′∈Q with Ts′=s′. To verify that T achieves only one fixed point, we suppose there exists v′∈Q with s′≠v′, such that Tv′=v′. Now,
Rewrite the above inequality in a proper form, then we have
By permitting t tends to infinity in the above inequality, we get ν(s′,v′)<ν(s′,v′), a contradiction. Thus, s′=v′ and, hence, T has only FP in Q.
Corollary 2.6. Suppose (Q,ν) is a complete b-metric space with constant b≥1. Assume there exist r∈(0,1] and h∈[0,1) with b2r+h(b2+b)<1, such that T:Q→Q satisfies
for all s,v∈Q. Then, T has only one FP in Q.
Proof. Define θ:Q×Q→[1,+∞) via θ(s,v)=b,∀s,v∈Q. Now, for s0∈Q and m∈N, we have
Also, from br+h≤b2r+h(b2+b)<1, we arrive at
So, all conditions of Theorem 2.6 are met. So, the result also follows.
Now, we present some examples of our results.
Example 2.1. Let Q=[0,+∞). Define T:Q→Q via Tv=14v and θ:Q×Q→[1,∞) by θ(v,s)=v+s+1. Also, define ν:Q×Q→[0,+∞) via
Then:
(1)ν is extended b-metric, which is not b-metric.
(2)(Q,ν) is complete.
(3) Let v0∈Q, take vn=Tnv0. Then, for m∈N, we have
(4) For any v,s0∈Q, we have
(5) For any v,s∈Q, we have
(6) For s,v∈Q, we have
We note that the hypotheses of Theorem 2.3 have been fulfilled for r=14 and h=12.
Example 2.2. Let Q={0,1,2,3,…}. Define T:Q→Q via
and θ:Q×Q→[1,∞) by
Also, define ν:Q×Q→[0,+∞) via
Then:
(1)ν is extended b-metric, which is not b-metric.
(2)(Q,ν) is complete.
(3) Let s0∈Q, take (st)=(Tts0). Then, for m∈N, we have
(4) For any v,q∈Q, we have
(5) For any v,s∈Q, we have
(6) For v,s∈Q, we have
We note that the hypotheses of Theorem 2.6 have been fulfilled for r=14 and h=14.
3.
Application
In this section, our goal is to present some applications of our findings.
We start this section by giving a solution to the following integral equation:
Now, let Q=C([0,1]) be the set of all continuous functions on [0,1]. Define ||.||∞:Q→[0,+∞) by
Also, define ν:Q×Q→[0,+∞) via
and θ:Q×Q→[1,+∞) via
Then, (Q,ν) is an extended b-metric space.
Now, let
Then, one can show that A is a closed subspace of Q. So, (A,ν) is complete.
Theorem 3.1. Suppose the following conditions:
(1) K:[0,1]×R→R is continuous, and
(2) There exists r∈[0,14), such that
for all f∈A.
Then, the integral equation (3.1) has a unique solution.
Proof. Define T:A→A by
Now, for f∈A, we have
So, we conclude that
For f,g∈Q, we have
Let f0∈A. Then, for t∈[0,1] and i∈N, we have |fi(t)|=|Ti(f0)(t)|≤||T||∞i||f||∞|t|. So, ||fi||∞≤||T||i∞. Therefore,
Let v,f∈Q. Then,
So, lim supi→+∞θ(v,Tif) exists and is finite. So, all conditions of Theorem 2.1 have been achieved. Accordingly, T has a fixed point in A⊆Q. So, the integral equation (3.1) has a solution in Q.
Our second application is to give a solution to equation of the form f(s)=0, where s∈Q=[0,+∞).
Theorem 3.2. For t≥1 and two integers m and k with 4m2<(1+t)2 and (1+t)≤k, the equation
has a unique real solution s′ in [0,+∞).
Proof. Let Q=[0,+∞). Define T:Q→Q by
Also, define θ:Q×Q→[1,+∞) by
On Q×Q, we define the complete extended b-metric ν by
Then:
(1) For s,v∈Q, we have
Indeed,
(2) For s0∈Q, put si=Tis0. Then, one can show that
(3)θ is continuous in its variables.
(4) For v,s∈Q, we have
So, all the conditions of Corollary 2.3 have been fulfilled. Therefore, T has a unique FP in [0,+∞).
Corollary 3.1. For k≥3, the equation
has a unique real solution s′ in [0,+∞).
Proof. We can show that the equation
is equivalent to
The result follows from Theorem 3.2 by taking m=1, t=k−1 and noting that 4m2<(1+t)2 and 1+t≤k.
Example 3.1. The equation
has a unique real solution s′ in [0,+∞).
Proof. The result follows from Corollary 3.1 by taking k=10.
4.
Conclusions
In this work, we have taken advantage of the notion of extended b-metric to present new contraction conditions. Next, we proved several new fixed point theorems in the context of extended b-metric spaces. Two examples are provided to show the validity and usefulness of our findings. Furthermore, two applications were added to support our findings.
Acknowledgments
The first author would like to thank the Prince Sultan University for facilitating publishing this paper through TAS lab.
Conflict of interest
The authors declare no conflicts of interest.









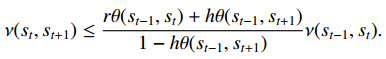

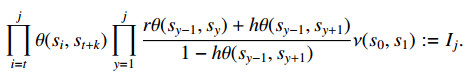




 DownLoad:
DownLoad: