A diffusive cancer model with virotherapy: Studying the immune response and its analytical simulation

1.   Introduction

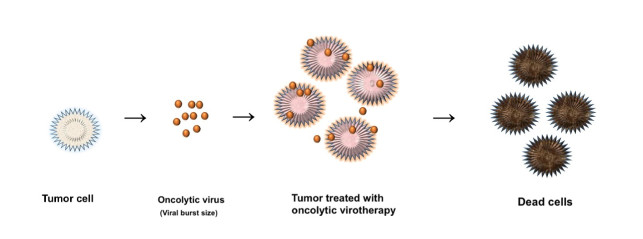
Recently, cancer therapies have been heavily developed in order to find a therapy that is able to decay the tumor in a short time without harming the neighboring healthy tissue. In the field of genetic engineering, scientists discovered a new cancer treatment by using genetically altered viruses ^[1]. Oncolytic viruses are genetically altered viruses that infect cancer cells. They grow in an abnormal tumor cell and destroy it without infecting healthy cells or normal tissue. The oncolytic viruses interact with the tumor cell and generate a burst of an oncolytic virus (see Figure 1). The burst size is the number of new viruses resulting from the lysis of an infected tumor cell, and some of the new viruses may infect nearby tumor cells. The burst size is used to measure the replicability of an oncolytic virus ^[2].

Mathematical models are able to describe biological and medical problems, such as cancer models with a variety of therapies ^[3,4], epidemic models ^[5], HIV infection models ^[6,7,8] and prey-predator models ^[9]. A few researchers have studied mathematical models of cancer with virotherapy and described the interaction between the virus and the tumor. Wodarz introduced a basic mathematical model that studied tumor growth in the presence of virotherapy treatment ^[10]. The model has been modified to study the relationship between burst size and virus replicability. The results showed that cancer cells decrease if the burst size is large ^[11]. On the other hand, some mathematical models have demonstrated the immune system response to virotherapy. Since the immune system treats viruses as foreign bodies and thus destroys them, it shows a negative response to virotherapy that may reduce the quality of viral treatment ^[12]. Also, many studies describe the interactions between uninfected and infected cells and different kinds of immune responses ^[13,14].

Herein, we will review the basic model of oncolytic virus replication which was introduced by Wodarz ^[15]. The model studies the tumor growth and the infection term and it is given by the following system of ordinary differential equations (ODEs):

where $f$ and $y$ are the uninfected and infected cells, respectively, the function $X$ represents the growth of $f$ and $y$ and the function $G$ denotes the rate at which tumor cells become infected by the virus. The coefficients $\bar \beta$ and $\bar{\delta}$ are the infection rate of the virus and the death rate of virus-infected cells, respectively, and the coefficient $\bar{r}$ is the logistical growth rate of uninfected cells. Then, Tian ^[2] proposed a following common basic model for the virotherapy of three populations:

where $v$ is the free virus population and $\bar{\gamma}$ is the death rate of the virus. The coefficient $\bar{b}\bar{\delta}$ refers to the burst size of new viral swarms resulting from killing an infected cell $y$. The model (2) was also modified in ^[16] to study the dynamics of oncolytic virotherapy, and it includes four populations, as follows:

where $z$ denotes the innate immune cell population, $\bar{s}$ is the rate of stimulation of the innate immune cell and $\bar{p}$ is the rate of immune clearance. Moreover, some models have demonstrated the spread of tumor cells under viral therapy and radiation therapy ^[17,18].

The immune response and its impact in both uninfected and infected cells were considered in the model (3) in Reference ^[19] as follows:

where the infected and uninfected cells stimulate the immune response at rates $s_1$ and $s_2$, respectively. The novelty of this paper is its study of the mathematical model in ^[19] by distinguishing between the naive and activated immune system cells. In addition, we study the spread of viruses and cells by taking a diffusion term into account. Thus, we obtain a system of partial differential equations (PDEs). The immune system cells can be activated by immunotherapy or biological therapy. Therefore, it is very important to distinguish between the naive and activated immune system cells in the mathematical model. Thus, the model introduced in this paper can be useful to study the effects of combining immunotherapy with virotherapy.

The paper is organized as follows. The second section introduces the studied mathematical model, the third section is the theoretical study of the system, the fourth section shows the analytical solutions obtained via the tanh-expansion method, the fifth section discuses the results and the last section is a summary of the work.

2.   Mathematical model

In this section, we reformulate the mathematical model in ^[19] by considering the five cell populations, which are uninfected cancer cells $f$, infected cancer cells $y$, the free virus $v$, the naive immune cells $z$ and the activated immune cells $z_{a}$, as follows:

where $d_{i}, i = 1, 2, 3, 4, 5$ denotes the diffusion terms of $f, y, v, z$ and $z_a$, respectively. The rest of the parameters are converted to dimensionless parameters in the following system of PDEs and described in Table 1.

The system becomes dimensionless by setting $t = \frac{\tau}{\delta}$, $F = C f$, $Y = C y$, $V = C v$, $Z = C z$ and $Z_a = C z_a$ and renaming the parameters as follows:

Thus, we obtain the following diffusive PDEs:

Then, the initial conditions become $F(0) = \frac{f_0}{C},$ $Y(0) = \frac{y_0}{C},$ $V(0) = \frac{v_0}{C},$ $Z(0) = \frac{x_0}{C},$ $Z_{a} (0) = \frac{x_{a_0}}{C}.$

3.   Theoretical study

3.1.   Positivity and boundedness of the solutions

Theorem 1. Let $(F(x, t), Y(x, t), V(x, t), Z(x, t), Z_a(x, t)) = (\hat f(\xi), \hat y(\xi), \hat v(\xi), \hat z(\xi), \hat z_a(\xi))\in R^{5}_{+}$, where $\xi = kx+ct+\xi_0$; then, the solutions $(\hat f(\xi), \hat y(\xi), \hat v(\xi), \hat z(\xi), \hat z_a(\xi))$ are nonnegative and bounded in the following region:

where $\zeta = \min\{p, \mu_2\}$.

Proof. First, we specify the initial value problems for System $(6)$ as follows:

As a result, the solutions are non-decreasing. In order to study the boundedness for the aforementioned system of PDEs, we will transfer the system to a system of ODEs using the traveling wave transformation. Let us define $\xi = kx+ct+\xi_0$; then, we get

From the first equation in System (7), we have

Let us assume the differential equation$\frac{d F_1}{dt} = r_1 F_1(1-F_1)$ with the initial condition $F_1(0) = F_0$, which satisfies

hence,

Note that $\frac{d \hat{f}}{dt} \leq \frac{d F_1}{dt},$ which implies that $\lim_{t \rightarrow \infty} \sup\hat{f} \leq \lim_{t \rightarrow \infty} \sup{F_1}.$ Therefore, we have

From the first and second equations in System (7), we have

which satisfy

Again, from the third equation in System (7), we have

which yields

Also, from the fourth and fifth equations in System (7), we note that

where $\zeta = \min\{p, \mu_2\}$. Thus, we obtain

and

3.2.   Equilibrium points

Model (6) has equilibrium points of the form $(F, Y, V, Z, Z_a)$ such that $F\geq 0, Y\geq0, V\geq0, Z\geq0$ and $Z_a\geq 0$. The equilibrium points of the system are the steady-state solutions, which are obtained by setting the following:

However, with help of Mathematica, we obtained five equilibrium points:

where

$E_2$ is positive if $b > 1+(\gamma/{\beta}),$ and $E_3$ is positive if $p < \lambda_z < p+s_2$.

3.3.   Basic reproduction number

The basic reproduction number is the number of cases that are generated by a signal virus in the population ^[20]. Let $P = (Y, F, V, Z, Z_a)$, model (7) is rewritten as

where

Next, the Jacobian matrix for $\upsilon_1 (P)$ and $\upsilon_2 (P)$ at $E_1$ are computed as follows:

where $\rho$ is the spectral radius. Thus, if $R_0 < 1$, the cancer will decline; if $R_0 = 1$, the cancer will stay alive and stable; if $R_0 > 1$, the cancer will experience growth and outbreak. Therefore, $E_0$ and $E_1$ always exist, $E_2$ exists if $R_0 > 1$, $E_3$ exists if $p+s_2 > \lambda_z > p$ and $E_4$ exists if $R_0 > 1$.

3.4.   Local stability analysis

We investigate the local stability of the equilibrium points by evaluating the Jacobian matrix of the nonlinear system ^[21].

Theorem 2. The trivial equilibrium $E_0$ of the system is locally unstable.

Proof. The Jacobian matrix of System (6) at $E_0$ is

It is obvious that the eigenvalues for $J(E_0)$ are as follows:

All eigenvalues are negative if $r < 0$. Hence, $E_0$ is locally unstable if $r > 0$.

Theorem 3. The equilibrium point $E_1$ is locally asymptotically stable if only if $R_0 < 1$.

Proof. By the calculation of the Jacobian matrix at $E_1$, we obtain

The characteristic polynomial is

The eigenvalues of $J(E_1),$ which are $\lambda_1 = -\mu_2$, $\lambda_2 = -r$ and $\lambda_3 = -(p+s_2),$ are negative. By the Routh-Hurwitz criteria, since $(\beta +\gamma +1)$ is positive, $\lambda_{4, 5}$ has a real negative part if $b\leq 1+\frac{\gamma}{\beta},$ which implies that $R_0 < 1$. Biologically, when the viral burst size $b$ is smaller than the critical value which is $1+\frac{\gamma}{\beta}$, the new produced viruses will be enough to infect tumor cells.

Theorem 4. The equilibrium point $E_2$ is locally asymptotically stable if $b > 1$ and $\beta < r$.

Proof. The jacobian matrix $J(E_2)$ is

where

The eigenvalues are $\lambda_1 = -\mu_2$ and $\lambda_2 = -\beta s_1 F_3 V_3- s_2 F_3-p,$ which are both negative, while $\lambda_{3, 4, 5}$ denotes the zeros of the polynomial $\lambda^3+A_1\lambda^2+A_2\lambda+A_3$. It is obvious that $A_1 > 0$ if $b > 1$, $A_2 > 0$ if $b > 1$, $\beta < r$ and $R_0 > 1$, $A_3 > 0$ if $b > 1$ and $R_0 > 1$, and

Therefore, by the Routh-Hurwitz criterion, $\lambda_{3, 4, 5}$ have negative real parts if $A_1 A_2-A_3 > 0,$ which occurs if $b > 1$ and $\beta < r$. Thus, $E_2$ is locally asymptotically stable.

Biologically, if the viruses are powerful, which means that the burst size is greater than the critical value, then the system has the equilibrium $E_2$ with the balance of tumor cells, infected tumor cells and viruses.

Theorem 5. The equilibrium point $E_3$ is locally asymptotically stable if $b < 1$, $b\beta < R_0$ and $R_0 < 1$. If $\lambda_z = 0,$ the point $E_3$ is locally asymptotically stable under the conditions that $\alpha \beta < \kappa$ and $b\beta < r$.

To find the eigenvalue, solve the Jacobian $J(E_3)$:

The characteristic polynomial of this matrix is evaluated as follows:

where $b_0, b_1, b_2, b_3$ and $b_4$ are defined in the Appendix. All coefficients are positive if $b < 1$. By using Descartes' rule, the number of sign changes is zero; thus, the point $E_3$ is locally asymptotically stable if $b < 1$.

Theorem 6. The equilibrium point $E_4$ is locally stable if $b < 1$, $b\beta < r$, $s_1 > s_2$, $\lambda_z > Z_{4a}$ and $Z_4 > Z_{4a}$.

Proof. To find the Jacobian at the equilibrium point $E_4$, we evaluate $|J(E_4) - \lambda I| = 0$, where $J(E_4)$ is given by

where $E_{1, 1} = r(1-Y_4-2F_4)-\alpha Z_{4a}-\beta V_4 -r F_4$. The characteristic polynomial is

where $a_0, a_1, a_2, a_3, a_4$ and $a_5$ are defined in the Appendix. All coefficients are positive if $b < 1$, $b\beta < r$, $\lambda_z > Z_{4a}$, $s_1 > s_2$ and $Z_4 > Z_{4a}$. By using Descartes' rule, the number of sign changes is zero; thus, the point $E_4$ is locally asymptotically stable if $b < 1$, $b\beta < r$, $\lambda_z > Z_{4a}$, $s_1 > s_2$ and $Z_4 > Z_{4a}$.

3.5.   Global stability

In this section, the global stability of the equilibrium points will be investigated by using Lyapunov functions ^[22], which must be positive definite.

Theorem 7. $E_1$ is globally asymptotically stable if $1+b \leq r \leq2, \; b\leq1$.

Proof. The Lyapunov function is defined at point $E_1$ as follows:

The derivative of $L_1$ is

where

The equilibrium equations at $E_1$ are

We found that $L_1^{\prime} \leq 0$ if $1+b \leq r \leq2, \; b\leq1$. Hence, $E_1$ is globally asymptotically stable if $1+b \leq r \leq\; 2, b\leq1$.

Theorem 8. $E_2$ is globally asymptotically stable if $2 < b, \; r > \beta$ $R_0 < 1$ and $2 < Y_2 < \frac{\gamma r}{b\beta}$.

Proof. The Lyapunov function is defined at $E_2$ as follows:

Thus, we have $L_2^{\prime}$ as follows:

The equilibrium equations are

Using the equilibrium equations in $L_2^{\prime}$ gives

where

Note that

and $C_V = 0$ if $A_3 = \frac{A_1}{b-1}$. Let $A_2 = A_3 = \frac{A_1}{b-1}$; then, $C_{FV} = -A_1\beta$ and $C_F = A_1 (r(2-Y_2)-\beta V_2+\frac{\beta}{b-1} V_2)$. We have that $C_F < 0$ if $Y_2 > 2$. Thus, we obtain $C_Y$ as

Since $Y_2 > 2$, $C_Y < 0$. Thus, $C_{Z_a}$ becomes

If $A_5 = \frac{A_1 }{\mu_2(b-1)}(\frac{\alpha_f \gamma}{\beta} + \kappa V_2+ \mu _1 Y_2)$ and we let $A_4 = A_1$, we obtain $C^*$ as follows:

We get that $L_2^{\prime} \leq 0$ if $2 < Y_2 < \frac{\gamma r}{b\beta}$. Hence, $E_2$ is globally asymptotically stable.

Theorem 9. $E_3$ is globally asymptotically stable if $b < 1$; then, $p < \lambda < \frac{p \left(\mu_2 r+\alpha_f s_2 Z_{3}\right)}{\mu _2 r+\alpha_f s_2}$, $\frac{\gamma \left(r+\frac{\alpha_f s_1 Z_{3}}{\mu_2}\right)}{1-b} < \beta$, and $r > \frac{2\lambda_z \alpha_f}{\mu_2}.$

Proof. The Lyapunov function at $E_3$ is defined as follows:

and its derivative is

After substituting the points $F_3, Z_3$ and $Z_{a_3}$ in $L_3^{\prime}$, we get

where

The equilibrium equations at $(F_3, 0, 0, Z_3, Z_{a3})$ are

If $A_4 = A_5$, then $B_{FZ} = 0$ and $B_{YZ} = 0$. If $A_3 = A_2$, then $B_{FV} < 0$, $A_3 = \frac{A_1 \beta F_3}{\gamma}$ and $B_V = 0$. If $A_5 = \frac{A_1 F_3 \alpha_f}{ \mu_2 }$, then $B_{Z_a} = 0$. Thus,

and since $b < 1$, we have that $\frac{\gamma \left(r+\frac{\alpha_f s_1 Z_{3}}{\mu_2}\right)}{1-b} < \beta$ and

and

$L_2^{\prime} \leq 0$ if $r > \frac{2\lambda_z \alpha_f}{\mu_2}$. Hence, $E_3$ is globally asymptotically stable.

4.   Analytical solution

Finding the solutions of the system helps to understand the dynamics of the solutions. Some researchers have found numerical solutions for biological systems by using Galerkin meshless method ^[23] or traveling wave solutions ^[24]. Since there are no initial conditions available, the best way is to apply an analytical method which does not require initial or boundary conditions. We shall the use tanh-expansion method to find the solutions ^[25]. The following are the steps to construct the solution:

(1) Transfer the system of PDEs given by (6) into the system ODEs given by (7) using a traveling wave transformation, which is defined by $\xi = k x+c t+\xi_0$.

(2) Assume that

and substituting $(14)$ into the equation of System $(7)$ gives a polynomial of $u$ and its derivatives:

(3) Assume that

where M is a positive integer and

where $\mu$ and $a_i$ are constants such that

(4) Apply the homogeneous balance theorem to find the value of $M$, i.e., balance the linear terms of highest order in the previous equation with the highest-order nonlinear terms.

(5) Substitute Eq (16) into the equations of System (15) to obtain an equation of $\Phi^i$.

(6) Equate the confections of $\Phi^i$ to zero to obtain the $a_i$'s and $\eta$'s. By following Steps (1) and (2), we obtain the following system of equations:

Then, we sum all of the equations to obtain a single equation, as follows:

where

Next, we follow Steps (3) and (4) and balance between the nonlinear term $u^2$ and the highest order of the derivative $u^{\prime\prime}$; we get $2M = 4+M-2$, which satisfies $M = 2$. Thus,

Substituting Eq (20) into ODE (19) gives

Note that

Substituting Eq (22) into Eq (21) and collecting all of the terms with the same power of $\Phi$ together implies the following:

this can be rewritten as

Then, we equate the constant $b_i$'s to zero to obtain the algebraic system of equations and find the $a_i$'s and $\eta$'s.

Thus, the solutions are in the following form:

where

and

5.   Discussion of results

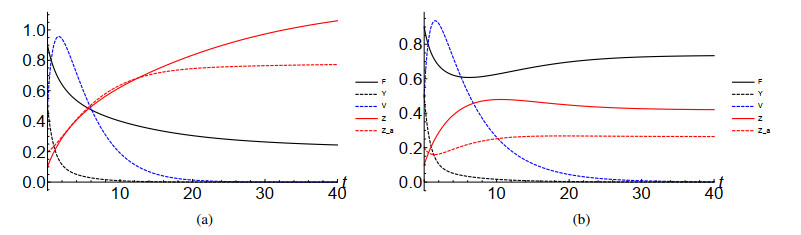
The presented mathematical model aims to elucidate the effects of combining viral therapy with the immune response and its spread. First, we ignored the diffusion terms and solved the problem by using the Runge-Kutta 4th-order method using the values of the non-dimensionless parameters according to Reference ^[16], as follows:

We considered two cases: (a) $\mu_1 = \mu_2 = 0.2, \; s_1 = 0.2, \; s_2 = 0.6$ and (b) $\mu_1 = \mu_2 = 0.7\; s_1 = 0.2, \; s_2 = 0.6$, where the initial conditions are $F = 0.9, \; Y = 0.5, \; V = 0.5, \; Z = 0.1$ and $Z_a = 0.2$.

The results in Figure 2 show that, in Case (a), the unaffected cells $F$ decreases during the treatment when the concentration of activated immune system cells is low. On the other hand, the high concentration of $Z_a$ helps to maintain the level of healthy cells in the body. Therefore, we predict that the combination of biological therapy and virotherapy reduces the side effects of the virotherapy, and the patient's body may become less weak during the treatment.

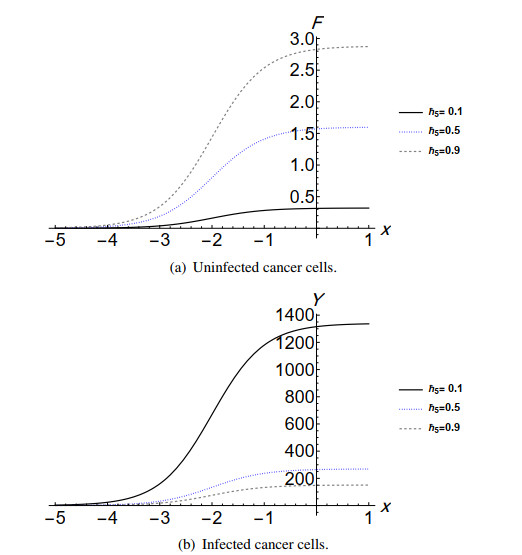
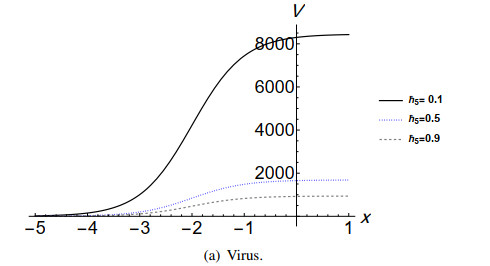
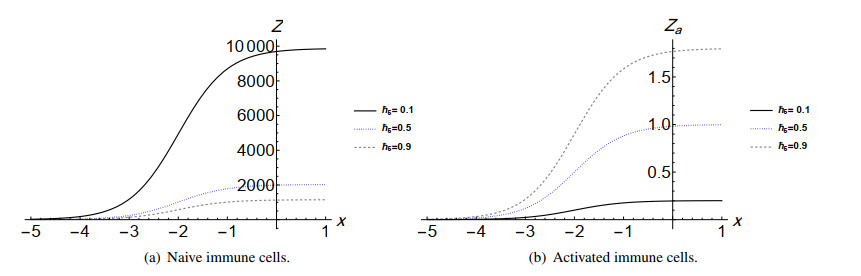
The immune response against cancer cells has been investigated for decades. It has been determined that the immune system actively patrols the body ^[26]. From this standpoint, we investigate the diffusion coefficient of the immune system $d_5$. The solutions of Model (6) are found by employing the tanh-expansion method to study the effect of the treatment on cancer growth. The solution is presented in Eq (24), which indicates that $d_5$ is dependent on $d_1, \; d_2, \; d_3$ and $d_4$. The diffusion of activated immune system cells ($d_5$) increases when the diffusion of the unaffected cells ($d_1$) or naive immune system cells ($d_4$) increases, while it decreases by increasing the diffusion of the virus ($d_2$) or infected cells ($d_3$).

Note that $\eta_5$ is another parameter that affects the solution, as we can see in Figures 3–5. The parameter $\eta_5$ is a coefficient that is associated with $Z_a$. When $\eta_5$ increases, the concentrations of uninfected cells $F$ and activated immune system cells $Z_a$ increase, while the concentrations of infected cells $y$, virus $v$ and naive immune system cells $Z$ decrease. We observed that the immune cells $Z$ have the highest concentrations compared to other components in the system, and this indicates the response of the immune system for viral treatment. {However, the immunotherapy has been widely used in different protocols to treat cancers ^[27]. We predict good results of the combination between immune therapy and virotherapy. The results are aligned with the clinical trial in Reference ^[28]. This clinical trial confirms the possibility of combining the immunotherapy and virotherapy.

6.   Conclusions

In this work, we modified a mathematical model of cancer and virotherapy to study the dynamics of virotherapy with tumor cells and the effects of the immune response. In addition, this modification distinguishes between two types of immune system cells, which are the activated cells and naive cells. The results predict that the high concentration of activated immune cells leads to enhanced results of virotherapy. The activated immune cells can be generated in the patient's body through biological therapy. Moreover, the model was analyzed by using the stability theory of nonlinear systems. We studied the stability of five equilibrium points and determined the conditions of the existence and local and global stability of the equilibrium points. As a result, the success of viral treatment depends on the size of the burst $b$, the viral infection rate $\beta$ and the clearance rate of viruses $\gamma$, which depend on the type of the virus. The treatment by virotherapy can be more effective by stimulating the activated immune cells. Furthermore, we found the analytical solutions for the studied model by using the tanh-expansion method because of a lack of initial and boundary conditions. We found that, if the concentration of activated immune cells $Z_a$ increases, the unaffected cells $f$ increase, which indicates the improvement of the treatment results.

However, for future work, the studied model can be solved numerically by finding the associated initial and boundary conditions based on real data, and by using the Galerkin method ^[23]. Also, diffusion terms can be added in many biological models to study the spread of the model components and deal with a system of PDEs.

Conflicts of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Appendix

The definitions of $b_0, b_1, b_2, b_3$ and $b_4$ that are related to the characteristic polynomial for $E_2$ are as follows:

The definitions of $a_0, a_1, a_2, a_3, a_4$ and $a_5$ that are related to the characteristic polynomial for $E_4$ are as follows: