1.
Introduction
The term "infectious diseases" refers to illnesses caused by living organisms, usually parasites and microorganisms, that spread from one host to another either directly or indirectly. Infectious diseases have been a significant concern in our society. These illnesses can sometimes pose severe threats and lead to epidemics. Medical research has rapidly advanced in identifying and controlling three primary characteristics: Infectivity, epidemic potential, and uncertainty, which have helped reduce the burden of such diseases. Infectious diseases are modelled mathematically as a dynamic transmission cycle involving interactions between susceptible and diseased hosts. These interactions are usually expressed as a coupled ordinary differential equation. The SIR model takes into account several variables while examining infectious disease systems. Several models that examine significant aspects in the research of infectious diseases include SIS, SIRV, SEIR, SVEIRS, SIQR, SEIRV, SEIQS, and others [1,2,3,4,5,6,7]. Understanding disease dynamics is complex due to factors like environmental fluctuations, making it challenging to collect precise data. For example, temperature variations can significantly impact the reproduction rate of disease-spreading bacteria, influencing the disease's dynamics. As a result, it's essential to consider how uncertainty in biological parameters affects disease behavior. If incorrect parameter values are used, model outputs may be biased, so sensitivity analysis is necessary for understanding how model outputs change in response to parameter variations. When studying the transmission of infectious diseases, sensitivity analysis is often used to develop strategies for slowing infection spread by targeting key model parameters, such as the primary reproduction number R0. The literature provides information on dynamic parameter sensitivities in infectious spread for traditional SIR and SEIR models to maximize the usefulness of observed data, with the primary source of uncertainty being the random variability of the included parameters.
Interactions between species can impact the quality of life for all involved. These interactions are crucial for an organism's survival since its primary objective is to stay alive. Without these relationships, life as we know it would be impossible. It's remarkable how fascinating organism interactions can be and can be studied using mathematical models, an exciting field within ecology research [5,7]. Different factors, such as environmental conditions, impact the growth and balance of living populations, and modeling can be an invaluable tool for understanding their dynamics. Organisms, typically proto-microorganisms and parasites can cause infectious illnesses through direct or indirect transmission from one host to another. Due to their reason to periodically spread like epidemics and cause serious problems, infectious diseases have recently become a significant worry in our culture. The three major components that lessen the severity of these disorders are infectivity, epidemic potential, and uncertainty. The medical community has made great strides in recognising and managing these components. The dynamic transmission cycle is a mathematical model of an infectious illness that involves interactions between susceptible and infected hosts. Typically, these interactions are expressed as a linked set of ordinary differential equations.
Fractional calculus is a mathematical analysis that extends beyond differentiation and integration conventions. Fractional calculus concerns derivatives and integrals of non-integer orders, such as fractions or decimals, while classical calculus concentrates on the powers of integers. The Caputo operator is a valuable tool for problem-solving and is commonly used to handle real-world challenges. The main difference between the Riemann-Liouville operator and other fractional operators is the singularity quality of the kernels. They are applied in roughly related ways to observe different model dynamics. It follows that using these operations would inevitably result in better outcomes. Researchers attempting to understand better a model's dynamics advise using fractional operators with non-singular kernels. Establishing the C-F derivative has addressed certain standard limits on fractional derivatives [8]. The C-F derivative outperforms the most commonly used techniques for assessing human knowledge [9]. The operator's performance and its benefits were validated using various approaches. Studies on numerous scientific, engineering, and mathematical models have proved their usefulness. However, experts from real-world cases are a more meaningful example [10,11]. Atangana and Baleanu introduced a derivative operator with a non-singular kernel. It utilizes the Mittag-Leffer function and is in a convenient area for modellers of real-world situations because of its non-local and non-singular kernel. Over the past few decades, the Atangana-Baleanu variant has obtained strong research value and applicability in diverse fields, particularly in biological models [12]. This fractional derivative introduced non-local and complex dynamic behavior and numerous natural results. In addition, since biological models are expected to have a memory effect and hereditary features, which can be defined more precisely using fractional calculus, the solution of the fractional order system is expected to obtain how to control epidemic diseases [13]. The authors of this study investigated the sensitivity of the model solution in delay differential systems using variational and direct methods [14]. Corruption and terrorism have become significant issues in many nations worldwide. However, more needs to be written about the relationship between the two. To address this, the author has developed a novel fractional-order mathematical model to explore the coexistence of terrorism and corruption [15]. This article examines the authors' mathematical model of COVID-19, which incorporates a fractional-order system and considers the effectiveness of vaccination [16].
Fractional-order models have become increasingly popular in control engineering, physics, neural networks, and medicine. They can predict the condition of a system at any future moment by considering its current state and all of its past states. Due to its practicality, researchers are interested in fractional-order calculus. The concept of fractional-order differentiation and integration was first introduced by two prominent figures in mathematics history, Riemann and Liouville. The R-L and Caputo fractional derivatives are examples of fractional differential operators that use a power law kernel. These operators have precise definitions and have been widely researched and applied across various disciplines [17]. However, their limited applicability and inability to represent other natural and artificial systems have hindered their development. To overcome these limitations, novel C-F fractional-order derivatives have been developed based on the exponential kernel, successfully describing various real-world events [18]. Several mathematical models with C-F fractional order have been discussed in the literature.
Numerous numerical techniques have been developed to solve biological models and fractional-order differential equations [19]. The Newton interpolation formula, the Toufik-Atangana approach, the Adam-Bashforth method, the predictor-corrector method, and the Runge-Kutta technique are a few of the numerous numerical algorithms that have been the subject of extensive literature [17,18,19,20,21,22,23]. To solve non-linear systems numerically, the Toufik-Atangana approach is widely used [24,25]. Recently, a novel numerical system called the Toufik-Atangana numerical system has emerged as a potential solution to the problems with the Adams-Bashforth approach [26,27]. Combining the fundamental theorem of fractional calculus with the two-step Lagrange polynomial, this new methodology develops a novel and very efficient numerical method [26]. Using this approach, problems can be resolved quickly and accurately. A biological model has been subjected to many fractional operators using the Toufik-Atangana numerical framework to get the required findings. Stability analysis is an essential method in numerical analysis that yields effective results. When expressed mathematically, stability is necessary for spectrum analysis of real-world problems [28]. Hyers expounded on Ulam's 1940 introduction of the U-H stability hypothesis in 1941. As previously stated, the optimal approximation or exact solution to the issue is the basis for computing the stability. Furthermore, it is simple to implement and evaluate the recommended stability ideas [28,29].
The following subjects in this work: The definitions and basic ideas of fractional calculus are covered in Section 2. We examine a non-integer C-F model for infectious diseases in Section 3. The positivity and sensitivity analysis of the model under discussion is covered in detail in Section 4. In Section 5, we focuses on the proposed model solution's existence, uniqueness, and stability in the U-H. In Section 6, we present the numerical method for the C-F operator Adams-Bashforth scheme. Section 7 features numerical findings and a graphic analysis. Finally, in Section 8, we discuss the findings of the investigation.
2.
Definitions and basic concepts
The essential definitions and theorems relevant to the C-F have been provided in this section.
Definition 2.1. [18,30] Suppose that ϑ ∈ H1(q1,q2), q1<q2, and ς∈(0,1), so the C-F fractional differential operator. Then, we have
where B(ς) is the normalization function with B(0)=B(1)=1.
However, if ϑ ∉ H1(q1,q2), then we have
Definition 2.2. [18,31] Suppose that ϑ ∈ H1(q1,q2), q1<q2, and ς∈(0,1), so the C-F fractional differential operator. Then, we have
Definition 2.3. [18,32] Suppose that ς is the order of integral in the C-F integral operator. Then, we have
3.
Fractional order of infectious diseases model
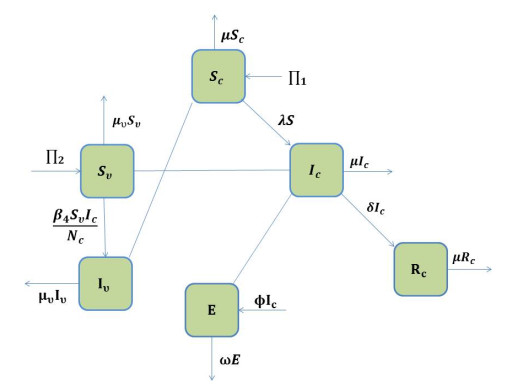
This section presents the generalized form of the infectious spread transmission dynamics with specific parameter values for a given population. In this paper, we build upon the fundamental SEIR contagious disease model by expanding it to the SEQIRDV model [33], which considers different disease stages and traits. There are seven subpopulations within the overall population N: susceptible (S), infected (I), exposed (E), recovered (R), quarantined (Q), dead (D), and vaccinated (V). Realistically, the natural death rate caused for each subpopulation is represented by a value μ. A second parameter, Π, indicates the recruitment of susceptible individuals in any infected population at any time k. At the disease transmission rate β, susceptible people can be exposed and become members of the diseased class. We assume that specific individuals receive vaccinations for a particular infectious disease at a rate of ν. The rate at which people contract the disease is β, and they move on to the affected group after a latent period of γ. Based on the vaccination's efficiency measure σ, the interaction of those who have had vaccinations falls into this category. With a predetermined period until death ρ, the infected population is confined for a proposed average length of δ, either entering the dead population with a disease mortality rate of τ or the recovered class with a recovery rate of ω. Depending on the availability of vaccines for the particular condition, the class "vaccinated" is added. The flowchart of the infectious dynamical disease system (3.1) is represented by Figure 1. After accounting for these variables, the dynamical system that results is as follows [33]:
with initial conditions S(0)≥0, E(0)≥0, I(0)≥0, Q(0)≥0, R(0)≥0, D(0)≥0 and V(0)≥0.
Fractional derivatives in mathematical biology offer a versatile framework for modeling various biological phenomena, including vaccination processes and recovery dynamics. By extending beyond traditional epidemic and noninfectious disease models, researchers gain a deeper understanding of the complex behaviors exhibited by biological systems. This enables them to develop innovative solutions to critical vaccination research and healthcare issues by incorporating fractional calculus into their mathematical models. Initially, we transformed the model with integer order into one with fractional order. We apply the C-F derivative in the system (3.1), and then we get
4.
Preliminary analysis of the model
4.1. Positivity and boundedness
In fractional order modeling of biological systems, the population remains positive and bounded over time to represent biological constraints accurately. Positivity and boundedness are essential in fractional order models to ensure stability, realistic behavior, and relevance to real-world situations. These features are necessary due to the complex dynamics introduced by fractional calculus. Positive states play a crucial role in maintaining a system's stability and meaningful behavior. In contrast, positive outputs are vital for applying and understanding the model's results in practical applications. Boundedness ensures that the system does not exhibit unlimited growth, which is essential for stability and control. Furthermore, boundedness guarantees that the behavior of a system remains predictable and controllable, thus facilitating the analysis of system performance and reaction. The proposed model has a built-in feature where its solutions are always positive and bounded. We ensure that all state variables have non-negative values for any time k>0. This [34] means a trajectory starting with a positive initial condition will stay favorable for k>0. Therefore, system (3.2) provides that
Since N(t)=S(k)+I(k)+E(k)+Q(k)+D(k)+R(k)+V(k) is total population, we have
then one has
Therefore, we have
which provides the feasible region for the infectious diseases model, and Ω is positively invariant. Thus, the proposed model (3.2) is well-posed mathematically.
4.2. Sensitivity analysis
This study gives us insights into each parameter's importance in the disease's spread. This information is crucial not only for planning experiments but also for integrating data and simplifying complex models. Sensitivity analysis is often used to assess the resilience of model predictions to changes in parameter values, as there are sometimes errors in data collection and assumed parameter values. This tool helps identify the characteristics that significantly impact the threshold R0 and should be the focus of intervention strategies. Sensitivity indices provide a way to measure the proportional change in a variable resulting from a change in the parameter. We use a variable's normalized forward sensitivity index concerning a specific parameter to achieve this objective. This index is defined as the ratio of the relative change in the variable to the relative change in the parameter. The sensitivity index can be determined using partial derivatives if a variable is differentiable concerning the parameter. We conducted a sensitivity study in this section to determine the impact of each parameter on the R0. A sensitivity analysis can also determine the critical parameters vital to illness management. This method ascertains the relative contribution of each parameter value to the R0. Therefore, we have
The system's qualitative characteristics are being considered while organising the relevant parameters based on their impact on the value of R0, which is quite beneficial. The results of this investigation will help identify the most crucial disease control factors. We can utilize sensitivity indices to determine the effect of a parameter change on the state variable. These indices are calculated using the definition provided in the paper [34,35]. To estimate the sensitivity index, we use partial derivatives, as shown below:
The sensitivity indices for different parameters are present in Table 1. These indices have been calculate using the starting values, except for σ. Figure 2 shows the sensitivity indices of R0 for the considered parameters of interest. The results indicate that Π, β, δ, and μ are highly significant characteristics, as seen in Table 1 and Figure 2. Based on the sensitivity analysis results, it was found that the R0 values increase or decrease in direct proportion to changes in the values of Π, β, σ, δ, μ, ν and γ. The reproduction number within the defined limits has been analyzed, considering the following factors. After reviewing the analyses and graphs, it is evident that precautionary measures should be taken to prevent the spread of the disease by improving adverse conditions and reducing factors that contribute to increased reproduction numbers. Figure 3(a) is the plot of R0 versus the β and Π. Figure 3(b) is the plot of R0 versus the γ and δ. Figure 3(c) is the plot of R0 versus the Π and μ. Figure 3(d) is the plot of R0 versus the σ and ν. Notably, we have observed that μ is quite sensitive, and raising this parameter could result in a notable drop in the R0 value. Consequently, limiting these factors can aid in the prevention of the spread of illness. The variables are considered when examining the relevant reproduction number within the specified limits. Based on the evaluations and visual representations, it is concluded that appropriate measures should be implemented to prevent the spread of the disease. This can be achieved by decreasing the factors that contribute to the positive growth rate of reproduction numbers and raising the factors that have a detrimental effect on it. Hence, it can be concluded that increasing awareness about quarantine and vaccination among affected individuals can significantly reduce the spread of infection within the population.
5.
Essential existence and uniqueness of the solutions
Here, we examine the uniqueness and existence of solutions using the fixed point theorem, which is essential for the proposed model [31,36]. The C-F fractional integral operator, when applied to system (3.2), yields
Define the following kernels:
then we have
Theorem 5.1. If the dissimilarity listed below holds:
Afterwards, the contraction mapping and Lipschitz condition are convinced by the kernel M1.
Proof. Assume that S and S1 are any two functions, then we get
Let Υ1=βϖ2+υ+μ, we do suppose that S,E,I,Q,R,D and V is bounded functions, i.e., ‖S(k)‖≤ϖ1, ‖E(k)‖≤ϖ2, ‖I(k)‖≤ϖ3, ‖Q(k)‖≤ϖ4, ‖R(k)‖≤ϖ5, ‖D(k)‖≤ϖ6 and ‖V(k)‖≤ϖ7.
Hence, kernel M1 satisfies the Lipschitz condition and since
then it is also a contraction for M1.
Similarly, kernels M2, M3, M4, M5, M6, and M7 satisfy the Lipschitz condition, respectively, as follows:
Equations (5.4) and (5.5) are used to apply the previously described kernels, which transform system (5.1) into
We now introduce the following recursive formulas:
where the initial condition are
With regard to the recursive formulas, the differences between successive terms can be represented as
Note that
After solving system (5.8), we apply the usual supremum norm to both sides of the first equation of system (5.8), then we obtain
Using Eq (5.10) and the triangle inequality, we get
Thus, using the Lipschitz constant Υ1 to propitiate the Lipschitz condition, the kernel M1 enables us to determine
Thus, we obtain
In a similar manner, we get
Theorem 5.2. If there ∃ a time k0>0, then the ensuing disparities are valid:
solutions exist for the infectious disease system.
Proof. Let S(k), E(k), I(k), Q(k), R(t), D(k), and V(k) be bounded functions and use the Lipschitz condition. Now, in Eqs (5.13) and (5.14), using the recursive method, we obtain
Thus, it is proven that the aforementioned solutions exist and continue to exist. To demonstrate the function is a solution of system (3.2), we make the following assumptions:
Then, we have
Repeating this process recursively, it becomes
At the point k0, we get
As r →∞ in Eq (5.20), then we get
Similarly, we get
We establish that a system of system (3.2) solutions is unique. Consider the possibility that there is another set of model (3.2) to determine the uniqueness of the solution. We have S1(k), E1(k), I1(k), Q1(k), R1(k), D1(k), and V1(k); then
When we apply the norm to Eq (5.21), we obtain
Using the kernel's Lipschitz condition, one can achieve
By reducing the complexity of Eq (5.23), we get
Theorem 5.3. The proposed model has a unique solution if the following conditions are hold:
Proof. Using Eq (5.24), we have
Implying that
we obtain
Continuing in the same manner, we have
As a result, we proved that system (3.2)'s system of solutions is unique.
Stability analysis
We employ nonlinear functional analysis to investigate the Ulam-Hyers (U-H) stability [28,37] of the proposed fractional model (3.2). Eighty-four years have passed since Professor Ulam presented the stability problem to the University of Wisconsin Mathematics Club. Ulam asked whether a proposition remains valid or approximately valid when the hypothesis is slightly modified [28,38]. This subject is intriguing and significant in multiple scientific disciplines, motivating numerous individuals to pursue its investigation. The current name for this topic is the U-H stability problem. Initially, the focus was on the stability of group homomorphisms. One year later, Hyers resolved the inquiry of the additive mappings across Banach spaces using the "contraction mapping theorem". After this significant advancement, numerous investigations were conducted on Ulam's challenge using diverse approaches and variations. Rassias extended the findings of Hyers [39]. Instead of using a positive constant, he employed a dominating function to regulate the estimate. This problem is commonly referred to as the Ulam-Hyers-Rassias stability problem or the generalized U-H stability problem.
In recent decades, numerous research articles have been published on U-H stability, focusing on ordinary differential equations (ODEs) [40,41]. ODEs result in productive outcomes, encompassing both linear and nonlinear equations [42,43]. Many recent studies have focused on the U-H stability concerning fractional systems [44]. The concepts of existence, uniqueness, and U-H stability have been established in various functional systems. U-H stability measures the difference in solutions of differential equations with fractional order. This stability ensures that controlled systems remain stable and perform predictably, even with slight variations in the system dynamics. When modeling physical processes with fractional-order dynamics, U-H stability guarantees that the model stays accurate even when minor changes or approximations are made to the governing equations. U-H stability is used to analyze the sensitivity of solutions to small changes in boundary data for fractional differential equations with boundary conditions. This analysis ensures the reliability of the solutions in practical applications. The concept of U-H stability is beneficial for analyzing and implementing fractional-order systems. It provides a framework to ensure that solutions remain stable even when subjected to minor disturbances, which is essential in numerous practical situations. For simplicity, we consider the proposed model (3.2) to be as follows:
where
Applying the fractional integral on (5.30), we obtain
Definition 5.1. The proposed model (3.2) is UH stable if there exists ς>0 and along with the condition for any ϵ>0 and ˉU∈B, if
then ∃ U∈B, and B in the model (3.2),
such that
where
Remark 5.1. Let a small perturbation κ∈C[0,T], such that κ(0)=0 with the following condition: ‖κ(k)‖≤ˉϵ, for k∈[0,T] and ˉϵ>0.
Lemma 5.1. Let the solution ˉUκ(k) of the perturbed system
hold the condition
where
Proof. Applying the fractional integral in Eq (5.33), we obtain
Also,
Using Remark 5.1, we obtain
This completes the proof.
Theorem 5.4. The proposed model (3.2) is UM stable if
Proof. Let ˉU be the solution of Eq (5.32) and with help of uniqueness, U be a unique solution of the system (5.30), then we have
Simplifying the above equation, we obtain
where
Hence, the proposed model (3.2) is UM stable.
6.
Numerical scheme
We present a numerical solution for the model (3.2) using the Adams-Bashforth (A-B) technique. Owolabi and Atangana et al. [45] introduced a three-step A-B technique with the C-F fractional derivative, which we used to determine the numerical scheme for the fractional-order system (3.2). Take into consideration the C-F derivative of the fractional differential equation
By utilising the C-F fractional integral on both sides of Eq (6.1), we obtain
We have divided the time interval into smaller intervals with steps of h, then we get ke+1=ke+h, k0=0, e=0,1,2,...,e−1. We put k=ke+1 and k=ke in Eq (6.2). We have found the difference in the resulting equations by performing a computation, then we get
We are estimated the integral ∫ke+1keF(Y,E(Y))dY with the approximation of ∫ke+1keQ2(Y)dY, where Q2(Y) is the Lagrange polynomial of points (ke−2,F(ke−2,E(ke−2))), (ke−1,F(ke−1,E(ke−1))) and (ke,F(ke,E(ke))). Thus,
where Lj(Y) is the Lagrange basis polynomials on the point ke,ke−1,ke−2.
Let Ee=E(ke), and v=ke+1−Yh, after replacing the Lagrange basis polynomials and performing integration, we obtain the following result:
Using Eq (6.5) in Eq (6.3), we have
The error with this technique is
The proposed model's numerical simulations are generated using the three-step A-B approach for the C-F fractional derivative in Eq (6.6).
Let the vectors
and
where the following are the functions specified by system (3.2), we have
We can express model (3.2) in vector form as shown below:
Equation (6.6) is utilized to obtain the solution of model (3.2), which is expressed through the iterative formula given below:
Let E0=E(k0)=[S(k0),E(k0),I(k0),Q(k0),R(k0),D(k0),V(k0)]T, Ee−2=E(ke−2), Ee−1=E(ke−1), Ee=E(ke) and Ee+1=E(ke+1), then
We have obtained the iterative formula:
Stability analysis of numerical scheme
Here, we are analysing the stability of the fractional A-B scheme
Now, rewrite Eq (6.11), then we have
Using Eq (5.30), we have
Afterward, we apply the Von-Neumann stability analysis for the terms in the aforementioned equation.
So that
which reduces to
A recursive formula is applied, when e=0, we have
Simplifying the previous equation (6.15), we have
If
then, we suppose that
we have
Simplifying the previous equation (6.15), we have
Hence, when applied to Eq (5.30), the three-step A-B method with the C-F derivative is conditionally stable.
7.
Numerical results and graphical analysis
In this section, we simulate the non-linear fractional proposed model using a novel numerical technique that uses the C-F non-integer operator. We displayed graphical findings for various fractional orders and infection rates during the simulation. To comprehend the system's behavior and operation, tracking and controlling the infection rate is imperative. Utilizing the numerical approach outlined in Section 6, we followed the instructions and finished the simulation results. We examined numerical findings for various fractional orders and time intervals using MATLAB R2016a. As such, we can see how adjusting the parameters and starting conditions affects the model's predictions through the simulations and improves our grasp of the dynamics of the model. The fractional order analysis's graphical results have been more illuminating and broadly applicable than other related efforts. The following parameter values have been applied to the simulation: S(0)=100, E(0)=50, I(0)=30, Q(0)=20, R(0)=18, D(0)=2, V(0)=60, Π=20, β=2×10−4, ν=1×10−3, μ=0.3, γ=5.1, σ=0.05, δ=5.1, τ=0.04, ω=0.03 and ρ=15. For this study, we have chosen specific orders to represent the complex nature of the system under examination, as arbitrary order derivatives offer greater degrees of freedom and provide a wide range of geometries. Figure 4 depicts the state variable plots of time graphically in the suggested model using the ABM method for different orders (ς): 0.99,0.96,0.93 and 0.90. The fractional suggested model (3.2) for various values of ς has been numerically simulated and shown in Figures 5 and 6.
When we place a classical order, the infected population is higher, but when we place an order with ς=0.85, the infected population is smaller, as illustrated in Figure 5. When placing a classical order, the recovered and quarantined population is smaller. However, when placing an order with ς=0.85, the recovered and quarantined population is more significant.
We consider a small order, leading to a more significant impact on the dead population than a more substantial higher order. Figure 7 depicts the 3D phase trajectory of the system (3.2) as the order of derivative = 1 and μ varies. Figure 8 depicts the time series graph of the system (3.2) when the order of derivative (ς)=0.99 and μ varies. When we place the value of μ=0.45, the susceptible, quarantined, and vaccinated population is smaller. However, when we set μ=0.30, the susceptible, quarantined, and vaccinated population is more significant, as shown in Figure 8. If we choose the smaller value for μ, we have large populations of these populations. The dead population becomes more extensive if we choose the smaller value for μ. Figure 9 depicts the time series graph of the system (3.2) when the order of derivative (ς)=0.99, δ varies and ν varies. The infected and quarantined populations are sensitive to parameter δ increasing order. The exposed and infected populations are sensitive to parameter ν. Figure 10 depicts the 3D phase trajectory of the system (3.2) as the order of derivative = 1 and β varies. Figure 11 depicts the time series graph of the system (3.2) when the order of derivative (ς)=0.99 and β varies. When we place the value of β is small, we get the susceptible, infected, and recovered population is more significant compared to the more considerable value of β. The dead population becomes more extensive if we choose the smaller value for β. Figure 12 depicts the 3D phase trajectory of the system (3.2) as the order of derivative = 1 and τ varies. Figure 13 depicts the time series graph of the system (3.2) when the order of derivative (ς)=0.99 and τ varies. The exposed and recovered populations are not very sensitive to parameter τ. We consider a small value for τ, leading to a more significant impact on the quarantined population than a more substantial value of τ.
The numerical simulation suggests we gain more reliable insights into behavior within specific ranges with more precise parameter information. We can explore the model's behavior under different input parameter values. Therefore, this study highlights the advantages of using numerical techniques in real-world disease models.
8.
Conclusions
In this paper, we discuss the SEIQRDV model, which focuses on the spread of infectious diseases and considers positivity, boundedness, and sensitivity. We have created a fractional order model based on a described integer order contagious disease model. Using fixed-point theory, we have proven the uniqueness and existence of solutions to this model under specific circumstances. We have also used a novel numerical technique supported by the A-B scheme to find the numerical solution. By plotting the model's output at different fractional orders and parameter values, we have observed how the population curves respond to these variations. However, it is important to note that the uncertainty resulting from random fluctuations in the model parameters cannot be eliminated. Additionally, determining which parameters are essential in the model can be challenging, causing sensitivity analysis for such a model to be difficult. The sensitivity analysis of the basic reproduction number has shown that the model's parameters have a significant impact. The results indicate that the recruitment and transmission rates are the most influential factors contributing to a substantial increase in the R0. These findings provide valuable insights into the mechanisms that affect the dynamics of infectious disease transmission and offer strategies for reducing disease transmission.
We observe that even slight changes in parameters such as β, δ, μ, ν, and τ result in different population dynamics. These efforts will enhance our understanding of this paradigm and enable us to obtain more information successfully. Moreover, the results indicate that as the number of infectious individuals in the community decreases, the number of recovered individuals in the system increases. This suggests a correlation between the decrease in the number of sick individuals and the increase in the number of those who have effectively recuperated from the illness. The proposed model provides valuable insights into disease transmission dynamics using fractional-order derivatives. The results of our investigation are crucial for improving the accuracy of the infectious disease model and formulating successful strategies. Furthermore, our investigation indicated that meaningful parameters can be found and examined even in uncertainty. These research results suggest expanding this work to encompass control theory and other fractional operators.
Author contributions
Parveen Kumar: Formal analysis, Writing–original draft, Methodology, Software, Validation; Sunil Kumar: Supervision, Conceptualization, Investigation, Writing–review and editing; Badr Saad T Alkahtani: Validation, Writing–review and editing, Conceptualization, Visualization; Sara S Alzaid: Investigation, Formal analysis, Visualization, Writing–original draft. All authors have read and agreed to the published version of the manuscript.
Acknowledgement
This research was funded by Researchers Supporting Project number (RSPD2024R526), King Saud University, Riyadh, Saudi Arabia.
Funding
This research was funded by Researchers Supporting Project number (RSPD2024R526), King Saud University, Riyadh, Saudi Arabia.
Conflict of interest
All authors declare no conflicts of interest.









 DownLoad:
DownLoad:


















