Fractional orthotriple fuzzy Choquet-Frank aggregation operators and their application in optimal selection for EEG of depression patients

1.   Introduction

The study of flow phenomena in porous media (see ^[1,2,3,4,5]) has been the subject of extensive research endeavors conducted by both theoretical and experimental investigators over the past 150 years, owing to its broad ranging applications across various scientific and technological domains such as agricultural engineering, geophysics, soil mechanics, groundwater hydrology, filtration processes, petroleum, ceramic, and textile engineering, and so on. Recently, it has been a subject of interest in biomechanics and biotechnology, also. The movement of gases and liquids through porous media is common to many chemical processes; for example a chemical catalytic reactor filled with porous pallets is impregnated. Therefore, researchers have always been attracted to this intriguing field. Vafai and Kim ^[6] derived an exact solution to examine the dynamics of the interface region between a porous medium and the fluid layers. A numerical investigation of a convective mixed non-Newtonian nanofluid in a two-lid square cavity in a porous medium was done by Nazari et al.^[7]. Motion of a micropolar Casson fluid in a porous material across a stretched platter was simulated numerically by Dabe et al. ^[8]. Awais et al.^[9] explored the heat-mass transfer phenomena for the Casson fluid submerged in a porous medium past a shrinking wall, subject to the Lorentz force and a heat source. Kodi et al.^[10] investigated unsteady magnetohydrodynamic flow of Jeffrey fluid in porous media with the influence of Soret effects, Hall current, and thermal radiation. Lio ^[11] conducted a comprehensive study on the dynamic boundary problem associated with the flow of non-Newtonian Bingham fluids within fractal porous media, employing both analytical and numerical methodologies. A modeling of chemically reactive porous media through a multiple scale approach was studied by Saeedmonir ^[12].

The investigation of transport phenomena of electrically conducting fluid through porous media under the influence of a magnetic field encompasses several scientific and technical domains, including metallurgy, nuclear engineering, aerodynamic, and earth science. Magnetohydrodynamics (MHD) is the field of physics that studies the dynamic behavior of the interaction of electrically conducting fluids (such as plasma, ionized gases, liquid metal, and saltwater) and magnetic fields. The field was first developed by Hannes Alfven in 1942. It combines the principles of both fluid dynamics and electromagnetism. This intriguing field has various applications in engineering, biotechnology and the chemical, petroleum, and metallurgical industries. These include MHD power generators and pumps, metal casting and solidification, liquid metal cooling and heat exchangers, ion propulsion, magnetic drug targeting, treatment of cancer tumors, magnetic therapy, and so on. Therefore, researchers (see ^{[13,14,15,16,17,18,19,20]}) are always urged to explore more research opportunities in this field and contribute sequentially to the advancement of magnetohydrodynamic flow. Geindreau and Auriyault ^[21] studied the behavior of MHD flows in porous media. The behavior of magnetohydrodynamics convective movement of heat through a vertical movable plate due to the impact of viscosity and thermal conduction was investigated by Seddeek and Salama ^[22]. Magnetohydrodynamic flow modeling past an unstable stretched sheet with heat radiation and fluctuating fluid characteristics was explored by Megahed et al.^[23]. The impact of heat production and Newtonian heating on dusty fluid movement in magnetohydrodynamics between two parallel plates was examined by Ali et al.^[24]. An estimaation of the Nusselt number for a flow between two horizontal plates with an MHD second-order slip model was done by Simsek and Hatice ^[25]. Awais et al.^[26] researched the behavior of activation energy and viscous dissipation on the MHD Eyring-Powell fluid with Darcy-Forchheimer and vacillating fluid characteristics.

Couette flow is a particular sort of flow where shearing actions of fluid layers take place between two parallel channels, where one is stationary and the other is in constant motion. The designation "Couette flow" is attributed to Maurice Marie Alfred Couette, a French physicist who conducted pioneering investigations on this particular type of flow during the late 19th century. However, the generalized Couette flow broadened this concept to more complex scenarios, such as investigating the rheological properties of non-Newtonian fluids or circumstances in which a fluid's characteristics vary over time or space. This model is similar to plain Couette flow but the difference is the applied external pressure gradient virtue of which the fluid motion takes place. The generalized form allows for a broader understanding of fluid behavior in different flow conditions. Also, several analytical and numerical works in literature are devoted to the study of conducting fluid flow between two parallel plates (see ^{[27,28,29,30,31,32,33,34,35,36]}).

Chemical reaction plays a crucial role in the study of fluid flows with their ability to influence temperature, the magnetic field, heat generation or absorption, material properties, electrical conductivity, species transport, altering rheological characteristics, and so on. A First-order chemical reaction is the reaction in which the reaction rate is directly proportional to concentration of a reactant or reacting species raised to the firsy power (see Eq (2.22)). This means that if the reaction rate is high, it will consume the species rapidly leading to significant variation in the concentration profile. In the case of a slow reaction rate, it will take a longer time to diffuse and transport within the flow resulting in a smoother concentration profile. The presence of first-order reactions plays a crucial role in mixing and generating coupled heat and mass transport phenomena between the fluid layers and the corresponding plates that can enhance or hinder reactant mixing. A first-order reaction can create concentration gradients in the fluid flow. As the reacting species is consumed or produced, its concentration changes along the flow direction. Maintaining the liquid flow under chemical reactions constitutes several significant challenges in technological problems. Therefore, researchers alwyas highlight the importance of chemical reactions in the studies of fluid flows. Redappa and Geetha ^[37] explored MHD induced convection of Cu, Ag, and $\text{Fe}_{3}\text{O}_{4}$ nanoparticles of Jeffrey nanofluid in a porous medium across a moving plate with a heat source and chemical reaction. Maiti et al.^[38] worked on the squeezing behavior of nanofluid flow between two aligned horizontal boundries with a first-order chemical reaction and velocity slip. Mythreye et al.^[39] conducted a comprehensive study on the influence of chemical reactions on a semi-infinite vertical permeable moving plate, considering heat absorption, magnetohydrodynamic convective heat transfer, and mass transfer. A thorough investigation of radiative and chemically reactive MHD nanofluid under heat and mass transfer through an infinite moving vertical plate was done by Arulmohzi et al.^[40]. A numerical investigation of magnetohydrodynamic heat-mass transport of Jeffrey fluid accross a stretched surface under a chemical reaction and thermal radiation was presented by Narayana et al.^[41]. Gulle et al.^[42] treated MHD Jeffrey fluid through an inclined erect plate under the effects of Soret ejection and chemical reaction. Nisar et al.^[43] proposed a semi-analytical solution for MHD natural convective Jeffrey fluid under a thermal source and chemical reaction. Idowu ^[44] considered the impact of heat and mass transportation on unsteady MHD oscillatory Jeffrey fluid flow through a horizontal channel under a chemical reaction.

The investigation of non-Newtonian fluid (see ^{[45,46,47,48,49]}) is a fascinating area of contemporary research since it differs from the conventional behaviors observed in a Newtonian fluid. Non-Newtonian fluids have a spectrum of viscosities that react differently to external stress in contrast to the linear stress-strain connection seen in Newtonian fluid. Many salt solutions and molten polymers are classified as non-Newtonian fluids. A few of them are toothpaste, corn starch, shampoo, cosmetics, paints, and blood. Shear-thickening and shear-thinning liquids are included in this category, with some examples including Bingham fluid, viscoelastic fluid, Jeffrey fluid, Casson fluid, Maxwell fluid, Carreau fluid, and second-grade fluid. Exploring the complexities of these non-Newtonian fluids not only broadens our comprehension of basic fluids but also holds immense potential for advancement of real-world applications.

Jeffrey fluid, a non-Newtonian fluids, is a rate-type material and shows a viscoelastic effect. It is appropriate, particularly for those fluids that exhibit shear-thinning behavior. It has multiple applications in polymer processing, the food and beverage industries, biomechanics, pharmaceuticals, and the gas and oil industries. Therefore, it has gained significient attention from a multitude of scientists and researchers. Mopuri et al.^[50] studied the behavior of magnetohydrodynamic Jeffrey fluid through an inclined vertical porous plate. Fiza et al.^[51] investigated the three-dimensional rotating MHD Jeffrey fluid flow across two parallel plates under the action of hall current. Analysis of heat transfer in the MHD Jeffrey fluid's channel flow under generalized boundary conditions was done by Aleem et al.^[52]. An examination of the hemodynamics of different properties of liquid on the peristaltic mechanism of MHD Jeffrey fluid was done by Devya et al.^[53]. M. Qasim ^[54] explained the phenomena of heat-mass transport of Jeffrey fluid over a stretched sheet. Dalir ^[55] studied the phenomena of heat transfer and entropy generation of Jeffrey fluid past a stretched sheet under forced convection. The impact of the Soret number on Jeffrey fluid flowing over an erect moving plate using the finite element method was analysed by Pramod et al.^[56]. A stability analysis on rheological behavior of Jeffrey fluid in the presence of gyrotactic microorganisms was done by Sarfraz et al.^[57].

Motivated by the above studies and given the practical applications of such models, the aim of this research is to understand the behavior of the time-dependent generalized Couette flow of Jeffrey fluid under the influence of varying magnetic intensity and with the implication of magnetic flux at varying angles of inclination/divergence. The impacts of heat and mass transfer, thermal radiation and first-order chemical reaction along with other non-dimensional parameters on fluid flow are investigated in the present model. The findings are visually represented through graphs (2-D and 3-D) and tables, providing valuable insights into the characteristics of velocity, energy, and concentration boundary layers.

1.1.   Novelty of the paper

This study educated a novel dimension by introducing a non-homogenous magnetic effect in a transverse direction of the fluid flow at various angles of inclination at different time intervals. We investigate the effects of this inclined induced magnetic field on the dynamic behavior of particles of non-Newtonian Jeffrey fluid with a generalized Couette flow model to understand the complex flow pattern of thermal, momentum, and concentration boundary layers. As far as the authors are aware, the specific problem addressed in this article has not been explored in the existing body of literature.

1.2.   Organization of the paper

Section 1 includes the literature assessment. Section 2 presents the mathematical modeling and formulation of the problem at hand. In Section 3, an exact solution to the problem is provided. The obtained results are then analyzed and discussed in Section 4, utilizing tables and graphs. Section 5 is desiginated for comparision and code validation. Finally, the principal findings of the study are summarized and listed in Section 6.

2.   Formulation of the mathematical model

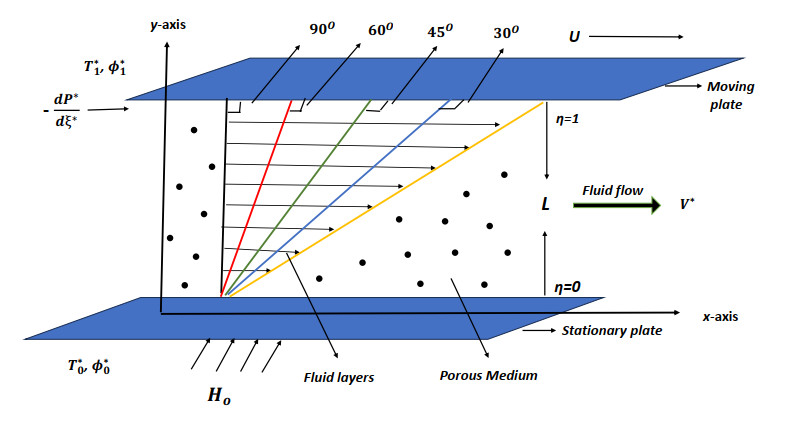
Consider an electrically conducting, incompressible magnetohydrodynamic Jeffrey fluid flowing with velocity $\vec{V^{*}}$ = $(u^{*}(\eta)$$\hat{i}$, 0, 0) between two infinite horizontal parallel plates with a channel of width $L$ through a saturated porous medium. The fluid motion takes place due to the movement of upper plate with a contant velocity $U$ in the $x$-axis direction and due to the external constant pressure gradient $\frac{dP^*}{d\xi^{*}}$ while the $y$-axis runs perpendicular to the fluid flow. The lower plate is stationary and is subjected to magnetic field $H_0$ at various degree of incidence $\theta$. The lower and upper boundries are maintained at temperature $\mathcal{T}^{*}$ = $\mathcal{T}^{*}_{o}$ and $\mathcal{T}^{*}$ = $\mathcal{T}^{*}_{1}$ under the first-order chemical reaction with species concentration $\phi^{*}$ = $\phi^{*}_{o}$ and $\phi^{*}$ = $\phi^{*}_{1}$, respectively. The flow configuration is shown in Figure 1.

2.1.   Governing equations

The governing flow equations are based on Navier-Stokes equations, Darcy's Law of drag force, and Fourier's law of heat conduction (see ^[35,44]).

Continuity equation:

Momentum equation:

Energy equation:

Concentration equation:

In momentum Eq (2.2), $\rho$ is fluid density, $P^*$ is the pressure gradient and $\vec{S}$ is the extra stress tensor for the Jeffrey fluid written as:

Here, $\mu$ is the coefficient of viscosity, $\lambda_{1}$ is the ratio of relaxation to retardation time, $\lambda_{2}$ is the retardation time, $\dot{r}$ is the shear rate (deformation tensor) which is give by

Also, $\vec{R}$ is Darcy's resistance in the porous medium (Darcy's Law) which is given by

where $K_D$ is the Darcy's permeability parameter in the porous medium.

Though the objective of our study is to examine the velocity profile at distinct angles of inclination (along $y$-axis) of the magnetic field vector $\vec{H^{*}}$ = (0, $H_0sin$$\theta$$\hat{j}$, 0) as the upper plates move from left to right. Therefore, we have $\vec{F_{L.f}}$ = $\vec{J}$$\times\vec{H^{*}}$, the induced Lorentz force, where $\vec{J}$ is the density of electric current, which is related to the fluid velocity by Ohm's law as:

Here $\sigma$ is electrical conductivity and $\vec{E}$ is the electrical field generated at a right angle to $\vec{V^{*}}$ and $\vec{H^{*}}$ which is evaluated as

By putting (2.10) into (2.9), we obtain

Now, $\vec{F_{L.f}}$ takes the form

Hence, considering the $x$-component of Lorentz force, we have

In energy Eq (2.3), the terms $k$, $C_p$, and $Q_s^*$, respectively, are the kinematic viscosity, specific heat, and heat absorption coefficients. $q_r$ is the radiative heat flux vector given by:

where $\alpha$ is the thermal diffusivity.

Using all of the above considerations, we obtained the following system of equations:

Momentum equation:

Energy equation:

Concentration equation:

The systems of equations from (2.15)–(2.17) are accompanied by the following initial and boundary conditions.

With the help of similarity transformation, we write the set of Eqs (2.15)–(2.18) in a dimensionless form by introducing the following non-dimensional quantities into the governing equations:

Hence, Eqs (2.15) to (2.18) now become:

The corresponding initial and boundary conditions become:

3.   Solution of the problem

To solve the system of Eqs (2.20)–(2.22), we apply the regular perturbation method (see ^[58,59,60]). We have converted the system of given partial differential equations (PDEs) into ordinary differential equations (ODEs) because there is no closed form of governing linear PDEs. The perturbation method is a powerful tool used to solve PDEs by expanding the solution as a power series in terms of a small parameter that can be treated as a perturbation or oscillation in the system. Hence, we have considered a perturbed or asymptotic solution for the velocity $u$($\eta$, $t$), temperature $\mathcal{T}$($\eta$, $t$), and concentration $\phi$($\eta$, $t$) profiles which enabled us to derive the expressions up to O($\gamma^{2}$) with $\gamma$ as a small amplitude characterizing the motion of the mobile oscillatory upper plate. The following steps are involved:

(1) Substitute the assumed series expansion into the original PDEs and equate the coefficient of like powers of $\gamma$.

(2) Solve each equations in the sequence seperately starting from the lower power of $\gamma$ and progressing to the higher order.

(3) Apply initial and boundary conditions to each order of the solution which helps to determine the unknown coefficients in the expansion.

(4) Determine the convergence and validity of the obtained solution as the perturbation method assumes that the solution is accurate with a certain range of $\gamma$ values which should be sufficiently small. Hence, we have

By substituting Eqs (3.1)–(3.3) into Eqs (2.20)–(2.23) and by equating harmonic and non-harmonic terms and disregarding higher-order terms of $\gamma$, we get the following system of ordinary differential equations.

Zero-order series O$(\gamma^{0})$:

First-order series O$(\gamma^{1})$:

The corresponding boundary conditions are

To solve the set of Eqs (3.4)–(3.9) subject the constraints in (3.10), we used the method of separation of variables (see ^[61,62]). This method is another mathematical technique used to solve certain types of ordinary differential equations. By separating the variables and integrating each side, we can obtain solutions that describe the relationship between the variables involved in the problem. This method provides an analytical exact solution which gives more accuracy compared to other numerical methods. Hence, we get

Putting Eqs (3.11)–(3.16) into Eqs (3.1)–(3.3), we obtain the exact asymptotic solution for the momentum, energy, and concentration curve as follows:

3.1.   Physical parameters

Now, it is imperative to evaluate certain physical quantities of primary interest which are shear stress or skin friction $(\tau_\eta)$, surface heat flux or the local Nusselt number $(Nu_\eta)$, and surface mass flux or the local Sherwood number $(Sh_\eta)$ which plays a significant role in the study of fluid dynamics. Evaluating skin friction is essential because it influences the stress at the boundries and helps in understanding the flow behavior, characterizing the drag forces and boundary layer thickness. Similarly, by evaluating Nusselt and Sherwood numbers at different time intervals, we can capture the time-dependent variations in the convective heat or mass transfer within the fluid or between the channels. It plays a crucial role in the study of dynamical systems analysis such as oscillating flows as proposed in the present research work. It has various engineering applications where heat and mass transfer are evaluated over time to enhance overall efficiency and productivity. There are represented in dimensionless form as (see ^[42]).

3.1.1.   Skin friction ($\tau$) at lower and upper channels

3.1.2.   The Nusselt number ($\mathcal{N}u$) at lower and upper channels

3.1.3.   The Sherwood number ($\mathcal{S}h$) at lower and upper channels

4.   Results and discussion

This section discusses the major findings of the proposed research work. The results are dipicted through graphs (2D and 3D) and tables. The objective of drawing 3-D graphs is to show clearly the complex flow behavior of fluid with increasing strength of magnetic source and changing its direction of implication because 3-D graphs are useful for qualitative flow visualization.

4.1.   The effect of the Reynolds number ($Re$)

Figures 2(a) and 2(b) respectively, present a positive influence of the Reynolds number $Re$ on the velocity $u(\eta)$ and temperature $\mathcal{T}(\eta)$ profile. It is a dimensionless quantity which predicts the transition from laminar to turbulent or fluctuations in fluid layers. It is the ratio of inertial force to viscous force. The flow is laminar and linear at the lower stationary plate due to a no-slip condition. As the $Re$ increases, the fluid becomes more complex and oscillatory while flowing toward the upper moving plate. This is due to the dominance of the inertial force over the viscous force causing the fluid to become less viscous and less resistive. It leads to a transition or fluctuations in the fluid layers moving from the lower to upper channel, consequently energizing the fluid motion and temperature.

4.2.   The effect of the permeability parameter ($K$)

Figures 3(a)–3(c) demonstrate a rising pattern of $u(\eta)$, $\mathcal{T}(\eta)$, and $\phi(\eta)$ profile with growing values of porosity parameter $K$ which describes the degree of permeability of a material or medium. It allows fluid to flow smoothly. Hence, the momentum profile is more uniform which can be seen through velocity graph 3(a). Similarly, in the context of temperature, permeability also influence heat transfer within porous medium and channels. Higher $K$ value facilitate better heat transfer between the fluid and solid boundries which increases the temperature profile as shown in Figure 3(b). Permeability also plays a crucial role in shaping the concentration profile within the generalized Couette flow system. It effects the transport or dispersion of solutes or particles between the medium and adjacent walls. Higher permeability $K$ values near the boundries leads to a smoother concentration profile as shown in Figure 3(c).

4.3.   The effect of the Jeffrey parameter ($\lambda_{1}$)

Figures 4(a)–4(c) depict the effect of the Jeffrey fluid parameter on the velocity $u(\eta)$, temperature $\mathcal{T}(\eta)$, and concentration $\phi(\eta)$ contour. The parameter $\lambda_1$ is related to the relaxation or retardation time of the fluid. The analysis reveals retardation in $u(\eta)$ with increasing values of $\lambda_1$ as shown in Figure 4(a). The escalating value of $\lambda_1$ corresponds to a longer relaxation time and high viscosity of the fluid consequently retards the fluid velocity. However, the fluid temperature and concentration increases with increasing $\lambda_1$ values as represented in Figures 4(b) and 4(c) because of heat and mass transfer mechanisms causing the movement of energy and solutes within the fluid.

4.4.   The effect of the magnetic field strength ($H$)

Case(ⅰ): Figures 5(a) and 5(b), respectively, are the 2D and 3D graphs of the velocity $u(\eta)$ contour under the influence of the magnetic field $H$. Both of the figures witness the decreasing behavior of velocity with the strength of the magnetic field intensity, which can be seen through the shaded region in the 3-D graph. The reason for this is that, when the bottom plate is magnetized strongly, the Lorentz force ${F_{L.f}}$ arises from the interaction of the strong magnetic fields and electrically conducting Jeffrey fluid, which creates a drag or resisitive force at the channel, which reduced the efficiency of the fluid flow and retards the velocity gradients near the walls.

4.5.   The effect of the magnetic field at distinct angle of divergence ($\theta$)

Case(ⅱ): Figures 6(a) and 6(b), respectively, depict the 2D and 3D plots of the velocity $u(\eta)$ at different angles of divergence $\theta$. The velocity decreases with changing the direction of the magnetic field, which can be observed in both the 2-D and 3-D plots. We can see that when there is no inclination that is $\theta$ = $0^{o}$, velocity curve (the blue shaded slope region) is bent further, showing the highest rate of fluid velocity. As the degree of inclination is increased, $\theta$ $> 0^{o}$, it creates pressure in the direction of the fluid flow which pushes the upper plate from left to right, that is, it is rolling or sliding the upper plate over the lower one. This phenomena creates a friction between the plates which creates drag or resistance that retards the fluid velocity toward the upper region. The other reason for this is because of the introduction of an inclined magnetic field transversely or vertically in the opposite direction of the fluid motion that retards the fluid velocity $u(\eta)$.

4.6.   The effect of heat generation parameter ($Qs$)

Figures 7(a) and 7(b) reveal the outcomes of heat source/generation parameter $Q_s$ on temperature $\mathcal{T}(\eta)$ and concentration $\phi(\eta)$. It is clear from the Figure 7(a) that $\mathcal{T}(\eta)$ rises with growing values of $Q_s$. The heat source can modify the temperature gradient across the fluid domain. Depending on the distribution and intensity of the heat source, the temperature gradient may become steeper or more uniform. A higher estimation of $Q_s$ increases the kinetic energy or internal energy of the fluid particles yielding an increment in thermal boundary layers, and consequently increasing the temperature. The systems involving chemical reactions and a heat source can influence reaction rates and species concentrations. The temperature rises due to the heat source thereby affecting the concentrations of reactants and products in the fluid. Therefore, we observed an inverse effect of $Q_s$ on $\phi(\eta)$ (see Figure 7(b)) because of the temperature gradient or thermal diffusion alters the mass transfer between the flow channels.

4.7.   The effect of the Schmidt number ($Sc$)

Figure 8 explains the influence of the Schmidt number $Sc$ on the concentration $\phi(\eta)$ profile. The Schmidt number is a dimensionless quantity defined by the ratio of the momentum diffusivity (kinematic viscosity) to mass diffusivity. Physically, $\phi(\eta)$ is diminishing with higher values of $Sc$. In Couette flow, the convective momentum transport due to the relative motion of the plates dominates over the mass diffusion resulting in less mass transfer/distribution from the plates to the flow region. Hence, the concentration gets declined.

4.8.   The effect of the Prandtl number ($Pr$)

The Prandtl number ($Pr$) is a dimensionless parameter that plays a crucial role in fluid dynamics and heat transfer. The Prandtl number also influences the diffusion of mass or concentration in fluid flows. Figures 9(a) and 9(b), respectively, exhibit the declining behavior of $\mathcal{T}(\eta)$ and $\phi(\eta)$ with growing values of $Pr$. A higher Prandtl number indicates the dominance of momentum diffusivity over thermal diffusivity and mass diffusivity. The fluid is less effective in diffusing energy and the solute within the flow medium. This means that thermal and species distribution has a slower rate of decay between fluid layers. Consequently, the temperature and concentration profiles decline.

4.9.   The effect of the chemical reaction parameter ($Kr$)

Attributes of the chemical reaction parameter $Kr$ on fluid the temperature $\mathcal{T}(\eta)$ and concentration $\phi(\eta)$ curve are outlined in Figures 10(a) and 10(b). We can observe in Figure 10(b), a decreasing pattern of species concentration with increasing value of the chemical reaction parameter. This is due to the reduction of the molecular diffusivity with a higher consumption of the chemical species during the reaction causing less mass transfer between the fluid and the adjacent channels. Consequently, chemical reaction influences the temperature profile and affects the energy balance between the plates. This is due to thermal radiation or absorption during the reaction increasing, the temperature as shown in Figure 10(a).

4.10.   The effect of the thermal radiation parameter ($R$)

A rise in the radiation parameter $\mathcal{R}$ increases the temperature $\mathcal{T}(\eta)$, which can be seen in Figure 11. This is due to the contribution of conductive heat/energy transmission from the heated plates to the fluid layers. Further, in the case of fluid exhibiting non-Newtonian behavior, the presence of a heat source and chemical reaction also influence the thermal radiation, and thus the temperature profile, because of the interaction with the fluid's rheological properties.

4.11.   The variation of skin friction ($\tau$) with diferent angles of inclination ($\theta$)

From Table 1, we can see that the nature of skin friction at both of the channels is osscilatory and increasing. The reason for this is when the direction of inclination ($\theta$) of the magnetic fields changes, the upper plate starts sliding or rolling over the lower one from left to right under the pressure gradient, which creates an oscillatory increasing behavior of the fluid near the upper plate and creats more stress or drag at the lower plate. This periodic nature is also due to internal fluctuation of fluid particles due to the Van der Waals forces (attraction and repulsion) between atoms due to the relative sliding or motion of the fluid layers. Further, increasing the degree of magnetization to the lower wall consequently increases the drag or Lorentz force in a transverse direction of the fluid flow resulting in a rising shear stress at the lower boundary than that of the upper boundary.

4.12.   The variation of skin friction ($\tau$) with different magnitudes of the magnetic field ($H$)

Evaluating skin friction at both boundaries becomes essential because of the implication of strong magnetic fields to the lower plate. It influences the shear stress at both of the boundries and helps in understanding the flow behavior, characterizing the drag forces and boundary layer thickness. In Table 2, we can see that the shear stress is greater at the lower boundary than that at the upper boundary because the fluid particles are attached more to the lower plate due to the no-slip condition and the viscosity. When a strong magnetic field is applied directly to the lower plate, it increases the electrical conductivity of Jeffrey fluid particles near the lower channel and starts moving upwards with a high velocity, resulting in a reduction of the shear stress toward the upper channel.

4.13.   The variation of the Nusselt number ($\mathcal{N}u$) at different intervals of time ($t$)

Table 3 indicates the increasing rate of heat transfer over time that is the thermal/heat flux, which represents the time rate of heat movement per unit area. Heat or thermal transmission occurs in generalized Couette flow as a result of temperature differences between plates due to the heat source. Therefore, as time passes, the rate of heat transmission ($\mathcal{N}u_\eta$) between the plates and the medium increases, as shown in Table 3.

4.14.   The variation of the Sherwood number ($\mathcal{S}h$) at different intervals of time ($t$)

The Sherwood number represents the rate of mass transfer or mass flux per unit area. In generalized Couette flow, mass flux occurs when there is a concentration gradient of solute in the flow medium between the channels. We have observed in Table 4 that the rate of mass transfer is less at the lower wall than that at the upper wall. The reason for this is that, as time passes, the fluid flows from the lower to upper region, and it attracts the particles or species from preceding layers leading to a concentration difference between the fluid layers and a thicker boundary layer forms near the upper flow area. It consequently increases mass diffusivity of the fluid and hence the mass flux ($\mathcal{S}h$).

5.   Comparision and code validation

For the accuracy and convergence of the proposed asymptotic analytical solution, we have compared our result with the work of Elshabrawy et al.^[36] for temperature profile at different values of the $y$-axis cordinate $\eta$ at $Qs = 0.2$ and $Pr = 0.4$ for the limiting case taking the thermal radiation $\mathcal{R}$ = $0$. We have found that our results are in good agreement with Elshabrawy et al.^[36] as displayed in Table 5.

6.   Conclusions

This section provides the key outcomes and a few of the potential implications of the present research work. The research focused on the behavior of an unsteady magnetohydrodynamic oscillatory flow of non-Newtonian Jeffrey fluid between two infinite horizontal parallel channels. The fluid was moving under the external pressure gradient along the direction of the upper channel and the lower fixed channel was magnetized transversely. We investigated two scenarios regarding the velocity distribution for the proposed generalized Couette flow. The first case involved changing the magnetic flux strength, while the second case examined the effects of a magnetic field at different angles of inclination while keeping its magnitude constant. The study also encompassed the dynamic impacts of first-order chemical reaction, thermal radiation, and various originating flow parameters on the velocity, temperature, and concentration profile. Moreover, the exact asymptotic solution of the generalized Couette flow was obtained using the perturbation method and the method of separation of variables and then computed on MATLAB. Further, the shear-stress, heat, and mass flux were also evaluated and represented through tables. Also, the present analytical solution for the temperature profile $\mathcal{T}(\eta, t)$ was compared with previously published research work for the limiting case, and the findings indicated a high level of abidance. The major findings of our proposed problem are listed below:

● The fluid velocity $u(\eta)$ increases with increasing the Reynolds number $(Re)$ and permeability parameter $(K)$ while it retards with increasing magnetic field strength $(H)$, angle of inclination $(\theta)$, and Jeffrey fluid parameter $(\lambda_1)$.

● Growing values of the Reynolds number $(Re)$, Jeffrey fluid parameter $(\lambda_1)$, porosity parameter $(K)$, heat generation parameter $(Qs)$, rate of chemical reaction $(Kr)$ and thermal radiation $(\mathcal{R})$ elavate the temperature profile $\mathcal{T}(\eta)$ while an inverse effect is observed on $\mathcal{T}(\eta)$ with rising values of the Prandtl number $(Pr)$.

● The concentration profile $\phi(\eta)$ enhanced with Jeffrey fluid parameter $(\lambda_{1})$ and porosity parameter $(K)$. However, it diminished with rising values of the Prandtl number $(Pr)$, Schmidt number $(Sc)$, heat source $(Qs)$, and chemical reaction parameter $(Kr)$.

● By increasing the magnetic field $H$ ($\theta$ fixed) and increasing divergence $\theta$ of magnetic field intensity ($H$ fixed) in both of the cases, we found an oscillatory nature of the local skin friction (shear stress) $\tau$ at both of the channels. Also its effect is stronger at the lower channel than that at the upper channel.

● Both the Nusselt number (heat flux) $\mathcal{N}u_\eta$ and the Sherwood number (mass flux) $\mathcal{S}h_\eta$ are increasing over time and are less at the lower wall than the values at the upper wall.

● The study has numerious potential applications in enviromental science (geophysics, river and estuary dynamics, atmospherical boundary layer, transport phenomena) and chemical science (chemical reactors, magnetic seperation processes, microfluidics, and lab-on-a-chip (LOC) devices).

● Future research should be explore phase transitions in multi-phase flows like liquid-gas, solid-liquid, and gas-solid interactions between two microchannels.

● Developing advanced computational and simulation techniques will improve turbulence models to control the laminar-turbulence transition and grid resolution for better understanding of the complex flow pattern and, hence, assist in solving boundary value problems.

Appendix

$\lambda$ = $\frac{1}{1+\lambda_{1}}$, $N$ = $\frac{H^2sin^2\theta+K}{\lambda}$, $m_1$ = $\sqrt{N}$, $m_2$ = - $\sqrt{N}$, $M$ = $\frac{H^2sin^2\theta+K+nR_e}{\lambda}$, $m_3$ = $\sqrt{M}$, $m_4$ = - $\sqrt{M}$, $E$ = $\mathcal{R}^2$+$Q_s$, $m_5$ = $\sqrt{E}$, $m_6$ = - $\sqrt{E}$, $F$ = $(\mathcal{R}^2+Q_s+nP_r)$, $m_7$ = $\sqrt{F}$, $m_8$ = - $\sqrt{F}$, $C$ = $K_rS_c$, $m_9$ = $\sqrt{C}$, $m_{10}$ = -$\sqrt{C}$, $D$ = $(K_rS_c+nS_c)$, $m_{11}$ = $\sqrt{D}$, $m_{12}$ = - $\sqrt{D}$, $C_1$ = $\frac{1}{\lambda N}$ - $C_2$, $C_2$ = - $\frac{1}{\lambda N}$$\left(\frac{\lambda N+(1-e^{m_2})}{e^{m_2}-e^{m_1}}\right)$, $C_3$ = - $C_4$, $C_4$ = $\frac{1}{e^{m_4}-e^{m_3}}$, $C_5$ = - $C_6$, $C_6$ = $\frac{1}{e^{m_6}-e^{m_5}}$, $C_7$ = - $C_8$, $C_8$ = $\frac{1}{e^{m_8}-e^{m_7}}$, $C_9$ = - $C_{10}$, $C_{10}$ = $\frac{1}{e^{m_{10}}-e^{m_9}}$, $C_{11}$ = - $C_{12}$, $C_{12}$ = $\frac{1}{e^{m_{12}}-e^{m_{11}}}$.

The graphs and tables are based on the following values of different parameters, wherever they need to be fixed:

$Re = 3$, $K = 0.5$, $\lambda_{1} = 0.5$, $H = 1$, $P = 1$, $n = 0.1$, $t = 1$, $Pr = 1$, $\mathcal{R} = 1$, $Qs = 1$, $Sc = 2$, $Kr = 1$, $\gamma = 0.2$, $\theta = 90^o$.

Superscripts:

^* - Dimensional quantity;

$'$ - Differentiation w.r.t $\eta$ and $\xi$.

Cordinates:

$\eta$ - $y$-axis cordinate;

$\xi$ - $x$-axis cordinate.

Author contributions

Shabiha Naz: Problem suggestion, Solution to the problem, Modeling, Write - up; Tamizharasi Renganathan: Visualization, Validation, Verification. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

We would like to thank the reviewers and editors for giving their valuable time and suggestions to improve this paper.

Conflict of interest

The authors declare that they have no conflicts of interest.