Extended dissipative analysis for memristive neural networks with two-delay components via a generalized delay-product-type Lyapunov-Krasovskii functional

1.   Introduction

Due to its diverse potential applications, including secure communication, information science and parallel image processing, the synchronization of coupled dynamical neural networks has received much attention in recent years ^[1,2]. Frequent impulsive effects are common phenomena of dynamical neural networks in actual situations, which means abrupt changes in the state of nodes of such neural neural networks caused by switching phenomena and instantaneous perturbations at certain moments. An impulsive differential dynamical system with continuous and discontinuous behavior can be represented by such a network, which is one of the most typical hybrid systems ^[3]. In fact, impulsive effects can greatly affect dynamical neural networks, and can be categorized into desynchronizing impulses and synchronizing impulses. In particular, if impulsive effects occur during the signal transmission between nodes, the term of coupling may be rewritten into a discontinuous form. It is therefore challenging to explore the synchronization of coupled dynamical neural networks with impulsive effects. Several interesting results have been obtained in ^[4,5,6,7]. In consideration of the difficulties in synchronization between all network nodes caused by the topological structure of a network and in the achievement of dynamical behaviors of all the nodes, there are many control strategies available to solve this issue, such as pinning control ^[8], impulsive control ^[9,10], adaptive control ^[11] and event-triggered control ^[12,13].

An example of discontinuous control is impulsive control, which is only applied at certain discrete moments to achieve a goal, and thus has been favored by many scholars for its low cost, high efficiency, and simple structure. A number of noteworthy studies have shown that impulsive control can synchronize complex neural networks ^{[14,15,16,17,18]}. Pinning control ^[8,9,19] is another method for synchronizing dynamical neural networks with only a small fraction of nodes controlled. In ^[8], a pinning control strategy has been successfully proposed to address synchronization issues of complex neural networks, and has been proven to be one of the most powerful methods. The method of combining impulsive control and pinning control was presented for dynamical networks with delays ^[9], in which a scheme of choosing the pinning nodes was given. This mechanism inherits the merits of the two methods, that is, the lower cost of control and saving resources. For just this reason, some excellent results about pinning impulsive control strategy have emerged. For instance, Yi et al. ^[20] examined how pinning impulsive controls synchronized neural networks with hybrid delays, where internal delay, three kinds of coupling delays and two impulsive effects are considered. As a method to achieve exponential synchronization, Shen et al. ^[21] presented impulsive pinning control, which uses the average impulsive interval and introduces impulse pinned proportions. More related work can be seen in ^[22,23,24]. Although the control methods mentioned above are easy to implement, the impulsive instants are artificially determined in advance or dependent on some special conditions. In other words, information transmission may be hampered by time-triggered control strategies that consume unnecessary resources and waste control resources. Therefore, researchers have turned their attention to event-triggered control, which is considered to be able to prevent these defects.

Event-triggered mechanism (ETM) has already attracted a huge amount of interest due to its practical advantages in low cost of controller updates and high efficiency ^{[25,26,27,28,29]}. That is to say, control mechanisms like this improve the efficiency with which limited bandwidth resources are used. More recently, there has been widespread adoption of the event- triggered impulsive control (ETIC) method by scholars, by which impulsive instants are generated when certain events occur according to the states of a system rather than being designed beforehand. More relevant studies on ETIC can be found in ^{[13,30,31,32]}, where ETIC is applied to various systems. For instance, a study of the Lyapunov stability problem of an impulsive system was carried out using ETIC ^[13] and the exponential stability was investigated for continuous-time dynamic systems and applied to memristive neural networks based on an ETIC approach ^[30]. All these studies are evidence of the superiority of the ETIC mechanism, though time delay is not included in the argument of the studies. On the other hand, there has been much discussion of SIS and SIR epidemic models in the field of epidemic disease spreading research ^[33]. In the view of contact among individuals, it is obvious that the infected propagation is related to the degree of individuals, which means the number of edges to connect the individuals with others. Therefore, many disease epidemic models can be characterized by complex networks. By applying ETIC to the network nodes, the disease can be controlled and resources can be saved, which has a certain reference value to the practical work. Some typical works are as follows: ^[34] design an epidemic control mechanism based on data instead of the subjective empirical method. ^[35] investigates the stability and optimal control for SIS epidemic systems with birth and death in directed complex networks and the reference therein.

It is noted that time delay is ubiquitous in actual systems on account of various factors, such as signal transmission, sampling and controller calculations ^[36]. A time delay within dynamic nodes is called an internal delay, while that during the transmission of information between nodes is called a coupling delay. In particular, delays that occur during signal exchange at impulsive instants are called impulsive delays. For impulsive delays, we need to analyze whether the information obtained at impulsive instants exists in the current interval or in a previous interval. Considering time delays usually weaken the synchronization performance of dynamical neural networks or make the analysis of the synchronization more complex and challenging, it is worthwhile to study the synchronization problem of complex networks with the existence of time delays. Meanwhile, scholars have made painstaking efforts and have achieved excellent results ^{[20,37,38,39,40,41,42]}. For example, an experiment in signed delayed neural networks was conducted by Mu et al. ^[43] in which quasi-bipartite synchronization was examined under impulsive conditions, in which the nodes have cooperative as well as antagonistic interactions. In ^[44], the synchronization problem of complex neural networks with the existence of impulsive delays and system inner delays with unknown boundaries was discussed. Nevertheless, in these studies about ETIC, either the impulse instants are artificially determined, or only one kind of time delay is considered. There are few studies on the event-triggered pinning impulsive control (EPIC) mechanism for synchronization of dynamical neural networks with hybrid delays to our knowledge. Therefore, the following are several main contributions in this paper pertaining to the exponential synchronization of dynamical neural networks with mixed delays under the appropriate EPIC method.

Motivated by the above discussion, this paper mainly focuses on the exponential synchronization problem of dynamical neural networks with mixed delays under the appropriate EPIC method. The main contributions are highlighted as follows:

1) An novel EPIC mechanism is designed to achieve synchronization for impulsive dynamical neural networks with hybrid delays. There are impulsive effects when signals are exchanged between nodes, which it should be noted that the coupling term is discontinuous. From a practical point of view, the system internal delay and impulsive delay in this paper are considered simultaneously, which are both limited. It becomes more challenging to analyze when mixed delays are present.

2) The designed event-triggered rule in the EPIC mechanism is based on the Lyapunov function, where only one node needs to be controlled and well-designed event-triggered conditions determine the impulsive instants, which is different from the predesigned impulse instants in ^[7] and ^[45]. Obviously, this mechanism can effectively reduce the cost of controller and update frequency of the controller. To ensure exponential synchronization, the parameter $\eta$ is introduced in the event-triggered rule, which differs from the proposed forced impulse sequence in ^[31]. In other words, no matter whether the event occurs or not, the exponential synchronization can be reached in the end.

3) According to proposed the EPIC strategy, some generalized inequalities related to hybrid delays are proposed. In view of the above, the synchronization of dynamical neural networks can be analyzed using LMIs technology to establish a number of sufficient criteria. Furthermore, Zeno behavior can be excluded. In order to analyze the synchronization of dynamical neural networks, LMIs technology is utilized to establish a number of sufficient criteria.

The remainder of this article is organized as follows. Section Ⅱ gives some useful preliminaries, which presents an important lemma for the achievement of exponential synchronization. The main results are derived in Section Ⅲ. A numerical example and simulation are provided in Section Ⅳ to illustrate the effectiveness of the proposed method. Finally, the conclusion of this paper is given in Section Ⅴ.

Notations: Throughout this paper, $\mathbb{Z}$, $\mathbb{Z}_{+}, \mathbb{R}$, and $\mathbb{R}_{+}$ denote the set of integer numbers, positive integer numbers, real numbers, and nonnegative real numbers, respectively. $\mathbb{R}^n$ stands for $n$-dimensional real spaces equipped with the Euclidean norm $\|\cdot\|$, and $\mathbb{R}^{n \times m}$ stands for the set of $n \times m$ real matrices. A positive (negative) definite matrix $W \in \mathbb{R}^{n \times n}$ is denoted by $W > 0 (W < 0).$ $\lambda_{\max }(W)$ $(\lambda_{\min}(W))$ denotes the maximum (minimum) eigenvalue of a matrix $W \in \mathbb{R}^{n \times n}$. $I$ represents an identity matrix. The symmetrical part of $W$ is defined as $W^s = (W+W^T)/2$. $\otimes$ stands for the Kronecker product. For $\mathfrak{J} \subseteq \mathbb{R}, \mathfrak{S} \subseteq \mathbb{R}^m(1 \leq m \leq n)$, $PC(\mathfrak{J}, \mathfrak{S}): = \{\phi: \mathfrak{J} \rightarrow \mathfrak{S} \mid \phi$ is piecewise right continuous $\}$.

2.   Preliminaries

By coupling of $N$ neurons in a neural network, we consider the following coupled impulsive dynamical neural networks with hybrid delays:

where $i = 1, 2, \cdots, N$, $x_i(t)\in\mathbb{R}^n$ denotes the state with respect to the $i$th neuron and $f(\cdot)\ {\text{and}} \ g(\cdot) \in\mathbb{R}^n$ are the activation functions. $c > 0$ represents the coupling strength. $u_i(t)$ is the $i$th control input, which is designed later. $\Gamma = diag\{\gamma_1, \gamma_2, \cdots, \gamma_n\} > 0$ is the inner coupling matrix. $H = (h_{ij})_{N\times N}$ indicates the coupling weights matrix, which is defined as follows: if there is a connection from neuron $j$ to neuron $i$, then $h_{ij} > 0$, otherwise $h_{ij} = 0$. Moreover, the diagonal elements of matrix $H$ is defined as $h_{ii} = -\sum_{j = 1, j\neq i}^Nh_{ij}$, $i = 1, 2, \cdots, N$. $\tau(t)$ and $\tau_k$ are system internal time-vary delay and impulsive delay, respectively, which meet $0 \leq \tau(t) \leq \tau$. $A, B_1, B_2 \in\mathbb{R}^{n\times n}$ are constant matrices. $C_k$ and $D_k$ denotes control gains. The impulsive sequence $\{t_k\}_{k = 1}^\infty$ determined by the event-triggered rule satisfies $t_k-\tau_k \in [t_{k-1}, t_k), k\in \mathbb{Z_+}$. We always assume that $x(t_k) = x(t_k^+),$ and $\phi_i(t) \in PC ([t_0-\tau, t_0], \mathbb{R}^n)$ is the initial condition of the $i$th neuron.

In this paper, the isolated dynamical model can be seen as an objective trajectory, which can be represented by the following equation:

where $\psi(\theta) \in PC ([t_0-\tau, t_0], \mathbb{R}^n)$ is the initial condition.

In this paper, the synchronization problem between (2.1) and (2.2) by using the EPIC method is investigated. Without loss of generality, the first node of dynamical networks is selected to be controlled, and the impulsive controller can be designed as follows:

where $\delta(t)$ is the Dirac function.

Remark 2.1. In this study, synchronizing the network requires only one node to be controlled. At the same time, the impulsive instants are determined by the ETM designed later. By reducing the cost of control updates and communication waste, it is more efficient than a general time-triggered mechanism. Meanwhile, the same control purpose can also be achieved in the case of reducing the number of controllers, which is compared with the impulsive control strategy triggered by events. From controller (2.3), it can be seen that the jump of state variable $x(t)$ at $t = t_k$ is dependent on the state information at the instants $t_k^–\tau_k$ and the current instants $t_k^-$, simultaneously. This paper only takes the synchronizing impulsive effects into account.

Let $e_i(t) = x_i(t) - s(t), i = 1, \cdots, N$ be the synchronization error. Then, the compact form of error system with impulsive controller (2.3) has the following form:

where $e(t) = \big[e^T_1(t), \cdots, e^T_N(t)\big] ^T,$ $\hat{f}(e_i(t)) = f (x_i(t)) -f(s(t))$, $\hat{F}(e(t)) = \big[\hat{f}^T(e_1(t)), \cdots, \hat{f}^T(e_N(t))\big]^T$, $\hat{g}(e_i(t-\tau(t))) = g(x_i(t-\tau(t))-g(s(t-\tau(t)))$, $\hat{G}(e(t-\tau(t))) = \big[\hat{g}^T(e_1(t-\tau(t))), \cdots, \hat{g}^T(e_N(t-\tau(t)))\big]^T$.

The initial condition $\chi(\theta) = [\chi_1(\theta), \cdots, \chi_N(\theta)]^T, \chi_i(\theta) = \varphi_i(\theta)-\psi(\theta) \in PC ([t_0-\tau, t_0], \mathbb{R}^{n})$. The norm of $\chi(\theta)$ is defined as $|\chi(\theta)| = \sup_{t_0-\tau \leq \theta \leq t_0} \|\chi(\theta)\|$.

Definition 2.1. The impulsive dynamical network (2.1) is deemed to achieve the globally exponential synchronization with (2.2), if there exist some constants $T > 0$, $\tilde{M} > 0$ and $\epsilon > 0$, such that $\forall \chi(\theta) \in PC([t_0-\tau, t_0], \mathbb{R}^{nN})$,

holds for all $t > T$.

Assumption 2.1. The activation functions of neurons $f(\cdot)$ and $g(\cdot)$ satisfy the Lipschitz condition, $f(0) = 0$ and $g(0) = 0$, that is, there exist positive constants $l_1, l_2$ such that $\forall \eta_1, \ \eta_2 \in \mathbb{R}^n$

Lemma 2.1. ^[46] For any vectors $x, y$, there exist a matrix $\mathcal{S} > 0$ and a constant $\xi > 0$, such that

Lemma 2.2. ^[47] For an irreducible matrix $H$ with non-negative off-diagonal elements, which satisfies the zero-row-sum condition, the following propositions can be formulated:

(1) If $\lambda$ is an eigenvalue of $H$ and $\lambda \neq 0$, then $Re(\lambda) < 0.$

(2) $H$ has an eigenvalue 0 with multiplicity 1 and its corresponding right eigenvector is $[1, 1, \cdots, 1]^T$.

(3) $\xi = [\xi_1, \xi_2, \cdots, \xi_N]^T \in \mathbb{R}^N$ is the left eigenvector of $H$ corresponding to the eigenvalue 0 and satisfies $\xi^TH = 0$, where $\xi_i \in(0, 1], i = 1, 2, \cdots, N.$

Next, by virtue of a suitable Lyapunov function $V(t)$ given in the sequel, the adopted ETM is defined as follows:

where $V_{t_0} = \sup_{t_0-\tau\leq s \leq t_0}V(s), \eta > 0, a_k > 0$ satisfies

Before an important lemma is presented, the following general impulsive delayed system should be considered first to ensure the universality of the proposed lemma.

where $z(t)\in \mathbb{R}^n$ represents the state of the general impulsive delayed system, $\tau(t)$ and $\tau_k$ represent the system internal delay and impulsive delay, respectively, and $0\leq \tau(t) \leq \tau$. $\{t_k\}_{k = 1}^\infty$ is the impulse sequence. $z_0(s)$ is the initial value of the general impulsive delayed system.

Lemma 2.3. A general impulsive system with mixed delays (2.7) is said to be global exponential stable, if the inequality (2.6) holds and there exists a $K_\infty$ function $\alpha_1, \alpha_2$, a differential nonnegative function $V(z(t)): \mathbb{R}^{n} \rightarrow \mathbb{R}_+$ and some positive constants $c_1, c_2, a_k, b_k$, $\tau_k, M, \eta, k\in \mathbb{Z}_+$ satisfies the following conditions:

and the derivative of $V(t)$ along (2.7) with initial conditions $z_0(s)\in PC([t_0-\tau, t_0], \mathbb{R}^n)$ satisfies

where $\{t_k, \ k\in \mathbb{Z}_+\}$ are triggering instants determined by the ETM (2.5), $t_k^{*}$ is given later, the triggering parameter $a_k$ and the impulsive parameter $b_k$ satisfy

where $a_0-b_0^{'} = 0$, $b_k^{'} = b_k +\ln \frac{1}{2}, \ k\in\mathbb{Z}_+$.

Proof. For the sake of simplicity, an auxiliary function is first introduced as

Then the ETM (2.5) can be rewritten as

Therefore, for $k = 1$, it can be obtained from the ETM (2.9) and the inequality (2.8) that

and

Thus, $\exists \ t_1^{*}\in[t_0, t_1),$ such that $t_1^{*} = \sup\big\{t\geq t_0, \ U(t)\leq \max\{U(t_0), V_{t_0}\}\big\}$, i.e. $U(t_1^{*}) = \max\{U(t_0), V_{t_0}\} = V_{t_0}$. For $t\in [t_1^{*}, t_1), U(t) \geq U(t_1^{*}),$ which implies for $\theta \in[-\tau, 0]$, when $t_0\leq t+\theta < t_1$,

when $t_0-\tau\leq t+\theta < t_0$,

To sum up, $U(t+\theta)\leq \mathtt{e}^MU(t), t\in [t_1^{*}, t_1).$

When $t = t_1$, on the basis of $(H_2)$ and ETM (2.9), one can get that

For $k = 2$, from the ETM (2.9),

and

Similarly, $\exists\ t_2^{*} \in[t_1, t_2),$ such that $t_2^{*} = \sup\big\{t\geq t_1, U(t)\leq \max\{U(t_1), V_{t_0}\}\big\}$, i.e. $U(t_2^{*}) = \max\{U(t_1), V_{t_0}\}$. For $t\in [t_2^{*}, t_2), U(t) \geq U(t_2^{*})\geq V_{t_0},$ which illustrates $\forall \theta \in[-\tau, 0]$, when $t_1\leq t+\theta < t_2$,

when $t_1\leq t+\theta < t_2$,

when $t_0-\tau\leq t+\theta < t_0$,

In conclusion, $U(t+\theta)\leq \mathtt{e}^MU(t), t\in [t_2^{*}, t_2).$

When $t = t_2$, we have

Repeating the above derivation by using the recursive approach, it is verifiable that $\forall k \in\mathbb{Z}_+$,

and

where $\Omega_k = \max_{ \forall m\in \{1, \cdots, k-1\}}\big\{a_k+\sum_{i = 1}^m(a_{k-i}-b_{k-i}^{'})\big\}.$ Then, $\exists \ t_k^{*}\in[t_{k-1}, t_k),$ such that $t_k^{*} = \sup\{t\geq t_{k-1}, U(t)\leq \max\{U(t_{k-1}), V_{t_0}\}\}$, i.e. $U(t_k^{*}) = \max\{U(t_{k-1}), V_{t_0}\}.$ For $t\in [t_k^{*}, t_k)$, $U(t)\geq U(t_k^{*}) \geq V_{t_0}$, which indicates that when $\theta\in[-\tau, 0]$,

Given the above, $\forall t\in[t_k^{*}, t_k)$, from the condition $(H_3)$,

Then, it leads to

Thus

That is

Accumulating the inequality (2.10), we have

Finally, considering (2.6), $t_k \rightarrow +\infty$ as $k \rightarrow +\infty$, which shows that the ETM (2.5) will not induce Zeno behavior.

From the above analysis, for any $k\in \mathbb{Z}_+$, one can derive that

That is

Combining $(H_1)$, it can be obtained that the system with mixed delays (2.7) is global exponential stable. □

Remark 2.2. It should be noted that the impulsive delay $\tau_k$ should satisfy $\tau_k \in [0, \frac{a_k}{c_1+c_2\mathtt{e}^{\eta \tau+M}+\eta}],$ which means that the impulsive delay is small-delay. Furthermore, $t_k-\tau_k \in [t_{k-1}, t_k)$ can prevent the case that the current state is affected by the state of former impulsive interval. On the other hand, $t_k \rightarrow + \infty$ as $k \rightarrow + \infty$ means that infinite triggers do not occur in a finite interval. In addition, this lemma shows how to deal with the stability of impulsive systems with mixed delays, so it can also be applied to the delayed dynamical network with impulsive effects proposed in this paper.

3.   Main results

In this part, the exponential synchronization for the directed impulsive dynamical network under the EPIC method is expounded. The theoretical analysis mentioned above is applied to the dynamical network to verify the feasibility and effectiveness of Lemma 2.3. With that in mind, some sufficient synchronization criterion will be established by choosing an appropriate Lyapunov function. Meanwhile, Zeno phenomenon can be avoided.

According to the fact that $H$ is an irreducible matrix, define diagonal matrix $\Xi = diag\{\xi_1, \cdots, \xi_N\}$, where $\xi_i (i = 1, \cdots, N)$ satisfies Lemma 2.2. It can be verified that $\Xi H+H^T\Xi$ is zero-row-sum and $\lambda_{\max}(\Xi H+H^T\Xi) = 0$.

Theorem 3.1. Suppose Assumption 2.1 holds. If there exist some positive constants $\zeta_1, \zeta_2, b_k, \eta, \tau_k$, positive-definite matrices $S_1, S_2\in \mathbb{R}^{n\times n}$ satisfy the following conditions.

Then, the exponential synchronization of the dynamical network (2.1) and the target trajectory (2.2) can be achieved under the ETM (2.5) and the impulsive pinning controller (2.3). In the meantime, there is no Zeno behavior for system (2.7) coupled with ETM (2.9).

Proof. Choose the Lyapunov function as:

Then from the error system (2.4), $D^+V(t)$ can be calculated as follows.

When $t\in[t_{k-1}, t_k)$ with $k\in\mathbb{Z}_+$,

According to Assumption 2.1 and Lemma 2.1,

Similarly,

The following inequality can be reduced from the fact that $\lambda_{\max}(\Xi H+H^T \Xi) = 0$.

Combining the inequalities mentioned above and conditions $(a)$, $(b)$, (3.1) can be further deduced as

Since $H$ is irreducible, $\forall j \neq 1, j \in \{1, \cdots, N\}$, there exist $m_1, m_2, \cdots, m_s \in \{1, \cdots, N\}$, such that $h_{m_1, j} > 0, \; h_{m_s, m_{s-1}} > 0, \cdots, h_{1, m_s} > 0$. Thus, for $\forall j = 2, 3, \cdots, N$,

Combining with the single controller (2.3), we obtain

Hence, when $t = t_k$, according to the condition $(c)$

It follows from the definition of $V(t)$ that

It is not hard to verify that the inequalities (3.2), (3.3) and (3.4) can satisfy the conditions of Lemma 2.3. With the aid of Lemma 2.3, we can calculate $\|e(t)\|\leq \mathtt{e}^{\frac{-\eta (t-t_0)+M}{2}}\sqrt{\frac{\max_{\forall i}\{\xi_i\}}{\min_{\forall i}\{\xi_i\}}}|\chi(\theta)|.$ Thus, the synchronization of (2.1) and (2.2) can be achieved and the Zeno behavior can be avoided. To sum up, the proof is completed. □

Remark 3.1. It should be noticed that Theorem 3.1 is the special case of Lemma 2.3. In other words, Lemma 2.3 is more general. In addition, the single event-triggered impulsive pinning controller actually acts on the whole directed network with impulsive effect, which not only saves the cost of the controller, but also improves the control efficiency. Compared with the single impulsive controller in ^[7], the impulsive instants are generated by the ETM (2.5) rather than designed in advance, which avoids the unnecessary waste of resources.

Note that the nonidentical parameters $a_k, b_k^{'}, C_k, D_k, \tau_k, k\in\mathbb{N}^+$ may raise the calculating burden. Therefore, for the sake of simplicity, we suppose that $b_k^{'} = a_k = a > 0, b_k = a-\ln{\frac{1}{2}}, C_k = C, D_k = D, \tau_k = \tilde{\tau}$. Accordingly, the event-triggered condition (2.5) can be weakened to

then we can derive the following results.

Corollary 3.1. Suppose Assumption 2.1 holds. If there exist some positive constants $\zeta_1, \zeta_2, a, b_k, \eta, \tilde{\tau}$, positive-definite matrices $S_1, S_2\in \mathbb{R}^{n\times n}$ satisfy the condition (a) and (b) of Theorem 3.1 and the following condition.

Then, the exponential synchronization of the dynamical network (2.1) and the target trajectory (2.2) can be achieved under the ETM (3.5), and the Zeno phenomenon also can be excluded.

If there is no delay in the dynamical network (2.1), i.e. $B_2 = 0, D_k = 0, k \in \mathbb{Z}_+$, then from the ETM (2.5),

where $\eta > 0$, $a_k > 0$ is defined by the (2.6).

Corollary 3.2. Assume the Assumption 2.1 holds. Under the ETM (3.6), the dynamical network (2.1) and (2.2) can obtain the exponential synchronization. If there exist positive definite matrix $S \in \mathbb{R}^{n\times n}$ and some positive constants $\zeta, d_k, \tilde{\mathcal{M}}$ satisfying

where

Proof. Under the conditions $(a)$ and $(b)$, one can get the following inequalities by the same analysis as Theorem 3.1.

where the Lyapunov function $V(t)$ is the same as Theorem 3.1. According to the ETM (3.6), let $W(t) = \mathtt{e}^{\eta(t-t_0)}V(t)$, $t \geq t_0$, for $k = 1$, we have

and

When $t = t_1$, it follows the fact (3.9) that

Repeat the preceding steps, for any $k\in \mathbb{Z}_+$, one can obtain

Furthermore, on the basis of the inequality (3.7), it can be reduced as

Finally

Thus, the exponential synchronization can be achieved.

On the other hand, the Zeno behavior also can be excluded, which is the same as the proof of Lemma 2.3. □

Remark 3.2. For a no-delay network, the parameter $\eta$ in event-triggered condition (3.6) plays a significant function in the proof of the synchronization process, which differs from the forced impulse sequence in ^[31]. In other words, the auxiliary function $W(t)$ can eventually be covered by an exponential function, that is, no matter whether the event occurs or not, the exponential synchronization can be reached in the end.

4.   Numerical simulation

In this part, some numerical examples are given to illuminate the effectiveness of the proposed EIPC strategy. Consider the dynamical neural networks (2.1) with $N = 5$ nodes. Choose $n = 3, c = 0.2, \tau = 1, \Gamma = I_n, A = -I_n$, $B_1 = \begin{bmatrix} 0.58 & -0.75 & -0.75\\ -0.75 & 0.58 & 1\\ -0.6 & 1 & 0.58 \end{bmatrix},$ $B_2 = \begin{bmatrix} 0.55 & -0.5 & 0.75\\ 1.25 & -0.8 & -1\\ 0.6 & -0.6 & -0.75 \end{bmatrix},$ $H = \begin{bmatrix} -2 & 1 & 0 & 0 & 1 \\ 1 & -2 & 1 & 0 & 0\\ 0 & 1 & -2 & 1 & 0\\ 0 & 0 & 1 & -2 & 1\\ 1 & 0 & 0 & 1 & -2 \end{bmatrix},$ $\Xi = diag\{ 0.3, 0.5, 1, 0.4, 0.4 \}.$ Let $f(x_i(t)) = \big(tanh(x_{i1}(t)), tanh(x_{i2}(t)), tanh(x_{i3}(t))\big)^T$, $g(x_i(t)) = 0.1*\big(tanh(x_{i1}(t)), tanh(x_{i2}(t)), tanh(x_{i3}(t))\big)^T$, $\eta = 0.003, \tilde{\tau} = 0.0112, a = 3$.

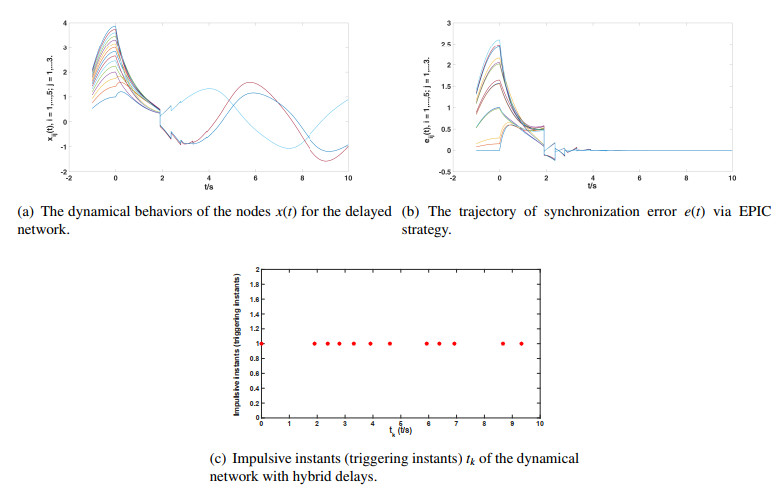
Then, the state trajectory of the dynamical neural networks (2.1) is shown in Figure 1a. By using the MATLAB matrix toolbox, the feasible solutions of LMIs in Theorem 3.1 can be obtained, which shows that $\zeta_1 = 216.4738, \zeta_2 = 2.5408.$ According to the Differential mean value theorem, it is easily designed $l_1 = 9.3696,$ and $l_2 = 0.101$, thus the Assumption 2.1 always can be ensured. $\tilde{C} = 0.127I_n, \tilde{D} = 0.08I_n, \hat{C} = -0.146I_n, \hat{D} = -0.055I_n$. It should noted that $C_{2k} = \tilde{C}, D_{2k} = \tilde{D}, C_{2k-1} = \hat{C}, D_{2k-1} = \hat{D}, k\in \mathbb{Z}_+,$ which is more universal than fixed gain matrix in ^[36]. All the conditions in Theorem 3.1 are satisfied by checking. Then, the exponential synchronization between (2.1) and (2.2) can be achieved, which illustrates that the proposed EIPC scheme is effective. The trajectory of the error is depicted in Figure 1b. At the same time, the triggering instants (impulsive instants) are shown in Figure 1c. It can be seen from the above figures that, when $\eta = 0.003$, the dynamical neural networks (2.1) and the target trajectory (2.2) can approximately synchronize in $4.5s$.

On the other hand, it can be found that the convergence rate of the synchronization error is related to the parameter $\eta$ in ETM (3.5). In other words, the impulsive instants $t_k$ determined by the ETM (3.5) with different parameters $\eta$ are different, which can be shown in Table 1. Correspondingly, the time to achieve synchronization is shown in Table 1, which indicates that when the parameter $\eta = 0.01$, the synchronization is faster, but the frequency of controller update is also faster, which means that the cost of the controller update is more. Nevertheless, when $\eta = 0.003$, the interevent time $t_k-t_{k-1}, k\in \mathbb{Z}_+$ are larger. As a specific numerical measure of synchronization effect, the less the synchronization time is realized, the better the synchronization effect is. As we can see from Table 1, when the value of the parameter $\eta$ is decreasing, the synchronization takes longer, but the control updates are fewer. The above illustrates that our proposed EIPC strategy is effective, but the specific selection of parameter $\eta$ depends on the specific situation.

5.   Conclusions

In this paper, an event-triggered impulsive pinning control method for coupled impulsive dynamical neural networks with hybrid delays has been presented and the impulsive effects are taken into account in modeling. Different from the literature in existence ^[14,22,25], impulsive instants rely on the ETM rather than being set in advance. Moreover, on the basis of the proposed EIPC strategy and stability theory, some sufficient synchronization conditions are established to address the exponential synchronization problem and eliminate the Zeno behavior. Finally, the feasibility of the EIPC algorithm has been verified by the numerical simulation.

Furthermore, in the future, considering that the information transmitted through the communication network of the epidemic model is vulnerable to impulsive malicious effects ^[34], the EIPC design strategy of dynamical networks acts on the disease epidemic model to provide a reference for practice is an interesting problem, which needs to be studied further.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgment

This work is supported by the Scientifc Research Startup Fund for Shenzhen High-Caliber Personnel of SZPT under Grant 6022310042k, the Research Foundation of Shenzhen Polytechnic under Grant 6022312044K, and the National Natural Science Foundation of China under Grant 2022A1515110967 and 2023A1515011809.

Conflict of interest

The authors declare no conflict of interest.