Moran random walk with reset and short memory

1.   Introduction

Numerous scientific fields have relied heavily on the study of random processes to gain understanding of a wide range of phenomena, from particle motion to population behavior. The random walk, a mathematical representation of a path made up of a series of random steps, is one of these stochastic processes that has shown to be very significant. The Moran process, so named after the biologist Patrick Moran who first presented it in the context of population genetics, is one prominent variation of the random walk.

Originating in population genetics, the Moran process provides a fundamental paradigm for comprehending the dynamics of genetic diversity within populations. The Moran process was developed by Patrick Moran in the middle of the 20th century as a straightforward yet effective method for researching evolutionary processes in finite populations.

Under particular rules governing reproduction, selection, and random genetic drift, individuals interact within a finite population in a discrete-time stochastic process known as the Moran process. In addition to taking into consideration the limiting size of populations, which can have significant long-term effects on genetic variation, Moran's formulation captures the fundamental mechanisms driving evolutionary change, such as genetic drift and selection.

Under particular rules governing reproduction, selection, and random genetic drift, individuals interact within a finite population in a discrete-time stochastic process known as the Moran process.

A-part from its use in population genetics, the Moran process has been proven useful in several other disciplines, such as epidemiology, ecology, and sociology. It has been adopted as a model for researching a variety of phenomena that are typified by random interactions and discrete events due to its adaptability and intuitive appeal.

Since its introduction, several variations of Moran random walk have been introduced from these models: age statistics of the population at a given step ^[1,2], the height of walks with resets and Moran models ^[3], the two-dimensional Moran model (number of resets, final altitude, height) ^[4], and the two-dimensional Moran random walk with time-dependent probability of reset ^[5]. In this work, we introduce a variation of this model, where we assume a population of size 1 that, at each step, has two possibilities, at random: either it is replaced by a new individual, or it continues to go up with a one-step size.

Our model is a mixture between a Moran process with a single component and an elephant walk. In this model, the walk at each time only takes steps of size 1 upwards or returns to zero, which is the Moran walk. However, the decision at each step (to go up or return to zero) depends randomly on the previous step: the walk only remembers the previous step, reproducing what is in memory with probability $p$ and the opposite of what is in memory with probability $1-p$, hence the connection with the elephant walk.

The examined model in this paper has some similarities with the Markov chain model explored in Brenaud's book ^[6]. However, there are key differences. In our model, transitions from $i$ to $i-1$ are almost surely (for all $i \geq 1$), and the probability of transitioning from $0$ to a state $i$ depends on $i-1$. It is important to note that our model allows for the possibility of moving from $i$ to zero (reset) with a probability, which also depends on $i$. Additionally, the transition from $i$, in our model, can lead to either $i+1$ or $0$, in contrast to the Brenaud book where it is limited to $i-1$.

The structure of this current paper is organized as follows. In Section 2, we present our Moran random walk with short memory. In Section 3, we state our main result concerning the cumulative distribution function of the height statistics associated with our random walk using the moment-generating function. Also, we find the mean of the height statistics. In Section 4, we illustrate numerically our random walk with different lengths: $n = 10,100, 1000, 10,000,100,000$, and $500,000$, for different values of the probabilities $p = 0.3, 0.5, 0.85$, and $r = 0.25, 0.5, 0.8$. In Sections 5 and 6, we find the explicit expressions of the mean and the variance of our random walk. In Section 7, we find the closed form of the characteristic function of our random walk. Also, we determine the limit law of our walk using the characteristic function tool. In Section 8, we prove our main results. Finally, in Section 9, we present the conclusions and perspectives of our work.

2.   Definitions and presentation of the model

Consider the one-dimensional Moran model with short memory $Y_n$. It starts from 0 at time 0 (i.e., $\mathbb{P}\left(Y_0 = 0\right) = 1$). The Moran model with one dimension is given by the following system: at time 1,

and for time $n > 1$, the walk $Y_n$, can only remember the step $n-1$ and decides to repeat the same step with probability $p$ or to do the opposite step with probability $1-p$, where $p\in(0, 1)$ and $r\in(0, 1)$. We define the event $A_n$, at time $n$, the random walk $Y_n$ decides to repeat the movement made at the time $n$,

We can write the random walk $Y_n$ at the time $n$, by

The state space of $Y_n$ is $\{0, \ldots, n\}$.

Remark 2.1. Some remarks about the probability $r$, Eq (2.1), and the mean of short memory:

● The probability $r$ is exclusively utilized during the initial step $n = 1$, in which the random walk lacks any recollection, prompting the use of $r$ to initiate the process.

● The event $\overline{A}_{n-1}$ is when, at time $n$, the random walk decides to reproduce the opposite step made at time $n-1$: more precisely if, for example, at step $n-1$ the random walk decides to go up by a step of size $1$ and then, according to event $\overline{A}_{n-1}$, it decides to go to zero at time $n$.

● By the definition of our model, for all $n\geq 2, \, \mathbb{P}(A_{n-1}) = p$,

● For all $n\geq 2$, in the event: $\left(A_{n-1}\cap\{Y_{n-1} = 0\}\right)\cup \left(\overline{A}_{n-1}\cap \{Y_{n-1}\neq 0\}\right)$, $Y_n = 0$.

● By short memory, we mean that the random walk, at any step, remembers only the previous step and not all the previous steps.

In the paper, ${\mathbb{E}}(Y_n)$, ${\mathbb{V}ar}(Y_n)$, represent respectively, the mean and the variance of $Y_n$.

This model has found numerous applications in game theory and financial markets. Specifically, in the case of a game where at each step, there is a chance of either winning or losing everything. Each step of the game involves repeating the same action as the previous step with a probability of $p$, or playing the opposite action with a probability of $1-p$. In this case the random variable $Y_n$ represents the result of the game at step $n$. Assuming that every time the player wins, their prize pool increases by $a$ dollars, and once they lose, they lose their entire fortune, in this scenario, the player's winnings up to the $n^{th}$ step, amount to $aY_n$. This model can be modeled by a Markov chain. With the aid of ^[7] and our results, we can obtain findings that appear to be interesting.

3.   Main result

In this section, we want to study the behavior of the height statistics, denoted by $H_n$, of the random walk $Y_n$. Precisely, we need to study the distribution of $H_n$. For this objective, we use the moment-generating function, denoted by $A_h(z)$, of the cumulative distribution function, denoted by $\mathbb{P}\Big(H_n\leq h\Big)$, of $H_n$, for all real number $z\in(0, \, 1)$. We define the height statistics, denoted by $H_n = \max(Y_0, Y_1, Y_2, \ldots, Y_n)$, of the random walk $Y_n$. For all $h$ integer number, we define $A_h(.)$ as the moment-generating function of $H_n$: for all $z\in(0, \, 1)$

The moment-generating function technique has been well developed in ^[8,9].

In this reference, the robustness of this technique is highlighted for explaining the distribution of a random variable defined by a recursive equation. We define the following sequences of probabilities: for all integer number $h$ and for all $n\geq 2$,

with the initial following conditions,

Lemma 3.1. The sequence $b_n$ satisfies the following recursion: for all $n\geq 1$,

Lemma 3.2. The sequence $c_n$ satisfies the following recursion: for all $n\geq h+3$,

In this section, we present our main result concerning the distribution of the height statistics $H_n$, of the random walk $Y_n$. We find a closed form of the generating function of $H_n$ and we deduce that the cumulative distribution function, $\mathbb{P}\Big(H_n\leq h\Big)$, of $H_n$.

Theorem 3.1. The cumulative distribution function of $H_n$ is given by: for all $0\leq h \leq n$,

where, for all $z\in(0, 1)$,

is the generating function of the cumulative distribution of $H_n$.

In the next corollary, we find the mean of the height $H_n$ using Theorem 3.1.

Corollary 3.1. The mean of $H_n$ can be obtained as

Here, we focus on the waiting time $\tau_h$ for the random walk to reach a given level $h$. Given a level $h$.

Theorem 3.2. The distribution of $\tau_h$ is given by, for all $n\geq 1$,

Remark 3.1. From Theorem 3.2, we can compute the mean of $\tau_h$ but the expression is very complicated. In fact, from Eq (8.12), we compute the sequence $(b_n(h))_n$ and finally we use Eq (8.11), to obtain the expression of $c_n(h)$.

4.   Simulations

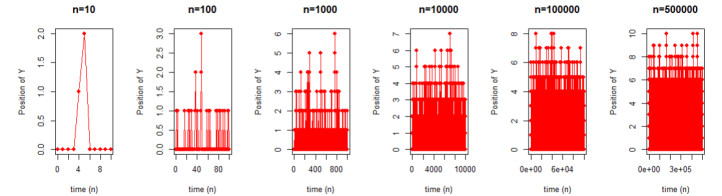
In this section, we use the R software to study the influence of the two probabilities $p$ and $r$ on the evolution of the random walk $Y_n$ with different lengths. In the first case, we take a small value of the probability $r$ that equals to 0.25 and we change the probability $p$ from 0.3, 0.5 to 0.85 where the lengths of the random walk $Y_n$ are equals to 10,100, 1000, 10,000,100,000, and 500,000. For the second case, the probability $r$ is fixed at 0.5, and the probability $p$ is changed from 0.3, 0.5 to 0.85; we treat the random walk $Y_n$ with different lengths that are equal to 10,100, 1000, 10,000,100,000, and 500,000. Finally, we finish with a high value of the probability $r$ (0.8) and the probability $p$ changes from 0.3 to 0.85 with the same lengths of $Y_n$.

From Figures 1–3, we observe that the maximum level of $Y_n$ and the height $H_n$ are dependent on the three parameters: $r$, $p$, and $n$.

$1)$ When $r$ and $n$ are fixed and $p$ is changed from 0.3, 0.5 to 0.85, we observe that $Y_n$ and $H_n$ are always increasing. For example, for fixed $n = 10$ and $r = 0.25$, and changed $p$ from 0.3, 0.5 and 0.85, the maximum level of $Y_n$ is increased from 0, 1, to 8 and the height $H_n$ are increased from 2, 3 to 8, respectively. For $n = 10,000$ and $r = 0.25$, and changed $p$ from 0.3, 0.5 and 0.85, the maximum level of $Y_n$ is increased from 2, 2, to 10 and the height $H_n$ is increased from 7, 12 to 48, respectively. For $n = 500,000$ and $r = 0.25$, and changed $p$ from 0.3, 0.5 and 0.85, the maximum level of $Y_n$ is increased from 7, 14 to 35 and the height $H_n$ is increased from 10, 19 to 69, respectively.

$2)$ When $r$ and $p$ are fixed and $n$ is changed from 10,100, 1000, 10,000,100,000, to 500,000, we observe that $Y_n$ and $H_n$ are always increasing. But the evolution of the walk $Y_n$ is very slow. For example, for fixed $r = 0.25$, and $p = 0.3$, and changed $n$ from 10,100, 1000, 10,000,100,000, to 500,000, the maximum level of $Y_n$ and the height $H_n$ are increased from 2, 3, 6, 8, 9 to 10, respectively. For example, for fixed $r = 0.25$, and $p = 0.5$, and changed $n$ from 10,100, 1000, 10,000,100,000, to 500,000, the maximum level of $Y_n$ and the height $H_n$ are increased from 3, 7, 9, 12, to 18, respectively. When $r = 0.25$, and $p = 0.85$ fixed and changed $n$ from 10,100, 1000, 10,000,100,000, to 500,000, the maximum level of $Y_n$ and the height $H_n$ are increased from 8, 18, 34, 48, to 68, respectively.

Also, Figure 1 shows that the maximum level of the random walk $Y_n$ equals 10 when $p = 0.3$, $r = 0.25$, and $n = 500,000$. Figure 2 shows that the maximum level of the random walk $Y_n$ equals 18 when $p = 0.5$, $r = 0.25$, and $n = 500,000$. Figure 3 shows that the maximum level of the random walk $Y_n$ equals 68 when $p = 0.85$, $r = 0.25$ and $n = 500,000$. That means that if $n$ and $p$ increase, then the maximum level of $Y_n$ increases. But this evolution of $Y_n$ is slow. Furthermore, the height $H_n$ does not exceed 10, 18, and 68 when $r = 0.25$, $p = 0.3, 0.5, 0.85$, and $n = 500,000$.

Figures 4–6 show that the maximum level of $Y_n$ and the height $H_n$ are also dependent on the three parameters: $r$, $p$, and $n$.

$1)$ When $r$ and $n$ are fixed and $p$ is changed from 0.3, 0.5 to 0.85, we observe that $Y_n$ and $H_n$ are always increasing. For example, for fixed $n = 100$, and $r = 0.5$, and changed $p$ from 0.3, 0.5, and 0.85, the maximum level of $Y_n$ and the height $H_n$ are increased from 3, 5, to 30, respectively. For $n = 1000$, and $r = 0.5$, and changed $p$ from 0.3, 0.5 and 0.85, the maximum level of $Y_n$ and the height $H_n$ are increased from 4, 7 to 40, respectively. For $n = 500,000$ and $r = 0.5$, and changed $p$ from 0.3, 0.5, and 0.85, the maximum level of $Y_n$ and the height $H_n$ are increased from 10, 24 to 69, respectively.

$2)$ When $r$ and $p$ are fixed and $n$ is changed from 10,100, 1000, 10,000,100,000, to 500,000, we observe that $Y_n$ and $H_n$ are always increasing. But the evolution of the walk $Y_n$ is very slow. For example, for fixed $r = 0.5$, and $p = 0.3$, and changed $n$ from 10,100, 1000, 10,000,100,000, to 500,000, the maximum level of $Y_n$ and the height $H_n$ are increased from 1, 3, 4, 7, 9 to 10, respectively. For example, for fixed $r = 0.5$, and $p = 0.5$, and changed $n$ from 10,100, 1000, 10,000,100,000, to 500,000, the maximum level of $Y_n$ and the height $H_n$ are increased from 3, 5, 7, 10, 19, to 18, respectively. When $r = 0.5$, and $p = 0.85$ fixed and changed $n$ from 10,100, 1000, 10,000,100,000, to 500,000, the maximum level of $Y_n$ and the height $H_n$ are increased from 8, 29, 39, 44, 59, to 68, respectively.

In addition, Figure 4 shows that the maximum level of the random walk $Y_n$ equals 10 when $p = 0.3$, $r = 0.5$, and $n = 500,000$. Figure 5 shows that the maximum level of the random walk $Y_n$ equals 24 when $p = 0.5$, $r = 0.5$, and $n = 500,000$. Figure 6 shows that the maximum level of the random walk $Y_n$ equals to 68 when $p = 0.85$, $r = 0.5$, and $n = 500,000$. That means that if $n$ and $p$ increase, then the maximum level of $Y_n$ increases. But this evolution of $Y_n$ is slow. Furthermore, the height $H_n$ does not exceed 10, 24, and 68 when $r = 0.5$, $p = 0.3, 0.5, 0.85$, and $n = 500,000$.

Figures 7–9 show that the maximum level of $Y_n$ and the height $H_n$ are also depended on the three parameters: $r$, $p$, and $n$.

$1)$ When $r$ and $n$ are fixed and $p$ is changed from 0.3, 0.5 to 0.85, we observe that $Y_n$ and $H_n$ are always increasing. For example, for fixed $n = 100$, and $r = 0.8$, and changed $p$ from 0.3, 0.5, and 0.85, the maximum level of $Y_n$ and the height $H_n$ are increased from 3, 6, to 21, respectively. For $n = 10,000$ and $r = 0.8$, and changed $p$ from 0.3, 0.5, and 0.85, the maximum level of $Y_n$ and the height $H_n$ are increased from 7, 11, to 48, respectively. For $n = 500,000$ and $r = 0.8$, and changed $p$ from 0.3, 0.5 and 0.85, the maximum level of $Y_n$ and the height $H_n$ are increased from 10, 19, to 68, respectively.

$2)$ When $r$ and $p$ are fixed and $n$ is changed from 10,100, 1000, 10,000,100,000, to 500,000, we observe that $Y_n$ and $H_n$ are always increasing. But the evolution of the walk $Y_n$ is very slow. For example, for fixed $r = 0.8$, and $p = 0.3$, and changed $n$ from 10,100, 1000, 10,000,100,000, to 500,000, the maximum level of $Y_n$ and the height $H_n$ are increased from 2, 3, 5, 7, 10 to 10, respectively. For example, for fixed $r = 0.8$, and $p = 0.5$, and changed $n$ from 10,100, 1000, 10,000,100,000, to 500,000, the maximum level of $Y_n$ and the height $H_n$ are increased from 1, 6, 7, 11, 14, to 19, respectively. When $r = 0.8$ and $p = 0.85$ fixed and changed $n$ from 10,100, 1000, 10,000,100,000, to 500,000, the maximum level of $Y_n$ and the height $H_n$ are increased from 8, 21, 34, 44, 70, to 70, respectively.

In addition, Figure 7 shows that the maximum level of the random walk $Y_n$ equals 10 when $p = 0.3$, $r = 0.8$, and $n = 500,000$. Figure 8 shows that the maximum level of the random walk $Y_n$ equals 19 when $p = 0.5$, $r = 0.8$, and $n = 500,000$. Figure 9 shows that the maximum level of the random walk $Y_n$ equals 70 when $p = 0.85$, $r = 0.8$, and $n = 500,000$. That means that if $n$ and $p$ increase, then the maximum level of $Y_n$ increases. But this evolution of $Y_n$ is slow. Furthermore, the height $H_n$ does not exceed to 10, 19, and 68 when $r = 0.8$, $p = 0.3, 0.5, 0.85$, and $n = 500,000$.

5.   Mean of the random walk $Y_n$

In this section, we study the mean of the random walk $Y_n$. We start by a technical lemma to find a recursive relation between the probability of the random walk $Y_n$ that equals 0 at the two successive times $n$ and $n-1$, denoted by $p_{n-1}(0)$, and $p_n(0)$. Furthermore, we find a closed form of $p_{n}(0)$. In addition, we find a recursive equation between the mean of $Y_n$, the mean of $Y_{n-1}$, and the probability of the random walk $Y_{n}$ at time $n-1$ on 0. Finally, we finish this section by the explicit expression of the mean of $Y_n$. For this, we denote by $p_n(0) = \mathbb{P}(Y_n = 0)$ the probability of the random walk $Y_n$, equal to 0 at time $n$.

The next lemma is a key lemma to find the explicit form of the first moment (mean) of the random walk $Y_n$. It leads to finding the explicit form of the probability that the random walk $Y_n$ equals 0, at time $n$.

Lemma 5.1. The sequence of probabilities $p_n(0)$, satisfies the following recursive equation: for all $n\geq 1$,

where $p_0(0) = 1$. Its explicit expression is given by: for all $n\geq 1$,

where $p_0(0) = 1$.

Proof. Using the conditional probability: for all $n\geq 1$, we have

By, iterating Eq (5.1) $n$ times and using the fact that

we get the desired result. □

Remark 5.1 When $r = p$ in Eq (5.2), we have the special case:

The next theorem uses Lemma 5.1 to find the first moment of the walk $Y_n$. We find a recursive equation related ${\mathbb{E}}(Y_n)$, ${\mathbb{E}}(Y_{n-1})$ and $p_{n-1}(0)$. This relation leads to the determination of the explicit form of $Y_n$.

Theorem 5.1. The mean of $Y_n$, satisfy the following recursive equation: for all $n\geq 1$,

Its explicit expression is given by:

Proof. Using Eq (2.1), one has

using Lemma 5.1, then we get

Iterating Eq (5.3) $n$ times, we obtain

where

Developing and simplifying

multiplying Eq (5.6) by $(1-2p)\, \, p^{n-1}$, then we get

Combining Eqs (5.5) and (5.7), then we obtain

Replacing the following identities

in Eq (5.8), we obtain

□

Remark 5.2. When $r = p$, we have the special case:

Corollary 5.1. Asymptotically, the mean of the random walk $Y_n$ converges to $\frac{1}{2(1-p)}$ for all $r\in(0, 1)$ and $p\in(0, 1)$.

Proof. The proof follows directly from Eq (5.4). □

6.   Variance of the random walk $Y_n$

In this section, we find the explicit form of the variance of the random walk $Y_n$. For this objective, we start with a key lemma to find a recursive equation between the three following quantities: ${\mathbb{E}}(Y^2_n)$, ${\mathbb{E}}(Y_n)$, and $\sum^{n-1}_{k = 1}p^{-k}{\mathbb{E}}(Y_{k})$. In addition, we need to calculate $\sum^{n-1}_{k = 1}p^{-k}{\mathbb{E}}(Y_{k})$, combining with the explicit form of the first moment of $Y_n$ defined in Theorem 5.1 to obtain an explicit form of the second moment of $Y_n$, denoted by ${\mathbb{E}}(Y^2_n)$. Finally, we state the closed form of the variance of $Y_n$.

We start by a technical lemma to find the recursive equation between: ${\mathbb{E}}(Y^2_n)$, ${\mathbb{E}}(Y_n)$, and $\sum^{n-1}_{k = 1}p^{-k}{\mathbb{E}}(Y_{k})$.

Lemma 6.1. The second moment of $Y_n$, satisfies the following recursive equation: $\forall n\geq 1$,

Proof. Using Eq (2.1), one has

hence

using Lemma 5.1, then we get

Iterating Eq (6.1) $n$ times, we obtain

and using Eq (5.5), we deduce

□

In the next lemma, we need to calculate $\sum^{n-1}_{k = 1}p^{-k}{\mathbb{E}}(Y_{k})$ using the explicit form of the mean of the walk $Y_n$, defined in (5.4). This lemma is a technical lemma used to find the explicit expression of the second moment of $Y_n$.

Lemma 6.2. One has: for all $n\geq 2$,

Proof. Applying Eq (5.4), we have

developing and after some calculations, we have

and get

Define the sequence $I_n$, for all $n\geq 1$, by

developing and simplifying,

replacing Eq (6.6) in Eq (6.5), we obtain

multiplying Eq (6.7) by $2p^n$, then we get

□

Now, we present the explicit form of the second moment of the random walk $Y_n$. It is used to find the explicit form of the variance of $Y_n$.

Proposition 6.1. The explicit form of the second moment of $Y_n$, is given by: $\forall n\geq 1$,

Proof. Replacing Eqs (5.4) and (6.4) in Eq (6.1), then we get

where the two sequences $A_n$ and $B_n$ are defined by

adding $A_n$ and $B_n$, and regrouping the terms

combining Eqs (6.9) and (6.10), then we obtain

□

In the next corollary, we present the explicit expression of the variance of $Y_n$ using Theorem 5.1 and Lemma 6.1.

Corollary 6.1. The variance of $Y_n$, is given by

Proof. Applying Eqs (5.4) and (6.8), we have

developing and simplifying

combining Eqs (6.12) and (6.13), then we have

□

Remark 6.1. When $r = p$, we have the special case:

7.   Distribution of the random walk $Y_n$

In this section, we define the characteristic function of the random walk $Y_n$, denoted by $\Phi_n(t)$, for all $t\in\mathbb{R}$. Furthermore, we find a recursive equation between $\Phi_n(t)$, $\Phi_{n-1}(t)$, $p_n(0)$, and $p_{n-1}(0)$. By iteration, we determine the explicit expression of $\Phi_n(t)$. In the next step, we study the convergence of $\Phi_n(t)$ asymptotically. Finally, we finish this section by the limit distribution of the random walk $Y_n$, denoted by $Y$. We start with the definition of the characteristic function, denoted by $\Phi_n(t)$,

In the next theorem, we present an important result concerning the closed form of the characteristic function of the random walk $Y_n$. It is used to determine the distribution of $Y_n$.

Theorem 7.1. The characteristic function $\Phi_n(t)$, of $Y_n$ satisfies the recursive equation:

Its explicit expression is given by: for all $n\geq 1$,

where $\Phi_n(0) = 1$.

Proof. Using Eqs (2.1) and (7.1), then we have: for all $t\in\mathbb{R}$

Using the following identities

Eq (7.3) can be written as

Iterating Eq (7.1) $n$ times, we get

Rewriting Eq (7.5), we obtain

applying Eq (5.6), we have

multiplying Eq (7.7) by $(1-p)p^{n-1}e^{int}$, then we get

Combining Eqs (7.6) and (7.8), we obtain

□

Now, we can deduce the distribution of the random walk $Y_n$ from Theorem 7.1.

Corollary 7.1. The distribution of the random walk $Y_n$, is given by: for all $n\geq 1$,

Proof. From Eq (7.6), we have

we conclude the proof by identification of the coefficients of $e^{itk}, \, k = 0, \ldots, n$. □

We prove in the next corollary that the characteristic function of the random walk $Y_n$ converges to $\Phi_Y(t)$, representing the characteristic function of the limit law of the random walk $Y_n$. Also, we find the explicit expression of $\Phi_Y(t)$.

Corollary 7.2. The distribution of $Y_n$ converges asymptotically to the random variable $Y$, with the characteristic function, denoted by $\Phi_Y(t)$, given by

Proof. From Eq (7.2), we have

passing to the limit, we get

□

The result presented in Corollary 7.2 is used to find the distribution of the random variable $Y = \lim_{n\rightarrow \infty }Y_n$.

Theorem 7.2. The distribution of the random variable $Y$, with $\Phi_Y(t)$, its characteristic function is given by:

Remark 7.1. Our model is different from the model in ^[4]. In ^[4], the distribution of $Y$ was proved by a shifted geometric with parameter $p$, which is different from the distribution given in Theorem 7.2.

Proof of Theorem 7.2. Starting from Eq (7.9), we have

Since

The proof is finished by identifying Eqs (7.2) and (7.10). □

8.   Proofs

Proof of Lemma 3.1. Applying Eq (3.2),

Define two sequence of probabilities $d_n(h)$ and $g_n(h)$, for all $n \geq 1$, by

using the conditional probability, we have

and

Replacing Eqs (8.2) and (8.3) in Eq (8.1),

using Eqs (3.1) and (3.2), then we get, for all $n\geq2$,

□

Proof of Lemma 3.2. Define the following events

observe that

From Eqs (3.2), (8.4) and (8.5), we have: for all $n \geq h+3$,

Then, Eq (3.5) is verified. □

Now, we are able to proof our main result concerning the distribution of the height statistics $H_n$.

Proof of Theorem 3.1. Applying Eq (3.1), we have

where $R_{n, k, h}$, $S_{n, k, h}$ and $T_{n, h}$, are defined by: for all $n \geq 1$, $0\leq k\leq h$ and $0\leq h\leq n$

Using the conditional probability

then, we have

Replacing Eq (3.3) in (8.8), we get

If, in Eq (8.7) we take $k = 0$, we have

where

Combining Eqs (8.6), (8.9), and (8.10), we deduce that, for all $0\leq h \leq n$,

Using Lemmas 3.1 and 3.2, we obtain the following recursion

In order to obtain the explicit form of $a_n(h)$, we use the moment-generating functions, let

By Eq (3.4), we have

and from Eq (8.11), we have

Finally, we conclude that

and that, for all $0\leq h \leq n$,

□

Finally, we proof our second main result about the waiting time $\tau_h$.

Proof of Theorem 3.2. For all $h$ and for all $n\geq 1$, we have

Then,

□

9.   Conclusions and perspectives

In this paper, we explore the statistical properties of the one-dimensional Moran random walk with short memory. Specifically, we investigate the cumulative distribution function and the mean of the height statistics $H_n$ using generating function techniques. Our analysis leads to the explicit form of the generating function $A_h(z)$ of $H_n$. Additionally, we establish that the cumulative distribution function $\mathbb{P}\Big(H_n \leq h\Big)$ of $H_n$ is equivalent to the coefficient of $z^n$ in the power series $A_h(z)$. Furthermore, we derive explicit expressions for the mean and variance of the random walk $Y_n$. Utilizing characteristic function tools, we determine the distribution of $Y_n$ and deduce its limit distribution.

For the remainder of our study, we plan to investigate a variant of the Moran random walk model with long memory. Specifically, at each step $n$, the walk randomly and uniformly selects a past step $k$, and decides to either repeat the same movement as step $k$ (move up by $+1$ or return to $0$) with probability $p$, or to perform the opposite of step $k$ with probability $1-p$. In our opinion, this model is highly intriguing as it combines elements of both the elephant random walk ^[10,11,12] and the Moran walk ^[3,4,5].

Author contributions

Mohamed Abdelkader: Conceptualization, Methodology, Software, Formal analysis, Writing-original draft; Rafik Aguech: Conceptualization, Software, Formal analysis, Writing-original draft. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The first author extends appreciation to King Saud University in Riyadh, Saudi Arabia for funding this research work through Researchers Supporting Project number (RSPD2024R1068).

Conflict of interest

All authors declare no conflicts of interest in this paper.