The characteristic polynomials of semigeneric threshold arrangements

1.   Introduction

A finite hyperplane arrangement $\mathcal{A}$ is a finite set of affine hyperplanes in some vector space $V\cong \mathbb{K}^{n}$, where $\mathbb{K}$ is a field, the classical theories of hyperplane arrangements are introduced in ^[15,16]. Literatures ^[2,18] list the important topics of hyperplane arrangement, many arrangements mentioned in them are the deformations of the braid arrangement

The key observation is that for this arrangement, geometric notions of faces, flats, top-cones, and so on can be encoded by combinatorial notions of set compositions, set partitions, partial orders, and so on. There are a lot of deformations of the braid arrangement^[6], such as: Shi arrangement^[9,17], Catalan arrangement^[1,8,11], and semigeneric braid arrangement^[10]. Their combinatorics were first investigated systematically by Stanley ^[16] and relete to objects studied classically in enumeration. A major role in this study is played by the characteristic polynomial, which is a combinatorial invariant of the hyperplane arrangement.

Indeed, the characteristic polynomial is related to several other invariants, such as the Poincaré polynomial of the complexified complement$M(\mathcal{A})$^[14], the number of chambers for real arrangements ^[4,5], the number of $F_q$-rational points^[7], Chern classes of certain vector bundles^[3], lattice points counting^[12,19], and Tutte polynomial^[13], etc.

In order to introduce the characteristic polynomial, we need to comprehend what an intersection lattice is. Let $L(\mathcal{A})$ be the collection of all intersections of elements of $\mathcal{A}$. We partially order $L(\mathcal{A})$ by the reverse of inclusion, so that $X \leqslant Y$ means $X \supseteq Y$. Then $L(\mathcal{A})$ is a geometric lattice, called the intersection lattice of $\mathcal{A}$, which has $V$ as its minimal element. Let $\mu$ be the Möbius function of $L(\mathcal{A})$. The characteristic polynomial $\chi_{\mathcal{A}}(t)$ of $\mathcal {A}$ is defined by

In ^[16], Stanley defined the generic arrangement as follows:

Let $L_1, \cdots, L_m$ be linear forms, not necessarily distinct, in the variables $x = \left(x_1, \ldots, x_n\right)$ over the field $\mathbb{K}$. Let $\mathcal{A}$ be defined by

where $a_1, \cdots, a_m$ are generic elements of $\mathbb{K}$. This means if $H_i = \operatorname{ker}\left(L_i(x)-a_i\right)$, then

He also presented a special case of generic arrangement, called the generic threshold arrangement:

where $a_{ij}$'s are generic elements. In this paper, we define the semigeneric threshold arrangement in $\mathbb{R}^n$:

where $a_i$'s are generic elements. We can see that $\mathcal{A}_n$ is a natural deformation of the generic threshold arrangement while we replace $a_{ij}$ with $a_i$. The generic threshold arrangement and semigeneric threshold arrangement don't have an inclusion relationship, but may intersect.

If we consider the hyperplanes with different $a_i$'s, then the graph corresponding to them is always a forest. The normals of those hyperplanes are always linearly independent, furthermore, the intersection of those hyperplanes is not empty. Therefore, the genericity of $a_i$'s can be guaranteed when they take any numbers in $\mathbb{R}$. We do not emphasize that $a_i$'s are generic elements in later sections.

Since the characteristic polynomial of $\mathcal{A}_n$ has not yet been determined, in this paper, we provide a formula for the characteristic polynomials of the semigeneric threshold arrangement and its subarrangements. The remainder of this paper is organized as follows: In Section 2, we provide a few definitions to support the results that follow. In Section 3, we obtain a necessary and sufficient condition for the subarrangements of $\mathcal{A}_n$ to be central from the perspective of simple graphs and provide a formula for their characteristic polynomials. In Section 4, we demonstrate two uses for this formula.

2.   Preliminaries

We aims to provide a formula for the characteristic polynomials of the subarrangements of $\mathcal{A}_n$. According to Whitney's theorem, it is needed to give a characterization of the central subarrangements of $\mathcal{A}_n$. In this process, two types of special graphs, pseudo even cycle and pseudo spanning forest, play an important role. Following are the definitions for the terms STG arrangement, pseudo even cycle, and pseudo spanning forest.

Definition 2.1. Let $G = (V(G), E(G))$ be a simple graph with $V(G) = [n] = \{1, \cdots, n\}$. The corresponding STG arrangement, short for semigeneric threshold graphical arrangement, is defined by

where $a_i\text{'s}$ are generic elements.

Notice that $\mathcal{A}_G$ is a subarrangement of $\mathcal{A}_n$. Particularly, if $G = K_n$, the complete graph on $[n]$, then $\mathcal{A}_G = \mathcal{A}_{n}$.

Following is the definition of the pseudo even cycle, which can be regarded as the generalization of the even cycle.

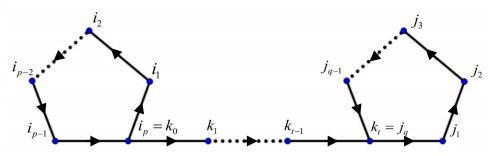
Definition 2.2. Let $G_1$ and $G_2$ be a $p$-cycle and a $q$-cycle, $G_3$ be a path of length $t$ whose ends are $k_0$ and $k_t$, where $p, q\in\{2r+1 \mid r\in {\mathbb{Z}}^+\}$, $t\geq0$. Particularly when $t = 0$, $G_3$ is a vertex. If $G_1, G_2, G_3$ satisfy the following conditions:

(1) $V(G_1\cap G_2) = \begin{cases}\{k_0\}, \quad t = 0, \\ \; \emptyset, \; \; \, \quad t > 0, \end{cases}$ (2) $V(G_1\cap G_3) = \{k_0\}$, (3) $V(G_2\cap G_3) = \{k_t\}$,

then we call $G_1\cup G_2\cup G_3$ a pseudo even cycle, denoted as $H^t_{p, q}$.

Figure 1 demonstrates that the length of a closed walk around $H^t_{p, q}$ is $p+q+2t$, an even number. That's why we call it a pseudo even cycle.

For the convenience of proofs in Section 3, we unify the concepts of even cycle and pseudo even cycle, providing the following definition.

Definition 2.3. We call a graph an extended even cycle if it's an even cycle or a pseudo even cycle.

The rank of $\mathcal{A}_G$ is the dimension of the space spanned by the normals to the hyperplanes in $\mathcal{A}_G$, denoted as $\operatorname{rank}(\mathcal{A}_G)$, which can be easily computed by the following pseudo spanning tree.

Definition 2.4. Let $G$ be a connected simple graph, $D$ be a spanning tree of $G$. We denote

where $e\in E(G)$ and $D\cup e$ contains an odd cycle, and call $\widetilde{G}$ the pseudo spanning tree of $G$.

Notice that the pseudo spanning tree of $G$ must exist but is not necessarily unique, as it depends on the selection of both $D$ and $e$.

If $G$ is not connected, we assume the connected components of $G$ are $C_1, \cdots, C_p$, where $p\geq2$. Denote $\widetilde{G} = \widetilde{C_1} \cup\cdots\cup\widetilde{C_p}$, and call it the pseudo spanning forest of $G$.

For a more intuitive understanding of Definition 2.4, we provide Example 2.1.

Example 2.1. Let $G$ be the simple graph in (a), then $D$ in (b) represents a spanning tree of $G$, and $\widetilde{G}$ in (c) represents a pseudo spanning tree of $G$.

3.   Main results

This section first provides a sufficient condition for $\mathcal{A}_G$ to be central if $G$ is a forest. Second, according to the extended even cycles in $G$, we present a necessary and sufficient condition for $\mathcal{A}_G$ to be central. Finally, we obtain a formula for the characteristic polynomials of the STG arrangements.

Lemma 3.1. If the simple graph $G$ is a forest, then $\mathcal{A}_G$ is central.

Proof. $\mathcal{A}_G$ is central if the intersection of all the hyperplanes in $\mathcal{A}_G$ contains at least one point $\left(x_1, \cdots, x_n\right)$. We can find such an assignment $\left(x_1, \cdots, x_n\right)$ satisfying $x_i+x_j = a_i \, (i j \in E(G))$. That can be done by just picking one from $\{x_1, \cdots, x_n\}$ at a time since the graph $G$ is a forest and $a_1, \cdots, a_{n-1}$ are generic elements. □

The following lemma characterizes central $\mathcal{A}_{G}$ if $G$ is a cycle.

Lemma 3.2. Let $G$ be a $k$-cycle with $V(G) = \left\{i_{1}, \cdots, i_{k}\right\}$ and $E(G) = \left\{i_{j} i_{j+1} \mid 1 \leq j \leq k\right\}$, where $i_{k+1} = i_{1}$. The corresponding STG arrangement of $G$ is

Then we have

(1) If $k$ is odd, $\mathcal{A}_{G}$ is central.

(2) If $k$ is even, $\mathcal{A}_{G}$ is central if and only if $\sum\limits_{j = 1}^{k}(-1)^{j} a_{\min\{i_j, i_{j+1}\}} = 0$.

Proof. The system of equations formed by the hyperplane equations in $\mathcal{A}_{G}$ is

where $b_{j} = a_{\min\{i_j, i_{j+1}\}}, 1 \leq j \leq k.$

Let $\beta = (b_1, \cdots, b_k)^\mathrm{T}$, $A$ and $\overline{A}$ be the coefficient matrix and augmented matrix of the above system of equations, respectively. Adjusting the order of columns in the matrix $\overline{A}$, we may assume

Making the following transformations to $\overline A$, we have

where $P(i, j(m))$ denotes the elementary matrix by adding $m$ multiple of $j$-th row of the identity matrix to $i$-th row of the identity matrix.

Distinctly, if $k$ is odd, $r(A) = r(\overline{A}) = k$, i.e., $\mathcal{A}_{G}$ is central. If $k$ is even, $\mathcal{A}_{G}$ is central if and only if $(-1)^{k} \sum\limits_{j = 1}^{k}(-1)^{j} b_{j} = 0$, i.e., $\sum\limits_{j = 1}^{k}(-1)^{j} a_{\min\{i_j, i_{j+1}\}} = 0$. □

The following lemma provides a necessary and sufficient condition for $\mathcal{A}_{H^t_{p, q}}$ to be central, where $H^t_{p, q}$ is a pseudo even cycle.

Lemma 3.3. For the pseudo even cycle $H^t_{p, q}$, we start from the edge $i_pi_1$, go along the direction of the arrows in Figure 1, end at the edge $j_{q-1}j_{q}$, sequentially replace the generic elements of the hyperplanes corresponding to the edges by $b_1, \cdots, b_{p+t+q}$. Then $\mathcal{A}_{H^t_{p, q}}$ is central if and only if

Proof. If $t > 0$, let $\beta = (b_1, \cdots, b_{p+t+q})^\mathrm{T}$, $A$ and $\overline{A}$ be the coefficient matrix and augmented matrix of the system of equations in $\mathcal{A}_{H^t_{p, q}}$, respectively. Adjusting the order of columns in the matrix $\overline{A}$, we may assume that

Making the following transformations to $\overline A$, we have

Therefore, $\mathcal{A}_{H^t_{p, q}}$ is central if and only if $r(A) = r(\overline A)$, i.e., $\sum\limits_{j = 1}^{p+t+q}(-1)^{j-1}b_j+\sum\limits_{j = p+1}^{p+t}(-1)^{j-1} b_j = 0$.

Similarly, if $t = 0$, $\mathcal{A}_{H^t_{p, q}}$ is central if and only if $\sum\limits_{j = 1}^{p+q}(-1)^{j} b_{j} = 0$. □

Following is a formula for computing $\operatorname{rank}(\mathcal{A}_G)$ according to the pseudo spanning forest of $G$.

Lemma 3.4. Let $G$ be a simple graph, $\widetilde{G}$ be a pseudo spanning forest of $G$ and $\mathcal{A}_G$ be the corresponding STG arrangement of $G$. Then $\operatorname{rank}(\mathcal{A}_G) = |E(\widetilde{G})|$, where $|E(\widetilde{G})|$ is the number of edges in $\widetilde{G}$.

Proof. We assume that $|E(\widetilde{G})| = m, |E(G)| = h, 1\leq m\leq h$. In the following, the normals to the hyperplanes in $\mathcal{A}_G$ will be simply called the normals of ${G}$. Let the normals of $\widetilde{G}$ be $\delta_{1}, \cdots, \delta_{m}$ and the normals of $G$ be $\delta_{1}, \cdots, \delta_{m}, \cdots, \delta_{h}$, respectively. We assume $G$ has connected components $C_1, \cdots, C_p$, $p\geq2$. The maximal linearly independent subset of $\{\delta_{1}, \cdots, \delta_{h}\}$ is the disjoint union of the maximal linearly independent subsets of normals of $C_1, \cdots, C_p$, and $|E(\widetilde{G})| = |E(\widetilde{C_1})|+\cdots+|E(\widetilde{C_p})|$, then we may assume $G$ is connected.

Case 1: If $G$ contains no odd cycle, then $\widetilde{G}$ is the spanning tree of $G$, i.e., $\delta_{1}, \cdots, \delta_{m}$ are linearly independent. If $E(G) = E(\widetilde{G})$, i.e., $m = h$, then $\{\delta_{1}, \cdots, \delta_{m}\}$ is a maximal linearly independent subset of $\{\delta_{1}, \cdots, \delta_{h}\}$. If $E(G)\neq E(\widetilde{G})$, for any $e \in E(G)-E(\widetilde{G})$, $\widetilde{G} \bigcup e$ must contain an even cycle. Let the normal corresponding to edge $e$ be $\delta \in \{\delta_{m+1}, \cdots, \delta_{h}\}$. Since the normals of an even cycle are linearly dependent, $\delta$ can be linearly expressed by $\delta_{1}, \cdots, \delta_{m}$. However, $e$ is taken at random, then $\{\delta_{1}, \cdots, \delta_{m}\}$ is a maximal linearly independent subset of $\{\delta_{1}, \cdots, \delta_{h}\}$.

Case 2: If $G$ contains any odd cycle, then $\widetilde{G}$ has a unique odd cycle $O$. We assume $|E(O)| = k$, and the normals of $O$ are $\{\delta_{1}, \cdots, \delta_{k}\}\subseteq \{\delta_{1}, \cdots, \delta_{h}\}$, take any edge $e \in E(O)$ and let its corresponding normal happens to be $\delta_{k}$. Since $O$ is an odd cycle, $\delta_k$ cannot be linearly expressed by the normals of $O\setminus e$, that is, $\delta_{1}, \cdots, \delta_{k-1}$. It is obvious that $\delta_k$ cannot be linearly expressed by the normals of $\widetilde{G}\setminus O$, that is, $\delta_{k+1}, \cdots, \delta_{m}$. In addition, $\delta_{1}, \cdots, \delta_{k-1}$ and $\delta_{k+1}, \cdots, \delta_{m}$ cannot linearly express each other, then

Therefore, $\delta_k$ cannot be linearly expressed by $\delta_{1}, \cdots, \delta_{k-1}, \delta_{k+1}, \cdots, \delta_{m}$, which are the normals of $\widetilde{G}\setminus e$. Since $\widetilde{G}\setminus e$ is the spanning tree of $G$, the normals of $\widetilde{G}\setminus e$ are linearly independent, therefore, $\delta_{1}, \cdots, \delta_{m}$ are linearly independent. If $E(G) = E(\widetilde{G})$, i.e., $h = m$, then $\{\delta_{1}, \cdots, \delta_{m}\}$ is a maximal linearly independent subset of $\{\delta_{1}, \cdots, \delta_{h}\}$. If $E(G)\neq E(\widetilde{G})$, i.e., $|E(\widetilde{G})| = m = |V(G)|$, then $\delta_{1}, \cdots, \delta_{m}$ are in the $m$-dimensional space. However, $m+1$ vectors in $m$-dimensional space are linearly dependent. Therefore, $\{\delta_{1}, \cdots, \delta_{m}\}$ is a maximal linearly independent subset of $\{\delta_{1}, \cdots, \delta_{h}\}$.

Above all, $\{\delta_{1}, \cdots, \delta_{m}\}$ is a maximal linearly independent subset of $\{\delta_{1}, \cdots, \delta_{h}\}$, i.e., $\operatorname{rank}(\mathcal{A}_G) = |E(\widetilde{G})|$. □

In the following, we provide a necessary and sufficient condition for the STG arrangement $\mathcal{A}_G$ to be central.

Theorem 3.1. The STG arrangement $\mathcal{A}_G$ is central if and only if all the subarrangements corresponding to the extended even cycles present in $G$ are central.

Proof. If $\mathcal{A}_G$ is central, then any subarrangement of $\mathcal{A}_G$ is central.

Conversely, we consider the following two cases:

Case 1: Let $C$ be a connected component of $G$ that does not contain any extended even cycles, i.e., $C$ contains no cycles or only an odd one, then $\widetilde{C} = C$. Let $M$ and $\overline M$ be the coefficient matrix and augmented matrix of the linear system of hyperplane equations for $\mathcal{A}_C$, respectively. Then, the row vectors of $M$ are the normals of $C = \widetilde C$, which are linearly independent. Therefore, $\operatorname{rank}(M) = |E(\widetilde{C})|$. Because $|E(\widetilde{C})| \leq |V(\widetilde{C})|$, i.e., the number of rows of $M$ does not exceed the number of columns of $M$. Then $\operatorname{rank}(\overline M) = |E(\widetilde{C})| = \operatorname{rank}(M)$, i.e., $\mathcal{A}_C$ is central.

Case 2: Let $C$ be a connected component of $G$ that contains extended even cycle. Assume the number of vertices in $C$ is $|V(C)| = l$, the number of edges in $C$ is $|E(C)| = p\; (l\le p\le C_l^2)$, the number of edges in $\widetilde{C}$ is $|E(\widetilde{C})| = r\le p$. Let the normals of $\widetilde{C}$ be $\delta_{1}, \cdots, \delta_{r}$ and the normals of $C$ be $\delta_{1}, \cdots, \delta_{r}, \cdots, \delta_{p}$. By Lemma 3.4, we know that the maximal linearly independent subset of $\{\delta_{1}, \cdots, \delta_{p}\}$ is $\{\delta_{1}, \cdots, \delta_{r}\}$. Let $M$ and $\overline{M}$ be the coefficient matrix and augmented matrix of the linear system of hyperplane equations for $\mathcal{A}_C$ as follows:

We can see that $\operatorname{rank}(M) = \operatorname{rank}(\delta_{1}, \cdots, \delta_{p}) = \operatorname{rank}(\delta_{1}, \cdots, \delta_{r}) = r$.

In the following, we discuss the rank of $\overline M$. Pick $e \in E(C) \setminus E(\widetilde{C})$, and assume its normal is $\delta_s \in \{\delta_{r+1}, \cdots, \delta_p\}$, then

is the augmented matrix of the linear system of hyperplane equations for $\mathcal{A}_{\widetilde{C}\cup e}$. From the definition of $\widetilde{C}$, we know $\widetilde{C}\cup e$ must contain a unique extended even cycle $O$. We may assume $\delta_{1}, \cdots, \delta_{h}, \delta_{s}$ are the normals of $O$, where $h \leq r$. Then, the augmented matrix of the linear system of hyperplane equations for $\mathcal{A}_{O}$ is

If $O$ is an even cycle, according to the proof of Lemma 3.2, $\mathcal{A}_O$ is central if and only if $\operatorname{rank}(\overline{T}) = \operatorname{rank}(\delta_1, \cdots, \delta_h, \delta_s) = h$. Therefore, $r(\overline N) = r$. However, $\delta_s$ can be taken as any element in $\{\delta_{r+1}, \cdots, \delta_p\}$, then $r(\overline M) = r$. There is a similar result in Lemma 3.3, so the same goes if $O$ is a pseudo even cycle.

Then $\operatorname{rank}(\overline M) = r = \operatorname{rank}(M)$, i.e., $\mathcal{A}_C$ is central.

Above all, $\mathcal{A}_G$ is central. □

Next, we cite Whitney's theorem ^[16] as Lemma 3.5.

Lemma 3.5. Let $\mathcal{A}$ be an arrangement in $n$-dimensional vector space, the characteristic polynomial of $\mathcal{A}$ is

where $\# \mathcal{B}$ is the number of hyperplanes in $\mathcal{B}$.

By Lemma 3.5, we can obtain a formula for the characteristic polynomial of the STG arrangement as follows.

Corollary 3.1. The characteristic polynomial of the STG arrangement $\mathcal{A}_G$ is:

where $B$ is the subgraph of $G$ such that $\mathcal{A}_B$ is a central arrangement, $u(B)$ is the number of connected components in $B$, and $v(B)$ is the number of odd cycles in $\widetilde{B}$.

Proof. The number of edges in $\widetilde B$ is $\operatorname{rank}(\mathcal{A}_B)$. The number of connected components in $B$ is $u(B) = n-\operatorname{rank}(\mathcal{A}_B)+v(B)$. Then

Therefore, the characteristic polynomial of $\mathcal{A}_G$ is

□

4.   Examples

In this section, we will illustrate the applications of Corollary 3.1 with two examples.

Example 4.1. For the graph $G$ in Figure 3, the corresponding STG arrangement $\mathcal{A}_{G}$ contains the following hyperplanes:

We let $a_1 = 1, a_2 = 2, a_3 = 2, a_4 = 3$, and compute the characteristic polynomial of $\mathcal{A}_G$.

According to Theorem 3.1, we must determine if the STG arrangements corresponding to the extended even cycles in $G$ are central. By Lemma 3.2, 3.3, the STG arrangement corresponding to the left even cycle in Figure 4 is central, whereas the other two are not. Therefore, for central STG arrangement $\mathcal{A}_B$, the corresponding graph $B$ should not contain any extended even cycles other than the left one.

Figure 5 lists the isomorphic subgraphs of $G$ which corresponding to central arrangements, and we label the numbers of each case under the subgraphs.

Table 1 lists the values of $u(B)-v(B)$, $|E(B)|$, and the number of distinct labelings of $B$ for each subgraph $B$ in Figure 5.

Thus, by Corollary 3.1, the characteristic polynomial of $\mathcal{A}_G$ is obtained as:

Example 4.2. For Figure 3 above, we will consider all the types of $\chi_{\mathcal{A}_G}(t)$ if $\mathcal{A}_G$ is taken with different generic elements. Let the STG arrangement of $G$ in Figure 3 be

We list all the types of $\chi_{\mathcal{A}_G}(t)$ in Table 2, where "T" indicates that the condition is satisfied, "F" indicates that the condition is not satisfied, and "$\backslash$" indicates that it is unnecessary to consider.

5.   Conclusions

In this paper, we study the characteristic polynomial of the semigeneric threshold arrangement $\mathcal{A}_n$, which is a deformation of the generic threshold arrangement. For the STG arrangement $\mathcal{A}_G$, we provide a necessary and sufficient condition for it to be central from the perspective of the simple graph $G$. Based on the above condition, a formula for the characteristic polynomial of the STG arrangement $\mathcal{A}_G$ is obtained.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The work was partially supported by Science and Technology Research Project of Jilin Province (No. JJKH20220719KJ, 20230101186JC) and NSF of China (No. 11501051).

Conflict of Interest

The authors declare no conflict of interest in this paper.