Sturm's Theorem for Min matrices

Efruz Özlem Mersin; Efruz Özlem Mersin

doi:10.3934/math.2023880

AIMS Mathematics

2023, Volume 8, Issue 7: 17229-17245. doi: 10.3934/math.2023880

Previous Article Next Article

Research article

Sturm's Theorem for Min matrices

Efruz Özlem Mersin ^,

Department of Mathematics, Faculty of Science and Arts, Aksaray University, Aksaray 68100, Turkey

Received: 17 February 2023 Revised: 29 April 2023 Accepted: 11 May 2023 Published: 18 May 2023
MSC : 15A18, 15B99

In the present paper, we study Min matrix $\mathcal{A}_{min} = \left[a_{min\left(i, j\right)}\right]_{i, j = 1}^n$ , where $a_s$ 's are the elements of a real sequence $\left\lbrace a_s\right\rbrace$ . We first obtain a recurrence relation for the characteristic polynomial for matrix $\mathcal{A}_{min}$ , and some relations between the coefficients of its characteristic polynomial. Next, we show that the sequence of the characteristic polynomials of the $i \times i \left(i \leq n\right)$ Min matrices satisfies the Sturm sequence properties according to different required conditions of the sequence $\left\lbrace a_s\right\rbrace$ . Using Sturm's Theorem, we get some results about the eigenvalues, such as the number of eigenvalues in an interval. Thus, we obtain the number of positive and negative eigenvalues of Min matrix $\mathcal{A}_{min}$ . Finally, we give an example to illustrate our results.

Keywords:

Citation: Efruz Özlem Mersin. Sturm's Theorem for Min matrices[J]. AIMS Mathematics, 2023, 8(7): 17229-17245. doi: 10.3934/math.2023880

Related Papers:

[1]	Rajish Kumar P, Sunil Jacob John . On redundancy, separation and connectedness in multiset topological spaces. AIMS Mathematics, 2020, 5(3): 2484-2499. doi: 10.3934/math.2020164
[2]	Seçil Çeken, Cem Yüksel . Generalizations of strongly hollow ideals and a corresponding topology. AIMS Mathematics, 2021, 6(12): 12986-13003. doi: 10.3934/math.2021751
[3]	Saad Ihsan Butt, Ahmet Ocak Akdemir, Muhammad Nadeem, Nabil Mlaiki, İşcan İmdat, Thabet Abdeljawad . $(m, n)$ -Harmonically polynomial convex functions and some Hadamard type inequalities on the co-ordinates. AIMS Mathematics, 2021, 6(5): 4677-4690. doi: 10.3934/math.2021275
[4]	Qian Liu, Jianrui Xie, Ximeng Liu, Jian Zou . Further results on permutation polynomials and complete permutation polynomials over finite fields. AIMS Mathematics, 2021, 6(12): 13503-13514. doi: 10.3934/math.2021783
[5]	Usman Babar, Haidar Ali, Shahid Hussain Arshad, Umber Sheikh . Multiplicative topological properties of graphs derived from honeycomb structure. AIMS Mathematics, 2020, 5(2): 1562-1587. doi: 10.3934/math.2020107
[6]	Ninghe Yang . Exact wave patterns and chaotic dynamical behaviors of the extended (3+1)-dimensional NLSE. AIMS Mathematics, 2024, 9(11): 31274-31294. doi: 10.3934/math.20241508
[7]	Ali N. A. Koam, Ali Ahmad, Yasir Ahmad . Computation of reverse degree-based topological indices of hex-derived networks. AIMS Mathematics, 2021, 6(10): 11330-11345. doi: 10.3934/math.2021658
[8]	R. Aguilar-Sánchez, J. A. Mendez-Bermudez, José M. Rodríguez, José M. Sigarreta . Multiplicative topological indices: Analytical properties and application to random networks. AIMS Mathematics, 2024, 9(2): 3646-3670. doi: 10.3934/math.2024179
[9]	Muhammad Riaz, Khadija Akmal, Yahya Almalki, S. A. Alblowi . Cubic m-polar fuzzy topology with multi-criteria group decision-making. AIMS Mathematics, 2022, 7(7): 13019-13052. doi: 10.3934/math.2022721
[10]	Maryam Salem Alatawi, Ali Ahmad, Ali N. A. Koam, Sadia Husain, Muhammad Azeem . Computing vertex resolvability of benzenoid tripod structure. AIMS Mathematics, 2022, 7(4): 6971-6983. doi: 10.3934/math.2022387

Abstract

1. Introduction

In today's world mathematics is necessary in all fields. It is an essential instrument for comprehension around us. It covers all the facts of life. Mathematics is the branch of science that deals with the reasoning of figures, numbers and order. In our daily life, we use mathematics in our routine work in various forms. There are many branches of mathematics like algebra, geometry, arithmetic, trigonometry, analysis and many other theories. Graph theory is the study of mathematical objects known as graph, which consist of vertices connected by edges. It is the mathematical theory which deals with the properties and applications of graphs. When we apply graph theory on chemistry then it is called chemical graph theory. In mathematical models graph theory is used to get a deep understanding of the physical properties of these chemical compounds. Some physical properties such as boiling point, melting point, density are associated to geometrical structure of the compound. Now a days, several ways are used in mathematical chemistry to understand chemical structure which are existing behind the chemical concepts, to create and inquire novel mathematical representation. In complete history of chemistry certain scientist, usually contemplates connections between mathematics with chemistry and the possibility of using mathematics to analyze and predict new chemical concepts. Mufti defined sanskruti and harmonic indices of certain graph structure ^[25]. Babujee calculated topological indices and new graph structures in 2012 ^[5]. Farahani worked on a new version of zagreb index of circumcoronene series of benzenoid in 2013 ^[7]. Hayat defined some degree based topological indices of certain nanotubes ^[8]. Imran worked on topological indices of certain interconnection networks in 2014 ^[14]. In 2016, Siddiqui computed zagreb indices and zagreb polynomials of some nanostars dendrimers ^[27]. Saleem computed retractions and homomorphisms on some operations of graphs ^[28]. Iqbal calculated eccentricity based topological indices of some benzenoid structures ^[12]. Yang examined two-point resistances and random walks on stellated regular graphs ^[29]. Islam defined M-polynomial and entropy of paraline graph of Napthalene in 2019 ^[11]. Iqbal worked on topological indices of subdivided and line graph of subdivided friendship graph ^[13]. In 2020, Afzal examined M-polynomial and topological indices of zigzag edge coronoid fused by starphene ^[1]. Archdeacon defined the medial graph and voltage-current duality ^[2]. Munir computed M-polynomial and degree-based topological indices of polyhex nanotubes ^[22]. Iqbal calculated ve topological indices of tickysim spinnaker model ^[15]. Azhar examined a note on valency dependence invariants of L(G(K)) Graph ^[4]. Jamil defined the first general zagreb eccentricity index ^[18]. Iqbal defined ABC4 and GA5 index of subdivided and line graph of subdivided dutch windmill graph ^[16]. Maji worked on the first entire zagreb index of various corona products and their bounds ^[23]. Imran describe computation of topological indices of NEPS of graphs ^[17]. Hayat computed topological indices for networks derived by applying graph operations from honeycomb structures ^[9], based on this idea we have computed the topological indices for transformed structures. Next we have few definitions ^[3,9]:

Definition 1:

Let K be a simple connected graph its M-polynomial is defined as;

$M(K;x, y) = \sum\limits_{S \leq a \leq b \leq T}m_{ab}(K)x^{a}y^{b}, \, \, \, \, \, \, \, \ \text{(i)}$

where: S = $Min\{d_\beta|\beta \in V(K)\}$ , T = $Max\{d_\beta|\beta \in V(K)\}$ , and $m_{ab}(K)$ is the number of edges $\gamma\beta\in E(K)$ such that $\{ d_\gamma, \ d_\beta\}$ = $\{{a}, {b}\}$ .

Definition 2:

When we place a new vertex in each face of a planar graph G, and attach that vertex with all the vertices of the respective face of G, we get the stellation of G and denote it as St(G).

Definition 3:

We introduce a node in each edge of the graph and join the nodes if their corresponding edges are adjacent and is denoted by Md(G).

Definition 4:

We introduce a node in each bounded faces of the graph and join the nodes by an edge if the faces share an edge in graph it is called bounded dual. It is represented as Bdu(G).

T. Réti introduced First and Second Zagreb indices are ^[26],

$\begin{eqnarray} M_1(K)& = &\sum\limits_{\gamma\beta \in E(K)}{(d_\gamma+d_\beta)}, \end{eqnarray}$

(1.1)

$\begin{eqnarray} M_2(K)& = &\sum\limits_{\gamma\beta \in E(K)}{(d_\gamma d_\beta)}. \end{eqnarray}$

(1.2)

Second modified Zagreb index is defined as ^[10],

$\begin{eqnarray} ^mM_2(k)& = &\sum\limits_{\gamma\beta \in E(K)}\bigg(\frac 1{d_\gamma d_\beta}\bigg). \end{eqnarray}$

(1.3)

Symmetric division and reciprocal general Randic index is ^[19],

$\begin{eqnarray} SDD(K)& = &\sum\limits_{\gamma\beta \in E(K)}\ \bigg\{\frac {min(d_\gamma, d_\beta)}{max(d_\gamma, d_\beta)}+\frac {max(d_\gamma, d_\beta)}{min(d_\gamma, d_\beta)}\bigg\}, \end{eqnarray}$

(1.4)

$\begin{eqnarray} RR_\alpha(K)& = &\sum\limits_{\gamma\beta \in E(K)}\frac 1{(d_\gamma d_\beta)^\alpha}. \end{eqnarray}$

(1.5)

Whereas, the General Randic index defined as ^[24],

$\begin{eqnarray} R_\alpha(K)& = &\sum\limits_{\gamma\beta \in E(K)}(d_\gamma d_\beta)^{\alpha}, \end{eqnarray}$

(1.6)

where $\alpha$ is an arbitrary real number.

In 1998, the Atomic Bond Connectivity Index is defined as ^[6],

$\begin{eqnarray} ABC(K)& = &\sum\limits_{\gamma\beta \in E(K)}\sqrt{\frac{d_{\gamma}+d_{\beta}-2}{d_\gamma d_\beta}}. \end{eqnarray}$

(1.7)

Geometric-Arithmetic index is ^[30],

$\begin{eqnarray} GA(K)& = &\sum\limits_{\gamma\beta\in E(K)}\frac{2\sqrt{d_{\gamma}d_{\beta}}}{d_{\gamma}+d_{\beta}}. \end{eqnarray}$

(1.8)

In 2015, the General Version of Harmonic Index is defined ^[31],

$\begin{eqnarray} H_k(K)& = &\sum\limits_{\gamma\beta \in E(K)}\bigg(\frac 2{d_{\gamma}+d_{\beta}}\bigg)^k. \end{eqnarray}$

(1.9)

First and Second Gourava Indices were introduced by Kalli which is defined as, respectively ^[20],

$\begin{eqnarray} GO_1(K)& = &\sum\limits_{\gamma\beta \in E(K)}\big[(d_{\gamma}+d_{\beta})+(d_\gamma d_\beta)\big], \end{eqnarray}$

(1.10)

$\begin{eqnarray} GO_2(K)& = &\sum\limits_{\gamma\beta \in E(K)}\big[(d_{\gamma}+d_{\beta})(d_\gamma d_\beta)\big]. \end{eqnarray}$

(1.11)

Kalli introduced the First and Second Hyper-Gourava Indices which is defined as, respectively ^[21],

$\begin{eqnarray} HGO_1(K)& = &\sum\limits_{\gamma\beta\in E(K)}\big[(d_{\gamma}+d_{\beta})+(d_\gamma d_\beta)\big]^2, \end{eqnarray}$

(1.12)

$\begin{eqnarray} HGO_2(K)& = &\sum\limits_{\gamma\beta\in E(K)}\big[(d_{\gamma}+d_{\beta})(d_\gamma d_\beta)\big]^2. \end{eqnarray}$

(1.13)

2. Methodology

At first, we obtain transformed pattern of molecular structures zigzag and triangular benzenoid named as $T_1$ and $T_2$ . Next we define M-polynomial and topological indices of these networks by applying the stellation, medial and bounded dual. Further we define edge partition depending upon degree based vertices of $T_1$ and $T_2$ and then calculate the indices.

3. Results and discussion

3.1. M-polynomial and degree based topological indices of $T_1$ structure

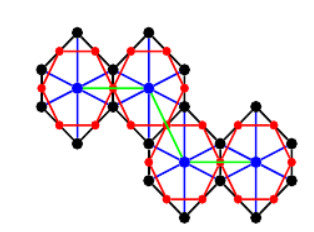
Now we will construct the stellation, medial and bounded dual operations on simple and undirected zigzag benzenoid structure. We get a new transformed network (say) $T_1$ , shown in for n = 2. After this we will compute M-polynomial and degree based topological indices of our newly obtained network. Where, blue is stellation, red is medial, green is bounded dual operations applied on $T_1$ .

Figure 1. Transformed structure

$T_1$ .

DownLoad: Full-Size Img PowerPoint

Following shows the types of edges and their count for network $T_1$ ; $n\geq2$ . Now, we will calculate the M-polynomial and vertex degree based topological indices namely first Zagreb index, second Zagreb index, second modified index, symmetric division index, general Randic index, reciprocal general Randic index, atomic bond connectivity index, geometric arithmetic index, general version of harmonic index, first and second gourava indices, first and second hyper gourava indices.

3.1.1. Theorem

Let $T_1$ , be the transformed network then its M-polynomial is

$M\big(T_1;x, y\big) = \big(8n+8\big)x^3y^4+8x^3y^7+\big(4n-4\big)x^3y^8+\big(4n+4\big)x^4y^4+\big(8n-4\big)x^4y^5+\big(8n-4\big)x^4y^6 \\ +\big(4n-2\big)x^5y^6+4x^5y^7+\big(8n-8\big)x^5y^8+2x^7y^8+\big(2n-3\big)x^8y^8.\\$

Proof:

Using definition of M-polynomial and information from Table 3, we have

$M(T_1;x, y) = \sum\limits_{a \leq b}m_{ab}x^{a}y^{b} = \sum\limits_{3\leq 4}m_{34}x^3y^4+\sum\limits_{3\leq 7}m_{37}x^3y^7+\sum\limits_{3\leq 8}m_{38}x^3y^8+\sum\limits_{4\leq4}m_{44}x^4y^4+\sum\limits_{4\leq5}m_{45}x^4y^5 \\ +\sum\limits_{4\leq6}m_{46}x^4y^6+\sum\limits_{5\leq6}m_{56}x^5y^6+\sum\limits_{5\leq7}m_{57}x^5y^7+\sum\limits_{5\leq8}m_{58}x^5y^8 +\sum\limits_{7\leq8}m_{78}x^7y^8+\sum\limits_{8\leq8}m_{88}x^8y^8\\ = |E_{3, 4}|x^3y^4+|E_{3, 7}|x^3y^7+|E_{3, 8}|x^3y^8+|E_{4, 4}|x^4y^4+|E_{4, 5}|x^4y^5+|E_{4, 6}|x^4y^6+|E_{5, 6}|x^5y^6 \\ +|E_{5, 7}|x^5y^7+|E_{5, 8}|x^5y^8+|E_{7, 8}|x^7y^8+|E_{8, 8}|x^8y^8\\ = \big(8n+8\big)x^3y^4+8x^3y^7+\big(4n-4\big)x^3y^8+\big(4n+4\big)x^4y^4+\big(8n-4\big)x^4y^5+\big(8n-4\big)x^4y^6 \\ +\big(4n-2\big)x^5y^6+4x^5y^7+\big(8n-8\big)x^5y^8+2x^7y^8+\big(2n-3\big)x^8y^8.$

Figure 2. M-polynomial of

$T_1$ .

DownLoad: Full-Size Img PowerPoint

3.1.2. Theorem

Let $T_1$ , be the transformed network and

be its M-polynomial. Then, the first Zagreb index $M_1\big(T_1\big)$ , the second Zagreb index $M_2\big(T_1\big)$ , the second modified Zagreb index $^mM_2\big(T_1\big)$ , the general Randic index $R_\alpha(T_1)$ , where $\alpha \ \epsilon \ N$ , reciprocal general Randic index $RR_\alpha(T_1)$ , where $\alpha \ \epsilon \ N$ , and the symmetric division degree index $SDD(T_1)$ obtained from M-polynomial are as follows:

$M_1(T_1) = 464n-48, \\ M_2(T_1) = 1176n-264, \\ ^mM_2(T_1) = \frac{11}{12}\big(n+1\big)+\frac{11}{30}\big(n-1\big)+\frac{13}{30}\big(2n-1\big)+\frac{1}{64}\big(2n-3\big) +\frac{223}{420}, \\ R_\alpha(T_1) = 12^\alpha(8n+8)+21^\alpha(8)+24^\alpha(4n-4)+16^\alpha(4n+4)+20^\alpha(8n-4)+24^\alpha(8n-4) \\ +30^\alpha(4n-2)+35^\alpha(4)+40^\alpha(8n-8)+56^\alpha(2)+64^\alpha(2n-3), \\ RR_\alpha(T_1) = \frac{8}{12^\alpha}\big(n+1\big)+\frac{8}{21^\alpha}+\frac{4}{24^\alpha}\big(n-1\big)+\frac{4}{4^{2\alpha}}\big(n+1\big) +\frac{4}{20^\alpha}\big(2n-1\big)+\frac{4}{24^\alpha}\big(2n-1\big) \\ +\frac{2}{30^\alpha}\big(2n-1\big)+\frac{4}{35^\alpha}+\frac{8}{40^\alpha}\big(n-1\big) +\frac{2}{56^\alpha}+\frac{1}{64^\alpha}\big(2n-3\big), \\ SDD(T_1) = \frac{74}{3}\big(n+1\big)+\frac{899}{30}\big(n-1\big)+\frac{314}{15}\big(2n-1\big)+2\big(2n-3\big)+\frac{14527}{420}.$

Proof: Let $f(x, y)$ = $M\big(T_1;x, y\big)$ be the M-polynomial of the transformed network $T_1$ . Then

Now, the required partial derivatives and integrals are obtained as:

By using the information given in Table 3 and formulas for Table 1;

$D_xf\big(x, y\big) = 3\big(8n+8\big)x^3y^4+24x^3y^7+3\big(4n-4\big)x^3y^8+4\big(4n+4\big)x^4y^4+4\big(8n-4\big)x^4y^5 \\ +4\big(8n-4\big)x^4y^6+5\big(4n-2\big)x^5y^6+20x^5y^7+5\big(8n-8\big)x^5y^8+14x^7y^8+8\big(2n-3\big)x^8y^8, \\ D_yf\big(x, y\big) = 4\big(8n+8\big)x^3y^4+56x^3y^7+8\big(4n-4\big)x^3y^8+4\big(4n+4\big)x^4y^4+5\big(8n-4\big)x^4y^5 \\ +6\big(8n-4\big)x^4y^6+6\big(4n-2\big)x^5y^6+28x^5y^7+ 8\big(8n-8\big)x^5y^8+16x^7y^8+8\big(2n-3\big)x^8y^8, \\ D_xD_yf\big(x, y\big) = 12\big(8n+8\big)x^3y^4+168x^3y^7+24\big(4n-4\big)x^3y^8+16\big(4n+4\big)x^4y^4+20\big(8n-4\big)x^4y^5 \\ +24\big(8n-4\big)x^4y^6+30\big(4n-2\big)x^5y^6+140x^5y^7+40\big(8n-8\big)x^5y^8+112x^7y^8 \\ +64\big(2n-3\big)x^8y^8, \\ S_xS_yf\big(x, y\big) = \frac{2}{3}\big(n+1\big)x^3y^4+\frac{8}{21}x^3y^7+\frac{1}{6}\big(n-1\big)x^3y^8+\frac{1}{4}\big(n+1\big)x^4y^4 +\frac{1}{5}\big(2n-1\big)x^4y^5 \\ +\frac{1}{6}\big(2n-1\big)x^4y^6+\frac{1}{15}\big(2n-1\big)x^5y^6+\frac{4}{35}x^5y^7+\frac{1}{5}\big(n-1\big)x^5y^8 \\ +\frac{1}{28}x^7y^8+\frac{1}{64}\big(2n-3\big)x^8y^8, \\ D_x^{\alpha}D_y^{\alpha}f(x, y) = 12^{\alpha}(8n+8)x^3y^4+21^{\alpha}(8)x^3y^7+24^{\alpha}(4n-4)x^3y^8+4^{2\alpha}(4n+4)x^4y^4+20^{\alpha}(8n-4)x^4y^5 \\ +24^{\alpha}(8n-4)x^4y^6+30^{\alpha}(4n-2)x^5y^6+35^{\alpha}(4)x^5y^7+40^{\alpha}(8n-8)x^5y^8+56^{\alpha}(2)x^7y^8 \\ +46^{\alpha}(2n-3)x^8y^8, \\ S_x^{\alpha}S_y^{\alpha}f\big(x, y\big) = \frac{8}{12^\alpha}\big(n+1\big)x^3y^4+\frac{8}{21^\alpha}x^3y^7 +\frac{4}{24^\alpha}\big(n-1\big)x^3y^8+\frac{4}{4^{2\alpha}}\big(n+1\big)x^4y^4 \\ +\frac{4}{20^\alpha}\big(2n-1\big)x^4y^5+\frac{4}{24^\alpha}\big(2n-1\big)x^4y^6+\frac{2}{30^\alpha}\big(2n-1\big)x^5y^6+\frac{4}{35^\alpha}x^5y^7 \\ +\frac{8}{40^{\alpha}}\big(n-1\big)x^5y^8+\frac{2}{56^\alpha}x^7y^8+\frac{1}{64^\alpha}\big(2n-3\big)x^8y^8, \\ S_yD_xf\big(x, y\big) = 6\big(n+1\big)x^3y^4+\frac{24}{7}x^3y^7+\frac{3}{2}\big(n-1\big)x^3y^8+4\big(n+1\big)x^4y^4+\frac{16}{5}\big(2n-1\big)x^4y^5 \\ +\frac{8}{3}\big(2n-1\big)x^4y^6+\frac{5}{3}\big(2n-1\big)x^5y^6+\frac{20}{7}x^5y^7+5\big(n-1\big)x^5y^8 \\ +\frac{7}{4}x^7y^8+(2n-3)x^8y^8, \\ S_xD_yf\big(x, y\big) = \frac{32}{3}\big(n+1\big)x^3y^4+\frac{56}{3}x^3y^7+\frac{32}{3}\big(n-1\big)x^3y^8+4\big(n+1\big)x^4y^4+5\big(2n-1\big)x^4y^5 \\ +6\big(2n-1\big)x^4y^6+\frac{12}{5}\big(2n-1\big)x^5y^6+\frac{28}{5}x^5y^7+\frac{64}{5}\big(n-1\big)x^5y^8 \\ +\frac{16}{7}x^7y^8+(2n-3)x^8y^8.$

Table 1. Derivation of some degree-based topological indices from M-polynomial ^[3].

$Topological$ $Index$	Derivation from M (K; x, y)
$First$ $Zagreb$	$(D_x+D_y)(M(K; x, y))\|_{x=1=y}$	(ii)
$Second$ $Zagreb$	$(D_xD_y)(M(K; x, y))\|_{x=1=y}$	(iii)
$Second$ $Modified$ $Zagreb$	$(S_xS_y)(M(K; x, y))\|_{x=1=y}$	(iv)
$general$ $Randic$	$(D_x^{\alpha}D_y^{\alpha})(M(K; x, y))\|_{x=1=y}$	(v)
$Reciprocal$ $general$ $Randic$	$(S_x^{\alpha}S_y^{\alpha})(M(K; x, y))\|_{x=1=y}$	(vi)
$Symmetric$ $Division$ $Index$	$(S_yD_x)+(S_xD_y)(M(K; x, y))\|_{x=1=y}$	(vii)

| Show Table

DownLoad: CSV

Table 2. Planar and non-planar graph.

$Graph$	$Planar$ / $Non-Planar$
$St(G_1, G_2)$	$Planar$
$Md(G_1, G_2)$	$Planar$
$Bdu(G_1, G_2)$	$Non-Planar$
$T_1$	$Non-Planar$
$T_2$	$Non-Planar$

| Show Table

DownLoad: CSV

Consequently,

$M_1(T_1) = (D_x+D_y)f(x, y)|_{x = 1 = y} = 464n-48, \\ M_2(T_1) = D_xD_yf(x, y)|_{x = 1 = y} = 1176n-264, \\ ^mM_2(T_1) = S_xS_yf(x, y)|_{x = 1 = y} = \frac{11}{12}\big(n+1\big)+\frac{11}{30}\big(n-1\big)+\frac{13}{30}\big(2n-1\big) +\frac{1}{64}\big(2n-3\big)+\frac{223}{420}, \\ R_\alpha(T_1) = D_x^{\alpha} D_y^{\alpha}f(x, y)|_{x = 1 = y} = 12^\alpha(8n+8)+(21)^\alpha8+24^\alpha(4n-4)+16^\alpha(4n+4) +20^\alpha(8n-4)\\ +24^\alpha(8n-4)+30^\alpha(4n-2)+(35)^\alpha4 +40^\alpha(8n-8)+(56)^\alpha2+64^\alpha(2n-3), \\ RR_\alpha(T_1) = S_x^{\alpha}S_y^{\alpha}f(x, y)|_{x = 1 = y} = \frac{8}{12^\alpha}\big(n+1\big)+\frac{8}{21^\alpha} +\frac{4}{24^\alpha}\big(n-1\big)+\frac{4}{4^{2\alpha}}\big(n+1\big) +\frac{4}{20^\alpha}\big(2n-1\big) \\ +\frac{4}{24^\alpha}\big(2n-1\big)+\frac{2}{30^\alpha}\big(2n-1\big)+\frac{4}{35^\alpha}+\frac{8}{40^\alpha}\big(n-1\big) +\frac{2}{56^\alpha}+\frac{1}{64^\alpha}\big(2n-3\big), \\ SDD(T_1) = (S_yD_x+S_xD_y)(x, y)|_{x = 1 = y} = \frac{74}{3}\big(n+1\big)+\frac{899}{30}\big(n-1\big)+\frac{314}{15}\big(2n-1\big)+2\big(2n-3\big)+\frac{14527}{420}.$

3.1.3. Theorem

For $T_1$ , the Atomic Bond Connectivity, Geometric Arithematic Index and General Harmonic Index are as follows, respectively.

$1) \ \ ABC(T_1) = 2n\sqrt{6}+(n+1)\frac{4\sqrt{15}}{3}+(14n+11)\frac{\sqrt14}{56}+(n-1)\frac{2\sqrt110}{5} \\ +(2n-1)\bigg(2\sqrt{\frac{7}{5}}+\frac{4}{\sqrt3}+\sqrt{\frac{6}{5}}\bigg)+\frac{16\sqrt{42}}{21}+\frac{\sqrt182}{14}, \\ 2) \ \ GA(T_1) = (n+1)\bigg(\frac{32\sqrt3}{7}+4\bigg)+(n-1)\frac{32\sqrt10}{13}+(32n-21)\frac{8\sqrt6}{55}+(2n-1)\bigg(\frac{16\sqrt5}{9}+\frac{4\sqrt30}{11}\bigg) \\ +(2n-3)+\frac{8\sqrt21}{5}+\frac{2\sqrt35}{3}+\frac{8\sqrt14}{15}, \\ 3) \ \ H_k(T_1) = (8n+8)\big(\frac2{7}\big)^k+(8n+4)\big(\frac{1}{5}\big)^k+(4n-4)\big(\frac2{11}\big)^k +(4n+4)\big(\frac1{4}\big)^k+(8n-4)\big(\frac2{9}\big)^k \\ +(4n-2)(\frac2{11})^k+4(\frac1{6})^k+(8n-8)(\frac2{13})^k+2(\frac2{15})^k+(2n-3)(\frac1{8})^k.$

Proof:

1). According to Eq (1.7)

$ABC(T_1) = \sum\limits_{\gamma\beta \in E(K)}\sqrt{\frac{d_{\gamma}+d_{\beta}-2}{d_\gamma d_\beta}}.$

By using the information given in Table 3.

$= (8n+8)\bigg(\sqrt{\frac{3+4-2}{3\times4}}\bigg)+8\bigg(\sqrt{\frac{3+7-2}{3\times7}}\bigg)+(4n-4)\bigg(\sqrt{\frac{3+8-2}{3\times8}}\bigg) \\ +(4n+4)\bigg(\sqrt{\frac{4+4-2}{4\times4}}\bigg)+(8n-4)\bigg(\sqrt{\frac{4+5-2}{4\times5}}\bigg)+(8n-4)\bigg(\sqrt{\frac{4+6-2}{4\times6}}\bigg) \\ +(4n-2)\bigg(\sqrt{\frac{5+6-2}{5\times6}}\bigg)+4\bigg(\sqrt{\frac{5+7-2}{5\times7}}\bigg)+(8n-8)\bigg(\sqrt{\frac{5+8-2}{5\times8}}\bigg) \\ +2\bigg(\sqrt{\frac{7+8-2}{7\times8}}\bigg)+(2n-3)\bigg(\sqrt{\frac{8+8-2}{8\times8}}\bigg)\\ = 2n\sqrt{6}+(n+1)\frac{4\sqrt{15}}{3}+(14n+11)\frac{\sqrt14}{56}+(n-1)\frac{2\sqrt110}{5} \\ +(2n-1)\bigg(2\sqrt{\frac{7}{5}}+\frac{4}{\sqrt3}+\sqrt{\frac{6}{5}}\bigg)+\frac{16\sqrt{42}}{21}+\frac{\sqrt182}{14}.\\$

Table 3. Types and count of edges for

$T_1$ .

$Types$ $of$ $edges$	$Count$ $of$ $edges$
$(3, 4)$	$8n+8$
$(3, 7)$	$8$
$(3, 8)$	$4n-4$
$(4, 4)$	$4n+4$
$(4, 5)$	$8n-4$
$(4, 6)$	$8n-4$
$(5, 6)$	$4n-2$
$(5, 7)$	$4$
$(5, 8)$	$8n-8$
$(7, 8)$	$2$
$(8, 8)$	$2n-3$

| Show Table

DownLoad: CSV

2). According to Eq (1.8)

$GA(T_1) = \sum\limits_{\gamma\beta\in E(K)}\frac{2\sqrt{d_{\gamma}d_{\beta}}}{d_{\gamma}+d_{\beta}}.$

By using the information given in Table 3.

$= (8n+8)\bigg(\frac{2\sqrt{3\times4}}{3+4}\bigg)+8\bigg(\frac{2\sqrt{3\times7}}{3+7}\bigg)+(4n-4)\bigg(\frac{2\sqrt{3\times8}}{3+8}\bigg) +(4n+4)\bigg(\frac{2\sqrt{4\times4}}{4+4}\bigg)\\ +(8n-4)\bigg(\frac{2\sqrt{4\times5}}{4+5}\bigg)+(8n-4)\bigg(\frac{2\sqrt{4\times6}}{4+6}\bigg) +(4n-2)\bigg(\frac{2\sqrt{5\times6}}{5+6}\bigg)+4\bigg(\frac{2\sqrt{5\times7}}{5+7}\bigg)\\ +(8n-8)\bigg(\frac{2\sqrt{5\times8}}{5+8}\bigg) +2\bigg(\frac{2\sqrt{7\times8}}{7+8}\bigg)+(2n-3)\bigg(\frac{2\sqrt{8\times8}}{8+8}\bigg)\\ = (n+1)\bigg(\frac{32\sqrt3}{7}+4\bigg)+(n-1)\frac{32\sqrt10}{13}+(32n-21)\frac{8\sqrt6}{55}+(2n-1)\bigg(\frac{16\sqrt5}{9}+\frac{4\sqrt30}{11}\bigg) \\ +(2n-3)+\frac{8\sqrt21}{5}+\frac{2\sqrt35}{3}+\frac{8\sqrt14}{15}.\\$

3). According to Eq (1.9)

$H_k(T_1) = \sum\limits_{\gamma\beta \in E(K)}\bigg(\frac 2{d_{\gamma}+d_{\beta}}\bigg)^k.$

By using the information given in Table 3.

$= (8n+8)\bigg(\frac{2}{3+4}\bigg)^{k}+8\bigg(\frac{2}{3+7}\bigg)^{k}+(4n-4)\bigg(\frac{2}{3+8}\bigg)^{k} +(4n+4)\bigg(\frac{2}{4+4}\bigg)^{k}+(8n-4)\bigg(\frac{2}{4+5}\bigg)^{k} \\ +(8n-4)\bigg(\frac{2}{4+6}\bigg)^{k}+(4n-2)\bigg(\frac{2}{5+6}\bigg)^{k}+4\bigg(\frac{2}{5+7}\bigg)^{k}+(8n-8)\bigg(\frac{2}{5+8}\bigg)^{k} +2\bigg(\frac{2}{7+8}\bigg)^{k} +(2n-3)\bigg(\frac{2}{8+8}\bigg)^{k}\\ = (8n+8)\big(\frac2{7}\big)^k+(8n+4)\big(\frac{1}{5}\big)^k+(4n-4)\big(\frac2{11}\big)^k +(4n+4)\big(\frac1{4}\big)^k+(8n-4)\big(\frac2{9}\big)^k \\ +(4n-2)(\frac2{11})^k+4(\frac1{6})^k+(8n-8)(\frac2{13})^k+2(\frac2{15})^k+(2n-3)(\frac1{8})^k.$

3.1.4. Theorem

For $T_1$ , the First, Second Gourava Indices and the First, Second Hyper Gourava Indices are as follows, respectively.

$1) \ \ GO_1(T_1) = 1640n-312, \\ 2) \ \ GO_2(T_1) = 13128n-4404, \\ 3) \ \ HGO_1(T_1) = 68064n-26124, \\ 4) \ \ HGO_2(T_1) = 5816720n-3573928.$

Proof:

1). According to Eq (1.10)

$\ \ \ GO_1(T_1) = \sum\limits_{\gamma\beta \in E(K)}[(d_{\gamma}+d_{\beta})+(d_\gamma d_\beta)].$

By using the information given in Table 3.

$= (8n+8)\big[(3+4)+(3\times4)\big]+8\big[(3+7)+(3\times7)\big]+(4n-4)\big[(3+8)+(3\times8)\big] +(4n+4)\big[(4+4)\\ +(4\times4)\big]+(8n-4)\big[(4+5)+(4\times5)\big]+(8n-4)\big[(4+6)+(4\times6)\big] +(4n-2)\big[(5+6)+(5\times6)\big]\\ +4\big[(5+7)+(5\times7)\big]+(8n-8)\big[(5+8)+(5\times8)\big] +2\big[(7+8)+(7\times8)\big]+(2n-3)\big[(8+8)+(8\times8)\big]\\ = 1640n-312.$

2). According to Eq (1.11)

$\ \ \ GO_2(T_1) = \sum\limits_{\gamma\beta \in E(K)}[(d_{\gamma}+d_{\beta})(d_\gamma d_\beta)].$

By using the information given in Table 3.

$= (8n+8)\big[(3+4)(3\times4)\big]+8\big[(3+7)(3\times7)\big]+(4n-4)\big[(3+8)(3\times8)\big] +(4n+4)\big[(4+4)(4\times4)\big]\\ +(8n-4)\big[(4+5)(4\times5)\big]+(8n-4)\big[(4+6)(4\times6)\big] +(4n-2)\big[(5+6)(5\times6)\big]+4\big[(5+7)(5\times7)\big]\\ +(8n-8)\big[(5+8)(5\times8)\big] +2\big[(7+8)(7\times8)\big]+(2n-3)\big[(8+8)(8\times8)\big]\\ = 13128n-4404.$

3). According to Eq (1.12)

$\ \ \ HGO_1(T_1) = \sum\limits_{\gamma\beta\in E(K)}[(d_{\gamma}+d_{\beta})+(d_\gamma d_\beta)]^2.$

By using the information given in Table 3.

$= (8n+8)[(3+4)+(3\times4)]^{2}+8[(3+7)+(3\times7)]^{2}+(4n-4)[(3+8)+(3\times8)]^{2} \\ +(4n+4)[(4+4)+(4\times4)]^{2}+(8n-4)[(4+5)+(4\times5)]^{2}+(8n-4)[(4+6)+(4\times6)]^{2} \\ +(4n-2)[(5+6)+(5\times6)]^{2}+4[(5+7)+(5\times7)]^{2}+(8n-8)[(5+8)+(5\times8)]^{2} \\ +2[(7+8)+(7\times8)]^{2}+(2n-3)[(8+8)+(8\times8)]^{2}\\ = 68064n-26124.$

4). According to Eq (1.13)

$\ \ \ HGO_2(T_1) = \sum\limits_{\gamma\beta\in E(K)}[(d_{\gamma}+d_{\beta})(d_\gamma d_\beta)]^2.$

By using the information given in Table 3.

$= (8n+8)[(3+4)(3\times4)]^{2}+8[(3+7)(3\times7)]^{2}+(4n-4)[(3+8)(3\times8)]^{2} +(4n+4)[(4+4)(4\times4)]^{2} \\ +(8n-4)[(4+5)(4\times5)]^{2}+(8n-4)[(4+6)(4\times6)]^{2}+(4n-2)[(5+6)(5\times6)]^{2} \\ +4[(5+7)(5\times7)]^{2}+(8n-8)[(5+8)(5\times8)]^{2}+2[(7+8)(7\times8)]^{2}+(2n-3)[(8+8)(8\times8)]^{2}\\ = 5816720n-3573928.$

3.2. M-polynomial and degree based topological indices of $T_2$ structure

Now we will construct the stellation, medial and bounded dual operations on simple and undirected triangular benzenoid structure. We get a new transformed network (say) $T_2$ , shown in for n = 5. After this we will compute M-polynomial and degree based topological indices of our newly obtained network. Where, blue is stellation, red is medial, green is bounded dual operations applied on $T_2$ .

Figure 3. Transformed structure

$T_2$ .

DownLoad: Full-Size Img PowerPoint

Following shows the types of edges and their count for network $T_2$ ; $n\geq5$ . Now, we will calculate the different M-polynomial and vertex degree based topological indices namely first Zagreb index, second Zagreb index, second modified index, symmetric division index, general Randic index, reciprocal general Randic index, atomic bond connectivity index, geometric arithmetic index, general version of harmonic index, first and second gourava indices, first and second hyper gourava indices.

Table 4. Types and count of edges for

$T_2$ .

$Types$ $of$ $edges$	$Count$ $of$ $edges$
$(3, 4)$	$6n+6$
$(3, 8)$	$9$
$(3, 10)$	$3n-6$
$(4, 4)$	$3n+3$
$(4, 5)$	$6n-6$
$(4, 6)$	$6n-6$
$(5, 6)$	$3n-3$
$(5, 8)$	$6$
$(5, 10)$	$6n-12$
$(6, 6)$	$6(n-1)^2$
$(6, 8)$	$3$
$(6, 10)$	$9n-18$
$(6, 12)$	$6[(n-(n-1))+(n-(n-2))+...$
	$+(n-4)+(n-3)]$
$(8, 10)$	$6$
$(10, 10)$	$3n-6$
$(10, 12)$	$6n-18$
$(12, 12)$	$3[(n-4)+(n-5)+...$
	$+(n-(n-1))]$

| Show Table

DownLoad: CSV

3.2.1. Theorem

Let $T_2$ , be the transformed network then its M-polynomial is

$M(T_2;x, y) = (6n+6)x^3y^4+9x^3y^8+(3n-6)x^3y^{10}+(3n+3)x^4y^4+(6n-6)x^4y^5+(6n-6)x^4y^6 \\ +(3n-3)x^5y^6+6x^5y^8+(6n-12)x^5y^{10}+6(n-1)^2x^6y^6+3x^6y^8+(9n-18)x^6y^{10} \\ +6[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)]x^6y^{12}+6x^8y^{10}+(3n-6)x^{10}y^{10} \\ +(6n-18)x^{10}y^{12}+3[(n-4)+(n-5)+...+(n-(n-1))]x^{12}y^{12}.$

Proof: Using definition of M-polynomial and information from Table 4, we have

$M(T_2;x, y) = \sum\limits_{a \leq b}m_{ab}x^{a}y^{b} = \sum\limits_{3\leq 4}m_{34}x^3y^4+\sum\limits_{3\leq 8}m_{38}x^3y^8+\sum\limits_{3\leq 10}m_{3 \ 10}x^3y^{10}+\sum\limits_{4\leq4}m_{44}x^4y^4 \\ +\sum\limits_{4\leq5}m_{45}x^4y^5+\sum\limits_{4\leq6}m_{46}x^4y^6+\sum\limits_{5\leq6}m_{56}x^5y^6+\sum\limits_{5\leq8}m_{58}x^5y^8+\sum\limits_{5\leq10}m_{5 \ 10}x^5y^{10} \\ +\sum\limits_{6\leq6}m_{66}x^6y^6+\sum\limits_{6\leq8}m_{68}x^6y^8+\sum\limits_{6\leq10}m_{6 \ 10}x^6y^{10} +\sum\limits_{6\leq12}m_{6 \ 12}x^6y^{12}+\sum\limits_{8\leq10}m_{8 \ 10}x^8y^{10} \\ +\sum\limits_{10\leq10}m_{10 \ 10}x^{10}y^{10}+\sum\limits_{10\leq12}m_{10 \ 12}x^{10}y^{12}+\sum\limits_{12\leq12}m_{12 \ 12}x^{12}y^{12}\\ = |E_{3, 4}|x^3y^4+|E_{3, 8}|x^3y^8+|E_{3, 10}|x^3y^{10}+|E_{4, 4}|x^4y^4+|E_{4, 5}|x^4y^5+|E_{4, 6}|x^4y^6+|E_{5, 6}|x^5y^6 \\ +|E_{5, 8}|x^5y^{8}+|E_{5, 10}|x^5y^{10}+|E_{6, 6}|x^6y^6+|E_{6, 8}|x^6y^8+|E_{6, 10}|x^6y^{10}+|E_{6, 12}|x^6y^{12} \\ +|E_{8, 10}|x^8y^{10}+|E_{10, 10}|x^{10}y^{10}+|E_{10, 12}|x^{10}y^{12}+|E_{12, 12}|x^{12}y^{12}\\ = (6n+6)x^3y^4+9x^3y^8+(3n-6)x^3y^{10}+(3n+3)x^4y^4+(6n-6)x^4y^5+(6n-6)x^4y^6 \\ +(3n-3)x^5y^6+6x^5y^8+(6n-12)x^5y^{10}+6(n-1)^2x^6y^6+3x^6y^8+(9n-18)x^6y^{10} \\ +6\big[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)\big]x^6y^{12}+6x^8y^{10}+(3n-6)x^{10}y^{10} \\ +(6n-18)x^{10}y^{12}+3\big[(n-4)+(n-5)+...+(n-(n-1))\big]x^{12}y^{12}.$

Figure 4. M-polynomial of

$T_2$ for n = 6.

DownLoad: Full-Size Img PowerPoint

Figure 5. M-polynomial of

$T_2$ .

DownLoad: Full-Size Img PowerPoint

3.2.2. Theorem

Let $T_2$ , be the transformed network and

$M(T_2;x, y) = (6n+6)x^3y^4+9x^3y^8+(3n-6)x^3y^{10}+(3n+3)x^4y^4+(6n-6)x^4y^5+(6n-6)x^4y^6 \\ +(3n-3)x^5y^6+6x^5y^8+(6n-12)x^5y^{10}+6(n-1)^2x^6y^6+3x^6y^8+(9n-18)x^6y^{10} \\ +6\big[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)\big]x^6y^{12}+6x^8y^{10}+(3n-6)x^{10}y^{10} \\ +(6n-18)x^{10}y^{12}+3\big[(n-4)+(n-5)+...+(n-(n-1))\big]x^{12}y^{12},$

be its M-polynomial. Then, the first Zagreb index $M_1\big(T_2\big)$ , the second Zagreb index $M_2\big(T_2\big)$ , the second modified Zagreb $^mM_2(T_2\big)$ , the general Randic index $R_\alpha(T_2)$ , where $\alpha \ \epsilon \ N$ , reciprocal general Randic index $RR_\alpha(T_2)$ , where $\alpha \ \epsilon \ N$ , and the symmetric division degree index $SDD(T_2)$ obtained from M-polynomial are as follows:

$M_1(T_2) = 678n-816+72(n-1)^2+108\big[(n-(n-1))+(n-(n-2)) \\ +...+(n-4)+(n-3)\big]+72\big[(n-4)+(n-5)+...+(n-(n-1))\big], \\ M_2(T_2) = 2424n-3774+216(n-1)^2+432\big[(n-(n-1))+(n-(n-2)) \\ +...+(n-4)+(n-3)\big]+432\big[(n-4)+(n-5)+...+(n-(n-1))\big], \\ ^mM_2(T_2) = \frac{11}{16}\big(n+1\big)+\frac{2}{5}\big(n-2\big)+\frac{13}{20}\big(n-1\big)+\frac{1}{20}\big(n-3\big)+\frac{53}{80} +\frac{1}{6}\big(n-1\big)^2\\ +\frac{1}{12}\big[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)\big] \\ +\frac{1}{48}\big[(n-4)+(n-5)+...+(n-(n-1))\big], \\ R_\alpha(T_2) = 12^\alpha(6n+6)+24^\alpha(9)+30^\alpha(3n-6)+4^{2\alpha}(3n+3)+20^\alpha(6n-6) +24^\alpha(6n-6) \\ +30^\alpha(3n-3)+40^\alpha(6)+50^\alpha(6n-12)+6(n-1)^2(36)^\alpha+48^\alpha(3)+60^\alpha(9n-18) \\ +72^\alpha[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)]6+80^\alpha(6)+100^\alpha(3n-6) \\ +120^\alpha(6n-18)+144^\alpha[(n-4)+(n-5)+...+(n-(n-1))]3, \\ RR_\alpha(T_2) = \frac{6}{12^\alpha}\big(n+1\big)+\frac{9}{24^\alpha}+\frac{3}{30^\alpha}\big(n-2\big)+\frac{3}{4^{2\alpha}}\big(n+1\big) +\frac{6}{20^\alpha}\big(n-1\big)+\frac{6}{24^\alpha}\big(n-1\big) \\ +\frac{3}{30^\alpha}\big(n-1\big)+\frac{6}{40^\alpha}+\frac{6}{50^\alpha}\big(n-2\big)+\frac{6}{36^\alpha}\big(n-1\big)^2 +\frac{3}{48^\alpha}+\frac{9}{60^\alpha}\big(n-2\big)+\frac{6}{80^\alpha} \\ +\frac{3}{100^\alpha}\big(n-2\big)+\frac1{72^\alpha}\big[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)\big]6 \\ +\frac{6}{120^\alpha}\big(n-3\big)+\frac{1}{144^\alpha}\big[(n-4)+(n-5)+...+(n-(n-1))\big]3, \\ SDD(T_2) = \frac{37}{2}\big(n+1\big)+\frac{157}{5}\big(n-1\big)+\frac{523}{10}\big(n-2\big)+\frac{61}{5}\big(n-3\big)+\frac{2371}{40}+12(n-1)^2 \\ +15[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)] \\ +6[(n-4)+(n-5)+...+(n-(n-1))].$

Proof: Let $f(x, y)$ = $M(T_2;x, y)$ be the M-polynomial of the transformed network $T_2$ . Then

Now, the required partial derivatives and integrals are obtained.

By using the information given in Table 4 and formulas for Table 1:

$D_xf(x, y) = 3(6n+6)x^3y^4+27x^3y^8+3(3n-6)x^3y^{10}+4(3n+3)x^4y^4+4(6n-6)x^4y^5 \\ +4(6n-6)x^4y^6+5(3n-3)x^5y^6+30x^5y^8+5(6n-12)x^5y^{10}+36(n-1)^2x^6y^6+18x^6y^8 \\ +6(9n-18)x^6y^{10}+36[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)]x^6y^{12} \\ +48x^8y^{10}+10(3n-6)x^{10}y^{10}+10(6n-18)x^{10}y^{12} +36[(n-4)+(n-5)+...\\ +(n-(n-1))]x^{12}y^{12}, \\ D_yf(x, y) = 4(6n+6)x^3y^4+72x^3y^8+10(3n-6)x^3y^{10}+4(3n+3)x^4y^4+5(6n-6)x^4y^5 \\ +6(6n-6)x^4y^6+6(3n-3)x^5y^6+48x^5y^8+10(6n-12)x^5y^{10}+36(n-1)^2x^6y^6+24x^6y^8 \\ +10(9n-18)x^6y^{10}+72[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)]x^6y^{12} \\ +60x^8y^{10}+10(3n-6)x^{10}y^{10}+12(6n-18)x^{10}y^{12} +36[(n-4)+(n-5)+...\\ +(n-(n-1))]x^{12}y^{12}, \\ D_xD_yf(x, y) = 12(6n+6)x^3y^4+216x^3y^8+30(3n-6)x^3y^{10}+16(3n+3)x^4y^4+20(6n-6)x^4y^5 \\ +24(6n-6)x^4y^6+30(3n-3)x^5y^6+240x^5y^8+50(6n-12)x^5y^{10}+216(n-1)^2x^6y^6 \\ +144x^6y^8+60(9n-18)x^6y^{10}+432[(n-(n-1))+(n-(n-2))+... \\ +(n-4)+(n-3)]x^6y^{12}+480x^8y^{10}+100(3n-6)x^{10}y^{10}+120(6n-18)x^{10}y^{12} \\ +432[(n-4)+(n-5)+...+(n-(n-1))]x^{12}y^{12}, \\ S_xS_yf(x, y) = \frac{1}{2}\big(n+1\big)x^3y^4+\frac{3}{8}x^3y^8+\frac{1}{10}\big(n-2\big)x^3y^{10} +\frac{3}{16}\big(n+1\big)x^4y^4+\frac{3}{10}\big(n-1\big)x^4y^5 \\ +\frac{1}{4}\big(n-1\big)x^4y^6+\frac{1}{10}\big(n-1\big)x^5y^6+\frac{3}{20}x^5y^8 +\frac{3}{25}\big(n-2\big)x^5y^{10}+\frac{1}{6}\big(n-1\big)^2x^6y^6+\frac{1}{16}x^6y^8 \\ +\frac{3}{20}\big(n-2\big)x^6y^{10} +\frac{1}{12}\big[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)\big]x^6y^{12} \\ +\frac{3}{40}x^8y^{10}+\frac{3}{100}\big(n-2\big)x^{10}y^{10}+\frac{1}{20}\big(n-3\big)x^{10}y^{12} \\ +\frac{1}{48}\big[(n-4)+(n-5)+...+(n-(n-1))\big]x^{12}y^{12}, \\ D_x^{\alpha}D_y^{\alpha}f(x, y) = 12^\alpha(6n+6)x^3y^4+24^\alpha(9)x^3y^8+30^\alpha(3n-6)x^3y^{10}+4^{2\alpha}(3n+3)x^4y^4+20^\alpha(6n-6)x^4y^5 \\ +24^\alpha(6n-6)x^4y^6+30^\alpha(3n-3)x^5y^6+40^\alpha(6)x^5y^8+50^\alpha(6n-12)x^5y^{10} \\ +(36)^{\alpha}(n-1)^26x^6y^6+48^\alpha(3)x^6y^8+60^\alpha(9n-18)x^6y^{10}+72^\alpha[(n-(n-1))+(n-(n-2)) \\ +...+(n-4)+(n-3)]6x^6y^{12}+80^\alpha(6)x^8y^{10}+100^\alpha(3n-6)x^{10}y^{10}+120^\alpha(6n-18)x^{10}y^{12} \\ +144^\alpha[(n-4)+(n-5)+...+(n-(n-1))]3x^{12}y^{12}, \\ S_x^{\alpha}S_y^{\alpha}f(x, y) = \frac{6}{12^\alpha}\big(n+1\big)x^3y^4+\frac{9}{24^\alpha}x^3y^8 +\frac{3}{30^\alpha}\big(n-2\big)x^3y^{10} +\frac{3}{4^{2\alpha}}\big(n+1\big)x^4y^4\\ +\frac{6}{20^\alpha}\big(n-1\big)x^4y^5 +\frac{6}{24^\alpha}\big(n-1\big)x^4y^6 +\frac{3}{30^\alpha}\big(n-1\big(n-1\big)x^5y^6 +\frac{6}{40^\alpha}x^5y^8\\ +\frac{6}{50^\alpha}\big(n-2\big)x^5y^{10} +\frac{6}{36^\alpha}\big(n-1\big)^2x^6y^6 +\frac{3}{48^\alpha}x^6y^8+\frac{9}{60^\alpha}\big(n-2\big)x^6y^{10} \\ +\frac1{72^\alpha}\bigg[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)\bigg]6x^6y^{12} \\ +\frac{6}{80^\alpha}x^8y^{10}+\frac{3}{100^\alpha}\big(n-2\big)x^{10}y^{10} +\frac{6}{120^\alpha}\big(n-3\big)x^{10}y^{12} \\ +\frac1{144^\alpha}\bigg[(n-4)+(n-5)+...+(n-(n-1))\bigg]3x^{12}y^{12}, \\ S_yD_xf(x, y) = \frac{9}{2}(n+1)x^3y^4+\frac{27}{8}x^3y^8+\frac{9}{10}(n-2)x^3y^{10}+3(n+1)x^4y^4+\frac{24}{5}(n-1)x^4y^5 \\ +4(n-1)x^4y^6+\frac{5}{2}(n-1)x^5y^6+\frac{15}{4}x^5y^8+3(n-2)x^5y^{10}+6(n-1)^2x^6y^6 +\frac{9}{4}x^6y^8\\ +\frac{27}{5}(n-2)x^6y^{10} +3[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)]x^6y^{12} \\ +\frac{24}{5}x^8y^{10}+3(n-2)x^{10}y^{10}+5(n-3)x^{10}y^{12} +3[(n-4)+(n-5)+...+(n-(n-1))]x^{12}y^{12}, \\ S_xD_yf(x, y) = 8(n+1)x^3y^4+24x^3y^8+10(n-2)x^3y^{10}+3(n+1)x^4y^4+\frac{15}{2}(n-1)x^4y^5 \\ +9(n-1)x^4y^6+\frac{18}{5}(n-1)x^5y^6+\frac{48}{5}x^5y^8+12(n-2)x^5y^{10}+6(n-1)^2x^6y^6 +4x^6y^8\\ +15(n-2)x^6y^{10}+12[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)]x^6y^{12} \\ +\frac{15}{2}x^8y^{10}+3(n-2)x^{10}y^{10}+\frac{36}{5}(n-3)x^{10}y^{12} \\ +3[(n-4)+(n-5)+...\\ +(n-(n-1))]x^{12}y^{12}.$

Consequently,

$M_1(T_2) = (D_x+D_y)f(x, y)|_{x = 1 = y} = 678n-816+72(n-1)^2+108\big[(n-(n-1))+(n-(n-2)) \\ +...+(n-4)+(n-3)\big]+72\big[(n-4)+(n-5)+...+(n-(n-1))\big], \\ M_2(T_2) = D_xD_yf(x, y)|_{x = 1 = y} = 2424n-3774+216(n-1)^2+432\big[(n-(n-1))+(n-(n-2)) \\ +...+(n-4)+(n-3)\big]+432\big[(n-4)+(n-5)+...+(n-(n-1))\big], \\ ^mM_2(T_2) = S_xS_yf(x, y)|_{x = 1 = y} = \frac{11}{16}\big(n+1\big)+\frac{2}{5}\big(n-2\big)+\frac{13}{20}\big(n-1\big)+\frac{1}{20}\big(n-3\big)+\frac{7}{10} +\frac{1}{6}\big(n-1\big)^2\\ +\frac{1}{12}\big[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)\big] \\ +\frac{1}{48}\big[(n-4)+(n-5)+...+(n-(n-1))\big], \\ R_\alpha(T_2) = D_x^{\alpha} D_y^{\alpha}f(x, y)|_{x = 1 = y} = 12^\alpha(6n+6)+24^\alpha(9)+30^\alpha(3n-6)+4^{2\alpha}(3n+3)+20^\alpha(6n-6) \\ +24^\alpha(6n-6)+30^\alpha(3n-3)+40^\alpha(6)+50^\alpha(6n-12)+6(n-1)^2(36)^\alpha+48^\alpha(3) \\ +60^\alpha(9n-18)+72^\alpha[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)]6 \\ +80^\alpha(6)+100^\alpha(3n-6)+120^\alpha(6n-18)+144^\alpha[(n-4)+(n-5)+...+(n-(n-1))]3, \\ RR_\alpha(T_2) = S_x^{\alpha}S_y^{\alpha}f(x, y)|_{x = 1 = y} = \frac{6}{12^\alpha}\big(n+1\big)+\frac{9}{24^\alpha}+\frac{3}{30^\alpha}\big(n-2\big)+\frac{3}{4^{2\alpha}}\big(n+1\big) +\frac{6}{20^\alpha}\big(n-1\big)+\frac{6}{24^\alpha}\big(n-1\big) \\ +\frac{3}{30^\alpha}\big(n-1\big)+\frac{6}{40^\alpha}+\frac{6}{50^\alpha}\big(n-2\big)+\frac{6}{36^\alpha}\big(n-1\big)^2 +\frac{3}{48^\alpha}+\frac{9}{60^\alpha}\big(n-2\big)+\frac{6}{80^\alpha} \\ +\frac{3}{100^\alpha}\big(n-2\big)+\frac1{72^\alpha}\big[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)\big]6 \\ +\frac{6}{120^\alpha}\big(n-3\big)+\frac{1}{144^\alpha}\big[(n-4)+(n-5)+...+(n-(n-1))\big]3, \\ SDD(T_2) = (S_yD_x+S_xD_y)(x, y)|_{x = 1 = y} = \frac{37}{2}\big(n+1\big)+\frac{157}{5}\big(n-1\big)+\frac{523}{10}\big(n-2\big)+\frac{61}{5}\big(n-3\big) +\frac{2371}{40} \\ +12(n-1)^2+15[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)] \\ +6[(n-4)+(n-5)+...+(n-(n-1))].$

3.2.3. Theorem

For $T_2$ , the Atomic Bond Connectivity, Geometric Arithmetic Index and General Harmonic Index are as follows, respectively.

$1) \ \ \ \ ABC(T_2) = (7n)\frac{\sqrt6}{4}+(n+1){\sqrt15}+(n-1)\bigg(3\sqrt{\frac{7}{5}}+{2\sqrt3}+3\sqrt{\frac{3}{10}}\bigg) \\ (n-2)\bigg(\frac{\sqrt330}{10}+\frac{3\sqrt26}{5}+\frac{3\sqrt210}{10}+\frac{9\sqrt2}{10}\bigg)+\frac{3\sqrt110}{10}+\frac3{2}+\frac{6}{\sqrt5} \\ +(n-1)^2{\sqrt10}+[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)]{2\sqrt2} \\ +[(n-4)+(n-5)+...+(n-(n-1))]\frac{\sqrt22}{4}, \\ 2) \ \ \ \ GA(T_2) = (24n+36)\frac{\sqrt3}{7}+(132n+48)\frac{\sqrt6}{55}+(50n-113)\frac{6\sqrt30}{143}+3(n+1) \\ +(8n)\frac{\sqrt5}{3}+(n-2)\bigg({4\sqrt2}+\frac{9\sqrt15}{4}+3\bigg)+\frac{24\sqrt10}{13}+6(n-1)^2 \\ +[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)]{4\sqrt2} \\ +3[(n-4)+(n-5)+...+(n-(n-1))], \\ 3) \ \ \ H_k(T_2) = (6n+6)(\frac2{7})^k+9(\frac2{11})^k+(3n-6)(\frac2{13})^k+(3n+3)(\frac1{4})^k+(6n-6) \\ (\frac2{9})^k+(6n-6)(\frac1{5})^k+(3n-3)(\frac2{11})^k+6(\frac2{13})^k+(6n-12)(\frac2{15})^k \\ +6(n-1)^2)(\frac1{6})^k+3(\frac1{7})^k+(9n-18)(\frac1{8})^k+6[(n-(n-1)) \\ +(n-(n-2))+...+(n-4)+(n-3)](\frac1{9})^k+6(\frac1{9})^k+(3n-6)(\frac1{10})^k \\ +(6n-18)(\frac1{11})^k+3[(n-4)+(n-5)+...+(n-(n-1))](\frac1{12})^k.$

Proof: Using Eqs 1.7–1.9 and Table 4, we get the results 1–3.

3.2.4. Theorem

For $T_2$ , the First, Second Gourava Indices and the First, Second Hyper Gourava Indices are as follows, respectively.

$1) \ \ \ GO_1(T_2) = 3102n-4590+288(n-1)^2+540[(n-(n-1))+(n-(n-2)) \\ +...+(n-4)+(n-3)]+504[(n-4)+(n-5)+...+(n-(n-1))], \\ 2) \ \ \ GO_2(T_2) = 40548n-74610+2592(n-1)^2+7776[(n-(n-1))+(n-(n-2)) \\ +...+(n-4)+(n-3)]+10368[(n-4)+(n-5)+...+(n-(n-1))], \\ 3) \ \ \ HGO_1(T_2) = 267984n-531210+13824(n-1)^2 \\ +48600[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)] \\ +84672[(n-4)+(n-5)+...+(n-(n-1))], \\ 4) \ \ \ HGO_2(T_2) = 66901488n-158433396+1119744(n-1)^2 \\ +10077696[(n-(n-1))+(n-(n-2))+...+(n-4)+(n-3)] \\ +35831808[(n-4)+(n-5)+...+(n-(n-1))].$

Proof: Using Eqs 1.10–1.13 and Table 4 we get the above results 1–4.

4. Conclusions

In this paper, we defined M-polynomial of the transformed zigzag benzenoid and transformed triangular benzenoid structures by applying stellation, medial and bounded dual operations to get networks named as $T_1$ and $T_2$ . With the help of M-polynomial, we computed certain degree-based topological indices such as first Zagreb index, second Zagreb index, second modified Zagreb index, general Randic index, reciprocal general Randic index, symmetric division degree index. We also computed atomic bound connectivity index, geometric arithmetic index, general harmonic index, first and second gourava indices, first and second hyper gourava indices. M-polynomial is used to calculate the certain degree based topological indices as a latest developed instrument in the chemical graph theory. In future, we can compute other indices on these structures and some additional transformed structures can be studied for a variety of topological indices to have an insight about their properties.

Acknowledgments

This work was supported by the Key teaching research project of quality engineering in Colleges and universities in Anhui Province. Anhui Vocational college of Electronics and Information Technology Guangzhou Zhuoya Education Investment Co., Ltd. Practical Education Base (subject No: 2020sjjd093). The authors are very thankful for this research funding. We are also very grateful to the reviewers for their valuable suggestions.

Conflict of interest

The authors declare no conflict of interest.

References

[1]	G. Pólya, G. Szegö, Problems and theorems in analysis II, Berlin: Springer, 1998. http://dx.doi.org/10.1007/978-3-642-61905-2
[2]	M. Catalani, A particular matrix and its relationships with Fibonacci numbers, arXiv: math/0209249.
[3]	R. Bhatia, Infinitely divisible matrices, Am. Math. Mon., 113 (2006), 221–235. http://dx.doi.org/10.2307/27641890 doi: 10.2307/27641890
[4]	R. Bhatia, Min matrices and mean matrices, Math. Intelligencer, 33 (2011), 22–28. http://dx.doi.org/10.1007/s00283-010-9194-z doi: 10.1007/s00283-010-9194-z
[5]	C. Da Fonseca, On the eigenvalues of some tridiagonal matrices, J. Comput. Appl. Math., 200 (2007), 283–286. http://dx.doi.org/10.1016/j.cam.2005.08.047 doi: 10.1016/j.cam.2005.08.047
[6]	L. Moyé, Statistical monitoring of clinical trials: fundamentals for investigators, New York: Springer, 2006. http://dx.doi.org/10.1007/0-387-27782-X
[7]	H. Neudecker, G. Trenkler, S. Liu, Problem section, Stat. Papers, 50 (2009), 221–223. http://dx.doi.org/10.1007/s00362-008-0174-8
[8]	K. Chu, S. Puntanen, G. Styan, Problem section, Stat. Papers, 52 (2011), 257–262. http://dx.doi.org/10.1007/s00362-010-0363-0
[9]	M. Mattila, P. Haukkanen, Studying the various properties of Min and Max matrices-elemantary vs. more advanced methods, Spec. Matrices, 4 (2016), 101–109. http://dx.doi.org/10.1515/spma-2016-0010 doi: 10.1515/spma-2016-0010
[10]	M. Bahşi, S. Solak, A particular matrix and its properties, Int. J. Math. Sci. Appl., 1 (2011), 971–974.
[11]	S. Solak, M. Bahşi, A particular matrix and its some properties, Sci. Res. Essays, 8 (2013), 1–5. http://dx.doi.org/10.5897/SRE11.410 doi: 10.5897/SRE11.410
[12]	M. Bahşi, S. Solak, Some particular matrices and their characteristic polynomials, Linear Multilinear A., 63 (2015), 2071–2078. http://dx.doi.org/10.1080/03081087.2014.940940 doi: 10.1080/03081087.2014.940940
[13]	J. Stuart, Nested matrices and inverse $M$ -matrices, Czech. Math. J., 65 (2015), 537–544. http://dx.doi.org/10.1007/s10587-015-0192-3 doi: 10.1007/s10587-015-0192-3
[14]	S. Jafari-Petroudi, B. Pirouz, A particular matrix, its inversion and some norms, Appl. Comput. Math., 4 (2015), 47–52. http://dx.doi.org/10.11648/j.acm.20150402.13
[15]	S. Jafari-Petroudi, B. Pirouz, A note on Hadamard inverse and Hadamard exponential of a matrix with Fibonacci numbers, Proceedings of The $7$ th National Conference on Mathematics, 2015, 28–29.
[16]	S. Jafari-Petroudi, M. Pirouz, A note on tribonacci numbers with particular matrices, Proceedings of The 28th International Conference of The Jangjeon Mathematical Society, 2015, 71.
[17]	S. Jafari-Petroudi, M. Pirouz, On the bounds for the spectral norm of particular matrices with Fibonacci and Lucas numbers, Int. J. Adv. Appl. Math. Mech., 3 (2016), 82–90.
[18]	S. Jafari-Petroudi, M. Pirouz, Toward special symmetric matrices with harmonic numbers, Proceedings of The 8th National Conference on Mathematics, 2016, 11–12.
[19]	E. Kılıç, T. Arıkan, Studying new generalizations of Max-Min matrices with a novel approach, Turk. J. Math., 43 (2019), 2010–2024.
[20]	T. Solmaz, M. Bahşi, Max and Min matrices with hyper-Fibonacci numbers, Asian-Eur. J. Math., 15 (2022), 2250084. http://dx.doi.org/10.1142/S179355712250084X doi: 10.1142/S179355712250084X
[21]	D. Özgul, M. Bahşi, Min matrices with hyper-Lucas numbers, J. Sci. Arts, 4 (2020), 855–864. http://dx.doi.org/10.46939/J.Sci.Arts-20.4-a07 doi: 10.46939/J.Sci.Arts-20.4-a07
[22]	C. Kızılateş, N. Terzioğlu, On $r$ -min and $r$ -max matrices, J. Appl. Math. Comput., 68 (2022), 4559–4588. http://dx.doi.org/10.1007/s12190-022-01717-y doi: 10.1007/s12190-022-01717-y
[23]	M. Jain, S. Iyengar, R. Jain, Numerical methods: problems and solutionsz, Bangalore: New Age International, 2007.
[24]	P. Ciarlet, J. Lions, Solution of equations in $\mathbb{R}^{n}$ , In: Handbook of numerical analysis, Amsterdam: Elsevier, (1994), 625–778.
[25]	M. Sturm, Analyse d' un Mémoire sur la résolution des équations numériques, In: Collected works of Charles François Sturm, Basel: Birkhäuser, 2009,323–326. http://dx.doi.org/10.1007/978-3-7643-7990-2_24
[26]	M. Sturm, Extrait d'un Mémoire sur L'intécration d'un système d'équations différentielles linéaires, présenté à l'Académie des sciences, In: Collected works of Charles François Sturm, Basel: Birkhäuser, 2009,334–342. http://dx.doi.org/10.1007/978-3-7643-7990-2_27
[27]	P. Sturm, Mémoire sur la résolution des équations numériques, In: Collected works of Charles François Sturm, Basel: Birkhäuser, 2009,345–390. http://dx.doi.org/10.1007/978-3-7643-7990-2_29
[28]	L. Greenberg, Sturm sequences for nonlinear eigenvalue problems, SIAM J. Math. Anal., 20 (1989), 182–199. http://dx.doi.org/10.1137/0520015 doi: 10.1137/0520015
[29]	E. Isaacson, H. Keller, Analysis of numerical methods, 2 Eds., New York: John Wiley-Sons, 1966.
[30]	J. Stoer, R. Bulirsch, Introduction to numerical analysis, New York: Springer-Verlag, 2002. http://dx.doi.org/10.1007/978-0-387-21738-3
[31]	A. Mostowski, M. Stark, Introduction to higher algebra, Pergamon: Elsevier, 1964. http://dx.doi.org/10.1016/C2013-0-10019-0
[32]	E. Mersin, M. Bahşi, Sturm theorem for the generalized Frank matrix, Hacet. J. Math. Stat., 50 (2021), 1002–1011. http://dx.doi.org/10.15672/hujms.773281 doi: 10.15672/hujms.773281

This article has been cited by:

1.	Deeba Afzal, Farkhanda Afzal, Sabir Hussain, Faryal Chaudhry, Dhana Kumari Thapa, Gohar Ali, Investigation on Boron Alpha Nanotube by Studying Their M-Polynomial and Topological Indices, 2022, 2022, 2314-4785, 1, 10.1155/2022/6136168
2.	Jia-Bao Liu, Hifza Iqbal, Khurram Shahzad, Topological Properties of Concealed Non-Kekulean Benzenoid Hydrocarbon, 2023, 43, 1040-6638, 1776, 10.1080/10406638.2022.2039230
3.	Kamel Jebreen, Hifza Iqbal, Muhammad Haroon Aftab, Iram Yaqoob, Mohammed Issa Sowaity, Amjad Barham, Study of eccentricity based topological indices for benzenoid structure, 2023, 45, 10269185, 221, 10.1016/j.sajce.2023.05.010
4.	Claudio Rocco, Jose A. Moronta, A Novel Perspective for Hosoya and M Polynomials for Analyzing Electric Power Network Topology, 2024, 1556-5068, 10.2139/ssrn.4806323
5.	Hifza Iqbal, Muhammad Haroon Aftab, Ali Akgul, Zeeshan Saleem Mufti, Iram Yaqoob, Mustafa Bayram, Muhammad Bilal Riaz, Further study of eccentricity based indices for benzenoid hourglass network, 2023, 9, 24058440, e16956, 10.1016/j.heliyon.2023.e16956

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(1616) PDF downloads(62) Cited by(5)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Tables(2)

AIMS Mathematics

Sturm's Theorem for Min matrices

Related Papers:

Abstract

1. Introduction

2. Methodology

3. Results and discussion

3.1. M-polynomial and degree based topological indices of $T_1$ structure

3.1.1. Theorem

3.1.2. Theorem

3.1.3. Theorem

3.1.4. Theorem

3.2. M-polynomial and degree based topological indices of $T_2$ structure

3.2.1. Theorem

3.2.2. Theorem

3.2.3. Theorem

3.2.4. Theorem

4. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Sturm's Theorem for Min matrices

Related Papers:

Abstract

1. Introduction

2. Methodology

3. Results and discussion

3.1. M-polynomial and degree based topological indices of T1 T_1 structure

3.1.1. Theorem

3.1.2. Theorem

3.1.3. Theorem

3.1.4. Theorem

3.2. M-polynomial and degree based topological indices of T2 T_2 structure

3.2.1. Theorem

3.2.2. Theorem

3.2.3. Theorem

3.2.4. Theorem

4. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

3.1. M-polynomial and degree based topological indices of $T_1$ structure

3.2. M-polynomial and degree based topological indices of $T_2$ structure