Exact wave patterns and chaotic dynamical behaviors of the extended (3+1)-dimensional NLSE

Ninghe Yang; Ninghe Yang

doi:10.3934/math.20241508

AIMS Mathematics

2024, Volume 9, Issue 11: 31274-31294. doi: 10.3934/math.20241508

Previous Article Next Article

Research article

Exact wave patterns and chaotic dynamical behaviors of the extended (3+1)-dimensional NLSE

Ninghe Yang ^,

Department of Mathematics, Northeast Petroleum University, Daqing 163318, China

Received: 15 September 2024 Revised: 25 October 2024 Accepted: 29 October 2024 Published: 04 November 2024
MSC : 34A05, 34C23, 35C05

In this paper, exact wave propagation patterns and chaotic dynamical behaviors of the extended (3+1)-dimensional nonlinear Schrödinger equation are studied. The topological structure of the dynamic system of the equation is studied by the complete discrimination system for the cubic polynomial method, in which the existence conditions of the soliton solutions and periodic solutions are obtained. Then, by the trial equation method, thirteen exact solutions are obtained, including solitary wave solutions, triangular function solutions, rational solutions and the elliptic function double periodic solutions, especially the elliptic function double periodic solutions. Finally, it is found that the system has chaotic behaviors when given the appropriate perturbations.

Keywords:

nonlinear Schrödinger equation,
the complete discrimination system for polynomial method,
exact solution,
chaotic behaviors

Citation: Ninghe Yang. Exact wave patterns and chaotic dynamical behaviors of the extended (3+1)-dimensional NLSE[J]. AIMS Mathematics, 2024, 9(11): 31274-31294. doi: 10.3934/math.20241508

Related Papers:

[1]	M. S. Hashmi, Rabia Shikrani, Farwa Nawaz, Ghulam Mustafa, Kottakkaran Sooppy Nisar, Velusamy Vijayakumar . An effective approach based on Hybrid B-spline to solve Riesz space fractional partial differential equations. AIMS Mathematics, 2022, 7(6): 10344-10363. doi: 10.3934/math.2022576
[2]	Ram Kishun Lodhi, Saud Fahad Aldosary, Kottakkaran Sooppy Nisar, Ateq Alsaadi . Numerical solution of non-linear Bratu-type boundary value problems via quintic B-spline collocation method. AIMS Mathematics, 2022, 7(4): 7257-7273. doi: 10.3934/math.2022405
[3]	Azhar Iqbal, Abdullah M. Alsharif, Sahar Albosaily . Numerical study of non-linear waves for one-dimensional planar, cylindrical and spherical flow using B-spline finite element method. AIMS Mathematics, 2022, 7(8): 15417-15435. doi: 10.3934/math.2022844
[4]	Emre Kırlı . A novel B-spline collocation method for Hyperbolic Telegraph equation. AIMS Mathematics, 2023, 8(5): 11015-11036. doi: 10.3934/math.2023558
[5]	Peng Zhong, Xuanlong Wu, Li Zhu, Aohao Yang . A new APSO-SPC method for parameter identification problem with uncertainty caused by random measurement errors. AIMS Mathematics, 2025, 10(2): 3848-3865. doi: 10.3934/math.2025179
[6]	Shanshan Wang . Split-step quintic B-spline collocation methods for nonlinear Schrödinger equations. AIMS Mathematics, 2023, 8(8): 19794-19815. doi: 10.3934/math.20231009
[7]	Osama Ala'yed, Rania Saadeh, Ahmad Qazza . Numerical solution for the system of Lane-Emden type equations using cubic B-spline method arising in engineering. AIMS Mathematics, 2023, 8(6): 14747-14766. doi: 10.3934/math.2023754
[8]	Mohammad Tamsir, Neeraj Dhiman, Deependra Nigam, Anand Chauhan . Approximation of Caputo time-fractional diffusion equation using redefined cubic exponential B-spline collocation technique. AIMS Mathematics, 2021, 6(4): 3805-3820. doi: 10.3934/math.2021226
[9]	Osama Ala'yed, Belal Batiha, Diala Alghazo, Firas Ghanim . Cubic B-Spline method for the solution of the quadratic Riccati differential equation. AIMS Mathematics, 2023, 8(4): 9576-9584. doi: 10.3934/math.2023483
[10]	Hasim Khan, Mohammad Tamsir, Manoj Singh, Ahmed Hussein Msmali, Mutum Zico Meetei . Numerical approximation of the time-fractional regularized long-wave equation emerging in ion acoustic waves in plasma. AIMS Mathematics, 2025, 10(3): 5651-5670. doi: 10.3934/math.2025261

Abstract

1. Introduction

Scientific innovations have enlightened the globe on different aspects of life, primarily on differential equations. Nonlinear partial differential equations, in particular have become handy across despaired dimensions. The nonlinear models have been used in plasma physics, engineering, fluid mechanics, nonlinear optics, biology, economics, chemistry, and many more fields. The necessity of understanding and using nonlinear evolution equations comes from their ability to model complex real-world phenomena. They attract physicists as much as they do mathematicians. Analyzing the exact solitary wave solutions for nonlinear evolution equations is an essential topic in the biographies of mathematical physics. Currently, many physical issues have been solved more confidently with the help of computer algebra. In recent years, creative methodologies have been developed to find multiple exact solutions to nonlinear differential equations. Among others, the homogeneous balance method ^[1,2], the tanh function method ^[3,4,5], the extended tanh function method ^[6], the hyperbolic function method ^[7,8], the rational expansion method ^[9], the sine-cosine method ^[10], the Jacobi elliptic function method ^[11,12,13], the exponential function method ^[14,15], the inverse scattering method ^[16], the Fan sub-equation technique ^[17,18,19], the F-expansion method ^[20,21], and the auxiliary equation method ^{[22,23,24,25]} provide additional power for the scientific arsenal. These methodologies are so effective and versatile that they can solve a wide range of nonlinear issues with great accuracy ^[26,27,28].

Localized transient waves that are non-dispersive and nonsingular, namely solitary waves (solitons), are solutions to nonlinear field theories ^[29,30,31]. Their importance is crucial throughout a broad spectrum of physics and technology, which is being noticed by many authors of the scientific literature ^[32,33,34]. According to a relativistic thermodynamic approach, exotic models offering more generality are being proposed instead of the traditional equilibrium models ^[35,36,37]. One analysis ^[38] presents an arbitrary N-fold Darboux transformation for the (HBK) equation obtaining the explicit (2N-1)-solitons solution using Vandermonde-like determinant. Another investigation the dynamics of waves for the generalized Gerdjikov-Ivanov equation, build some phase solutions and the graphic pattern of waves in terms of Whitham modulation theory and finite-gap integration ^[39]. The wave phenomenon propagation concepts used in the model's description through media with complex inner kinetics are based on the relaxational nature of the occurrence. Disturbances undermining thermodynamic balance maintain slow and fast mechanical waves and the processes striving to restore equilibrium. It means that the Vakhnenko equation ^[40,41] becomes the known nonlinear equation encompassing soliton solutions, describing the evolution of high-frequency waves in a relaxing medium; this specific form is rather typical of this equation.

$\begin{equation} \frac{\partial}{\partial x}\left(\frac{\partial}{\partial t}+ f \frac{\partial}{\partial x}\right)f +f = 0. \end{equation}$

(1.1)

This equation, having ( $f$ ) as a dimensionless pressure, ( $x$ ) as a space variable, and ( $t$ ) as a temporal one, represents a very complex system of dynamics that may turn into solitary behavior. Nevertheless, dealing with the Vakhnenko equation, a new dimension, is very tough because of its one-way nature. The study has been extended widely to unravel the mysteries behind it. For instance, it has been reported that various soliton solutions underlie wave propagations of varying features in the framework. An example is the demonstration of soliton solutions in the Vakhnenko equation, and their coverage in ^[42]. Additionally, further studies have revealed many more than just the solitons that resemble loops and humps, but some of them have turned out to be cusp-like structures ^[43]. Moreover, the research has shown the existence of N-soliton solutions that are applied to Eq (1.1), which increases the knowledge about the dynamics that the framework already has ^[44]. Furthermore, the latest work has gone into solitary wave solutions, which are diverse, and solitary wave solutions in the environs of the Vakhnenko equation ^[45,46], which can help unveil more about the nonlinear effects encapsulated by this equation. In trying to comprehend and utilize these solutions, we use a method belonging to the Riccati-Bernoulli sub-ode together with Bäcklund transformation. Such a hybrid approach opens a new channel for investigating the enigmatic driving forces behind symbols in the Vakhnenko equation, a gateway to nonlinear dynamics study and other fields. Following ^[42], we introduced new independent variables ( $X$ ) and ( $T$ ) that we have in the study. This method introduced the promise of new insights into the system dynamics code

$\begin{equation} \begin{split} &x = T + F \left(X, T \right) + x_o, \qquad t = X.\\ &f \left(x, t \right) = \frac{\partial F}{\partial X}\left(X, T \right). \end{split} \end{equation}$

(1.2)

Drawing upon the foundational equation (1.2), we have

$\begin{equation} \frac{\partial}{\partial X} = \frac{\partial}{\partial t}+ f \frac{\partial}{\partial x}, \qquad \frac{\partial}{\partial T} = \left(1 + \frac{\partial F}{\partial T} \right)\frac{\partial}{\partial x}. \end{equation}$

(1.3)

Hence, Eq (1.1) can be reformulated as:

$\begin{equation} \frac{\partial}{\partial T}\left(\frac{\partial^2 F}{\partial X^2} \right)+\left(\frac{\partial F}{\partial X} \right)\left(\frac{\partial F}{\partial T} \right) + \left(\frac{\partial F}{\partial X} \right) = 0. \end{equation}$

(1.4)

The proposed methodology ^[47,48,49] stands out for its superiority in solving uniquely complex algebraic problems, and its versatility spans the expanses of different scientific fields like physics, fluid dynamics, biology, chemistry, and optical fiber communications. Implementing the Riccati–Bernoulli sub-ode technique and the Bäcklund transformation method facilitates converting partial differential equations into coupled systems of algebraic types. This change gives researchers a chance to discover the exact things related to the involved dynamical system and helps them improve their comprehension of these processes ^[50,51,52]. This strategy is crucial for settling the finite number of numerical solutions, rendering all the solutions tolerated for the considered equations valid. Another added advantage of this technique is its built-in resilience in transcending the waves of single-wave solutions, making it one of the most influential and anticipatory techniques compared to the existing methods ^[53,54,55].

2. Algorithm

Suppose we have a non-linear partial differential equation in two independent variable ( $x$ ) and ( $t$ ), given by

$\begin{equation} G_1\left(g, g_x, g_t, g_{xx}, g_{tt}, g_{xt}, \ldots \right) = 0, \end{equation}$

(2.1)

where $g = g(x, t)$ is an unknown function and ( $G_1$ ) is a polynomial in $g = g(x, t)$ and its various partial derivatives and nonlinear terms involved. Here is the scientific method outline for solving such equations.

Let us denote the independent variables ( $x$ ) and ( $t$ ) as a single variable ( $\Theta$ ) by defining,

$\begin{equation} \begin{aligned} & G(x , t) = g(\Theta), \quad \Theta = k_1{x_1}+ k_2{x_2}+ k_3{t} \ldots +\Theta_o, \end{aligned} \end{equation}$

(2.2)

where $k_1, k_2, k_3, \ldots \Theta_o$ are constants.

This transformation allows us to convert the given equation (2.1) into an ordinary differential equation represented as:

$\begin{equation} G_2\left(g, g'(\Theta) , g''(\Theta), gg'(\Theta), \ldots \right) = 0. \end{equation}$

(2.3)

Assume that Eq (2.3) has a solution in the form of a finite series:

$\begin{equation} {g}(\Theta) = \sum\limits_{i = -m}^{m} c_i{\phi(\Theta)}^i. \end{equation}$

(2.4)

Under the constraints where, $c_m \neq 0$ and $c_{-m} \neq 0$ simultaneously, we consider the presumptive solution for $g(\Theta)$ . Additionally, we apply the Bäcklund transformation method to obtain the solution for $\phi(\Theta)$ .

$\begin{equation} \phi(\Theta) = \frac{-\mu b + a \varphi(\Theta)}{a + b \varphi(\Theta)}. \end{equation}$

(2.5)

With the constants ( $\mu$ ), ( $a$ ), and ( $b$ ), assuming that $b\neq0$ , and introducing the function $\varphi(\Theta)$ , defined as:

$\begin{equation} \frac{d{\varphi}}{d\Theta} = \mu +{\varphi(\Theta)^2}. \end{equation}$

(2.6)

Reference ^[56] presents the post-solution analysis of Eq (2.6), detailing the conditions that led to various observed scenarios. The parameter ( $\mu$ ) is subsequently leveraged to derive further analysis and ascertain the solution $\varphi(\Theta)$ .

$\begin{align} (i) &\quad\text{If}\quad \mu < 0, \quad\text{then}\quad \varphi(\Theta) = -\sqrt{-\mu}\tanh(\sqrt{-\mu}\Theta), \quad \text{or}\quad \varphi(\Theta) = -\sqrt{-\mu}\coth(\sqrt{-\mu}\Theta). \end{align}$

(2.7)

$\begin{align} (ii) &\quad\text{If}\quad \mu > 0, \quad\text{then}\quad \varphi(\Theta) = \sqrt{\mu}\tan(\sqrt{\mu}\Theta), \quad\text{or}\quad \varphi(\Theta) = -\sqrt{\mu}\cot(\sqrt{\mu}\Theta). \end{align}$

(2.8)

$\begin{align} (iii) &\quad\text{If}\quad \mu = 0, \quad\text{then}\quad \varphi(\Theta) = \frac{-1}{\Theta}. \end{align}$

(2.9)

Nonlinear and highest-order derivative components are added in order to achieve a more accurate and finer equilibrium state, which is derived from a homogeneous balance and linear perturbation analysis. The following formula gives us a relationship between the degree of the nonlinear term and the highest-order derivative to determine the integer ( $m$ ) ^[57]. This integer ( $m$ ) is instrumental in determining the assumed series solution for the series solution assumed in Eq (2.4).

$\begin{equation} D\left[\frac{d^z g}{d\Theta^z}\right] = m + z, \quad D\left[g^j \frac{d^z g}{d\Theta^z}\right]^u = mj + u(z + m). \end{equation}$

(2.10)

The series solution from (2.5) is substituted and solved computational tools. Finally, the coefficients obtained are substituted back in to Eq (2.4) to determine $g(\Theta)$ .

3. Execution of the problem

We are going to make use of the described procedure to get the solitary wave precisely $F \left(X, T \right)$ here in this section. This breakthrough was actually made based on a highly sophisticated wave transformation process.

$\begin{equation} \begin{aligned} F(X, T) = f(\psi), \quad \text {where} \quad \psi = k X - \omega T, \end{aligned} \end{equation}$

(3.1)

where ( $k$ ) and ( $\omega$ ) are constants. By employing the aforementioned complex wave transformation, Eq (1.4) undergoes a transformation, resulting in the following nonlinear ordinary differential equation (ODE):

$\begin{equation} -\left(\omega k \right)F''' - \omega \left( F'\right)^2 + F' = 0. \end{equation}$

(3.2)

Using Eq (2.4), this involves adding up the following expressions: Eqs (2.4) and (2.5). Perform the substitution into Eq (3.2), and after that, you obtain a system of algebraic equations that contain the coefficients of $\phi^i(\psi)$ , and their value must equal zero. By solving this system of algebraic equations using Maple, the following results are obtained:

Case:1

$\begin{equation} \begin{split} c_{{0}} = c_{{0}}, c_{{1}} = -{\frac {c_{{-1}}}{\mu}}, c_{{-1}} = c_{{-1}}, \omega = -3/8\, {c_{{-1}}}^{-1}, k = 1/6\, {\frac {c_{{-1}}}{\mu}}, \mu = \mu, a = a, b = b. \end{split} \end{equation}$

(3.3)

Case:2

$\begin{equation} \begin{split} c_{{0}} = c_{{0}}, c_{{1}} = c_{{1}}, c_{{-1}} = 0, \omega = \omega, k = -1/6\, c_{{ 1}}, \mu = 3/2\, {\frac {1}{\omega\, c_{{1}}}}, a = a, b = b. \end{split} \end{equation}$

(3.4)

Solution Set. 1: The case 1 based on Eq (1.4) is therefore explained. Consequently, solitary wave solutions can be obtained with the given condition $\mu < 0$ .

$\begin{equation} \begin{split} &F_1(x, t) = c_{{-1}} \left( a-b\sqrt {-\mu}\tanh \left( \sqrt {-\mu} \left( 1/6\, { \frac {c_{{-1}}X}{\mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) \left( -\mu\, b-a\sqrt {-\mu}\tanh \left( \sqrt {-\mu} \left( 1/6\, {\frac {c_{{-1}}X}{\mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) ^{-1}+\\ &c_{{0}}-c_{{-1}} \left( -\mu\, b-a \sqrt {-\mu}\tanh \left( \sqrt {-\mu} \left( 1/6\, {\frac {c_{{-1}}X}{ \mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) {\mu}^{-1} \left( a-b\sqrt {-\mu}\tanh \left( \sqrt {-\mu} \left( 1/6\, {\frac {c _{{-1}}X}{\mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) ^ {-1}. \end{split} \end{equation}$

(3.5)

$\begin{equation} \begin{split} &F_2(x, t) = c_{{-1}} \left( a-b\sqrt {-\mu}\coth \left( \sqrt {-\mu} \left( 1/6\, { \frac {c_{{-1}}X}{\mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) \left( -\mu\, b-a\sqrt {-\mu}\coth \left( \sqrt {-\mu} \left( 1/6\, {\frac {c_{{-1}}X}{\mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) ^{-1}+\\ &c_{{0}}-c_{{-1}} \left( -\mu\, b-a \sqrt {-\mu}\coth \left( \sqrt {-\mu} \left( 1/6\, {\frac {c_{{-1}}X}{ \mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) {\mu}^{-1} \left( a-b\sqrt {-\mu}\coth \left( \sqrt {-\mu} \left( 1/6\, {\frac {c _{{-1}}X}{\mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) ^ {-1}. \end{split} \end{equation}$

(3.6)

Solution Set. 2: The case 1 based on Eq (1.4) is therefore explained. Consequently, solitary wave solutions can be obtained with the given condition $\mu > 0$ .

$\begin{equation} \begin{split} &F_3(x, t) = c_{{-1}} \left( a+b\sqrt {\mu}\tan \left( \sqrt {\mu} \left( 1/6\, { \frac {c_{{-1}}X}{\mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) \left( -\mu\, b+a\sqrt {\mu}\tan \left( \sqrt {\mu} \left( 1/ 6\, {\frac {c_{{-1}}X}{\mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) ^{-1}+\\ &c_{{0}}-c_{{-1}} \left( -\mu\, b+a\sqrt {\mu} \tan \left( \sqrt {\mu} \left( 1/6\, {\frac {c_{{-1}}X}{\mu}}+3/8\, { \frac {T}{c_{{-1}}}} \right) \right) \right) {\mu}^{-1} \left( a+b \sqrt {\mu}\tan \left( \sqrt {\mu} \left( 1/6\, {\frac {c_{{-1}}X}{\mu} }+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) ^{-1}. \end{split} \end{equation}$

(3.7)

$\begin{equation} \begin{split} &F_4( x, t) = c_{{-1}} \left( a-b\sqrt {\mu}\cot \left( \sqrt {\mu} \left( 1/6\, { \frac {c_{{-1}}X}{\mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) \left( -\mu\, b-a\sqrt {\mu}\cot \left( \sqrt {\mu} \left( 1/ 6\, {\frac {c_{{-1}}X}{\mu}}+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) ^{-1}+\\ &c_{{0}}-c_{{-1}} \left( -\mu\, b-a\sqrt {\mu} \cot \left( \sqrt {\mu} \left( 1/6\, {\frac {c_{{-1}}X}{\mu}}+3/8\, { \frac {T}{c_{{-1}}}} \right) \right) \right) {\mu}^{-1} \left( a-b \sqrt {\mu}\cot \left( \sqrt {\mu} \left( 1/6\, {\frac {c_{{-1}}X}{\mu} }+3/8\, {\frac {T}{c_{{-1}}}} \right) \right) \right) ^{-1}. \end{split} \end{equation}$

(3.8)

Solution Set. 3: The case 2 based on Eq (1.4) is therefore explained. Consequently, solitary wave solutions can be obtained with the given condition $\mu < 0$ .

$\begin{equation} \begin{split} F_{5}(x, t) = &c_{{0}}+c_{{1}} \left( -3/2\, {\frac {b}{\omega\, c_{{1}}}}-1/2\, a\sqrt {-6\, {\frac {1}{\omega\, c_{{1}}}}}\tanh \left( 1/2\, \sqrt {-6\, {\frac {1}{\omega\, c_{{1}}}}} \left( -1/6\, c_{{1}}X-\omega\, T \right) \right) \right) \\ & \left( a-1/2\, b\sqrt {-6\, {\frac {1}{\omega\, c_{{1} }}}}\tanh \left( 1/2\, \sqrt {-6\, {\frac {1}{\omega\, c_{{1}}}}} \left( -1/6\, c_{{1}}X-\omega\, T \right) \right) \right) ^{-1}. \end{split} \end{equation}$

(3.9)

$\begin{equation} \begin{split} F_{6}(x, t) = &c_{{0}}+c_{{1}} \left( -3/2\, {\frac {b}{\omega\, c_{{1}}}}-1/2\, a\sqrt {-6\, {\frac {1}{\omega\, c_{{1}}}}}\coth \left( 1/2\, \sqrt {-6\, {\frac {1}{\omega\, c_{{1}}}}} \left( -1/6\, c_{{1}}X-\omega\, T \right) \right) \right) \\ & \left( a-1/2\, b\sqrt {-6\, {\frac {1}{\omega\, c_{{1} }}}}\coth \left( 1/2\, \sqrt {-6\, {\frac {1}{\omega\, c_{{1}}}}} \left( -1/6\, c_{{1}}X-\omega\, T \right) \right) \right) ^{-1}. \end{split} \end{equation}$

(3.10)

Solution Set. 4: The case 2 based on Eq (1.4) is therefore explained. Consequently, solitary wave solutions can be obtained with the given condition $\mu > 0$ .

$\begin{equation} \begin{split} F_{7}(x, t) = &c_{{0}}+c_{{1}} \left( -3/2\, {\frac {b}{\omega\, c_{{1}}}}+1/2\, a\sqrt {6}\sqrt {{\frac {1}{\omega\, c_{{1}}}}}\tan \left( 1/2\, \sqrt {6} \sqrt {{\frac {1}{\omega\, c_{{1}}}}} \left( -1/6\, c_{{1}}X-\omega\, T \right) \right) \right)\\ & \left( a+1/2\, b\sqrt {6}\sqrt {{\frac {1}{ \omega\, c_{{1}}}}}\tan \left( 1/2\, \sqrt {6}\sqrt {{\frac {1}{\omega\, c_{{1}}}}} \left( -1/6\, c_{{1}}X-\omega\, T \right) \right) \right) ^ {-1}. \end{split} \end{equation}$

(3.11)

$\begin{equation} \begin{split} F_{8}( x, t) = &c_{{0}}+c_{{1}} \left( -3/2\, {\frac {b}{\omega\, c_{{1}}}}-1/2\, a\sqrt {6}\sqrt {{\frac {1}{\omega\, c_{{1}}}}}\cot \left( 1/2\, \sqrt {6} \sqrt {{\frac {1}{\omega\, c_{{1}}}}} \left( -1/6\, c_{{1}}X-\omega\, T \right) \right) \right) \\ & \left( a-1/2\, b\sqrt {6}\sqrt {{\frac {1}{ \omega\, c_{{1}}}}}\cot \left( 1/2\, \sqrt {6}\sqrt {{\frac {1}{\omega\, c_{{1}}}}} \left( -1/6\, c_{{1}}X-\omega\, T \right) \right) \right) ^ {-1}. \end{split} \end{equation}$

(3.12)

Solution Set. 5: The case 2 based on Eq (1.4) is therefore explained. Consequently, solitary wave solutions can be obtained with the given condition $\mu = 0$ .

$\begin{equation} \begin{split} F_{9}(x, t) = c_{{0}}+c_{{1}} \left( -3/2\, {\frac {b}{\omega\, c_{{1}}}}-{\frac {a}{- 1/6\, c_{{1}}X-\omega\, T}} \right) \left( a-{\frac {b}{-1/6\, c_{{1}}X- \omega\, T}} \right) ^{-1}. \end{split} \end{equation}$

(3.13)

4. Results and discussion

Through this exploration, a sequence of events is summarized into an outline for dissecting the theory of how waves propagate in mediums with intricate internal dynamics, which are inspired by the relaxation character driven by the phenomenon. The Bäcklund transformation utilizes the differential equation to remodel these systems into ordinary differential equations that can be handled by transformation friendly techniques. This enables the discovery of the solutions to equations. Our unique contribution is the Riccati–Bernoulli sub-ode method, allows us to determine the remaining coefficients of the series solution and thus get a clearer image of the underpinning dynamics. Moreover, the solving of the equation system and its series solution is detailed with both solutions split into Riccati–Bernoulli sub-ode algorithm. This rigorous analysis yields three distinct families of solutions: hyperbolic, rational, and trigonometric. Moreover, as is the case with different analytical solutions, each solution is individual, despite the governing mathematical structures being different owing to the variational equations.

The particular framework is adaptive to such patterns as kink and lump (which tend to be a proper basis for adaptations at different physical levels). Kink solitons act as a key, which helps in the theoretical realization of topological line solitons and dislocations in particle physics and solids, respectively. Furthermore, lump solitons become important in nonlinear optics as well as oceanography, where they bring about the creation of rogue waves and short pulses of light upon interaction with an optical beam. MATLAB gave us the perfect settings, and we adjusted specific parameters to perfectly match the analytical solutions with the detailing of each individual solution as a result. As a result of this, the graphs serve not only as the means to the liquid but also facilitate deeper comprehension of the properties that could be used to calculate the dynamics of the liquids precisely.

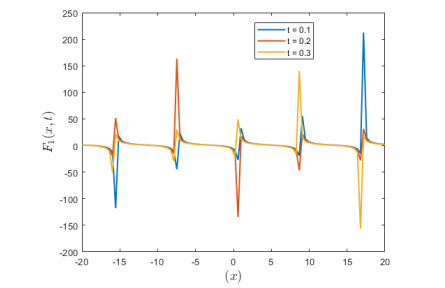
Figure 1: To start out with, the spatial domain's nature stands out as that of a localized perturbation, with its distinct shape and amplitude. As it propagates along the medium, the profile of its spatial form stays undistorted, which proves its resistance to breaking and shaping powers. But even further, the soliton finds the medium that slowly, calmingly, brings everything in to order. This can be demonstrated by observing the long-term degradation of the soliton amplitude. The medium undergoes the relaxation stage when its amplitude is absorbing the energy from the soliton, it diminishes over the length.

Figure 1. Evolution of the soliton solution of function

$F_1$ , showcasing its dynamic behavior over time.

DownLoad: Full-Size Img PowerPoint

Figure 2: Illustrates the periodic lump solutions, i.e., one specificity of the wave soliton structures that has periodic behavior. It leads to solutions that appear in the form of amplitude and shape periodic variations of the wave packet and that, because of their periodicity, are quite well reflected in the form of a repetition of humps or peaks in the picture of waves. Lump solutions of a periodic nature arise naturally from the interaction of nonlinear structure, modulation effects, dispersion, and other spectral factors inherent to wave dynamics. Distinct from conventional linear waves that travel uniformly, the periodicity of these lump solutions is now intrinsically entailed within their behavior, reflecting the periodicity in the physics that creates them. Also, as we move to greater time intervals, the wave amplitude increases, showing that these are solutions that are dispersive in nature and that they evolve dynamically over time.

Figure 2. Evolution of the solution of function

$F_{2}$ , showcasing its dynamic behavior over time.

DownLoad: Full-Size Img PowerPoint

Figure 3: This plot shows the way the periodic hyperbolic soliton solution is spatially and temporally propagating in the medium, that is, the vertical motion of an image with a certain amplitude having an oscillating behavior in space. Nonetheless, the original form of the periodic hyperbolic soliton actually manifests as a standing wave with a uniform amplitude; this should be viewed as a stable, non-uniform wave motion, so that the periodic wave packet oscillates as a soliton. While the soliton advances to the right in the spatial dimension, the bottoms of the light suction trough grow higher and higher, as the solid tells us that the intensity of the wave grows stronger as you go down in the wave.

Figure 3. Evolution of the solution of function

$F_{3}$ , showcasing its dynamic behavior over time.

DownLoad: Full-Size Img PowerPoint

Figure 4: In this depiction, the plot represents the spacial progress of the bright soliton solution. This solution characterizes its amplitude as a constant feature that is never changed. Lack of movable amplitude for up-bright solitons is an inherent property that expresses their stability against dissipative effects. Even when the process of relaxation appears in the medium, the original wavefront kink is kept the same in the amplitude along its path.

Figure 4. Evolution of the soliton solution of function

$F_{6}$ , showcasing its dynamic behavior over time.

DownLoad: Full-Size Img PowerPoint

Figure 5: In this representation, the plot is to solely portray the characteristic of a dark soliton solution flow within the medium through its unique amplitude, which continues to be unchanged throughout the evolution of the solution. First, the dark kink arises in the amplitude profile as a local counterpart to the wave trough, which is an illustration of the violent disturbance within the medium. The amplitude of the kink is astonishingly stable as it spreads in space independent of the amount of time since the space–time terms do not interfere with the propagation of the kink.

Figure 5. Evolution of the dark soliton solution of function

$F_{7}$ , showcasing its dynamic behavior over time.

DownLoad: Full-Size Img PowerPoint

As the time parameter increases, the amplitude of the wave packet also increases in a periodic lump plot depicted in Figure 6. This is attributed to wave dispersion, where different frequencies move at different velocities, thereby causing the wave to spread out and the energy to concentrate more in some areas, leading to higher peaks. However, the lump solution remains stable but dynamic, showing that there is consistency in the nature of waves despite them being dynamic too. Understanding such phenomena is important mostly in fields like optics and acoustics, which deal with significant issues of wave propagation as well as dispersion. This graphic representation offers important information about the intricate processes involved in development over a period for waves.

Figure 6. Evolution of the periodic lump solution of function

$F_{8}$ , showcasing its dynamic behavior over time.

DownLoad: Full-Size Img PowerPoint

5. Conclusions

The Ricatti–Bernoulli sub-ode method has been successfully implemented to develop a wide range of solitary wave solutions of the Vakhnenko system, an essential nonlinear description for the dynamics of high-frequency waves in relaxation media. They have two different components, the lump and the kink, which show the location of wave movement and wave propagation within the fluid. The implemented tools are suitable in most cases for bringing to the fore the different physical properties of waves dispersed in various wave systems. The presented method is reliable and easy to use for gaining a diversity of options for problem solving and therefore adds to the arsenal of current analytical techniques in nonlinear waves. On the other hand, it is able to extend beyond the Vakhnenko equation to embrace a wider variety of nonlinear evolution equations, like the ones belonging to this class. By generating solitary wave solutions, the work not only adds to the theoretical knowledge about wave propagation in non-dispersive mediums but also empowers the experiments and interpretations of the waves and the modeling of complex wave phenomena. Through this process, different types of waves expose the hidden mechanisms that govern the waves' propagation processes, thus providing a deep understanding of the underlying physical aspects.

Author contributions

Khudhayr A. Rashedi, Saima Noor, Tariq S. Alshammari and Imran Khan: Writing-original draft, Formal analysis, Validation, Writing–review & editing. The authors contributed equally to this work. All the authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (KFU241278).

Funding

This work was supported by the Deanship of Scientific Research, Vice Presidency for Graduate Studies and Scientific Research, King Faisal University, Saudi Arabia (KFU241278).

Conflict of interest

The authors declare that they have no conflicts of interest.

References

[1]	J. Shang, W. Li, D. Li, Traveling wave solutions of a coupled Schrödinger-Korteweg-de Vries equation by the generalized coupled trial equation method, Heliyon, 9 (2023), e15695. http://dx.doi.org/10.1016/j.heliyon.2023.e15695 doi: 10.1016/j.heliyon.2023.e15695
[2]	B. Liu, Q. Zhao, X. Li, Step-like initial value problem and Whitham modulation in fluid dynamics to a generalized derivative nonlinear Schrödinger equation, Phys. Fluids, 36 (2024), 066109. http://dx.doi.org/10.1063/5.0210864 doi: 10.1063/5.0210864
[3]	S. Rizvi, A. Seadawy, N. Farah, S. Ahmad, Application of Hirota operators for controlling soliton interactions for Bose-Einstein condensate and quintic derivative nonlinear Schrödinger equation, Chaos Soliton. Fract., 159 (2022), 112128. http://dx.doi.org/10.1016/j.chaos.2022.112128 doi: 10.1016/j.chaos.2022.112128
[4]	N. Karjanto, Modeling wave packet dynamics and exploring applications: a comprehensive guide to the nonlinear Schrödinger equation, Mathematics, 12 (2024), 744. http://dx.doi.org/10.3390/math12050744 doi: 10.3390/math12050744
[5]	Y. Jiang, C. Wang, Exact solutions and dynamic properties of perturbed Fokas-Lenells equation, J. Opt., in press. http://dx.doi.org/10.1007/s12596-024-01823-z
[6]	N. Raza, M. Osman, A. Abdel-Aty, S. Abdel-Khalek, H. Besbes, Optical solitons of space-time fractional Fokas-Lenells equation with two versatile integration architectures, Adv. Differ. Equ., 2020 (2020), 517. http://dx.doi.org/10.1186/s13662-020-02973-7 doi: 10.1186/s13662-020-02973-7
[7]	A. Arnous, A. Elsherbeny, A. Secer, M. Ozisik, M. Bayram, N. Shah, et al., Optical solitons for the dispersive concatenation model with spatio-temporal dispersion having multiplicative white noise, Results Phys., 56 (2024), 107299. http://dx.doi.org/10.1016/j.rinp.2023.107299 doi: 10.1016/j.rinp.2023.107299
[8]	W. Rabie, H. Ahmed, M. Hashemi, M. Mirzazadeh, M. Bayram, Generating optical solitons in the extended (3+1)-dimensional nonlinear Kudryashov's equation using the extended F-expansion method, Opt. Quant. Electron., 56 (2024), 894. http://dx.doi.org/10.1007/s11082-024-06787-9 doi: 10.1007/s11082-024-06787-9
[9]	Y. Zhang, X. Lü, Data-driven solutions and parameter discovery of the extended higher-order nonlinear Schrödinger equation in optical fibers, Physica D, 468 (2024), 134284. https://doi.org/10.1016/j.physd.2024.134284 doi: 10.1016/j.physd.2024.134284
[10]	Y. Li, Y. Kai, Wave structures and the chaotic behaviors of the cubic-quartic nonlinear Schrödinger equation for parabolic law in birefringent fibers, Nonlinear Dyn., 111 (2023), 8701–8712. http://dx.doi.org/10.1007/s11071-023-08291-3 doi: 10.1007/s11071-023-08291-3
[11]	H. Triki, F. Azzouzi, A. Biswas, S. Moshokoa, M. Belic, Bright optical solitons with Kerr law nonlinearity and fifth order dispersion, Optik, 128 (2017), 172–177. http://dx.doi.org/10.1016/j.ijleo.2016.10.026 doi: 10.1016/j.ijleo.2016.10.026
[12]	Y. Wu, M. Vivas-Cortez, H. Ur Rehman, E. Sherif, A. Rashid, Bifurcation study, phase portraits and optical solitons of dual-mode resonant nonlinear Schrödinger dynamical equation with Kerr law non-linearity, Heliyon, 10 (2024), e34416. http://dx.doi.org/10.1016/j.heliyon.2024.e34416 doi: 10.1016/j.heliyon.2024.e34416
[13]	P. Albayrak, M. Ozisik, A. Secer, M. Bayram, S. Das, Optical solitons of stochastic perturbed Radhakrishnan-Kundu-Lakshmanan model with Kerr law of self-phase-modulation, Mod. Phys. Lett. B, 38 (2024), 2450122. http://dx.doi.org/10.1142/S0217984924501227 doi: 10.1142/S0217984924501227
[14]	A. Biswas, M. Ekici, A. Dakova, S. Khan, S. Moshokoa, H. Alshehri, et al., Highly dispersive optical soliton perturbation with Kudryashov's sextic-power law nonlinear refractive index by semi-inverse variation, Results Phys., 27 (2021), 104539. http://dx.doi.org/10.1016/j.rinp.2021.104539 doi: 10.1016/j.rinp.2021.104539
[15]	K. Ahmed, N. Badra, H. Ahmed, W. Rabie, M. Mirzazadeh, M. Eslami, et al., Investigation of solitons in magneto-optic waveguides with Kudryashov's law nonlinear refractive index for coupled system of generalized nonlinear Schrödinger's equations using modified extended mapping method, Nonlinear Anal.-Model., 29 (2024), 205–223. http://dx.doi.org/10.15388/namc.2024.29.34070 doi: 10.15388/namc.2024.29.34070
[16]	N. Ozdemi, S. Altun, A. Secer, M. Ozisik, M. Bayram, Revealing optical soliton solutions of Schrödinger equation having parabolic law and anti-cubic law with weakly nonlocal nonlinearity, J. Taibah Univ. Sci., 18 (2024), 2270237. http://dx.doi.org/10.1080/16583655.2023.2270237 doi: 10.1080/16583655.2023.2270237
[17]	S. Arshed, G. Akram, M. Sadaf, A. Ul Nabi, A. Alzaidi, Optical soliton solutions of perturbed nonlinear Schrödinger equation with parabolic law nonlinearity, Opt. Quant. Electron., 56 (2024), 50. http://dx.doi.org/10.1007/s11082-023-05564-4 doi: 10.1007/s11082-023-05564-4
[18]	M. Aamir Ashraf, A. Seadawy, S. Rizvi, A. Althobaiti, Dynamical optical soliton solutions and behavior for the nonlinear Schrödinger equation with kudryashov's quintuple power law of refractive index together with the dual-form of nonlocal nonlinearity, Opt. Quant. Electron., 56 (2024), 1243. http://dx.doi.org/10.1007/s11082-024-07096-x doi: 10.1007/s11082-024-07096-x
[19]	E. Zayed, K. Alurrfi, A. Arnous, M. Hashemi, M. Bayram, Effects of high dispersion and generalized non-local laws on optical soliton perturbations in magneto-optic waveguides with sextic-power law refractive index, Nonlinear Dyn., 112 (2024), 8507–8525. http://dx.doi.org/10.1007/s11071-024-09518-7 doi: 10.1007/s11071-024-09518-7
[20]	T. Han, Z. Li, K. Shi, G. Wu, Bifurcation and traveling wave solutions of stochastic Manakov model with multiplicative white noise in birefringent fibers, Chaos Soliton. Fract., 163 (2022), 112548. http://dx.doi.org/10.1016/j.chaos.2022.112548 doi: 10.1016/j.chaos.2022.112548
[21]	T. Han, Y. Jiang, J. Lyu, Chaotic behavior and optical soliton for the concatenated model arising in optical communication, Results Phys., 58 (2024), 107467. http://dx.doi.org/10.1016/j.rinp.2024.107467 doi: 10.1016/j.rinp.2024.107467
[22]	J. Zhang, Optical solitons in optical metamaterials with anti-cubic nonlinearity, Optik, 251 (2022), 168329. https://doi.org/10.1016/j.ijleo.2021.168329 doi: 10.1016/j.ijleo.2021.168329
[23]	L. Tang, Bifurcations and dispersive optical solitons for the nonlinear Schrödinger-Hirota equation in DWDM networks, Optik, 262 (2022), 169276. http://dx.doi.org/10.1016/j.ijleo.2022.169276 doi: 10.1016/j.ijleo.2022.169276
[24]	I. Samir, O. El-Sham, R. El-barkoki, H. Ahmed, W. Abbas, M. Hashemi, Extraction of solitons in optical fibers for the (2+1)-dimensional perturbed nonlinear Schrödinger equation via the improved modified extended tanh function technique, Contemp. Math., 5 (2024), 2397–2410. http://dx.doi.org/10.37256/cm.5220244301 doi: 10.37256/cm.5220244301
[25]	K. Ahmed, H. Ahmed, N. Badra, W. Rabie, Optical solitons retrieval for an extension of novel dual-mode of a dispersive non-linear Schrödinger equation, Optik, 307 (2024), 171835. http://dx.doi.org/10.1016/j.ijleo.2024.171835 doi: 10.1016/j.ijleo.2024.171835
[26]	H. Rehman, I. Iqbal, M. Medani, A. Awan, U. Perveen, R. Alroobaea, Analyzing the dynamics of multi-solitons and other solitons in the perturbed nonlinear Schrödinger equation, Mod. Phys. Lett. B, in press. http://dx.doi.org/10.1142/S0217984924504682
[27]	A. Farooq, M. Khan, W. Ma, Exact solutions for the improved mKdv equation with conformable derivative by using the Jacobi elliptic function expansion method, Opt. Quant. Electron., 56 (2024), 542. http://dx.doi.org/10.1007/s11082-023-06258-7 doi: 10.1007/s11082-023-06258-7
[28]	A. Arnous, A. Biswas, Y. Yıldırım, Q. Zhou, W. Liu, A. Alshomrani, et al., Cubic-quartic optical soliton perturbation with complex Ginzburg-Landau equation by the enhanced Kudryashov's method, Chaos Soliton. Fract., 155 (2022), 111748. http://dx.doi.org/10.1016/j.chaos.2021.111748 doi: 10.1016/j.chaos.2021.111748
[29]	A. Elsherbeny, M. Mirzazadeh, A. Arnous, A. Biswas, Y. Yıldırım, A. Asiri, Optical bullets and domain walls with cross-spatio dispersion having parabolic law of nonlinear refractive index, J. Opt., in press. http://dx.doi.org/10.1007/s12596-023-01398-1
[30]	A. Biswas, Theory of optical bullets, J. Opt. A, 4 (2002), 84–97. http://dx.doi.org/10.1163/156939302X01254 doi: 10.1163/156939302X01254
[31]	K. Hosseini, M. Matinfar, M. Mirzazadeh, A (3+1)-dimensional resonant nonlinear Schrödinger equation and its Jacobi elliptic and exponential function solutions, Optik, 207 (2020), 164458. http://dx.doi.org/10.1016/j.ijleo.2020.164458 doi: 10.1016/j.ijleo.2020.164458
[32]	S. Kumar, A. Kukkar, Dynamics of several optical soliton solutions of a (3+1)-dimensional nonlinear Schrödinger equation with parabolic law in optical fibers, Mod. Phys. Lett. B, in press. http://dx.doi.org/10.1142/S0217984924504530
[33]	W. Rabie, H. Ahmed, I. Samir, M. Alnahhass, Optical solitons and stability analysis for NLSE with nonlocal nonlinearity, nonlinear chromatic dispersion and Kudryashov's generalized quintuple-power nonlinearity, Results Phys., 59 (2024), 107589. http://dx.doi.org/10.1016/j.rinp.2024.107589 doi: 10.1016/j.rinp.2024.107589
[34]	C. Liu, Applications of complete discrimination system for polynomial for classifications of traveling wave solutions to nonlinear differential equations, Comput. Phys. Commun., 181 (2010), 317–324. http://dx.doi.org/10.1016/j.cpc.2009.10.006 doi: 10.1016/j.cpc.2009.10.006
[35]	C. Liu, Trial equation method based on symmetry and applications to nonlinear equations arising in mathematical physics, Found. Phys., 41 (2011), 793–804. http://dx.doi.org/10.1007/s10701-010-9521-4 doi: 10.1007/s10701-010-9521-4
[36]	C. Liu, Canonical-like transformation method and exact solutions to a class of diffusion equations, Chaos Soliton. Fract., 42 (2009), 441–446. http://dx.doi.org/10.1016/j.chaos.2009.01.006 doi: 10.1016/j.chaos.2009.01.006
[37]	C. Liu, The classification of travelling wave solutions and superposition of multi-solutions to Camassa-Holm equation with dispersion, Chinese Phys., 16 (2007), 1832. http://dx.doi.org/10.1088/1009-1963/16/7/004 doi: 10.1088/1009-1963/16/7/004
[38]	Y. Kai, J. Ji, Z. Yin, Study of the generalization of regularized long-wave equation, Nonlinear Dyn., 107 (2022), 2745–2752. http://dx.doi.org/10.1007/s11071-021-07115-6 doi: 10.1007/s11071-021-07115-6
[39]	Y. Kai, S. Chen, K. Zhang, Z. Yin, A study of the shallow water waves with some Boussinesq-type equations, Waves Random Complex, 34 (2024), 1251–1268. http://dx.doi.org/10.1080/17455030.2021.1933259 doi: 10.1080/17455030.2021.1933259
[40]	L. Guo, W. Xu, The traveling wave mode for nonlinear Biswas-Milovic equation in magneto-optical wave guide coupling system with Kudryashov's law of refractive index, Results Phys., 27 (2021), 104500. http://dx.doi.org/10.1016/j.rinp.2021.104500 doi: 10.1016/j.rinp.2021.104500
[41]	Y. Chen, Exact chirped solutions for the generalized nonlinear Schrödinger equation in highly-nonlinear optical fibers, Optik, 281 (2023), 170814. http://dx.doi.org/10.1016/j.ijleo.2023.170814 doi: 10.1016/j.ijleo.2023.170814
[42]	S. Li, Nonlinear chirped optical solitons of the perturbation Fokas-Lenells equation in optical fibers, Optik, 276 (2023), 170627. http://dx.doi.org/10.1016/j.ijleo.2023.170627 doi: 10.1016/j.ijleo.2023.170627
[43]	Y. Zhao, L. Guo, Optical wave solutions of the nonlinear Schrödinger equation with an anti-cubic nonlinear in presence of Hamiltonian perturbation terms, Optik, 274 (2023), 170593. http://dx.doi.org/10.1016/j.ijleo.2023.170593 doi: 10.1016/j.ijleo.2023.170593
[44]	Y. Li, Y. Kai, Chaotic behavior of the Zakharov-Kuznetsov equation with dual-power law and triple-power law nonlinearity, AppliedMath, 3 (2023), 1–9. http://dx.doi.org/10.3390/appliedmath3010001 doi: 10.3390/appliedmath3010001
[45]	Y. Kai, S. Chen, K. Zhang, Z. Yin, Exact solutions and dynamic properties of a nonlinear fourth-order time-fractional partial differential equation, Waves Random Complex, in press. http://dx.doi.org/10.1080/17455030.2022.2044541

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)