Tensor Conjugate-Gradient methods for tensor linear discrete ill-posed problems

1.   Introduction

In this paper, we consider the solution of large minimization problems of the form

where the Frobenius norm of singular tube of $\mathcal{A}$ rapidly attenuates to zero with the increase of the index number. In particular, $\mathcal{A}$ has ill-determined tubal rank. Many of its singular tubes are nonvanishing with tiny Frobenius norm of different orders of magnitude. Problem (1.1) with such a tensor is called tensor linear discrete ill-posed problems. They arise from the restoration of color image and video, see e.g., ^[1,2,3,4,5]. Throughout this paper, the operation $*$ represents tensor t-product introduced in ^[1] and $\lVert \cdot \rVert _F$ denotes the tensor Frobenius norm, represented by

We assume that the observed tensor $\mathcal{B}\in \mathbb{R}^{m\times p\times n}$ is polluted by an error tensor $\mathcal{E}\in \mathbb{R}^{m\times p\times n}$, i.e.,

where $\mathcal{B}^*\in \mathbb{R}^{m\times p\times n}$ is an unknown and unavailable error-free tensor related to $\mathcal{B}$. $\mathcal{B}^*$ is determined by $\mathcal{A}*\mathcal{X}^* = \mathcal{B}^*$, where $\mathcal{X}^*$ represents the explicit solution of problem (1.1) that is to be found. We assume that the upper bound of the Frobenius norm of $\mathcal{E}$ is known, i.e.,

Straightforward solution of (1.1) generally is not meaningful due to propagation and severe amplification of the error $\mathcal{E}$ into the solution of (1.1) and the ill-posedness of $\mathcal{A} = [a]_{i, j, k = 1}^{l, m, n}$. In this paper we use Tikhonov regularization to reduce this effect and this regularization replaces (1.1) with penalty least-squares problems of the form

where $\mu > 0$ is a regularization parameter. We assume that

where $\mathcal{N}(\mathcal{A})$ denotes the null space of the tensor $\mathcal{A}$ under $*$, is the set of all solutions $\mathcal{X}$ of the equation $\mathcal{A}*\mathcal{X} = \mathcal{O}$. $\mathcal{I}$ is the identity tensor and $\mathcal{O}\in \mathbb{R}^{m\times p\times n}$ is a tensor whose elements are all zero, respectively.

The normal equation of the minimization problem (1.5) is

then

is the unique solution of the Tikhonov minimization problem (1.5) under the assumption (1.6).

There are many methods for solving large-scale tensor linear discrete ill-posed problems (1.1). Recently, a tensor Golub–Kahan bidiagonalization method ^[4] and a GMRES method ^[5] were introduced for solving large-scale linear ill-posed problems (1.1) by iteratively solving (1.5). The randomized tensor singular value decomposition (rt-SVD) method in ^[6] was presented for computing super large data sets, and has prospects in image data compression and analysis. Ugwu and Reichel ^[7] proposed a new random tensor singular value decomposition (R-tSVD), which improves the truncated tensor singular value decomposition (T-tSVD) in ^[1]. Kilmer et al. ^[2] presented a tensor Conjugate-Gradient method (tCG) for tensor linear systems $\mathcal{A}*\mathcal{X} = \mathcal{B}$ corresponding to the least-squares problems (1.1), where the regularization parameter in the tCG method is user-specified.

This paper mainly extends CG methods from matrix problems to tensor problems. Using matrix methods to solve the problem of image restoration and denoising is to flatten the three-dimensional data of color images into matrix form in turn for processing. Based on t-product, we extend the matrix method to tensor, which can preserve the data correlation between three-dimensional tensor sections. The tensor problem is projected into the Fourier domain, which makes use of the particularity of t-product structure. We further discuss the tCG method for the approximate solution of (1.1) in the Fourier domain. The discrepancy principle is used to determine a suitable regularization parameter of the tCG method. The proposed automatic determination strategy is called the tCG method with automatic determination of regularization parameters (A-tCG-FFT). A least-squares method based on the tCG method is provided for (1.1), which is called A-tCGLS-FFT. A preconditioned version of the A-tCG-FFT method is presented, which is abbreviated as A-tPCG-FFT. The Conjugate Gradient method only needs to save the current and last gradient values, which takes up less memory resources. Moreover, only the previously calculated gradient information is needed in each iteration process, so parallel calculation can be carried out and the calculation efficiency can be improved. Moreover, the way of projecting tensor problem into Fourier domain also greatly avoids the time and space complexity required to smooth tensor problem into matrix problem.

The rest of this paper is organized as follows. Section 2 introduces some symbols and preliminary knowledge that will be used in the context. Section 3 presents the A-tCG-FFT, A-tCGLS-FFT and A-tPCG-FFT methods for solving the minimization problem (1.5). Section 4 gives several examples on image and video restoration and Section 5 draws some conclusions.

2.   Preliminaries

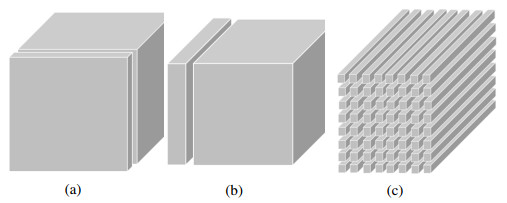
This section gives some notations and definitions, and briefly summarizes some results that will be used later. For a third-order tensor $\mathcal{A}\in \mathbb{R}^{l\times m\times n}$, Figure 1 shows the frontal slices $\mathcal{A}(:, :, k)$, lateral slices $\mathcal{A}(:, j, :)$ and tube fibers $\mathcal{A}(i, j, :)$, and we abbreviate $A_k = \mathcal{A}(:, :, k)$ for simplicity. An $ln\times m$ matrix is obtained by the operator ${\textbf{unfold}}(\mathcal{A})$, whereas the operator ${\textbf{fold}}$ folds this matrix back to the tensor $\mathcal{A}$, i.e.,

Definition 1. Let $\mathcal{A}\in \mathbb{R}^{l\times m\times n}$, then a block-circulant matrix of $\mathcal{A}$ is denoted by ${\bf{bcirc}}(\mathcal{A})$, i.e.,

Definition 2. ^[1] Given two tensors $\mathcal{A}\in \mathbb{R}^{l\times m\times n}$ and $\mathcal{B}\in \mathbb{R}^{m\times p\times n}$, the t-product $\mathcal{A}*\mathcal{B}$ is defined as

where $\mathcal{C}\in \mathbb{R}^{l\times p\times n}$.

The following remarks will be used in Section 3.

Remark 2.1. ^[8] For suitable tensors $\mathcal{A}$ and $\mathcal{B}$, it holds that

(1) ${\bf{bcirc}}(\mathcal{A}*\mathcal{B}) = {\bf{bcirc}}(\mathcal{A})*{\bf{bcirc}}(\mathcal{B})$.

(2) ${\bf{bcirc}}(\mathcal{A}^T) = {\bf{bcirc}}(\mathcal{A})^T$.

(3) ${\bf{bcirc}}(\mathcal{A}+\mathcal{B}) = {\bf{bcirc}}(\mathcal{A})+{\bf{bcirc}}(\mathcal{B})$.

Let $F_n$ be an n-by-n unitary discrete Fourier transform matrix, i.e.,

where $\omega = e^{\frac{-2\pi i}{n}}$, then we get the tensor $\hat{\mathcal{A}}$ generated by using FFT along each tube of $\mathcal{A}$, i.e.,

where $\otimes$ is the Kronecker product, $F_{n}^{H}$ is the conjugate transposition of $F_n$ and $\hat{A}_i$ denotes the frontal slices of $\hat{\mathcal{A}}$.

We also need the following remark.

Remark 2.2. ^[9] For appropriately sized tensors $\mathcal{A}$ and $\mathcal{B}$,

(1) ${\bf{bdiag}}(\widehat{\mathcal{A}*\mathcal{B}}) = {\bf{bdiag}}(\hat{\mathcal{A}}){\bf{bdiag}}(\hat{\mathcal{B}})$.

(2) ${\bf{bdiag}}(\widehat{\mathcal{A}+\mathcal{B}}) = {\bf{bdiag}}(\hat{\mathcal{A}}+\hat{\mathcal{B}})$.

(3) ${\bf{bdiag}}(\hat{\mathcal{A}^H}) = {\bf{bdiag}}(\hat{\mathcal{A}})^H$. Additionally, if ${\bf{bdiag}} (\mathcal{A})$ is symmetric, ${\bf{bdiag}}(\hat{\mathcal{A}})$ is also symmetric.

(4) ${\bf{bdiag}}(\hat{\mathcal{A}^{-1}}) = {\bf{bdiag}}(\hat{\mathcal{A}})^{-1}$.

Then the t-product of $\mathcal{A}$ and $\mathcal{B}$ in (2.1) can be expressed by

and (2.1) is reformulated as

It is easy to implement (2.1) in MATLAB. Using MATLAB notation, let $\hat{\mathcal{M}}$ = fft$(\mathcal{M}, [\ ], 3)$ be the tensor obtained by applying the FFT along the third dimension. Then (2.1) can be computed by taking the FFT along tube of $\mathcal{A}$ and $\mathcal{B}$ to obtain $\hat{\mathcal{A}}$ = fft$(\mathcal{A}, [\ ], 3)$ and $\hat{\mathcal{B}}$ = fft$(\mathcal{B}, [\ ], 3)$. Then for the matrix-matrix product of each pair of front slices of $\hat{\mathcal{A}}$ and $\hat{\mathcal{B}}$, there is

and then taking the inverse FFT along the third dimension to obtain $\mathcal{C}$ = ifft$(\hat{\mathcal{C}}, [\ ], 3)$. We refer to Table 1 for more notations.

3.   Tensor Conjugate-Gradient methods

3.1.   The A-tCG-FFT method

Based on the tensor conjugate gradient (tCG) method proposed by Kilmer et al. ^[10], this section presents a method to solve the regularization (1.5) by using the CG process in Fourier domain, where an suitable regularization parameter is automatically determined by the discrepancy principle. This method is abbreviated as A-tCG-FFT. The A-tCG-FFT improves the tCG method presented in ^[2] where the regularization parameter was user-specified. The following result shows the equivalent equation of (1.5) in the Fourier domain.

Theorem 3.1. Let $\hat{\mathcal{A}}$ = fft$(\mathcal{A}, [\ ], 3)$, $\hat{\mathcal{B}}$ = fft$(\mathcal{B}, [\ ], 3)$ and $\hat{\mathcal{X}}$ = fft$(\mathcal{X}, [\ ], 3)$. Then, solving the tensor regularization (1.5) is equivalent to solving a sequence of regularized least-squares problems of the matrix form

where $\lVert \cdot \rVert$ represents the 2-norm of the matrix, and $\hat{X}_k = \hat{\mathcal{X} }(:, :, k)$, $\hat{A}_k = \hat{\mathcal{A} }(:, :, k)$ and $\hat{B}_k = \hat{\mathcal{B} }(:, :, k)$.

The normal equation of (3.1) can be represented as

Once getting $\hat{\mathcal{X}}$, we have the approximation solution of (1.1) with the form $\mathcal{X}$ = iff$(\hat{\mathcal{X}}, [\ ], 3)$.

Proof. Following Remarks 2.1 and 2.2, (1.8) is represented as

Thus, by using (2.4) we have

which implies (3.2).

Now we discuss the determination of a suitable regularization parameter for (3.1). Let $\hat{\mathcal{B}}^{*}$ = fft$(\mathcal{B}^*, [\; ], 3)$ and $\hat{\mathcal{B}}$ = fft$(\mathcal{B}, [\; ], 3)$, and denote $\hat{B}_k^* = \hat{B}^*(:, :, k)$ and $\hat{B}_{k} = \hat{\mathcal{B}}(:, :, k)$. The assumption in (1.4) implies that

where $\hat{E}_k = \hat{B}_k-\hat{B}_k^*$. The availability of the bound (3.3) allows us to determine $\mu$ by the discrepancy principle. Especially, the solution $\hat{X}_k$ of (3.1) satisfies

where $\eta > 1$ is usually a user-specified constant and is independent of $\delta_k$. For more details on the discrepancy principle, see e.g., ^[11].

In ^[12,13], the method of selecting regularization parameter through an a-priori strategy and a-posteriori parameter choice rule is mentioned to verify the convergence estimation between exact solution and regularization solution. Here, we choose regularization parameter to be obtained by automatically updating the polynomial function

where $0 < \rho < 1$ and $\mu_0 = \lVert \hat{\mathcal{A}}\rVert$. Then, we obtain a suitable regularization parameter by iteratively applying (3.5) until (3.4) is satisfied.

Algorithm 1 summarizes the A-tCG-FFT method for solving (1.5). Algorithm 1 contains two nested iterations. The outer iteration updates $\mu$ by applying (3.5) so that the discrepancy principle is satisfied. The inner iteration is to use the CG method (CG-iteration) to solve the $k$-th normal equation (3.2) with the value of $\mu_j$ determined by the outer iteration, and $\left\langle M, N\right \rangle$ represents the inner product between matrices $M$ and $N$. The inner iteration is stopped when the norm of the residual

of the $i$-th iterate $X_{k, \mu_{j}, i}$ is less than a tolerance $tol$.

In the following Corollay 3.1, the rationality of the two methods for initial $X_0$ is expounded.

Corollary 3.1. Let $X_0 = 0$ be the initial solution of the inner iteration of Algorithm 1, then we have the initial residual

Otherwise, if $X_0 = X_{k, \mu _{j-1}}$, then we have

Proof. Denote

It is easy to see that

for $X_0 = 0$. Let $X_0 = X_{k, \mu _{j-1}}$, then we have

Theorem 3.2. If $\hat{X}_k^*$ is the exact solution of the symmetric positive definite equations (1.7), $X_{k, \mu _{j}, i}$ and $X_{k, \mu _{j}, i+1}$ are generated by the inner CG-iteration of Algorithm 1, then

where ${\boldsymbol{A}} = \hat{A}_k^H\hat{A}_k+\mu _jI$, $\kappa({\boldsymbol{A}}) = \frac{\lambda _{max}({\boldsymbol{A}})}{\lambda_{min}({\boldsymbol{A}}) }$. Here $\lambda_{max}({\boldsymbol{A}})$ and $\lambda_{min}({\boldsymbol{A}})$ are the maximum and minimum eigenvalues of ${\boldsymbol{A}}$ respectively.

Theorem 3.2 illustrates the convergence of Algorithm 1. Refer to ^[14] for the detailed proof process.

3.2.   The A-tCGLS-FFT method

In the actual numerical calculation, if $\hat{A}_k^H\hat{A}_k$ is singular and $\mu$ is very small, then $\hat{A}_k^H\hat{A}_k+\mu _{j}I$ is ill-conditioned. Inspired by the idea in ^[15] for the numerical stability of a linear system in matrix form, in this section, we use the CGLS method instead of the CG method in Algorithm 1.

The main difference between Algorithms 2 and 1 is the updating of $z_i = \hat{B}_k-\hat{A}_kX_{k, \mu _{j}, i}$ in Algorithm 2 rather than the residuals (3.6) of Algorithm 1. We refer to ^[16] for more details for a corresponding linear system in matrix form.

3.3.   A preconditioned tensor Conjugate-Gradient method

In this subsection, we consider the acceleration of Algorithm 1 by preconditioning. In Algorithm 1, the coefficient matrix $\hat{A}_k^H\hat{A}_k+\mu I$ of the $k$-th normal equation (3.2) is symmetric and positive definite. We set $M = \hat{A}_k^H\hat{A}_k+\mu I$ and apply approximate Cholesky decomposition to $M$. The process of approximate Cholesky decomposition can be directly realized by Matlab function $chol$, then $M_{chol} = chol(M)$ can be obtained. Let $M_L = M_{chol}^{H}$ and $M_R = M_{chol}$, then there is $M = M_LM_R$, where $M_L$ is a lower triangular nonsingular sparse matrix and $M_R = M_L^H$. Then we solve the preconditioned normal equations

instead of (3.2) in Algorithm 1, where $\tilde{A} = M_{L}^{-1} \left(\hat{A}_k^H\hat{A}_k+\mu I \right)M_{R}^{-1}$, $\tilde{X} = M_R\hat{X}_k$ and $\tilde{B} = M_{L}^{-1}\hat{A}_k^H\hat{B}_k$.

Let $\hat{X}_{k, i}$ and $\tilde{X}_{k, i}$ represent the $i$-th iterate of (3.8) and (3.2) in the inner CG- iteration of Algorithm 1 under a certain regularization parameter $\mu$, respectively. Then we have

Denote $\tilde{P}_{k, i} = M_R\hat{P}_{k, i}$ and $\hat{t}_{k, i} = M_{L}^{-1}\hat{R}_{k, i}$, then we have

According to the definition of matrix inner product $\left \langle A, B \right \rangle = tr(A^TB)$, where $tr$ denotes the trace of a square matrix. Then, we have

According to (3.10) and (3.11), we get

and

Then, we have

and

Finally, we have

Based on (3.10)–(3.16), we have the preconditioned process of Algorithm 1. Algorithm 3 lists the A-tPCG-FFT method.

The following result gives the convergence of Algorithm 3.

Theorem 3.3. If $\hat{X}_k^*$ is the true solution of the symmetric positive definite equation (1.7), $X_{k, \mu _{j}, 0}$ is the initial solution in the internal CG iteration of Algorithm 3, and $X_{k, \mu _{j}, i}$ is the $i$-th iterate, then

where ${\boldsymbol{A}} = \hat{A}_k^H\hat{A}_k+\mu _jI$ and $\kappa(M)$ is the same as that in Theorem 3.2.

Proof. Let ${\textbf{A}} = \hat{A}_k^H\hat{A}_k+\mu _jI$, Taking ${\textbf{A}}$ as $M_{L}^{-1}{\textbf{A}}M_{R}^{-1}$ in the similar result of Algorithm 1 in ^[17] results in (3.17).

We can expect from Theorem 3.3 that Algorithm 3 generally achieves better convergence than Algorithm 1 since

We will illustrate this in numerical experiments in Section 4.

4.   Numerical examples

This section presents three examples to show the application of Algorithms 1–3 on the restoration of image and video. All calculations were performed in MATLAB R2018a on computers with intel core i7 and 16GB RAM.

Let $\mathcal{X}_{iter}$ denote the iterative solution to (1.5). The quality of the approximate solution $\mathcal{X}_{iter}$ is defined by the relative error

and the signal-to-noise ratio (SNR)

where $\mathcal{X}_{true}$ denotes the uncontaminated data tensor and $E(\mathcal{X}_{true})$ is the average gray-level of $\mathcal{X}_{true}$.

In (1.5), we generate a noise tensor $\mathcal{E}$ and simulate the error in the data tensor $\mathcal{B} = \mathcal{B}_{true}+\mathcal{E}$. $\mathcal{E}$ is a noise tensor with a random term of normal distribution, the mean value is zero, and the variance selection corresponds to a specific noise level $\nu = \frac{\lVert \mathcal{E} \rVert _F}{\lVert \mathcal{B}_{true} \rVert _F}$.

We summarize the cross-channel blurring and within-channel blurring in the original blurring process in ^[3] that will be used in the following examples. The complete blurring model is presented in the form of

where

and $A_{blur}$ is a $3\times 3$ matrix with the sum of each row equal to 1, which denotes cross-channel blurring as in ^[18].

and ${\textbf{vec}}(\cdot)$ is an operator that transforms a matrix into a vector by stacking columns of the matrix from left to right. $A^{(1)}\in \mathbb{R}^{n\times n}$ and $A^{(2)}\in \mathbb{R}^{n\times n}$ define within-channel blurring, which are the horizontal inner blurring matrix and the vertical inner blurring matrix, respectively, see ^[18] for more details. A special case to consider is $a_{rr} = a_{gg} = a_{bb} = \mu$, $a_{gr} = a_{rg} = a_{gb} = a_{bg} = \beta$ and $a_{br} = a_{rb} = \gamma$. If the formula (4.1) is calculated directly in MATLAB, the results are stored in the matrix and cannot be calculated effectively. Therefore, t-product structure is considered, and (4.1) is presented in the following tensor form

where $\mathcal{A}_{\upsilon}\in \mathbb{R}^{n\times n\times 3}$ and $\mathcal{A}_{\omega }\in \mathbb{R}^{n\times n\times 3}$. Each blurring matrix $A^{(i)}$ is defined as follows:

where $\sigma$ is a parameter that controls the amount of smoothing. Therefore, if $\sigma$ is larger, the problem becomes more ill posed.

Example 4.1. $({\bf{Color\ image)}}$ This example shows the restoration of a blurred penguin color image by Algorithms 1 – 3. This example compares the effects of A-tCG-FFT, A-tCGLS-FFT and A-tPCG-FFT in color image deblurring, and the image is contaminated by cross-channel blur and additive noise. The cross-channel bluring is determined by the matrix

For the within-channel blurring, we set $\sigma = 4$ and $r = 7$. Let $\mathcal{A}_{\upsilon\left(:, :, 1 \right)} = \mu A^{\left(2 \right)}, \mathcal{A}_{\upsilon\left(:, :, 2 \right)} = \beta A^{\left(2 \right)}$, $\mathcal{A}_{\upsilon\left(:, :, 3 \right)} = \gamma A^{\left(2 \right)}$, and $\mathcal{A}_{\omega} = \mathcal{I}$. The condition number of the obtained front slice of $\mathcal{A}$ is $cond(\mathcal{A}(:, :, k)) = 8.7257e+04(k = 1, 2, 3)$. Let the two noise levels be $\nu = 10^{-2}$ and $\nu = 10^{-3}$, respectively. Formula (4.2) can be used to generate the blurred images, and $\mathcal{B} = \mathcal{B}_{true}+\mathcal{E}$ adds noise to the blurred image. Figure 2 shows the original image and the blurred and noisy image with $\nu = 10^{-3}$.

The essence of Algorithms 1–3 is to solve three inner and outer loops in the Fourier domain in turn. Each outer iteration uses the discrepancy principle to select the appropriate regularization parameter $\mu$. We specify $\eta = 1.05$ and $\rho = \frac{1}{2}$. We set the initial solution of inner iteration as $X_0 = X_{k, \mu _{j-1}}$, and the convergence criterion of the inner iteration is given by the residual norm being less than $tol = 10^{-6}$.

Table 2 lists CPU time, SNR and relative error of three algorithms for the restoration of penguin image. We can see from Table 2 that the A-tPCG-FFT algorithm needs the least CPU time among all the methods, while the A-tCG-FFT algorithm is the most time consuming. There is little difference between SNR and relative errors for all the methods.

Figure 3 shows the change of relative error with CPU time for the algorithms to process the third slice of penguin image with $\nu = 10^{-3}$ in Table 2. Figure 3 shows the iterative solution of the inner iteration and outer iteration of the three algorithms. It can be seen that when the regularization parameters are selected, the relative error norm values of the iterative solutions obtained by the inner iteration process of the three algorithms are gradually decreasing. Similarly, after the three algorithms automatically update the regularization parameters in the outer iteration, the iterative solutions corresponding to the updated regularization parameters are all smaller than the relative error norm of the iterative solutions before updating. We can still get from Figure 3 that the A-tPCG-FFT algorithm converges the fastest among all methods.

Figure 4 displays the recovered penguin image for Algorithms 1–3 corresponding to the results with $\nu = 10^{-3}$ in Table 2.

From Example 4.1 we can see that the A-tPCG-FFT method displays the best convergence among three methods.

Example 4.2 (Color video) We recover 10 consecutive frames (frames 41 to 50) of blurred and noised vipbarcode color video from MATLAB. Each frame has $240\times 240$ pixels. We store 10 original video frames in the tensor $\mathcal{X}_{true}\in \mathbb{R}^{240\times 30\times 240}$, obtained by stacking the grayscale images that constitute the three channels of each blurred color frame.

These frames are blurred by (4.2), where $\mathcal{A}_{\upsilon}$ is a 3-way tensors such that $\mathcal{A}_{\upsilon\left(:, :, 1 \right)} = A^{\left(1 \right)}$, $\mathcal{A}_{\upsilon\left(:, :, i \right)} = \mathcal{O}$ for $i = 2, \dots30$, and $\mathcal{A}_{\omega} = \mathcal{I}$. Using $\sigma = 3$ and $r = 5$ to build the blurring matrices with periodic boundary conditions. The condition number of the obtained first slice of $\mathcal{A}$ is $1.6191e+03$, and the condition number of the remaining frontal sections of $\mathcal{A}$ is infinite. Use $\mathcal{B} = \mathcal{B}_{true}+\mathcal{E}$ adds noise to the blurred image, and the considered noise levels are $\nu = 10^{-2}$ and $\nu = 10^{-3}$. We set the initial solutions of their iterations as $X_0 = X_{k, \mu _{j-1}}$, and under the convergence condition that the residual norm is less than $tol = 10^{-6}$. Using the discrepancy principle to determine regularization parameters, specify $\eta = 1.1, \alpha _0 = \frac{1}{2}$ and $\rho = \frac{1}{2}$. Table 3 records the concrete results of recovering these 10 frames of video data, including relative error, SNR and CPU time. Because the same criteria for selecting parameters and stopping iteration are set, these three algorithms differ slightly in relative error and SNR. However, the A-tPCG-FFT algorithm has a strong advantage in stopping iteration CPU time.

Below we analyze the video recovery process of the 50th frame. Figure 5 shows the 50th original frame of this video file and the blurred and noisy video frame with $\nu = 10^{-3}$.

Figure 6 shows the variation of the relative errors of the third piece of the 50th video frame with CPU time when the three algorithms process $\nu = 10^{-3}$ in Table 3.

As can be seen from Figure 6, the convergence speed of algorithm A-tPCG-FFT is the fastest among the three algorithms. We can also get from Figure 6 that with the automatic updating of regularization parameters by the outer iteration and the progress of the inner iteration algorithm, the relative error norms of the iterative solutions obtained by the three algorithms are gradually decreasing.

Figure 7 is the result of the restoration of the blurred and noisy image of the 50th frame by A-tCG-FFT, A-tCGLS-FFT, and A-tPCG-FFT.

According to the results of Example 4.2, A-tCGLS-FFT and A-tPCG-FFT require less CPU time compared to A-tCG-FFT when recovering the data of each frame of video, so when processing multi-frame video data, this lead time will be accumulated in each process. That is to say, the more video frames, the more obvious the time advantages of A-tCGLS-FFT and A-tPCG-FFT, especially A-tPCG-FFT.

5.   Conclusions

Based on the matrix conjugate gradient method, this paper presents three types of tensor Conjugate-Gradient methods for solving large-scale linear discrete ill-posed problems in tensor form. Firstly, we project the tensor equation to Fourier domain, and propose a strategy to automatically determine the regularization parameters of the tensor conjugate gradient method in the Fourier domain (A-tCG-FFT). In addition, we developed the A-tCGLS-FFT method and the preconditioned version of A-tCG-FFT. These proposed methods are used in different examples of color image and video restoration. Numerical experiments show that the tensor conjugate gradient methods are effective in solving ill-posed problems with t-product structure the Fourier domain.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

The authors would like to thank the referees for their helpful and constructive comments. TThis research was supported in part by the Sichuan Science and Technology Program (grant 2022ZYD0008).

Conflict of interest

The authors declare no conflict of interest.