Controlling stability through the rate of decay of the delay feedback kernels

1.   Introduction

The problem of concern here is the following Hopfield neural network (HNN) system with two types of delays: discrete and distributed

for $i = 1, 2, \dots, m,$ where $m$ is the number of existing units, $\varkappa _{i}$ are the state of the neuron number $i$ at the instant $t$, $c_{i} > 0$ are the rates of the passive delay, $a_{ij}, b_{ij}, d_{ij}$ denote the connection weight matrices, $I_{i}$ stand for the external inputs assumed constants, $f_{j}$ are the activation functions, $k_{j}$ are the delay feedback kernels, $\tau > 0$ is the discrete delay and $\varphi _{i}$ describe the history of the states.

The activation functions in the discrete and distributed delays are in general different but we are considering them here equal just for simplicity.

The continuous deterministic HNN is a recurrent artificial neural network that is used in many applications to model the dynamics of systems with a large number of inputs and unknown parameters. The first model introduced in ^[8] had the form

Hopfield ^[8] introduced this continuous deterministic model to describe the time evolution of the state of electronic devices with a large number of amplifiers in conjunction with feedback circuits made up of wires, resistors and capacitors. Such circuits have integrative time delays due to capacitance. Since then, HNN has been used to describe various systems that occur in engineering, biology and economy ^{[1,2,3,7,9,10,11,12,15,18,20,21,23]}.

Many complex processes with delays can be modeled as Hopfield neural network (HNN) systems with discrete and/or continuously distributed delays. Time retardation in electronic neural networks occur on account of the finite switching speed of amplifiers and can lead to instabilities in the form of oscillations ^{[4,5,6,13,14,17,19,22,24,25,26,27,28]}.

Guo ^[6] analyzed the global asymptotic stability for (1.1) with piecewise continuous kernels. The global and local stability of the equilibrium states of (1.1) has been investigated under various conditions on the different coefficients, activation functions and delays ^{[4,5,6,13,14,17,19,22,24,25,26,27,28]}. In addition, there is an interest in determining the speed of convergence to the equilibrium states. For this purpose, various exponential stability results have been established, see for example ^[19]. In all these papers, the main condition for exponential asymptotic stability is $\int_{0}^{\infty }e^{\beta s}K(s)ds < \infty$ for some $\beta > 0$ in addition to the standard condition of the dominance of the damping on the other coefficients ^{[13,16,17,19,22,24,28]}.

Yin and Fu ^[25] studied the $\mu$-stability issue for a class of NNs (1.1) subject to impulses with a diagonal $K$ and unbounded time-varying lags. They used a Lyapunov-Krasovskii functional to derive some conditions in the form of linear matrix inequalities. The $\mu$-stability, roughly means that the states converge asymptotically to equilibrium at the rate $1/\mu (t)$ in a certain norm. Cui et al. ^[4] extended (1.1) to a reaction-diffusion cellular NN. The delays there were unbounded and time-varying and the distributed delays were bounded. In both papers, the function $\mu (t)$ must satisfy the conditions

where $\beta _{1}, \beta _{2}$ and $\beta _{3}$ are nonnegative scalars.

Zhang and Jin ^[26] established conditions for existence, uniqueness and global asymptotic stability of the stationary state of HNN with fixed or distributed time delays. The results apply in case the interconnection matrices are symmetric and nonsymmetric. The activation functions are continuous and non-monotonic functions.

The most important issue in this field is the stability of the equilibrium. The first results have been shown for simple HNNs with some specific activation functions like the Sigmoid function $f(u)$ = $\frac{1}{1+e^{-u/T}}$, Hyperbolic tangent function $f(u) = \tanh (u/T)$, Inverse tangent function $f(u) = \frac{2}{\pi }\tan ^{-1}(u/T)$, Threshold function $f(u) = \left\{ \begin{array}{c} -1, \; u < 0, \\ 1, \; u > 0, \end{array} \right.$ Gaussian radial basis function $f(u) = \exp \{-\left\Vert u-m\right\Vert ^{2}/\sigma ^{2}\}$ and the Linear function $f(u) = au+b$. Because of the need in applications, these activation functions have been extended to bounded, monotone and differentiable functions. In turn, these conditions have been weakened to a mere Lipschitz continuity condition. These conditions on the monotonicity, boundedness and differentiability of the activation functions have been improved thereafter to simply a global (or local) Lipschitz continuity condition. There are also a fairly large number of papers dealing with different conditions on the different coefficients involved in the system. Indeed, for the parameters, the LMI method, M-Matrix and other techniques are very efficient. They have been used and improved in an impressive number of references that cannot fit in this limited size paper. Unfortunately, in spite of the many appearing cases in the applications (as mentioned in the book of Kosko), this issue has not received much attention. In this work, we want to fill this gap by establishing reasonable conditions on the kernels ensuring exponential stability and other types of stability.

The existence and uniqueness of the equilibrium has been discussed under different conditions and using different methods, such as fixed point theorems. Therefore, the well-posedness is guaranteed in our case as we are assuming standard conditions for the (dominance conditions of the) parameters and also on the activation functions (Lipschitz continuity), we obtain easily the existence and uniqueness of a solution as our kernels remain of (dissipative) fading memory type.

Here, the focus will be on the kernels $k_{j}\left(t\right)$ in problem (1.1). We extend the class of kernels satisfying

to a much wider class for which we have exponential stability as well as stability with general decay. Our result is proved under rather standard conditions on the other parameters and functions in the system but is ready to be adopted for more general situations. Indeed, in the existing papers, it is either kernels of exponential type or of subexponential type which are considered. In the present work, we do not use these assumptions. Instead, we assume the following condition: let $\eta _{j}\left(t\right)$ be nonnegative continuous functions satisfying

and

This new class of kernels is much wider than the existing one in the market. It contains the proper exponentially decaying functions. Moreover, it contains polynomially decaying functions and many more functions. Therefore, this improves earlier results and allows the treatment of more problems by allowing a larger class of admissible kernels. As consequence, the rates of stability are general and not necessarily exponential.

It is our objective here to derive sufficient conditions for stability with general rate, including as a special case, the exponential stability. Our results are obtained using new suitably selected functionals of Lyapunov-type in this theory and improve the existing results using completely different arguments. In view of the previous results, we shall assume the existence of continuously differentiable solutions.

2.   Preliminaries

In this part of the paper, we shall present our assumptions, definitions and useful lemmas.

We start with the presumptions:

${\bf{(B1)}}$ The delay kernel functions $k_{j}$ are piecewise continuous nonnegative functions such that $\kappa _{j}: = \int_{0}^{\infty }k_{j}(s)\, ds < \infty$.

${\bf{(B2)}}$ The functions $f_{i}$ are Lipschitz continuous on $\mathbb{R}$ with $L_{i}$, $i = 1, 2, \dots, m$ as Lipschitz constants, that is

${\bf{(B3)}}$ The initial data $\varphi _{i}(t)$, $t\leq 0$ are continuous functions.

Definition 1. The point $\varkappa ^{\ast } = (\varkappa _{1}^{\ast }, \dots, \varkappa _{m}^{\ast })^{T}$ is called an equilibrium point of problem (1.1) if for $i$ = $1, 2, \dots, m,$

Definition 2. The equilibrium point $\varkappa ^{\ast }$ is said to be globally $\mu$-stable if there exists a constant $A > 0$ and a positive function $\mu (t)$ such that $\lim_{t\rightarrow \infty }\mu (t) = \infty$ and

where $\Vert \cdot \Vert$ denotes any norm in $\mathbb{R} ^{m}.$

The existence of a unique equilibrium for this kind of problems has been shown for instance in ^[26,27] when the functions $f_{j}$ are Lipschitz continuous. It has been proved also for 'Non-Lipschitz' continuous functions (see ^[5]).

These results apply for our case here. In fact, one can consult any result in Hopfield neural network theory even without (discrete and distributed) delays, as delays do not affect the proofs. As a matter of fact, they do not appear in the system satisfied by the equilibrium. However, there will be conditions on their coefficients.

3.   General stability

This part is devoted to the study the stability of the equilibrium state $\varkappa ^{\ast }$ for (1.1). If we let

then it is clear that the stability of $\varkappa ^{\ast }$ is equivalent to the stability of the zero state for the problem

where

${\bf{(B4)}}$ The initial data $\varphi _{i}(t)$ are such that $\psi _{i}\in L^{2}(-\infty, 0),$ $i = 1, 2, \dots, m.$

To investigate the stability of the system (1.1), we employ the 'energy' functional

The first lemma is a straightforward consequence of (B2) and (3.2).

Lemma 1. Let assumption (B2) hold. Then

and

Lemma 2. Let presumptions (B1)–(B3) hold. Then for $t\geq 0$

where

Proof. The differentiation of $E(t)$ in (3.3), along solutions of (3.1), yields for $t\geq 0$

By Lemma 2 we can write for $t\geq 0$

From Cauchy-Schwartz inequality we have the bound

Consequently, for $t\geq 0$

□

Theorem 1. Let assumptions (B1)–(B4) hold. If

then $E(t)$ is uniformly bounded.

Proof. Consider the functionals

and

Note that

and

Moreover,

and

Let

Then, $\mathcal{E}(0) < \infty$ and

or for $t\geq 0$,

This may be rewritten simply as

From the condition stated in the theorem and (3.10) we see that $\mathcal{E}^{\prime }(t)\leq 0$, $t\geq 0$. Therefore,

The proof is complete. □

We now specify our main condition on the kernels

${\bf{(B5)}}$ There are nonnegative continuous functions $\eta _{j}(t)$ such that

and

Theorem 2. Let assumptions (B1)–(B5) hold and

for some $\varepsilon > 0.$ Then, if $\lim_{t\rightarrow \infty }\eta (t) = \bar{\eta} = 0$ we have

and

in case $0 < \bar{\eta}\leq \infty,$ for some positive constants $C_{i},$ $i = 1, 2, 3, 4.$

Remark 1. If $\eta (t) = \frac{\mu ^{\prime }(t)}{\mu (t)}$ for some differentiable function $\mu (t),$ then we obtain

for some positive constants $A$ and $\sigma.$

Proof Theorem 2. For $0 < \delta < 1/2$, consider the functional

where

$\lambda _{1j}$ as in (3.4), and $V_{2}$ as in (3.6). Here $\beta$ is selected so small that $e^{\beta \tau }\leq 1+\varepsilon$ ($\varepsilon$ is in the statement of the theorem).

By direct differentiation we have

Next, we estimate $V_{2}^{\prime }(t)$ in light of our new assumption (B5) on the kernels. Clearly, for $t\geq 0$,

Taking into account (3.11)–(3.13), the differentiation along solutions of (3.1) yields for $t\geq 0$

or

In view of (3.4), we find for $t\geq 0$

or

where

From the hypotheses we have $\alpha > 0$.

We discuss two cases:

Case 1. $\lim_{t\rightarrow \infty }\eta (t) = 0$

Let $t^{\ast } > 0$ be large enough so that

Therefore

This implies that

By continuity and Theorem 1, we may derive a similar estimate on $[0, t^{\ast }]$.

Case 2. $0 < \bar{\eta}\leq \infty$

In this case

In case $\bar{\eta} = +\infty$, we consider any positive constant $\xi$, $\eta (t)\geq \xi$.

In view of (3.14) and (3.16), we see that

where

Therefore,

A continuity argument and Theorem 1 gives a similar estimates on $[0, t_{\ast }].$ The proof is complete. □

4.   Numerical illustration

In this section, we shall present numerical examples validating the efficiency of the above theoretical results.

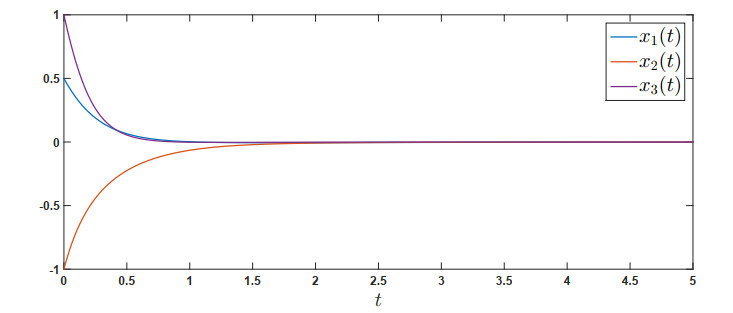
Example 1. Consider the following Hopfield neural network system, composed of three neurons

where the associated functions and parameters are selected as follows:

Through some simple calculations, we get $L_{1} = L_{2} = L_{3} = \frac{1}{4}, \; \kappa _{i} = \frac{1}{4e}$, and we choose $\eta _{i}(t)$ = $\frac{1}{4(1+\sqrt{ 1+t})}, \; i = 1, 2, 3.$

Hence, the assumptions (B1)–(B5) are met. By virtue of Theorem 2, then the solutions of the system (4.1) decay to the stationary states. These can be depicted in Figure 1.

Example 2. Consider the system (4.1) in which the related functions and parameters are chosen as

Via a simple calculation, we obtain $L_{1} = L_{2} = L_{3} = \frac{1}{16}, \; \kappa _{i} = 1, \; \eta _{i}(t) = \frac{1}{2(1+t)}, \; i = 1, 2, 3.$

Therefore, as the hypotheses (B1)–(B5) of Theorem 2 are fulfilled, the solutions of the system (4.1) decay to steady points. We can see these in Figure 2.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Conflict of interest

The authors declare no conflict of interest.