A new generalization of edge-irregular evaluations

1.   Introduction

Let $G = (V, E)$ be a simple graph with vertex set $V$ and edge set $E$. A labeling of a graph is a map that carries graph elements to the positive or non-negative integers. If the domain is the vertex set alone or the set of all vertices and edges, the labelings are respectively called vertex labelings or total labelings. Thus, for a vertex $k$-labeling $\omega: V(G) \to \{ 1, 2, \dots, k \}$, the associated weight of an edge $e = xy \in E(G)$ is $w_{\omega}(xy) = \omega(x) + \omega(y)$. A vertex labeling $\omega$ is called edge-irregular if all of the edges have distinct weights. The maximal integer $k$ minimized over all edge-irregular $k$-labelings is known as the edge-irregularity strength of $G$, ${\rm{es}}(G)$.

The notion of the edge-irregularity strength was introduced by Ahmad et al. in ^[1], and there is an estimated lower bound of this graph invariant for all simple graphs with maximum degree $\Delta(G)$ in the following form:

For certain families of graphs, specifically paths, stars, double stars and the Cartesian product of two paths ^[1], as well as for complete $m$-ary trees ^[2], Toeplitz graphs ^[4], plane graphs ^[22] and complete $m$-partite graphs ^[23], the exact value of the edge-irregularity strength has been determined.

Koam et al., in ^[16], introduced a modular edge-irregular labeling as a modification of the modular irregular labeling defined in ^[8].

For a graph $G = (V, E)$ of size $m$, a function $\omega: V(G) \to \{1, 2, \dots, k\}$ is said to be a modular edge-irregular $k$-labeling if the edge-weight function $\mu: E(G) \to \mathbb Z_{m}$ defined by $\mu(xy) = w_{\omega}(xy) = \omega(x) + \omega(y)$ is bijective and called the modular edge-weight of the edge $xy$, where $\mathbb Z_{m}$ is the group of integers modulo $m$. The modular edge-irregularity strength, denoted as ${\rm{mes}}(G)$, is defined as the minimum $k$ for which $G$ has a modular edge-irregular labeling by using a number of labels of at most $k$. If there is no such labeling for the graph $G$, then the value of ${\rm{mes}}(G)$ is defined as $\infty$.

Let us note that Muthugurupackiam and Ramya in ^[18,19] defined the even (odd) modular edge-irregular labelings, where the set of modular edge-weights contains only even (odd) integers.

Definitely, every modular edge-irregular $k$-labeling of a graph is also its edge-irregular $k$-labeling. This shows a relationship between the edge-irregularity strength and the modular edge-irregularity strength. Thus, for any simple graph $G$, the following holds:

The relationship given by (1.2) gives a lower bound of the parameter ${\rm{mes}}(G)$. The existence of modular edge-irregular labelings for several families of graphs is investigated in ^[16], particularly for paths, stars, cycles, caterpillars, $n$-suns and friendship graphs, and the precise value of the modular edge-irregularity strength that proves the sharpness of the lower bound presented in (1.2) is determined.

For a graph $G$, the authors of ^[7] define a labeling $\rho: V(G) \cup E(G) \to \{1, 2, \dots, k\}$ as an edge-irregular total $k$-labeling if, for every two different edges $xy$ and $x'y'$ of $G$ there is $wt_{\rho}(xy) \neq wt_{\rho}(x'y')$, where the total edge-weight of an edge $xy$ is defined as $wt_{\rho}(xy) = \rho(x) +\rho(xy) +\rho(y)$. The total edge-irregularity strength of a graph $G$, denoted as ${\rm{tes}}(G)$, is defined as the minimum $k$ for which $G$ has an edge-irregular total $k$-labeling.

One can see that, if $\omega: V(G) \to \{1, 2, \dots, k\}$ is an edge-irregular $k$-labeling of a simple graph $G$ with ${\rm{es}}(G) = k$ and we extend this labeling to the total labeling $\rho$ of $G$ such that

then the resulting labeling $\rho$ is an edge-irregular total labeling of $G$. Thus, for any simple graph $G$,

A lower bound on the total edge-irregularity strength of a simple graph with maximum degree $\Delta(G)$ is given in ^[7] as follows:

Ivančo and Jendrol' ^[13] posed the conjecture that, for an arbitrary graph different from $K_5$, the total edge-irregularity strength is exactly the lower bound presented by (1.4).

The conjecture of Ivančo and Jendrol' has been verified for trees ^[13], for complete graphs and complete bipartite graphs ^[14], for the Cartesian product of two paths $P_n \square P_m$ ^[15], for the corona product of a path with certain graphs ^[20] and for large dense graphs with $\tfrac{|E(G)|+2}3 \le \tfrac{\Delta(G)+1}2$ in ^[10]. Some other results on the total edge-irregularity strength can be found in ^[3,5,6,9].

An interesting modification of the irregularity strength of graphs is a strength of graphs. We refer the reader to ^[12] which deals with this graph invariant and presents a lower bound for the strength of a graph in terms of its independence number.

A total labeling $\rho: V(G) \cup E(G) \to \{1, 2, \dots, k\}$ is called a modular edge-irregular total $k$-labeling of the graph $G$ of size $m$ if the edge-weight function $\lambda: E(G) \to \mathbb Z_{m}$ defined by $\lambda(xy) = wt_{\rho}(xy) = \rho(x) + \rho(xy) + \rho(y)$ is bijective and called the modular total edge-weight of the edge $xy$. The {modular total edge-irregularity strength} of a graph $G$, denoted as ${\rm{mtes}}(G)$, is known as the maximal integer $k$, minimized over all modular edge-irregular total $k$-labelings, and it is rated to $\infty$ if no such function is possible.

In this paper, we are dealing with a boundary estimation of the modular total edge-irregularity strength. For certain families of graphs, we investigate the existence of modular edge-irregular total $k$-labelings and determine the precise values of the modular total edge-irregularity strength in order to prove the tightness of the presented lower bound.

2.   Main results

Since every modular edge-irregular total $k$-labeling of a graph $G$ is also its edge-irregular total $k$-labeling then we have

Extending a modular edge-irregular $k$-labeling to the modular edge-irregular total $k$-labeling (similar to the above construction for extending an edge-irregular $k$-labeling to the edge-irregular total $k$-labeling) gives the following relationship:

In general, the converse of (2.1) does not hold. The next theorem gives a condition when an edge-irregular total $k$-labeling of a graph is also its modular edge-irregular total $k$-labeling.

Theorem 2.1. Let $G$ be a graph with ${\rm{tes}}(G) = k$. If the total edge-weights under a corresponding edge-irregular total $k$-labeling constitute a set of consecutive integers, then

The exact values of the total edge-irregularity strength for cycles and stars are determined as follows.

Theorem 2.2. ^[7] Let $C_n$ be a cycle on $n\ge 3$ vertices. Then, ${\rm{tes}}(C_n) = \left\lceil \tfrac{n+2}{3}\right\rceil$.

Theorem 2.3. ^[7] Let $K_{1, n}$ be a star on $n+1$ vertices, $n\ge 2$. Then, ${\rm{tes}}(K_{1, n}) = \left\lceil \tfrac{n+1}{2}\right\rceil$.

From the previous theorems, it follows that the lower bound of the total edge-irregularity strength in (1.4) is sharp. In addition, it is shown in ^[7] that, under the condition of the described edge-irregular total $\left\lceil \tfrac{n+2}{3}\right\rceil$-labeling for cycles and the edge-irregular total $\left\lceil \tfrac{n+1}{2}\right\rceil$-labeling for stars, the corresponding total edge-weights in both two considered cases constitute the set of consecutive integers. Then, with respect to Theorem 2.1, we have the following corollaries.

Corollary 2.1. Let $C_n$ be a cycle on $n\ge 3$ vertices. Then, ${\rm{mtes}}(C_n) = \left\lceil \tfrac{n+2}{3}\right\rceil$.

Corollary 2.2. Let $K_{1, n}$ be a star on $n+1$ vertices, $n\ge 2$. Then, ${\rm{mtes}}(K_{1, n}) = \left\lceil \tfrac{n+1}{2}\right\rceil$.

The previous corollaries imply the sharpness of the lower bound of the modular total edge-irregularity strength given in (2.1).

In ^[17], an $n$-sun $S\!(n)$ on $2n$ vertices is defined as a cycle $C_n$ with an edge terminating in a vertex of degree $1$ attached to each vertex. Koam et al., in ^[16], proved that

Now, we present the modular total edge-irregularity strength for $n$-suns.

Theorem 2.4. Let $S\!(n)$ be an $n$-sun on $2n$ vertices, $n\ge 3$. Then,

Proof. Let $S\!(n)$ be the $n$-sun with $V(S\!(n)) = \{x_i, y_i: 1\le i\le n\}$ and $E(S\!(n)) = \{ x_ix_{i+1}, x_iy_i: 1\le i\le n\}$, where $x_{n+1} = x_1$. The fact that $\left\lceil \tfrac{2n+2}{3}\right\rceil$ is a lower bound for ${\rm{tes}}(S\!(n))$ follows from (1.4). To show that $\left\lceil \tfrac{2n+2}{3}\right\rceil$ is an upper bound for the total edge-irregularity strength of $n$-sun, we describe a total $\left\lceil \tfrac{2n+2}{3}\right\rceil$-labeling for $S\!(n)$.

Let $k = \left\lceil \tfrac{2n+2}{3}\right\rceil$. For $n\ge 6$, we construct the function $\rho$ as follows:

Evidently, the total labeling $\rho$ is a $k$-labeling. Moreover, given the total labeling $\rho$ for weights of the edges of $S\!(n)$, we have

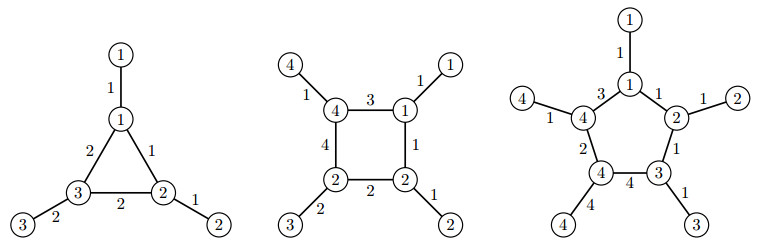
It is a matter of performing a routine check to see that the determined total edge-weights constitute a sequence of consecutive integers from $3$ up to $2n+2$. It means that the total labeling $\rho$ is an edge-irregular total $\left\lceil \tfrac{2n+2}{3}\right\rceil$-labeling. Figure 1 shows the optimal edge-irregular total labelings for $S\!(3)$, $S\!(4)$ and $S\!(5)$, where the total edge-weights in all cases form a sequence of consecutive integers. Thus, with respect to Theorem 2.1, we get that ${\rm{tes}}(S\!(n)) = {\rm{mtes}}(S\!(n)) = \left\lceil \tfrac{2n+2}{3}\right\rceil$ for any $n\ge 3$. This concludes the proof. □

A friendship graph $f_n$, $n\ge 1$, can be visualized as $n$ triangles sharing a common central vertex and is otherwise independent, where $|V(f_n)| = 2n+1$ and $|E(f_n)| = 3n$. For the friendship graph $f_n$ of order $2n+1$, it has been proved in ^[16] that

According to (2.2), these results give an upper bound of the modular total edge-irregularity strength for $f_n$. The existence of edge-irregular total labelings of the friendship graph was investigated in ^[7], wherein the authors proved that ${\rm{tes}}(f_{n}) = \left\lceil \tfrac{3n+2}{3}\right\rceil$. Since the described edge-irregular total $\left\lceil \tfrac{3n+2}{3}\right\rceil$-labeling of the friendship graph $f_n$, $n\ge 1$, allocates the corresponding total edge-weights from the set of consecutive integers $\{ 3, 4, \dots, 3n+2 \}$, then, from Theorem 2.1, we get the next corollary.

Corollary 2.3. Let $f_{n}$ be a friendship graph of size $3n$, $n\ge 1$. Then, ${\rm{mtes}}(f_{n}) = \left\lceil \tfrac{3n+2}{3}\right\rceil$.

A wheel $W_n$, $n\ge 3$, is a graph obtained by joining all vertices of a cycle $C_n$ to a further vertex called the center. Haryeni et al. investigated the modular edge-irregularity strength of wheels and proved the following result ^[11].

Theorem 2.5. ^[11] Let $W_{n}$ be a wheel of order $n+1$. If $n$ is odd and $n\ge 5$, then

They also showed that the upper bound given in Theorem 2.5 is tight. From the relationship given by (2.2), we have an upper bound of the modular total edge-irregularity strength for $W_n$ for odd $n$. On the other hand, the authors of ^[7] present a construction of an edge-irregular total $\left\lceil \tfrac{2n+2}{3}\right\rceil$-labeling of the wheel with $n+1$ vertices for all $n\ge 3$, where the total edge-weights constitute the set of consecutive integers $\{ 3, 4, \dots, 2n+2 \}$. Given Theorem 2.1, we have the following corollary.

Corollary 2.4. Let $W_{n}$ be a wheel on $n+1$ vertices, $n\ge 3$. Then, ${\rm{mtes}}(W_{n}) = \left\lceil \tfrac{2n+2}{3}\right\rceil$.

In the last part of the paper, we focus on circulant graphs and study the existence of the modular edge-irregular total labelings for three classes of this family of graphs. Let $n$, $m$ and $a_1, a_2, \dots, a_m$ be positive integers. For $1\le a_1 < a_2 < \dots < a_m \le \tfrac{n}{2}$, the circulant graph $C_n(a_1, a_2, \dots, a_m)$ is a regular graph with the vertex set $V = \{ v_0, v_1, \dots, v_{n-1} \}$ and the edge set $E = \{ v_iv_{i+a_j}: i = 0, 1, \dots, n-1, j = 1, 2, \dots, m \}$, where indices are taken modulo $n$. If $a_m < \tfrac{n}{2}$, then $C_n(a_1, a_2, \dots, a_m)$ is a $2m$-regular circulant graph with $mn$ edges. If $a_m = \tfrac{n}{2}$, then the circulant graph is a $(2m-1)$-regular one of size $\tfrac{n(2m-1)}{2}$. Partial results on the existence of edge-irregular total labelings for the circulant graph $C_n(1, 2)$, for $n$ even, can be found in ^[21].

We will determine the exact value of the parameter $\rm{mtes}$ for each of the three classes of circulant graphs, namely, $C_n(1, 2)$, $C_n(1, 3)$ and $C_n\left(1, \tfrac{n}{2}\right)$.

Theorem 2.6. Let $C_n(1, 2)$ be a circulant graph on $n$ vertices, $n\ge 5$. Then,

Proof. Let $C_n(1, 2)$ be the circulant graph with the vertex set $V(C_n(1, 2)) = \{v_i: 0\le i \le n-1\}$ and the edge set $E(C_n(1, 2)) = \{v_iv_{i+1}, v_iv_{i+2}: 0\le i \le n-1\}$, where indices are taken modulo $n$. For $n\ge 5$, the circulant graph $C_n(1, 2)$ is a $4$-regular graph with $n$ vertices and $2n$ edges. Put $k = \left\lceil \tfrac{2n+2}{3}\right\rceil$. According to the lower bound given in (1.4), we have that ${\rm{tes}}(C_n(1, 2)) \ge k$.

The graph $C_5(1, 2)$ is isomorphic to $K_5$, and, in ^[14], it is proved that ${\rm{tes}}(C_n(1, 2)) = 5$. An edge-irregular total $5$-labeling of the circulant graph $C_5(1, 2)$ is depicted in Figure 2. Figure 3 illustrates appropriate edge-irregular total $\left\lceil \tfrac{2n+2}{3}\right\rceil$-labelings for circulant graphs $C_n(1, 2)$ for $n = 6, 7, 8$.

In order to show that ${\rm{tes}}(C_n(1, 2)) \le k$ for $n\ge 9$, it only remains to describe a suitable total $k$-labeling for $C_n(1, 2)$. Let us consider a labeling $\alpha: V(C_n(1, 2)) \cup E(C_n(1, 2)) \to \{1, 2, \dots, k\}$ defined in the following way:

We can see that the numbers of all edge labels and vertex labels are at most $k$. For the total edge-weights under the condition of the total labeling $\alpha$, we get

The total weights of edges $v_iv_{i+1}$, $i = 0, 1, \dots, n-1$, successively assume odd values of $3, 5, \dots, 2n+1$. We continue to then obtain

Thus, the total weights of edges $v_iv_{i+2}$, $i = 0, 1, \dots, n-1$, successively attain even values of $4, 6, \dots, 2n+2$.

This means that the total edge-weights of the circulant graph $C_n(1, 2)$, $n\ge 9$, constitute the set of consecutive integers from $3$ up to $2n+2$. According to Theorem 2.1, it follows that the total labeling $\alpha$ is a modular edge-irregular total $\left\lceil \tfrac{2n+2}{3}\right\rceil$-labeling of the circulant graph $C_n(1, 2)$ for $n\ge 6$, and we are done. □

Theorem 2.7. Let $C_n(1, 3)$ be a circulant graph on $n$ vertices, $n\ge 7$. Then,

Proof. Consider a circulant graph $C_n(1, 3)$ with the vertex set $V(C_n(1, 3)) = \{v_i: 0\le i \le n-1\}$ and the edge set $E(C_n(1, 3)) = \{v_iv_{i+1}, v_iv_{i+3}: 0\le i \le n-1\}$, where indices are taken modulo $n$. For $n\ge 7$, we have a $4$-regular graph with $n$ vertices and $2n$ edges. Put $k = \left\lceil \tfrac{2n+2}{3}\right\rceil$. From (1.4), we have that ${\rm{tes}}(C_n(1, 3)) \ge k$. Edge-irregular total $k$-labelings for circulant graphs $C_n(1, 3)$ for $n = 7, 8, 9$ are shown in Figure 4.

To show that $k$ is an upper bound for the total edge-irregularity strength of $C_n(1, 3)$ given $n\ge 10$, we describe a total $k$-labeling $\beta: V(C_n(1, 3)) \cup E(C_n(1, 3)) \to \{1, 2, \dots, k\}$ as follows:

Observe that the numbers of all vertex labels and edge labels are at most $k$ and the total edge-weights have the following values:

It is a routine matter to verify that the total edge-weights successively attain consecutive integers $3, 4, \dots, 2n+2$, and we arrive at the desired result. □

Theorem 2.8. Let $n$ be an even positive integer, $n\ge 4$, and let $C_n\left(1, \tfrac{n}{2} \right)$ be a circulant graph on $n$ vertices. Then,

Proof. Let $n$ be an even positive integer, $n\ge 4$. Consider the circulant graph $C_n\left(1, \tfrac{n}{2} \right)$ with the vertex set $V\left(C_n\left(1, \tfrac{n}{2} \right)\right) = \{v_i: 0\le i \le n-1\}$ and the edge set $E\left(C_n\left(1, \tfrac{n}{2} \right)\right) = \{v_iv_{i+1}: 0\le i \le n-1\} \cup \{v_iv_{i+\tfrac{n}{2}}: 0\le i \le \tfrac{n}{2}-1\}$, where indices are taken modulo $n$. Since $C_n\left(1, \tfrac{n}{2} \right)$ is a $3$-regular graph of order $n$ and size $\tfrac{3n}{2}$, then, from (1.4), it follows that ${\rm{tes}}\left(C_n\left(1, \tfrac{n}{2} \right)\right)\ge \tfrac{n}{2}+1$. To prove the equality, it suffices to prove the existence of an edge-irregular total $(\tfrac{n}{2}+1)$-labeling of the circulant graph $C_n\left(1, \tfrac{n}{2} \right)$. We define the total labeling $\gamma$ as follows:

One can easily check that the vertex labels and edge labels of $C_n\left(1, \tfrac{n}{2} \right)$, under the condition of the labeling $\gamma$, are at most $\tfrac{n}{2}+1$, i.e., $\gamma$ is a total $(\tfrac{n}{2}+1)$-labeling.

The total edge-weights admit the following values:

We can detect that, given the total $k$-labeling $\gamma$, the total edge-weights successively attain consecutive values from $3$ up to $\tfrac{3n}{2}+2$; applying Theorem 2.1, we obtain the desired result. □

3.   Conclusions

In this paper, we have introduced a new graph invariant, i.e., the modular total edge-irregularity strength, as a modification of the modular edge-irregularity strength and total edge-irregularity strength. We estimated a lower bound of this new graph invariant and determined the precise values of the modular total edge-irregularity strength for certain families of graphs, namely, cycles, stars, $n$-sun graphs, friendship graphs, wheels and circulant graphs $C_n(1, 2)$, $C_n(1, 3)$, $C_n\left(1, \tfrac{n}{2}\right)$, in order to prove the sharpness of the presented lower bound.

The results obtained in this paper give examples of graphs for which their total edge-irregularity strength equals their modular total edge-irregularity strength. It is natural to ask for a characterization of all graphs for which the equality between these graph parameters hold. Up to now, all known results suggest that, for most graphs, they will be the same.

Open Problem: Characterize graphs $G$ for which ${\rm{tes}}(G) = {\rm{mtes}}(G)$.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

This research was supported by a UPAR grant from United Arab Emirates University (UAEU), Al Ain, UAE via grant no. G00003739. This work was also supported by the Slovak Research and Development Agency under contract no. APVV-19-0153 and by VEGA 1/0243/23.

Conflict of interest

The authors declare no conflicts of interest.