On the edge irregularity strength for some classes of plane graphs

1.   Introduction

Let $G$ be a connected, simple and undirected graph with vertex set $V(G)$ and edge set $E(G)$. Graph labeling is a mapping of elements of the graph, i.e. vertex and/or edges to a set of numbers (usually positive integers), called labels. If the domain is the vertex-set or the edge-set, the labeling is called vertex labeling or edge labeling respectively. Similarly if the domain is $V(G)\cup E(G)$, then the labeling is called total labeling. In 1988, Chartrand et al. ^[19] defined irregular labeling for a graph G as an assignment of labels from the set of natural numbers to the edges of $G$ such that the sums of the labels assigned to the edges of each vertex are different. The minimum value of the largest label of an edge over all existing irregular labelings is known as the irregularity strength of $G$, and it is denoted by $s(G)$. The work of Chartrand et al. ^[19] opened a new horizon for graph theorists with a lot of research in this domain as confessed by the numerous articles investigating $s(G)$ for various families of graphs (see ^{[7,10,18,20,21,26,27]}).

In 2007, Baca et al. in ^[15] investigated two modifications of the irregularity strength of graphs, namely total edge irregularity strength denoted by $tes(G)$, and total vertex irregularity strength denoted by $tvs(G)$. Results on the total vertex irregularity strength and the total edge irregularity strength can be found in ^{[1,2,4,8,11,16,23,25,27,28,29,30]}.

Motivated by the work of Chartrand et al. ^[19], Ahmad et al. in ^[3] introduced edge irregular $k$-labelings of graphs. A vertex $k$-labeling of graph $G$ $\phi : V(G) \rightarrow \{1, 2, \cdots, k\}$ can be defined as an edge irregular k-labeling for $G$ if for every two different edges $e$ and $f$ it is $w_{\phi} (e) \neq w_{\phi} (f)$, where the weight $w_{\phi} (e)$ of an edge $e = xy \in E(G)$ is defined as $w_{\phi} (xy) = \phi(x) + \phi(y)$. The minimum $k$ for which the graph $G$ has an edge irregular $k-$labeling is called the edge irregularity strength of $G$, denoted by es(G). In the same work ^[3], the authors proved a general lower bound of $es(G)$ and then determined exact values for several families of graphs such as paths, stars, double stars and Cartesian product of two paths. Over the last years, $es(G)$ has been investigated for different families of graphs including trees with the help of algorithmic solutions and amalgamated families of graph through corona product and Toeplitz graphs ^{[5,6,9,12,13,14,31,32,33,34,35]}.

A lot of work has focused on graph labeling and that is evident from the recent survey by Gallian ^[22]. Still there is great potential of expansion in this area. That is why in this paper, we determine the exact value of edge irregularity strength for some classes of plane graphs. A planar graph is a graph that can be drawn on the plane in such a way that its edges do no intersect and only meet at their endpoints. A plane graph is a particular drawing of a planar graph on the Euclidean plane.

2.   Main results

The following theorem establishes a general lower bound for the edge irregularity strength of a graph $G$ (see ^[3]).

Theorem 1. ^[3] Let $G = (V, E)$ be a simple graph with maximum degree $\Delta$. Then

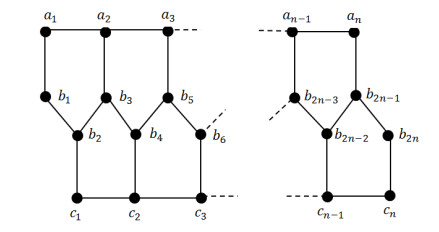
We first discuss edge irregularity strength of plane graph $C_n$ that is defined in ^[17] as follows: Let $P_1, P_2$ and $P_3$ be paths on vertices $a_1, a_2, \ldots, a_n$; $b_1, b_2, \ldots, b_{2n}$ and $c_1, c_2, \ldots, c_n$, respectively. Form the graph $C_n$ from the disjoint union $P_1\cup P_2\cup P_3$ by adding the edges $\{a_ib_{2i-1}, \, \, c_ib_{2i}:1\le i\le n\}$. Graph $C_n$ is shown in Figure 1.

In the following theorem, we determine the exact value of the edge irregularity strength of $C_n$.

Theorem 2. Let $n$ be an integer with $n\ge 3$. Then $es(C_n) = 3n-1.$

Proof. Let $C_n$ be the graph with vertex set $V(C_n) = \{a_i, c_i:1\le i\le n\}\cup\{b_i:1\le i\le 2n\}$ and edge set $E(C_n) = \{a_ia_{i+1}, c_ic_{i+1}: 1\le i \le n-1\}\cup \{b_ib_{i+1}: 1\le i \le 2n-1 \}\cup \{a_ib_{2i-1}, c_ib_{2i}: 1 \le i \le n \}$. The maximum degree of $C_n$ is $\Delta(C_n) = 3.$ The order and size of graph $C_n$ is $4n$ and $6n-3$, respectively. From Theorem 1, we have $es(C_n)\ge\max\left\{ \lceil\frac{6n-2}{2}\rceil, 3\right\} = \left \lceil\frac{6n-2}{2}\right\rceil = 3n-1$. To prove the equality, it suffices to prove the existence of an optimal edge irregular $(3n-1)$-labeling.

We construct the labeling $\psi_1:V(C_n) \rightarrow \{1, 2, 3, \ldots, 3n-1\}$ in the following way:

$\psi_1(a_i) = 2n-1+i$ for $1\le i \le n$, $\psi_1(c_i) = i$ for $1\le i \le n$,

The edge weights are as follows:

We can see that all vertex labels are at most $3n-1$. The edge weights under the labeling $\psi_1$ are distinct for all pairs of distinct edges and the labeling $\psi_1$ provides the upper bound on $es(C_n),$ i.e $es(C_n) \le 3n-1.$ Combining with the lower bound, we conclude that $es(C_n) = 3n-1$. This completes the proof.

Let $A_n$ denotes the plane graph consisting of faces of length $s$ where $s = 3, 4, 5$ and one external infinite face. Note that graph $A_n$ is similar to $C_n$ if one adds edges $b_{2i-1}b_{2i+1}$. The vertex set is $V(A_n) = \{a_i, b_i, c_i, d_i:1\le i\le n\}$ and the edge set is $E(A_n) = \{a_ia_{i+1}, c_ic_{i+1}, d_id_{i+1}, b_ic_{i+1}: 1\le i \le n-1\}\cup \{a_ib_i, b_ic_i, c_id_i: 1 \le i \le n \}.$ Moreover $\vert V(A_n)\vert = 4n$ and $\vert E(A_n)\vert = 7n-4$, see ^[11,24]. The graph $A_n$ is shown in Figure 2.

In the following theorem, we determine the exact value of the edge irregularity strength of $A_n$.

Theorem 3. Let $n$ be an integer with $n\ge 3$. Then $es(A_n) = \lceil\frac{7n-3}{2}\rceil$.

Proof. Let $A_n$ be the graph with vertex set $V(A_n)$ and edge set $E(A_n)$ as defined previously. The maximum degree of $A_n$ is $\Delta(A_n) = 5$. From Theorem 1, we have that $es(A_n)\ge\max\left\{ \lceil\frac{7n-3}{2}\rceil, 5\right\} = \left \lceil\frac{7n-3}{2}\right\rceil$. To prove the equality, it suffices to prove the existence of an optimal edge irregular $\left \lceil\frac{7n-3}{2}\right\rceil$-labeling. Let $\psi_2: V(A_n)\rightarrow \{1, 2, \dots, \left \lceil\frac{7n-3}{2}\right\rceil$} such that

The edge weights are as follows:

We can see that all vertex labels are at most $\lceil\frac{7n-3}{2}\rceil$. The edge weights under the labeling $\psi_2$ are distinct for all pairs of distinct edges and the labeling $\psi_2$ provides the upper bound on $es(A_n),$ i.e $es(A_n)\le \lceil\frac{7n-3}{2}\rceil.$ Combining with the lower bound, we conclude that $es(A_n) = \lceil\frac{7n-3}{2}\rceil$. This completes the proof.

A quadrilateral snake $Q_n$ is a plane graph obtained from a path $b_1, b_2, \dots, b_n$ by adding new vertices $a_1, a_2, a_3\ldots, a_{2(n-1)}$ and new edges $a_{2i-1}a_{2i}$, respectively and joining $a_{2i-1}$ to $b-i$ and $a_{2i}$ to $b_{i+1}$. The double quadrilateral snake $D(Q_n)$ is obtained from $Q_n$ by adding new vertices $c_1, c_2, \dots, c_{2(n-1)}$ and new edges $c_{2i-1}c_{2i}, c_{2i-1}b_{i}$ and $c_{2i}b_{i+1}$ for $1\le i\le n-1$. It is clear that $\vert V(D(Q_n))\vert = 5n-4$ and $\vert E(D(Q_n))\vert = 7(n-1)$. The graph $D(Q_n)$ is shown in Figure 3.

Theorem 4. Let $n$ be an integer with $n\ge 3$. Then $es(D(Q_n)) = \left\lceil\frac{7n-6}{2}\right\rceil.$

Proof. Let $D(Q_n)$ be the plane graph with vertex set $V(D(Q_n)) = \{a_i, c_i:1\le i\le n\}\cup\{b_i:1\le i\le \frac{n}{2}+1\}$ and edge set $E(D(Q_n)) = \{a_{2i-1}a_{2i}, c_{2i-1}c_{2i}$ : $1\le i \le \frac{n}{2}\}\cup \{b_ib_{i+1}: 1\le i \le \frac{n}{2}\}\cup \{a_{2i-1}b_i: 1 \le i \le \frac{n}{2}+1\}\cup\{a_{2i}b_{i+1}$ : $1\le i\le \frac{n}{2}\}\cup\{c_{2i}b_{i+1} : 1\le i\le \frac{n}{2}\}\cup\{c_{2i-1}b_i$ : $1\le i\le \frac{n}{2}+1\}$ where $n\ge 3$. The maximum degree of $D(Q_n)$ is $\Delta(D(Q_n)) = 6$. From Theorem 1, we have that $es(D(Q_n))\ge\max\left\{ \lceil\frac{7n-6}{2}\rceil, 6\right\} = \left \lceil\frac{7n-6}{2}\right\rceil$. To prove the equality, it suffices to prove the existence of an optimal edge irregular $\left \lceil\frac{7n-6}{2}\right\rceil$-labeling.

Let $\psi_3: V(D(Q_n)) \to \{ 1, 2, \dots, \left \lceil\frac{7n-6}{2}\rceil\right\}$ be the vertex labeling such that

The edge weight are as follows:

We can see that all vertex labels are at most $\lceil\frac{7n-6}{2}\rceil$. The edge weights under the labeling $\psi_3$ are distinct for all pairs of distinct edges and the labeling $\psi_3$ provides the upper bound on $es(D(Q_n))$, i.e. $es(D(Q_n))\le \lceil\frac{7n-6}{2}\rceil.$ Combining with the lower bound, we conclude that $es(D(Q_n)) = \lceil\frac{7n-6}{2}\rceil.$ This completes the proof.

3.   Remarks and Conclusion

The problem studied in this paper is about edge irregularity strength of three classes of plane graphs. According to result for lower bound of $es(G)$ in Theorem 1 and all three upper bounds in Theorems 2, 3 and 4, we obtain the exact value for edge irregularity strength of these graphs.

The graphs considered in this paper are quite restricted. From our understanding, the $es(G)$ is indeed hard to compute for general graph $G$, or even for planar graphs. As families of planar graphs, we expect to study outerplanar graphs, planar graphs with bounded maximum degree, or with faces of small size, planar 2-trees, planar 3-trees, etc. They are common graph families in the literature of graph labeling and provide insight for other families of planar graphs that include them.

Presented graphs have bounded tree-width and path-width. Although this might be a mere observation, one can find a path decomposition such that the induced subgraphs in each partitions are identical (except possibly for the last one) and have $\lceil \frac{E}{n} \rceil$ edges. For example, for $D(Q_n)$ the path decomposition is defined by associating the 2-connected components to the nodes of the path. Two consecutive subgraphs have one vertex in common (cutvertex) and each subgraph has 7 edges (recall that $E(D(Q_n)) = 7n-7$. One can compute the labeling for the first subgraph and propagate by linearly increasing the labels. If the edge irregularity is satisfied for the first two subgraphs, then it should hold for the entire graph. Such an approach (if correct) could potentially broaden the targeted graphs.

Acknowledgments

The authors would like to thank the referees for their constructive and valuable comments that improved the paper.

Conflict of interest

All authors declare no conflict of interest in this paper.