Reflexive edge strength of convex polytopes and corona product of cycle with path

1.   Introduction

By a graph $G$ we mean a finite nonempty set $V(G)$ of vertices together with a set $E(G)$ of unordered pairs of vertices, called edges of $G$. The graph $G$ is called a simple graph if there is no multiple edges or loops, otherwise, it is a multigraph. For other terminologies and notations that are not defined in this paper, see ^[1]. Besides, it is well known that a simple graph is impposible to completely irregular, which is to have all vertices of distinct degrees. But, it is logical in multigraphs. Therefore, Chartrand et al. ^[2] introduced an irregular labeling by replacing the parallel edges incident on every vertex of a multigraph to a positive integer set on edges of a simple graph of order at least 3, and consequently the simple graph becomes irregular. Tanna ^[3] rephrased the definition of such graph labeling in the following way.

Definition 1. ^[3] A function $\delta$ is called an irregular labeling of a graph $G$ if $\delta:E(G)\rightarrow \{1, \, 2, \, \ldots, \, k\}$ has the property that the associated vertex weights are pairwise distinct, $w_{\delta}(u)\neq w_{\delta}(v)$ for all vertices $u$, $v\in V(G)$ and $u\neq v$. The weight of a vertex $v\in V(G)$ is

where the sum is over all vertices $u$ adjacent to $v$. An irregularity strength $s(G)$ is defined as the minimum $k$ for which $G$ has the irregular labeling using labels at most $k$.

Subsequently, Bača et al. ^[4] extended this study by proposing the irregular total labelings, i.e., a vertex irregular total labeling and an edge irregular total labeling, which are not only considered the vertex weight, but also the edge weight. Gallian in his comprehensive survey ^[5] listed the latest and most relevant articles of graph labelings.

Definition 2. ^[4] For a graph $G = (V, E)$, a labeling $\rho:V(G)\cup E(G)\rightarrow \{1, \, 2, \, \ldots, \, k\}$ is a total $k$-labeling. The total $k$-labeling is an edge irregular total $k$-labeling if every two different edges $xy$ and $x^\prime y^\prime$ have the distinct weights, $w_{\rho}(xy)\neq w_{\rho}(x^\prime y^\prime)$, where

for all edges $xy$, $x^\prime y^\prime\in E(G)$ and $xy\neq x^\prime y^\prime$. Likewise, the total $k$-labeling is called a vertex irregular total $k$-labeling if every two different vertices $x$ and $y$ have the distinct weights, $w_{\rho}(x)\neq w_{\rho}(y)$, where

for all vertices $x$, $y\in V(G)$ and $x\neq y$. The minimum $k$ for which such labelings exist is called a total edge irregularity strength of $G$, denoted by $tes(G)$ (resp. a total vertex irregularity strength of $G$, denoted by $tvs(G)$).

Motivated by the notions of irregular labeling and irregular total labelings, Tanna et al. ^[6] introduced the irregular reflexive labelings, i.e., an edge irregular reflexive labeling and a vertex irregular reflexive labeling, by allowing the vertex labels representing the vertex degrees contributed by the loops. They made two observations, (a) the vertex labels are non-negative even integers, which represent the fact that each loop contributes twice to the vertex degree; and (b) the vertex label 0 is permissible to represent a loopless vertex. We focus on the edge irregular reflexive labeling in the following study. For more existing studies on edge irregular reflexive labeling of graphs, see ^{[7,8,9,10,11,12,13,14,15]}.

Definition 3. ^[3] A total $k$-labeling $\varphi$ is a combination of an edge labeling $\varphi_e:E(G)\rightarrow \{1, \, 2, \, \ldots, \, k_e\}$ and a vertex labeling $\varphi_v:V(G)\rightarrow \{0, \, 2, \, \ldots, \, 2k_v\}$, in which labeling $\varphi$ is a total $k$-labeling of a graph $G$ such that $\varphi(x) = \varphi_v(x)$ if $x\in V(G)$ and $\varphi(x) = \varphi_e(x)$ if $x\in E(G)$, where $k = \, \mbox{max}\, \{k_e, 2k_v\}$. The total $k$-labeling $\varphi$ is called an edge irregular reflexive $k$-labeling of $G$ if any two different edges $xy$, $x^\prime y^\prime$ of $G$ have the distinct edge weights $wt_{\varphi}(xy)\neq wt_{\varphi}(x^\prime y^\prime)$, where

The smallest value $k$ for such labeling exists is called a reflexive edge strength of $G$, denoted by $res(G)$.

A lower bound for $res(G)$ was obtained by Tanna et al. ^[6], which is needed in what follows.

Lemma 1. ^[6] For a graph $G$,

In this paper, we investigate the reflexive edge strength on certain convex polytopes and a corona product of cycle with path (denoted as $C_n\odot P_m$ for $n\ge 3$ and $m\ge 2$), which is an extend of previous studies of Bača et al. ^[16,17] and Tarawneh et al. ^[18], respectively. In these previous studies, Bača et al. ^[16,17] stated an antiprism $\mathcal A_{n}$, convex polytopes $\mathcal D_{n}$ and $\mathcal R_{n}$ have a magic labeling of type $(1, \, 1, \, 0)$, wherease Tarawneh et al. ^[18] proved the edge irregularity strength on $C_n\odot P_m$ for $n\ge 4$ and $m = 2, 3$. For other existing studies of convex polytopes, we can refer to ^{[19,20,21,22,23]}. Eventually, we obtained the exact reflexive edge strength for these graphs. The definitions of graphs are defined in the following Sections 2 and 3.

2.   Convex polytope graphs

Convex polytopes are one of the families of plane graphs, where the plane graph is said to be a planar graph if it can be drawn on the plane in such a way that no intersection of any two edges and each edge only incident with its endpoints. In the following, we focus on the antiprism $\mathcal A_{n}$ for $n\ge 4$, convex polytopes $\mathcal D_{n}$ and $\mathcal R_{n}$ for $n\ge 3$.

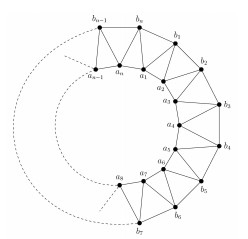
The antiprism $\mathcal A_{n}$ was previously defined by Bača ^[16]. Zhang and Gao ^[24] then redefined it as a graph that consists of an inner cycle of vertices $a_1, \, a_2, \, a_3, \dots, \, a_n$, an outer cycle of vertices $b_1, \, b_2, \, b_3, \dots, \, b_n$, and a set of $2n$ spokes of edges $a_ib_i$ and $b_ia_{i+1}$ (includes $b_na_1$ if $i = n$), as shown in Figure 1.

Therefore, a vertex set and an edge set of $\mathcal A_{n}$ are defined as $V(\mathcal A_{n}) = \{a_i, \, b_i\mid 1\le i\le n\}$ and $E(\mathcal A_{n}) = \{a_ia_{i+1}, \, b_ib_{i+1}, \, a_ib_i, \, b_ia_{i+1}\mid 1\le i\le n-1\}\cup\{a_1a_n, \, b_1b_n, \, a_1b_n, \, a_nb_n\}$, respectively.

Theorem 2.1. For $n\ge 4$,

Proof. According to the fact that $\mathcal A_{n}$ has $4n$ edges. By referring to Lemma 1,

Therefore, the following proves that $k$ is an exact upper bound for $res(\mathcal A_{n})$ by distinguishing between two cases, where $n\ge 4$.

Case 1. $n$ is even.

Define a total $k$-labeling $\varphi$ of $\mathcal A_{n}$ as follows.

We notice that the maximum values of vertex label and edge label of $n\equiv0, 4\, (\mbox{mod}\, 6)$ are the same, that is, $k = \Big\lceil\frac{4n}{3}\Big\rceil$. For $n\equiv2\, (\mbox{mod}\, 6)$, the maximum value of vertex label is $k = \Big\lceil\frac{4n}{3}\Big\rceil+1$, which is greater than all edge labels. Thus, labeling $\varphi$ is a total $k$-labeling of $\mathcal A_{n}$. From Table 1, we can easily see that the edge weights of $\mathcal A_{n}$ are distinct integers in $\{1, \, 2, \, \ldots, \, 4n\}$ under the total $k$-labeling $\varphi$.

Case 2. $n$ is odd.

As referred to Lemma 1, $res(\mathcal A_{5})\ge 8$. Through the vertex labels and edge labels as illustrated in Figure 2, we obtain $res(\mathcal A_{5}) = 8$.

For $n\ge 7$, we define a total $k$-labeling of $\mathcal A_{n}$ in the following ways.

We can see that the maximum value of vertex label of $n\equiv1, \, 5\, (\mbox{mod}\, 6)$ is greater than all edge labels, which is $k = \Big\lceil\frac{4n}{3}\Big\rceil$ and $k = \Big\lceil\frac{4n}{3}\Big\rceil+1$, respectively. For $n\equiv3\, (\mbox{mod}\, 6)$, the maximum value of vertex label is $k = \Big\lceil\frac{4n}{3}\Big\rceil$, which is equal to the maximum value of edge label. Hence, labeling $\varphi$ is a total $k$-labeling of $\mathcal A_{n}$. By referring to Table 1, it clearly shows that the edge weights of $\mathcal A_{n}$ are distinct integers in $\{1, \, 2, \, \ldots, \, 4n\}$ under the total $k$-labeling $\varphi$. Thus, the total $k$-labeling $\varphi$ is an edge irregular reflexive $k$-labeling of $\mathcal A_{n}$, where $n\ge 4$. The theorem holds.

Example 1. Figure 3 illustrates (a) the edge irregular reflexive $6$-labeling of $\mathcal A_{4}$; (b) the edge irregular reflexive $10$-labeling of $\mathcal A_{7}$; and (c) the edge irregular reflexive $20$-labeling of $\mathcal A_{14}$.

The following convex polytope $\mathcal D_{n}$ consists of a vertex set $V(\mathcal D_{n}) = \{a_i, \, b_i, \, c_i, \, d_i\mid 1\le i\le n\}$ and an edge set $E(\mathcal D_{n}) = \{a_ia_{i+1}, \, a_ib_i, \, b_ic_i, \, b_{i+1}c_i, \, c_id_i, \, \, d_id_{i+1}\mid 1\le i\le n-1\}\cup\{a_1a_n, \, a_nb_n, \, b_1c_n, \, b_nc_n, \, c_nd_n, \, d_1d_n\}$, where the vertices $a_1, \, a_2, \, \ldots, \, a_n$ and $d_1, \, d_2, \, \ldots, \, d_n$ are on an inner cycle and outer cycle of $\mathcal D_{n}$, respectively, see Figure 4.

Theorem 2. For $n\ge 3$, $res(\mathcal D_{n}) = 2n$.

Proof. Since $\mathcal D_{n}$ has $6n$ edges, by Lemma 1, $res(\mathcal D_{n})\ge k = 2n$. Therefore, we prove that $k = 2n$ is an upper bound for $res(\mathcal D_{n})$, where $n\ge 3$. Now, define a total $k$-labeling $\varphi$ of $\mathcal D_{n}$ as follows.

Evidently, the maximum value of vertex label is $k = 2n$, which is equal to the maximum value of edge label under the labeling $\varphi$. Thus, labeling $\varphi$ is a total $k$-labeling of $\mathcal D_{n}$. Next, we show the edge weights of $\mathcal D_{n}$ are distinct under the total $k$-labeling $\varphi$.

The above edge weight computations verify that all edges of $\mathcal D_{n}$ have distinct integers in $\{1, \, 2, \, \ldots, \, 6n\}$. Thus, the total $k$-labeling $\varphi$ is an edge irregular reflexive $k$-labeling of $\mathcal D_{n}$. The theorem holds.

Example 2. Figure 5 shows (a) the edge irregular reflexive $10$-labeling of $\mathcal D_{5}$; and (b) the edge irregular reflexive $16$-labeling of $\mathcal D_{8}$.

The convex polytope $\mathcal R_{n}$ is formerly defined by Bača ^[17] that it is a combination of an antiprism $\mathcal A_{n}$ and a prism graph, where these two graphs are Archimedean convex polytopes. Figure 6 depicts $\mathcal R_{n}$ consists of an inner cycle of vertices $c_1, \, c_2, \, c_3, \dots, \, c_n$, an interior cycle of vertices $b_1, \, b_2, \, b_3, \dots, \, b_n$, an outer cycle of vertices $a_1, \, a_2, \, a_3, \dots, \, a_n$, and a set of $3n$ spokes of edges $a_ib_i$, $b_ic_i$, and $b_ic_{i+1}$ (includes $b_nc_1$ if $i = n$).

Therefore, a vertex set and an edge set of $\mathcal R_{n}$ are defined as $V(\mathcal R_{n}) = \{a_i, \, b_i, \, c_i\mid 1\le i\le n\}$ and $E(\mathcal R_{n}) = \{a_ia_{i+1}, \, a_ib_i, \, b_ib_{i+1}, \, b_ic_i, \, b_ic_{i+1}, \, c_ic_{i+1}\mid 1\le i\le n-1\}\cup$$\{a_1a_n, \, a_nb_n, \, b_1b_n, \, b_nc_1, \, b_nc_n, \, c_1c_n\}$, respectively.

Theorem 3. For $n\ge 3$, $res(\mathcal R_{n}) = 2n$.

Proof. The size of $\mathcal R_{n}$ is $6n$. According to Lemma 1, $res(\mathcal R_{n})\ge k = 2n$. Hence, the following proves $k = 2n$ is an upper bound for $res(\mathcal R_{n})$ by distinguishing two cases, where $n\ge 3$.

Case 1. $n$ is odd.

Define a total $k$-labeling $\varphi$ of $\mathcal R_{n}$ as follows.

Clearly, the maximum value of edge label is equal to the maximum value of vertex label, which is $k = 2n$ under the labeling $\varphi$. Thus, labeling $\varphi$ is a total $k$-labeling of $\mathcal R_{n}$. Then, we summarise the edge weights of $\mathcal R_{n}$ and show it via Table 2. We can easily see that all edge weights of $\mathcal R_{n}$ are distinct integers in $\{1, \, 2, \, \ldots, \, 6n\}$.

Case 2. $n$ is even.

Define a total $k$-labeling $\varphi$ of $\mathcal R_{n}$ as follows.

Evidently, as same as Case 3, the maximum value of edge label is $k = 2n$, which is equal to the maximum value of vertex label under the labeling $\varphi$. Thus, labeling $\varphi$ is a total $k$-labeling of $\mathcal R_{n}$. According to Table 2, the edge weights of $\mathcal R_{n}$ also have the distinct integers in $\{1, \, 2, \, \ldots, \, 6n\}$ under the total $k$-labeling $\varphi$. Thus, the total $k$-labeling $\varphi$ is an edge irregular reflexive $k$-labeling of $\mathcal R_{n}$, $n\ge 3$. The theorem holds.

Example 3. Figure 7 shows (a) the edge irregular reflexive $8$-labeling of $\mathcal R_{4}$; and (b) the edge irregular reflexive $22$-labeling of $\mathcal R_{11}$.

3.   Corona product of cycle and path

Corona product of cycle and path, denoted by $C_n\odot P_m$ is obtained from a copy of $C_n$ (with $n$ vertices) and $n$ copies of $P_m$ by joining the $i$-th vertex of $C_n$ to every vertex in $i$-th copy of $P_m$. It consists of a vertex set and an edge set that are defined as $V(C_n\odot P_m) = \{x_i, y_i^j\mid 1\le i\le n, 1\le j\le m\}$ and $E(C_n\odot P_m) = \{x_iy_i^j\mid 1\le i\le n, 1\le j\le m\}$$\cup\{y_i^jy_i^{j+1}\mid 1\le i\le n, 1\le j\le m-1\}\cup\{x_ix_{i+1}\mid 1\le i\le n-1\}\cup\{x_1x_n\}$, respectively.

Theorem 4. For $n\ge 3$ and $m\ge 2$,

Proof. Since $C_n\odot P_m$ has $2nm$ edges, by Lemma 1, we have

Therefore, we prove that $k$ is an upper bound for $res(C_n\odot P_m)$, where $n\ge 3$ and $m\ge 2$. Define a total $k$-labeling $\varphi$ of $C_n\odot P_m$ as follows.

Next, the edges are labeled in the following ways.

Case 1. $n = 3, 4, 5$,

(i) For $1\le j\le m$,

(ii) For $1\le j\le m-1$,

(iii) $\varphi(x_1x_2) = 2\Big\lceil \frac{2m-1}{3}\Big\rceil.$

Case 2. $n\ge 6$.

(i) For $1\le j\le m$,

(ii) For $1\le j\le m-1$,

(iii) $\varphi(x_1x_2) = \varphi(x_2x_3) = 2\Big\lceil \frac{2m-1}{3}\Big\rceil.$

Evidently, the maximum value of vertex label is greater than or equal to the edge labels under the labeling $\varphi$, which is $k = \Big\lceil \frac{2nm}{3}\Big\rceil$ if $nm\not\equiv 1\, (\mbox{mod}\, 3)$, otherwise, $k = \Big\lceil \frac{2nm}{3}\Big\rceil +1$. Thus, labeling $\varphi$ is a total $k$-labeling of $C_n\odot P_m$. The distinct edge weights of $C_n\odot P_m$ under the total $k$-labeling $\varphi$ is shown as Table 3.

We can see that the edge weights of all edges in $C_n\odot P_m$ are distinct integers in the set $\{1, 2, \ldots, 2nm\}$ Thus, the total $k$-labeling $\varphi$ is an edge irregular reflexive $k$-labeling of $C_n\odot P_m$. This completes the proof.

Example 4. Figure 8 shows (a) the edge irregular reflexive $8$-labeling of $C_4\odot P_3$; (b) the edge irregular reflexive $8$-labeling of $C_5\odot P_2$; and (c) the edge irregular reflexive $16$-labeling of $C_6\odot P_4$.

4.   Conclusions

We successfully determined $res(\mathcal A_{n})$ for $n\ge 4$, $res(\mathcal D_{n})$ and $res(\mathcal R_{n})$ for $n\ge 3$ as well as $res(C_n\odot P_m)$ for $n\ge 3$, $m\ge 2$. These results provided further support to the following conjecture.

Conjecture 1. ^[8] Any graph $G$ with maximum degree $\Delta (G)$ satisfies:

where $r = 1$ for $\vert E(G)\vert \equiv 2, 3(\mathit{\mbox{mod}}\, 6)$, and zero otherwise.

From this study, the following problems naturally arise. A double antiprism $\mathcal {AA}_{n}$ is a convex polytope which consists of 3 cycles with each cycle has $n$ vertices and a set of $4n$ spokes of edges incident on the vertices.

Problem 1. Prove that the sharp upper bound of $res(\mathcal {AA}_{n})\le \Big\lceil\frac{7n}{3}\Big\rceil$ if $7n\not\equiv 2, 3\, (\mathit{\mbox{mod}}\, \, 6)$, otherwise, $res(\mathcal {AA}_{n})\le \Big\lceil\frac{7n}{3}\Big\rceil+1$.

Moreover, any graph is said to be a convex polytope if it can be drawn on the plane without the intersection of any two edges. Therefore, many classes of convex polytopes can be obtained by either combining the graphs or adding edges on the existing convex polytope graph. For example, by adding a set of $2n$ spokes of edges $b_ib_{i+1}$ and $c_ic_{i+1}$ on $\mathcal D_{n}$ forms another class of convex polytope, called $\mathcal B_{n}$ for $n\ge 3$ which has $8n$ edges.

Problem 2. Prove that the exact upper bound of $res(\mathcal B_{n})\le \Big\lceil\frac{8n}{3}\Big\rceil$ if $4n\equiv 0, 2\, (\mathit{\mbox{mod}}\, 3)$, otherwise, $res(\mathcal B_{n})\le\Big\lceil\frac{8n}{3}\Big\rceil+1$.

Furthermore, the problem could be extended to be more general through the consideration of characterizing the convex polytope graphs.

Problem 3. Characterize the convex polytopes $G$ of same sizes have the same upper bound of reflexive edge strength.

Besides, an interesting corona product of graphs, i.e., a corona product of star and cycle (denoted by $K_{1, m}\odot C_n$ for $m$, $n\ge 3$) which is never been investigated and still open in the study of irregular labeling or irregular reflexive labeling.

Problem 4. Prove that the sharp upper bound of $res(K_{1, m}\odot C_n)\le \Big\lceil\frac{m+2n(m+1)}{3}\Big\rceil$ if $m+2nm+2n\not\equiv 2, 3\, (\mathit{\mbox{mod}}\, 6)$, otherwise, $res(K_{1, m}\odot C_n)\le \Big\lceil\frac{m+2n(m+1)}{3}\Big\rceil+1$.

Instead of corona product of graphs, many challenging graph operations, e.g., strong product of graphs are still open in the edge irregular reflexive labeling.

Problem 5. Determine the reflexive edge strength of the strong product of two paths, $res(P_n\boxtimes P_m)$, where $n$, $m\ge 2$.

Problem 6. Find the edge irregular reflexive labeling on strong product of two cycles, $res(C_n\boxtimes C_m)$, where $n$, $m\ge 3$.

Acknowledgments

The authors would like to thank the referees for their valuable comments. This research is supported by the Fundamental Research Grant Scheme (FRGS), Ministry of Higher Education, Malaysia with Reference Number FRGS/1/2020/STG06/UMT/02/1 (Grant Vot. 59609).

Conflict of interest

All authors declare no conflicts of interest in this paper.