1.
Introduction
Let L be a finite lattice with a least element 0 and A(L) be the set of all atoms. Before reading the paper, to familiarize with the notation and concepts used here, we strongly recommend the readers to read the first part of this work [3]. The annihilating-ideal graph of a lattice L, denoted by AG(L), and defined by the graph whose vertex set is the set of all non-trivial ideals of L and two distinct vertices I and J being adjacent if and only if I∧J=0, which was introduced by Afkhami et al. [1]. Note that the graph AG(L) is an r-partite graph for some r∈N.
One of the most important topological properties of a graph is its genus. The genus of graphs associated with algebraic structures has been studied by many authors, see [2,4,5,11]. The planar and crosscap one annihilating-ideal graph of lattices were characterized by Shahsavar [13] and Parsapour et al. [10], respectively. Also, whether the line graph associated with the annihilating-ideal graph of a lattice is planar or projective was characterized by Parsapour et al. [12]. Moreover, the authors of [9] characterized all lattices L whose line graph of AG(L) is toroidal. Recently, Asir et al. [3], provided the classification of lattices with the number of atoms less than or equal to 4 whose annihilating-ideal graph can be embedded in the non-orientable surface of crosscap two.
Note that a graph is planar if and only if it does not contain either of two forbidden graphs K5 and K3,3. An analogous characterization for embeddings of graphs on surfaces is known for the projective plane, which has 103 forbidden subgraphs, see [6]. For surfaces in general, it is known that the set of forbidden minors is finite and an explicit upper bound can be given, see [14]. In this paper, we have identified a class of minimal r-partite graphs that are not crosscap two graphs. So, these graphs may be realized as forbidden subgraphs for crosscap two.
The aim of this paper is to find the lattices with at least 5 atoms whose annihilating-ideal graph has non-orientable genus two embedding. This lead to the addition of r-partite graphs, where r≥5, to the family of crosscap two graphs. First of all, we observe that, by Proposition 3.3 [3], |A(L)|≤6 whenever the crosscap of AG(L) is two. Therefore, the lattices under consideration has either 5 or 6 atoms, and the corresponding classifications are done in Theorems 2.2 and 3.1. The reader can find an interesting connection between AG(L) and multipartite graphs in Examples 2.1 and 3.1.
Before moving into our main results, we have collected the crosscap lower bound of some graphs which will be used in the subsequent sections. In what follows, the notations K4−e and K4,5−e denote graphs with an arbitrary edge removed from K4 and K4,5 respectively. Also, K8−3e denotes a graph with three arbitrary edges removed from K8. Moreover, K6,3∪(K4−e), denotes a graph, that includes the vertices and edges of K6,3 with partition (X,Y), |X|=6, as well as the edges of K4−e, a subgraph induced by any 4 arbitrary vertices in the partition X.
Proposition 1.1. Let G be a graph.
(i) [3, Proof of Theorem 3] If G is isomorphic to K6,3∪(K4−e) or K4,5−e, then ˜γ(G)≥3.
(ii) If G is isomorphic to K8−3e or K2,2,2,2, then ˜γ(G)≥3.
Proof. (ⅱ) The non-embeddability of K8−3e in the Klein bottle directly follows from Euler's polyhedral equation. The non-embeddability of K2,2,2,2 in the Klein bottle is a straightforward consequence of the characterization [8] of the graphs that triangulate both the torus and Klein bottle; note that it is well-known that K2,2,2,2 triangulates the torus, see [7]. □
Let us directly move on to the lattices with 5 atoms.
2.
The case when |A(L)|=5
Before going into the characterization of crosscap two AG(L) for number of atoms of size 5, we rectify missing cases in projective characterization given in [10]. In particular, the authors have not discussed the sets of the form Uijk for 1≤i≠j≠k≤5 in Theorem 2.7. To be precise, let |∪5n=1Un|=5. From the proof of Theorem 2.7(ⅰ) [10], the following two possibilities should be considered.
Case 1. |Uij|=2 for unique 1≤i≠j≤5. Then, Theorem 2.7(ⅰ) of [10] says that AG(L) is projective whenever |∪k≠i,j(Uik∪Ujk)|≤2 with |Uik|,|Ujk|≤1. But consider any one of U(ij)c,U(ik)c,U(jk)c as non-empty. More generally, let us assume U(pq)c≠∅ for some Upq≠∅ with 1≤p,q≤5. Then the sets X=Ui∪Uj∪Uij∪{[Ipq,I(pq)c]} and Y=∪k≠i,jUk form K5,3 in AG(L) and so ˜γ(AG(L))≥2. Therefore, U(pq)c=∅ whenever Upq≠∅.
Case 2. For some fixed i, |∪5j=1Uij|≤3, |Uij|≤1 and |Ukℓ|≤1 for at most one pair k,ℓ with 1≤i≠j≠k≠ℓ≤5 such that every vertex of Ukℓ is adjacent to a maximum of one vertex from ∪5j=1Uij.
If |U(pq)c|≥2 for some Upq≠∅ and 1≤p,q≤5, then the sets X=Up∪Uq∪Upq and Y=∪r≠p,qUr∪U(pq)c form K3,5 in AG(L), a contradiction. Also if |U(pq)c|,|U(p1q1)c|=1 for some |Upq|,|Up1q1|≠∅ and 1≤p,q,p1,q1≤5, then the sets X=Up∪Uq∪Upq∪{[Ip1q1,I(p1q1)c]} and Y=∪r≠p,qUr∪U(pq)c form K4,4−e which has crosscap two, a contradiction. Therefore, |∪U(pq)c|≤1, where the union is taken over all Upq≠∅.
Suppose |Ukℓ|=1 for some 1≤k,ℓ≤5 with a vertex in Ukℓ adjacent to exactly one vertex of ∪5j=1Uij, say a vertex in Uij. We now claim that ∪U(pq)c=∅, where the union is taken over all Upq≠∅. In order to prove the claim, when either U(ij)c≠∅ or U(kℓ)c≠∅, let us take U(ij)c≠∅, then X=Ui∪Uj∪Uij and Y=∪m≠i,jUm∪Ukℓ∪U(ij)c form K3,5. Further, if U(ij′)c≠∅ for some 1≤j′≠j≤5, then, X=Ui∪Uj∪Uij∪[Iij′,I(ij′)c] and Y=∪m≠i,jUm∪Ukℓ form K4,4−e. Thus, ∪U(pq)c=∅.
Based on the addition of above mentioned cases in projective characterization, we can summarize it as follows.
Theorem 2.1. Let L be a lattice with |A(L)|=5 and let |∪5n=1Un|=5. Then, ˜γ(AG(L))=1 if and only if |Uij|≤2 for all 1≤i≠j≤5 and one of the following conditions hold:
(i) There is a unique Uij such that |Uij|=2 with Ui′j′,U(ij)c=∅ for i′,j′∈{1,…,5}∖{i,j}, |∪p∈{i,j};q∉{i,j}Upq|≤2 and ∪Upq≠∅U(pq)c=∅. Moreover, if Up1q1,Up2q2≠∅, then {p1,q1}∩{p2,q2}≠∅.
(ii) |Uij|≤1 for all 1≤i≠j≤5. For some fixed i∈{1,…,5}, |∪5j=1Uij|≤3, atmost one of the sets Ukℓ such that |Ukℓ|=1, where 1≤i≠k≠ℓ≤5 and |∪Upq≠∅U(pq)c|≤1. Moreover, if Ukℓ has a vertex, then it is adjacent to atmost one vertex in ∪5j=1Uij and if such adjacency exists, then ∪Upq≠∅U(pq)c=∅.
We are now in a position to state and prove the main result of this section.
Theorem 2.2. Let L be a lattice with |A(L)|=5 and let 1≤i≠j≠k≠l≠m≤5. Then, ˜γ(AG(L))=2 if and only if one of the following conditions hold:
(i) |∪5n=1Un|=8, there exists Ui with |Ui|=4 and Upq=Ujkl=Ujklm=∅ for all 1≤p≠q≤5.
(ii) |∪5n=1Un|=7, one of the following cases is satisfied:
[a] There exists Ui such that |Ui|=3 with |∪j≠iUij|≤2 and |∪k,ℓ,m,n≠iUkℓ∪Ukℓm∪Ukℓmn|≤1. Moreover, if |∪k,ℓ,m,n≠iUkℓ∪Ukℓm∪Ukℓmn|=1, then ∪j≠iUij=∅ and if ∪k,ℓ,m,n≠iUkℓ∪Ukℓm∪Ukℓmn=∅, then |∪j≠iUij|∈{1,2}.
[b] There exist Ui and Uj such that |Ui|=|Uj|=2 with |∪k,ℓ∉{i,j}Ukℓ|≤1. Moreover:
[b1] If |∪k,ℓ∉{i,j}Ukℓ|=1, then ∪m=i,j;pq≠ij(Umn∪Upqr)∪U(ij)c∪Uij∪U(i)c∪U(j)c=∅.
[b2] If ∪k,ℓ∉{i,j}Ukℓ=∅, then |∪m=i,j;mn≠ijUmn∪U(ij)c|≤1. Also, if |∪m=i,j;mn≠ijUmn∪U(ij)c|=1, then |Uij|≤1 and ∪pq≠ij;pqr≠(ij)cUpqr∪U(i)c∪U(j)c=∅. Moreover, if ∪m=i,j;mn≠ijUmn∪U(ij)c=∅, then |Uij|≤2. In addition, if |Uij|=2, then ∪pq≠ij;pqr≠(ij)cUpqr∪U(i)c∪U(j)c=∅ and if |Uij|≤1, then |∪p=i,j;pq≠ijUpqr|≤2 together with |Upqr|≤1, and either ∪p=i;q≠jUpqr∪U(j)c=∅ or ∪p=jUpqr∪U(i)c=∅.
(iii) |∪5n=1Un|=6. There exists Ui such that |Ui|=2 with |∪j,k≠iUjk|≤2 and Uj′k′=∅ when Ujk≠∅ for all j′,k′∉{j,k}. Moreover:
[a] There is Ujk such that |Ujk|=2 for j,k≠i with ∪ℓ∉{j,k}Uiℓ=∅, |∪m∈{j,k};p,q,r≠i(Uim∪Upqr)|≤2 in which |Uim|,|Upqr|≤1 and U(st)c=∅ if Ust≠∅ for all 1≤s≠t≤5.
[b] There exist Ujk,Uj1k1 such that |Ujk|=|Uj1k1|=1 where j,k,j1,k1≠i and |{j,k}∩{j1,k1}|=1 with ∪ℓ∉{j,k}∩{j1,k1}Uiℓ=∅, |∪m={j,k}∩{j1,k1};p,q,r≠i(Uim∪Upqr)|≤2 in which |Uim|,|Upqr|≤1 and U(st)c=∅ if Ust≠∅ for all 1≤s≠t≤5.
[c] There is a unique Ujk such that |Ujk|=1 for all j,k≠i with |∪ℓ∉{j,k}Uiℓ∪U(jk)c|≤1. Also, if |∪ℓ∉{j,k}Uiℓ∪U(jk)c|=1, then |∪m∈{j,k}Uim|≤2 in which each |Uim|≤1 and ∪p,q,r,s≠iUpqr∪Upqrs=∅. Furthermore, one of the following is satisfied in the case of ∪ℓ∉{j,k}Uiℓ∪U(jk)c=∅:
[c1] If |∪m∈{j,k}Uim|=3 or 4, then exactly one of the sets Uim, for m=j,k, has more than one element and ∪p,q,r,s≠iUpqr∪Upqrs=∅.
[c2] If |Uim|=2 and Uim′=∅ for m≠m′∈{j,k}, then U(im)c=∅ and |∪p,q,r≠iUpqr|≤1. Also, Upqrs=∅ for p,q,r,s≠i whenever |∪p,q,r≠iUpqr|=1.
[c3] If |∪m∈{j,k}Uim|≤2 in which each |Uim|≤1, then U(im)c=∅ and 1≤|∪m∈{j,k};p,q,r≠i(Uim∪Upqr)|≤3. Also, Upqrs=∅ for p,q,r,s≠i whenever |∪m∈{j,k};p,q,r≠i(Uim∪Upqr)|=3 together with |∪p,q,r≠iUpqr|=2.
[d] ∪j,k≠iUjk=∅ and |∪m≠iUim|≤4 in which |Uim|≤3. Also, if two of Uim's has 2 elements, then ∪p,q,r,s≠iUpqr∪Upqrs=∅, and if exactly one set Uim has more than 1 element, then |∪p,q,r≠iUpqr|≤1 together with ∪Uim≠∅U(im)c=∅. Furthermore, one of the following is satisfied in case of |Uim|≤1 for all m≠i:
[d1] If |∪m≠iUim|=4, then ∪Uim≠∅U(im)c=∅.
[d2] If |∪m≠iUim|≤3, then |∪Uim≠∅U(im)c|≤1. Also, if |∪Uim≠∅U(im)c|=1, then ∪p≠i,pqr≠(im)cUpqr=∅. If ∪Uim≠∅U(im)c=∅, then |∪p,q,r≠i;pqr≠(im)cUpqr|≤2 whenever |∪m≠iUim|=3, and 2≤|∪p,q,r≠i;pqr≠(im)cUpqr|≤4 with atmost one |Upqr|∈{2,3} whenever |∪m≠iUim|≤2. Further, in the last part, if |∪p,q,r≠i;pqr≠(im)cUpqr|=2, then exactly one non-empty set exists in the collection {Upqr:p,q,r≠i;pqr≠(im)c}.
(iv) |∪5n=1Un|=5 and one of the following cases is satisfied:
[a] There is a Uij such that |Uij|=4, ∪ℓ,m∉{i,j}Uℓm∪U(ij)c=∅, |∪p∈{i,j};q∉{i,j}Upq|≤2 in which |Upq|≤1 and Up′q′,U(pq)c=∅ when |Upq|=1 where p′,q′∉{p,q}.
[b] There is a Uij such that |Uij|=3, ∪ℓ,m∉{i,j}Uℓm∪U(ij)c=∅, |∪p∈{i,j};q∉{i,j}Upq|≤3, where the choice i or j for p is placed at most two times in the union, in which at most one of Upq's has two elements and |∪Upq≠∅U(pq)c|≤1. Further, if |Upq|=2 for some p∈{i,j};q∉{i,j}, then ∪p′,q′∉{p,q}Up′q′∪∪Upq≠∅U(pq)c=∅, and if |∪p∈{i,j};q∉{i,j}Upq|=3 with |Upq|≤1, then the three choices for q is not distinct. Moreover, if |∪Upq≠∅U(pq)c|=1, then |∪p∈{i,j};q∉{i,j}Upq|≤2 with the choice for two pairs of p,q's are not mutually disjoint.
[c] There is a Uij such that |Uij|=2 with |∪ℓ,m∉{i,j}Uℓm∪U(ij)c|≤1. Further, if |∪ℓ,m∉{i,j}Uℓm∪U(ij)c|=1, then |∪p∈{i,j};q∉{i,j}Upq|≤2 with |Upq|≤1 and Up′q′,U(pq)c=∅ when |Upq|=1, where p′,q′∉{p,q}. Moreover, if ∪ℓ,m∉{i,j}Uℓm∪U(ij)c=∅, then 2≤|∪p∈{i,j};q∉{i,j}Upq|≤4 in which at most one of the sets Upq has two elements, where the choice i or j for p is placed at most once in the union, and one of the following is satisfied:
[c1] If |Urs|=2 for some r∈{i,j},s∉{i,j}, then ∪Upq≠∅U(pq)c=∅ and at most one of the sets Utu is non-empty with the property that {r,s}∩{t,u}=∅.
[c2] If |Upq|≤1 for all p∈{i,j},q∉{i,j}, then |∪Upq≠∅U(pq)c|≤1. Also, if |U(pq)c|=1 for some |Upq|=1, then every non-empty set Urs should have the property that {r,s}∩{p,q}≠∅.
[d] |Uij|≤1 for all 1≤i≠j≤5.
[d1] If |∪1≤p≠q≤5Upq|=5, then ∪Upq≠∅U(pq)c=∅, and at least one of the sets Up1q1,Up2q2,Up3q3 or Up4q4 must be empty whenever the indices satisfy the condition {p1,q1}∩{p2,q2}=∅ and {p3,q3}∩{p4,q4}=∅.
[d2] If |∪1≤p≠q≤5Upq|=4, then |∪Upq≠∅U(pq)c|≤1. Moreover, if ∪Upq≠∅U(pq)c=∅, then the subgraph induced by the set ∪1≤p≠q≤5Upq has more than one edge and if |∪Upq≠∅U(pq)c|=1, say |U(rs)c|=1, then the vertex in Urs is adjacent to at most two vertices of ∪Upq≠∅;pq≠rsUpq. Further, if there is an adjacency between the vertex of Urs and a vertex of ∪Upq≠∅;pq≠rsUpq, then the subgraph induced by the set ∪Upq≠∅;pq≠rsUpq is an empty graph.
[d3] If |∪1≤p≠q≤5Upq|∈{2,3}, then |∪Upq≠∅U(pq)c|≤3. Moreover:
● If |∪Upq≠∅U(pq)c|=3, then |U(pq)c|=3 for some 1≤p≠q≤5 and no non-empty set Urs exist with {r,s}∩{p,q}=∅.
● Let |∪Upq≠∅U(pq)c|=2. If a unique set U(pq)c≠∅ for 1≤p≠q≤5, then at most one non-empty set Urs exists with {r,s}∩{p,q}=∅. If two sets U(p1q1)c,U(p2q2)c≠∅ for 1≤p1,q1,p2,q2≤5, then no non-empty set Urs exists with {r,s}∩{pf,qf}=∅ for 1≤f≤2.
● If |∪Upq≠∅U(pq)c|=1, then exactly one non-empty set Urs exists with {r,s}∩{p,q}=∅.
[d4] If |∪1≤p≠q≤5Upq|=1, then |∪Upq≠∅U(pq)c|∈{2,3}.
Proof. If |∪5n=1Un|≥9, then AG(L) contains K5,4 as a subgraph so that |∪5n=1Un|≤8.
Case 1. Let |∪5n=1Un|=8. Suppose |U1|=4. If ∪k,p≠1Uij∪Ukℓm∪Upqrs≠∅ for some 1≤i<j≤5, then AG(L) contains K4,5−e and by Proposition 1.1, we have ˜γ(AG(L))≥3. Therefore, ∪k,p≠1Uij∪Ukℓm∪Upqrs=∅. Now the graph AG(L) (except the vertices of degree one and two) is a subgraph of H1 (as given in [3, Figure 1(a)]) and so by [3, Lemma 3.5], we get ˜γ(AG(L))=2. If |U1|=3, then the subgraph induced by the sets X=U1∪U5 and Y=U2∪U3∪U4 contains H4 in AG(L) and so by [3, Lemma 3.6], ˜γ(AG(L))≥3. Also, if |U1|=2, then AG(L) contains K2,2,2,2 as a subgraph and by Proposition 1.1, ˜γ(AG(L))≥3.
Case 2. Let |∪5n=1Un|=7.
Case 2.1. Suppose |U1|=3. If the subgraph induced by ⟨V(AG(L))−{∪5n=1Un}⟩ has an edge (I,J), then the vertices I1,I′1,I′′1,I2,I3,I4,I5,[I,J] form K8−3e and so by Proposition 1.1, we have ˜γ(AG(L))≥3. Therefore each vertex of U1mn is adjacent to exactly two vertices in AG(L) which are also adjacent. Also if I,J∈∪i,p,s≠1Uij∪Upqr∪Ustuv, then the subgraph induced by I1,[I′1,I],[I′′1,J],I2,I3,I4 and I5 form K7 in AG(L), a contradiction. Thus |∪i,p,s≠1Uij∪Upqr∪Ustuv|≤1 and among all the remaining sets we have to examine only those sets of the form U1k.
Let I∈∪i,p,s≠1Uij∪Upqr∪Ustuv. If U1k≠∅ for some k≠1, then, the subgraph G21=AG(L)−{I,(Ik,Iℓ),(Ik,Im),(Ik,In)} contains K4,4−e with partite sets X=U1∪U1k and Y=Uk∪Uℓ∪Um∪Un where ℓ,m,n∈{2,3,4,5}∖{k} and e=(I1k,Ik). Note that any N2-embedding of K4,4−e has one hexagonal and six rectangular faces. Since I is adjacent to three vertices I1,I′1 and I′′1 of X, the vertex I must be inserted into the hexagonal face of the N2-embedding of K4,4−e. If Ik is in the hexagonal face, then Ik is in exactly two distinct rectangular faces so that the three edges incident with Ik, namely (Ik,Iℓ),(Ik,Im),(Ik,In), cannot be drawn without edge crossing, a contradiction. If not, I1k∈X must be in the hexagonal face. Therefore, the hexagonal face does not contain all the three vertices of X namely I1,I′1 and I′′1. Thus, I cannot be embedded, a contradiction. Hence, U1k=∅ for all 2≤k≤5.
Assume ∪i,p,s≠1Uij∪Upqr∪Ustuv=∅. Suppose |∪5k=2U1k|≥3 and let I1ℓ,I1m,I1n∈∪5k=2U1k. Then, the subgraph AG(L)−{I1m,I1n} contains K4,4−e with partitions X=U1∪U1ℓ and Y=U2∪U3∪U4∪U5. Clearly, any N2-embedding of K4,4−e has one hexagonal and six rectangular faces. The vertices I1m and I1n are adjacent to three vertices of Y in AG(L). So it requires at least two hexagonal faces in a N2-embedding of K4,4−e, a contradiction. Thus, |∪5k=2U1k|≤2.
Further, AG(L) is projective whenever ∪1≤i<j≤5Uij=∅ with ∪p,s≠1Upqr∪Ustuv=∅. Thus, ˜γ(AG(L))=2 if |∪i,p,s≠1Uij∪Upqr∪Ustuv|=1 with ∪5k=2U1k=∅ or ∪i,p,s≠1Uij∪Upqr∪Ustuv=∅ with |∪5k=2U1k|∈{1,2}.
Case 2.2. Suppose |U1|=2. Then, |U2| must be 2.
If |Uij|≥2 for some i≠1,2, then the contraction of AG(L) induced by the set {I1,[I′1,Iij],I2,[I′2,I′ij],I3,I4,I5} form K7. So, |Uij|≤1 for all i,j∉{1,2}.
Suppose |Uij|=1 for some i≠1,2. If I∈∪k=1,2;pq≠12(Ukℓ∪Upqr)∪U(ij)c∪U1345∪U2345, then I is adjacent to one of I1, I2 or Iij. The latter case, that is (I,Iij)∈E(AG(L)), is not possible because ⟨∪5n=1Un∪{[I,Iij]}⟩≅K8−2e. Also if either (I,I1)∈E(AG(L)) or (I,I2)∈E(AG(L)), then we can merge such an edge so that K8−3e is a minor subgraph of AG(L). Thus, in this case, V(AG(L))∖{∪5n=1Un∪U12i∪U12j}=∅.
Suppose Uij=∅ for all i≠1,2. Let I,J∈∪k=1,2;kℓ≠12Ukℓ∪U345. If I,J∈U345, then the partition sets {I,J,I3,I4,I5} and {U1∪U2} form K5,4 in AG(L). If not, we have |Ukℓ|≥1 for some k∈{1,2} and kℓ≠12 so that the partition sets Uk∪Uℓ∪{I,J} and ∪m≠k,ℓUm form K5,4−e in AG(L). Thus, |∪k=1,2;kℓ≠12Ukℓ∪U345|≤1.
Let I∈∪k=1,2;kℓ≠12Ukℓ∪U345.
● In the case of |U12|≥2, note that I is adjacent to either the vertices of U1 or U2, say U1. Here, the contraction of AG(L) contains K6,3∪(K4−e) with partite sets {I1,[I′1,I],I2,I′2,I12,I′12} and ∪m≠1,2Um.
● In the case of ∪pq≠12;pqr≠345Upqr∪U1345∪U2345≠∅, by contracting a single edge in AG(L), we get the contraction of AG(L) contains H4.
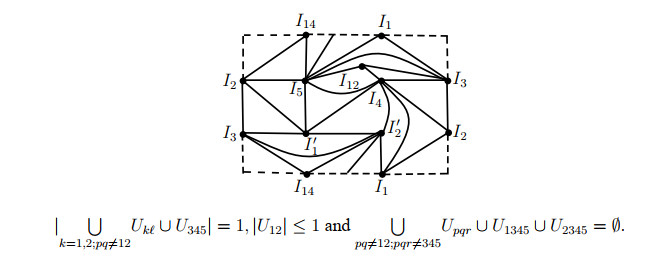
Thus, |∪k=1,2;kℓ≠12Ukℓ∪U345|=1, |U12|≤1 and ∪pq≠12;pqr≠345Upqr∪U1345∪U2345=∅. For this case, with the help of Figure 1, we get ˜γ(AG(L))=2.
Let ∪k=1,2;kℓ≠12Ukℓ∪U345=∅.
● In the case of |U12|≥3, AG(L) contains K3,7 with partite sets U1∪U2∪U12 and U3∪U4∪U5.
● In the case of |U12|=2, we have ∪pq≠12;pqr≠345Upqr∪U1345∪U2345=∅. If not, there exists some J∈∪pq≠12;pqr≠345Upqr∪U1345∪U2345, then J is adjacent to either I1 or I2, say (J,I1)∈E(AG(L)) so that the contraction of AG(L) contains K6,3∪(K4−e) with partite sets {[J,I1],I′1,I2,I′2,I12,I′12} and U3∪U4∪U5.
● In the case of |U12|≤1:
(a) If |Upqr|≥2 for pq≠12 and pqr≠345, then AG(L) contains K3,6∪(K4−e) with partite sets Up∪Uq∪Ur∪Upqr and ∪m≠p,q,rUm. Therefore, |Upqr|≤1 for pq≠12 and pqr≠345.
(b) If J∈∪p=1;q≠2Upqr∪U1345 and K∈∪p=2Upqr∪U2345, then the contraction of AG(L) induced by the set {I1,[I′1,K],I2,[I′2,J],I3,I4,I5} form K7. Therefore, either ∪p=1;q≠2Upqr∪U1345=∅ or ∪p=2Upqr∪U2345=∅.
(c) If |∪p=1;q≠2Upqr|≥3, that is |U134|=|U135|=|U145|=1, then consider the subgraph AG(L)−{I135,I145,(I1,I4),(I′1,I4),(I3,I4),(I1,I3),(I′1,I3)} which contains K5,3 with partite sets X=U1∪U3∪U4∪U134 and Y=U2∪U5. Notice that any N2-embedding of K5,3 has one hexagonal face and six rectangular faces. Also in AG(L), the vertex I4 is adjacent to the vertices of {I1,I′1,I3}⊆X and I135 is adjacent to I4 as well as {I2,I′2}⊆Y. Since degK5,3(I4)=3, three rectangular faces cannot adopt all these edges incident with I3 together with the edges incident with I135. Therefore, I4 must be in the hexagonal face. A similar technique also proves that I3 is a part of the hexagonal face. To an extent, the hexagonal face can adopt the vertices I135 and I145 with its edges together with an edge incident to either I4 or I3. We let the edge (I1,I4) be embedded in the hexagonal face. Here the two other edges incident with I4, namely (I′1,I4) and (I3,I4) can be embedded in two rectangle faces that contains I4. Now we have to embed two more edges incident with I3, namely (I1,I3) and (I′1,I3) but we are left-out with only one rectangular face that contains I3, a contradiction. Therefore, |∪p=1;q≠2Upqr|≤2; likewise |∪p=2Upqr|≤2.
Thus, in the case of ∪k=1,2;kℓ≠12Ukℓ∪U345=∅, either |U12|=2 with ∪pq≠12;pqr≠345Upqr∪U1345∪U2345=∅ or |U12|≤1 with |∪p=1,2;pq≠12Upqr|≤2 and |Upqr|≤1 together with either ∪p=1;q≠2Upqr∪U1345=∅ or ∪p=2Upqr∪U2345=∅. For all these cases, by using Figure 2, we get ˜γ(AG(L))=2.
Thus, ˜γ(AG(L))=2 if |∪i≠1,2Uij|=1 with ∪k=1,2;pq≠12(Ukℓ∪Upqr)∪U(ij)c∪U12∪U1345∪U2345=∅ or ∪i≠1,2Uij=∅ with |∪k=1,2;kℓ≠12;pq≠12Ukℓ∪Upqr|≤1. Also, if |∪k=1,2;kℓ≠12;pq≠12Ukℓ∪Upqr|=1, then |U12|≤1 and U1345=U2345=∅. Moreover, if ∪k=1,2;kℓ≠12;pq≠12Ukℓ∪Upqr=∅, then |U12|≤2. In addition, U1345=U2345=∅ whenever |U12|=2 and either U1345=∅ or U2345=∅ whenever |U12|≤1.
Case 3. Let |∪5n=1Un|=6. Then |U1|=2. If |∪i≠1Uij|≥3, then the graph G21 is contained in AG(L) and so ˜γ(AG(L))≥3. Therefore, |∪i≠1Uij|≤2. Further, if |Uij|=|Ukℓ|=1 for some {i,j}∩{k,ℓ}=∅, then the graph (H4∪(u1,u2))−(v2,v4) is contained in AG(L) and by [3, Lemma 3.6], we have ˜γ(AG(L))≥3. That is, E(⟨∪i≠1Uij⟩)=∅.
Case 3.1. Assume |∪i≠1Uij|=2. Let |Uij|=2 for some i≠1. If I∈(∪k≠i,jU1k)∪U(ij)c, then the sets X=Ui∪Uj∪Uij and Y=U1∪Uk∪Uk′∪I, where k′∈{2,3,4,5}∖{i,j,k} form K4,5 in AG(L), a contradiction. Therefore, ∪k≠i,jU1k=U(ij)c=∅.
If U1i or U1j has two elements, say |U1i|≥2, then the subgraph G22=AG(L)−{I1i,I′1i,(Ik,Ii),(Ik,Ij),(Ik,Iij),(Ik,I′ij)} contains K5,3 with partite sets X=Ui∪Uj∪Uk∪Uij and Y=U1∪Uk′, where k∈{2,3,4,5}∖{i,j} and k′∈{2,3,4,5}∖{i,j,k}. Note that any N2-embedding of K5,3 has one hexagonal, six rectangular faces and out of which three faces contains the vertex Ik because degK5,3(Ik)=3. Since I1i and I′1i are adjacent to Ij,Ik,Ik′ in AG(L), it requires two distinct faces that contains Ik to embed the vertices I1i and I′1i. So, after embedding I1i and I′1i in any N2-embedding of K5,3, it may adopt at most three distinct edges with one end in Ik and another end in one of the vertices of X. But, Ik is adjacent to {Ii,Ij,Iij,I′ij}⊂X, a contradiction. Thus, |U1i|,|U1j|≤1.
Suppose |U1i|,|U1j|=1 and ∪p≠1Upqr≠∅. Then, ˜γ(AG(L))≥3. Suppose |U1i|=1 and U1j=∅. If U(1i)c≠∅, then the sets X=Ui∪Uj∪Uij∪{[I1i,I(1i)c]} and Y=U1∪Um∪Un, where m,n∈{1,…,5}∖{1,i,j} form K5,4 in AG(L), a contradiction. Also, if I,J∈∪p≠1Upqr, then it is not difficult to verify that ˜γ(AG(L))≥3.
Thus, ˜γ(AG(L))=2 if ∪k∉{i,j}U1k=∅, |∪k∈{i,j},p≠1(U1k∪Upqr)|≤2 with |U1k|,|Upqr|≤1 and U(mn)c=∅ if Umn≠∅ for all 1≤m,n≤5.
Moreover, it is not difficult to verify that the same argument is also valid for |Uij|=|Umn|=1 for some i,m≠1. Since E(⟨∪i≠1Uij⟩)=∅, let {i,j}∩{m,n}=ℓ. So ˜γ(AG(L))=2 whenever ∪k≠ℓU1k=∅, |U1ℓ|≤1, |U1ℓ∪∪p≠1Upqr|≤2 and U(mn)c=∅ if Umn≠∅ for all 1≤m,n≤5.
Case 3.2. Suppose |Uij|=1 for some unique i≠1. If I,J∈∪k≠i,jU1k∪U(ij)c, then the sets X=Ui∪Uj∪Uij and Y=U1∪I∪J∪∪k≠i,jUk form K3,6∪(K4−e) in AG(L) and so by Proposition 1.1, ˜γ(AG(L))≥3. Therefore, |∪k≠i,jU1k∪U(ij)c|≤1.
Case 3.2.1. Suppose I∈∪k≠i,jU1k∪U(ij)c. If |U1i|≥2, then the graph induced by sets X={I1,I′1,Ii,I1i,I′1i,[Iij,I]} and Y=∪k≠i,jUk contains a minor K6,3∪(K4−e) in AG(L) and so by Proposition 1.1, ˜γ(AG(L))≥3. Therefore, |U1i|,|U1j|≤1. Further, if J∈Upqr∪Upqrs for some p≠1, then the set {I1,[I′1,J],I2,I3,I4,I5,[Iij,I]} form K7 in AG(L), a contradiction. For the remaining cases, by using Figure 3(a), we have ˜γ(AG(L))=2.
Case 3.2.2. Suppose ∪k≠i,jU1k∪U(ij)c=∅. Let max{|U1i|,|U1j|}=|U1i| and ℓ,m∈{2,3,4,5}∖{i,j}. Clearly |U1i|≤3, otherwise, the sets X=U1∪Ui∪U1i and Y=Uj∪Uℓ∪Um form K7,3 in AG(L). If |U1i|≥2 and |U1j|≥2, then AG(L)−{I1j,I′1j,Iij,(Ij,Iℓ),(Ij,I′ℓ)} contains K5,3 with X=U1∪Ui∪U1i and Y=Uj∪Uℓ∪Um which is similar to the graph G15 (refer Case 4.2.2 of [3, Theorem 5.2]) so that ˜γ(AG(L))≥3.
Let |U1i|=3. If I∈∪p≠1Upqr∪Upqrs, then the subgraph AG(L)−{Iij,I,(I1,Ii),(I′1,Ii)} contains K6,3 with X=U1∪Ui∪U1i and Y=Uj∪Uℓ∪Um. Note that any N2-embedding of K6,3 has only rectangular faces. Further, in AG(L), Iij is adjacent to I1,I′1,Iℓ,Im and I is adjacent to I1,I′1. So, to embed the vertices Iij and I, it requires two distinct rectangular faces that contain both I1 and I′1. Next, to embed the edges (I1,Ii) and (I′1,Ii), it requires two more distinct rectangular faces with diagonals I1,Ii and I′1,Ii. In such a case, one cannot construct the remaining five distinct rectangular faces by using the existing vertices and edges, a contradiction. Therefore, ∪p≠1Upqr∪Upqrs=∅. In this case, that is |U1i|=3, |U1j|≤1 with ∪p≠1Upqr∪Upqrs=∅, and by the help of Figure 3(b), we get ˜γ(AG(L))=2.
Let |U1i|=2. Then, U(1i)c=∅; otherwise, the minor subgraph induced by the set {I1,[I′1,Iij],I2,I3,I4,I5,[I1i,I(1i)c]} form K7 in AG(L). Suppose |U1j|=1. If I∈∪p≠1Upqr∪Upqrs, then AG(L)−{I1j,Iij,I,(I1,Ii),(I′1,Ii)} contains K5,3 with X=U1∪Ui∪U1i and Y=Uj∪Uℓ∪Um. By using the structure of the graph G15 (refer Case 4.2.2 of [3, Theorem 5.2]), we have ˜γ(AG(L))≥3. Suppose U1j=∅. If |∪p≠1;pqr≠(1i)cUpqr|≥2 or ∪p≠1;pqr≠(1i)cUpqr,U2345≠∅, then the reader can verify that ˜γ(AG(L))≥3. Therefore, ˜γ(AG(L))=2 whenever |U1j|=1 with ∪p≠1Upqr∪Upqrs=∅ or U1j=∅ with |∪p≠1;pqr≠(1i)cUpqr|≤1 and U2345=∅ while |∪p≠1;pqr≠(1i)cUpqr|=1.
Let |U1i|,|U1j|≤1. Then, U(1i)c,U(1j)c=∅ whenever U1i,U1j≠∅. Note that by Theorem 2.8 [10], ˜γ(AG(L))=1 if ∪p≠1Upqr=∅.
Thus, ˜γ(AG(L))=2 if |U1i∪U1j|=2 with |∪p≠1;pqr≠(1i)c,(1j)cUpqr|=1 (or) |U1i∪U1j|=1 with |∪p≠1;pqr≠(1i)c,(1j)cUpqr|=2, U2345=∅ or |∪p≠1;pqr≠(1i)c,(1j)cUpqr|=1 (or) |U1i∪U1j|=∅ with 1≤|∪p≠1Upqr|≤2.
Case 3.3. Suppose Uij=∅ for all i≠1. Then, the subgraph induced by the neighborhood set of each vertex in U1mn for all 2≤m,n≤5 is an edge and so it does not play any role in determining the value of the crosscap. If |∪2≤k≤5U1k|≥5 or |U1k|≥4 or |Upqr|≥4 for p≠1, then K3,x where x≥7 is a subgraph of AG(L) and so ˜γ(AG(L))≥3.
Case 3.3.1. Let |U1k|∈{2,3}. Clearly, U(1m)c=∅ whenever U1m≠∅ for all 2≤m≤5; otherwise, K3,6∪(K4−e) is a subgraph of AG(L). If |Upqr|=2 for p≠1, then pqr≠(1k)c and so {p,q,r}∩{k}≠∅. Therefore, we assume that p=k. Now the subgraph G23=AG(L)−{(Ip,Iq),(Ip,Ir),(Ip,Iℓ)} contains K6,4−4e with partite set X=Up∪Uq∪Ur∪Uℓ∪Upqr and Y=U1∪U1k, where ℓ∈{2,3,4,5}∖{p,q,r}. Clearly, every face in any N2-embedding of K6,4−4e is rectangular. So to embed the edges (Ip,Iq),(Ip,Ir) and (Ip,Iℓ), it requires three rectangular faces which contains Ip, a contradiction to degK6,4−4e(Ip)=2.
Suppose |U1k|=3 for some 2≤k≤5. Then ˜γ(AG(L))=2 provided |∪ℓ≠kU1ℓ|≤1 with U(1k)c,U(1ℓ)c=∅ and |∪p≠1,pqr≠(1k)c,(1ℓ)cUpqr|≤1.
Suppose |U1k|=2 for some 2≤k≤5. If |U1ℓ|=2 for some ℓ∈{2,3,4,5}∖k, then |∪p≠1,pqr≠(1k)c,(1ℓ)cUpqr∪U2345|=∅, otherwise, AG(L) contains G23. Therefore, ˜γ(AG(L))=2 provided |∪ℓ≠kU1ℓ|≤2 with U(1k)c,U(1ℓ)c=∅. Moreover, if |U1ℓ|=2, then |∪p≠1,pqr≠(1k)c,(1ℓ)cUpqr∪U2345|=∅ and if |U1ℓ|≤1, then |Upqr|≤1 for all p≠1 and pqr≠(1k)c,(1ℓ)c.
Case 3.3.2. Suppose |U1k|≤1 for all k∈{2,3,4,5}.
Suppose |∪U1k≠∅U(1k)c|≥2, say I,J∈∪U1k≠∅U(1k)c. Then, the contraction of AG(L) induced by {I1}∪{[I′1,I′(1kc)]}∪{[I1k,I(1k)c]}∪∪ℓ≠1Uℓ in AG(L) form K7, a contradiction. Thus |∪U1k≠∅U(1k)c|≤1.
Claim A: If |∪2≤k≤5U1k|=4, then ∪p≠1Upqr=∅; equivalently, ∪2≤k≤5U(1k)c=∅.
Let |∪2≤k≤5U1k|=4. Assume on the contrary that Upqr≠∅ for some p≠1. Then pqr=(1m)c where m∈{2,3,4,5}∖{p,q,r}. Now the subgraph AG(L)−{I1q,I1r,I1m,(Ip,I1),(Ip,I′1)} contains K4,4 with partite sets X=U1∪Up∪U1p and Y=Uq∪Ur∪Um∪U(1m)c. Note that each face of any N2-embedding of K4,4 is rectangular, the vertices I1q,I1r,I1m are adjacent to Ip∈X and two vertices of Y, and Ip is adjacent to I1,I′1∈X. So to embed the remaining three vertices and two edges, it requires five rectangular faces which contains Ip but degK4,4(Ip)=4, a contradiction. Therefore, the claim holds.
Claim B: If |∪2≤k≤5U1k|≤3 and |∪U1k≠∅U(1k)c|=1, then Upqr=∅ for all p≠1,pqr≠(1k)c.
If U(1k)c≠∅ for 2≤k≤5 and Upqr≠∅ for p≠1 and pqr≠(1k)c, then the contraction of AG(L) induced by ⟨{I1}∪{[I′1,Ipqr]}∪{[I1k,I(1k)c]}∪∪ℓ≠1Uℓ⟩ contains K7, a contradiction.
Claim C: In case of |∪2≤k≤5U1k|≤3 and ∪U1k≠∅U(1k)c=∅.
Claim C1: If |∪2≤k≤5U1k|=3, then |Upqr|≤2 for p≠1,pqr≠(1k)c.
Suppose ∪U1k≠∅U(1k)c=∅ and |Upqr|≥3 for some p≠1,pqr≠(1k)c. This implies that |U1p|=|U1q|=|U1r|=1. Now consider the graph AG(L)−{Ir,I1p,I1q,I1r} which contains K5,3 with partite sets X=Up∪Uq∪Upqr and Y=U1∪Uℓ where ℓ∉{1,p,q,r}. Notice that any N2-embedding of K5,3 has one hexagonal face and six rectangular faces. Label the hexagonal face as F1. Now, try to embed the left-out vertices of AG(L) into a N2-embedding of K5,3. In AG(L), Ir is adjacent to I1,I′1,Ip,Iq and Iℓ so that Ir should be embedded into the face F1. Since I1p and I1q are adjacent to both Ir and Iℓ, we have both I1p and I1q embedded together with Ir in F1 and further the face F1 should have the path Ip−Iℓ−Iq. The point to remember here is the other neighbors of Ip and Iq in F1 are I1 and I′1. Also, I1r is adjacent to Iℓ,Ip and Iq, so to embed I1r it requires a rectangular face, say F2, that contains the path Ip−Iℓ−Iq. The point here is the fourth vertex of F2 must be either I1 or I′1. At last, since degK3,5(Ip)=3, there must be another rectangular face, say F3, in any N2-embedding of K5,3 that should have Ip. But, the edge (Ip,Iℓ) is already used twice for forming the faces F1 and F2 so that the two neighbors of Ip in F3 must be I1 and I′1. This contradicts the fact that at least one of the edges (Ip,I1) or (Ip,I′1) was used twice in F1 and F2. Thus, the claim holds true.
Claim C2: If |∪2≤k≤5U1k|≤2, then 2≤|∪p≠1,pqr≠(1k)cUpqr|≤4 with at most one |Upqr|∈{2,3}. Further, if |∪p≠1,pqr≠(1k)cUpqr|=2, then there exists Upqr such that |Upqr|=2.
First recall that if |∪2≤k≤5U1k|∈{1,2}, ∪U1k≠∅U(1k)c=∅ and |∪p≠1,pqr≠(1k)cUpqr|≤2 with |Upqr|≤1, then by Theorem 2.8 of [10], AG(L) is projective.
● If |Upqr|≥4 for some p≠1, then AG(L) contains K7,3 with partite sets Up∪Uq∪Ur∪Upqr and U1∪Um where m∈{2,…,5}∖{p,q,r}.
● Suppose there exist two sets Up1q1r1 and Up2q2r2 from the collection {Upqr:p≠1,pqr≠(1k)c} each having more than two elements. Clearly |{p1,q1,r1}∩{p2,q2,r2}|=2. So let us take p1=p2=p and q1=q2=q. Now, consider the graph AG(L)−{Ipqr2,I′pqr2,(Ip,Iq),(Ip,Ir1),(Iq,Ir1),(I1,Ir2),(I′1,Ir2)} which is isomorphic to K5,3 with partite sets X=Up∪Uq∪Ur1∪Upqr1 and Y=U1∪Ur2. Any N2-embedding of K5,3 has one hexagonal face and six rectangular faces. Note that Ipqr2 and I′pqr2 are adjacent to I1,I′1 and Ir1. To embed the vertices Ipqr2 and I′pqr2 into a N2-embedding of K5,3, we have two possibilities; (ⅰ) both Ipqr2 and I′pqr2 together with its edges are embedded in two rectangular faces, or (ⅱ) Ipqr2 and I′pqr2 together with its edges are embedded in hexagonal and rectangular faces respectively.
(ⅰ) In this case, both rectangular faces must have I1,I′1 and Ir1. Now, embedding of the edges (Ir1,Ip) and (Ir1,Iq) together with the fact that degK5,3(Ir1)=3 implies that the hexagonal face must contain Ir1. So, the edges either (Ir1,I1) or (Ir1,I1) belong to the hexagonal face, a contradiction because it is used twice in two rectangular faces.
(ⅱ) In this case, to embed the edges (Ip,Iq),(Ip,Ir1) and (Iq,Ir1), at least two rectangular faces are required. Finally, to embed the edges (I1,Ir2) and (I′1,Ir2), it requires two more rectangular faces in which the diagonals are I1,Ir2 and I′1,Ir2 respectively. But, such a case does not exist and so ˜γ(AG(L))≥3.
● Suppose |∪p≠1,pqr≠(1k)cUpqr|≥5. Then, the possibilities from the collection {Upqr:p≠1,pqr≠(1k)c} are (ⅰ) one set with three elements and two singleton sets, and (ⅱ) one set with two elements and three singleton sets. For case (ⅰ), the graph AG(L)−{I4,I245,I345,(I2,I3)} has K5,3 with partite sets X=U2∪U3∪U234 and Y=U1∪U5 which behave as a similar structure of the graph given in Claim C1. So ˜γ(AG(L))≥3. We leave it to the reader to prove ˜γ(AG(L))≥3 for case (ⅱ).
Thus, the claim holds true.
Case 4. Let |∪5n=1Un|=5 and let max1≤p<q≤5|Upq|=|Uij|. Clearly AG(L) is projective when Uij=∅. If |Uij|≥5, then the sets X=Ui∪Uj∪Uij and Y=∪k≠i,jUk form K3,7 in AG(L), a contradiction.
Case 4.1. Assume that |Uij|∈{3,4}. If Uℓm≠∅ or Uℓmn≠∅ for some ℓ,m,n∉{i,j}, then the sets X=Ui∪Uj∪Uij and Y=Uℓ∪Um∪Un∪Uℓm∪Uℓmn form K5,4 in AG(L), a contradiction. So, any non-empty two index sets Upq and three index sets Upqr must have either i or j as one of their indices. Therefore, every vertex in Uijk, for any k, is adjacent to exactly two vertices in AG(L), hence, these vertices do not play any role in finding the crosscap value. Thus, we avoid the sets Uijk for all k from V(AG(L)). Also, if Uik,Uiℓ,Uim≠∅ for k,ℓ,m∉{i,j}, then G24=AG(L)−{Iik,Iiℓ,Iim,(Ii,Ij)} contains K5,3 with partite sets X=Ui∪Uj∪Uij and Y=Uk∪Uℓ∪Um. Notice that any N2-embedding of K5,3 has one hexagonal and six rectangular faces. Also, in AG(L), Iik is adjacent to Ij,Iℓ,Im; Iiℓ is adjacent to Ij,Ik,Im and Iim is adjacent to Ij,Ik,Iℓ. So to embed the vertices Iik,Iiℓ,Iim in a N2-embedding of K5,3, it requires either one hexagon with a rectangular face or three rectangular faces which contains Ij. If Iik,Iiℓ,Iim are embedded in three rectangular faces, then since degK5,3(Ij)=3, no other face contains Ij so the edge (Ii,Ij) cannot be drawn without crossing. If not, two vertices must be inserted in the hexagonal face and the other vertex should be inserted in a rectangle face. In such cases, the third face which contains Ij does not exist because each edge occurs in exactly two faces. So ˜γ(AG(L))≥3. Therefore one of the sets Uik or Uiℓ or Uim must be empty for k,ℓ,m∉{i,j}. A slight modification of the proof would show that one of the sets Ujk or Ujℓ or Ujm must be empty for k,ℓ,m∉{i,j}.
Case 4.1.1. Suppose |Uij|=4. If |Upq|≥2 for p∈{i,j} and q∉{i,j}, then the subgraph AG(L)−{Ipq,I′pq,(Ii,Ij)} has a similar structure to the graph G16 (refer Case 5.1 [3, Theorem 5.2]) so that ˜γ(AG(L))≥3. Therefore, at most two sets from {Uik,Uiℓ,Uim} and two sets from {Ujk,Ujℓ,Ujm}, where k,ℓ,m∉{i,j}, may have an element.
Further, if Upq≠∅ for p∈{i,j} and q∉{i,j}, then we claim that the set Up′q′∪U(pq)c=∅, where p′∈{i,j}∖{p} and q≠q′∉{i,j}. Suppose not, I∈Up′q′∪U(pq)c, then the graph AG(L)−{[Ipq,I]} contains K6,3 with partite sets X=Ui∪Uj∪Uij and Y=∪k≠i,jUk. Since the merged vertex [Ipq,I] is adjacent to all the five vertices of ∪5n=1Un, it requires a face of length at least five in an N2-embedding of K6,3. A contradiction to the fact that every face in any N2-embedding of K6,3 is a rectangle.
Thus, in the case of |Uij|=4, ˜γ(AG(L))=2 provided ∪ℓ,m∉{i,j}Uℓm∪U(ij)c=∅, |∪p∈{i,j};q∉{i,j}Upq|≤2, in which |Upq|≤1 and Up′q′,U(pq)c=∅ when |Upq|=1, where p′,q′∉{p,q}.
Case 4.1.2. Suppose |Uij|=3. In every part of the case, let k,ℓ,m∈{1,…,5}∖{i,j}. If |Upq|=3 for p∈{i,j} and q∈{k,ℓ,m}, then the graph AG(L)−{Ipq,I′pq,I′′pq,(Ip′,Iq′),(Ip′,Iq′′)}, where p′∈{i,j}∖{p} and distinct q′,q′′∈{k,ℓ,m}∖{q}, contains a similar structure of the graph G′15 (refer Case 5.2 [3, Theorem 5.2]) so that ˜γ(AG(L))≥3. Also, if |Upq|=|Up′q′|=2 for distinct p,p′∈{i,j} and distinct q,q′∈{k,l,m}, then AG(L)−{Ipq,I′pq,Ip′q′,I′p′q′,(Ip,Ip′)} contains a similar structure of the graph G15 (refer to Case 4.2.2 [3, Theorem 5.2]) so that ˜γ(AG(L))≥3. Therefore, at most one set from the collection {Uik,Uiℓ,Uim,Ujk,Ujℓ,Ujm} has two elements.
(ⅰ) Without loss of generality, let us take |Uik|=2. Then, by Case 4.1, we have |Uiℓ∪Uim|≤1 and at most two sets from the collection {Ujk,Ujℓ,Ujm} have an element. But, our next claims are:
Claim A: |Uiℓ∪Uim∪Ujk|≤1 and Ujℓ∪Ujm∪U(ik)c=∅.
Suppose |Uiℓ∪Uim∪Ujk|=2. Since |Uiℓ∪Uim|≤1 and |Ujk|≤1, we choose I∈Uiℓ∪Uim and J∈Ujk. Now the graph AG(L)−{Iik,I′ik,(Ii,Ij),(Ij,[I,J])} contains K6,3 with partite sets X=Ui∪Uj∪Uij∪{[I,J]} and Y=Uk∪Uℓ∪Um. Note that all the faces in any N2-embedding of K6,3 are rectangular. Since Iik and I′ik are adjacent to Ij,Iℓ and Im, to embed the vertices Iik and I′ik, it requires two distinct rectangular faces that should have the vertex Ij in its boundary. Since degK6,3(Ij)=3, there is exactly one more rectangular face containing Ij, in which the two edges (Ij,Ii) and (Ij,[I,J]) cannot be embedded so that ˜γ(AG(L))≥3.
Suppose I∈Ujℓ∪Ujm∪U(ik)c. Then, K5,3 is a subgraph of the graph AG(L)−{Iik,I′ik,I} with partite sets X=Ui∪Uj∪Uij and Y=Uk∪Uℓ∪Um. Note that ˜γ(K5,3)=2. Since Iik−I−I′ik is a path in AG(L), these three vertices should be embedded into a single face of a N2-embedding of K5,3. First, embed the path Iik−I−I′ik together with the edges (Iik,Ij),(Iik,Iℓ),(Iik,Im),(I′ik,Ij),(I′ik,Iℓ) and (I′ik,Im) into a face. Then, clearly the middle vertex I of the path cannot adopt any edge incident with I, so the edges (I,Ii) and (I,Ik) cannot be embedded. Therefore, ˜γ(AG(L))≥3. Thus, the claim holds true.
Claim B: If |Uiℓ∪Uim∪Ujk|=1, say |Uiℓ|=1, then U(iℓ)c=∅.
If |Uiℓ|=1 with U(iℓ)c≠∅, then just replace I by Iiℓ and J by I(iℓ)c in the proof of the case |Uiℓ∪Uim∪Ujk|=2, and we get ˜γ(AG(L))≥3.
(ⅱ) Let |Uik|=1. Here, our claim is:
Claim C: |Uiℓ∪Uim∪Ujk∪Ujℓ∪Ujm∪U(ik)c|≤2, |Ujℓ∪Ujm∪U(ik)c|≤1 and |∪Upq≠∅U(pq)c|≤1. Further, if |∪Upq≠∅U(pq)c|=1, then Ujℓ∪Ujm=∅ and |Uiℓ∪Uim∪Ujk|≤1.
A slight modification of the proof of Claim B would show that |Ujℓ∪Ujm∪U(ik)c|≤1 and |∪Upq≠∅U(pq)c|≤1.
Suppose |Uiℓ∪Uim∪Ujk∪Ujℓ∪Ujm∪U(ik)c|=3. Since |Uiℓ∪Uim|≤1 and |Ujℓ∪Ujm∪U(ik)c|≤1, let I∈Uiℓ∪Uim, J∈Ujk and K∈Ujℓ∪Ujm∪U(ik)c. Then the sets X=Ui∪Uj∪Uij∪{[I,J]}∪{K,Iik} and Y=Uk∪Uℓ∪Um form K7,3.
Let |∪Upq≠∅U(pq)c|=1. If U(ik)c≠∅, then clearly Ujℓ∪Ujm=∅ and |Uiℓ∪Uim∪Ujk|≤1. If Upq,U(pq)c≠∅ for pq≠ik, then we have to show that pq≠jℓ,jm. If not, then X=Ui∪Uj∪Uij and Y=Uk∪Uℓ∪Um form K5,3 in the subgraph AG(L)−{Iik,[Ipq,I(pq)c]}. Note that ˜γ(K5,3)=2. Since the vertex Iik is adjacent to the vertex [Ipq,I(pq)c], the vertices Iik and [Ipq,I(pq)c] have to be embedded in a single face of any N2-embedding of K5,3. Here, the vertex [Ipq,I(pq)c] is adjacent to all of the five vertices of ∪5n=1Un and the vertex Iik is adjacent to exactly three vertices of ∪5n=1Un. Clearly, a single face cannot embed such eight edges onto it, a contradiction. Therefore, the claim holds true.
Thus, in the case of |Uij|=3, we have ˜γ(AG(L))=2 provided ∪ℓ,m∉{i,j}Uℓm∪U(ij)c=∅, |∪p∈{i,j};q∉{i,j}Upq|≤3, where the choice i or j for p is placed at most two times in the union, in which at most one of the sets Upq has two elements and |∪Upq≠∅U(pq)c|≤1. Further, if |Upq|=2 for some p∈{i,j};q∉{i,j}, then ∪p′,q′∉{p,q}Up′q′∪∪Upq≠∅U(pq)c=∅, and if |∪p∈{i,j};q∉{i,j}Upq|=3 with |Upq|≤1, then the three choices for q are not distinct. Moreover, if |∪Upq≠∅U(pq)c|=1, then |∪p∈{i,j};q∉{i,j}Upq|≤2 with the choice for two pairs of p,q's are not mutually disjoint.
Case 4.2. Assume |Uij|=2. If |∪ℓ,m∉{i,j}Uℓm∪U(ij)c|≥2, then the sets X=Ui∪Uj∪Uij and Y=V(AG(L))∖X form K4,5 in AG(L), a contradiction.
Further, if four non-empty sets exist other than Uij in such a way that two sets of the form Uik and two other sets of the form Ujk for k≠i,j are non-empty, say Uiℓ,Uim≠∅ and Ujℓ,Ujn≠∅ for distinct ℓ,m,n∉{i,j}. Then, the sets X={Ii,Ij,Iij,[Iiℓ,Ijn]} and Y={Iℓ,Im,In,[Iim,Ijℓ]} form (H3∪(u2,u3))−(u2,v1). Therefore, by [3, Lemma 3.6], we have ˜γ(AG(L))≥3.
Case 4.2.1. Suppose |∪ℓ,m∉{i,j}Uℓm∪U(ij)c|=1 and let I∈∪ℓ,m∉{i,j}Uℓm∪U(ij)c. If |Upq|≥2 for some p∈{i,j} and q∉{i,j}, then clearly ˜γ(AG(L))≥3. Let |Upq|=1 for some p∈{i,j} and q∉{i,j}. If J∈Up′q′∪Up′q′′ for p′∈{i,j}∖{p} and q′,q′′∉{i,j,q}, then the sets X={Ii,Ij,Iij,I′ij,[Ipq,J]} and Y={Iq,Iq′,Iq′′,I} form K5,4−e in AG(L) so that ˜γ(AG(L))≥3. Further, similar verification gives us ˜γ(AG(L))≥3 whenever U(pq)c≠∅ or there exist p∈{i,j} such that Upq≠∅ for all q∉{i,j}.
Therefore, in the case of |Uij|=2 with |∪ℓ,m∉{i,j}Uℓm∪U(ij)c|=1, ˜γ(AG(L))=2 provided |∪p∈{i,j};q∉{i,j}Upq|≤2 with |Upq|≤1 and Up′q′,U(pq)c=∅ when |Upq|=1 where p′,q′∉{p,q}.
Case 4.2.2. Suppose ∪ℓ,m∉{i,j}Uℓm∪U(ij)c=∅. If there exist p,p1∈{i,j} and q,q1∉{i,j} with pq≠p1q1 such that |Upq|,|Up1q1|=2, then AG(L) contains a structure of K3,8−4e and it can be verified that ˜γ(AG(L))≥3. So assume |Upq|=2 for unique p∈{i,j} and q∉{i,j}. If |Up′q′∪Up′q′′|>1 for p′∈{i,j}∖{p} and q′,q′′∈{1,…,5}∖{i,j,q}, then the sets X=Up∪Uq∪Upq and Y=Up′∪Uq′∪Uq′′∪Up′q′∪Up′q′′ form K4,5 in AG(L), a contradiction. If |Up′q′∪Up′q′′|=1, then |Upq′∪Upq′′∪Up′q|≤1 with Upq′=∅ if |Up′q′′|=1 and Upq′′=∅ if |Up′q′|=1 because of the facts that no two sets of the form Uik and no two sets of the form Ujk are non-empty, and the edges (Ip′q′,Ipq′′) and (Ip′q′′,Ipq′) are in AG(L). Similarly, if Up′q′,Up′q′′=∅, then |Upq′∪Upq′′|≤1 and |Up′q|≤1. Moreover, U(pq)c=∅ whenever Upq≠∅.
Finally, assume |Upq|≤1 for all p∈{i,j} and q∉{i,j}. Since no two sets from Uik and no two sets from Ujk are non-empty, |∪p∈{i,j};q∉{i,j}Upq|≤4, where the choice i or j for p is placed at most once in the union. If the subgraph induced by ⟨∪p∈{i,j};q∉{i,j}Upq⟩ in AG(L) has an edge, then U(pq)c=∅ for all Upq≠∅. If not, |∪p∈{i,j};q∉{i,j}U(pq)c|≤1, where the union is taken over all non-empty Upq. Also, by Theorem 2.1, AG(L) is projective whenever |∪p∈{i,j};q∉{i,j}Upq|≤2 with |Upq|≤1 and ∪Upq≠∅U(pq)c=∅. Further, if two non-empty sets Up1q1 and Up2q2 exists in the collection {Upq:p∈{i,j};q∉{i,j}}, then {p1,q1}∩{p2,q2}≠∅.
Therefore, in the case of |Uij|=2 with ∪ℓ,m∉{i,j}Uℓm∪U(ij)c=∅, we have ˜γ(AG(L))=2 provided 2≤|∪p∈{i,j};q∉{i,j}Upq|≤4 in which at most one of the sets Upq has two elements, where the choice i or j for p is placed at most once in the union. Moreover, one of the following is satisfied:
(a) If |Upfqf|=2 for some pf∈{i,j},qf∉{i,j}, then ∪Upq≠∅U(pq)c=∅. Further, at most one of the sets Upgqg is non-empty with the property that {pf,qf}∩{pg,qg}=∅.
(b) If |Upq|≤1 for all p∈{i,j},q∉{i,j}, then |∪Upq≠∅U(pq)c|≤1. Further, if |U(pq)c|=1 for some |Upq|=1, then every non-empty set Upf,qf should have the property that {pf,qf}∩{p,q}≠∅.
Case 4.3. Suppose |Uij|=1. If |∪1≤p≠q≤5Upq|≥6, then K8−3e is a minor of AG(L) and so by Proposition 1.1, ˜γ(AG(L))≥3. Therefore, |∪1≤p≠q≤5Upq|≤5.
(ⅰ) Let |∪1≤p≠q≤5Upq|∈{4,5}. Suppose non-empty sets Up1q1,Up2q2,Up3q3,Up4q4 exists which satisfies the conditions {p1,q1}∩{p2,q2}=∅ and {p3,q3}∩{p4,q4}=∅. If {p1,q1}∩{p3,q3}=∅ or {p2,q2}∩{p4,q4}=∅, then the vertex subset {∪5n=1Un∪[Ip1q1,Ip2q2]∪[Ip3q3,Ip4q4]} form K7. So, let us take p1∈{p1,q1}∩{p3,q3} and p2∈{p2,q2}∩{p4,q4}. Then, the sets X=Up1∪Uq1∪Ut∪Up1q1∪Up3q3 and Y=Up2∪Uq2∪Up2q2∪Up4q4, where t∈{1,…,5}∖{p1,p2,q1,q2}, form K5,4−4e in AG(L). Note that ˜γ(K4,5−4e)=2. Now it is not hard to demonstrate that the edges (Ip1,Iq1),(Iq1,Ip3q3),(Ip1,It),(Iq1,It),(Ip1q1,It),(Ip3q3,It),(Ip2,Iq2) and (Iq2,Ip4q4) of AG(L) cannot be embedded into any N2-embedding of K4,5−4e.
Also, notice that the set ∪Upq≠∅U(pq)c=∅ when |∪1≤p≠q≤5Upq|=5. Otherwise, either K7 or a graph similar to the structure of the graph G24, given in Case 4.1 of Theorem 2.2, will be a subgraph of AG(L).
Claim A: |∪Upq≠∅U(pq)c|≤1 when |∪1≤p≠q≤5Upq|=4. Moreover, if ∪Upq≠∅U(pq)c=∅, then the subgraph induced by the set ∪1≤p≠q≤5Upq has more than one edge and if |∪Upq≠∅U(pq)c|=1, say |U(rs)c|=1, then the vertex in Urs is adjacent to at most two vertices of ∪Upq≠∅;pq≠rsUpq. Further, if there is an adjacency between the vertex of Urs and a vertex of ∪Upq≠∅;pq≠rsUpq, then the subgraph induced by the set ∪Upq≠∅;pq≠rsUpq is an empty graph.
Assume that |∪1≤p≠q≤5Upq|=4. Since |Upq|≤1 for all 1≤p≠q≤5, let us take Up1q1,Up2q2,Up3q3,Up4q4≠∅.
Let |∪Upq≠∅U(pq)c|≥2. If |U(p1q1)c|≥2, then the graph AG(L)−{∪pq≠p1q1Upq,(p1,q1)} is similar to the graph G24 (Case 4.1 of Theorem 2.2) with partite sets X=Up1∪Uq1∪Up1q1 and Y=∪r≠p1,q1Ur∪U(p1q1)c so that ˜γ(AG(L))≥3. Suppose |U(p1q1)c|,|U(p2q2)c|≥1. If {p3,q3}∩{p4,q4}=∅, then the graph induced by the set {∪5n=1Un∪[Ip1q1,I(p1q1)c]∪[Ip2q2,I(p2q2)c]∪[Ip3q3,Ip4q4]} contains K8−3e so that ˜γ(AG(L))≥3. Also, if {p3,q3}∩{p4,q4}≠∅, say p3∈{p3,q3}∩{p4,q4}, then the sets X=Up3∪Up3q3∪Up4q4∪{[Ip1q1,I(p1q1)c]}∪{[Ip2q2,I(p2q2)c]} and Y=∪r≠p3Ur contains K5,4−2e in AG(L). Note that ˜γ(K5,4−2e)=2 and every face in any N2-embedding of K5,4−2e is rectangular. Since ⟨Y⟩=K4 and K4 cannot be embedded in N2 along with rectangular embedding, we have ˜γ(AG(L))≥3.
Let |U(p1q1)c|=1. If Ip1q1 is adjacent to all vertices of Up2q2∪Up3q3∪Up4q4, then the sets X=Up1∪Uq1∪Up1q1 and Y=∪r≠p1,q1Ur∪Up2q2∪Up3q3∪Up4q4∪U(p1q1)c form K3,7 in AG(L). Suppose Ip1q1 is adjacent to Ip2q2. As mentioned earlier, Ip3q3 is not adjacent to Ip4q4. If Ip2q2 is adjacent to either Ip3q3 or Ip4q4, say Ip3q3, then the set {∪5n=1Un∪[Ip1q1,I(p1q1)c]∪[Ip2q2,Ip3q3]} form K7. Therefore, E(⟨Up2q2∪Up3q3∪Up4q4⟩)=∅. Thus, the claim holds true.
Claim B: |∪Upq≠∅U(pq)c|≤3 when |∪1≤p≠q≤5Upq|≤3.
Assume that |∪1≤p≠q≤5Upq|≤3. If |U(pq)c|≥4 for 1≤p≠q≤5, then AG(L) contains K3,7 with partite sets X=Up∪Uq∪Upq and Y=∪k≠p,qUk∪U(pq)c. If three sets U(p1q1)c,U(p2q2)c,U(p3q3)c are non-empty, then the three merged vertices [Ipfqf,I(pfqf)c], for all 1≤f≤3, together with the vertices in ∪5n=1Un form K8−3e. If |U(p1q1)c|,|U(p2q2)c|≥2, then the sets X=Up1∪Uq1∪Up1q1 and Y=∪r≠p1,q1Ur∪U(p1q1)c form K3,5 which has crosscap 2. Clearly, the path I(p2q2)c−Ip2q2−I′(p2q2)c together with its edges, could not be embedded into any N2-embedding of K3,5.
Claim C: [C1] If |∪Upq≠∅U(pq)c|=3, then |U(pq)c|=3 for 1≤p≠q≤5 and no non-empty set Urs exists with {r,s}∩{p,q}=∅.
[C2] Let |∪Upq≠∅U(pq)c|∈{2,1}. If there exists a unique set U(pq)c≠∅ for 1≤p≠q≤5, then at most one non-empty set Urs exist with {r,s}∩{p,q}=∅. If two sets U(p1q1)c,U(p2q2)c≠∅ for 1≤p1,q1,p2,q2≤5 and {p1,q1}∩{p2,q2}≠∅, then no non-empty set Urs exist with {r,s}∩{pf,qf}=∅ for 1≤f≤2.
The proofs of claims [C1] and [C2] are merely verifications that can be done by the reader.
Now, to determine conditions for ˜γ(AG(L))=2 (given in the statement), we have to eliminate projective conditions of AG(L) which was given in Theorem 2.1. □
Example 2.1. As an illustration, we consider the case (ⅲ)[c] in Theorem 2.2. Let |U1|=2,|Ui|=1 for i=2,3,4,5, and |U14|=|U23|=1. If |U12|=|U13|=1, then the corresponding 6-partite graph, given in Figure 4(a), is a crosscap two graph. Also, if |U2345|=1, then the crosscap of corresponding 6-partite graph, given in Figure 4(b), is not equal to two. Moreover, the 6-partite graph G in Figure 4(b) is minimal with respect to ˜γ(G)≠2.
3.
The case when |A(L)|=6
Finally we look into the lattice with 6 atoms. We close the paper by presenting its statement and proof.
Theorem 3.1. Let L be a lattice with |A(L)|=6. Then, ˜γ(AG(L))=2 if and only if one of the following conditions hold:
(i) |∪6n=1Un|=7, there is Ui such that |Ui|=2 with ∪1≤p≠q≤6Upq=∅, ∪j,k,ℓ,m,n≠i(Ujkℓ∪Ujkℓm∪Ujkℓmn)=∅ and at most three sets Uipq's has exactly one element.
(ii) |∪6n=1Un|=6, |∪1≤i≠j≤6Uij|≤2, ∪Uij,Uijk≠∅(U(ij)c∪U(ijk)c)=∅ and one of the following cases is satisfied:
[a] In case of ∪1≤i≠j≤6Uij=∅:
[a1] If there is a unique |Uijk|=3 for 1≤i≠j≠k≤6 or |Uijk|=|Uℓmn|=2 for some ijk≠ℓmn and 1≤i,j,k,ℓ,m,n≤6, then there exist at most eight distinct non-empty Upqr's (including Uijk,Uℓmn) in which at most two distinct Upqr's are non-empty such that the intersection of all the sets at their indices has exactly two elements, where 1≤p≠q≠r≤6.
[a2] If there is a unique |Uijk|=2 for 1≤i≠j≠k≤6, then there exist at most nine distinct non-empty Upqr's (including Uijk) in which at most three distinct Upqr's are non-empty such that the intersection of all the sets at their indices has exactly two elements, where 1≤p≠q≠r≤6.
[a3] If |Uijk|≤1 for all 1≤i≠j≠k≤6, then there exist at most ten distinct non-empty Uijk's in which exactly three distinct Uijk's are non-empty such that the intersection of all the sets at their indices has exactly two elements, where 1≤i≠j≠k≤6.
[b] If |Uij|=1 for some unique 1≤i≠j≤6, then ∪{ℓ,m,n}∩{i,j}=∅Uℓmn=∅, and |∪{ℓ,m,n}∩{i,j}≠∅Uℓmn|≤6 with at most two distinct non-empty Uℓmn's in which at most one set Uℓmn has two elements such that the intersection of all the sets at their indices has exactly two elements.
[c] If |Uij|=2 for some unique 1≤i≠j≤6, then ∪{ℓ,m,n}∩{i,j}=∅Uℓmn=∪1≤k≤6Uijk=∅, and |∪|{ℓ,m,n}∩{i,j}|=1Uℓmn|≤4 with |Uℓmn|≤1 in which at most two distinct Uℓmn's are non-empty such that the intersection of all the sets at their indices has exactly two elements.
[d] If |Uij|=|Uik|=1 for some 1≤i≠j≠k≤6, then ∪{i}or{j,k}⊈{ℓ,m,n}∩{i,j,k}Uℓmn=∅, and |∪{i}or{j,k}⊆{ℓ,m,n}∩{i,j,k}Uℓmn|≤5 with |Uℓmn|≤1 in which at most two distinct Uℓmn's are non-empty such that the intersection of all the sets at their indices has exactly two elements.
Proof. Suppose that |∪6n=1Un|≥8. Then AG(L) contains K2,2,2,2 or K8−3e as a subgraph so that by Proposition 1.1, we have ˜γ(AG(L))≥3. Thus, |∪6n=1Un|≤7.
Case 1. Let |∪6n=1Un|=7. Then, |U1|=2 and |U2|=…=|U6|=1. Clearly, K7−e is a subgraph of AG(L). If I∈∪i≠1(Uij∪Uijk∪Uijkℓ∪Uijkℓm), then merge the vertices I and I1 so that K7 is a subgraph of AG(L), a contradiction. If U1j≠∅ for some j=2,…,6, then X=U1∪Uj∪U1j and Y=∪j′≠1,jUj′ form a subgraph H3 (refer [3, Lemma 3.6]) in AG(L) and so ˜γ(AG(L))≥3. Therefore, ∪i,jUij=∅.
If |U1jk|≥2 for some 2≤j,k≤6, then AG(L) contains K3,6∪(K4−e) as a minor, so by Proposition 1.1 we have ˜γ(AG(L))≥3. So, |U1jk|≤1 for all 2≤j,k≤6.
Suppose |∪U1jk|≥4. Then, it is not hard to verify that K8,3−4e is a subgraph of AG(L) with the partition set X⊃{∪U1jk∪U1}. Further, assume that a vertex in X is adjacent to at least six vertices of X or, two vertices in X is adjacent to at least five vertices of X. Note that any N2-embedding of K8,3−4e has two hexagonal and seven rectangular faces. Since the maximum degree of vertices of X in K8,3−4e is 3, at most one vertex of X may adopt 5 distinct edges from ⟨X⟩. But, ⟨X⟩ contains either a vertex of degree 6 or two vertices of degree 5, a contradiction.
Thus, ˜γ(AG(L))=2 whenever ∪k≠1(Uij∪Ukℓm∪Ukℓmn∪Ukℓmnp)=∅ with at most three U1ℓm's having one element.
Case 2. Let |∪6n=1Un|=6. Then |U1|=…=|U6|=1. If the subgraph induced by V(AG(L))∖{∪6n=1Un} has an edge (I,J), then merge the vertices I and J so that the resulting vertex is adjacent to all the vertices of ∪6n=1Un. Therefore, K7 is a minor of AG(L), a contradiction. Thus, ⟨V(AG(L))∖{∪6n=1Un}⟩ is an empty graph.
If |∪i,jUij|≥3, then the structure given for G21 is a subgraph of AG(L), so that ˜γ(AG(L))≥3. Therefore, |∪i,jUij|≤2.
Case 2.1. Assume Uij=∅ for all 1≤i,j≤6. As mentioned earlier, we have U(ijk)c=∅ when Uijk≠∅.
If |Uijk∪Uijℓ∪Uijm∪Uijn|≥4, then the subgraph AG(L)−{(Ii,Ik),(Ij,Ik),(Ik,Iijℓ),(Ik,Iijm),(Ik,Iijn)} contains K3,7−3e with partite sets X=Ui∪Uj∪Uk∪Uijk∪Uijℓ∪Uijm∪Uijn and Y=Uℓ∪Um∪Un (take ℓ,m,n∈{1,…,6}∖{i,j,k} in case of ℓ,m,n does not exist in the union of the assumption). Note that any N2-embedding of K3,7−3e have two hexagonal and six rectangular faces. The edges (Ii,Ik),(Ij,Ik),(Ik,Iijℓ),(Ik,Iijm) can be inserted without crossing in two hexagonal faces. In such a case one cannot find a rectangular face with diagonals Ik and Iijn and so ˜γ(AG(L))≥3.
Also, if |Uijk|≥4 for some 1≤i≠j≠k≤6, then the sets X=Ui∪Uj∪Uk∪Uijk and Y=∪ℓ≠i,j,kUℓ form K7,3 in AG(L).
(ⅰ) Assume |Uijk|=3 for some 1≤i≠j≠k≤6. If |Uℓmn|≥2 for some ℓmn≠ijk, then the the subgraph AG(L)−{Iℓmn,I′ℓmn,(Ii,Ij),(Ii,Ik),(Ij,Ik)} is similar to the structure of G16 (refer Case 5.1 of [3, Theorem 5.2]) so that ˜γ(AG(L))≥3. If |Uijℓ|=|Uijm|=1, then the graph AG(L)−{Iijℓ,Iijm,(Ik,Ii),(Ik,Ij)} contains K6,3 with partite sets X=Ui∪Uj∪Uk∪Uijk and Y=Uℓ∪Um∪Un. Note that every face in any N2-embedding of K6,3 is rectangular, Iijℓ is adjacent to Ik,Im,In and Iijm is adjacent to Ik,Iℓ,In. So, to embed the vertices Iijℓ and Iijm, it requires two rectangular faces that contains Ik. Now the edges (Ik,Ii) and (Ik,Ij) cannot be embedded into a single rectangular face which has Ik, a contradiction. Similarly, we get ˜γ(AG(L))≥3 whenever |Upqr|=|Upqs|=|Upqt|=1 for 1≤p≠q≠r≠s≠t≤6 with pq≠ij.
(ⅱ) Assume |Uijk|=2 for some 1≤i≠j≠k≤6. If |Uℓmn|=|Upqr|=2 for ℓmn,pqr≠ijk, then clearly ˜γ(AG(L))≥3. If |Uijℓ|=2 with Uijm≠∅ for 1≤ℓ≠m≤6, then the graph AG(L)−{(Ik,Ii),(Ik,Ij),(Ik,Iijℓ),(Ik,I′ijℓ),(Ik,Iijm)} contains K8,3−3e with partite sets X=Ui∪Uj∪Uk∪Uijk∪Uijℓ∪Uijm and Y=∪n≠i,j,kUn. Note that ˜γ(K8,3−3e)=2, and any N2-embedding of K8,3−3e have one hexagonal and nine rectangular faces. Now, to recover a N2-embedding of AG(L) from a N2-embedding of K8,3−3e, we have to embed five edges in which one end is at Ik and the another end at a vertex of X. So it is required that Ik has to be part of at least four faces of a N2-embedding of K8,3−3e, a contradiction to degK8,3−3e(Ik)=3.
Suppose |Upqr|=2 for pq≠ij. If |Uijℓ|=|Uijm|=1 for 1≤ℓ≠m≤6, then the subgraph AG(L)−{Ipqr,I′pqr,(Ik,Ii),(Ik,Ij),(Ik,Iijℓ),(Ik,Iijm),(Ii,Ij)} contains K3,7−2e with partite sets X=Ui∪Uj∪Uk∪Uijk∪Uijℓ∪Uijm and Y=Uℓ∪Um∪Un. Note that any N2-embedding of K3,7−2e have one hexagonal and 8 rectangular faces. Clearly, each rectangular face can adopt at most one new edge and so to embed the edges (Ik,Ii),(Ik,Ij),(Ik,Iijℓ),(Ik,Iijm) it requires one hexagonal and two rectangular faces which contains Ik. In addition, we have to embed the vertices Ipqr and I′pqr. Here, the vertices Ipqr and I′pqr are adjacent to at least one of Ii or Ij or Ik. If it is Ik, then clearly the edge (Ik,Ipqr) cannot be embedded. So, let Ipqr,I′pqr be adjacent to Ii. But, Ii is used in embedding the first five edges. So, the remaining two rectangular faces are required to embed the edges (Ii,Ipqr) and (Ii,I′pqr). In such a case, the edge (Ii,Ij) could not be embedded in N2, a contradiction. For all the remaining cases, one can retrieve a N2-embedding of AG(L) from Figure 5.
If |Uijk|≤1 for all 1≤i≠j≠k≤6, then by eliminating the projective cases, we will get the result as in the statement.
Case 2.2. Assume 1≤|∪i,jUij|≤2. Let Uij≠∅ for some 1≤i≠j≤6. Clearly, U(ij)c=∅ and Upqr=∅ for all {p,q,r}∩{i,j}=∅.
Choose p and q such that {p,q}∩{i,j}≠∅. If Upqr1,Upqr2,Upqr3≠∅ with r1,r2,r3∉{i,j}, then, the subgraph AG(L)−{Ipqr2,Ipqr3,(Ir1,Ip),(Ir1,Iq),(Ir1,Iij)} contains K5,3 with partite sets X=Up∪Uq∪Ur1∪Uij∪Upqr1 and Y=Ur∪Ur2∪Ur3, where r∉{p,q,r1,r2,r3}. Any N2-embedding of K5,3 have one hexagonal and six rectangular faces. Note that Ipqr2,Ipqr3 are adjacent to Ir1 and two vertices of Y. So, to embed the vertices Ipqr2,Ipqr3 together with edges (Ir1,Ip),(Ir1,Iq) and (Ir1,Iij), it requires a hexagon with three rectangular faces or five rectangular faces which contains Ir1, a contradiction to degK5,3(Ir1)=3.
(ⅰ) Assume |Uij|=1 for some unique 1≤i≠j≤6. Choose ℓ,m and n in such a way that {ℓ,m,n}∩{i,j}≠∅. If |Uℓmn|≥3, then AG(L) contains K3,7 as a subgraph, a contradiction. Also, if |Uℓmn|=|Uℓ1m1n1|=2, then the graph AG(L)−{Iℓ1m1n1,I′ℓ1m1n1,(Ii,Ij)} contains a subgraph similar to the structure of G16 (refer Case 5.1 of [3, Theorem 5.2]) and so ˜γ(AG(L))≥3. Thus, ˜γ(AG(L))=2 whenever ∪{ℓ,m,n}∩{i,j}=∅Uℓmn∪U(ij)c=∅ and, |∪{ℓ,m,n}∩{i,j}≠∅Uℓmn|≤6 in which at most one set Uℓmn has two elements with at most two distinct sets Uℓmn's non-empty such that the intersection of all the sets at their indices has exactly two elements.
(ⅱ) Assume |∪i,jUij|=2.
Suppose |Uij|=2 for 1≤i≠j≤6. If Uijk≠∅ for some 1≤k≤6, then K6,3 with partite sets X=Ui∪Uj∪Uk∪Uij∪Uijk and Y=Up∪Uq∪Ur, where p,q,r∈{1,…,6}∖{i,j,k}. Every face in any N2-embedding of K6,3 is rectangular. So, to embed the edges (Ik,Ii),(Ik,Ij),(Ik,Iij),(Ik,I′ij), it requires four rectangular faces all of which contains Ik but degK3,6(Ik)=3, a contradiction. Thus, ˜γ(AG(L))=2 when ∪{ℓ,m,n}∩{i,j}=∅Uℓmn∪∪kUijk∪U(ij)c=∅, and |∪|{ℓ,m,n}∩{i,j}|=1Uℓmn|≤4 in which |Uℓmn|≤1 with at most two distinct sets Uℓmn's non-empty such that the intersection of all the sets at their indices has exactly two elements.
Suppose distinct Uij,Upq≠∅ for 1≤i,j,p,q≤6. Then, {i,j}∩{p,q}≠∅. So let |Uij|=|Uik|=1 for some 1≤i≠j≠k≤6. Let us take ℓ,m and n such that {ℓ,m,n}∩{i,j,k} contains either {i} or {j,k}. If |Uℓmn|≥2, then the subgraph AG(L)−{Iℓmn,I′ℓmn,(Ii,Ij),(Ii,Ik),(Ij,Iik),(Ik,Iij)} contains K5,3 with partite sets X=Ui∪Uj∪Uk∪Uij∪Uik and Y=Up∪Uq∪Ur where p,q,r∈{1,…,6}∖{i,j,k}. Note that Iℓmn,I′ℓmn are adjacent to three vertices of K5,3 and so to embed the vertices Iℓmn,I′ℓmn together with edges (Ii,Ij),(Ii,Ik), it requires one hexagonal and one rectangular face. Thereafter one cannot find two rectangular faces with diagonal vertices Ij,Iik and Ik,Iij respectively. Therefore, either (Ij,Iik) or (Ik,Iij) cannot be embedded without crossing. Therefore, ˜γ(AG(L))≥3.
Thus, ˜γ(AG(L))=2 when ∪{i}or{j,k}⊈{ℓ,m,n}∩{i,j,k}Uℓmn∪U(ij)c∪U(ik)c=∅, and |∪{i}or{j,k}⊆{ℓ,m,n}∩{i,j,k}Uℓmn|≤5 in which |Uℓmn|≤1 with at most two distinct sets Uℓmn's non-empty such that the intersection of all the sets at their indices has exactly two elements. □
Example 3.1. As an illustration, we consider the case (ii)[a1] in Theorem 3.1. Let |Ui|=1 for i=1,…,6, |U123|=|U134|=2 and |U126|=|U145|=|U245|=1. If |U356|=1, then the corresponding crosscap two 8-partite graph is given in Figure 6. Also, if |U125|=1, then the crosscap of corresponding 8-partite graph, as in Figure 7, is not equal to two. Moreover, the 8-partite graph G in Figure 7 is minimal with respect to ˜γ(G)≠2.
4.
Conclusions
Note that no complete set of forbidden subgraphs for the two-crosscap surface (Klein bottle) is known yet. In this regard, an open problem will be to determine a family of graphs that has crosscap number two. This series of papers provides a class of r-partite graphs, where 3≤r≤8, that (1) can be embedded or (2) cannot be embedded in the two-crosscap surface. This was done by using the complete classification of all lattices whose annihilating-ideal graph has crosscap number two.
For the future work, one can determine all forbidden r-partite, r≥4, subgraphs for the crosscap two surface. Also, it would be interesting to classify all lattices whose annihilating-ideal graph can be embedded in the non-orientable surfaces of crosscap three.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
This research project was funded by the Deanship of Scientific Research (DSR) at King Abdulaziz University, under grant no. KEP-44-130-42. The first, second and fourth authors, therefore, acknowledge with thanks DSR for technical and financial support.
Conflict of interest
The authors declare no conflicts of interest regarding the publishing of this paper.









 DownLoad:
DownLoad:









