Controllability of fractional stochastic evolution inclusion via Hilfer derivative of fixed point theory

Abdelkader Moumen; Ammar Alsinai; Ramsha Shafqat; Nafisa A. Albasheir; Mohammed Alhagyan; Ameni Gargouri; Mohammed M. A. Almazah; Abdelkader Moumen; Ammar Alsinai; Ramsha Shafqat; Nafisa A. Albasheir; Mohammed Alhagyan; Ameni Gargouri; Mohammed M. A. Almazah

doi:10.3934/math.20231014

AIMS Mathematics

2023, Volume 8, Issue 9: 19892-19912. doi: 10.3934/math.20231014

Previous Article Next Article

Research article Special Issues

Controllability of fractional stochastic evolution inclusion via Hilfer derivative of fixed point theory

1.
Department of Mathematics, Faculty of Sciences, University of Hail, Hail 55425, Saudi Arabia
2.
Department of mathematics, Kuvempu University, Shivamogga, Karnataka-577451, India
3.
Department of Mathematics and Statistics, The University of Lahore, Sargodha 40100, Pakistan
4.
Department of Mathematics, College of Science and Arts (Magardah), King Khalied University, Magardah 61421, Saudi Arabia
5.
Department of Mathematics, College of Humanities and Science in Al Aflaj, Prince Sattam Bin Abdulaziz University, Saudi Arabia, 11912
6.
Department of Mathematics, College of Sciences and Arts (Muhyil), King Khalied University, Muhyil 61421, Saudi Arabia

Received: 09 April 2023 Revised: 29 May 2023 Accepted: 05 June 2023 Published: 14 June 2023
MSC : 34A07, 34A08, 60G22

In this study, we use the Hilfer derivative to analyze the approximate controllability of fractional stochastic evolution inclusions (FSEIs) with nonlocal conditions. By assuming that the corresponding linear system is approximately controllable, we obtain a novel set of adequate requirements for the approximate controllability of nonlinear FSEIs in meticulous detail. The fixed-point theorem for multi-valued operators and fractional calculus are used to achieve the results. Finally, we use several instances to demonstrate our findings.

Keywords:

Citation: Abdelkader Moumen, Ammar Alsinai, Ramsha Shafqat, Nafisa A. Albasheir, Mohammed Alhagyan, Ameni Gargouri, Mohammed M. A. Almazah. Controllability of fractional stochastic evolution inclusion via Hilfer derivative of fixed point theory[J]. AIMS Mathematics, 2023, 8(9): 19892-19912. doi: 10.3934/math.20231014

Related Papers:

[1]	Muammer Ayata, Ozan Özkan . A new application of conformable Laplace decomposition method for fractional Newell-Whitehead-Segel equation. AIMS Mathematics, 2020, 5(6): 7402-7412. doi: 10.3934/math.2020474
[2]	Aslı Alkan, Halil Anaç . A new study on the Newell-Whitehead-Segel equation with Caputo-Fabrizio fractional derivative. AIMS Mathematics, 2024, 9(10): 27979-27997. doi: 10.3934/math.20241358
[3]	Javed Hussain . On the series solution of the stochastic Newell Whitehead Segel equation. AIMS Mathematics, 2023, 8(9): 21591-21605. doi: 10.3934/math.20231100
[4]	Aslı Alkan, Halil Anaç . The novel numerical solutions for time-fractional Fornberg-Whitham equation by using fractional natural transform decomposition method. AIMS Mathematics, 2024, 9(9): 25333-25359. doi: 10.3934/math.20241237
[5]	Laiq Zada, Rashid Nawaz, Sumbal Ahsan, Kottakkaran Sooppy Nisar, Dumitru Baleanu . New iterative approach for the solutions of fractional order inhomogeneous partial differential equations. AIMS Mathematics, 2021, 6(2): 1348-1365. doi: 10.3934/math.2021084
[6]	M. Mossa Al-Sawalha, Khalil Hadi Hakami, Mohammad Alqudah, Qasem M. Tawhari, Hussain Gissy . Novel Laplace-integrated least square methods for solving the fractional nonlinear damped Burgers' equation. AIMS Mathematics, 2025, 10(3): 7099-7126. doi: 10.3934/math.2025324
[7]	Shabir Ahmad, Aman Ullah, Ali Akgül, Fahd Jarad . A hybrid analytical technique for solving nonlinear fractional order PDEs of power law kernel: Application to KdV and Fornberg-Witham equations. AIMS Mathematics, 2022, 7(5): 9389-9404. doi: 10.3934/math.2022521
[8]	Zihan Yue, Wei Jiang, Boying Wu, Biao Zhang . A meshless method based on the Laplace transform for multi-term time-space fractional diffusion equation. AIMS Mathematics, 2024, 9(3): 7040-7062. doi: 10.3934/math.2024343
[9]	Azzh Saad Alshehry, Naila Amir, Naveed Iqbal, Rasool Shah, Kamsing Nonlaopon . On the solution of nonlinear fractional-order shock wave equation via analytical method. AIMS Mathematics, 2022, 7(10): 19325-19343. doi: 10.3934/math.20221061
[10]	Muhammed Naeem, Noufe H. Aljahdaly, Rasool Shah, Wajaree Weera . The study of fractional-order convection-reaction-diffusion equation via an Elzake Atangana-Baleanu operator. AIMS Mathematics, 2022, 7(10): 18080-18098. doi: 10.3934/math.2022995

Abstract

1. Introduction

Fractional calculus (FC) is a subject that dates back to 1695 and is regarded to be as old as ordinary calculus. Ordinary calculus made it impossible to model nonlinear real-world phenomenon in nature, hence fractional calculus became popular among researchers. The fractional derivative is the derivative of arbitrary order in applied mathematics and mathematical analysis. In the nineteenth century, Riemann Liouville ^[1] implemented the fractional derivative when simulating real-world problems. Some of the Nobel contributions of mathematicians are listed here, Caputo ^[2], Kemple and Beyer ^[3], Abbasbandy ^[4], Jafari and Seifi ^{[5, 6]}, Miller and Ross ^[7], Podlubny ^[8], Kilbas and Trujillo ^[9], Diethelm et al. ^[10], Hayat et al. ^[11], Debanth ^[12], Momani and Shawagfeh ^[13], etc. Fractional calculus has become one of the fascinating science and engineering research areas in recent years. Viscoelasticity and damping, diffusion and wave propagation, electromagnetism and heat transfer, biology, signal processing, robotics system classification, physics, mechanics, chemistry, and control theory are the most important scientific fields that use fractional calculus at the moment.

Researchers are interested in FC because of its wide applications in physics, engineering, and real-life sciences. Fractional differential equations accurately represent these physical facts. Fractional differential equations are significantly greater generalizations of integer-order differential equations. Fractional differential equations (FDEs) have generated much interest in recent years. As a result of their frequent appearance in diverse applications, such as quantum mechanics ^[14], chaotic dynamics ^[15], plasma physics ^{[16, 17]}, theory of long-range interaction ^[18], mechanics of non-Hamiltonian systems ^[19], physical kinetics ^[20], anomalous diffusion and transport theory ^[21], mechanics of fractional media ^[22], astrophysics ^[23], and so on. FDEs have been the subject of numerous investigations. Many works have been dedicated to developing efficient methods for solving FDEs, but it is important to remember that finding an analytical or approximate solution is difficult, therefore, accurate methods for obtaining FDE solutions are still being researched. In the literature, there are several analytical and numerical approaches for solving FDEs. For example, the generalized differential transform method (GDTM) ^[24], adomian decomposition method (ADM) ^[25], homotopy analysis method (HAM) ^[26], variational iteration method (VIM) ^[27], homotopy perturbation method (HPM) ^[28], Elzaki transform decomposition method (ETDM) ^[29], iterative Laplace transform method (ILTM) ^[30], fractional wavelet method (FWM) ^{[31, 32]}, residual power series method (RPSM) ^{[33, 34]}.

In this paper, we used two powerful techniques with the aid of the Antagana-Baleanu fractional derivative operator and Laplace transform for solving time fractional NWSEs. The two well-known methods that we implement are LTDM and VITM. The suggested techniques give series form solutions having quick convergence towards the exact solutions. Four non-linear NWSEs case study issues are resolved using the given methodology. Newell and Whitehead ^[35] developed the non-linear NWSE. The diffusion term's influence interacts with the reaction term's nonlinear effect in the Newell-Whitehead-Segel equation model. The fractional NWSE is written in the following way:

$\begin{equation} D_{\tau}^{\Im}\mu(\xi, \tau ) = kD_{\xi}^{2}\mu(\xi, \tau)+g\mu-h\mu^{r}, \end{equation}$

(1.1)

where $r$ is a positive integer and $g, h$ are real numbers with $k > 0$ . The first term $D_{\tau}^{\Im}\mu(\xi, \tau)$ on the left hand side in (1.1) shows the deviations of $\mu(\xi, \tau)$ with time at a fixed location, while the right hand side first term $D_{\xi}^{2}\mu(\xi, \tau)$ shows the deviations with spatial variable $\xi$ of $\mu(\xi, \tau)$ at a specific time and the right hand side remaining terms $g\mu-h\mu^{r},$ is the source terms. $\mu(\xi, \tau)$ is a function of the spatial variable $\xi$ and the temporal variable $\tau$ in (1.1), with $\xi\in R$ and $\tau\geq0$ . The function $\mu(\xi, \tau)$ might be considered the (nonlinear) temperature distribution in an infinitely thin and long rod or as the fluid flow velocity in an infinitely long pipe with a small diameter. Many researchers find the analytical solution of NWSEs ^{[36, 37]} due to their wide range of applications in mechanical and chemical engineering, ecology, biology, and bioengineering.

2. Preleminaries

Some basic definitions related to fractional calculus are expressed here in this section.

Definition 2.1. The Caputo fractional-order derivative is given as

$\begin{equation} ^{LC}D^{\Im}_{{\tau}}\{{g}({{\tau}})\} = \frac{1}{(n-{\Im})}\int_{0}^{{{\tau}}}({{\tau}}-k)^{{n}-{\Im}-1}{g}^{{n}}(k)dk, \end{equation}$

(2.1)

where ${n} < {\Im} \leq {n}+1.$

Definition 2.2. The Caputo fractional-order derivative via Laplace transformation $^{LC}D^{{\Im}}_{{\tau}}\{{g}({{\tau}})\}$ is defined as

$\begin{equation} \mathbb{L}\{^{LC}D^{{\Im}}_{{\tau}}\{{g}({{\tau}})\}\}({\omega}) = \frac{1}{{\omega}^{{n}-{\Im}}}\left[{\omega}^{n}\mathbb{L}\{{g}(\xi, {{\tau}})\}({\omega})-{\omega}^{{n}-1}{g}(\xi, 0)-\cdots-{g}^{{n}-1}(\xi, 0)\right]. \end{equation}$

(2.2)

Definition 2.3. The Atangana-Baleanu derivative in Caputo manner is given as

$\begin{equation} ^{ABC}D^{{\Im}}_{{\tau}}\{{g}({{\tau}})\} = \frac{A({\Im})}{1-{\Im}}\int_{a}^{{{\tau}}}{g}^{'}(k)E_{{\Im}}\left[-\frac{{\Im}}{1-{\Im}}(1-k)^{{\Im}}\right]dk, \end{equation}$

(2.3)

where $A({\gamma})$ is a normalization function such that $A(0) = A(1) = 1, {g}\in H^1(a, b), b > a, {\Im}\ \in[0, 1]$ and $E_{{\gamma}}$ represent the Mittag-Leffler function.

Definition 2.4. The Atangana-Baleanu derivative in Riemann-Liouville manner is given as

$\begin{equation} ^{ABC}D^{{\Im}}_{{\tau}}\{{g}({{\tau}})\} = \frac{A({\Im})}{1-{\Im}}\frac{d}{d{{\tau}}}\int_{a}^{{{\tau}}}{g}(k)E_{{\Im}}\left[-\frac{{\gamma }}{1-{\Im}}(1-k)^{{\Im}}\right]dk. \end{equation}$

(2.4)

Definition 2.5. The Laplace transform connected with the Atangana-Baleanu operator is define as

$\begin{equation} ^{AB}D^{{\Im}}_{{\tau}}\{{g}({{\tau}})\}({\omega}) = \frac{A({\gamma}){\omega}^{{\Im}}\mathbb{L}\{{g}({{\tau}})\}({\omega})-{\omega}^{{\Im}-1}{g}(0)}{(1-{\Im})\left({\omega}^{{\Im}}+\frac{{\Im}}{1-{\gamma}}\right)}. \end{equation}$

(2.5)

Definition 2.6. Consider $0 < {\Im} < 1$ , and ${g}$ is a function of ${\Im}$ , then the fractional-order integral operator of ${\Im}$ is given as

$\begin{equation} ^{ABC}I^{{\Im}}_{{\tau}}\{{g}({{\tau}})\} = \frac{1-{\Im}}{A({\Im})}{g}({{\tau}})+\frac{{\Im}}{A({\Im})\Gamma({\Im})}\int_{a}^{{{\tau}}}{g}(k)({{\tau}}-k)^{{\Im}-1}dk. \end{equation}$

(2.6)

3. The idea of LTDM

The solution by LTDM for partial differential equations having fractional-order is described in this section.

$\begin{equation} D_\tau^\Im{\mu(\xi, \tau)}+\mathcal{\bar{G}}_1(\xi, \tau)+\mathcal{N}_1(\xi, \tau) = \mathcal{F}(\xi, \tau), \quad 0 < \Im \leq 1, \end{equation}$

(3.1)

with some initial sources

$\mu(\xi, 0) = \xi(\xi)\quad\rm{and}\quad\frac{\partial}{\partial\tau}\mu(\xi, 0) = \zeta(\xi),$

where $D_\tau^\Im = \frac{\partial^\Im}{\partial \tau^\Im}$ is the fractional-order $AB$ operator having order $\Im, \mathcal{\bar{G}}_1$ is linear operator and $\mathcal{N}_1$ is non-linear and $\mathcal{F}(\xi, \tau)$ indicates the source term.

Employing the Laplace transform to (3.1), and we acquire

$\begin{equation} L[D_\tau^\Im{\mu(\xi, \tau)}+\mathcal{\bar{G}}_1(\xi, \tau)+\mathcal{N}_1(\xi, \tau)] = L[\mathcal{F}(\xi, \tau)]. \end{equation}$

(3.2)

By the virtue of Laplace differentiation property, we have

$\begin{equation} L[\mu(\xi, \tau)] = \Theta(\xi, \omega)-\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}L[\mathcal{\bar{G}}_1(\xi, \tau)+\mathcal{N}_1(\xi, \tau)], \end{equation}$

(3.3)

where

$\Theta(\xi, \omega) = \frac{1}{\omega^{\Im+1}}[\omega^{\Im}g_{0}(\xi)+\omega^{\Im-1}g_{1}(\xi)+\cdots+g_{1}(\xi)]+\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}\mathcal{F}(\xi, \tau).$

Now, applying inverse Laplace transform yields (3.3) into

$\begin{equation} \mu(\xi, \tau) = \Theta(\xi, \omega)-L^{-1}\left\{\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}L[\mathcal{\bar{G}}_1(\xi, \tau)+\mathcal{N}_1(\xi, \tau)]\right\}, \end{equation}$

(3.4)

where $\Theta(\xi, \omega)$ demonstrates the terms occurring from source factor. LTDM determines the solution of the infinite sequence of $\mu(\xi, \tau)$

$\begin{equation} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau). \end{equation}$

(3.5)

and decomposing the nonlinear operator $\mathcal{N}_1$ as

$\begin{equation} \mathcal{N}_1(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mathcal{A}_m, \end{equation}$

(3.6)

where $\mathcal{A}_m$ are Adomian polynomials given as

$\begin{equation} \mathcal{A}_m = \frac{1}{m!}\left[\frac{\partial^m}{\partial\ell^m}\left\{\mathcal{N}_1\left(\sum\limits_{k = 0}^{\infty}\ell^k\xi_k, \sum\limits_{k = 0}^{\infty}\ell^k\tau_k\right)\right\}\right]_{\ell = 0}. \end{equation}$

(3.7)

Putting (3.5) and (3.7) into (3.4), gives

$\sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \Theta(\xi, \omega)-L^{-1}\left\{\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}L[\mathcal{\bar{G}}_1(\sum\limits_{m = 0}^{\infty}\xi_m, \sum\limits_{m = 0}^{\infty}\tau_m)+\sum\limits_{m = 0}^{\infty}\mathcal{A}_m]\right\}.$

(3.8)

The following terms are described:

$\begin{align} \mu_0(\xi, \tau)& = \Theta(\xi, \omega) \end{align}$

(3.9)

$\begin{align} \mu_1(\xi, \tau)& = L^{-1}\left\{\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}L[\mathcal{\bar{G}}_1(\xi_0, \tau_0)+\mathcal{A}_0]\right\}. \end{align}$

(3.10)

Thus all components for $m\geq1$ are calculated as

$\begin{equation} \mu_{m+1}(\xi, \tau) = L^{-1}\left\{\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}L[\mathcal{\bar{G}}_1(\xi_m, \tau_m)+\mathcal{A}_m]\right\}. \end{equation}$

(3.11)

4. VITM formulation

The VITM solution for FPDEs is defined in this section.

$\begin{equation} D_{\tau}^{\Im}{\mu(\xi, \tau)}+\mathcal{M}\mu(\xi, \tau)+\mathcal{N}\mu(\xi, \tau)-\mathcal{P}(\xi, \tau) = 0, \quad m-1 < {\Im} \leq m, \end{equation}$

(4.1)

with initial source

$\begin{equation} \mu(\xi, 0) = g_1(\xi), \end{equation}$

(4.2)

where $D_\mathfrak{\tau}^{\Im} = \frac{\partial^{\Im}}{\partial \mathfrak{\tau}^{\Im}}$ is stand for fractional-order $AB$ operator, $\mathcal{M}$ is a linear operator and $\mathcal{N}$ is nonlinear term and $\mathcal{P}$ indicates the source term.

The Laplace transform is applied to Eq (4.1), we have

$\begin{equation} L[D_{\tau}^{\Im}{\mu(\xi, \tau)}]+L[\mathcal{M}\mu(\xi, \tau)+\mathcal{N}\mu(\xi, \tau)-\mathcal{P}(\xi, \tau)] = 0. \end{equation}$

(4.3)

By the property of $LT$ differentiation, we get

$\begin{equation} L[{\mu(\xi, \tau)}] = \frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\Im)}L\left[\mathcal{M}\mu(\xi, \tau)+\mathcal{N}\mu(\xi, \tau)-\mathcal{P}(\xi, \tau)\right]. \end{equation}$

(4.4)

The iteration technique for (4.4) as

$\begin{equation} \mu_{m+1}(\xi, \tau) = \mu_{m}(\xi, \tau)+\Im(s)\left[\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\Im)}L\left[\mathcal{M}\mu(\xi, \tau)+\mathcal{N}\mu(\xi, \tau)-\mathcal{P}(\xi, \tau)\right]\right], \end{equation}$

(4.5)

where $\Im(s)$ is Lagrange multiplier and

$\begin{equation} \Im(s) = -\frac{\omega^{\Im}+\Im(1-\Im)}{\omega^{\Im}}, \end{equation}$

(4.6)

with the application of inverse Laplace transform, (4.5) series form solution is given by

$\begin{align*} \mu_{0}(\xi, \tau)& = \mu(0)+L^{-1}\left[\Im(s)L[-\mathcal{P}(\xi, \tau)]\right]\\ \mu_{1}(\xi, \tau)& = L^{-1}\left[\Im(s)L[\mathcal{M}\mu(\xi, \tau)+\mathcal{N}\mu(\xi, \tau)]\right]\\ &\;\;\vdots\\ \mu_{n+1}(\xi, \tau)& = L^{-1}\left[\Im(s)L\left[\mathcal{M}\left[\mu_{0}(\xi, \tau)+\mu_{1}(\xi, \tau)+\cdots+\mu_{n}(\xi, \tau)\right]\right]\right.\\ &\quad\left.+\mathcal{N}\left[\mu_{0}(\xi, \tau)+\mu_{1}(\xi, \tau)+\cdots+\mu_{n}(\xi, \tau)\right]\right]. \end{align*}$

5. Convergence analysis

Here we discuss uniqueness and convergence analysis.

Theorem 5.1. The result of (3.1) is unique for $LTDM_{ABC}$ , when

$0 < (\theta_{1}+\theta_{2})\left(1-{{\Im}}+{{\Im}}\frac{\tau^{\mu}}{\Gamma(\mu+1)}\right) < 1.$

Proof. Let $H = (C[J], ||.||)$ with the norm $||\phi(\tau)|| = \max_{\tau\in J}|\phi(\tau)|$ be the Banach space, for all continuous function on $J.$ Let $I: H\rightarrow H$ is a non-linear mapping, where

$\mu^{C}_{l+1} = \mu^{C}_{0}+L^{-1}[p({{\Im}}, {{\upsilon}}, {\omega})L[\mathcal{L}(\mu_{l}(\xi, \tau))+\mathbb{N}(\mu_{l}(\xi, \tau))]], \quad l\geq0.$

Suppose that $|\mathcal{L}(\mu)-\mathcal{L}(\mu^{*})| < \theta_{1}|\mu-\mu^{*}|$ and $|\mathbb{N}(\mu)-\mathbb{N}(\mu^{*})| < \theta_{2}|\mu-\mu^{*}|$ , where $\mu: = \mu(\xi, \tau)$ and $\mu^{*}: = \mu^{*}(\xi, \tau)$ are two different function values and $\theta_{1}, \theta_{2}$ are Lipschitz constants.

$\begin{align} ||I\mu-I\mu^{*}||&\leq \max\limits_{t\in J}|L^{-1}\left[q({{\Im}}, {{\upsilon}}, {\omega})L[\mathcal{L}(\mu)-\mathcal{L}(\mu^{*})]+q({{\Im}}, {{\upsilon}}, {\omega})L[\mathbb{N}(\mu)-\mathbb{N}(\mu^{*})]|\right]\\ &\leq \max\limits_{t\in J}\left[\theta_{1}L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L[|\mu-\mu^{*}|]]+\theta_{2}L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L[|\mu-\mu^{*}|]]\right]\\ &\leq \max\limits_{t\in J}(\theta_{1}+\theta_{2})\left[L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L|\mu-\mu^{*}|]\right]\\ &\leq(\Im_{1}+\theta_{2})\left[L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L||\mu-\mu^{*}||]\right]\\ & = (\theta_{1}+\theta_{2})\left(1-{{\Im}}+{{\Im}}\frac{\tau^{{{\Im}}}}{\Gamma{{{\Im}}+1}}\right)||\mu-\mu^{*}||, \end{align}$

(5.1)

where $I$ is contraction as

$0 < (\theta_{1}+\theta_{2})\left(1-{{\Im}}+{{\Im}}\frac{\tau^{{{\Im}}}}{\Gamma{{{\Im}}+1}}\right) < 1.$

From Banach fixed point theorem, the result of (3.1) is unique.

Theorem 5.2. The $LTDM_{ABC}$ result of (3.1) is convergent.

Proof. Let $\mu_{m} = \sum_{r = 0}^{m}\mu_{r}(\xi, \tau)$ . To show that $\mu_{m}$ is a Cauchy sequence in $H$ . For $n\in\mathbb{N}$ , let

$\begin{align} ||\mu_{m}-\mu_{n}||& = \max\limits_{\tau\in J}|\sum\limits_{r = n+1}^{m}\mu_{r}|\\ &\leq \max\limits_{\tau\in J} \left|L^{-1}\left[q({{\Im}}, {{\upsilon}}, {\omega})L\left[\sum\limits_{r = n+1}^{m}(\mathcal{L}(\mu_{r-1})+\mathbb{N}(\mu_{r-1}))\right]\right]\right|\\ & = \max\limits_{\tau\in J} \left|L^{-1}\left[q({{\Im}}, {{\upsilon}}, {\omega})L\left[\sum\limits_{r = n+1}^{m-1}(\mathcal{L}(\mu_{r})+\mathbb{N}(u_{r}))\right]\right]\right|\\ &\leq \max\limits_{\tau\in J}\left|L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L[(\mathcal{L}(\mu_{m-1})-\mathcal{L}(\mu_{n-1})+\mathbb{N}(\mu_{m-1})-\mathbb{N}(\mu_{n-1}))]]\right|\\ &\leq\theta_{1}\max\limits_{\tau\in J}\left|L^{-1}[q({{\Im}}, {{\upsilon}}, {\omega})L[(\mathcal{L}(\mu_{m-1})-\mathcal{L}(\mu_{n-1}))]]\right|\\ &\quad+\theta_{2}\max\limits_{\tau\in J}\left|L^{-1}[p({{\Im}}, {{\upsilon}}, {\omega})L[(\mathbb{N}(\mu_{m-1})-\mathbb{N}(\mu_{n-1}))]]\right|\\ & = (\theta_{1}+\theta_{2})\left(1-{{\Im}}+{{\Im}}\frac{\tau^{{{\Im}}}}{\Gamma({{\Im}}+1)}\right)||\mu_{m-1}-\mu_{n-1}||. \end{align}$

(5.2)

Let $m = n+1$ , then

$\begin{equation} ||\mu_{n+1}-\mu_{n}||\leq \theta||\mu_{n}-\mu_{n-1}||\leq \theta^{2}||\mu_{n-1}\mu_{n-2}||\leq \cdots \leq \theta^{n}||\mu_{1}-\mu_{0}||, \end{equation}$

(5.3)

where

$\theta = (\theta_{1}+\theta_{2})\left(1-{{\Im}}+{{\Im}}\frac{\tau^{{{\Im}}}}{\Gamma({{\Im}}+1)}\right).$

Similarly, we have

$\begin{align} ||\mu_{m}-\mu_{n}||&\leq ||\mu_{n+1}-\mu_{n}||+||\mu_{n+2}\mu_{n+1}||+\cdots+||\mu_{m}-\mu_{m-1}||\\ &\leq (\theta^{n}+\theta^{n+1}+\cdots+\theta^{m-1})||\mu_{1}-\mu_{0}||\\ &\leq \theta^{n}\left(\frac{1-\theta^{m-n}}{1-\theta}\right)||\mu_{1}||. \end{align}$

(5.4)

As $0 < \theta < 1$ , we get $1-\theta^{m-n} < 1$ . Therefore, we have

$\begin{equation} ||\mu_{m}-\mu_{n}||\leq \frac{\theta^{n}}{1-\theta}\max\limits_{t\in J}||\mu_{1}||. \end{equation}$

(5.5)

Since $||\mu_{1}|| < \infty$ and $||\mu_{m}-\mu_{n}||\rightarrow 0$ , when $n \rightarrow \infty$ . As a result, $\mu_m$ is a Cauchy sequence in $H$ , implying that the series $\mu_m$ is convergent.

6. Applications

Four cases of nonlinear NWSEs are presented to demonstrate the suggested technique's capability and reliability.

Example 1. The NWSE has given in (1.1) for $g = 2, h = 3, k = 1$ and $r = 2$ becomes

$\begin{equation} D_{\tau}^{\Im}\mu(\xi, \tau ) = D_{\xi}^{2}\mu(\xi, \tau)+2\mu(\xi, \tau)-3\mu^{2} (\xi, \tau), \quad 0 < \theta\leq 1, \end{equation}$

(6.1)

with initial source $\mu(\xi, 0) = \Upsilon.$

Applying Laplace transform to (6.1), we get

$\begin{equation} \frac{\omega^{\Im}L[\mu(\xi, \tau)]-\omega^{-1}\mu(\xi, 0)}{\omega^{\Im}+\Im(1-\omega^{\Im})} = L\left[D_{\xi}^{2}\mu(\xi, \tau)+2\mu(\xi, \tau)-3\mu^{2}(\xi, \tau)\right]. \end{equation}$

(6.2)

On taking Laplace inverse transform, we get

$\begin{equation} \mu(\xi, \tau) = \Upsilon+L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left[D_{\xi}^{2}\mu(\xi, \tau)+2\mu(\xi, \tau)-3\mu^{2}(\xi, \tau)\right]\right]. \end{equation}$

(6.3)

Assume that the solution, $\mu(\xi, \tau)$ in the form of infinite series given by

$\begin{equation} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau), \end{equation}$

(6.4)

where $\mu^{2} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ are the so-called Adomian polynomials that represent the nonlinear terms, thus (6.3) having certain terms are rewritten as

$\begin{equation} \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \Upsilon+L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}} L\left[D_{\xi}^{2}\mu(\xi, \tau)+2\mu(\xi, \tau)-3\sum\limits_{m = 0}^{\infty}\mathcal{A}_m\right]\right]. \end{equation}$

(6.5)

According to (3.7), the decomposition of nonlinear terms by Adomian polynomials is defined as

$\begin{equation} \mathcal{A}_0 = \mu_{0}^2, \quad\mathcal{A}_1 = 2\mu_{0}\mu_{1}, \quad\mathcal{A}_2 = 2\mu_{0}\mu_{2}+(\mu_{1})^{2}. \end{equation}$

(6.6)

Thus, on comparing both sides of (6.5)

$\begin{equation*} \mu_0(\xi, \tau) = \Upsilon. \end{equation*}$

For $m = 0$ , we have

$\begin{equation*} \mu_1(\xi, \tau) = \Upsilon(2-3\Upsilon)\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]. \end{equation*}$

For $m = 1$ , we have

$\begin{equation*} \mu_2(\xi, \tau) = 2\Upsilon(2-3\Upsilon)(1-3\Upsilon)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \end{equation*}$

The approximate series solution is expressed as

$\begin{equation*} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \mu_0(\xi, \tau)+\mu_1(\xi, \tau)+\mu_2(\xi, \tau)+\cdots. \end{equation*}$

Therefore, we have

$\begin{align*} \mu(\xi, \tau)& = \Upsilon+\Upsilon(2-3\Upsilon)\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+2\Upsilon(2-3\Upsilon)(1-3\Upsilon)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align*}$

Particularly, putting $\Im = 1$ , we get the exact solution

$\begin{equation} \mu(\mu, \tau) = \frac{-\frac{2}{3}\Upsilon\exp({2\tau})}{-\frac{2}{3}+\Upsilon-\Upsilon\exp({2\tau})}. \end{equation}$

(6.7)

The analytical results by VITM:

The iteration formulas for (6.1), we have

$\begin{equation} \mu_{m+1}(\xi, \tau) = \mu_{m}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{m}(\xi, \tau)+2\mu_{m}(\xi, \tau)-3\mu_{m}^{2}(\xi, \tau)\right\}\right], \end{equation}$

(6.8)

where $\mu_0(\xi, \tau) = \Upsilon.$

For $m = 0, 1, 2, \ldots$ , we have

(6.9)

(6.10)

Therefore, we obtain

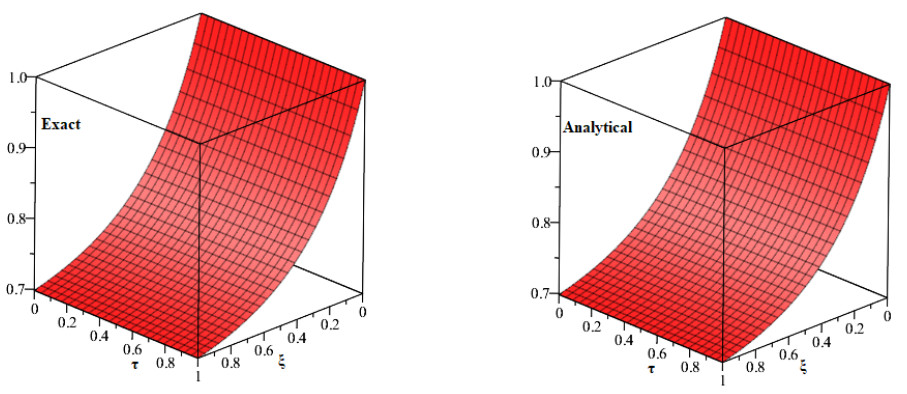
$\begin{align} \mu(\xi, \tau)& = \sum\limits_{m = 0}^{\infty}\mu_{m}(\xi, \tau) = \Upsilon+\Upsilon(2-3\Upsilon)\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+2\Upsilon(2-3\Upsilon)(1-3\Upsilon)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align}$

(6.11)

Particularly, putting $\Im = 1$ , we get the exact solution, see Figure 1 and Table 1.

$\begin{equation} \ \mu(\xi, \tau) = \frac{-\frac{2}{3}\Upsilon\exp({2\tau})}{-\frac{2}{3}+\Upsilon-\Upsilon\exp({2\tau})}. \end{equation}$

(6.12)

Figure 1. The solution graph of Example 1, the exact solution and the analytical solution at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Table 1.

$\mu(\xi, \tau)$ Comparison of the exact solution, our methods solution and absolute error (AE) of Example 1.

$\tau=0.0001$	Exact solution	Our methods solution	AE of our methods	AE of our methods	AE of our methods
${\Upsilon}$	$\Im=1$	$\Im=1$	$\Im=1$	$\Im=0.9$	$\Im=0.8$
0	0.000000000000000	0.000000000000000	0.0000000000E+00	0.0000000000E+00	0.0000000000E+00
0.1	0.100000170000000	0.100000100000000	7.0000000000E-08	2.4390000000E-07	1.5317000000E-06
0.2	0.200000280000000	0.200000200000000	8.0000000000E-08	5.4790000000E-07	3.1233000000E-06
0.3	0.300000330000000	0.300000300000000	3.0000000000E-08	9.1180000000E-07	4.7750000000E-06
0.4	0.400000320000000	0.400000400000000	8.0000000000E-08	1.3357000000E-06	6.4866000000E-06
0.5	0.500000250000000	0.500000500000000	2.5000000000E-07	1.8197000000E-06	8.2582000000E-06
0.6	0.600000120000000	0.600000600000000	4.8000000000E-07	2.3636000000E-06	1.0089700000E-05
0.7	0.699999930000000	0.700000700000000	7.7000000000E-07	2.9675000000E-06	1.1981300000E-05
0.8	0.799999680000000	0.800000800000000	1.1200000000E-06	3.6315000000E-06	1.3932800000E-05
0.9	0.899999370000000	0.900000900000000	1.5300000000E-06	4.3554000000E-06	1.5944400000E-05
1.0	0.999999000000000	1.000001000000000	2.0000000000E-06	5.1390000000E-06	1.8016000000E-05

| Show Table

DownLoad: CSV

Example 2. The NWSE has given in (1.1) for $g = 1, h = 1, k = 1$ and $r = 2$ becomes

$\begin{equation} D_{\tau}^{\Im}\mu(\xi, \tau ) = D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)(1-\mu(\xi, \tau)), \quad 0 < \Im\leq1, \end{equation}$

(6.13)

with initial source

$\begin{equation*} \mu(\xi, 0) = \frac{1}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{2}}. \end{equation*}$

Applying Laplace transform to (6.13), we get

$\begin{equation} \frac{\omega^{\Im}L[\mu(\xi, \tau)]-\omega^{-1}\mu(\xi, 0)}{\omega^{\Im}+\Im(1-\omega^{\Im})} = L\left[D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)(1-\mu(\xi, \tau))\right]. \end{equation}$

(6.14)

On taking Laplace inverse transform, we get

$\begin{equation} \mu(\xi, \tau) = \frac{1}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{2}}+L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left[D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)(1-\mu(\xi, \tau))\right]\right]. \end{equation}$

(6.15)

Assume that the solution, $\mu(\xi, \tau)$ in the form of infinite series given by

$\begin{equation} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau), \end{equation}$

(6.16)

where $\mu^{2} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ are the so-called Adomian polynomials that represent the nonlinear terms, thus (6.15) having certain terms are rewritten as

$\begin{equation} \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \frac{1}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{2}} +L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left[D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)-\sum\limits_{m = 0}^{\infty}\mathcal{A}_m\right]\right]. \end{equation}$

(6.17)

Applying the proposed analytical approach and the nonlinear terms can be obtained with the aid of Adomian's polynomials stated in (3.7), we acquire

$\begin{equation*} \mu_0(\xi, \tau) = \frac{1}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{2}}. \end{equation*}$

For $m = 0$ , we have

$\begin{equation*} \mu_1(\xi, \tau) = \frac{5}{3}\frac{\exp\left({\frac{\xi}{\sqrt{6}}}\right)}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{3}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]. \end{equation*}$

For $m = 1$ , we have

$\begin{equation*} \mu_2(\xi, \tau) = \frac{25}{18}\left(\frac{\exp\left({\frac{\xi}{\sqrt{6}}}\right)\left(-1+2\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{4}}\right)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \end{equation*}$

The approximate series solution is expressed as

$\begin{equation*} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \mu_0(\xi, \tau)+\mu_1(\xi, \tau)+\mu_2(\xi, \tau)+\cdots. \end{equation*}$

Therefore, we obtain

$\begin{align*} \mu(\xi, \tau)& = \frac{1}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{2}}+\frac{5}{3}\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{3}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]+\frac{25}{18}\left(\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)\left(-1+2\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)}{\left(1+\exp\left({\frac{\xi}{\sqrt{6}}}\right)\right)^{4}}\right)\\ &\quad\times\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align*}$

Particularly, putting $\Im = 1$ , we get the exact solution

$\begin{equation} \mu(\mu, \tau) = \left(\frac{1}{1+\exp\left(\frac{\xi}{\sqrt{6}}-\frac{5}{6}\tau\right)}\right)^{2}. \end{equation}$

(6.18)

The analytical results by VITM:

The iteration formulas for (6.13), we have

$\begin{equation} \mu_{m+1}(\xi, \tau) = \mu_{m}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{m}(\xi, \tau)+\mu_{m}(\xi, \tau)(1-\mu_{m}(\xi, \tau))\right\}\right], \end{equation}$

(6.19)

where

$\begin{equation*} \mu_0(\xi, \tau) = \frac{1}{(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)}. \end{equation*}$

For $m = 0, 1, 2, \ldots$ , we have

$\begin{align} \mu_{1}(\xi, \tau)& = \mu_{0}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{0}(\xi, \tau)+\mu_{0}(\xi, \tau)(1-\mu_{0}(\xi, \tau))\right\}\right]\\ \mu_1(\xi, \tau)& = \frac{5}{3}\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{3}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right] \end{align}$

(6.20)

$\begin{align} \mu_{2}(\xi, \tau)& = \mu_{1}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{1}(\xi, \tau)+\mu_{1}(\xi, \tau)(1-\mu_{1}(\xi, \tau))\right\}\right]\\ \mu_2(\xi, \tau)& = \frac{25}{18}\left(\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)\left(-1+2\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{4}}\right)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right] \\\;\;\vdots\notag \end{align}$

(6.21)

Therefore, we obtain

$\begin{align} \mu(\xi, \tau)& = \sum\limits_{m = 0}^{\infty}\mu_{m}(\xi, \tau) = \frac{1}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{2}}+\frac{5}{3}\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{3}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+\frac{25}{18}\left(\frac{\exp\left(\frac{\xi}{\sqrt{6}}\right)\left(-1+2\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)}{\left(1+\exp\left(\frac{\xi}{\sqrt{6}}\right)\right)^{4}}\right)\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align}$

(6.22)

Particularly, putting $\Im = 1$ , we get the exact solution, see Figures 2, 3 and Table 2.

$\begin{equation} \mu(\xi, \tau) = \left(\frac{1}{1+\exp\left(\frac{\xi}{\sqrt{6}}-\frac{5}{6}\tau\right)}\right)^{2}. \end{equation}$

(6.23)

Figure 2. The exact solution and analytical solution of Example 2 at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. The two and three dimensional different fractional order graphs of

$\Im$ example 2.

DownLoad: Full-Size Img PowerPoint

Table 2.

$\mu(\xi, \tau)$ Comparison of exact solution, our methods solution and Absolute Error (AE) of Example 2.

$\tau=0.0001$	Exact solution	Our methods solution	AE of our methods	AE of our methods	AE of our methods
${\xi}$	$\Im=1$	$\Im=1$	$\Im=1$	$\Im=0.9$	$\Im=0.8$
0	0.250020833800000	0.250020833700000	1.0000000000E-10	3.3580800000E-05	1.2032390000E-04
0.1	0.239919747900000	0.239919747800000	5.0941566800E-11	3.2881658260E-05	1.1781851670E-04
0.2	0.230035072700000	0.230035072600000	8.1583004800E-11	3.2156851240E-05	1.1522127190E-04
0.3	0.220374241800000	0.220374241700000	1.3295068340E-10	3.1408781520E-05	1.1254074080E-04
0.4	0.210943948200000	0.210943948100000	1.7637132220E-10	3.0639941880E-05	1.0978578190E-04
0.5	0.201750129200000	0.201750129000000	1.5669454130E-10	2.9852894210E-05	1.0696543270E-04
0.6	0.192797956100000	0.192797956000000	1.0301314750E-10	2.9050141560E-05	1.0408873760E-04
0.7	0.184091829000000	0.184091828700000	2.3924337590E-10	2.8234000470E-05	1.0116457590E-04
0.8	0.175635376500000	0.175635376200000	2.9445508530E-10	2.7407274000E-05	9.8202291510E-05
0.9	0.167431461100000	0.167431460800000	3.1297190840E-10	2.6572425380E-05	9.5210825130E-05
1.0	0.159482188800000	0.159482188600000	2.6399135400E-10	2.5731952810E-05	9.2199048510E-05

| Show Table

DownLoad: CSV

Example 3. The NWSE has given in (1.1) for $g = 1, h = 1, k = 1$ and $r = 4$ becomes

$\begin{equation} D_{\tau}^{\Im}\mu(\xi, \tau ) = D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)-\mu^{4}(\xi, \tau), \quad 0 < \Im\leq1 \end{equation}$

(6.24)

with initial source

$\begin{equation*} \mu(\xi, 0) = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}. \end{equation*}$

Applying Laplace transform to (6.24), we get

(6.25)

On taking Laplace inverse transform, we get

$\begin{equation} \mu(\xi, \tau) = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}+L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left[D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)-\mu^{4}(\xi, \tau)\right]\right]. \end{equation}$

(6.26)

Assume that the solution, $\mu(\xi, \tau)$ in the form of infinite series given by

$\begin{equation} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau), \end{equation}$

(6.27)

where $\mu^{4} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ are the so-called Adomian polynomials that represent the nonlinear terms, thus (6.26) having certain terms are rewritten as

$\begin{equation} \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}} +L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}} L\left[D_{\xi}^{2}\mu(\xi, \tau)+\mu(\xi, \tau)-\sum\limits_{m = 0}^{\infty}\mathcal{A}_m\right]\right]. \end{equation}$

(6.28)

According to (3.7), the decomposition of nonlinear terms by Adomian polynomials is defined as

$\begin{equation} \mathcal{A}_0 = \mu_{0}^4, \quad\mathcal{A}_1 = 4\mu_{0}^{3}\mu_{1}, \quad\mathcal{A}_2 = 4\mu_{0}^{3}\mu_{2}+6\mu_{0}^{2}\mu_{1}^{2}. \end{equation}$

(6.29)

Thus, on comparing both sides of (6.30)

$\begin{equation*} \mu_0(\xi, \tau) = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}. \end{equation*}$

For $m = 0$ , we have

$\begin{equation*} \mu_1(\xi, \tau) = \frac{7}{5}\frac{\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{5}{3}}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]. \end{equation*}$

For $m = 1$ , we have

$\begin{equation*} \mu_2(\xi, \tau) = \frac{49}{50}\frac{\left(2\exp\left(\frac{3\xi}{\sqrt{10}}\right)-3\right)\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{8}{3}}}\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \end{equation*}$

The approximate series solution is expressed as

$\begin{equation*} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \mu_0(\xi, \tau)+\mu_1(\xi, \tau)+\mu_2(\xi, \tau)+\cdots. \end{equation*}$

Therefore, we obtain

$\begin{align*} \mu(\xi, \tau)& = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}+\frac{7}{5}\frac{\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{5}{3}}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+\frac{49}{50}\frac{\left(2\exp\left(\frac{3\xi}{\sqrt{10}}\right)-3\right)\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{8}{3}}}\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align*}$

Particularly, putting $\Im = 1$ , we get the exact solution

$\begin{equation} \ \mu(\xi, \tau) = \frac{1}{2}\tanh\left(-\frac{3}{2\sqrt{10}}\left(\xi-\frac{7}{\sqrt{10}}\tau\right)\right). \end{equation}$

(6.30)

The analytical results by VITM:

The iteration formulas for (6.24), we have

$\begin{equation} \mu_{m+1}(\xi, \tau) = \mu_{m}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{m}(\xi, \tau)+\mu_{m}(\xi, \tau)-\mu_{m}^{4}(\xi, \tau)\right\}\right], \end{equation}$

(6.31)

where

$\begin{equation*} \mu_0(\xi, \tau) = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}. \end{equation*}$

For $m = 0, 1, 2, \ldots$ , we have

$\begin{align} \mu_{1}(\xi, \tau)& = \mu_{0}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{0}(\xi, \tau)+\mu_{0}(\xi, \tau)-\mu_{0}^{4}(\xi, \tau)\right\}\right], \\ \mu_1(\xi, \tau)& = \frac{7}{5}\frac{\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{5}{3}}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right], \end{align}$

(6.32)

$\begin{align} \mu_{2}(\xi, \tau)& = \mu_{1}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{1}(\xi, \tau)+\mu_{1}(\xi, \tau)-\mu_{1}^{2}(\xi, \tau)\right\}\right], \\ \mu_2(\xi, \tau)& = \frac{49}{50}\frac{\left(2\exp\left(\frac{3\xi}{\sqrt{10}}\right)-3\right)\exp^{\frac{3}{\sqrt{10}}\xi}}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{8}{3}}}\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \\ \;\;\vdots\notag \end{align}$

(6.33)

Therefore, we obtain

$\begin{align} \mu(\xi, \tau)& = \sum\limits_{m = 0}^{\infty}\mu_{m}(\xi, \tau)\\ & = \frac{1}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{2}{3}}}+\frac{7}{5}\frac{\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{5}{3}}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+\frac{49}{50}\frac{\left(2\exp\left(\frac{3\xi}{\sqrt{10}}\right)-3\right)\exp\left(\frac{3\xi}{\sqrt{10}}\right)}{\left(1+\exp\left(\frac{3\xi}{\sqrt{10}}\right)\right)^{\frac{8}{3}}}\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align}$

(6.34)

Particularly, putting $\Im = 1$ , we get the exact solution, see Figures 4, 5 and Table 3.

$\begin{equation} \mu(\xi, \tau) = \frac{1}{2}\tanh\left(-\frac{3}{2\sqrt{10}}\left(\xi-\frac{7}{\sqrt{10}}\tau\right)\right). \end{equation}$

(6.35)

Figure 4. The exact solution and analytical solution graph of Example 3 at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. The error graph of Example 3 at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Table 3.

$\mu(\xi, \tau)$ Comparison of exact solution, our methods solution and Absolute Error (AE) of Example 3.

$\tau=0.0001$	Exact solution	Our methods solution	AE of our methods	AE of our methods	AE of our methods
${\xi}$	$\Im=1$	$\Im=1$	$\Im=1$	$\Im=0.9$	$\Im=0.8$
0	0.630004621400000	0.630004623000000	1.6000000000E-09	7.1080200000E-05	2.5467930000E-04
0.1	0.609938405400000	0.609938406700000	1.3721312690E-09	7.2077200130E-05	2.5825129220E-04
0.2	0.589628520300000	0.589628521400000	1.1413782460E-09	7.2815436450E-05	2.6089584380E-04
0.3	0.569148496800000	0.569148497700000	8.7201231790E-10	7.3288425700E-05	2.6259010230E-04
0.4	0.548573070400000	0.548573071000000	6.9266503090E-10	7.3494089020E-05	2.6332630440E-04
0.5	0.527977019100000	0.527977019700000	5.8687018460E-10	7.3434320340E-05	2.6311129590E-04
0.6	0.507434030100000	0.507434030300000	1.9085441870E-10	7.3114619290E-05	2.6196573810E-04
0.7	0.487015628200000	0.487015628200000	1.4619007300E-11	7.2545024110E-05	2.5992429560E-04
0.8	0.466790202200000	0.466790202100000	1.0115621760E-10	7.1738176370E-05	2.5703268760E-04
0.9	0.446822151300000	0.446822151000000	3.7765613140E-10	7.0709457140E-05	2.5334660600E-04
1.0	0.427171171700000	0.427171171200000	5.2356035770E-10	6.9477036140E-05	2.4893040880E-04

| Show Table

DownLoad: CSV

Example 4. The NWSE has given in (1.1) for $g = 3, h = 4, k = 1$ and $r = 3$ becomes

$\begin{equation} D_{\tau}^{\Im}\mu(\xi, \tau ) = D_{\xi}^{2}\mu(\xi, \tau)+3\mu(\xi, \tau)-4\mu^{3}(\xi, \tau) , \ \ 0 < \Im\leq1, \end{equation}$

(6.36)

with initial source

$\begin{equation*} \mu(\xi, 0) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}. \end{equation*}$

Applying Laplace transform to (6.36), we get

$\begin{equation} \frac{\omega^{\Im}L[\mu(\xi, \tau)]-\omega^{-1}\mu(\xi, 0)}{\omega^{\Im}+\Im(1-\omega^{\Im})} = L\left[D_{\xi}^{2}\mu(\xi, \tau)+3\mu(\xi, \tau)-4\mu^{3}(\xi, \tau)\right]. \end{equation}$

(6.37)

On taking Laplace inverse transform, we get

$\begin{equation} \mu(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}+L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left[D_{\xi}^{2}\mu(\xi, \tau)+3\mu(\xi, \tau)-4\mu^{3}(\xi, \tau)\right]\right]. \end{equation}$

(6.38)

Assume that the solution, $\mu(\xi, \tau)$ in the form of infinite series given by

$\begin{equation} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau), \end{equation}$

(6.39)

where $\mu^{3} = \sum_{m = 0}^{\infty}\mathcal{A}_m$ are the so-called Adomian polynomials that represent the nonlinear terms, thus (6.38) having certain terms are rewritten as

$\begin{equation} \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)} +L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}} L\left[D_{\xi}^{2}\mu(\xi, \tau)+3\mu(\xi, \tau)-4\sum\limits_{m = 0}^{\infty}\mathcal{A}_m\right]\right]. \end{equation}$

(6.40)

According to (3.7), the decomposition of nonlinear terms by Adomian polynomials is defined as,

$\begin{equation} \mathcal{A}_0 = \mu_{0}^3, \quad\mathcal{A}_1 = 3\mu_{0}^{2}\mu_{1}, \quad\mathcal{A}_2 = 3\mu_{0}^{2}\mu_{2}+3\mu_{0}\mu_{1}^{2}. \end{equation}$

(6.41)

Thus, on comparing both sides of (6.40)

$\begin{equation*} \mu_0(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}. \end{equation*}$

For $m = 0$ , we have

$\begin{equation*} \mu_1(\xi, \tau) = \frac{9}{2}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{2}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]. \end{equation*}$

For $m = 1$ , we have

$\begin{align*} \mu_2(\xi, \tau)& = \frac{81}{4}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)\left(-\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{3}}\\ &\quad\times\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \end{align*}$

The approximate series solution is expressed as

$\begin{equation*} \mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_m(\xi, \tau) = \mu_0(\xi, \tau)+\mu_1(\xi, \tau)+\mu_2(\xi, \tau)+\cdots. \end{equation*}$

Therefore, we obtain

$\begin{align*} \mu(\xi, \tau)& = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}+\frac{9}{2}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{2}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+\frac{81}{4}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)\left(-\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{3}}\\ &\quad\times\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align*}$

Particularly, putting $\Im = 1$ , we get the exact solution

$\begin{equation} \ \mu(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi-\frac{9}{2}\tau\right)}. \end{equation}$

(6.42)

The analytical results by VITM:

The iteration formulas for (6.36), we have

$\begin{equation} \mu_{m+1}(\xi, \tau) = \mu_{m}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{m}(\xi, \tau)+3\mu_{m}(\xi, \tau)-4\mu_{m}^{3}(\xi, \tau)\right\}\right], \end{equation}$

(6.43)

where

$\begin{equation*} \mu_0(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}. \end{equation*}$

For $m = 0, 1, 2, \ldots$ , we have

$\begin{align} \mu_{1}(\xi, \tau)& = \mu_{0}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{0}(\xi, \tau)+3\mu_{0}(\xi, \tau)-4\mu_{0}^{3}(\xi, \tau)\right\}\right], \\ \mu_1(\xi, \tau)& = \frac{9}{2}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{2}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right], \end{align}$

(6.44)

$\begin{align} \mu_{2}(\xi, \tau)& = \mu_{1}(\xi, \tau)-L^{-1}\left[\frac{\omega^{\Im}+\Im(1-\omega^{\Im})}{\omega^{\Im}}L\left\{\frac{\omega^{\Im}}{\omega^{\Im}+\Im(1-\omega^{\Im})}D_{\xi}^{2}\mu_{1}(\xi, \tau)+3\mu_{1}(\xi, \tau)-4\mu_{1}^{3}(\xi, \tau)\right\}\right], \\ \mu_2(\xi, \tau)& = \frac{81}{4}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)\left(-\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{3}}\\ &\quad\times\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]. \\\;\;\vdots\notag \end{align}$

(6.45)

Therefore, we obtain

$\begin{align} &\mu(\xi, \tau) = \sum\limits_{m = 0}^{\infty}\mu_{m}(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)}\\ &\quad+\frac{9}{2}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{2}}\left[\frac{\Im\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)\right]\\ &\quad+\frac{81}{4}\sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)\exp\left(\frac{\sqrt{6}}{2}\xi\right)\left(-\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)}{\left(\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi\right)\right)^{3}}\\ &\quad\times\left[\frac{\Im^{2}\tau^{2\Im}}{\Gamma(2\Im+1)}+2\Im(1-\Im)\frac{\tau^{\Im}}{\Gamma(\Im+1)}+(1-\Im)^{2}\right]+\cdots. \end{align}$

(6.46)

Particularly, putting $\Im = 1$ , we get the exact solution, see Figures 6, 7 and Table 4.

$\begin{equation} \mu(\xi, \tau) = \sqrt{\frac{3}{4}}\frac{\exp\left(\sqrt{6}\xi\right)}{\exp\left(\sqrt{6}\xi\right)+\exp\left(\frac{\sqrt{6}}{2}\xi-\frac{9}{2}\tau\right)}. \end{equation}$

(6.47)

Figure 6. The exact solution and analytical solution graph of Example 4 at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. The error graph of Example 4 at

$\Im = 1$ .

DownLoad: Full-Size Img PowerPoint

Table 4.

$\mu(\xi, \tau)$ Comparison of Exact solution, Our methods solution and Absolute Error (AE) of example 4.

$\tau=0.0001$	Exact solution	Our methods solution	AE of our methods	AE of our methods	AE of our methods
${\xi}$	$\Im=1$	$\Im=1$	$\Im=1$	$\Im=0.9$	$\Im=0.8$
0	0.433022444800000	0.433022445000000	1.7320508080E-10	7.9386816730E-06	2.2292879540E-05
0.1	0.459505816600000	0.459505816600000	3.2194421390E-11	7.9089032580E-06	2.2209048130E-05
0.2	0.485791725000000	0.485791725200000	1.6732056440E-10	7.8207979170E-06	2.1961331750E-05
0.3	0.511688623000000	0.511688622800000	2.1377960370E-10	7.6762722350E-06	2.1556125910E-05
0.4	0.537016284000000	0.537016284300000	3.7853826310E-10	7.4809626080E-06	2.1006564010E-05
0.5	0.561610593500000	0.561610593600000	1.3316432970E-10	7.2385076780E-06	2.0326137420E-05
0.6	0.585327390000000	0.585327389900000	4.4316889200E-11	6.9562540670E-06	1.9533837800E-05
0.7	0.608045207500000	0.608045207500000	4.4341099960E-11	6.6414869210E-06	1.8649762960E-05
0.8	0.629666845500000	0.629666845900000	4.6131349780E-10	6.3016518320E-06	1.7694707350E-05
0.9	0.650119804000000	0.650119803700000	7.6816056310E-10	5.9421274000E-06	1.6687344050E-05
1.0	0.669355693000000	0.669355693500000	4.9676049840E-10	5.5740946070E-06	1.5651582380E-05

| Show Table

DownLoad: CSV

7. Results and discussion

, show the behavior of the exact and proposed methods solution at $\Im = 1$ in (AB fractional derivative) manner of Example 1. The comparison of the exact and analytical solution of Example 2 is shown Figure 2, whereas the graphical view for various fractional orders is demonstrated with the help of figures. In Figure 3, the two and three dimensional different fractional order graphs of Example 2. The figures show that our solution approaches the exact solution as the fractional order goes towards the integer-order. Figure 4, demonstrate the layout of the exact and analytical solution while shows the error comparison of the exact and analytical results of Example 3. The error confirms the efficiency of the suggested techniques. The graphical view of Example 4 for exact and our solution can be seen in , however, shows the error comparison of both results. Furthermore, the behavior of the exact and proposed method solution with the aid of absolute error at different orders of $\Im$ is shown in Tables 1–4. Finally, it is clear from the figures and tables that the proposed methods have a sufficient degree of accuracy and quick convergence towards the exact solution.

8. Conclusions

The LTDM and VITM were used for solving time fractional Newell-Whitehead-Segel equation. The solution we obtained is a series that quickly converges to exact solutions. Four cases are studied, which shows that the proposed methods solutions strongly agree with the exact solution. It is found that the suggested techniques are easy to implement and need a small number of calculations. This shows that LTDM and VITM are very efficient, effective, and powerful mathematical tools easily applied in finding approximate analytic solutions for a wide range of real-world problems arising in science and engineering.

Acknowledgements

This research received funding support from the National Science, Research and Innovation Fund (NSRF), Thailand.

Conflict of interest

The authors declare that they have no competing interests.

References

[1]	Y. K. Chang, J. J. Nieto, W. S. Li, Controllability of semilinear differential systems with nonlocal initial conditions in Banach spaces, J. Optim. Theory Appl., 142 (2009), 267–273. https://doi.org/10.1007/s10957-009-9535-2 doi: 10.1007/s10957-009-9535-2
[2]	L. Górniewicz, S. K. Ntouyas, D. O'Regan, Existence and controllability results for first-and second-order functional semilinear differential inclusions with nonlocal conditions, Numer. Funct. Anal. Optim., 28 (2007), 53–82. https://doi.org/10.1080/01630560600883093 doi: 10.1080/01630560600883093
[3]	L. Górniewicz, S. K. Ntouyas, D. O'Regan, Controllability results for first and second order evolution inclusions with nonlocal conditions, Ann. Pol. Math., 89 (2007), 65–101. https://doi.org/10.4064/ap89-1-5 doi: 10.4064/ap89-1-5
[4]	N. U. Ahmed, Nonlinear stochastic differential inclusions on balance space, Stoch. Anal. Appl., 12 (1994), 1–10. https://doi.org/10.1080/07362999408809334 doi: 10.1080/07362999408809334
[5]	G. Da Prato, J. Zabczyk, Stochastic Equations in Infinite Dimensions, Cambridge: Cambridge university press, 2014.
[6]	X. Fu, Approximate controllability for neutral impulsive differential inclusions with nonlocal conditions, J. Dyn. Control Syst., 17 (2011), 359–386. https://doi.org/10.1007/s10883-011-9126-z doi: 10.1007/s10883-011-9126-z
[7]	N. I. Mahmudov, Approximate controllability of semilinear deterministic and stochastic evolution equations in abstract spaces, SIAM J. Control Optim., 42 (2003), 1604–1622. https://doi.org/10.1137/S0363012901391688 doi: 10.1137/S0363012901391688
[8]	P. Muthukumar, C. Rajivganthi, Approximate controllability of impulsive neutral stochastic functional differential system with state-dependent delay in Hilbert spaces, J. Control Theory Appl., 11 (2013), 351–358. https://doi.org/10.1007/s11768-013-2061-7 doi: 10.1007/s11768-013-2061-7
[9]	R. P. Agarwal, B. de Andrade, G. Siracusa, On fractional integro-differential equations with state-dependent delay, Comput. Math. Appl., 62 (2011), 1143–1149. https://doi.org/10.1016/j.camwa.2011.02.033 doi: 10.1016/j.camwa.2011.02.033
[10]	G. M. Mophou, G. M. N'Guérékata, Existence of mild solutions of some semilinear neutral fractional functional evolution equations with infinite delay, Appl. Math. Comput., 216 (2010), 61–69. https://doi.org/10.1016/j.amc.2009.12.062 doi: 10.1016/j.amc.2009.12.062
[11]	X. B. Shu, Y. Lai, Y. Chen, The existence of mild solutions for impulsive fractional partial differential equations, Nonlinear Anal. Theory Method. Appl., 74 (2011), 2003–2011. https://doi.org/10.1016/j.na.2010.11.007 doi: 10.1016/j.na.2010.11.007
[12]	J. Cui, L. Yan, Existence result for fractional neutral stochastic integro-differential equations with infinite delay, J. Phys. A Math. Theor., 44 (2011), 335201. https://doi.org/10.1088/1751-8113/44/33/335201 doi: 10.1088/1751-8113/44/33/335201
[13]	J. Wang, Y. Zhou, Existence and controllability results for fractional semilinear differential inclusions, Nonlinear Anal. Real World Appl., 12 (2011), 3642–3653. https://doi.org/10.1016/j.nonrwa.2011.06.021 doi: 10.1016/j.nonrwa.2011.06.021
[14]	Z. Yan, H. Zhang, Existence of solutions to impulsive fractional partial neutral stochastic integro-differential inclusions with state-dependent delay, Electron. J. Differ. Equ., 2013 (2013), 1–21.
[15]	S. Duan, J. Hu, Y. Li, Exact controllability of nonlinear stochastic impulsive evolution differential inclusions with infinite delay in Hilbert spaces, Int. J. Nonlinear Sci. Numer. Simul., 12 (2011), 23–33. https://doi.org/10.1515/ijnsns.2011.023 doi: 10.1515/ijnsns.2011.023
[16]	A. Debbouche, D. Baleanu, Controllability of fractional evolution nonlocal impulsive quasilinear delay integro-differential systems, Comput. Math. Appl., 62 (2011), 1442–1450. https://doi.org/10.1016/j.camwa.2011.03.075 doi: 10.1016/j.camwa.2011.03.075
[17]	A. Debbouche, D. Baleanu, Exact null controllability for fractional nonlocal integrodifferential equations via implicit evolution system, J. Appl. Math., 2012 (2012), 931975. https://doi.org/10.1155/2012/931975 doi: 10.1155/2012/931975
[18]	A. Debbouche, D. F. Torres, Approximate controllability of fractional nonlocal delay semilinear systems in Hilbert spaces, Int. J. Control, 86 (2013), 1577–1585. https://doi.org/10.1080/00207179.2013.791927 doi: 10.1080/00207179.2013.791927
[19]	S. Kumar, N. Sukavanam, Approximate controllability of fractional order semilinear systems with bounded delay, J. Differ. Equ., 252 (2012), 6163–6174. https://doi.org/10.1016/j.jde.2012.02.014 doi: 10.1016/j.jde.2012.02.014
[20]	N. I. Mahmudov, Approximate controllability of fractional neutral evolution equations in Banach spaces, Abstr. Appl. Anal., 2013 (2013), 531894. https://doi.org/10.1155/2013/531894 doi: 10.1155/2013/531894
[21]	Z. Yan, Approximate controllability of fractional neutral integro-differential inclusions with state-dependent delay in Hilbert spaces, IMA J. Math. Control Informa., 30 (2013), 443–462. https://doi.org/10.1093/imamci/dns033 doi: 10.1093/imamci/dns033
[22]	H. M. Ahmed, M. M. El-Borai, W. El-Sayed, A. Elbadrawi, Null controllability of Hilfer fractional stochastic differential inclusions, Fractal Fract., 6 (2022), 721. https://doi.org/10.3390/fractalfract6120721 doi: 10.3390/fractalfract6120721
[23]	T. Sathiyaraj, J. Wang, P. Balasubramaniam, Controllability and optimal control for a class of time-delayed fractional stochastic integro-differential systems, Appl. Math. Optimi., 84 (2021), 2527–2554. https://doi.org/10.1007/s00245-020-09716-w doi: 10.1007/s00245-020-09716-w
[24]	X. Ma, X. B. Shu, J. Mao, Existence of almost periodic solutions for fractional impulsive neutral stochastic differential equations with infinite delay, Stoch. Dynam., 20 (2020), 2050003. https://doi.org/10.1142/S0219493720500033 doi: 10.1142/S0219493720500033
[25]	M. Liu, L. Chen, X. B. Shu, The existence of positive solutions for $\Phi$ -Hilfer fractional differential equation with random impulses and boundary value conditions, Wave. Random Complex Media, 2022, 1–19. https://doi.org/10.1080/17455030.2023.2176695 doi: 10.1080/17455030.2023.2176695
[26]	L. Shu, X. B.Shu, J. Mao, Approximate controllability and existence of mild solutions for Riemann-Liouville fractional stochastic evolution equations with nonlocal conditions of order $1 < \alpha < 2$ , Fract. Calc. Appl. Anal., 22 (2019), 1086–1112. https://doi.org/10.1515/fca-2019-0057 doi: 10.1515/fca-2019-0057
[27]	Y. Guo, X. B. Shu, F. Xu, C. Yang, HJB equation for optimal control system with random impulses, Optimization, 2022, 1–25. https://doi.org/10.1080/02331934.2022.2154607 doi: 10.1080/02331934.2022.2154607
[28]	L. Byszewski, V. Lakshmikantham, Theorem about the existence and uniqueness of a solution of a nonlocal abstract Cauchy problem in a Banach space, Appl. Anal., 40 (1991), 11–19. https://doi.org/10.1080/00036819008839989 doi: 10.1080/00036819008839989
[29]	J. Alzabut, A. G. M. Selvam, R. A. El-Nabulsi, V. Dhakshinamoorthy, M. E. Samei, Asymptotic stability of nonlinear discrete fractional pantograph equations with non-local initial conditions, Symmetry, 13 (2021), 473. https://doi.org/10.3390/sym13030473 doi: 10.3390/sym13030473
[30]	K. Abuasbeh, R. Shafqat, Fractional Brownian motion for a system of fuzzy fractional stochastic differential equation, J. Math., 2022 (2022), 3559035. https://doi.org/10.1155/2022/3559035 doi: 10.1155/2022/3559035
[31]	K. Abuasbeh, R. Shafqat, A. Alsinai, M. Awadalla, Analysis of the mathematical modelling of COVID-19 by using mild solution with delay caputo operator, Symmetry, 15 (2023), 286. https://doi.org/10.3390/sym15020286 doi: 10.3390/sym15020286
[32]	K. Abuasbeh, R. Shafqat, A. Alsinai, M. Awadalla, Analysis of controllability of fractional functional random integroevolution equations with delay, Symmetry, 15 (2023), 290. https://doi.org/10.3390/sym15020290 doi: 10.3390/sym15020290
[33]	K. Abuasbeh, R. Shafqat, A. U. K. Niazi, M. Awadalla, Oscillatory behavior of solution for fractional order fuzzy neutral predator-prey system, AIMS Math., 7 (2022), 20383–20400. https://doi.org/10.3934/math.20221117 doi: 10.3934/math.20221117
[34]	A. Moumen, R. Shafqat, A. Alsinai, H. Boulares, M. Cancan, M. B. Jeelani, Analysis of fractional stochastic evolution equations by using Hilfer derivative of finite approximate controllability, AIMS Math., 7 (2023), 16094–16114. https://doi.org/10.3934/math.2023821 doi: 10.3934/math.2023821
[35]	A. Moumen, R. Shafqat, Z. Hammouch, A. U. K. Niazi, M. B. Jeelani, Stability results for fractional integral pantograph differential equations involving two Caputo operators, AIMS Math., 8 (2023), 6009–6025. https://doi.org/10.3934/math.2023303 doi: 10.3934/math.2023303
[36]	A. A. A. Ghafli, R. Shafqat, A. U. K. Niazi, K. Abuasbeh, M. Awadalla, Topological structure of solution sets of fractional control delay problem, Fractal Fract., 7 (2023), 59. https://doi.org/10.3390/fractalfract7010059 doi: 10.3390/fractalfract7010059
[37]	R. Sakthivel, R. Ganesh, S. M. Anthoni, Approximate controllability of fractional nonlinear differential inclusions, Appl. Math. Comput., 225 (2013), 708–717. https://doi.org/10.1016/j.amc.2013.09.068 doi: 10.1016/j.amc.2013.09.068
[38]	R. Sakthivel, S. Suganya, S. M. Anthoni, Approximate controllability of fractional stochastic evolution equations, Comput. Math. Appl., 63 (2012), 660–668. https://doi.org/10.1016/j.camwa.2011.11.024 doi: 10.1016/j.camwa.2011.11.024
[39]	Y. Ren, L. Hu, R. Sakthivel, Controllability of impulsive neutral stochastic functional differential inclusions with infinite delay, J. Comput. Appl. Math., 235 (2011), 2603–2614. https://doi.org/10.1016/j.cam.2010.10.051 doi: 10.1016/j.cam.2010.10.051
[40]	I. Podlubny, Fractional differential equations, Math. Sci. Eng., 1999,340.
[41]	F. Jarad, T. Abdeljawad, Generalized fractional derivatives and Laplace transform, Discrete Cont Dyn. S, 13 (2020), 709–722. https://doi.org/10.3934/dcdss.2020039 doi: 10.3934/dcdss.2020039
[42]	B. C. Dhage, Multi-valued mappings and fixed points Ⅱ, Tamkang J. Math., 37 (2006), 27–46. https://doi.org/10.5556/j.tkjm.37.2006.177 doi: 10.5556/j.tkjm.37.2006.177

This article has been cited by:

1.	Manal Alqhtani, Khaled M. Saad, Rasool Shah, Wajaree Weera, Waleed M. Hamanah, Analysis of the Fractional-Order Local Poisson Equation in Fractal Porous Media, 2022, 14, 2073-8994, 1323, 10.3390/sym14071323
2.	Naveed Iqbal, Thongchai Botmart, Wael W. Mohammed, Akbar Ali, Numerical investigation of fractional-order Kersten–Krasil’shchik coupled KdV–mKdV system with Atangana–Baleanu derivative, 2022, 2022, 2731-4235, 10.1186/s13662-022-03709-5
3.	Pongsakorn Sunthrayuth, Muhammad Naeem, Nehad Ali Shah, Rasool Shah, Jae Dong Chung, Numerical Simulations of the Fractional Systems of Volterra Integral Equations within the Chebyshev Pseudo-Spectral Method, 2022, 14, 2073-8994, 2575, 10.3390/sym14122575
4.	Azzh Saad Alshehry, Rasool Shah, Nehad Ali Shah, Ioannis Dassios, A Reliable Technique for Solving Fractional Partial Differential Equation, 2022, 11, 2075-1680, 574, 10.3390/axioms11100574
5.	Muhammad Naeem, Humaira Yasmin, Nehad Ali Shah, Jeevan Kafle, Kamsing Nonlaopon, Analytical Approaches for Approximate Solution of the Time-Fractional Coupled Schrödinger–KdV Equation, 2022, 14, 2073-8994, 2602, 10.3390/sym14122602
6.	Sabur Uddin, Shazia Karim, F. S. Alshammari, Harun-Or Roshid, N. F. M. Noor, Fazlul Hoque, Muhammad Nadeem, Ali Akgül, Adnan Maqsood, Bifurcation Analysis of Travelling Waves and Multi-rogue Wave Solutions for a Nonlinear Pseudo-Parabolic Model of Visco-Elastic Kelvin-Voigt Fluid, 2022, 2022, 1563-5147, 1, 10.1155/2022/8227124
7.	M. Mossa Al-Sawalha, Osama Y. Ababneh, Rasool Shah, Amjad khan, Kamsing Nonlaopon, Numerical analysis of fractional-order Whitham-Broer-Kaup equations with non-singular kernel operators, 2022, 8, 2473-6988, 2308, 10.3934/math.2023120
8.	Saleh Alshammari, Naveed Iqbal, Mohammad Yar, Yusuf Gurefe, Analytical Investigation of Nonlinear Fractional Harry Dym and Rosenau-Hyman Equation via a Novel Transform, 2022, 2022, 2314-8888, 1, 10.1155/2022/8736030
9.	Xiankang Luo, Muhammad Nadeem, Laplace residual power series method for the numerical solution of time-fractional Newell–Whitehead–Segel model, 2023, 0961-5539, 10.1108/HFF-01-2023-0001
10.	Sultan Alyobi, Rasool Shah, Adnan Khan, Nehad Ali Shah, Kamsing Nonlaopon, Fractional Analysis of Nonlinear Boussinesq Equation under Atangana–Baleanu–Caputo Operator, 2022, 14, 2073-8994, 2417, 10.3390/sym14112417
11.	Haifa A. Alyousef, Rasool Shah, Kamsing Nonlaopon, Lamiaa S. El-Sherif, Samir A. El-Tantawy, An Efficient Analytical Method for Analyzing the Nonlinear Fractional Klein–Fock–Gordon Equations, 2022, 14, 2073-8994, 2640, 10.3390/sym14122640
12.	Aisha Abdullah Alderremy, Rasool Shah, Naveed Iqbal, Shaban Aly, Kamsing Nonlaopon, Fractional Series Solution Construction for Nonlinear Fractional Reaction-Diffusion Brusselator Model Utilizing Laplace Residual Power Series, 2022, 14, 2073-8994, 1944, 10.3390/sym14091944
13.	Nehad Ali Shah, Essam R. El-Zahar, Ali Akgül, Adnan Khan, Jeevan Kafle, Yusuf Gurefe, Analysis of Fractional-Order Regularized Long-Wave Models via a Novel Transform, 2022, 2022, 2314-8888, 1, 10.1155/2022/2754507
14.	Azzh Saad Alshehry, Muhammad Imran, Rasool Shah, Wajaree Weera, Fractional-View Analysis of Fokker-Planck Equations by ZZ Transform with Mittag-Leffler Kernel, 2022, 14, 2073-8994, 1513, 10.3390/sym14081513
15.	Meshari Alesemi, Jameelah S. Al Shahrani, Naveed Iqbal, Rasool Shah, Kamsing Nonlaopon, Analysis and Numerical Simulation of System of Fractional Partial Differential Equations with Non-Singular Kernel Operators, 2023, 15, 2073-8994, 233, 10.3390/sym15010233
16.	M. Mossa Al-Sawalha, Ravi P. Agarwal, Rasool Shah, Osama Y. Ababneh, Wajaree Weera, A Reliable Way to Deal with Fractional-Order Equations That Describe the Unsteady Flow of a Polytropic Gas, 2022, 10, 2227-7390, 2293, 10.3390/math10132293
17.	Yelu Wang, Jun Tian, Yongjun Zhou, Yu Zhao, Wei Feng, Keqiang Mao, Assessing Dynamic Load Allowance of the Negative Bending Moment in Continuous Girder Bridges by Weighted Average Method, 2022, 12, 2079-6412, 1233, 10.3390/coatings12091233
18.	Badriah M. Alotaibi, Rasool Shah, Kamsing Nonlaopon, Sherif. M. E. Ismaeel, Samir A. El-Tantawy, Investigation of the Time-Fractional Generalized Burgers–Fisher Equation via Novel Techniques, 2022, 15, 2073-8994, 108, 10.3390/sym15010108
19.	Aisha Abdullah Alderremy, Rasool Shah, Nehad Ali Shah, Shaban Aly, Kamsing Nonlaopon, Evaluation of Fractional-Order Pantograph Delay Differential Equation via Modified Laguerre Wavelet Method, 2022, 14, 2073-8994, 2356, 10.3390/sym14112356
20.	M. Mossa Al-Sawalha, Rasool Shah, Kamsing Nonlaopon, Imran Khan, Osama Y. Ababneh, Fractional evaluation of Kaup-Kupershmidt equation with the exponential-decay kernel, 2023, 8, 2473-6988, 3730, 10.3934/math.2023186
21.	Mohammad Alshammari, Naveed Iqbal, Davis Bundi Ntwiga, Azhar Hussain, A Comparative Study of Fractional-Order Diffusion Model within Atangana-Baleanu-Caputo Operator, 2022, 2022, 2314-8888, 1, 10.1155/2022/9226707
22.	Naveed Iqbal, Moteb Fheed Saad Al Harbi, Saleh Alshammari, Shamsullah Zaland, Muhammad Nadeem, Analysis of Fractional Differential Equations with the Help of Different Operators, 2022, 2022, 1687-9139, 1, 10.1155/2022/1333109
23.	Naveed Iqbal, Abeer M. Albalahi, Mohammed S. Abdo, Wael W. Mohammed, Reny George, Analytical Analysis of Fractional-Order Newell-Whitehead-Segel Equation: A Modified Homotopy Perturbation Transform Method, 2022, 2022, 2314-8888, 1, 10.1155/2022/3298472
24.	Pongsakorn Sunthrayuth, Muhammad Naeem, Nehad Ali Shah, Rasool Shah, Jae Dong Chung, On the Solution of Fractional Biswas–Milovic Model via Analytical Method, 2023, 15, 2073-8994, 210, 10.3390/sym15010210
25.	Azzh Saad Alshehry, Roman Ullah, Nehad Ali Shah, Rasool Shah, Kamsing Nonlaopon, Implementation of Yang residual power series method to solve fractional non-linear systems, 2023, 8, 2473-6988, 8294, 10.3934/math.2023418
26.	Fatemah Mofarreh, Asfandyar Khan, Rasool Shah, Alrazi Abdeljabbar, A Comparative Analysis of Fractional-Order Fokker–Planck Equation, 2023, 15, 2073-8994, 430, 10.3390/sym15020430
27.	Azzh Saad Alshehry, Naila Amir, Naveed Iqbal, Rasool Shah, Kamsing Nonlaopon, On the solution of nonlinear fractional-order shock wave equation via analytical method, 2022, 7, 2473-6988, 19325, 10.3934/math.20221061
28.	Humaira Yasmin, Naveed Iqbal, Ibrahim Mahariq, A Comparative Study of the Fractional-Order Nonlinear System of Physical Models via Analytical Methods, 2022, 2022, 1563-5147, 1, 10.1155/2022/7488996
29.	Noufe H. Aljahdaly, Rasool Shah, Muhammed Naeem, Mohammad Asif Arefin, Yusuf Gurefe, A Comparative Analysis of Fractional Space-Time Advection-Dispersion Equation via Semi-Analytical Methods, 2022, 2022, 2314-8888, 1, 10.1155/2022/4856002
30.	Taher S. Hassan, Ismoil Odinaev, Rasool Shah, Wajaree Weera, Dynamical Analysis of Fractional Integro-Differential Equations, 2022, 10, 2227-7390, 2071, 10.3390/math10122071
31.	Rasool Shah, Azzh Saad Alshehry, Wajaree Weera, A Semi-Analytical Method to Investigate Fractional-Order Gas Dynamics Equations by Shehu Transform, 2022, 14, 2073-8994, 1458, 10.3390/sym14071458
32.	Naveed Iqbal, Mohammad Alshammari, Wajaree Weera, Numerical analysis of fractional-order nonlinear Gardner and Cahn-Hilliard equations, 2022, 8, 2473-6988, 5574, 10.3934/math.2023281
33.	Abd-Allah Hyder, Mohamed A. Barakat, Doaa Rizk, Rasool Shah, Kamsing Nonlaopon, Study of HIV model via recent improved fractional differential and integral operators, 2023, 8, 2473-6988, 1656, 10.3934/math.2023084
34.	Aisha Abdullah Alderremy, Fractional Numerical Simulation of Coupled Approximate Long Wave and Modified Boussinesq Equations Involving Mittag-Leffler Kernel, 2022, 14, 2073-8994, 1632, 10.3390/sym14081632
35.	Thongchai Botmart, Badriah Alotaibi, Rasool Shah, Lamiaa El-Sherif, Samir El-Tantawy, A Reliable Way to Deal with the Coupled Fractional Korteweg-De Vries Equations within the Caputo Operator, 2022, 14, 2073-8994, 2452, 10.3390/sym14112452
36.	Saleh Alshammari, Naveed Iqbal, Mohammad Yar, Yusuf Gurefe, Fractional-View Analysis of Space-Time Fractional Fokker-Planck Equations within Caputo Operator, 2022, 2022, 2314-8888, 1, 10.1155/2022/4471757
37.	Muhammad Naeem, Humaira Yasmin, Rasool Shah, Nehad Ali Shah, Jae Dong Chung, A Comparative Study of Fractional Partial Differential Equations with the Help of Yang Transform, 2023, 15, 2073-8994, 146, 10.3390/sym15010146
38.	E. M. Elsayed, Rasool Shah, Kamsing Nonlaopon, J. Vanterler da C. Sousa, The Analysis of the Fractional-Order Navier-Stokes Equations by a Novel Approach, 2022, 2022, 2314-8888, 1, 10.1155/2022/8979447
39.	Wedad Albalawi, Rasool Shah, Kamsing Nonlaopon, Lamiaa S. El-Sherif, Samir A. El-Tantawy, Laplace Residual Power Series Method for Solving Three-Dimensional Fractional Helmholtz Equations, 2023, 15, 2073-8994, 194, 10.3390/sym15010194
40.	Muhammad Naeem, Humaira Yasmin, Rasool Shah, Nehad Ali Shah, Kamsing Nonlaopon, Investigation of Fractional Nonlinear Regularized Long-Wave Models via Novel Techniques, 2023, 15, 2073-8994, 220, 10.3390/sym15010220
41.	M. Mossa Al-Sawalha, Azzh Saad Alshehry, Kamsing Nonlaopon, Rasool Shah, Osama Y. Ababneh, Approximate analytical solution of time-fractional vibration equation via reliable numerical algorithm, 2022, 7, 2473-6988, 19739, 10.3934/math.20221082
42.	M. Mossa Al-Sawalha, Rasool Shah, Kamsing Nonlaopon, Osama Y. Ababneh, Numerical investigation of fractional-order wave-like equation, 2022, 8, 2473-6988, 5281, 10.3934/math.2023265
43.	Thongchai Botmart, Ravi P. Agarwal, Muhammed Naeem, Adnan Khan, Rasool Shah, On the solution of fractional modified Boussinesq and approximate long wave equations with non-singular kernel operators, 2022, 7, 2473-6988, 12483, 10.3934/math.2022693
44.	A. A. Alderremy, Shaban Aly, Rabia Fayyaz, Adnan Khan, Rasool Shah, Noorolhuda Wyal, C. Rajivganthi, The Analysis of Fractional-Order Nonlinear Systems of Third Order KdV and Burgers Equations via a Novel Transform, 2022, 2022, 1099-0526, 1, 10.1155/2022/4935809
45.	Ahmed M. Zidan, Adnan Khan, Rasool Shah, Mohammed Kbiri Alaoui, Wajaree Weera, Evaluation of time-fractional Fisher's equations with the help of analytical methods, 2022, 7, 2473-6988, 18746, 10.3934/math.20221031
46.	Haresh P. Jani, Twinkle R. Singh, Aboodh transform homotopy perturbation method for solving fractional‐order Newell‐Whitehead‐Segel equation, 2022, 0170-4214, 10.1002/mma.8886
47.	Yogeshwari F. Patel, Jayesh M. Dhodiya, Dhrien Pandit, Exact solution of nonlinear Newell–Whitehead–Segel equation using semi‐analytical approach, 2022, 0170-4214, 10.1002/mma.8843
48.	Naveed Iqbal, Saleh Alshammari, Thongchai Botmart, Evaluation of regularized long-wave equation via Caputo and Caputo-Fabrizio fractional derivatives, 2022, 7, 2473-6988, 20401, 10.3934/math.20221118
49.	Humaira Yasmin, Naveed Iqbal, A Comparative Study of the Fractional Coupled Burgers and Hirota–Satsuma KdV Equations via Analytical Techniques, 2022, 14, 2073-8994, 1364, 10.3390/sym14071364
50.	Wedad Albalawi, Rasool Shah, Nehad Ali Shah, Jae Dong Chung, Sherif M. E. Ismaeel, Samir A. El-Tantawy, Analyzing Both Fractional Porous Media and Heat Transfer Equations via Some Novel Techniques, 2023, 11, 2227-7390, 1350, 10.3390/math11061350
51.	Azzh Saad Alshehry, Humaira Yasmin, Fazal Ghani, Rasool Shah, Kamsing Nonlaopon, Comparative Analysis of Advection–Dispersion Equations with Atangana–Baleanu Fractional Derivative, 2023, 15, 2073-8994, 819, 10.3390/sym15040819
52.	Dowlath Fathima, Reham A. Alahmadi, Adnan Khan, Afroza Akhter, Abdul Hamid Ganie, An Efficient Analytical Approach to Investigate Fractional Caudrey–Dodd–Gibbon Equations with Non-Singular Kernel Derivatives, 2023, 15, 2073-8994, 850, 10.3390/sym15040850
53.	Zaiyong Feng, Jun Mao, Zhengrong Xiang, Xuhuan Wang, Stability of short memory fractional-order hybrid systems, 2024, 90, 05779073, 1057, 10.1016/j.cjph.2024.03.024
54.	Mashael M. AlBaidani, Abdul Hamid Ganie, Fahad Aljuaydi, Adnan Khan, Application of Analytical Techniques for Solving Fractional Physical Models Arising in Applied Sciences, 2023, 7, 2504-3110, 584, 10.3390/fractalfract7080584
55.	Abdulrahman B. M. Alzahrani, Numerical Analysis of Nonlinear Coupled Schrödinger–KdV System with Fractional Derivative, 2023, 15, 2073-8994, 1666, 10.3390/sym15091666
56.	Aslı Alkan, Halil Anaç, A new study on the Newell-Whitehead-Segel equation with Caputo-Fabrizio fractional derivative, 2024, 9, 2473-6988, 27979, 10.3934/math.20241358
57.	Zhi-Yong Fan, Khalid K. Ali, M. Maneea, Mustafa Inc, Shao-Wen Yao, Solution of time fractional Fitzhugh–Nagumo equation using semi analytical techniques, 2023, 51, 22113797, 106679, 10.1016/j.rinp.2023.106679
58.	Ma’mon Abu Hammad, Albandari W. Alrowaily, Rasool Shah, Sherif M. E. Ismaeel, Samir A. El-Tantawy, Analytical analysis of fractional nonlinear Jaulent-Miodek system with energy-dependent Schrödinger potential, 2023, 11, 2296-424X, 10.3389/fphy.2023.1148306
59.	Sara Maghsoudi-Khouzani, Ali Kurt, New semi-analytical solution of fractional Newell–Whitehead–Segel equation arising in nonlinear optics with non-singular and non-local kernel derivative, 2024, 56, 1572-817X, 10.1007/s11082-023-06126-4
60.	Abdulrahman B. M. Alzahrani, Ghadah Alhawael, Novel Computations of the Time-Fractional Coupled Korteweg–de Vries Equations via Non-Singular Kernel Operators in Terms of the Natural Transform, 2023, 15, 2073-8994, 2010, 10.3390/sym15112010
61.	Mashael M. AlBaidani, Abdul Hamid Ganie, Adnan Khan, The dynamics of fractional KdV type equations occurring in magneto-acoustic waves through non-singular kernel derivatives, 2023, 13, 2158-3226, 10.1063/5.0176042
62.	Muhammad Z. Baber, Hadi Rezazadeh, Muhammad S. Iqbal, Nauman Ahmed, Muhammad W. Yasin, Mohammad Ali Hosseinzadeh, Investigation of soliton solutions for the NWHS model with temperature distribution in an infinitely long and thin rod, 2024, 0217-9849, 10.1142/S0217984924503925
63.	S Kumbinarasaiah, A N Nirmala, A numerical investigation of a well-known nonlinear Newell-Whitehead-Segel equation using the rank polynomial of the star graph, 2024, 99, 0031-8949, 065209, 10.1088/1402-4896/ad4067
64.	Abdul Hamid Ganie, Mashael M. AlBaidani, Adnan Khan, A Comparative Study of the Fractional Partial Differential Equations via Novel Transform, 2023, 15, 2073-8994, 1101, 10.3390/sym15051101
65.	Aisha A. Alderremy, Humaira Yasmin, Rasool Shah, Ali M. Mahnashi, Shaban Aly, Numerical simulation and analysis of Airy's-type equation, 2023, 21, 2391-5471, 10.1515/phys-2023-0144
66.	Umut Bektaş, Halil Anaç, A hybrid method to solve a fractional-order Newell–Whitehead–Segel equation, 2024, 2024, 1687-2770, 10.1186/s13661-023-01795-2
67.	Basma Abdul Hadi Ibrahim, Nihad Shareef Khalaf, Samer R. Yaseen, 2024, 3061, 0094-243X, 040039, 10.1063/5.0203677
68.	Yuto Nakamura, Shintaro Sato, Naofumi Ohnishi, Proper orthogonal decomposition method of constructing a reduced-order model for solving partial differential equations with parametrized initial values, 2024, 9, 26668181, 100654, 10.1016/j.padiff.2024.100654
69.	Yousef Jawarneh, Humaira Yasmin, M. Mossa Al-Sawalha, Rasool Shah, Asfandyar Khan, Fractional comparative analysis of Camassa-Holm and Degasperis-Procesi equations, 2023, 8, 2473-6988, 25845, 10.3934/math.20231318
70.	L.K. Yadav, G. Agarwal, M.M. Gour, A. Akgül, Md Yushalify Misro, S.D. Purohit, A hybrid approach for non-linear fractional Newell-Whitehead-Segel model, 2024, 15, 20904479, 102645, 10.1016/j.asej.2024.102645
71.	NEHAD ALI SHAH, MOHAMMED KBIRI ALAOUI, ALI AKGUL, AHMED M. ZIDAN, JAE DONG CHUNG, THE NEW ANALYSIS OF FRACTIONAL-ORDER MULTI-DIMENSIONAL DIFFUSION EQUATIONS BY ZZ TRANSFORM WITH MITTAG-LEFFLER KERNEL, 2023, 31, 0218-348X, 10.1142/S0218348X23400819
72.	Mashael M. AlBaidani, Abdul Hamid Ganie, Adnan Khan, Computational Analysis of Fractional-Order KdV Systems in the Sense of the Caputo Operator via a Novel Transform, 2023, 7, 2504-3110, 812, 10.3390/fractalfract7110812
73.	Liaqat Ali, Guang Zou, Na Li, Kashif Mehmood, Pan Fang, Adnan Khan, Analytical treatments of time-fractional seventh-order nonlinear equations via Elzaki transform, 2024, 145, 0022-0833, 10.1007/s10665-023-10326-y
74.	Abdul Hamid Ganie, Adnan Khan, N. S. Alharthi, Fikadu Tesgera Tolasa, Mdi Begum Jeelani, Nan-Jing Huang, Comparative Analysis of Time‐Fractional Coupled System of Shallow‐Water Equations Including Caputo’s Fractional Derivative, 2024, 2024, 2314-4629, 10.1155/jom/2440359
75.	Richard Olu Awonusika, Approximate analytical solution of a class of highly nonlinear time–fractional-order partial differential equations, 2025, 13, 26668181, 101090, 10.1016/j.padiff.2025.101090
76.	Aljawhara H Almuqrin, CGL Tiofack, DV Douanla, A Mohamadou, Weaam Alhejaili, Sherif ME Ismaeel, Samir A El-Tantawy, On the “Tantawy technique” and other methods for analyzing fractional Fokker–Plank type equations, 2025, 1461-3484, 10.1177/14613484251319893
77.	Aljawhara H. Almuqrin, Sherif M. E. Ismaeel, C. G. L. Tiofack, A. Mohamadou, Badriah Albarzan, Weaam Alhejaili, Samir A. El-Tantawy, Solving fractional physical evolutionary wave equations using advanced techniques, 2025, 2037-4631, 10.1007/s12210-025-01320-w

Reader Comments

Your name:*

Email:*
© 2023 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(2081) PDF downloads(134) Cited by(2)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Mathematics

Controllability of fractional stochastic evolution inclusion via Hilfer derivative of fixed point theory

Related Papers:

Abstract

1. Introduction

2. Preleminaries

3. The idea of LTDM

4. VITM formulation

5. Convergence analysis

6. Applications

7. Results and discussion

8. Conclusions

Acknowledgements

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Catalog

AIMS Mathematics

Controllability of fractional stochastic evolution inclusion via Hilfer derivative of fixed point theory

Related Papers:

Abstract

1. Introduction

2. Preleminaries

3. The idea of LTDM

4. VITM formulation

5. Convergence analysis

6. Applications

7. Results and discussion

8. Conclusions

Acknowledgements

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog