On fuzzy numerical model dealing with the control of glucose in insulin therapies for diabetes via nonsingular kernel in the fuzzy sense

1.   Introduction

Insulin and glucagon enzymes are produced by the pancreas and assist in glucose management. While blood sugar concentrations rise, glucagon is released into the bloodstream by the pancreas. Whenever plasma concentrations are inadequate, glycogen is generated by collapsing glucagon and producing fructose from intravascular components, which improves insulin sensitivity. Diabetes mellitus, often known as diabetes, is an illness that arises if the insulin-glucose connection requires replacement ^[1]. As a consequence of diverse underlying etiologies of diabetic complications involving persistent hyperglycemia, diabetes mellitus causes disruptions in nutrients, carb, and lipid consumption as a consequence of impaired glucose function, impaired insulin, or perhaps both. Type 1 (hyperglycemic) and type 2 (hypoglycemic) diabetes are the main types of diabetes that individuals can have ^[2]. Patients with hypoglycemia may be capable of incorporating a continuous glucose monitor (CGM) to optimize and maintain their glycemic concentration. The patient would be aseptically if any irregularities in plasma glucose were discovered. If insulin concentrations are excessively high, a mixture of CGM and insulin injections is applied to regulate glucagon.

Treatments such as glucose fortification and diet modification are currently available for diabetics. A syringe or an insulin pen is typically used to inject medication subcutaneously ^[3,4]. As a result, scientists have recently collaborated to overcome an innovation challenge in order to produce a synthetic pancreas that can perform the same endocrine functions as a genuine and normal pancreas ^[5,6]. Scientists have recently ^[7] discovered an alternative pancreas, or automatic monitoring mechanism. The proliferation of CGMs is an attempt to put the paradigm of shuttered monitoring into practice. Considering the valuable information accessible, numerous strategies are being created. Closed loop systems, model predictive influence and shaky reasoning regulation are only a few of the applications because of its capability to handle a broad plethora of different restrictions on a traditional premise. Optimal tracking regulation is the more frequently implemented communication measure. It was extremely complicated to fix the challenge of diabetes modulation in artificial pancreas experiments. The primary objectives of an artificial pancreas system are to reduce hypoglycemic episodes and ensure safe recovery from them ^[8,9,10,11], as well as to accurately alter its settings for glycaemia control in type 1 and type 2 diabetics as well as healthy people ^[12,13].

According to several academics and scientists exploring them fractional generalizations of integer-order frameworks constitute a fairly rigorous description of physical phenomena ^{[14,15,16,17,18,19,20,21,22]}. The implementation of fractional DEs has gained in popularity subsequently, and it is now widely employed in numerical simulations in scientific disciplines. Numerous major achievements, including articles and monographs, have been released in the associated domains ^{[23,24,25,26,27,28,29,30]}. For modeling purposes, the fractional derivative operators based on power law, exponential decay and Mittag-Leffler kernels can be used ^{[31,32,33,34,35,36,37,38]}. These are regarded as appropriate for understanding challenging real concerns, such as complications exhibiting anomalous tendencies, which may be duplicated by employing varying-order differential operators. These techniques have been productively employed in a variety of scientific domains, but biological models have received less consideration. The Atangana-Baleanu-Caputo (ABC)-fractional operator expressing the hereditary property is credited with this crucial breakthrough. The generalized Mittag-Leffler function outperforms the exponential decay and index law kernels due to resilient reminiscence linked in the Atangana-Baleanu fractional derivative. Moreover, the Atangana-Baleanu fractional order derivative is also Liouville-Caputo and Caputo-Fabrizio, indicating that it has both Markovian and non-Markovian features. Because the transmission of certain viral infections is aberrant, neither classical differentiation nor fractional with constant can be employed in these circumstances, although they might be highly valuable strategies for simulating epidemiological challenges ^[39,40,41].

Very recently, fractional calculus and DEs have been expanded to fuzzy set theory and fuzzy fractional order DEs, respectively; see ^[42]. Agrawal et al. ^[43] explored the idea of finding fractional DEs with correlating fuzziness and expanded Riemann-Liouville differentiability to develop a formulation which is a unification of the Hukuhara difference and the Riemann-Liouville derivative. Several authors have devoted their interests to the notion of a Hukuhara difference, which was contemplated by Bede et al. ^[44,45]. Several researchers have investigated the existence and uniqueness of solutions via fuzzifications ^[46]. It is extremely time consuming to estimate increasingly efficient results for each fuzzy fractional DE when interacting with fuzzy fractional DEs. Researchers have invested a considerable amount of time into analyzing fuzzy fractional DEs, employing diverse strategies such as perturbation methods, integral transform methods, and spectral techniques ^[47,48]. As a consequence of this relevance, we will implement a fractional instance application of strongly generalized differentiability to the control of glucose in insulin treatments for the diabetes model. The main objective of this study is to construct and investigate the Atangana-Baleanu derivative in the Caputo perspective for a comprehensive glucose-insulin governing process that has a memory and is capable of retaining all preconceptions under the complexity of the uncertainty criterion. This is a key distinction from other current derivatives, and using this derivative is convenient, which reduces the complexity of the numerical results. This paper establishes the Atangana-Baleanu derivative in the parameterization interval formulation of fuzzy valued functions (FVFs) in the notion of Caputo. Furthermore, we extend this research by using Banach fixed point and Lipschitz conditions under generalized Hukuhara differentiability in order to verify the existence and uniqueness of solutions. We suggest using an impulsive differential equation model to examine plasma glucose control in diabetics receiving impulsive insulin doses. It is a deterministic mathematical system related to fractional derivatives and diabetes mellitus. The Adams-Bashforth-Moulton technique was used in a numerical method to address the structure for this research's simulations. The outcome of the present investigation suggests that managing plasma glucose using the fractional-order model is an appropriate option.

Owing to the above propensity, we will suggest ABC fractional differentiability, also known as ABC gH-differentiability, that is predicated on the generalized Hukuhara difference. To develop this conceptualization, a straightforward technique is applied that is determined by a blending of strongly generalized differentiability and the fractional ABC derivative. Taking into account the uncertain ABC fractional derivative, we examined the model for diabetes. Furthermore, the uniqueness and existence conditions of the system alternatives are presented via the contraction mapping theorem and the Lipschitiz strategy. Numerical simulation via the varying fractional order and uncertainty parameters is analyzed in a different manner. It is expected that the projected approach will be helpful in new venues in epidemiological research.

The remaining portion of the paper is organized as follows: Section 2 presents definitions and formulas for the fractional derivatives and fuzzy set theory. Section 3 illustrates the computational procedure for the suggested fuzzy fractional model for diabetes mellitus. Section 4 is devoted to the implementation of the fuzzy fractional diabetes model utilizing the ABC fractional derivative. Also, numerical simulations have been performed in consideration of an uncertainty parameter in Section 5. At the end, Section 6 describes the conclusions.

2.   Preliminaries

Here, we recall certain fundamental ideas and definitions from fuzzy set theory and fractional calculus; see ^[14,23,42].

Definition 2.1. ^[49,50] A fuzzy number $\mu$ of mapping $\mu:\mathfrak{R}\mapsto[0, 1]$ satisfies the subsequent assumptions:

(a) $\mu$ is upper semi continuous.

(b) $\mu\big[\eta x_{1}+(1-\eta)y_{1}\big]\geq\min\big\{\mu(x_{1}), \mu(y_{1})\big\}$.

(c) $\mu$ is normal, that is, there exists $x_{0}\in\mathfrak{R}; \mu(x_{0}) = 1$.

(d) $cl\big\{y\in\mathfrak{R}, \mu(y) > 0\big\}$ is compact.

Definition 2.2. ^[49] The parameterized version of a fuzzy number $\mu$ can be expressed as

Th following characterizations hold:

(a) $\underline{\mu}({\bf{r}}_{1})$ is a left continuous, bounded and increasing mapping over $[0, 1]$ and right continuous at $0;$

(b) $\bar{\mu}({\bf{r}}_{1})$ is a right continuous, bounded and decreasing mapping over $[0, 1]$ and right continuous at $0;$

(c) $\underline{\mu}({\bf{r}}_{1})\leq\bar{\mu}({\bf{r}}_{1})$.

${\bf{r}}_{1}$ is known to be a crisp number if $\underline{\mu}({\bf{r}}_{1})\leq\bar{\mu}({\bf{r}}_{1}) = 0$.

Definition 2.3. ^[51] For ${\bf{r}}_{1}\in[0, 1]$ and two fuzzy numbers $\mu$ and $\nu$, the fuzzy algebraic operations are defined as follows:

Assume that FVF $\omega({\bf{t}}_{1})\in\mathbb{C}^{\mathcal{F}}(\mathcal{J})\cap\mathbb{L}^{\mathcal{F}}(\mathcal{J})$ and its parametric form is described as follows:

Definition 2.4. ^[52] The Hausdorff distance $\tilde{d}:\mathfrak{R}_{\mathcal{F}}\times\mathfrak{R}_{\mathcal{F}}\mapsto\mathfrak{R}_{+}\bigcup\{0\}$ is described as follows:

where $\mathfrak{R}_{\mathcal{F}}$ represents the set of all fuzzy numbers, and $(\mathfrak{R}_{\mathcal{F}}, \tilde{d})$ is a complete metric space.

A metric $\tilde{d}$ has the subsequent properties:

(i) $\tilde{d}(\mu_{1}\oplus\mu_{3}, \mu_{2}\oplus\mu_{3}) = \tilde{d}(\mu_{1}, \mu_{2}), \; \forall\; \mu_{1}, \mu_{2}, \mu_{3}\in\mathfrak{R}_{\mathcal{F}}$;

(ii) $\tilde{d}(\mu_{1}\oplus\mu_{3}, 0) = \tilde{d}(\mu_{1}, 0)+\tilde{d}(\mu_{3}, 0), \; \forall\; \mu_{1}, \mu_{2}, \mu_{3}\in\mathfrak{R}_{\mathcal{F}}$;

(iii) $\tilde{d}(\mu_{1}\oplus\mu_{2}, \mu_{1}\oplus\mu_{3}) = \tilde{d}(\mu_{2}, \mu_{3}), \; \forall\; \mu_{1}, \mu_{2}, \mu_{3}\in\mathfrak{R}_{\mathcal{F}}$;

(iv) $\tilde{d}(\mu_{1}\oplus\mu_{2}, \mu_{3}\oplus\mu_{4}) = \tilde{d}(\mu_{1}, \mu_{3})+\tilde{d}(\mu_{2}, \mu_{4}), \; \forall\; \mu_{1}, \mu_{2}, \mu_{3}\in\mathfrak{R}_{\mathcal{F}}$;

(v) $\tilde{d}(\mu_{1}\ominus\mu_{2}, \mu_{3}\ominus\mu_{4}) = \tilde{d}(\mu_{1}, \mu_{3})+\tilde{d}(\mu_{2}, \mu_{4}), \; \forall\; \mu_{1}, \mu_{2}, \mu_{3}\in\mathfrak{R}_{\mathcal{F}}$;

(vi) $\tilde{d}(a\odot\mu_{1}) = \vert a\vert\tilde{d}(\mu_{1}, \mu_{2}), \; \forall\; \mu_{1}, \mu_{2}\in\mathfrak{R}_{\mathcal{F}}$.

Definition 2.5. ^[53] The generalized Hukuhara (${\bf{g}}{\bf{H}}$) derivative of a mapping $\omega({\bf{t}}_{1})$ as a solution of model (3.1) can be described as

where $\frac{d\omega(\tau)}{d{\bf{t}}_{1}}\vert_{{\bf{g}}{\bf{H}}}\in\mathbb{C}^{\mathcal{F}}(\mathcal{J})\cap\mathbb{L}^{\mathcal{F}}(\mathcal{J})$, and

The condition (i) is identical to the Hukuhara difference of $\omega(\tau+\hbar)\ominus\omega(\tau)$ definition. Assuming the definition of ${\bf{g}}{\bf{H}}$-difference and an ${\bf{r}}_{1}$-cut of both sides of the aforementioned derivative (2.6), the derivative in the accompanying interval yields the following:

Case (i): (1-differentiability)

Case (ii): (2-differentiability)

To define the ABC derivative in a parameterized version, we must first establish the Lebesgue integral of $\omega({\bf{t}}_{1})$ in interval form, which is as follows:

3.   Fuzzy fractional model for diabetes mellitus

Suppose a mathematical framework comprises glucose level $\mathcal{G}$, glucose uptake activity $\mathcal{X}$ and insulin level $\mathcal{I}$. Numerous variables have been examined, and a mathematical formulation has been created depending on the proportions of these components. The fundamental parameters, $\mathcal{G}_{\mathfrak{b}}$ and $\mathcal{I}_{\mathfrak{b}}$, are also included in this approach ^[54]. Nonlinear fuzzy fractional order DEs are employed to explain the new diabetes mellitus model with fuzzy fractional ABC derivative, as follows:

where $\wp({\bf{r}}_{1}) = (\underline{\wp}({\bf{r}}_{1}), \bar{\wp}({\bf{r}}_{1})) = ({\bf{r}}_{1}-1, 1-{\bf{r}}_{1})$, and ${\bf{r}}_{1}\in[0, 1]$.

For the sake of simplicity, we express the fuzzy ABC fractional diabetes model (3.1) as follows:

where $\Omega({\bf{t}}_{1})\in\mathbb{C}^{\mathcal{F}}(\mathcal{J})\bigcap\mathbb{L}^{\mathcal{F}}(\mathcal{J}),$ $\Omega({\bf{t}}_{1}) = (\Phi_{1}, \Phi_{2}, \Phi_{3})$ denotes the state of variables, and $\Lambda$ is a continuous vector function such that

where $\tilde{\mathcal{G}}({\bf{t}}_{1})$ is the random blood glucose intensity, $\tilde{\mathcal{X}}({\bf{t}}_{1})$ is the serum insulin variability for the secluded compartment, $\tilde{\mathcal{I}}({\bf{t}}_{1})$ is the serum insulin intensity, $\tilde{\mathcal{G}}_{\mathfrak{b}}$ is the normal pre-injection level of glucose concentrations, $\tilde{\mathcal{I}}_{\mathfrak{b}}$ is the normal pre-injection level of insulin sensitivity, and $\varphi_{1}$ is the insulin autonomous metabolic absorption in liver tissue and adipose cells. $\varphi_{2}$ is the proportion of reduction in muscle glucose absorption capacity, $\varphi_{3}$ is the insulin production growth in glycemic accumulation potential in $\tilde{\mathcal{I}}_{\mathfrak{b}}$, $\varphi_{4}$ is the percentage of transfer of pancreatic islets upon glycemic inoculation and glycogen accumulation, $\varphi_{5}$ is the glycemic target value, and $\varphi_{6}$ is the insulin decomposition proportion in the bloodstream. Two glucose/insulin systems are used to explain the coupling of the mathematical model of glycemic behavior. These algorithms can forecast hyperglycemia since they are based on regularly modified evidence ^[54].

4.   The fuzzy fractional diabetes model via the interval Atangana-Baleanu fractional derivative in the Caputo sense

In the system (3.2), let us assume the mapping $\Omega({\bf{t}}_{1})$ is the solution of the FV AB-fractional diabetes model in the view of Caputo, which is stated in interval parameterized form below.

Definition 4.1. The FV AB-fractional derivative in the view of Caputo is described in parametric form as follows:

where ${\bf{B}}(\alpha)$ is the normalization function such that ${\bf{B}}(0) = {\bf{B}}(1) = 1$. Also, $E_{\alpha}$ signifies the Mittag-Leffler function. Thus, we have

Since the symbol of the generalized Mittag-Leffler $\bar{E}_{\alpha}({\bf{t}}_{1})$ is determined by $\alpha$ and ${\bf{t}}_{1}$, and ${\bf{B}}(\alpha) > 0$, $\alpha < 1$.

The ABC fractional derivative's upper and lower limits are as follows:

Now, we will investigate the relationship between the solutions of our fuzzy fractional differential equation and the fuzzy integral equation that corresponds to it. Assume that

When two aspects are analyzed, the interval parameterized version is

Utilizing (4.1) yields the following:

Case (i):

Case (ii):

For every case, in view of (4.2), the parameterized version of the ABC fractional derivative and the verification in each case vary. So, the solution can be established theoretically and numerically. The Case (ii) represents the ABC-fractional differential equations with parameterized forms utilizing the generalized Hukuhara differentiability. Now, taking these considerations into account, the results in each scenario are as follows:

In Case (i):

In Case (ii):

The parameterized version of the above system can be given as

In view of the interval parameterized formulations, the integral operator correlated with the ABC fractional derivative operator on a FVF is represented as

It is described this way:

The ${\bf{r}}_{1}$-cut of the fractional integral is the accumulation of ${\bf{r}}_{1}$-cuts because it is a composition. Relying on (4.2) and the consequence of this fractional integral on the ABC fractional derivative, the following can also be clarified:

where

Therefore, for ${\bf{r}}_{1}\in[0, 1]$, we have

and

or, more generically,

4.1.   Existence analysis

Theorem 4.1. Suppose there is a continuous FVF $\Lambda({\bf{t}}_{1}, \Omega({\bf{t}}_{1}))$ and a non-negative kernel $\bar{E}_{\alpha}$ for every ${\bf{t}}_{1}$, $\alpha > 0$ with fuzzy initial condition has a solution in the following form:

Proof. The parameterized version of (3.2) is as follows:

According to Case (i),

In Case (ii),

Invoking the AB fractional operator on both sides of the above equation, we have the following:

In Case (i),

In Case (ii),

where

Therefore, we have the following:

In Case (i),

In Case (ii),

Taking into account the fuzzy formulation in Case (i),

In Case (ii),

Generally, we have

Corollary 4.1. In case the kernel $\bar{E}_{\alpha}$ for every ${\bf{t}}_{1}$ and $\alpha$ is negative the mentioned above relation are true conversely.

In Case (i),

In Case (ii),

In order to illustrate the existence of the solution, we first propose and describe the lower and upper solutions of the model in parameterized form. Here, $\underline{\Omega}({\bf{t}}_{1};{\bf{r}}_{1})$ and $\bar{\Omega}({\bf{t}}_{1};{\bf{r}}_{1})$ are the optimal solutions of the subsequent minimization and maximization problems, respectively:

such that

and

such that

where

and

Some remarkable cases of the above mentioned optimization problems are presented as follows:

I. Suppose there is a linear mapping $\Lambda,$ along with $\frac{\partial\underline{\Lambda}}{\partial\Omega}\geq0$ and $\frac{\partial\bar{\Lambda}}{\partial\Omega}\geq0$, and then we have

II. Suppose there is a linear mapping $\Lambda,$ along with $\frac{\partial\underline{\Lambda}}{\partial\Omega} < 0$ and $\frac{\partial\bar{\Lambda}}{\partial\Omega} < 0$, and then we have

4.2.   Uniqueness Analysis

Theorem 4.2. Assume that there is a continuous FVF $\Lambda({\bf{t}}_{1}, \Omega({\bf{t}}_{1}))$ on $\Delta$ of a plane $({\bf{t}}_{1}, \Omega)$ holding the Lipchitz assumption in $\Delta$ with respect to $\Omega$,

and then the model (3.1) has a unique fuzzy solution $\Omega({\bf{t}}_{1})$ when the subsequent assumption holds:

Proof. In order to prove the result, suppose the operator $\mathcal{F}:\mathbb{C}^{\mathcal{F}}(\mathcal{J})\cap\mathbb{L}^{\mathcal{F}}(\mathcal{J})\mapsto\mathcal{F}:\mathbb{C}^{\mathcal{F}}(\mathcal{J})\cap\mathbb{L}^{\mathcal{F}}(\mathcal{J})$ is the solution having both (non-negative and negative) kernels.

In Case (i),

In Case (ii),

In Case (i),

Since $\Omega_{1}(0) = \Omega_{2}(0),$ and by means of property (iii) of Definition 2.4, we have

Again, utilizing properties (iv) and (vi) of Definition 2.4,

Since $\Big(\frac{1-\alpha}{{\bf{B}}(\alpha)}\mathcal{L}+\frac{\alpha}{{\bf{B}}(\alpha)\Gamma(\alpha)}\mathcal{L}{\bf{t}}_{1}^{\alpha}\Big) = \mathcal{L} < 1$ is a Lipchitz constant. Consequently, we have

This shows that the operator $\mathcal{F}$ is a contraction mapping on $\mathbb{C}^{\mathcal{F}}(\mathcal{J})\cap\mathbb{L}^{\mathcal{F}}(\mathcal{J})$. By the Banach fixed point theorem, (3.2) has a unique solution. By applying an analogous technique, we can deduce the same result for Case (ii).

5.   Adams-Bashforth-Moulton approach for fuzzy fractional ABC fractional derivative for diabetes model

This section consists of a reliable and widely utilized numerical approach for finding and obtaining fractional order fuzzy initial value problems; see ^[55,56]. Let us assume the general fractional differential equations

Choosing $t_{0} = 0, \; \hbar = 0.01, t_{n_{1}+1} = t_{n_{1}}+\hbar, \; \underline{\mathcal{G}}(0) = ({\bf{r}}_{1}-1)\underline{\mathcal{G}}_{0}, \; \underline{\mathcal{X}}(0) = ({\bf{r}}_{1}-1)\underline{\mathcal{X}}_{0}, \; \underline{\mathcal{I}}(0) = ({\bf{r}}_{1}-1)\underline{\mathcal{I}}_{0},$ $\bar{\mathcal{G}}(0) = (1-{\bf{r}}_{1})\bar{\mathcal{G}}_{0}, \; \bar{\mathcal{X}}(0) = (1-{\bf{r}}_{1})\bar{\mathcal{X}}_{0}, \; \bar{\mathcal{I}}(0) = (1-{\bf{r}}_{1})\bar{\mathcal{I}}_{0}$ in (3.1), where $\hbar$ denotes the step-size, the corrector values are

Moreover, the corresponding predictor terms are as follows:

where

and

5.1.   Numerical simulation

The glucose-insulin process can be modeled mathematically in a variety of ways. One of the most well-known models presented by ^[55,56] is a three-compartment model (3.1). The DEs are required to transform this system to a fuzzy fractional-order system in the fuzzy ABC derivative sense. The justification for this is that Saleem et al. ^[8] demonstrated that the fractional-order model identifies the glucose-insulin combination more effectively than the classical model.

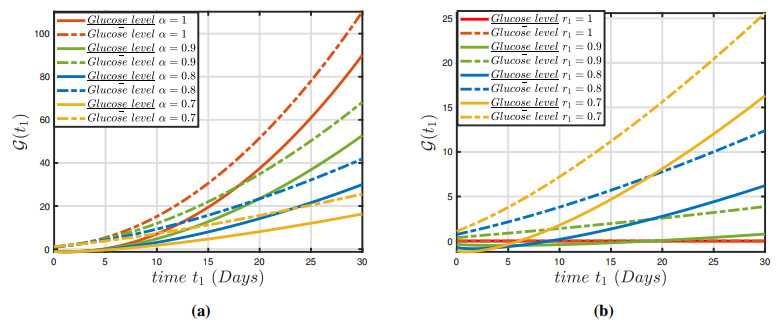
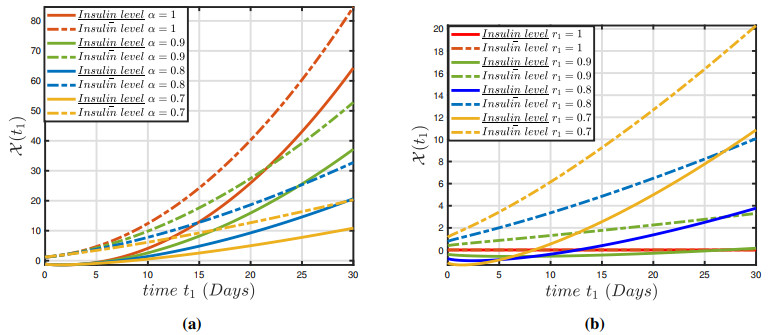
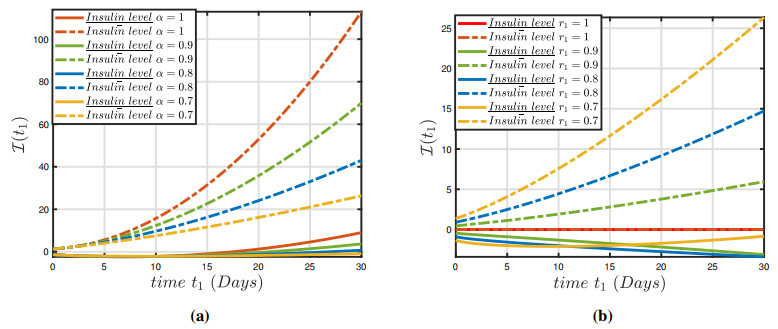
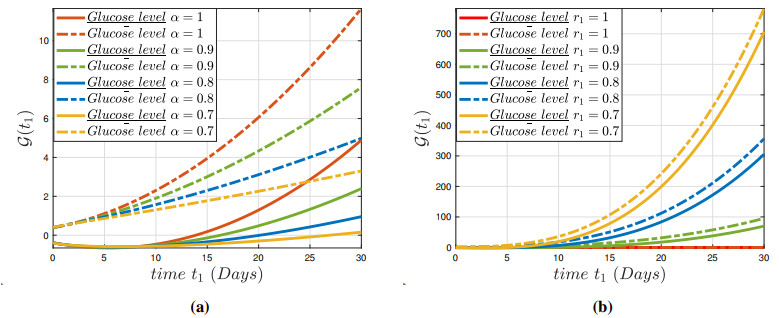
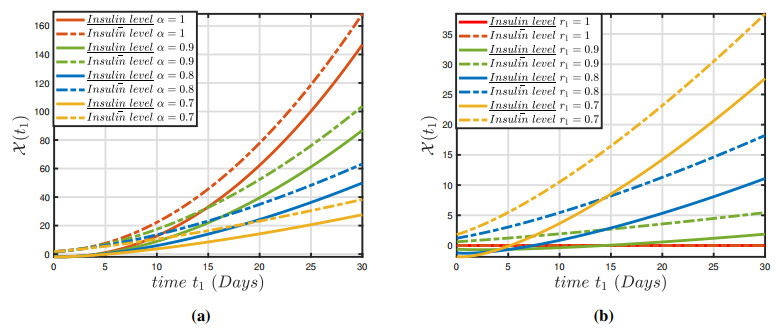
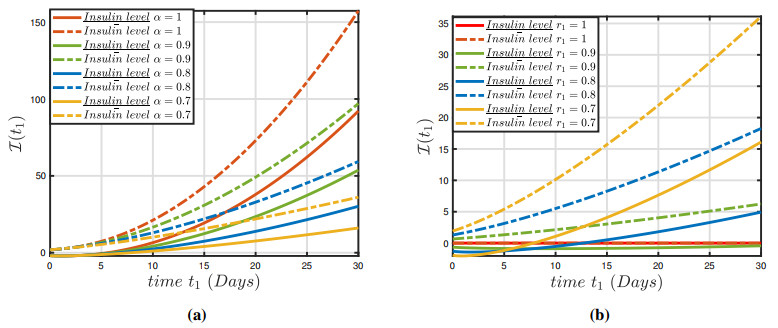
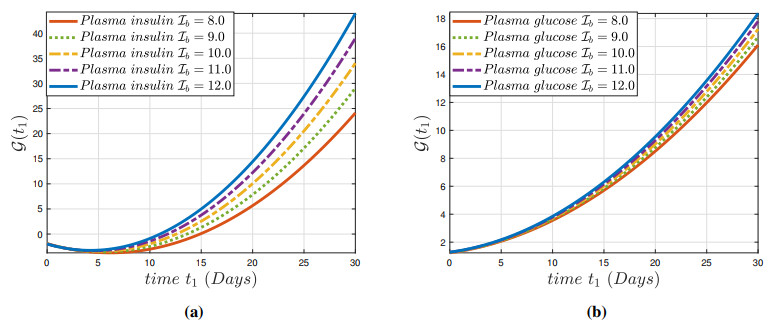
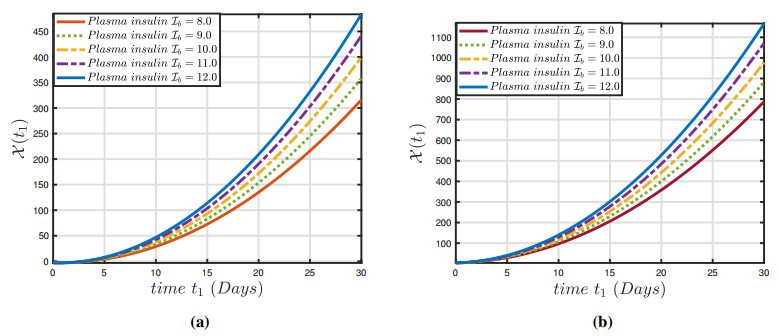
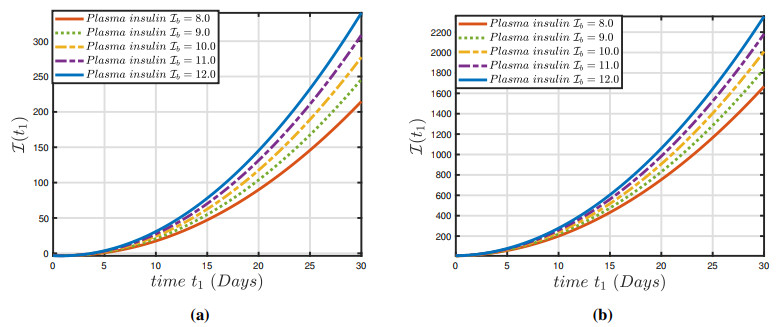
The numerical findings of the fuzzy fractional model (3.1) have been established for a system of nonlinear fuzzy fractional DEs via the fuzzy ABC derivative operator and the parameters are defined in Table 1. In view of (3.1), various numerical techniques utilizing the variation in parameters presented in Table 1 and restricted intervals can examine the impact of these variables on the dynamics of the fractional-order framework. This analysis demonstrates that changing the parameters has an impact on the model's behavior. Figures 1(a)–3(a) depict the constrained approximation for a normal individual and hyperglycemia depending on normal glucose, insulin ambient concentration, and insulin in plasma glucose for solutions. Furthermore, Figures 1(b)–3(b) depicts the constrained approximation for a normal individual and hyperglycemia individual depending on normal glucose, insulin ambient concentration and insulin in glucose for fuzzy solutions depending on an integer-order approach. Figures 4(a)–6(a) illustrate the entire behavior of the glucose-insulin network in both a healthy individual and a patient with hyperglycemia individual with both lower and upper solutions with varying fractional order and constant uncertainty ${\bf{r}}_{1} = 0.4$. The findings of the model depict the real and control scenario of consistent glucose system for mechanical pancreatic design. Also, Figures 4(b)–6(b) show the complete structure of the glucose-insulin network in both a healthy individual and a patient with hyperglycemia, with both lower and upper solutions with integer order and varying uncertainty. The results of the model present the solution for the upper case and a biassed approach for the upper solution in the control case of a consistent glucose system for mechanical pancreatic design. The technique will generate fuzzy solutions that occur in pairs for non-integer values, which are highly reliable and precise in the specified space. We can notice in Figure 7 that the conventional approach $\alpha = 1$ is unable to stabilize the blood sugar insulin mechanism for both healthy and hyperglycemia individual, and thus it does not meet the requirement for the preservation of a closed-loop configuration for a synthetic pancreas. It is apparent from Figure 8 that uncertainty values ensure balance and allow for persistent glucose system analysis. In Figure 9, the representations of the glucose-insulin systems via fuzzy ABC for a healthy individual and hyperglycemia individual in each category are compared with the recovery after plasma insulin injection. Although the behaviors of the glucose-insulin systems are nearly identical, the fuzzy ABC derivative provides pertinent and viable results in a closed-loop proposed methodology that aids in the development of the synthetic pancreas.

6.   Conclusions

This paper describes the mathematical and contextual research of the bio-medical glycemic system using a nonlinear fuzzy fractional-order framework with an ABC derivative for the treatment of diabetes complications. It demonstrates the consistency, uniqueness, and applicability of glucose intensity regulation in healthy people and individuals with hypoglycemic disorders. The hypoglycemic model built with the fuzzy fractional ABC derivative demonstrates excellent correlation in terms of controlling the glucose-insulin mechanism. The approach focuses on continuous glucose monitoring for a restricted amount of time, and the results are confined to standard levels for both normal people and individuals with hypoglycemic disorders. An investigation of predictive findings is used to examine the effects of various configurations since the generated systems are considerably more complicated to handle as parameterized governing equations than conventional fuzzy DEs. In terms of the significance of these models, we must leverage the interpretation of the uncertain ABC derivative to identify the solutions to the uncertain models. The effects of variation on the proportion of diabetics with time-concerned problems and the severity of diabetes mellitus are depicted graphically. By simulation analysis, we can demonstrate that when $\alpha = 1$ the ABC non-integer order derivative exhibits significant absorption features. For future research, we will extend this model to the fuzzy fractal-fractional operator and simulate this research with real data that depends on the control mechanism.

Acknowledgements

This research was supported by Taif University Researchers Supporting Project of Saudi Arabia (No. TURSP-2020/86), the National Natural Science Foundation of China (No. 71601072), the Fundamental Research Funds for the Universities of Henan Province (No. NSFRF210314) and the Innovative Research Team of Henan Polytechnic University (No. T2022-7).

Conflict of interest

The authors declare that they have no competing interests.