Numerical solution of stochastic and fractional competition model in Caputo derivative using Newton method

1.   Introduction

During the 1970s and the 1980s, most industrialized countries experienced a fall in productivity. However, this phenomenon did not affect the USA which, especially in the 1990s, has seen a growth in productivity and an even larger economic growth thanks to the development of ICT and to the rise of the "new economy." Fontela (2002) argues that this is a typical mesoeconomic effect, whose dimension lies between the impact of structural changes in the technology of production (effects on efficiency) and the effects at the macroeconomic level (effects on growth).

Fontela began studying these issues in the 1980s by applying surplus distribution measures based on macroeconomic accounting systems in order to understanding the distribution dynamics that appear simultaneously with progress and innovation benefits. In his seminal paper (Fontela, 1989), the principal finding was that "a growth process does not only imply a path of generation of total factor productivity (TFP), it also includes an internal transfer between industries of the gains of TFP." Moreover, in Fontela (1993), he states that "the rule of distribution will finally be dictated by the structure of the different markets [...] with perfect competition in all markets for products and primary factors, consumers will benefit immediately following price decrease but in all cases of more or less imperfect competition, the results will be less clear.

In this paper, starting from Fontela research we use the decomposition of total factor productivity surplus (TFPS) by proposed Garau (1996) deriving the price system comparing symmetrical input–output tables at current prices and at previous year prices, derived from the supply and use tables released by Istat (2018). In this paper there are two types of results. The first concerns the identification of policy areas on which to intervene to reduce the inefficiencies of market mechanisms. The second refers instead to the improvement of the ability to correctly measure the phenomena in question and the fundamental insertion of the same in a modeling context.

The remainder of this paper is organized as follows. Section 2 illustrates and justifies theoretically Fontela's system of surplus distribution. In Section 3, we propose a method for calculating implicit price indexes using input–output tables. Section 4 presents Garau's (1996) purchasing power transfer (PPT) distributional rules. Section 5 illustrates the results of our research and, finally, in the last section, we draw some conclusions and show some possible ways of extending total factor productivity surplus/purchasing power transfer (TFPS/PPT) analyses to support the dissemination of Fontela's idea and use it as a tool for economic analysis and policy evaluation.

2.   Theoretical framework

To better understand processes of productivity fall, it is useful to refer to Baumol (1967) and his model of unbalanced growth. The model considers two sectors: one is increasingly more productive and the other is in stagnation. In an economy characterized by perfect labor mobility, such an unbalance determines a reduction in costs and prices in the first sector, especially if there is substitutability between goods, and this could determine the disappearance of the sector whose productivity is not growing. Sectors with stagnant productivity often produce goods with inelastic prices (e.g., artistic activities); therefore, surplus transfers end up subsidizing these activities. If, instead, the production of the two sectors is maintained in a fixed proportion, one would observe a progressive spillover of labor toward the less productive sector. This hypothesis has been empirically tested in different works (Baumol et al., 1985, Appelbaum and Schekatt, 1994).

Another cause of this differential evolution can be found in the market structure of different sectors. Fontela et al. (2000) found that, in general, there is an inverse correlation between prices and productivity, except for sectors such as agriculture, whose prices are distorted by government intervention. In short, their analysis allows us to state that one of the main causes of unbalanced growth is the market structure, thus acknowledging the existence of imperfect competition, where prices do not adjust according to technical changes. The relationship between technical changes, market structure, and prices has been analyzed by Carter (1990) in a model where, similar to Baumol's (1967), an economic system composed of subsets of sectors, innovative sectors, and sectors where no change in technology is observed is considered. The results clearly show that the distribution of innovation gains depends strongly on the market structure and determines both an increase in profits, when the advantages go to capital holders, and a reduction in prices, when the benefits go to the consumers in the form of increased purchasing power.

The contributions of Baumol (1967) and Carter (1990) allows a better understanding of the mechanism of unbalanced growth, which characterizes the new economy in the following way (Fontela, 2002). The 1990s productivity growth in the USA is certainly based on the introduction of ICT in most productive sectors. In fact, as one would expect, under perfect competition, this should produce a reduction in prices of all goods that incorporate the new technology, and this process can be accelerated by the intervention of the government for the dismantlement of public monopolies (e.g., telecommunications). At the same time, the wages of specialized workers would increase and the surplus would possibly be partially absorbed by those sectors owning ICT patents. If the price and income elasticity of goods and services with high technological content is high, one should see a chain effect where a rise in demand stimulates innovation, prices fall, and demand increases again. This dynamic, typical of the new economy, will finalize when the system is saturated with high-tech goods and, in any case, only a high rate of innovation would allow the system to keep growing in the final phase. Because the growth mechanism described here is highly unbalanced, it is necessary to try to govern it through public policies capable of avoiding social and financial global crises (Fontela, 2002).

Further, it is important to study the effects of innovation to understand what the public sector can do to help firms innovate and therefore stimulate economic growth, as well as what could be done to avoid the benefits of innovation being entirely allocated to the private sector and enterprises (Mazzucato, 2014). This topic is linked to a correct design of cluster policies (called smart specialization strategy at the European and regional levels) and to firm subsidies. In general, when government resources are used, especially when their use can produce distortions, it would be opportune to perform an ex-ante impact evaluation of any interventions to better define their implementation and report their costs and benefits to the society as a whole.

3.   Fontela's TFPS model

Fontela (1989) calls TFPS the difference between output and inputs, both measured at constant prices. The idea is based on the input–output table deflation at current prices to obtain an "unbalanced" table at constant prices, that is, a table in which the row total does not coincide with the column total; the difference between the two totals provides the TFPS. To obtain national accounting data at constant prices, it is possible to adopt two different methodologies (Garau, 1996): the first uses price indexes and the second quantity indexes. In the first case, we start from a table with the prices and quantities of the current year.

In the second case we start from a table with prices and quantities of the base year:

Considering now the methodology proposed by Fontela (1989) for the calculation of TFPS, we can write:

where $TFP{S_{i, t}}$ corresponds to the amount of real resource flows between time t and time 0, ${q_{i, j, t}}$ is the flow of output of sector i towards sector j and ${p_{i, j, 0}}$ is the market price in its base year value. Since $\sum\nolimits_j {{p_{i, j, t}} \cdot {q_{i, j, t}}} = \sum\nolimits_j {{p_{j, i, t}} \cdot {q_{j, i, t}}}$, the expression (3) can be rewritten in terms of price variations as follows (Fontela, 1989):

Equation (3) measures the creation of the TFPS using the index number approach, while Equation (4) can be interpreted as the distributional rule of the TFPS. As is self-evident, such a distribution depends on the price variations of outputs (first element on the right-hand side) and inputs (second element on the right-hand side). Let us now assume that, for a given period t: ${\bf{X}}$ and $\overline {\bf{X}}$, ${\bf{l}}$ and $\overline {\bf{l}}$, ${\bf{k}}$ and $\overline {\bf{k}}$, ${\bf{m}}$ and $\overline {\bf{m}}$, ${\bf{f}}$ and $\overline {\bf{f}}$, ${\bf{e}}$ and $\overline {\bf{e}}$ are the matrix of intermediate flows, a vector of labor income, capital return, import flows, final demand, and export demand, respectively in current and constant prices. According to the accounting constraint, the following equations hold:

where $\iota$ is a unit vector. As we cannot observe $\overline {\bf{k}}$, the value added $(\overline {\bf{l}} + \overline {\bf{k}})$ must, of course, be obtained as a residual. However, if we are able to deflate every single item in Equation (5), including ${\bf{k}}$, or at least identify a proper deflator for the overall value added, it is quite plausible that the equilibrating relationship represented in Equation (6) does not hold.

As pointed out by Flexner (1959), although we were able to remove all statistical discrepancies due to calculation and statistical approximations, Equation (6) would be inadequate to represent a constant price relationship whenever productivity changes arise between base year and current values; this must be reflected by a balancing item in Equation (6).

Accordingly, we may argue that a well-defined system of accounts may provide a measure of productivity resulting from the difference between the amount of goods produced and the amount of production inputs used. Such a measure will take a positive value only if the quantity variation of the output is greater than the variation of all inputs. Therefore, the relationship in Equation (6) does not hold, and the balancing term has a precise economic meaning, which is called TFPS by Fontela (1989):

For a given period, t, the following definition of TFPS hold:

where ${\bf{S}}\left[ {{s_{i, j}}} \right] = {\bf{X}} - \overline {\bf{X}}$, ${{\bf{s}}_{\bf{k}}}\left[ {s{k_i}} \right] = {\bf{k}} - \overline {\bf{k}}$, ${{\bf{s}}_{\bf{l}}}\left[ {s{l_i}} \right] = {\bf{l}} - \overline {\bf{l}}$, ${{\bf{s}}_{\bf{m}}}\left[ {s{m_i}} \right] = {\bf{m}} - \overline {\bf{m}}$, ${{\bf{s}}_{\bf{f}}}\left[ {s{f_i}} \right] = {\bf{f}} - \overline {\bf{f}}$ and ${{\bf{s}}_{\bf{e}}}\left[ {s{e_i}} \right] = {\bf{e}} - \overline {\bf{e}}$.

By considering a given year t:

1. ${s_{i, j}} > 0$, it means that industry j is transferring surplus to industry i, and the reverse applies when ${s_{i, j}} < 0$, that is, industry j is paying relatively less for the inputs provided by industry i. Particularly interesting is the net industry contribution of industry i: ${s_{n, i}} = {\sum\nolimits_j s _{j, i}} - {\sum\nolimits_j s _{i, j}}$. When ${s_{n, i}} > 0$, industry i transfers its surplus to the rest of the economy more than it is gaining from all the other sectors.

2. Industry i is transferring surplus to its primary inputs when $s{l_i}$ and $s{k_i}$ are positive.

3. When the price of some commodity falls, industries transfer additional surplus to consumers making $s{f_i} < 0$.

4. From the trade side, we have an inflow of productivity gains from the rest of the world $s{e_i} > 0$ and $s{m_i} < 0$. The reverse applies when $s{e_i} < 0$ and $s{m_i} > 0$. Then, we can compute, as in Fontela et al. (2003), net outflow $s{m_i} - s{e_i} > 0$ or the net inflow in the opposite situation, $s{m_i} - s{e_i} < 0$.

Even if the double deflation method is widely used, it can hide some important processes behind economic growth, such as technical progress. An equilibrating system of accounts cannot be used at constant prices without the loss of some important effects concerning economic growth such as efficiency, rent spillovers, and all those elements that may concern disembodied technical change. Instead, a single deflation procedure would allow one to determine a measure of productivity gains (Flexner, 1959; Fontela, 1989; Babeau, 1994; Garau, 1996) and understand the process of generating economic growth.

Moreover, the use of a constant price method not only gives us the opportunity to obtain information on the internal productivity generation process, but also identifies the external determinants of growth that are behind the change in the terms of trade if proper price indexes are used to deflate imports and exports. This would yield interesting results, since the literature on economic growth has now recognized the role of knowledge spillovers as the most important driving force behind economic growth. As knowledge is incorporated into commodities, trade with highly technological countries means high quality and sophisticated inputs (either intermediate or capital goods) that improve efficiency and, in turn, competition among regions. Such a potential finding has been identified by Flexner (1959), while estimates of external rent spillovers for the Swiss economy may be found in Antille and Fontela (2003).

4.   Implicit price indexes and TFPS transfers

We now consider the construction of sector price indexes to deflate the 2014 Italian input–output table^*. In particular, we use symmetrical input–output tables at current prices and at previous year prices, derived from the supply and use tables released by Istat. If we compare the values of the two tables, we obtain:

which represents the implicit price index between time t and time t-1. Proceeding backward, we have:

^* Make and use tables (2018), availables from: http://www.istat.it

Taking the reciprocal of the latter we obtain:

Comparing expressions (9) and (10) we obtain:

We can generalize the above to obtain implicit price index I related to period t, t-n for the generic i sector of the input–output table:

It should be emphasized that these price indexes are not "pure"; in fact, we have to consider that Istat makes adjustments for the tables at previous year prices for balancing, which also modifies quantities in addition to prices. However, these adjustments are negligible for quantities, that is, they will not change quantities substantially since, if this were to happen, the input–output table at the previous year prices would not reflect production for year t and the tables would thus not be comparable. As such, the quantity adjustment is remarkably small and, as a result, it is considered negligible. Through the procedure described above, we obtain implicit price indexes for all matrices and vectors of the input–output system, which are then used to deflate the input–output table and, subsequently, compute the TFPS using Equation (8).

5.   Optimal TFPS and market surplus

In the model proposed by Fontela (1989), the effect of the TFPS variation due to the behavior of the agents and markets in the economic system is not highlighted. In particular, the ability of some agents to change prices is not reflected in $TFPS_{ij}$. As a result, Garau (1996) proposes a model based on the $TFPS_{ij}$ decomposition. Price is divided into two parts:

- $p_{ij0}^*$ represents the potential market price if agents are not able to obtain extra profits (price under competition);

- $p_{ij0}^{**}$ is an index of market bias and represents the ability of economic agents to gain from market imperfections (market surplus).

Considering the above, $TFPS_{ij}$ can be decomposed as follows:

Optimal $TFPS_{ij}$ is defined as

while $MS_{ij}$ is defined as

Then the $PPT_{ij}$ is given by

Considering the difference between the terms in last equation, we observe that:

- $TFPS_{ij}^*$ has a positive value if the second term is larger than the first; this means that the $i$ sector generates and distributes purchasing power derived from an increase in productivity;

- $MS_{ij}$, conversely, has a negative value if the second term is larger than the first; this means that a negative value corresponds to a redistribution of purchasing power.

We can estimate $TFPS_{ij}^*$ using the Törnqvist price index (Wolf, 1985, 1989; Fontela, 1994) as a proxy for $p_{ij}^*$. The Törnqvist price index can be calculated as follows:

As we can see, this index is unique for an entire row of the input–output table, that is, we consider that the price charged by sector $i$ for its products used as intermediate inputs is the same for all purchasing sectors $j$. For each sector, the relationship between prices is derived by comparing the values contained in the intersectoral matrices of the two tables.

In the formula, $w_{i, t}$ represents the value share of the asset produced by sector $j$ on the total value of the aggregate for period t:

The same holds for $w_{i, t-n}$. At this point, we deflate the input–output table for 2014 using the Törnqvist price index and reapply the TFPS calculation procedure to obtain $TFPS_{ij}^*$. Then, market surplus ($MS_{ij}$) is obtained as a residue:

It is important to underline that the sign of the sectoral $PPT_{ij}$ depends on the signs of $TFPS_{ij}^*$ and $MS_{ij}$; the possible combinations are:

6.   Results

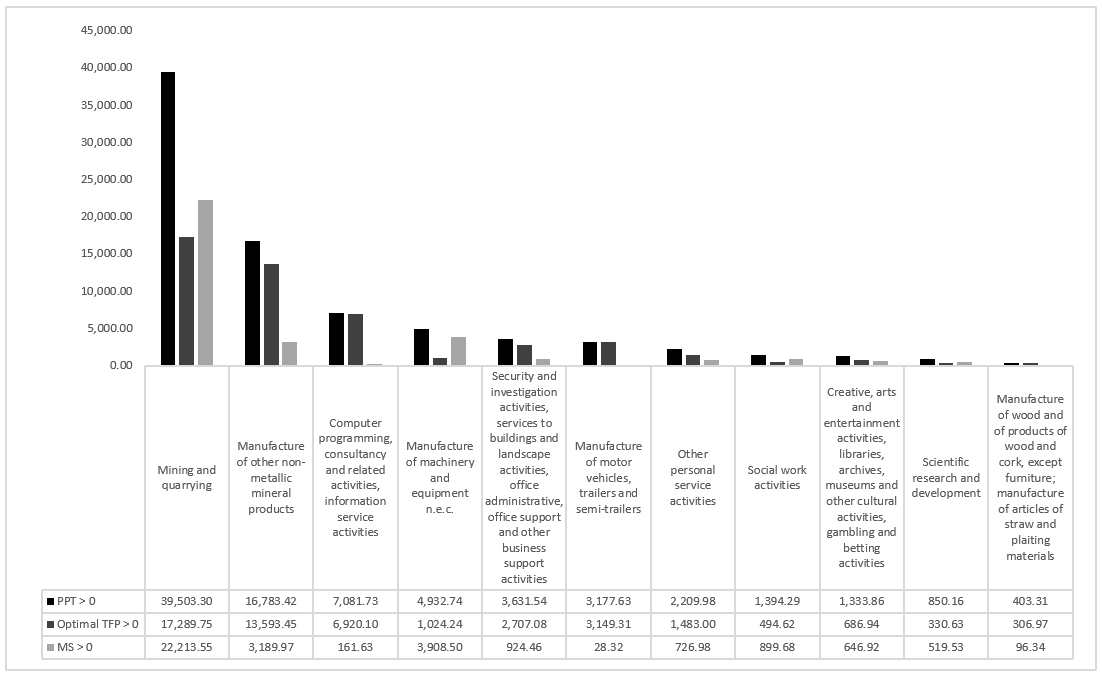
In the following figures, we present the sectoral results showing performance in terms of the optimal TFPS and MS. We distinguish between a first set of figures, grouped sectors with PPTs above zero (Figures 1–3) and a second set of figures (Figures 4–6), where the sectors with negative PPT are presented. The paper contains all tables necessary to understand the destination of the surplus and the actors absorbing or creating it.

The best performance is shown by mining and quarrying and the manufacture of other non-metallic mineral products, with optimal TFPSs equal to 17.290 and 13.539 million euros, respectively. These two sectors also show positive MS, which means that, for both sectors, the PPT results from the efficiency of the system (capacity of the system to create surplus of productivity) and from the capacity of agents to create additional surplus using their market power reduce sales prices. However, from a redistributive viewpoint, for both sectors, 50% of MS is transferred to the rest of the world through imports, while the remaining 50% is transferred to other sectors through an increase in intermediate input remuneration. Another efficient sector is the supply of electricity, gas, steam, and air conditioning, with an optimal TFPS of 10.298 million euros. However, part of this surplus, around 54%, is retained in the form of extra profits, which means that agents are able, through market distortions, to maintain higher prices, thus generating a negative MS. Of major importance are the results for the land transport and transport by pipelines sector (see Figure 5). In this case, we have an efficient sector, which creates a productivity surplus of 4.53 billion euros, but through market power (MS of $-4.708$ billion euros of which 79% to the detriment of other productive sectors) agents arrive to retain or increase their prices more than the generated TFPS and, finally, we observe a negative PPT. In other words, the productivity surplus generated by market efficiency is retained in the form of extra profits.

In terms of optimal negative TFPS, we observe that the construction sector has the worst performance, with a value of $-26.584$ million euros. In particular, a greater share of surplus is retained by investments, as well as by intermediate inputs. On the import side, the sector transfers surplus to the rest of the world. Looking at the MS circuit, we observe a small surplus generation of 5.058 billion euros, which is negligible compared to the productivity loss. Moreover, this quota is transferred mostly to public consumption. This extremely negative performance is in line with the trend of the sector's VA which is constantly decreasing from 2007 to 2015 (in the same period the total VA of the economy increases until 2011, decreases until 2013 and finally starts again in the 2014), the moment in which we observe a period of stability but not yet a restart. Another non-performing sector is financial service activities, except insurance and pension funding, which is characterized by a strongly negative optimum TFPS of $-24.865$ million euros. It should be noted that this sector retains surplus from other production sectors through intermediate inputs, but also from added value, imports, and consumers (households). The MS registers a value of 7.605 billion euros, which is too low to compensate for the productivity surplus loss, and we also register a negative PPT. Finally, a negative optimal TFPS is also characteristic of the food, beverage, and tobacco industry, with a value of $-6.609$ billion euros (see Figure 4). In this case, the sector retains surplus from other sectors through intermediate input prices, as well as from added value, imports, and consumers (households). Finally, this sector registers a negative MS, generating extra profit for economic agents of $-200$ million euros.

Lastly, the following sectors deserve special attention:

- Human health activities. This sector is not efficient, even its inefficiency is close to zero ($-853$ million euros). However, the sector redistributes surplus through market power, reducing prices versus intermediate inputs, VA, and the rest of the world, and augmenting prices for households.

- Coke and refined petroleum products is the sector with the worst performance in terms of MS, with a value of $-13.733$ million euros. The sector is not efficient (optimal optimum TFPS equal to $-350$ million euros, close to zero), but the strong market power allows it to increase intermediate input prices and, in fact, this sector retains surplus from other sectors by around 98%.

7.   Conclusions

Fontela (1989) concludes his seminal paper by describing an alternative model of growth where the long-term trend of increasing relative prices in services changes to allow TFPS transfers. Nowadays the service sector mainly refers to renewable energies, green economy, or the Internet of Things (Rifkin, 2014), as these are sectors where the concentration of research and innovation will probably produce TFP gains able to push the economy towards a new paradigm.

The main findings of our analysis concerning 2009–2014 are the capacity of the Italian economy to produce a TFPS of approximately 3.7 billion euros, even if the strong inefficiencies of some sectors, underlined by a market surplus of 6.4 billion euros, lead to an overall negative PPT ($-2.74$ billion euros). In the previous section, we looked at the relative positions of different sectors, distinguishing sectors that create TFPS from those who absorb them. Here, the focus is on the global relationships among institutional agents (consumers, workers, PA, external trade, firms). At the optimal level (see Table 2), we observe a transfer of resources, mainly from consumption and investments and only secondarily from value added to import and export. Conversely, at the market surplus level (Table 3), the negative performance is mainly due to the absorption of surplus by consumption (public and households) and investments against exports and VA components. Table 1 (PPT) also underlines the role of resource absorbers by public consumption, exports, and imports to the detriment of the different VA components, household consumption, and investment.

In summary, our analysis emphasizes, at the global level, the existence of a highly unbalanced growth mechanism, where TFPS flows from VA and internal components of final demand versus external trade and public consumption. The Italian economy must complete the reduction of sectoral inefficiencies (e.g., coke and refineries, wholesale trade, and telecommunications), but it must also reconstitute the ability, through radical interventions, to create a PPT to be distributed to less performing sectors and to the labor force. The slowdown in productivity underlined by the PNRR^† must be contrasted with the search for new engines of growth but also with awareness on the key role for the social cohesion for worse performing sectors (e.g., education and health) and less strong ones (employee and autonomous work versus financial rents). In other words, the unbalanced growth model is socially sustainable.

^† Governo italiano (2021) Piano Nazionale di Ripresa e Resilienza, available from: https://www.governo.it/sites/governo.it/files/PNRR.pdf

If a sector is able to produce TFPS and thanks to a good situation of competition it does not hold back the surplus created, then the sectors that exchange goods with this sector will benefit from it, in other words the TFPS created in one sector also spreads to other sectors. For this reason, policy makers are interested in limiting Market Surplus situations, eliminating the barriers that protect a sector and thus allowing the TFPS to flow freely. All this happens more, as highlighted by Babeau (1978) and previously by Masse and Bernard (1969), during an inflation resurging such as, for example, that we are living today after the Pandemic. It is therefore extremely useful for policy makers to incorporate the measure of TFPS and Market Surplus into the models, because in this way they can provide in advance those Market Surplus situations (those that can also determine speculative maneuvers) which are candidates to hinder the full revival of the economy.

It is to replace the old unbalanced growth model observed in our data by implementing a change of pace, as in other European countries, which can be facilitated by the intelligent use of the opportunities offered by the Next Gen Eu Fund to redefine development through the green and digital axes. Our methodology tells us that, on the one hand, imbalanced growth dynamics are natural, as not all sectors generate TFPS in the same way, but on the other hand, it is clear that these mechanisms must be sustainable, especially when the innovation of certain sectors (ICT in the 1990s) is exhausted. Therefore, the rent and inefficiency positions of other sectors are no longer sustainable.

From a theoretical viewpoint, we identified three areas for the in-depth analysis of our methodology. The first concerns the attempt to estimate labor and capital prices substantially, which is required to better understand the mechanism behind surplus redistribution. In this regard, the new decomposition of labor productivity explaining China productivity growth suggested by He and Walheer (2021), could be a good instruments to better measure the part of TFPS absorbed by labor. Second, we try to integrate our measures in a modeling context and, more precisely, within the CGE models, in which analyses of the redistribution of productivity surpluses and innovation and technology transfer policies can be adequately integrated (Garau and Lecca, 2015). CGE models are useful if one wants to capture the short-and long-term effects of productivity gains and then determine what the redistribution of these gains will be among economic agents.

The third point concerns the use of these models to assess public policy. Two examples are relevant in this regard: the first concerns the usefulness of such a model for policymakers who are concerned about both productivity gains and the allocation of welfare gains to different economic agents. The second example pertains to the transposition of the model into a spatial context (Garau, 1997; Antille and Fontela, 2003) to understand how the growth dynamics of some regions can contribute to the growth of other regions. In other words, this extension of our methodology would lead to an improvement in the spillover effects measure of regional, national, and European policies designed to strengthen economic and social cohesion. Such original results could be today refined considering the new regional tables (Fidelio) and Multi Regional Input Output (MRIO) frameworks as the basis of an analysis of international supply chains, also in the light of the recomposition of the profitability criteria of international trade.

Acknowledgments

We are very grateful to the fund "Fondo di Ateneo per la Ricerca: 2467/2019".

Conflict of interest

The author declares no conflicts of interest in this paper.