1.
Introduction
The well-known Black-Scholes (B-S) equation [1] for multi-asset option pricing is the following d-dimensional partial differential equation (PDE):
for (S,t)∈(0,∞)d×[0,T) with the final condition v(S,T)=vT(S), where v(S,t) is the value of the option in the multi-asset S=(S1,S2,…,Sd) at time t. T is the maturity time, σi is the volatility of underlying asset Si, ρij is the correlation between i-th and j-th assets, and r is the risk-free interest rate.
However most of the financial derivatives specially linear ones have analytical solutions, but they are not often easy to implement. Therefore the numerical methods would be suitable to find numerical approximations of them. Various numerical methods have been considered for one and multi-dimensional Black-Scholes equations. For instance, mesh free methods [9], high-order option pricing schemes [10,14], alternating direction implicit schemes [2,7] and etc. Furthermore, not only the numerical methods are so common to implement for the financial derivatives, but also they have been implemented for other variety problems and equations frequently [3,11,12,15].
One of the most common and simple numerical methods to implement for solving PDEs is FDMs. The main problem of FDMs for pricing multi-asset options with non-linear payoffs is significant numerical errors around their boundary points and also the strike price K. Several studies have been done to achieve an accurate numerical solution of multi-asset options. Jeong et al. [8] proposed a useful remedy to reduce numerical error around Smax by using the standard Monte Carlo simulation at this boundary point. Here we improved their methodology by using the antithetic variate method in Monte Carlo simulation [4], and furthermore a space transformation [13,16] that causes more nodal points around the strike price to get more robust solution.
2.
FDM for the two-asset B-S equation with combination of the GS and the MC simulation
Two-dimensional B-S equation with two assets x=S1 and y=S2 is the following PDE:
for (x,y,τ)∈Ω×[0,T) with the initial condition u(x,y,0)=u0(x,y) which is the Eq (1.1) with d=2 and a variable changing τ=T−t in the truncated domain Ω=(0,xmax)×(0,ymax). Suppose LBS is the operator of the right hand side of Eq (2.1). Now we discretize the time interval with a uniform time step Δτ=T/Nτ and the following grid stretching transformation that makes non-uniform space discretization of the interval [xmin,xmax] with more nodal points around K:
where c1=arcsinh(15(xmin−K)/K) and c2=arcsinh(15(xmax−K)/K). Therefore x(w)∈[xmin,xmax] for any w∈[0,1]. The grid stretching transformation by locating more nodal points around the strike price K, leads to reduce the numerical errors around K for the options with non-smooth payoffs which can be applied to even higher order finite difference methods in both single and multi-asset Black-Scholes equations. At first for the x-direction, we discretize the interval [0,1] uniformly to Nx sub-intervals, then we use the transformation (2.2) in [0,xmax] and define hxi=xi+1−xi for i=0,…,Nx−1. we discretize the interval [0,ymax] to Ny sub-intervals similarly. Let for i=0,…,Nx, j=0,…,Ny and n=0,…,Nτ define unij≈u(xi,yj,τn) and use the operator splitting method for solving Eq (2.1) with the following two discrete fractional time step equations:
where α≥0, β≥0 and α+β=1. We can choose different sets of values of α and β to achieve us implicit or explicit schemes in both (2.3) and (2.4). These schemes have first-order accuracy in general [5]. Here we take the implicit scheme by choosing α=1 and β=0 for both Eqs (2.3) and (2.4) which leads to a consistent and stable scheme and thereby the scheme is convergent with the first order of accuracy in time. Furthermore, with the operators (LxBSu)n+12ij and (LyBSu)n+1ij as follows, we obtain the second order of accuracy in space as the central finite difference approximations have been used for the space derivatives.
where the derivatives approximations are defined as
By substituting above derivatives in Eq (2.3), the following equations will be achieved:
where αi, βi and γi are the lower, main and upper diagonal of the tridiagonal matrix of the above system of equations respectively and fij is the constant vector of the system which are defined as:
for fixed j and the linear boundary condition at the boundaries. For instance u0j=2u1j−u2j, for j=1,…,Ny and similarly for uNx,j, ui0 and ui,Ny or at the end point of the domain, we apply the Monte Carlo simulation with the antithetic variate method (AMC) or the standard Monte Carlo simulation (MC). The solution of the above system of equations will be the vector u121:Nx,j. Similarly by substituting the derivatives approximations with respect to y in (2.4), we have another system of equations to solve for finding the value of the two-asset option.
Note that with the AMC and the MC simulations we obtain the option value VAMC and VMC respectively at time t=0 and (x,y)=(xmax,ymax) as follow:
where
and M is the number of replications in the antithetic and the standard Monte Carlo simulation which in this work we choose M=106, Λ is a payoff function, z, Σ and Φ are the random vector from a standard normal distribution, the volatility matrix and a vector with the size of multi-asset respectively. For instance, for the case of two-asset Σ and Φ are as follows:
where the elements of the volatility matrix will be obtained by solving the following system of equations:
Then with the exponential interpolation between V (which is VAMC or VMC) and the payoff value u0Nx,Ny, we obtain the option price at the end point of the domain for every time step:
3.
Numerical results
Here we solve numerically the B-S equation in one and two-dimensional space for different options with these parameters: T=1, K1=K2=100, r=0.03, σx=σy=0.3, ρ=0.5.
3.1. Power option
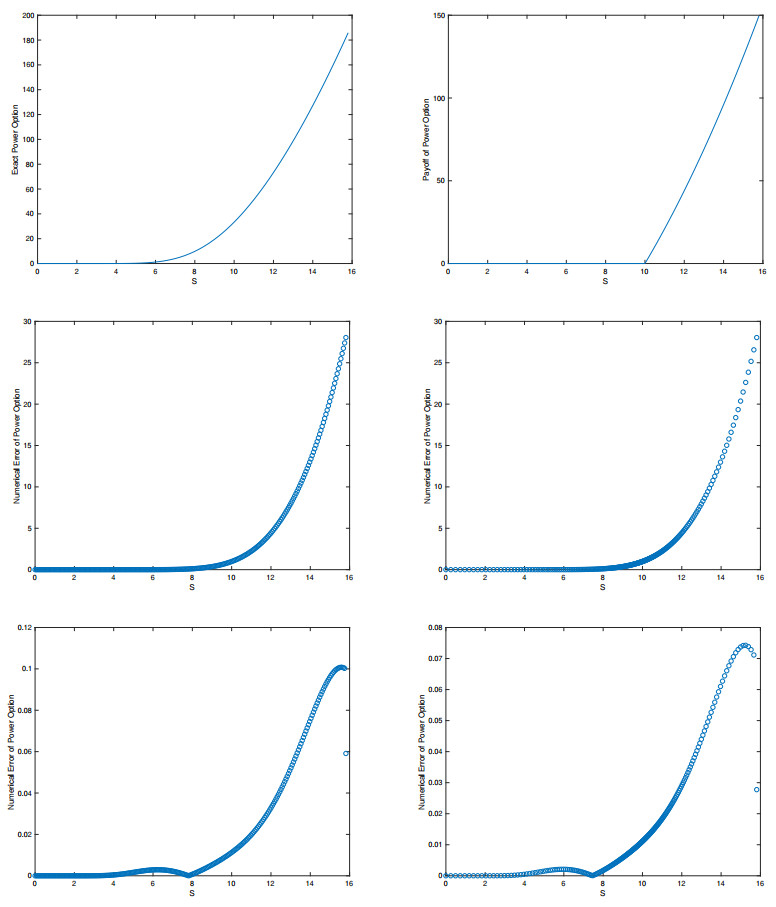
A power call option has a payoff max(xp−K,0) where p∈R+ is a power. The closed-form solution of the power option is given by [18]:
where
Note that the power option with p=1 is the call option. Figure 1 shows the comparison of the numerical errors of one-asset power call option with different schemes: The equidistance discretization in space with the linear boundary condition (Equi&L), the grid stretching discretization around the strike price with linear boundary condition (GS&L), the equidistance discretization in space with Monte Carlo simulation at Smax (Equi&MC) and the grid stretching discretization with the antithetic Monte Carlo simulation at Smax (GS&AMC).
Table 1 shows the RMSE of the power option with Nx=250 and Δτ=1720 for p=1, p=2 and p=3 in the whole domain Ω=(0,Smax) and the interesting domain around the strike price Ωe=[0.7p√K,1.3p√K] for the different schemes and different Smax. Keep in mind that in the grid stretching transformation (2.2) we must substitute p√K instead of K. We can see the MC and AMC simulation at the end point of the domain reduce RMSE significantly for bigger p and none of the GS, MC and AMC improve the accuracy of the numerical approximation for the call option (p=1).
3.2. European call option on the maximum of two assets
Now we consider a European call option on the maximum of two assets with the payoff u(x,y,0)=max{max{x,y}−K,0}. Then the following exact analytical solutions of the option [17] will be compared to the numerical solutions.
where M is the cumulative bivariate normal distribution function and defined as
and other parameters are as follows:
Figure 2 shows the comparison of the numerical solutions of the call option on the maximum of two assets with the different schemes and (xmax,ymax)=(250,250).
Now in Table 2 we compare the RMSE of these four schemes in the whole region Ω=(0,xmax)×(0,ymax) and in the most interesting region ΩK=(0.7K,1.3K)×(0.7K,1.3K) with different domain sizes (xmax,ymax)=(L,L) and Nx=Ny=L at t=0.
3.3. European call on the minimum of two assets
A European call on the minimum of two assets has the payoff u(x,y,0)=max{min{x,y}−K,0} and the closed form solution as follows [17]
where its parameters are the same as the European call option on the maximum of two assets. In Figure 3 and Table 3 we compare the four above mentioned schemes for this two-asset option.
3.4. Two-asset correlation call option
Here we consider a two-asset correlation call option wich pays off:
This option has been priced by [18]:
where ρ is the correlation coefficient between the returns on the two assets and
Now we solve numerically this option. Figure 4 shows the comparison of the numerical solutions of two-asset correlation call option with the different schemes.
Table 4 shows the RMSE of the equidistance discretization (Equi) and the grid stretching discretization around the strike price with Monte Carlo simulation at the last point of the boundary (xmax,ymax)=(L,L) (GS&MC)with different L in the whole region Ω=[0,L]×[0,L] and the most interesting region ΩK=[0.7K,1.3K]×[0.7K,1.3K] respectively.
3.5. Two-asset butterfly option
A butterfly option can be regarded as a combination of two long calls with strikes K1 and K2 and two short calls both with strike K=(K1+K2)/2. Thus, for given values K1,K2>0 with K1<K2, the payoff of a two-asset European butterfly option is:
and has the following analytical solution:
where the M(a,b;ρ) is the cumulative bivariate normal distribution function (3.4) and other parameters are defined in (3.5) and (3.6). where d(i)1 and d(i)2 will be obtained by substituting Ki in 3.5 for i=1,2.
Here we consider a two-asset butterfly option with K1=50, K2=150. Figure 5 shows the comparison of the numerical solutions of the two-asset butterfly option with the equidistance and the grid stretching discretization schemes. Since u0Nx,Ny=0 we can not use the Monte Carlo simulation at the end point of the domain in (2.24).
Now in Table 5 we compare the RMSE of the equidistance discretization (Equi) and the grid stretching discretization (GS) for the space in the whole region Ω=(xmax,ymax) and the most interesting region ΩK=[0.7K1,1.3K2]×[0.7K1,1.3K2] with different domain sizes (xmax,ymax)=(L,L) and Nx=Ny=L at t=0. We can see in this option the GS scheme does not have any superiority over Equi for the bigger domain.
3.6. Two-asset cash-or-nothing call option
The payoff function of a two-asset cash-or-nothing option is given by
which c is a constant. The closed form solution for the two-asset cash-or-nothing option is as follows
where M(a,b;ρ) is the cumulative bivariate normal distribution function (3.4) and dx and dy are the same as (3.10). Now we consider a two-asset cash-or-nothing call option with c=100, then the exact analytical solutions of the option [6] will be compared to the numerical solutions. Figure 6 shows the comparison of the numerical solutions of the option with the different four schemes and also Table 6 demonstrates the RMSE of the four schemes with different domain sizes (xmax,ymax)=(L,L), Nx=Ny=L and Δτ=1720 in the whole region Ω and the in interesting region ΩK. Since the payoff of this option is constant at the end point of the domain, we can see that the MC and AMC simulations do not have any superiority for the bigger domain.
4.
Conclusions
We applied the FDM for solving numerically one and two-dimensional B-S equations with different space discretization and boundary conditions. Also, RMSE has been applied for estimating error of the method as it is common to use and consider the numerical errors for all nodal points of the region. Numerical experiments illustrated that by applying the antithetic Monte Carlo simulation for the end point of the space domain and discretization with grid stretching to put more nodal points around the non-smooth point of the payoff function, we obtained more accurate numerical solutions in the considered exotic options with non-constant payoff at the end point of the space domain. These remedies can be considered and implemented for other options, higher dimensional models, nonlinear B-S equations and also other financial derivatives.
Acknowledgments
The authors would like to thank the reviewers for their helpful suggestions and comments, which improved the quality of this article.
Conflict of interest
The authors declare that they have no conflicts of interest.









 DownLoad:
DownLoad:








