Approximate solution of nonlinear Black–Scholes equation via a fully discretized fourth-order method

Azadeh Ghanadian; Taher Lotfi; Azadeh Ghanadian; Taher Lotfi

doi:10.3934/math.2020060

AIMS Mathematics

2020, Volume 5, Issue 2: 879-893. doi: 10.3934/math.2020060

Previous Article Next Article

Research article

Approximate solution of nonlinear Black–Scholes equation via a fully discretized fourth-order method

Azadeh Ghanadian ,
Taher Lotfi ^,

Department of Mathematics, Hamedan Branch, Islamic Azad University, Hamedan, Iran

Received: 06 October 2019 Accepted: 11 December 2019 Published: 06 January 2020
MSC : 41A15, 65M20

In this work, a new fourth-order finite difference (FD) approximation (for both structured and unstructured grid of nodes) is contributed and equipped with the fourth-order Runge–Kutta scheme to tackle the financial nonlinear partial differential equation (PDE) of Black–Scholes. This timedependent PDE problem is converted to a set of ordinary differential equations (ODEs). It is proved that under several criteria the procedure is time stable. Computational illustrations presented here, show that our approach is fast and accurate. The proposed technique reduces the computational cost, when more accurate results are requested.

Keywords:

Citation: Azadeh Ghanadian, Taher Lotfi. Approximate solution of nonlinear Black–Scholes equation via a fully discretized fourth-order method[J]. AIMS Mathematics, 2020, 5(2): 879-893. doi: 10.3934/math.2020060

Related Papers:

[1]	Din Prathumwan, Thipsuda Khonwai, Narisara Phoochalong, Inthira Chaiya, Kamonchat Trachoo . An improved approximate method for solving two-dimensional time-fractional-order Black-Scholes model: a finite difference approach. AIMS Mathematics, 2024, 9(7): 17205-17233. doi: 10.3934/math.2024836
[2]	Hijaz Ahmad, Muhammad Nawaz Khan, Imtiaz Ahmad, Mohamed Omri, Maged F. Alotaibi . A meshless method for numerical solutions of linear and nonlinear time-fractional Black-Scholes models. AIMS Mathematics, 2023, 8(8): 19677-19698. doi: 10.3934/math.20231003
[3]	Zhongdi Cen, Jian Huang, Aimin Xu . A posteriori grid method for a time-fractional Black-Scholes equation. AIMS Mathematics, 2022, 7(12): 20962-20978. doi: 10.3934/math.20221148
[4]	Ashish Awasthi, Riyasudheen TK . An accurate solution for the generalized Black-Scholes equations governing option pricing. AIMS Mathematics, 2020, 5(3): 2226-2243. doi: 10.3934/math.2020147
[5]	Min-Ku Lee, Jeong-Hoon Kim . Closed-form approximate solutions for stop-loss and Russian options with multiscale stochastic volatility. AIMS Mathematics, 2023, 8(10): 25164-25194. doi: 10.3934/math.20231284
[6]	Weiping Gao, Yanxia Hu . The exact traveling wave solutions of a class of generalized Black-Scholes equation. AIMS Mathematics, 2017, 2(3): 385-399. doi: 10.3934/Math.2017.3.385
[7]	Jafar Biazar, Fereshteh Goldoust . Multi-dimensional Legendre wavelets approach on the Black-Scholes and Heston Cox Ingersoll Ross equations. AIMS Mathematics, 2019, 4(4): 1046-1064. doi: 10.3934/math.2019.4.1046
[8]	Kazem Nouri, Milad Fahimi, Leila Torkzadeh, Dumitru Baleanu . Numerical method for pricing discretely monitored double barrier option by orthogonal projection method. AIMS Mathematics, 2021, 6(6): 5750-5761. doi: 10.3934/math.2021339
[9]	Muhammad Asim Khan, Norma Alias, Umair Ali . A new fourth-order grouping iterative method for the time fractional sub-diffusion equation having a weak singularity at initial time. AIMS Mathematics, 2023, 8(6): 13725-13746. doi: 10.3934/math.2023697
[10]	Abdulghani R. Alharbi . Traveling-wave and numerical solutions to nonlinear evolution equations via modern computational techniques. AIMS Mathematics, 2024, 9(1): 1323-1345. doi: 10.3934/math.2024065

Abstract

1. Introductory notes

In financial mathematics, options have become famous, so that in many cases more money is invested in them than in the underlying assets, both for hedging and for speculation ^[14]. There is a systematic procedure to obtain how much they are worthwhile, and hence they can be bought and sold with some confidence ^[36].

Options are basically traded directly among large financial institutes – also known as over-the-counter (i.e., OTC deals). These options often have nonstandard features that are tailored to the special requirements of the parties involved.

An asset is any financial object such as shares in a company, whose valuation is provided now, but is liable to modification in the future ^[10]. To discuss further, a call option of European type furnishes its owner the right (but without any obligation) to buy from the writer a specific asset for a specific price at a specific time in the future.

A fundamental option model is the following Black–Scholes partial differential equation (PDE) excluding the costs of transaction in a complete market ^[8]:

$\begin{equation} V_t+\frac{1}{2}\sigma^2 S^2 V_{SS}+(r-q)SV_S-rV = 0, \end{equation}$

(1.1)

wherein $r$ is the rate of interest without risk, $q$ is the yield of dividend, and the initial conditions as comes next:

$\begin{equation} V(S, T) = \max{\{E-S, 0\}}, \quad \text{put type}, \end{equation}$

(1.2)

$\begin{equation} V(S, T) = \max{\{S-E, 0\}}, \quad \text{call type}, \end{equation}$

(1.3)

by considering $E$ as the price of strike. The price of option, the underlying asset price and the 2nd derivative of $V$ in terms of $S$ are denoted by $V$ , $S$ and $V_{SS}$ , respectively.

Although several disadvantages are existed in (1.1), it is widely considered by traders and investors because of its simplicity, and also because, in several situations, it provides a fair valuation for price of options in the complete markets, see also the discussions of ^[21,33].

The most significant drawbacks of (1.1) are the followings. It considers a geometric Brownian motion (GBM), where the market might deviate from that assumption, as well as it assumes constant volatility, while the market is characterized by changing (stochastic) volatility regimes ^[28].

Therefore in practice, there are several caveats on the PDE of Black–Scholes (1.1), see ^[4] for more discussions. Theoretical models sometimes take a situation into account, wherein a portfolio optimization is exercised without the costs of transaction. Accordingly, more practical models at which the costs of transaction are considered, should be taken into account, see for example ^[18] and the references cited there. Noting that, the transaction costs reduce the expected return and thus cannot be ignored.

Two major resources for transaction costs are basically exist–fixed and impact costs. The first one is various types of fees (bank fee and so on) and generally they are functions with linear or piece-wise linear features of transaction size. The costs of impact are more challenging to model and generally have nonlinearity. Technically speaking, these costs are modifications in the considered asset's price that are caused by our own trading of that specific asset ^[7].

Pricing European-style option under the transaction costs, which are modeled by nonlinear PDEs is a the main topic of this research, because of the importance of considering transaction costs into (1.1).

It is recalling that for some time ago the Monte Carlo simulations were only employed for pricing European options while there is no such thing in recent years and they can successfully be applied for options with nonlinear volatilities ^[22]. However, the problem in pricing such options is that a model with time-dependent coefficients must be tackled, and this strategy relies on a several conditional expectations which are hard to compute. Thus numerical schemes for PDEs such as second-order finite difference (FD) or local/global RBF meshfree methods should be investigated, refer to ^[20,34].

In literature, different other techniques have been proposed, see e.g., ^[1] and a common note is the employment of high-order discretization schemes. To be more precise, the author in ^[1] discussed several merits of a 4th-rate compact scheme compared to the traditional solvers. To see some solvers for tackling the dynamic of financial models when come out as stochastic differential equations (SDEs), refer to ^[29,30]. See ^[16] for further details.

In this work, the derivatives involved in the PDE are estimated by higher order FD approximants contributed for both uniform and non-uniform grid of points. Then, a semi-discretization procedure ^[19] for discretizing on the asset variable is done to derive a set of (nonlinear) ordinary differential equations (ODEs).

After reviewing the preliminaries in Section 2, this paper presents a fully discretized high order FD method and compare its ability to simulate the governing equation of Black–Scholes under the transaction costs. We derive and propose new fourth-order FD discretization on any forms of discretization, i.e., for uniform and non-uniform discretizations in Section 3.

A classical 4th-rate explicit Runge–Kutta method is used along time in Section 4. The motivation in selecting such a scheme is that the fully discretized approach be of fourth-order accuracy in both time and space. An intensive numerical report will be furnished in Section 5 to validate the efficacy and usefulness of our scheme in option pricing under the costs of transaction. The simulation results confirmed that our fourth-order method is fruitful for studying the nonlinear Black–Scholes problem. Section 6 finalizes the work.

2. The literature

The paper ^[23] discussed an improved volatility to develop the reliability of the option pricing PDE (1.1) as follows:

$\begin{equation} \sigma = \sigma_0\sqrt{(1+\zeta\ \text{sign}(V_{SS}))}, \end{equation}$

(2.1)

from a model of binomial at which

$\begin{equation} \zeta = \dfrac{\mu}{\sigma_0\sqrt{\Delta t}}. \end{equation}$

(2.2)

Herein, $\mu$ is the proportional cost of transaction, $\Delta t$ is the period of transaction, $\sigma_0$ is the initial constant of volatility.

Authors in ^[15] presented a correction of constant volatility of the following form:

$\begin{equation} \sigma^2 = \sigma_0^2\left(1+\vartheta\ (S\ V_{SS})^{\frac{1}{3}}\right), \end{equation}$

(2.3)

wherein

$\begin{equation} \vartheta = 3\left(\zeta^2\ \theta/(2\pi)\right)^{\frac{1}{3}}, \end{equation}$

(2.4)

and $\theta$ , $\zeta$ are nonnegative constants representing the the risk premium measure and transaction cost measure, respectively. One may refer to the work ^[22] for several further related discussions.

Barles–Soner ^[7] proposed another practical model for the implied volatility as follows:

$\begin{equation} \sigma^2 = \sigma_0^2\left(1+ Z \ [\exp{(r(T-t))}a^2\ S^2\ V_{SS}]\right), \end{equation}$

(2.5)

wherein the maturity time is $T$ , $a = \mu\sqrt{\gamma \mathcal{N}}$ , with factor of risk of aversion $\gamma$ and $\mathcal{N}$ number of options for solding.

Computing the solution $Z (\cdot)$ based on the following first-order ODE which is nonlinear makes the overall pricing procedure challenging:

$\begin{equation} \left\{ \begin{array}{l} Z '(x) = \dfrac{1+ Z (x)}{2\sqrt{x Z (x)}-x}, \quad x\neq0, \\ Z (0) = 0. \end{array}\right. \end{equation}$

(2.6)

The implicit solution of (2.6) can be written as comes next ^[9]:

$\begin{equation} \left\{ \begin{array}{ll} x = \left(-\dfrac{\text{Arcsinh}\sqrt{ Z }}{\sqrt{1+ Z }}+\sqrt{ Z }\right)^2, &\text{if}\ Z \gt 0, \\ x = -\left(\dfrac{\text{arcsin}\sqrt{- Z }}{\sqrt{1+ Z }}-\sqrt{- Z }\right)^2, &\text{if}\ -1 \lt Z \lt 0. \end{array}\right. \end{equation}$

(2.7)

In this work, we use the exact solution (2.7) whenever required. Recalling that $Z(x)$ is an increasing function to $(-1, \infty)$ . To find the exact solution based on (2.7) algebraic nonlinear equations must be solved. In fact, for different values of $x$ , corresponding nonlinear equations must be solved using iterative methods. Here the Newton's method without memory which has already been coded inside the built-in function $\mathtt{Chop[FindRoot[]]}$ is used. A $\mathtt{Chop[]}$ command has already been imposed so as to replace values smaller than $10^{-10}$ with zero in order to accelerate the use of the problem and avoid accumulation and rood-off errors.

The improved nonlinear Black–Scholes model (1.1) & (2.5) has a unique viscosity solution ^[7].

Here by employing $U(S, \tau) = V(S, t)$ , $\tau = T-t$ , and considering (2.5), we present a novel computational scheme for the following PDE problem:

$\begin{equation} \left\{ \begin{array}{l} U_\tau = \dfrac{1}{2}\sigma_0^2\left(1+ Z \ [\exp{(r\tau)}a^2 S^2 U_{SS}]\right) S^2 U_{SS}+(r-q)S U_S-r U, \\ S \gt 0, \\ \tau\in [0, T), \\ U(S, 0)\ \text{payoff}. \end{array}\right. \end{equation}$

(2.8)

The problem (2.8) with its nonlinearity does not have a theoretical solution and this makes it requisite to present a robust scheme for pricing in the presence of transaction costs.

The parabolic PDE (2.8) is on the unbounded domain ^[27] below:

$\begin{equation} (S, \tau)\in[0, +\infty)\times (0, T]. \end{equation}$

(2.9)

Now we need to truncate (2.9) into a bounded domain for the sake of numerical computation. Thus, we have

$\begin{equation} (S, \tau)\in[0, s_{\max}]\times (0, T], \end{equation}$

(2.10)

wherein $s_{\max}$ , is a positive constant large enough for minimizing the error of truncating the domain.

It is recalled that for an option of call type, the boundary conditions are defined by ^[4]:

$\begin{equation} \left\{ \begin{array}{l} U(0, \tau) = 0, \\ \lim\limits_{S\rightarrow\infty}U(S, \tau) = S_{\max}-E\exp{\left(-r\tau\right)}. \end{array}\right. \end{equation}$

(2.11)

3. Constructing a fourth-order scheme

Here, by employing a similar spirit as in [12,chapters 3-4] or ^[2,5] but with further terms in the expansions of Taylor, a 4th-rate FD scheme is built on unstructured grid of nodes.

In fact, in unstructured nodes and to preserve the 4th rate of speed on such grids, five and six points are required for estimating the 1st and 2nd derivatives of a given smooth function.

Let us assume that $g(s)$ is sufficiently smooth and we have the following grid of points:

$\begin{equation} \{s_1, s_2, \cdots, s_{m-1}, s_m\}. \end{equation}$

(3.1)

Consider the following five adjacent nodes:

$\begin{equation} \{\{s_{i-2}, g(s_{i-2})\}, \{s_{i-1}, g(s_{i-1})\}, \{s_{i}, g(s_{i})\}, \{s_{i+1}, g(s_{i+1})\}, \{s_{i+2}, g(s_{i+2})\}\}, \end{equation}$

(3.2)

and compute the interpolatory polynomial $p(z)$ passing through the adjacent points, and thence its first differentiation $p'(z)$ .

By employing $z = s_i$ and several symbolic computations, one obtains the following FD formulation on unstructured grids:

$\begin{equation} g'(s_{i}) = \alpha_{i-2}g\left(s_{i-2}\right)+\alpha_{i-1}g\left(s_{i-1}\right) +\alpha_{i}g\left(s_{i}\right)+\alpha_{i+1}g\left(s_{i+1}\right)+\alpha_{i+2}g\left(s_{i+2}\right) +\mathcal{O}\left(h^4\right), \end{equation}$

(3.3)

wherein the maximum spacing of local grid is $h$ , one obtains

$\begin{equation} \begin{split} \alpha_{i-2}& = -\frac{\psi _{i-1, i} \psi _{i, i+1} \psi _{i, i+2}}{\psi _{i-2, i-1} \psi _{i-2, i} \psi _{i-2, i+1} \psi _{i-2, i+2}}, \\ \alpha_{i-1}& = \frac{\psi _{i-2, i} \psi _{i, i+1} \psi _{i, i+2}}{\psi _{i-2, i-1} \psi _{i-1, i} \psi _{i-1, i+1} \psi _{i-1, i+2}}, \\ \alpha_{i}& = \frac{1}{\psi _{i-2, i} \psi _{i, i-1} \psi _{i, i+1} \psi _{i, i+2}} Y _1, \\ \alpha_{i+1}& = \frac{\psi _{i-2, i} \psi _{i, i-1} \psi _{i, i+2}}{\psi _{i-2, i+1} \psi _{i+1, i-1} \psi _{i+1, i} \psi _{i+1, i+2}}, \\ \alpha_{i+2}& = \frac{\psi _{i-2, i} \psi _{i, i-1} \psi _{i, i+1}}{\psi _{i-2, i+2} \psi _{i+2, i-1} \psi _{i+2, i} \psi _{i+2, i+1}}, \end{split} \end{equation}$

(3.4)

using $\psi _{l, q} = s_{l}-s_{q}$ and

$\begin{equation} \begin{split} Y _1 = &s_{i-2} (s_{i-1} (\psi _{i+1, i}+\psi _{i+2, i})\\ &+3 s_i^2-2 (s_{i+1}+s_{i+2})s_i+s_{i+1} s_{i+2})+s_i (-4 s_i^2+3 (s_{i+1}+s_{i+2}) s_i\\ &-2 s_{i+1} s_{i+2})+s_{i-1} (3 s_i^2-2 (s_{i+1}+s_{i+2}) s_i+s_{i+1} s_{i+2}). \end{split} \end{equation}$

(3.5)

The sided FD formulas must be constructed similarly and used for the points on the boundaries and only the one near to the boundaries to have a unified fourth order of convergence. It is noted that in case of applying these formulas on structured grids, then the fourth order of convergence is preserved.

In a similar manner, FD approximants for the 2nd derivative terms can be obtained applying a similar methodology as above. So, let us consider the following set of points:

$\begin{equation} \{\{s_{i-3}, g(s_{i-3})\}, \{s_{i-2}, g(s_{i-2})\}, \{s_{i-1}, g(s_{i-1})\}, \{s_{i}, g(s_{i})\}, \{s_{i+1}, g(s_{i+1})\}, \{s_{i+2}, g(s_{i+2})\}\}, \end{equation}$

(3.6)

and calculate the 2nd-derivative interpolatory function $p''(z)$ based on $z$ . At this moment, by considering $z = s_i$ and a symbolic language like Wolfram Mathematica ^[37], one obtains

$\begin{equation} \begin{split} g''(s_{i}) = &\beta_{i-3}g\left(s_{i-3}\right)+\beta_{i-2}g\left(s_{i-2}\right)+\beta_{i-1}g\left(s_{i-1}\right)\\ &+\beta_{i}g\left(s_{i}\right)+\beta_{i+1}g\left(s_{i+1}\right)+\beta_{i+2}g\left(s_{i+2}\right) +\mathcal{O}\left(h^4\right), \end{split} \end{equation}$

(3.7)

where

$\begin{equation} \begin{split} \beta_{i-3}& = \frac{ Y _2}{\psi _{i-3, i-2} \psi _{i-3, i-1} \psi _{i-3, i} \psi _{i-3, i+1} \psi _{i-3, i+2}}, \\ \beta_{i-2}& = \frac{ Y _3}{\psi _{i-3, i-2} \psi _{i-2, i-1} \psi _{i-2, i} \psi _{i-2, i+1} \psi _{i-2, i+2}}, \\ \beta_{i-1}& = \frac{ Y _4}{\psi _{i-2, i-1} \psi _{i-1, i-3} \psi _{i-1, i} \psi _{i-1, i+1} \psi _{i-1, i+2}}, \\ \end{split} \end{equation}$

(3.8)

$\begin{equation*} \begin{split} \beta_{i}& = \frac{ Y _5}{\psi _{i-3, i} \psi _{i, i-2} \psi _{i, i-1} \psi _{i, i+1} \psi _{i, i+2}}, \\ \beta_{i+1}& = \frac{ Y _6}{\psi _{i-3, i+1} \psi _{i+1, i-2} \psi _{i+1, i-1} \psi _{i+1, i} \psi _{i+1, i+2}}, \\ \beta_{i+2}& = \frac{ Y _7}{\psi _{i-3, i+2} \psi _{i+2, i-2} \psi _{i+2, i-1} \psi _{i+2, i} \psi _{i+2, i+1}}. \end{split} \end{equation*}$

Here, we have

$\begin{equation} \begin{split} Y _2 = &s_{i-1} (-6 s_i^2+4 (s_{i+1}+s_{i+2}) s_i-2 s_{i+1} s_{i+2})+2 s_i (4 s_i^2\\ &-3 (s_{i+1}+s_{i+2}) s_i+2 s_{i+1} s_{i+2})+s_{i-2}(-6 s_i^2\\ &+4 (s_{i+1}+s_{i+2}) s_i-2 s_{i+1} s_{i+2}+s_{i-1} (4 s_i-2 (s_{i+1}+s_{i+2}))), \\ Y _3 = &2 (s_{i-3} (s_{i-1} (\psi _{i+1, i}+\psi _{i+2, i})+3 s_i^2-2 (s_{i+1}\\ &+s_{i+2}) s_i+s_{i+1} s_{i+2})+s_i (-4 s_i^2+3 (s_{i+1}+s_{i+2}) s_i-2 s_{i+1} s_{i+2})\\ &+s_{i-1} (3 s_i^2-2 (s_{i+1}+s_{i+2}) s_i+s_{i+1} s_{i+2})), \\ Y _4 = &2 (s_{i-3} (s_{i-2} (\psi _{i+1, i}+\psi _{i+2, i})+3 s_i^2-2 (s_{i+1}\\ &+s_{i+2}) s_i+s_{i+1} s_{i+2})+s_i (-4 s_i^2+3 (s_{i+1}+s_{i+2}) s_i-2 s_{i+1} s_{i+2})\\ &+s_{i-2} (3 s_i^2-2 (s_{i+1}+s_{i+2}) s_i+s_{i+1} s_{i+2})), \\ Y _5 = &2 (s_{i-2} (s_{i-1} (\psi _{i+1, i}+\psi _{i+2, i}-s_i)+6 s_i^2-3 (s_{i+1}+s_{i+2}) s_i+s_{i+1} s_{i+2})+s_{i-3} (s_{i-1} (\psi _{i+1, i}\\ &+\psi _{i+2, i}-s_i)+s_{i-2} (\psi _{i+1, i}+\psi _{i+2, i}+s_{i-1}-s_i)+6 s_i^2-3 s_{i+1} s_i-3 s_{i+2} s_i+s_{i+1} s_{i+2})\\ &+s_i (2 s_i (3 s_{i+1}-5 s_i)+s_{i-1} (6 s_i-3 s_{i+1}))+(3 s_i (2 s_i-s_{i+1})+s_{i-1} (s_{i+1}-3 s_i)) s_{i+2}), \\ Y _6 = &2 (s_i (s_{i-1} (2 \psi _{i, i+2}+s_i)+s_i (3 s_{i+2}-4 s_i))+s_{i-2} (s_i (2 \psi _{i, i+2}+s_i)\\ &+s_{i-1} (\psi _{i+2, i}-s_i))+s_{i-3} (2 s_i \psi _{i, i+2}\\ &+s_{i-1} (\psi _{i+2, i}-s_i)+s_{i-2} (\psi _{i-1, i}+\psi _{i+2, i})+s_i^2)), \\ Y _7 = &2 (s_i (s_{i-1} (2 \psi _{i, i+1}+s_i)+s_i (3 s_{i+1}-4 s_i))+s_{i-2} (s_i (2 \psi _{i, i+1}\\ &+s_i)+s_{i-1} (\psi _{i+1, i}-s_i))+s_{i-3} (2 s_i \psi _{i, i+1}\\ &+s_{i-1} (\psi _{i+1, i}-s_i)+s_{i-2} (\psi _{i-1, i}+\psi _{i+1, i})+s_i^2)). \end{split} \end{equation}$

(3.9)

To obtain (3.9), basically the procedure is to write the Taylor expansion of (3.7) up to fourth order and ignoring the larger errors terms. This can be done using a computer algebra system (CAS), here Mathematica, so as to obtain the weights properly and to keep the fourth order of convergence.

The procedure for obtaining the weights for the points $\{s_1, s_2, s_3, s_{m-1}, s_m\}$ to keep the fourth convergence order should be investigated by the six adjacent points as described above but for that specific node. The relations (3.3) and (3.7) are applicable on both non-uniform and uniform meshes and in case of equidistant discretion nodes, can yield in more accurate formulations.

4. Constructing the set of equations and time stepping

Considering all the weights of the diffusion and convection terms along with the structure of (2.8), we can build a system of semi–discretized ODEs, see ^[17] for more details. This is pursued in this section using the notion of differentiation matrices.

By matrix of differentiation, we typically mean a matrix that interlinks a function derivative evaluated at the nodes to the function of the function values at these nodes. To illustrate further, we have:

$\begin{equation} \frac{\partial }{{\partial S}}\underline {\rm{u}} \simeq {D_S}\underline {\rm{u}} , \end{equation}$

(4.1)

wherein $\underline {\rm{u}}$ is the function values vector and $D_S$ is the differentiation matrix. They are required when tackling PDEs by RBF–like or FD–like approximations.

Stencil weights are a special case of matrix of differentiation. Applying the novel approximations in (3.3) & (3.7), the differentiation matrices for the 1st and 2nd derivative of the function could be constructed and filled.

The set of ODEs after incorporating the boundaries can be given in the following compact matrix form:

$\begin{equation} \begin{split} \dfrac{dU}{d\tau}& = \Gamma(\tau) U(\tau), \\ U(0)& = \text{payoff function}, \end{split} \end{equation}$

(4.2)

where the time dependent coefficient matrix $\Gamma(\tau)$ is continuous on an interval in $\mathbb{R}$ .

Now, the system (4.2) is solved by the fourth–order explicit Runge–Kutta scheme as a temporal solver (considering the time discretization size $\psi \tau$ ), refer to ^[31] for an implementation. This is considered to have a fourth order discretization for both the spatial and temporal variables.

Consider $\mathbf{u}^\iota$ as an estimate to the true solution $\mathbf{u}(\tau_\iota)$ , then we can construct our final (explicit) method. Select $k +1$ temporal nodes, a time step size $\Delta \tau = \frac{T}{k} > 0$ , $\tau_{\iota+1} = \tau_{\iota}+\Delta \tau$ , $0\leq \iota\leq k$ and $\mathbf{u}^0 = p(s)$ , then the fourth–order RK method (RK4) ^[13] is provided as follows:

$\begin{equation} \mathbf{u}^{\iota+1} = \mathbf{u}^{\iota} +\frac{\Delta \tau}{6}\left(\phi_{1}+2\phi_{2} +2\phi_{3}+\phi_{4}\right), \end{equation}$

(4.3)

where

$\begin{align} \phi_{1}& = G\left(\tau_{\iota}, \mathbf{u}^{\iota}\right), \end{align}$

(4.4)

$\begin{align} \phi_{2}& = G\left(\tau_{\iota} +\frac{\Delta \tau}{2}, \mathbf{u}^{\iota} +\frac{\Delta \tau}{2}\phi_{1}\right), \end{align}$

(4.5)

$\begin{align} \phi_{3}& = G\left(\tau_{\iota} +\frac{\Delta \tau}{2}, \mathbf{u}^{\iota} +\frac{\Delta \tau}{2}\phi_{2}\right), \end{align}$

(4.6)

$\begin{align} \phi_{4}& = G\left(\tau_{\iota} +\Delta \tau, \mathbf{u}^{\iota}+\Delta \tau\phi_{3}\right). \end{align}$

(4.7)

The quartic order refers to the localized error of truncation to be of $\mathcal{O}(\Delta \tau^5)$ , and the total accumulated error is $\mathcal{O}(\Delta \tau^4)$ . The following theorem addresses a criterion at which the fourth–order proposed scheme is time stable when $a = 0$ . A remark for the case when $a\neq0$ will be given after the proof.

Theorem 4.1. As long as (4.2) is linear and reads the Lipschitz condition, then the iterative time–stepping scheme (4.3) is stable conditionally along time.

Proof. Here the Lipschitz condition gives (4.2) an existence and uniqueness of the solution. Besides, reminding that methods are $A$ –stable as long as there are no stability restrictions for the following ODE problem:

$\begin{equation} {U' = \lambda U, \ Re (\lambda) \lt 0}. \end{equation}$

(4.8)

This concept was furnished by Dahlquist for linear multi–step schemes (see for details [13,pages 40-50]). Incorporating the time–stepping method (4.3) on the system of ODEs (4.2) yields:

$\begin{align} \mathbf{u}^{\iota+1} = \left(\frac{(\Delta \tau \Gamma)^0}{0!} +\frac{(\Delta \tau \Gamma)^1}{1!} +\frac{(\Delta \tau \Gamma)^2}{2!} +\frac{(\Delta \tau \Gamma)^3}{3!} +\frac{(\Delta \tau \Gamma)^4}{4!}\right) \mathbf{u}^{\iota}. \end{align}$

(4.9)

The explicit method (4.9) is time–stable if the matrix eigenvalues are:

$\begin{equation} \left(I +\Delta \tau \Gamma +\frac{(\Delta \tau \Gamma)^2}{2} +\frac{(\Delta \tau \Gamma)^3}{3!} +\frac{(\Delta \tau \Gamma)^4}{4!}\right), \end{equation}$

(4.10)

have modulus less or equal than one. Viewing (4.9) as an iterative map, it would be clear that the eigenvalues of this matrix are

$\begin{equation} 1 +\Delta \tau \omega_\mathfrak{i} +\frac{(\Delta \tau \omega_\mathfrak{i})^2}{2} +\frac{(\Delta \tau \omega_\mathfrak{i})^3}{6} +\frac{(\Delta \tau \omega_\mathfrak{i})^4}{24}, \end{equation}$

(4.11)

where $\omega_\mathfrak{i}$ are the eigenvalues of matrix $\Gamma$ . Thus, the A–stability is reduced to

$\begin{equation} \left| 1+\Delta \tau \omega_\mathfrak{i} +\frac{(\Delta \tau \omega_\mathfrak{i})^2}{2} +\frac{(\Delta \tau \omega_\mathfrak{i})^3}{6} +\frac{(\Delta \tau \omega_\mathfrak{i})^4}{24} \right| \leq 1, \qquad \mathfrak{i} = 1, 2, \ldots, m. \end{equation}$

(4.12)

Therefore, our proposed method is time–stable if the time step size $\Delta \tau$ reads (4.12). For similar strategy in order to find the stability of condition of our solver one may also refer to the discussions given in ^[32]. The stability function in (4.12) shows a conditional stable behavior for (4.3). The proof is complete now.

Theorem 1 is mostly useful for the linear case of (2.8). For the nonlinear case, the information on the stability of the method is difficult to cope with. As such, stability criterion in (4.12) is in fact a requisite criterion for the stability of nonlinear problems but it is not sufficient, see for more ^[11].

To establish the convergence of the proposed scheme which is the combination of the adaptive fourth-order FD scheme with a sixth-order RK method, it is now enough to recall the Dahlquist theorem [26,Chapter 6.7]. It states that as long as we assume that the starting values are correct and there is no round-off/cancellation errors, then the a multistep method (4.3) is convergent if and only if it is stable and consistent. This is valid as long as the stability condition (4.12) on the temporal step size holds and the the maximum spacing for spatial and temporal sizes tend to zero.

5. Simulation reports

Here, we study the usefulness of our procedure for solving the time–dependent PDE problem (2.8) applying two different types of nodes, i.e., uniform nodes denoted by PMU and the nonuniform nodes denoted by PMNU.

The non–equidistant distribution of the discretization points for $S$ can be used based on ^[6] as follows:

$\begin{equation} s_i = \frac{1}{\xi_s}\sinh\left(x_i\sinh^{-1}\left(\xi_s(s_{\max}-E)\right) -(1-x_i)\sinh^{-1}(\xi_sE)\right)+E, \qquad 1\leq i\leq m, \end{equation}$

(5.1)

whereas $m\gg1$ and $x_i$ are structured points on $[0, 1]$ and are denser around the strike $E$ . We choose $\xi_s = 0.04915$ in (5.1).

Some other notes are as follows:

● Traditional structured 2nd-rate FD discretization scheme equipped with the explicit Euler's method discussed in ^[9] is also used for comparisons and denoted by SFD.

● Here, we consider $s_{\min} = 0$ , $s_{\max} = 3E$ .

● Mathematica 11.0, ^[35] is employed for calculations.

● The specifications of our machine are 16.00 GB of RAM and Windows 7 with Intel(R) Core(TM) i5–2430M CPU 2.40GHz processor.

● The absolute errors (AE) and the $l_2$ norm of the errors are reported for error compariosns.

Although three different methods have been compared here but the results are in agreement and also can compte the numerical results have recently been obtained in ^[3]. There are several other competitive and efficient schemes of higher orders in literature for doing option pricing such as the ones in ^[24,25] that we do not compare our scheme with them since they mainly tackle models without transaction costs.

Test 5.1. ^[7] This problem compares the effectiveness of various approaches for solving (2.8) in case of a vanilla call option having the following conditions:

$\begin{equation} a = 0, \ \sigma = 0.2, \ E = 100＄, \ q = 0, \ r = 0.1, \ T = 1\ \mathit{\text{year}}. \end{equation}$

(5.2)

The results are provided in Table 1 for the Test 5.1. The reference prices are obtained from the exact solution. Computational workouts show that by increasing the number of spatial discretization, PMNU and specially PMNU perform much better and produces accurate results in contrast to those of SFD.

Table 1. Numerical comparisons of different methods for Test 5.1.

	$m$	$\Delta \tau$	Scheme	Approximate solution	Absolute error	Time
$S=90$	17	0.0002	SFD	6.9043	$4.458\times10^{-2}$
		0.00125	PMU	7.1199	$1.709\times10^{-1}$
		0.00125	PMNU	6.9043	$4.459\times10^{-2}$
$S=100$			SFD	13.0481	$2.214\times10^{-1}$
			PMU	13.3539	$8.429\times10^{-2}$
			PMNU	13.2226	$4.704\times10^{-2}$
$S=110$			SFD	21.1375	$1.111\times10^{-1}$
			PMU	21.3755	$1.267\times10^{-1}$
			PMNU	21.2115	$3.718\times10^{-2}$
$l_2$			SFD		$2.518\times10^{-1}$	0.49
			PMU		$2.289\times10^{-1}$	0.37
			PMNU		$\mathbf{7.472\times10^{-2}}$	0.38
$S=90$	33	0.0002	SFD	6.9278	$2.115\times10^{-2}$
		0.00125	PMU	6.9995	$5.053\times10^{-2}$
		0.00125	PMNU	6.9397	$9.202\times10^{-3}$
$S=100$			SFD	13.2046	$6.498\times10^{-2}$
			PMU	13.3036	$3.396\times10^{-2}$
			PMNU	13.2608	$8.801\times10^{-3}$
$S=110$			SFD	21.1983	$5.037\times10^{-2}$
			PMU	21.2699	$2.119\times10^{-2}$
			PMNU	21.2421	$6.654\times10^{-3}$
$l_2$			SFD		$8.490\times10^{-2}$	0.85
			PMU		$6.447\times10^{-2}$	0.59
			PMNU		$\mathbf{1.436\times10^{-2}}$	0.62
$S=90$	65	0.0002	SFD	6.9392	$9.734\times10^{-3}$
		0.00125	PMU	6.9594	$1.044\times10^{-2}$
		0.00125	PMNU	6.9481	$8.158\times10^{-4}$
$S=100$			SFD	13.2538	$1.582\times10^{-2}$
			PMU	13.2796	$9.945\times10^{-3}$
			PMNU	13.2688	$7.987\times10^{-4}$
$S=110$			SFD	21.2384	$1.030\times10^{-2}$
			PMU	21.2564	$7.672\times10^{-3}$
			PMNU	21.2481	$6.163\times10^{-4}$
$l_2$			SFD		$2.124\times10^{-2}$	1.42
			PMU		$1.633\times10^{-2}$	0.97
			PMNU		$\mathbf{1.297\times10^{-3}}$	1.01
$S=90$	129	0.0002	SFD	6.9466	$2.298\times10^{-3}$
		0.00125	PMU	6.9517	$2.796\times10^{-3}$
		0.00125	PMNU	6.9492	$3.210\times10^{-4}$
$S=100$			SFD	13.2658	$3.855\times10^{-3}$
			PMU	13.2721	$2.496\times10^{-3}$
			PMNU	13.2699	$2.925\times10^{-4}$
$S=110$			SFD	21.2462	$2.560\times10^{-3}$
			PMU	21.2505	$1.798\times10^{-3}$
			PMNU	21.2489	$2.101\times10^{-4}$
$l_2$			SFD		$5.167\times10^{-3}$	2.73
			PMU		$4.157\times10^{-3}$	1.66
			PMNU		$\mathbf{4.824\times10^{-4}}$	1.80

| Show Table

DownLoad: CSV

To illustrate convergence rate of the whole scheme, we report the approximated real rate of convergence (ROC), applying the following formula

$\begin{equation} \text{ROC} \simeq \left| \log_2 \dfrac{AE(4m)-AE(2m)}{AE(2m)-AE(m)} \right|, \end{equation}$

(5.3)

where $AE(2m)$ is the solution of based on $2m$ nodes. If we use the obtained AE in $l_2$ from , we obtain the following ROCs, $\{1.39, 1.98\}$ for SFD, $\{1.77, 1.98\}$ for PMU and $\{2.20, 4.00\}$ for PMNU. The ROCs show that despite there is a kink for the initial condition in option pricing under transaction costs, but the main proposed scheme PMNU quickly reaches the fourth order of convergence. This too upholds the theoretical discussions of Section 3.

Test 5.2. We assume same parameters as in Test 5.1 but with $a = 0.01$ . The choice of a small value for $a$ is based on the real situations from the market as discussed in ^[7].

The reference solution here are: $u(E+10, 1)\simeq22.2960$ , $u(E, 1)\simeq14.6457$ , $u(E-10, 1)\simeq8.4032$ . The numerical results are furnished in for $a = 0.01$ .

Table 2. Numerical results of various schemes for Test 5.2.

	$m$	$\Delta \tau$	Scheme	Approximate solution	Absolute error	Time
$S=90$	17	0.0002	SFD	8.2660	$1.371\times10^{-1}$
		0.000625	PMU	8.4889	$8.577\times10^{-2}$
		0.0005	PMNU	8.3746	$2.850\times10^{-2}$
$S=100$			SFD	14.4156	$2.300\times10^{-1}$
			PMU	14.6887	$4.306\times10^{-2}$
			PMNU	14.6165	$2.912\times10^{-2}$
$S=110$			SFD	22.1537	$1.422\times10^{-1}$
			PMU	22.3622	$6.620\times10^{-2}$
			PMNU	22.2711	$2.482\times10^{-2}$
$l_2$			SFD		$3.032\times10^{-1}$	4.47
			PMU		$1.165\times10^{-1}$	2.58
			PMNU		$\mathbf{4.772\times10^{-2}}$	3.15
$S=90$	33	0.0002	SFD	8.3551	$4.806\times10^{-2}$
		0.000625	PMU	8.4249	$2.179\times10^{-2}$
		0.0005	PMNU	8.3976	$5.589\times10^{-3}$
$S=100$			SFD	14.5844	$6.127\times10^{-2}$
			PMU	14.6627	$1.709\times10^{-2}$
			PMNU	14.6402	$5.498\times10^{-3}$
$S=110$			SFD	22.2473	$4.863\times10^{-2}$
			PMU	22.3086	$1.263\times10^{-2}$
			PMNU	22.2911	$4.855\times10^{-3}$
$l_2$			SFD		$9.181\times10^{-2}$	8.16
			PMU		$3.044\times10^{-2}$	5.45
			PMNU		$\mathbf{9.222\times10^{-3}}$	5.53
$S=90$	65	0.0002	SFD	8.3864	$1.671\times10^{-2}$
		0.000625	PMU	8.4058	$2.675\times10^{-3}$
		0.0005	PMNU	8.4021	$1.050\times10^{-3}$
$S=100$			SFD	14.6273	$1.830\times10^{-2}$
			PMU	14.6482	$2.583\times10^{-3}$
			PMNU	14.6445	$1.103\times10^{-3}$
$S=110$			SFD	22.2821	$1.389\times10^{-2}$
			PMU	22.2978	$1.896\times10^{-3}$
			PMNU	22.2947	$1.238\times10^{-3}$
$l_2$			SFD		$3.923\times10^{-3}$	16.68
			PMU		$4.175\times10^{-3}$	9.58
			PMNU		$\mathbf{1.963\times10^{-3}}$	11.61

| Show Table

DownLoad: CSV

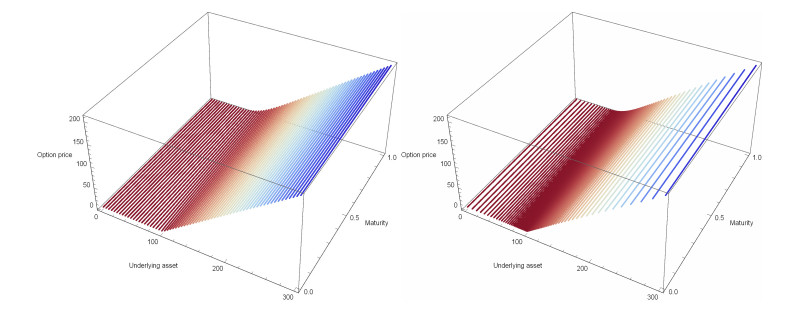
Because the costs of transaction are imposed for this experiment, the numerical solution is plotted for our fourth order procedures in Figure 1 so as to not only emphasize that the uniform and nonuniform discretizations applied in this work with fourth order are useful, but also to show the non-oscillatory positive behavior of the PMNU and PMNU.

Figure 1. Numerical solution of PMU and PMNU showing a stable and a positive behavior in Test 5.2 using

$n = 65$ and Table 2 in left and right, respectively.

DownLoad: Full-Size Img PowerPoint

Results in show that once $a\neq0$ , viz the nonlinearity involved, the pricing procedure is getting harder due to non-constant system matrix in (4.2) with nonlinear entries.

In addition, the approximate solutions (option prices) become higher than the linear case in with $a = 0$ illustrating the effect of transaction costs.

6. End notes

In this paper, after introducing the governing nonlinear equation in Section 2 for an important financial model, the details for the construction of new non-uniform fourth-order FD estimates of the 1st and 2nd derivatives of a given function are discussed in Section 3. Applying a semi-discretization approach, we have constructed an ODE system, which is nonlinear as long as the transaction cost is involved.

To march along time and to have a fully discretized fourth order convergent method, we have implemented the famous explicit Runge–Kutta scheme of fourth order. It was proved that under several conditions for the linear case (non–time–varying system (4.2)) the proposed method is time stable and subsequently a finer step size should be chosen for the time–varying case (nonlinear PDE model).

The emphasis in this paper was on proposing a fully fourth order method not only on the uniform grid of points but also for the non-equidistant distribution of the nodes with more concentration around the non-differentiable area of the initial condition.

The theoretical findings have been supported via several numerical investigations in Section 5 and it was illustrated that our scheme is fast, accurate as well as reduces the computational time for option pricing under transaction costs.

Future works could focus on applying this high order approach for American option pricing under transaction costs when the free boundary value problem is tackled with a penalty approach.

Acknowledgements

We would like to thank three anonymous referees whose insightful comments and suggestions helped us improve the first version of this work.

Conflicts of interest

The writers state that they have no conflicts of interest.

References

[1]	Y. Adam, Highly accurate compact implicit methods and boundary conditions, J. Comput. Phys., 24 (1977), 10-22. doi: 10.1016/0021-9991(77)90106-1
[2]	A. Akgül, F. Soleymani, How to construct a fourth-order scheme for Heston-Hull-White equation?, AIP Conference Proceedings, 2116 (2019), 240002.
[3]	Z. Al-Zhour, M. Barfeie, F. Soleymani, et al. A computational method to price with transaction costs under the nonlinear Black-Scholes model, Chaos Soliton. Fract., 127 (2019), 291-301. doi: 10.1016/j.chaos.2019.06.033
[4]	J. Ankudinova, M. Ehrhardt, On the numerical solution of nonlinear Black-Scholes equations, Comput. Math. Appl., 56 (2008), 799-812. doi: 10.1016/j.camwa.2008.02.005
[5]	A. Babucke, M. J. Kloker, Accuracy analysis of the fundamental finite-difference methods on non-uniform grids, Internal report, Stuttgart University, 2009.
[6]	L. V. Ballestra, C. Sgarra, The evaluation of American options in a stochastic volatility model with jumps: An efficient finite element approach, Comput. Math. Appl., 60 (2010), 1571-1590. doi: 10.1016/j.camwa.2010.06.040
[7]	G. Barles, H. M. Soner, Option pricing with transaction costs and a nonlinear Black-Scholes equation, Financ. Stoch., 2 (1998), 369-397. doi: 10.1007/s007800050046
[8]	F. Black, M. Scholes, The pricing of options and corporate liabilities, J. Polit. Econ., 81 (1973), 637-654. doi: 10.1086/260062
[9]	R. Company, L. Jódar, J. R. Pintos, A numerical method for European option pricing with transaction costs nonlinear equation, Math. Comput. Model., 50 (2009), 910-920. doi: 10.1016/j.mcm.2009.05.019
[10]	M. Cummins, F. Murphy, J. J. H. Miller, Topics in Numerical Methods for Finance, Springer, New York, 2012.
[11]	B. Düring, M. Fournié, A. Jüngel, High order compact finite difference schemes for a nonlinear Black-Scholes equation, Int. J. Theor. Appl. Financ., 6 (2003), 767-789. doi: 10.1142/S0219024903002183
[12]	B. Fornberg, A Practical Guide to Pseudospectral Methods, Cambridge University Press, UK, 1996.
[13]	E. Hairer, G. Wanner, Solving Ordinary Differential Equations II, Springer-Verlag, Berlin Heidelberg, 1996.
[14]	D. J. Higham, An Introduction to Financial Option Valuation, Cambridge University Press, UK, 2004.
[15]	M. Jandačka, D. Ševčovič, On the risk adjusted pricing methodology based valuation of vanilla options and explanation of the volatility smile, J. Appl. Math., 2005 (2005), 235-258. doi: 10.1155/JAM.2005.235
[16]	M. K. Kadalbajoo, A. Kumar, L. P. Tripathi, An efficient numerical method for pricing option under jump diffusion model, Int. J. Adv. Eng. Sci. Appl. Math., 7 (2015), 114-123. doi: 10.1007/s12572-015-0136-z
[17]	R. Knapp, A method of lines framework in mathematica, J. Numer. Anal. Indust. Appl. Math., 3 (2008), 43-59.
[18]	N. Krejić, M. Kumaresan, A. Rožnjik, VaR optimal portfolio with transaction costs, Appl. Math. Comput., 218 (2011), 4626-4637.
[19]	G. H. Meyer, The Time-Discrete Method of Lines for Options and Bonds: A PDE Approach, World Scientific Publishing, USA, 2015.
[20]	S. Milovanović, L. von Sydow, Radial basis function generated finite differences for option pricing problems, Comput. Math. Appl., 75 (2018), 1462-1481. doi: 10.1016/j.camwa.2017.11.015
[21]	R. Mohammadi, Quintic B-spline collocation approach for solving generalized Black-Scholes equation governing option pricing, Comput. Math. Appl., 69 (2015), 777-797. doi: 10.1016/j.camwa.2015.02.018
[22]	M. Monoyios, Option pricing with transaction costs using a Markov chain approximation, J. Econ. Dyn. Control, 28 (2004), 889-913. doi: 10.1016/S0165-1889(03)00059-9
[23]	A. Parás, M. Avellaneda, Dynamic hedging portfolios for derivative securities in the presence of large transaction costs, Appl. Math. Financ., 1 (1994), 165-193. doi: 10.1080/13504869400000010
[24]	P. Roul, A high accuracy numerical method and its convergence for time-fractional Black-Scholes equation governing European options, Appl. Numer. Math., (2020), DOI: https://doi.org/10.1016/j.apnum.2019.11.004.
[25]	P. Roul, V. M. K. P. Goura, A new higher order compact finite difference method for generalised Black-Scholes partial differential equation: European call option, J. Comput. Appl. Math., 363 (2020), 464-484. doi: 10.1016/j.cam.2019.06.015
[26]	T. Sauer, Numerical Analysis, 2 Eds., Pearson Publication, USA, 2012.
[27]	D. Ševčovič, M. Žitnanská, Analysis of the nonlinear option pricing model under variable transaction costs, Asia-Pac. Financ. Mark., 23 (2016), 153-174. doi: 10.1007/s10690-016-9213-y
[28]	R. U. Seydel, Tools for Computational Finance, 6 Eds, Springer, United Kingdom, 2017.
[29]	A. R. Soheili, F. Soleymani, Construction of some accelerated methods for solving scalar stochastic differential equations, Int. J. Comput. Sci. Math., 7 (2016), 537-547. doi: 10.1504/IJCSM.2016.081680
[30]	A. R. Soheili, F. Soleymani, A new solution method for stochastic differential equations via collocation approach, Int. J. Comput. Math., 93 (2016), 2079-2091. doi: 10.1080/00207160.2015.1085029
[31]	M. Sofroniou, R. Knapp, Advanced Numerical Differential Equation Solving in Mathematica, Wolfram Mathematica, Tutorial Collection, USA, 2008.
[32]	F. Soleymani, Pricing multi-asset option problems: A Chebyshev pseudo-spectral method, BIT, 59 (2019), 243-270. doi: 10.1007/s10543-018-0722-0
[33]	F. Soleymani, A. Akgül, Improved numerical solution of multi-asset option pricing problem: A localized RBF-FD approach, Chaos Soliton. Fract.,119 (2019), 298-309. doi: 10.1016/j.chaos.2019.01.003
[34]	D. Tavella, C. Randall, Pricing Financial Instruments - The Finite Difference Method, John Wiley & Sons Inc., New York, 2000.
[35]	M. Trott, The Mathematica GuideBook for Numerics, Springer, NY, USA, 2006.
[36]	P. Ursone, How to Calculate Options Prices and their Greeks, Wiely, UK, 2015.
[37]	P. R. Wellin, R. J. Gaylord, S. N. Kamin, An Introduction to Programming with Mathematica, Cambridge University Press, UK, 2005.

This article has been cited by:

1.	Mohammad Mehdizadeh Khalsaraei, Ali Shokri, Zahra Mohammadnia, Hamid Mohammad Sedighi, Efthymios G. Tsionas, Qualitatively Stable Nonstandard Finite Difference Scheme for Numerical Solution of the Nonlinear Black–Scholes Equation, 2021, 2021, 2314-4785, 1, 10.1155/2021/6679484
2.	Tayyebeh Nadaf, Taher Lotfi, Stanford Shateyi, Revisiting the Copula-Based Trading Method Using the Laplace Marginal Distribution Function, 2022, 10, 2227-7390, 783, 10.3390/math10050783
3.	Gholamreza Farahmand, Taher Lotfi, Malik Zaka Ullah, Stanford Shateyi, Finding an Efficient Computational Solution for the Bates Partial Integro-Differential Equation Utilizing the RBF-FD Scheme, 2023, 11, 2227-7390, 1123, 10.3390/math11051123
4.	Dongming Wei, Yogi Ahmad Erlangga, Gulzat Zhumakhanova, A finite element approach to the numerical solutions of Leland’s model, 2024, 89, 10590560, 582, 10.1016/j.iref.2023.07.076

Reader Comments

Your name:*

Email:*
© 2020 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(5221) PDF downloads(639) Cited by(4)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(1) / Tables(2)

AIMS Mathematics

Approximate solution of nonlinear Black–Scholes equation via a fully discretized fourth-order method

Related Papers:

Abstract

1. Introductory notes

2. The literature

3. Constructing a fourth-order scheme

4. Constructing the set of equations and time stepping

5. Simulation reports

6. End notes

Acknowledgements

Conflicts of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

AIMS Mathematics

Approximate solution of nonlinear Black–Scholes equation via a fully discretized fourth-order method

Related Papers:

Abstract

1. Introductory notes

2. The literature

3. Constructing a fourth-order scheme

4. Constructing the set of equations and time stepping

5. Simulation reports

6. End notes

Acknowledgements

Conflicts of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog