Fuzzy cosets in AG-groups

1.   Introduction

The concept of fuzzy sets along with various operations has been introduced by Zadeh in 1965 ^[1]. Due to the diverse applications of fuzzy sets ranging from engineering, computer science and social behaviour studies; the researchers have taken a keen interest in the subject in its related fields. Rosenfeld is the pioneer, who initiated fuzzification of algebraic structures ^[2]. He introduced basic definitions which are common and popular among the researchers. Rosenfeld introduced the notions of fuzzy subgroupoids and fuzzy subgroups and obtained some of their basic properties. Most of the recent works on fuzzy groups follow Rosenfeld's definitions. Anthony and Sherwood further redefined and characterized fuzzy subgroups ^[3,4]. Bhattacharya and Mukherjee introduced the notion of fuzzy normal subgroups, fuzzy relation and fuzzy cosets. They provided fuzzy generalizations of some remarkable results such as, Lagrange's theorem and Cayley's theorem ^[5,6,7,8,9]. Many other papers on fuzzy subgroups have also appeared which generalize various concepts of group theory such as conjugate subgroups, normal subgroups, quotient groups and cosets, congruence relations, homomorphism, isomorphism, series in groups and many more ^{[10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]}.

Abel-Grassmann's concept of groupoids (AG-groupoids) is about forty years old and, related to this concept, so far more than hundred research papers have been published and many more either lie on the archives or waiting to see the light. Though it was slowly and gradually explored, yet during the last couple of years, it attracted the attention of many researchers and ample research was carried out in this area.

In 1972, Kazim and Naseeruddin introduced AG-groupoids ^[26] and called it "left almost semigroup" or "LA-semigroup". In the literature this structure is also known by various names; right modular groupoid" ^[27], "left invertive groupoid" ^[28] or commonly by Abel Grassmann's groupoid (AG-groupoid) suggested by Stevanovic and Protic ^[29]. AG-groupoids have many applications in the theory of flocks ^[30], differential geometry, geometry and algebra ^[31,32,33]. Stevanovic and Protic ^[29] constructed the notion of n-inflation of the AG-groupoids. They also made such a constructions for AG{*}-groupoids ^[34]. They also discussed the properties of n-inflations of AG-groupoids, inflation's of the AG-band and semi-lattices.

An AG-groupoid (or LA-semigroups) is a nonassociative groupoid in general, in which the left invertive law "$(ab)c = (cb)a$ holds for all $a, \, b, \, c$". An AG-groupoid generalizes a commutative semigroup, and lies midway between a groupoid and a commutative semigroup. Even though the structure of AG-groupoid is nonassociative and noncommutative, it still holds many interesting properties which are usually found in commutative and associative algebraic structures. Very recently enumerations of AG-groupoids up to order 6 have been carried out with the help of GAP package for AG-groupoids called "AGGROUPOIDS" ^[35]. Presently, numerous examples of AG-groupoids are available for study, and various conjectures and conclusions can be drawn from the available data.

In general, an AG-group is a nonassociative structure. Unlike groups and other structures, commutativity and associativity imply each other in AG-groups and thus AG-groups become abelian group if any one of them is allowed in AG-group. It is a generalization of the abelian group and a special case of quasi-group. The structure of AG-group is very interesting in which one has to play with brackets. The order of an element cannot be defined in AG-groups, i.e. AG-groups cannot be locally associative, otherwise, it becomes an abelian group. However, the order of an element up to 2 can be found and is called involution. Further, achievement was made when AG-groups were enumerated up to order 12 ^[35]. An AG-groupoid $(G, \, \cdot)$ is called an AG-group or left almost group (LA-group), if there exists a unique left identity $e\in G$ (i.e. $ea = a$ for all $a\in G$), for all $a\in G$ there exists $a^{-1}\in G$ such that $a^{-1}a = aa^{-1} = e$. Dually, a right AG-groupoid $(G, \, \cdot)$ is called a right AG-group or right almost group (RA-group), if there exists a unique right identity $e\in G$ (i.e. $ae = a$ for all $a\in G$), for all $a\in G$ there exists $a^{-1}\in G$ such that $a^{-1}a = aa^{-1} = e$.

In this paper, fuzzy AG-subgroup ^[36,37] is further generalized and the notions of fuzzy cosets, conjugate fuzzy AG-subgroups, fuzzy quotient AG-subgroup, fuzzy AG-subgroup of the quotient (factor) AG-subgroup, fuzzy homomorphism of AG-group is introduced. These notions will provide a new direction for the researchers in this area. At the end of the paper, fuzzy version of famous Lagrange's theorem for finite AG-group is also introduced. The results in this paper are taken from the PhD thesis of the first author ^[38].

2.   Preliminaries

In the rest of this paper $G$ denotes an AG-group unless otherwise stated and $e$ denotes the left identity of $G$.

Definition 1. ^[37] Let $A$ be any fuzzy subset of an AG-group $G$ i.e. $A\in FP(G)$. Then $A$ is called a fuzzy AG-subgroup of $G$ if for all $x, \, y$ in $G$:

$\rm(i)$ $\mu_{A}(xy)\geq\mu_{A}(x)\wedge\mu_{A}(y)$,

$\rm(ii)$ $\mu_{A}(x^{-1})\geq\mu_{A}(x)$.

The set of all fuzzy AG-subgroups of $G$ is denoted by $F(G)$. If $A\in F(G)$, then

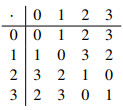
Example 1. In the AG-group $G$ of order $4$ with the following Cayley's table,

The fuzzy AG-subgroup $A$ of $G$ is defined by

where $t_{0} > t_{1} > t_{2}$; and $t_{0}, \, t_{1}, \, t_{2}\in[0, \, 1].$

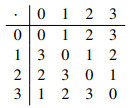
Example 2. Consider the AG-group $G$ of order $4$ with the following Cayley's table,

The fuzzy AG-subgroup $A$ of $G$ is defined by

where $t_{0}, \, t_{1}\in[0, 1]$ and $t_{0} > t_{1}.$

Proposition 1. ^[37] If $A\in F(G)$, then $\mu_{A}(x^{-1}) = \mu_{A}(x)$ and $\mu_{A}(e)\geq\mu_{A}(x)$ for all $x\in G$; where $e$ is the left identity of $G$.

Definition 2. Let $A\in F(G)$ and $u\in G$. Then $B$ is called fuzzy conjugate (with respect to $u$) denoted by, $A\overset{c}{\sim}B_{u}$, if $\mu_{B_{u}}(x) = \mu_{A}\left((ux)u^{-1}\right)$ for all $x\in G$ or simply by

Remark 1. It is noted that a fuzzy conjugate subgroup of a fuzzy subgroup is again a fuzzy subgroup, while the fuzzy conjugate of a fuzzy AG-subgroup may or may not be a fuzzy AG-subgroup.

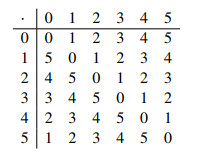
Example 3. The fuzzy conjugates of a fuzzy AG-subgroup $A$ are given as follows:

where $t_{0} > t_{1} > t_{2}$ and $t_{0}, \, t_{1}, \, t_{2}\in[0, \, 1]$ of an AG-group $G$ of order $6$ in the following table:

are given bellow:

Similarly, we can calculate $B_{3} = A, B_{4},$ and $B_{5}$. Here, both $B_{1} = B_{4}$ and $B_{2} = B_{5}$ are not fuzzy AG-subgroups of $G$, as

and

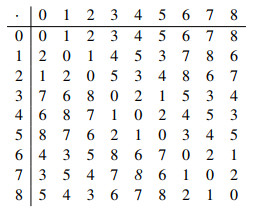
Example 4. The fuzzy conjugates of a fuzzy AG-subgroup $C$ are given by:

where $s_{3} > s_{4}$ and $s_{3}, \, s_{4}\in[0, \, 1]$, for any AG-group $G$ of order $9$ with the following table:

are given bellow:

and

Hence, $D_{0}, \, D_{1}$ and $D_{2}$ are the fuzzy conjugates of a fuzzy AG-subgroup $C$, in which $D_{1}$ and $D_{2}$ are not fuzzy AG-subgroups of $G$ as

and

Definition 3. Let $A\in F(G)$. Then $A$ is called a fuzzy normal AG-subgroup of $G$ if

In other words, $A$ is fuzzy normal AG-subgroup of $G$ if $A$ is self fuzzy conjugate. $FN(G)$ denotes the set of all fuzzy normal AG-subgroups of $G$.

Example 5. Let $G$ be an AG-group of order $6$ as defined in Example 3, and let $A$ be fuzzy AG-subgroup of $G$, defined by

where $t_{0} > t_{1}$ and $t_{0}, \, t_{1}\in[0, \, 1]$. The fuzzy conjugates of a fuzzy AG-subgroup $A$ of $G$, are given bellow:

Similarly, we can calculate $B_{3} = B_{4} = B_{5} = A.$ Hence $A$ is fuzzy normal AG-subgroup of $G$, as $A$ is self conjugate.

Lemma 1. Let $A\in F(G)$. Then $\mu_{A}(xy) = \mu_{A}(yx)$, for all $x, \, y\in G$.

Proof. Suppose that $A\in F(G)$. Then

Similarly, we can show that $\mu_{A}(yx)\geq\mu_{A}(xy)$, for all $x, \, y\in G$. Consequently, $\mu_{A}(xy)\geq\mu_{A}(yx)\geq\mu_{A}(xy)$, for all $x, \, y\in G$. Hence $\mu_{A}(yx) = \mu_{A}(xy)$.

In the following, a fuzzy coset of fuzzy AG-subgroups and binary operation on fuzzy coset is defined. Various examples of a fuzzy coset of fuzzy AG-subgroups are also constructed, and some of the properties of fuzzy coset of fuzzy AG-subgroups are investigated.

Definition 4. Let $A\in F(H)$ where $H$ is an AG-subgroup of $G$, i.e., $H\leq G$ and $x\in G$, then the set $Ax$ defined by

is called fuzzy coset of $H$ in $G$ with respect to the fuzzy AG-subgroup $A$ of $H$.

It should be noted that, if $A\in F(G)$, then by Lemma 1, $\mu_{A}(xy) = \mu_{A}(yx)$ for all $x, \, y\in G$. This implies that, each fuzzy left and fuzzy right coset of AG-subgroups always coincide with each other. Therefore, instead of fuzzy left (fuzzy right) coset the term fuzzy coset of AG-subgroup $H$ in $G$ is used.

Example 6. Consider the AG-group $G$ of order $4$ as in Example 2. Let $H = \{0, \, 2\}$ be an AG-subgroup $($abelian group$)$ of $G$:

A fuzzy subset $A$ of $H$ defined by

where $t_{0}, \, t_{1}\in[0, \, 1]$ and $t_{0} > t_{1}$, is a fuzzy AG-subgroup of $H$ in $G$.

All the disjoint fuzzy coset of $H$ in $G$ with respect to fuzzy AG-subgroup $A$ of $H$ are obtained as follow:

Hence $A$ and $A2$ are the two nonempty disjoint fuzzy cosets of $H$ in $G$ with respect to fuzzy AG-subgroup $A$ of $H$.

Example 7. Consider the AG-group $G$ of order $6$ as in Example 3. Let $H = \{0, \, 2, \, 4\}$ be an AG-subgroup of $G$ of order $3$.

A fuzzy AG-subgroup $A$ of $H$ in $G$ is given by:

where $t_{0} > t_{1}$, and $t_{0}, \, t_{1}\in[0, \, 1]$.

All the disjoint fuzzy cosets of $H$ in $G$ with respect to $A$ of $H$ are obtained as follow:

Hence $A, \, A2$ and $A4$ are three nonempty disjoint fuzzy cosets of $H$ in $G$ with respect to fuzzy AG-subgroup $A$ of $H$.

Example 8. Consider the AG-group $G$ of order $9$ as in Example 4. Let

and

be any four nonabelian AG-subgroups of $G$.

Here $A, \, B, \, C$ and $D$ are fuzzy AG-subgroups of $H_{1}, \, H_{2}, \, H_{3}$ and $H_{4}$ respectively defined by:

and

Then the following disjoint fuzzy cosets of $H_{1}$ in $G$ with respect to $A$ are obtained,

and for all $x\in(G-H)$

Hence $A, \, A1$ and $A2$ are the three nonempty disjoint fuzzy cosets of $H_{1}$ in $G$ with respect to fuzzy AG-subgroup $A$ of $H_{1}$.

Similarly, all the disjoint fuzzy cosets of $B, \, C$ and $D$ of $H_{2}, \, H_{3}$ and $H_{4}$ in $G$ respectively can be calculated in the same way.

3.   Fuzzy quotient AG-subgroups

It is important to note that if $G$ is a group and $H$ is any subgroup of $G$, then $(Ha)(Hb)\neq Hab$, unless $H$ is normal in $G$. There is no such condition in AG-groups because of the medial law, i.e. if $Ha$ and $Hb$ belongs to $G/ H$, where $G$ is an AG-group and $H$ is an AG-subgroup of $G$, then

without having any extra condition on $H$ ^[39]. Therefore, using this idea, a fuzzy quotient AG-subgroup or a fuzzy factor AG-subgroup can be defined in the following result.

Theorem 1. Let $H\leq G$ and $A\in F(H)$. Show that the set $G/ A = \{Ax\, :\, x\in G\}$ forms an AG-group under the binary operation defined by $Ax\cdot Ay = A\left(xy\right)\, \, {\rm for \; all} \, x, \, y\in G$.

Proof. First we show that the binary operation is well defined. Let $x, \, y, \, x_{\circ}, \, y_{\circ}\in G$ such that $Ax = Ax_{\circ}$ and $Ay = Ay_{\circ}$.

We show that $Ax\cdot Ay = Ax_{\circ}\cdot Ay_{\circ}$, i.e. $A\left(xy\right) = A\left(x_{\circ}y_{\circ}\right)$. By definition of fuzzy cosets $A$ of $H$ we get,

and

Now, for all $x, \, y\in G$,

Therefore,

Now, we show that $\mu_{A}\left(\left(x^{-1}y^{-1}\right)\left(x_{\circ}y_{\circ}\right)\right) = \mu_{A}(e)$ in Eq (3.1). Since, $Ax = Ax_{\circ}$ using definition of fuzzy cosets, for all $h\in H$ we obtain

Similarly, since $Ay = Ay_{\circ}$, again using the definition of fuzzy cosets, for all $h\in H$ we obtain

Now, we have

substituting $h$ by $\left(\left(x_{\circ}y_{\circ}\right)y^{-1}\right)$ in Eq (3.2) we get,

Therefore, Eq (3.1) implies that $\mu_{A}\left(h\left(x^{-1}y^{-1}\right)\right)\geq\mu_{A}\left(h\left(x_{\circ}^{-1}y_{\circ}^{-1}\right)\right)$.

Similarly, one can prove that $\mu_{A}\left(h\left(x_{\circ}^{-1}y_{\circ}^{-1}\right)\right)\geq\mu_{A}\left(h\left(x^{-1}y^{-1}\right)\right).$ Consequently, we have

Hence, the binary operation of cosets is well-defined.

Now we show that $G/ A$ forms an AG-group under the binary operation "$\cdot$".

Groupoid: $G/ A$ is a groupoid as the binary operation "$\cdot$" is closed in $G/ A$.

AG-groupoid: $G/ A$ satisfies the left invertive law under the binary operation "$\cdot$". Since for all $x, \, y, \, z\in G$,

Hence, $G/ A$ is an AG-groupoid.

Nonassociative: Again for all $x, \, y, \, z\in G$,

Therefore, $\left(Ax\cdot Ay\right)Az\neq Ax(Ay\cdot Az)$ in general. Hence, $G/ A$ is a nonassociative AG-groupoid.

Existence of Left Identity: For all $x\in G$,

but

This implies that $A$ is the left identity of $G/ A$.

Existence of Inverses: For all $x\in G$,

and

Thus $Ax^{-1}$ is the inverse of $Ax$ for all $x\in G$. Hence, $G/ A$ is an AG-group.

Remark 2. An AG-group $G/A$, defined in Theorem 1, is called fuzzy quotient AG-subgroup or fuzzy factor AG-subgroup.

Definition 5. Let $G$ be a finite AG-group and $H\leq G$, if $A\in F(H)$, then $G/A$ is an AG-group by Theorem 1. The number of distinct cosets of $H$ in $G$ with respect to $A\in F(H)$ in $G/ A$ (called the index of $H$ in $G$ with respect to $A$) written as $[G:\, A]$.

Example 9. Consider the AG-group $G$ of order $4$ as in Example 1. Let $H = \{0, \, 1\}$ be any AG-subgroup of $G$.

A fuzzy AG-subgroup $A$ of $H$ in $G$ is defined by:

The distinct fuzzy cosets of $H$ in $G$ with respect to $A$ in $G$ are $A$ and $A1$. Therefore, $G/ A = \{A, \, A1\}$ is an AG-group under the binary operation between two cosets defined by

Here $[G:\, A] = 2$.

Example 10. Consider the AG-group $G$ of order $6$ as in Example 3. Let $H = \{0, \, 2, \, 4\}$ be an AG-subgroup of $G$ of order $3$.

A fuzzy AG-subgroup $A$ of $H$ in $G$ is given by:

where $t_{0} > t_{1}$, and $t_{0}, \, t_{1}\in[0, \, 1]$.

All the distinct fuzzy cosets of $H$ in $G$ with respect to $A$ of $H$ are $A, \, A2$ and $\, A4$. Therefore, $G/ A = \{A, \, A2, \, A4\}$ is an AG-group under the binary operation between two cosets defined by

$G/ A$ satisfies the left invertive law; for all $x, \, y, \, z\in G$,

$G/ A$ is nonassociative; because

and

This implies that

$A$ is the left identity of $G/A$, but not the right one, because $A\cdot Ax = A0\cdot Ax = A(0\cdot x) = Ax$, for all $x\in G$, but $A2\cdot A = A(2\cdot0) = A4$.

Each fuzzy coset in $G/ A$ is the inverse of itself, since all the properties of AG-group are satisfied. Hence $G/ A$ is an AG-group as shown in Theorem 1. Here $[G:\, A] = 3$.

In the following fuzzy AG-subgroup of the quotient AG-group is defined.

4.   Fuzzy AG-subgroup of $(G/ H)$

Theorem 2. Let $A\in F(G)$ and $H$ be any AG-subgroup of $G$. If $B$ is any fuzzy subset of $G/ H$, defined by

then $B\in F(G/ H)$.

Proof. By definition of coset in AG-groups, for all $x, \, y\in G$, $Hx\cdot Hy = H(xy)$ by medial law. Therefore, for all $x, \, y\in G,$ we get

This implies that for all $x, \, y\in G$,

and

This implies that for all $x\in G$,

Hence $B\in F(G/ H)$.

Remark 3. The fuzzy AG-subgroup defined in Theorem 2, is called the Fuzzy AG-subgroup of the Quotient (or Factor) AG-subgroup.

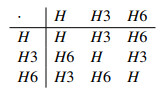
Example 11. Let $G$ be the AG-group of order $9$ as defined in Example 4. Let $H = \left\{ 0, \, 1, \, 2\right\}$ be an AG-subgroup of $G$. The distinct cosets of $H$ in $G$ are $H = \{0, \, 1, \, 2\}$, $H3 = \{3, \, 4, \, 5\}$ and $H6 = \{6, \, 7, \, 8\}$. Therefore, $G/ H = \left\{ H, \, H3, \, H6\right\}$ is an AG-group defined in the following Cayley's table:

Consider a fuzzy AG-subgroup $A$ of $G$ defined by

where $t_{0} > t_{1} > t_{2}$ and $t_{0}, \, t_{1}, \, t_{2}\in[0, \, 1]$.

Let $B\in FP\left(G/ H\right)$ be defined by

Then the membership $\mu_{B}\left(Hx\right)$ of $Hx\in\left(G/ H\right)$ for all $x\in G$ is given by:

Therefore, $B = \left\{ \left(H, \, t_{0}\right), \, \left(H3, \, t_{2}\right), \, \left(H6, \, t_{2}\right)\right\}.$ It can be easily verified that $B\in F\left(G/ H\right)$.

Example 12. Consider the AG-group $G$ of order $6$ as defined in Example 3. Let $H = \left\{ 0, \, 2, \, 4\right\}$ be an AG-subgroup of $G$. The distinct cosets of $H$ in $G$ are $H = \{0, \, 2, \, 4\}$ and $H3 = \{1, \, 3, \, 5\}$. Therefore, $G/ H = \{H, \, H1\}$ is an AG-group.

Define a fuzzy AG-subgroup $A$ of $G$ by:

where $t_{0} > t_{1} > t_{2}$ and $t_{0}, \, t_{1}, \, t_{2}\in[0, \, 1]$.

Let $B\in FP\left(G/ H\right)$ defined by

Then the membership $\mu_{B}\left(Hx\right)$ where $Hx\in\left(G/ H\right)$ for all $x\in G$ are given by:

Therefore, $B = \left\{ \left(H, \, t_{0}\right), \, \left(H1, \, t_{2}\right)\right\}.$ It can be easily verified that $B\in F\left(G/ H\right)$.

Theorem 3. If $H$ is an AG-subgroup of an AG-group $G$ and $A\in F(H),$ then $Ax = Ay\Leftrightarrow A_{\ast}\left(x\right) = A_{\ast}\left(y\right)$, for all $x, \, y\in G$.

Proof. Let $Ax = Ay$, for all $x, \, y\in G$. This implies that

putting $h = y$ in Eq (4.1), we get

Therefore, $A_{\ast}(y)\subseteq A_{\ast}(x)$.

Again putting $h = x$ in Eq (4.1), we get

This implies that $A_{\ast}(x)\subseteq A_{\ast}(y)$. Thus $A_{\ast}(y)\subseteq A_{\ast}(x)\subseteq A_{\ast}(y)$. Hence, $A_{\ast}(x) = A_{\ast}(y)$.

Conversely, let

Now for any $x, \, y\in G$, and $h\in H$, it follows that

This implies that $\mu_{A}(hx^{-1})\geq\mu_{A}(hy^{-1})$.

Similar, we can show that $\mu_{A}(hy^{-1})\geq\mu_{A}(hx^{-1})$.

Consequently, $\mu_{A}(hx^{-1}) = \mu_{A}(hy^{-1})$. This implies that $Ax = Ay$ (by definition of cosets).

Theorem 4. If $H\leq G$ and $A\in FN(H)$ such that $Ax = Ay$. Then $\mu_{A}(x) = \mu_{A}(y)$, for all $x, \, y\in G$.

Proof. Let $x, \, y\in G$ such that

Therefore,

Similarly, we can show that $\mu_{A}(x)\geq\mu_{A}(y)$. This implies that $\mu_{A}(x)\geq\mu_{A}(y)\geq\mu_{A}(x).$ Hence, $\mu_{A}(x) = \mu_{A}(y)$.

Proposition 2. If $H\leq G$ and $A\in FN(H)$. Then $\left(Ax\right)(xh) = \left(Ax\right)(hx) = \mu_{A}(h)$ for any $x\in G$ and $h\in H$.

Proof. Using definition of fuzzy cosets of $H$ in $G$ with respect to $A\in F(H)$, for any $x\in G$ and $h\in H$,

Also

Hence $\left(Ax\right)(xh) = \left(Ax\right)(hx) = \mu_{A}(h)$, for all $x\in G$ and $h\in H$.

5.   Fuzzy homomorphism of AG-groups

Definition 6. (Extension Principle) Let $X$ and $Y$ be any two non-empty sets, and $f$ is a function from $X$ into $Y$. Let $A\in FP(X)$ and $B\in FP(Y)$, define the fuzzy subsets $f(A)\in FP(Y)$ and $f^{-1}(B)\in FP(X),$ for all $y\in Y$, by

and for all $x\in X$,

here $f(A)$ is called the image of $\mu$ under $f$ and $f^{-1}(B)$ is called the pre-image (or the inverse image) of $B$ under $f$.

In the following some important results on fuzzy homomorphism from AG-groups $G$ into $G'$ are discussed.

Theorem 5. Let $A\in F(G)$ and $G'$ be an AG-group. Suppose $f$ is a homomorphism of $G$ into $G'$. Show that $f\left(A\right)\in F(G')$.

Proof. Here we have two cases:

$(1)$ Let $u, \, v\in G'$. Suppose either $u\notin f(G)$ or $v\notin f(G)$ or both $u, \, v\notin f(G)$. Then

Now assume that $u\notin f(G)$. Then $u^{-1}\notin f(G)$. Thus

Hence $f\left(A\right)\in F(G')$. $(2)$ Now suppose $u, \, v\in f(G),$ then there exist $x, \, y\in G$ such that $u = f(x)$ and $v = f(y)$. Then (by Definition 6)

Also

Hence $f(A)\in F(G')$.

Theorem 6. Let $B\in F(G')$ of an AG-group $G'$ and $f$ is a homomorphism from $G$ into $G'$. Show that $f^{-1}\left(B\right)\in F(G)$.

Proof. Suppose $x, \, y\in G$. Then (by Definition 6)

Further,

Hence $f^{-1}(B)\in F(G)$.

Theorem 7. Let $A\in FN(G)$ and $G'$ be an AG-group. If $f$ is an epimorphism from $G$ onto $G'$. Then $f\left(A\right)\in FN(G')$.

Proof. By Theorem 5, $f\left(A\right)\in F(G')$. Now let $x, \, y\in G'$. Since $f$ is onto, then $f(u) = x$ for some $u\in G$. Thus

Therefore, it follows that $f(A)\in FN(G')$.

Theorem 8. Let $B\in FN(G')$ and $G'$ be an AG-group. If $f$ is a homomorphism from $G$ into $G'$. Then $f^{-1}\left(B\right)\in FN(G)$.

Proof. By Theorem 6, $f^{-1}\left(B\right)\in F(G)$. Now let $x, \, y\in G$. Then

Therefore, it follows that $f^{-1}\left(B\right)\in FN(G)$.

Theorem 9. For any $H\leq G,$ if $A\in FN(H)$. Then the following assertions hold:

(1) $G/ A\cong G/ A_{\ast}$;

(2) If$B\in FP\left(G/ A\right)$, defined by $B\left(Ax\right) = \mu_{A}\left(x\right)$ for all $x\in G,$ then $B\in FN\left(G/ A\right)$.

Proof. Let $H\leq G$ and $A\in FN(H)$.

$(1)$ Both $G/ A$ and $G/ A_{\ast}$ are AG-groups by Theorem 1. Define a mapping $\phi:G/ A\rightarrow G/ A_{\ast}$ by

By Theorem 3, $\phi$ is an isomorphism, and $Ax\cdot Ay = A\left(xy\right)$ and $A_{\ast}x\cdot A_{\ast}y = A_{\ast}\left(xy\right)$ holds for all $x, \, y\in G.$

$(2)$ Let$B\in FP\left(G/ A\right)$ be defined by

We show that $B\in FN\left(G/ A\right).$ For all $x, \, y\in G$,

and

Hence $B\in F\left(G/ A\right)$.

Next we show that $B\in FN\left(G/ A\right)$. For $x, \, y\in G$,

Hence $B\in FN\left(G/ A\right)$.

Theorem 10. Let $H\leq G$ and $A\in FN(H)$. Then $B\in FP\left(G/ A_{\ast}\right)$ defined by $B(A_{\ast}x) = \mu_{A}(x)$ for all $x\in G$ is a fuzzy normal AG-subgroup in $G/ A_{\ast}$.

Proof. Let $H\leq G$ and $A\in FN(H)$. Let $B\in FP\left(G/ A_{\ast}\right)$ defined by $B(A_{\ast}x) = \mu_{A}(x)$. We will show that $B\in FN\left(G/ A_{\ast}\right)$. First we will show that the mapping $\mu_{B}:G/ A_{\ast}\rightarrow [0, \, 1]$ iswell-defined.

For any $x\in G$ we have

This implies that the mapping $\mu_{B}$ is well defined.

Now we show that $B$ is fuzzy AG-subgroup of $G/ A_{\ast}$. Let $A_{\ast}x$ and $A_{\ast}y$ be any arbitrary elements in $G/ A_{\ast}$. Then

and

This implies that $B$ is fuzzy AG-subgroup of $G/ A_{\ast}$.

Next we show that $B$ is a fuzzy normal AG-subgroup of $G/ A_{\ast}$. For any $A_{\ast}x$ and $A_{\ast}y$ in $G/ A_{\ast}$,

Hence $B\in FN\left(G/ A_{\ast}\right)$.

Theorem 11. Let $H\leq G$ and $A\in F(G)$. Define a mapping $\theta:G\rightarrow G/ A$ as follows:

Then $\theta$ is homomorphism with kernel $A_{\ast}x$.

Proof. Since $\theta(xy) = A\left(xy\right) = Ax\cdot Ay = \theta(x)\cdot\theta(y)\, \, {\rm for \ all} \, \, x, \, y\in G,$ $\theta$ is homomorphism. Further, kernel of $\theta$ consists of all $x\in G$ for which

Thus $Ker\, \theta = A_{\ast}$.

Remark 4. Such a homomorphism exists for every fuzzy AG-subgroup $A$ of $H$ in $G$ and is called natural homomorphism from $G$ onto $G/ A$.

Definition 7. Let $A\in F(G)$, and $\theta$ be a homomorphism from $G$ into $G/ A$. Then $Ker\, \theta = \{x\in G\, :\, Ax = Ae\} = \{x\in G\, :\, A_{*}x = A_{*}e\}$.

In the following, we introduce fuzzy Lagrange's Theorem for AG-groups of finite order.

6.   Fuzzy Lagrange's theorem

Theorem 12. (Fuzzy Lagrange's Theorem for Finite AG-group): Let $G$ be a finite AG-group, $H$ an AG-subgroup of $G$ and $A\in F(H)$. Then the index of $H$ in $G$ with respect to $A$ divides the order of $G$.

Proof. It follows from Theorem 11 that there is a homomorphism $\theta$ from $G$ onto $G/ A$, the set of all fuzzy cosets of $A$, defined in (11). Let $H$ be an AG-subgroup of $G$ defined by $H = \{x\in G\, :\, Ax = Ae\}$. Let $x\in H$, then $Ax = Ae\Leftrightarrow A_{\ast}x = A_{\ast}e$ (by Theorem 3). Therefore $H = \{x\in G\, :\, A_{\ast}x = A_{\ast}e\}$. Now $G$ is a disjoint union of the cosets of an AG-group $G$ with respect to $H,$ i.e.

where $x_{1}\in H$ and $x_{i}\in(G-H)$, for all $1 < i\leq k$. Then we show that corresponding to each $Hx_{i}; \, \, 1\leq i\leq k$, given in (6.1), there is a fuzzy coset belonging to $G/ A$, and further this correspondence is one-one. To see this, consider any coset $Hx_{i}$ for any $h\in H$, $\psi(hx_{i}) = A\left(hx_{i}\right) = Ah\cdot Ax_{i} = Ae\cdot Ax_{i} = A\left(ex_{i}\right) = Ax_{i}$. Thus $\psi$ maps each element of $Hx_{i}$ into the fuzzy cosets $Ax_{i}$.

Next we show that $\psi$ is well-defined. Consider $Hx_{i} = Hx_{j}$ for each $i, \, j\, \, \text{where}\, \, 1\leq i\leq k\quad \text{and }{1\leq j\leq k}$. Then

Thus $\psi$ is well-defined.

Further, we show that $\psi$ is one-one, for each $i, \, j$ where $1\leq i\leq k$ and $1\leq j\leq k$. Consider

From the above discussion, it is now clear that the number of distinct cosets of $H$ (index) in $G$ equals the number of fuzzy cosets of $A$, which is a divisor of the order of $G$. Hence we conclude that the index of $H$ in $G$ with respect to $A$ also divides the order of $G$.

7.   Conclusions

In this paper, a study of fuzzy AG-subgroups of AG-groups is initiated. Fuzzy cosets, quotient AG-subgroups relative to fuzzy AG-subgroups and fuzzy quotient AG-subgroups are defined, various notions and results are provided. Fuzzy Lagrange's theorem for finite AG-groups is stated and proved. The results in this paper are among the very few where non-associative fuzzy algebraic structures have been studied.

Conflict of interest

The authors declare that they have no conflict of interest.