A note on a ZIKV epidemic model with spatial structure and vector-bias

1.   Introduction

It is commonly recognized that Zika virus (ZIKV) belongs to a mosquito-borne flavivirus, which is primarily in tropical and subtropical regions, and spreads through the biting of infected Aedes aegypti. As reported in World Health Organization (WHO), 72 countries and territories have appeared local circulation of the ZIKV, which brings major threatens to the global public health in developing countries ^[2,9].

In recent years, reaction-diffusion equation models have been carried out to explore the impacts of the heterogeneity of spatial environment and population mobility on the spread of ZIKV (see, for example, but not limited to, ^{[5-8,12,13,19]}). In the above mentioned work, Fitzgibbon et al. ^[8] firstly proposed the diffusive vector-host model to investigate Zika outbreak in Rio de Janeiro, Brazil for the year of 2015-2016. The authors mainly focused on the final size and spatial distribution of the outbreak by numerically study, and later, the threshold-type results of the model characterized by the basic reproduction number (BRN) have been resolved by Magal et al. in ^[12]. Subsequently, Cai et al. ^[5] analytically and numerically studied the spatiotemporal transmission dynamics of the proposed model as in ^[8,12]. Further, in ^[6], the authors confirmed that epidemic equilibrium (EE) is globally asymptotically stable (GAS) by using the technique of Lyapunov function when the diffusion coefficients are all constants. It should be mentioned that the BRN for the model in ^[5,6,8,12] was defined by the spectral radius of the next generation operator ^[17], which generally has the relationship with the principal eigenvalue of associated elliptic system. Due to the fact that the BRN is lack of visualize, Magal et al. ^[13] developed an approach to link the BRN for the model in ^[8,12] and the local BRN, and explored the effects of the spatial heterogeneity and diffusion rates on the BRN. The local BRN was obtained from the reaction-diffusion model by dropping the diffusion terms.

Very recently, Duan and Huang ^[7] studied the model in ^[8,12] by incorporating general incidence rate. Taking into account the the vector-bias infection mechanism ^[3,4,10,11] in the vector-borne disease model, Wang and Chen ^[19] studied the model in ^[8,12] by adopting vector-bias infection terms. Assume that $\Omega\subset\mathbb{R}^n$ is a bounded domain with a smooth boundary $\partial\Omega$. Let $x\in \Omega$ and $t\in \mathbb{R}$ be the location and time variables, respectively. We use the symbols $H_u(x)$, $H_i(x, t)$, $V_u(x, t)$ and $V_i(x, t)$ to represent the densities of uninfected hosts, infected hosts, uninfected vectors and infected vectors, respectively. The uninfected hosts are assumed to be stationary in space since it amounts fairly small number comparing to the total population ^[18]. The deterministic reaction-diffusion system in ^[19] involving $H_i$, $V_u$ and $V_i$ reads as follows:

for $x\in\Omega, \ t > 0$, coupled with the following boundary and initial conditions:

where $H_u(\cdot)\in C^\alpha(\bar{\Omega}, \mathbb{R})$ is nonnegative and nontrivial; the parameter functions $d_1(\cdot)\in C^{1+\alpha}(\bar{\Omega})$ and $d_2(\cdot)\in C^{1+\alpha}(\bar{\Omega})$ are the diffusion rates of the hosts and vectors, respectively; $\beta_1(\cdot)$ (resp. $\beta_2(\cdot)$) is the biting rate of infected hosts (resp. uninfected vectors); the constant $b$ (resp. $c$) represents the transmission probability from infected host (resp. vector) to uninfected vectors (hosts); the parameter function $\lambda(\cdot)$ represents the loss rate of the infected hosts; the parameter functions $\alpha(\cdot)$ and $\mu(\cdot)$ stand for the breeding rate and the loss rate of the vectors due to environmental crowding. Here $\beta_i(\cdot) (i = 1, 2), \lambda(\cdot), \alpha(\cdot), \mu(\cdot)\in C(\bar{\Omega})$ are strictly positive. The constant $p$ (resp. $l$) stands for the probabilities that a mosquito randomly arrives at a human and picks the human if he is infectious (resp. susceptible). $\frac{\partial}{\partial\vartheta}$ denotes the normal derivative along $\partial\Omega$.

Taking into account the conservation law of the total vector population, and let $V:\ = V_u+V_i$, then $V(\cdot, t)$ fulfills the reaction-diffusion system:

It is well-known from ^[12] that for any $V_0\in C(\bar{\Omega}, \mathbb{R}_+)$, (1.2) possesses a unique global classical solution $V(\cdot, t)$ and satisfies

where $\bar{V}(\cdot)$ is the unique positive solution of the problem

Obviously, (1.1) admits two disease-free equilibria: the trivial and semi-trivial equilibrium, labeled by $E_0 = (0, 0, 0)$ and $E_1 = (0, \bar{V}(\cdot), 0)$, respectively. $E_0$ was proved to be always unstable.

By a routine process as those in [17,Theorem 3.5], the basic reproduction number $\Re_0$ for (1.1) in ^[19] is defined by

i.e., the spectral radius of $-\mathbb{C}{\mathbb{B}}^{-1}$, where $\mathbb{B}, \mathbb{C}: [C(\bar{\Omega})]^2\rightarrow [C(\bar{\Omega})]^2$ are defined as

and

for any $(\varphi, \psi)\in [C(\bar{\Omega})]^2$.

By defining the BRN, $\Re_0$, the authors further made an attempt to investigate the relationship between the BRN and the principal eigenvalue of associated eigenvalue problem. The main results in ^[19] are listed below.

Theorem 1.1. Denote by $\Psi(t)$ the solution semiflow generated by (1.1). Let $\omega(\varphi)$ be the omega limit set of the orbit $O^+(\varphi): = \{\Psi(t)\phi:\ t\geq0\}$. Let $\mathbb{X}_0:\ = \{\varphi\in C(\bar{\Omega}; \mathbb{R}^3_+):\ \varphi_1+\varphi_3\neq0$ and $\varphi_2+\varphi_3\neq0\}, \partial\mathbb{X}_0:\ = \{\varphi\in C(\bar{\Omega}; \mathbb{R}^3_+):\ \varphi_1+\varphi_3 = 0\ \mathit{\mbox{or}}\ \varphi_2+\varphi_3 = 0\}$. Then for $\forall (H_i^0(\cdot), V_u^0(\cdot), V_i^0(\cdot))\in\mathbb{X}_0$, we have the following assertions.

(i) If $\Re_0 < 1$, then $E_1$ is GAS, i.e., $E_1$ is locally stable and satisfies

(ii) If $\Re_0 > 1$, then $E_0$ and $E_1$ are uniform weak repellers, i.e., there exists $\zeta > 0$ small enough satisfying

(iii) If $\Re_0 > 1$, then (1.1) is uniformly persistent, that is, there is $\eta > 0$ satisfying

Furthermore, (1.1) admits at least one EE.

Although the threshold-type results for model (1.1) have been achieved in terms of the BRN, the detailed information (rather than the uniform persistence result) on the dynamics of model when $\Re_0 > 1$ was left and unsolved. It comes naturally to investigate the following question: Whether does model (1.1) admit a unique global stable EE? This constitutes the main motivation of the current paper. Our goal of this paper is to investigate that when $\Re_0 > 1$, (1.1) admits a unique EE, and it is GAS. The methods used here is inspired by the recent study ^[12].

2.   Global dynamics when $\Re_0 > 1$

2.1.   Asymptotic autonomous system

It is noted in (1.3) that $\lim\limits_{t\to\infty}\|V(\cdot, t)-\bar{V}(\cdot)\|_\infty = 0$, which allows us to consider the following problem:

If the EE of model (2.1), $(\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))\in C^2(\bar{\Omega})\times C^2(\bar{\Omega})$, exists, it then satisfies

In the whole section, we always assume that model (2.1) has EE, $(\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))$, then we prove that $(\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))$ is positive, unique and GAS in the set $\mathbb{M}: = \ \{(H_i^0(\cdot), V_i^0(\cdot))\in C(\bar{\Omega}; \mathbb{R}_+^2):\ H_i^0(\cdot)+V_i^0(\cdot)\not = 0\}$.

2.1.1.   The uniqueness of EE

We prove the uniqueness and positivity of $(\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))$ by the following lemmas. The way used here is similar to the ideas of ^[1], which based on the fact that the model (2.2) is cooperative and sub-linear.

Lemma 2.1. The nontrivial nonnegative equilibrium $(\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))$ of model (2.1) is strictly positive.

Proof. As $(\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))$ is nontrivial, we obtain $\tilde{H}_i(\cdot)\neq0$ or $\tilde{V}_i(\cdot)\neq0$. But from the first equation of (2.2), one can get $(\lambda(\cdot)-\nabla\cdot d_1(\cdot)\nabla)H_i = \frac{c\beta_1(\cdot)lH_u(\cdot)}{pH_i+lH_u(\cdot)}V_i$, which implies that $\tilde{H}_i(\cdot)\neq0$ and $\tilde{V}_i(\cdot)\neq0$. According to the maximum principle, the assertion directly follows. This proves Lemma 2.1.

We next pay our attention to the fixed point problem: for any $\mathfrak{B}_1, \mathfrak{B}_2 > 0$, defining $\mathbb{S} = \{ \phi\in C(\bar{\Omega}; \mathbb{R}_+):\ \|\phi\|_{\infty} \leq \mathfrak{B}_1\}$ and $\mathbb{L}:\ \mathbb{S}\subset C(\bar{\Omega})\to C(\bar{\Omega})$ by

where $\mathbb{L}_1(\phi): = \bigg[\big(\mathfrak{B}_2-\lambda(\cdot)\big)\phi+c\beta_1(\cdot)(\mu(\cdot)\bar{V}(\cdot)-\nabla\cdot d_2(\cdot)\nabla)^{-1}\frac{b\beta_2(\cdot)p\phi}{p\phi+lH_u(\cdot)}(\bar{V}(\cdot)-V_i)^+ -\frac{c\beta_1(\cdot)p\phi}{p\phi+lH_u(\cdot)}(\mu(\cdot)\bar{V}(\cdot)-\nabla\cdot d_2(\cdot)\nabla)^{-1}\frac{b\beta_2(\cdot)p\phi}{p\phi+lH_u(\cdot)}(\bar{V}(\cdot)-V_i)^+\bigg]$.

Lemma 2.2. Consider the elliptic system (2.2). $\tilde{H}_i(\cdot)$ is a nontrivial fixed point of $\mathbb{L}$. Specifically, there exists a sufficiently large $\mathfrak{B}_1^* > 0$ such that for all $\mathfrak{B}_1 > \mathfrak{B}_1^*$ and $\mathfrak{B}_2 > 0$, $\mathbb{L}(\tilde{H}_i(\cdot)) = \tilde{H}_i(\cdot)$.

Proof. From the second equation of (2.2), one knows that $\tilde{V}_i(\cdot)$ fulfills

Substituting it into the first equation of (2.2) and adding a term $\mathfrak{B}_2\tilde{H}_i(\cdot)$ to both side of the obtained equation yield

We further rewrite the above equation as

Here $\mathcal{N}(\cdot) = c\beta_1(\cdot)lH_u(\cdot)$. We further rewrite $\mathcal{N}(\cdot) = c\beta_1(\cdot)\big(p\tilde{H}_i(\cdot)+lH_u(\cdot)-p\tilde{H}_i(\cdot)\big)$ by a zero trick. This together with Lemma 2.1 yields the assertion, which proves Lemma 2.2.

Lemma 2.3. There exists a sufficiently large number $\mathfrak{B}_2^* > 0$ such that for all $\mathfrak{B}_2 > \mathfrak{B}_2^*$ and $\mathfrak{B}_1 > 0$, $\mathbb{L}$ is monotone, i.e., $\mathbb{L}(H_i^1)\leq\mathbb{L}(H_i^2)$ for all $H_i^1, H_i^2\in\mathbb{S}$ with $H_i^1\leq H_i^2$.

Proof. We only need to verify that $\mathbb{L}_1(H_i)\leq\mathbb{L}_1(H_i+m)$ with $m > 0$ for any $H_i, H_i+m\in\mathbb{S}$. In fact,

where

Obviously, $\mathcal{A}$ is monotonically increasing with respect to $\phi$. We focus on the following set:

With the help of the elliptic estimate, the above set is bounded, which in turn implies that $\mathcal{B}$ is monotonically increasing with respect to $\phi$ if $\mathfrak{B}_2$ is large. Hence, $\mathbb{L}_1(H_i+m)\geq \mathbb{L}_1(H_i)$. Therefore, $\mathbb{L}$ is monotone if $\mathfrak{B}_2$ is large. This proves Lemma 2.3.

For $\forall g_1, g_2 \in C(\bar{\Omega}, \mathbb{R})$, if $g_1(x) < g_2(x)$ for all $x\in \bar{\Omega}$, we write $g_1\ll g_2$.

Lemma 2.4. For $\forall \theta\in(0, 1)$ and $H_i\in\mathbb{S}$ with $H_i\gg0$, we have $\theta\mathbb{L}(H_i)\ll\mathbb{L}(\theta H_i)$.

Proof. Recall from Lemma 2.2 that

then $\theta\mathbb{L}(H_i)\ll\mathbb{L}(\theta H_i)$. The assertion now just based on the fact that $(\mathfrak{B}_2-\nabla\cdot d_1(\cdot)\nabla)^{-1}$ is strongly positive. This proves Lemma 2.4.

Lemma 2.5. The EE of model (2.1) is unique whenever it exists.

Proof. Assume for the contrary that $(H_i^\ast, V_i^\ast)$ and $(H_i^{\ast\ast}, V_i^{\ast\ast})$ are two different positive equilibrium. Then from the second equation of model (2.2), one can easily get $H_i^\ast\neq H_i^{\ast\ast}$. In the following, we always let $H_i^\ast\not\leq H_i^{\ast\ast}$. By virtue of $\tilde{H}_i(\cdot)$ is a nontrivial fixed point of $\mathbb{L}$ and the (1.1) is uniformly persistent whenever $\Re_0 > 1$, then the upper and lower bounds of $\tilde{H}_i(\cdot)$ are guaranteed.

Let us define $\rho = \max\{\tilde{\rho}\geq 0:\ \tilde{\rho}H_i^\ast\leq H_i^{\ast\ast}\}$. We then directly have $\rho\in (0, 1)$ and $\rho H_i^\ast\leq H_i^{\ast\ast}$ and $\rho H_i^\ast(x_0) = H_i^{\ast\ast}(x_0)$ for some $x_0\in \bar{\Omega}$. By Lemma 2.2, with sufficiently large numbers $\mathfrak{B}_1$ and $\mathfrak{B}_2$, such that $\mathbb{L}(H_i^\ast) = H_i^\ast$ and $\mathbb{L}(H_i^{\ast\ast}) = H_i^{\ast\ast}$. This combined with Lemmas 2.3 and 2.4 gives

Thus $\rho H_i^\ast\ll H_i^{\ast\ast}$, which contradicts with $\rho H_i^\ast(x_0) = H_i^{\ast\ast}(x_0)$. This proves Lemma 2.5.

2.1.2.   Global stability of EE of (2.1)

Let

and

By simple calculation, $\partial G_1/\partial V_i\geq0$ and $\partial G_2/\partial H_i\geq0$, then the limit system (2.1) is cooperative. It then follows from ^[15] that the solution semiflow of (2.1), $\tilde{\Psi}(t):\ C(\bar{\Omega}; \mathbb{R}^2)\rightarrow C(\bar{\Omega}; \mathbb{R}^2)$, i.e., $\tilde{\Psi}(t)(H_i^0, V_i^0) = (H_i(\cdot, t), V_i(\cdot, t))$, $\forall t\geq0$, is monotone. In what follows, we always say that $t > 0$ and the limit process are all uniformly on $\bar{\Omega}$. The following results provide the information that the solution of (2.1), $(H_i, V_i)$, is strictly positive and bounded under the condition that $\big(H_i^0(\cdot), V_i^0(\cdot)\big)\in C(\Omega; \mathbb{R}^+_2)$.

Lemma 2.6. Consider the limit system (2.1). Then the solution $(H_i(\cdot, t), V_i(\cdot, t))$ of (2.1) is strictly positive and bounded, provided that $\big(H_i^0(\cdot), V_i^0(\cdot)\big)\in C(\Omega; \mathbb{R}^+_2)$.

Proof. Similar to Lemma 3.7 in ^[12], the strictly positivity of $(H_i(\cdot, t), V_i(\cdot, t))$ can be obtained directly, as (2.1) is cooperative.

Let $\mathbb{M}_1 = \max\{\|\bar{V}(\cdot)\|_\infty, \|V_i^0(\cdot)\|_\infty\}$ and $\mathbb{M}_2 = \max\{c\|\beta_1\|_\infty \mathbb{M}_1/\lambda_m, \|H_{i0}\|_\infty\}$, where $\lambda_m = \min\{\lambda(x):\ x\in\bar{\Omega}\}$. From the $V_i$-equation of (2.1), together with the comparison principle, one can get that $V_i(\cdot, t)\leq \mathbb{M}_1$. Further, by the $H_i$-equation of (2.1), we directly have that for $x\in\Omega$ and $t > 0$, $\frac{\partial}{\partial t}H_i-\nabla\cdot d_1(\cdot)\nabla H_i\leq -\lambda(\cdot)H_i+c\beta_1\mathbb{M}_1$. Again from the standard comparison principle, $0\leq H_i(\cdot, t)\leq \mathbb{M}_2$. This proves Lemma 2.6.

Lemma 2.7. The EE of (2.1) is GAS whenever it exists, i.e.,

Proof. By Lemmas 2.5 and 2.6, we let $(\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))$ be the unique positive EE of (2.1). We introduce the following auxiliary system,

Let $(\underline{H_i}(\cdot), \underline{V_i}(\cdot)) = \gamma(\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))$ and $(\bar{H_i}(\cdot), \bar{V_i}(\cdot)) = \kappa(\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))$, we may choose sufficiently small $\gamma > 0$ and sufficiently large $\kappa$ such that $(\underline{H_i}(\cdot), \underline{V_i}(\cdot))\leq(H_i^0(\cdot), V_i^0(\cdot))\leq(\bar{H_i}(\cdot), \bar{V_i}(\cdot))$. Due to the monotonicity of $\tilde{\Psi}(t)$, by [15,Corollary 7.3.6], we have

in $C(\bar{\Omega}; \mathbb{R}^2)$ as $t\rightarrow \infty$. Hence, $\tilde{\Psi}(t)(H_i^0(\cdot), V_i^0(\cdot))\rightarrow (\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))$ in $C(\bar{\Omega}; \mathbb{R}^2)$ as $t\rightarrow \infty$.

2.2.   Global stability of $EE$ of (1.1)

In the following, by the theory of asymptotically autonomous semiflows, see, for example, [16,Theorem 4.1], we show the main result of this paper.

Theorem 2.1. Let $(\tilde{H}_i(\cdot), \tilde{V}_u(\cdot), \tilde{V}_i(\cdot))$ be the unique $EE$ of (1.1). Let $\mathbb{X}_0$ and $\Re_0$ be defined in Theorem 1.1. Then for any $(H_i^0(\cdot), V_u^0(\cdot), V_i^0(\cdot))\in \mathbb{X}_0$, EE is GAS provided that $\Re_0 > 1$, i.e., the solution of (1.1) fulfills

Proof. Combined with (iii) of Theorem 1.1 and the previous lemmas in last subsection, the existence and uniqueness of EE of (1.1) is ensured. We are now in a position to rewrite the $H_i$ and $V_i$ equations of (1.1) as

with $\mathcal{G}(\cdot, t) = \frac{b\beta_2(\cdot)pH_i}{pH_i+lH_u(\cdot)}(V_u-(\bar{V}(\cdot)-V_i)^+)-\mu(\cdot)\big(V_u+V_i-\bar{V}(\cdot)\big)V_i$. Thanks to $|V_u-(\bar{V}(\cdot)-V_i)^+|\leq|V_u+V_i-\bar{V}(\cdot)|$, one knows that $\mathcal{G}(\cdot, t)\rightarrow0$ in $C(\bar{\Omega}; \mathbb{R})$ as $t\rightarrow \infty$. According to [14,Proposition 1.1], one knows that (2.3) is asymptotic to (2.1). By Theorem 1.1, the $\omega$-limit set of system (2.3) is contained in a stable set $\mathbb{M}$. Further by the generalized results in [16,theorem 4.1], one directly obtain that $(H_i, V_i)\rightarrow (\tilde{H}_i(\cdot), \tilde{V}_i(\cdot))$ in $C(\bar{\Omega}; \mathbb{R}^2)$ as $t\rightarrow \infty$. On the other hand, as $V_u+V_i\rightarrow \bar{V}(\cdot)$ and $\tilde{V}_u(\cdot)+\tilde{V}_i(\cdot) = \bar{V}(\cdot)$, it gives $V_u \rightarrow \tilde{V}_u(\cdot)$ in $C(\bar{\Omega}; \mathbb{R})$ as $t\rightarrow \infty$. This proves Theorem 2.1.

3.   Numerical simulations

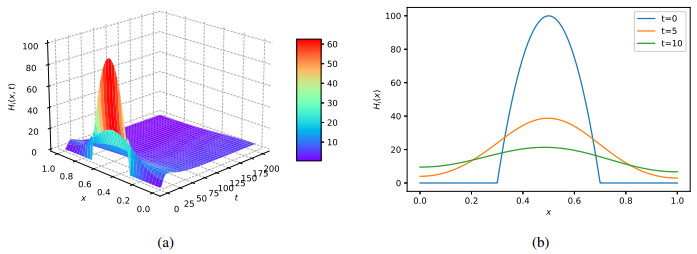
In this section, we perform the numerical simulation to validate the main result that the EE is GAS when $\Re_0 > 1$. Let $\Omega = (0, 1) \subset \mathbb{R}$. We consider system (1.1) with the parameter setting as follows:

Direct calculation gives the corresponding basic reproduction number $\Re_0 \approx1.9393$. For illustrative purpose only, we choose the following initial condition

Solution curves of $H_i(x, t)$, $V_u(x, t)$ and $V_i(x, t)$ are shown in Figures 1, 2 and 3. From Theorem $2.1$, $H_i(x, t)$, $V_u(x, t)$ and $V_i(x, t)$ will approach to the unique EE of (1.1). Figures 1, 2 and 3 demonstrate the spatial distribution of the densities of infected hosts, uninfected vectors and infected vectors after the initial epidemic.

Acknowledgments

We thank the anonymous referee for valuable comments which have led to a substantial improvement in the revision. J. Wang was supported by National Natural Science Foundation of China (Nos. 12071115, 11871179) and Heilongjiang Provincial Key Laboratory of the Theory and Computation of Complex Systems, China.

Conflict of interest

All authors declare no conflicts of interest in this paper.