1.
Introduction
In the domain of operations research, the parallel machine scheduling problem (PMSP) is important and difficult. The importance of PMSP comes from its ability to optimize the use of several machines and allocate a specific set of jobs to satisfy the customer's demands. This is vital for industries where resource optimization is essential, such as maximizing productivity and minimizing overall machine time. Additionally, a wide range of industries, especially in high-demand environments like data centers or manufacturing facilities, can adapt PMSP models for various scenarios, ranging from small-scale operations to large, complicated systems [1]. The challenges of PMSP stem from its complex nature, which has gained popularity and led to its classification as NP-hard [1,2]. This means that finding an optimal solution is computationally costly and becomes more difficult as the number of jobs and machines increases. Real-world scenarios frequently include dynamic changes and uncertainties, such as machine breakdowns or different job durations. Machine constraints and multiple objectives must be considered and balancing them can complicate the scheduling process. Therefore, the challenge of developing effective algorithms contributes to the complexity of the problem. According to [3], the successful solution of the PMSP requires simultaneous determination of assignment and sequencing policies for the available parallel machines and jobs.
Academic literature primarily categorizes research on PMSP into three main groups [3]: identical, uniform, and unrelated PMSP (UPMSP). UPMSP can be regarded as a general representation of the other two groups, wherein distinct machines are employed to execute identical jobs but possess varying processing capacities or capabilities. However, addressing real-world UPMSPs poses a significant challenge for both practitioners and researchers, primarily due to their inherent complexity. Notably, UPMSPs are typically classified as NP-hard, even without considering the multi-objective functions [4]. In addition, UPMSPs are considered more realistic than the other groups because machine speeds, technology, and machine types in the shop may differ from one another. Therefore, solving UPMSPs has attracted many researchers and professionals from scientific and engineering disciplines [5]. UPMSPs have found widespread application in production scheduling and manufacturing systems, particularly in semiconductor manufacturing [6], electronic assembly [4], and manufacturing electricity costs [7].
The most effective method for both exact and approximate solutions in small problem instances intended for single-objective optimization is linear programming [8]. In recent years, considerable attention has been given to multi-objective optimization, as seen by a substantial body of literature, particularly in the years 2019 and 2020 [9]. For instance, Sarçiçek [10] proposed a multi-objective UPMSP model that aims to minimize makespan and maximize machine preferences for jobs with sequence-dependent setup times and introduces a simulated annealing metaheuristic to address large-scale problems. Additionally, Meng et al. [11] presented a mathematical model that integrates identical UPMSPs in a structural metal-cutting facility to minimize total makespan and total tardiness. A new metaheuristic algorithm combines the variable neighborhood structure strategy (VNSGA-III) and the non-dominated sorting genetic algorithm III (NSGA-III). Experimental results show that the suggested algorithm statistically outperforms the comparison algorithms. In the meantime, in [12], the UPMSP model was adapted and expanded based on previous mathematical models by focusing on minimizing makespan and a set of constraints for small instances. Then, different types of simulated annealing were suggested to solve large-scale instances in the packaging industry. The comprehensive evaluation and performance analysis show that the proposed methods often outperform state-of-the-art methods.
The most multi-objective scheduling challenges across all fields were minimizing makespan and total tardiness, which also happened to be the multi-objective that most researchers looked at [13,14]. The application of fuzzy sets enhanced the accuracy of schedules to evaluate UPMSPs and deal with the complexities of real-world problems [1,15]. For example, in the transport industry, where the operators are the resources and the jobs are the freight delivery of the real-world UPMSP problem, Rivera Zarate [16] employed a fuzzy relational system to represent the decision makers' preferences and solve the three objective functions: minimizing completion time and risk and maximizing delivery reliability. The outranking-based particle swarm optimization algorithm (O-PSO) is a metaheuristic developed in that study. The study demonstrated its ability to generate high-quality solutions in comparison to a commonly used policy. Another study conducted by [17] aimed to minimize makespan and total cost simultaneously within manufacturing production systems, and a fuzzy programming method was employed to solve large-scale instances of the proposed UPMSP problem. Meanwhile, Zhou et al. [18] developed a tri-objective optimization model for UPMSP to minimize the total cost of the order delay and early penalty, makespan, and workload imbalance; the processing time is fuzzy due to many uncertain variables associated with actual production. A metaheuristic of Pareto-based discrete particle swarm optimization (PDPSO) was employed to evaluate the model across various scales. The findings indicate that the proposed PDPSO surpasses the other algorithms, particularly for small and medium-sized instances.
Prior studies have proposed fuzzy UPMSPs to enhance performance metrics and determine appropriate schedules across a range of scenarios. Such methods encompass exact methods [15,19], heuristic methods [20], and artificial swarm intelligence methods [21]. Therefore, quite a few metaheuristic algorithms have been proposed for UPMSP, with many demonstrating the capability to achieve near-optimal solutions within reasonable time frames [9]. Even though various algorithms have exhibited commendable performance results, the multiple and conflicting objectives remain an open issue [22]. The primary objectives under consideration are the minimization of makespan and total tardiness. Machine scheduling commonly employs makespan, but it can surpass due dates, thereby requiring the inclusion of an additional objective. As a result, even if the optimal makespan solution is identified, many jobs will probably be completed after their due dates. Consequently, simultaneously considering total tardiness and makespan minimization could lead to increased efficiency. While scheduling machines commonly use this multi-objective [14], the information required to define the time parameters and constraint conditions may be vague or not precisely measurable. This is because most real-world problems are fuzzy. For improvement in the quality of the schedule and making it more reflective of scheduling issues that occur in the real world, fuzzy sets can be utilized to evaluate UPMSPs.
Limited research has been conducted on UPMSP with the multi-objective makespan and total tardiness in the fuzzy environment [15]. Recently, Pourpanah et al. [23] conducted a comprehensive review of the artificial fish swarm algorithm (AFSA). The authors revealed that most modifications of AFSA focus on controlling the parameter values of the algorithm, particularly the visual distance, maximum step length, and crowding factor, along with updates and enhancements to existing behaviors or the development of new ones. AFSA has seen a lot of modifications recently to enhance optimization's effectiveness, most of which aimed for a balance among the exploration and exploitation procedures. Even so, currently used fish swarm algorithms have not yet achieved a global optimum at remarkably high convergence rates. Thus, AFSA development still has a tremendous deal of potential.
In recent years, the improved and modified AFSA became a valuable tool that can be efficiently applied in a variety of applications. Zhao et al. [24] adopted the improved AFSA for route planning of autonomous vessels by introducing a directional operator to improve efficiency, a probability weight factor to avoid local optima, and an adaptive operator to achieve better convergence performance. Tan & Mohamad-Saleh [25] presented a new algorithm of AFSA to improve the performance of global and local search techniques in optimization. The proposed algorithm includes several improvements, such as hybridizing characteristics, introducing normative communication and memory behaviors, and adapting parameters in terms of visuals and steps. Meanwhile, Huang et al. [26] proposed three adaptive step methods to speed up and address the shortcomings of the standard AFSA for solving sensor layout optimization problems in fiber grating networks. Research by Wang et al. [27] customized four operators and an adaptive factor to enhance the algorithm's convergence performance and suggested a modified AFSA when combined with a local path optimizer to resolve the path planning issue. Jin et al. [28] proposed a modified AFSA for unit commitment optimization to overcome the disadvantages of premature convergence and local extremes in the original algorithm. The improvements include variable vision, adjusting the movement strategy, and combining the mutation operation of genetic algorithms. A study by Gao et al. [29] introduced novel AFSA by using Cauchy mutation to accelerate the algorithm's speed of convergence to solve the parameter selection problem for the twin support vector machine. Li et al. [30] proposed improving AFSA to determine the best scheduling to minimize time delay for the multidimensional knapsack problem. These modifications attempted to improve the algorithm's performance in terms of convergence, optimality, and escape from local optimality, among others. However, the development of the algorithm continues to this day.
While there is limited research on the use of modified AFSA in machine scheduling, Tirkolaee et al. [31] introduced an improved version of AFSA to solve flow shop scheduling (FSS) problems. The aims were to minimize total cost and total energy consumption by adding self-adaptive behavior to enhance the algorithm's performance. To our knowledge, AFSA has never been used to solve the scheduling problem on unrelated machines for the proposed multi-objective problem under fuzzy environments. Therefore, in this study, a modified AFSA is proposed to minimize the proposed multi-objective problem with considerations of fuzzy triangular numbers to mitigate the uncertainty associated with the processing times and due dates. The proposed modified AFSA is a new algorithm designed to solve UPMSP by exploiting the capabilities of the AFSA, which is modified through three aspects: the addition of new behavior for the four main behaviors, the use of improved visual and step parameters, and converting AFSA from a continuous to a discrete solution space to deal with the discrete proposed model. Therefore, after creating a random fish population to represent UPMSP solutions, the proposed modified AFSA starts with the best individual solution generated by the standard AFSA. Additionally, the AFSA's constant value is replaced with improved visual and step parameters, and the performance is updated based on the best and current individual using aspiration behavior expression. Subsequently, the fitness value of the best individual is calculated using a transformation method to convert the continuous solution into a discrete solution. Therefore, all solutions will be updated according to the previous steps and implemented until the termination criterion is satisfied.
In short, the main contributions of this research are described as follows:
• Adapt and extend the linear multi-objective model introduced by [32] for UPMSP by embedding triangular fuzzy parameters.
• Apply the total integral value defuzzification method that converts a fuzzy output into a crisp output value.
• Modify standard continuous AFSA to deal with the discrete UPMSP model in solving the proposed UPMSP model.
• Evaluate the performance of the proposed modified algorithm by conducting computational experiments and comparing the results with AFSA and five versions of modified AFSA algorithms. The evaluation results confirmed the superior performance of the modified algorithm.
The performance of the proposed algorithm was compared against standard AFSA and three modified versions proposed by Zhao et al. [24] and Tan & Mohamad-Saleh [25] and three versions of methods outlined by Huang et al. [26].
This paper is structured as follows: Section 2 presents the problem formulation, while Section 3 explains the preliminaries. The standard AFSA is described in Section 4, and the proposed modified AFSA is detailed in Section 5. Section 6 provides computational and statistical results, along with the analysis of the evaluation process. Finally, Section 7 discusses the conclusions and future research directions.
2.
Problem formulation
Based on the classification scheme of scheduling problems by Graham et al. [33], the UPMSP for the multi-objective can be indicated as R//(Cmax+∑Tj), where R denotes an unrelated machine and Cmax+∑Tj represents a proposed multi-objective function. The following assumptions are considered before formulating the mathematical model for the proposed multi-objective UPMSP.
Assumptions:
1- Every machine and job are available at the start of time.
2- Parallel machines are unrelated (each job's processing time differs and is determined by the machine).
3- Preemption is not allowed.
4- There is only one job that each machine can process at once.
Indices and sets:
N: A set of jobs.
M: A set of machines.
j,k : Index for jobs, j,k∈N={1,…,n}.
N0: Indicates a set of jobs that involve a dummy job, N0={0,1,…,n}.
i: Index for machine, i∈M={1,…,m}.
Parameters and decision variables:
pij : The processing time of job j on machine i, which could differ depending on different machines.
dj: The due date of job j.
Cj: The completion time of job j.
Cmax: The maximum completion time (makespan).
w: The value of weight.
v: Sufficiently large number.
Tj: The tardiness of job j.
The notation definitions above and the current model have been inspired by the models that were introduced in papers [34,35]. Meanwhile, the proposed multi-objective model for UPMSP is extended to the linear multi-objective model introduced by [32], which is formulated as follows:
Subject to:
Equation (1) works to minimize multi-objective functions' makespan and total tardiness simultaneously. Constraint (2) guarantees that every job is done by just one machine. When job jth is executed after the job kth on the machine ith, the Xikj value is equal to 1; otherwise, the value will be 0. Constraint (3) demonstrates that there is only one job that is scheduled first at each machine, which means Xikj=1 when the kth job is the first job on a machine ith, otherwise Xikj=0. Constraint (4) specifies the job's flow balance at each machine, which means only one preceding job and one succeeding job. Constraint (5) determines the machine's initial job. Constraint (6) gives zero completion time at job 0. Constraint (7) ensures that the completion time of job jth equals the completion time of the preceding job plus the processing time of job jth at each machine; this can be performed using a large number v. When Xikj=1 if the job jth is ordered after job kth, then v(1−Xikj)=0 and Cj=Ck+pij. Otherwise, when job jth is not ordered after job kth, then Xikj=0, and thus, v(1−Xikj)=v. Constraint (8) demonstrates that the maximum completion time for all machines is equal to the makespan. Constraint (9) calculates each job's tardiness value. Constraint (10) ensures that no value for any of the decision variables can be negative. Constraint (11) illustrates binary variables.
3.
Preliminaries
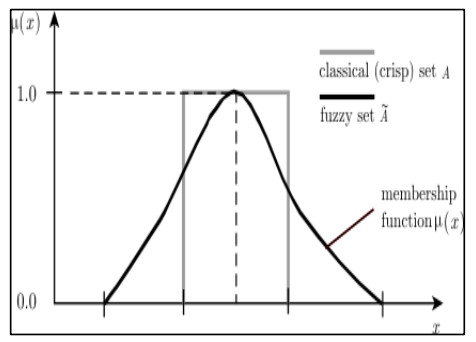
In the literature, fuzzification refers to the process of converting a crisp set into a specific fuzzy set [36]. The primary objective of a fuzzy scheduling process is to identify the "best" solution, or decision, given the presence of uncertain data. Zadeh [37] introduced the fuzzy set theory, which expands the classical set theory's 0–1 integer range to include the values [0, 1]. This section introduces some basic prerequisites for fuzzy sets and triangular fuzzy numbers that will be used later.
Definition 1 [38]: A fuzzy set ˜A in X is specified by the function μ˜A:X→[0,1], a set of ordered pairs if X is a collection of items represented by x:
As shown in Figure 1, the membership function μ˜A(x) of the fuzzy set ˜A is the relationship between various crisp values x and values in the interval [0,1].
In fuzzy theory applications, the most widely used and basic model of fuzzy numbers is called a triangular fuzzy number (TFN), which is represented by ˜A = (a1,a2,a3). The parameter a2 is the maximum possible evaluation data value of x, and parameters a1 and a3 denote the lower and upper bounds of the evaluation data's available area [39]. The graph of the membership function (x) in Figure 2 has a triangular shape, with the base over the interval [a1,a3] and the vertex at x=a2.
Definition 2: Let ˜A=(a1,a2,a3) and ˜B=(b1,b2,b3) be two TFNs. The main operations are also TFNs and can be performed as follows [40]:
The fuzzy mathematical model is the proposed deterministic model that has been fuzzified using TFNs for the primary parameters of processing time and due date stated here as follows:
Considering the above model, an optimal solution cannot be obtained in such a fuzzy environment [41]. Defuzzification is the process of transforming a fuzzy output into a single, crisp output value. A study conducted a performance evaluation and comparison of the nine defuzzification methods introduced in [42] to understand the impact of fuzziness on the fuzzy parameters in the UPMSP. The integral method introduced by [43] was found to have significantly better performance than the other methods based on comprehensive testing. To calculate the maximum fuzzy makespan and tardiness, it is necessary to use a method that compares TFNs. According to [43], the total integral value can be used and denoted as:
for triangular fuzzy number A=(a,b,c), and given α∈ [0, 1].
4.
Artificial fish swarm algorithm
A novel swarm intelligence-based optimization technique known as the artificial fish swarm algorithm (AFSA) was introduced by Li Xiao Lei [44], which involves randomly searching for a set of solutions to solve NP-hard problems [23]. Compared to other intelligent algorithms, AFSA has a limited number of parameters to manage, making it relatively simple to implement. The amount of time needed to find good solutions is reasonable, and the algorithm is parallel, has a strong global search capability, converges quickly, and is less sensitive to the needs of the objective functions. These benefits have led to the successful application of AFSA and its variants in a diverse array of optimization problems [25], such as flexible job shop scheduling problems [45], logistics distribution [46], network design problems [47], wireless sensor networks [48], cloud computing [49], the traveling salesman problem [50], and the exam timetabling problem [51]. Furthermore, Peraza et al. [52] demonstrated the successful implementation of AFSA in various benchmarking optimization problems. The basic idea behind AFSA is to mimic the various environmental behaviors that schooling fish exhibit in the water, where a fish serves as a fictitious representation of a true fish within a population, and the movements of the swarm are random. This algorithm trains each artificial fish (AF) to react to its current position and teaches it four basic behaviors: prey, swarm, follow, and random. Prey behavior is the foundation of the algorithm's convergence; swarm behavior improves the algorithm's stability and global convergence; follow behavior accelerates the convergence of the algorithm; and random behavior balances the contradiction of the other three behaviors. Here is a description of AFSA's behaviors:
Preying behavior: This essential behavior enables AF to get to locations where there is a greater concentration of food. This behavior is modeled within a radius of a fish's neighborhoods by using an AF's current location and its nearest neighbors as determined by the AF's field of view. Let Xi be the current position of the ith AF, and Xj be an arbitrary state of an AF as follows:
Visual is the visual length between two AFs that are placed in Xi and Xj, where the Euclidean distance can be defined as distij=∥Xi−Xj∥, and R is a random vector with each element between 0 and 1.
In minimization problems, if f(Xj)≤f(Xi), the ith AF moves a step toward Xj and, using the following formula:
where Xprey is the position of the ith AF after executing praying behavior, which is next to the Xj−Xi, and ∥Xprey−Xi∥≤S. However, if f(Xj)>f(Xi), another position Xj is randomly selected by applying Eq (1). If the fitness value (objective function), which could be the amount of food the AF is currently concentrating, fails to be satisfied after trying for a given number of iterations, Xi randomizes its next step as follows:
Swarming behavior: In this behavior, the fish collect and move toward the center position to avoid crowding. Let n denote the total number of AFs, nf be the number of neighbors within the ith AF's visual range with distij<Visual, and Xcenter be the central position of the swarm, which is the average of all AFs' positions:
The ith AF relocates in the direction of Xcenter if f(Xcenter)≤f(Xi) and nfn⋗μ, where μ∈[0,1] is the crowding factor; this indicates that there is greater availability of food in the center and that the location is not overcrowded. As a result, Xi takes a movement toward the neighbor's center as follows:
otherwise, the ith AF will carry out the preying behavior.
Following behavior: For ith AF, if at least another jth AF is represented where ∥Xj−Xi∥≤Visual and f(Xj)>f(Xi) with low crowded factor, i.e., nfn<μ, then ith AF move one step toward the jth AF position is as follows:
If there are no neighbors around Xi or if none of them satisfy the condition, then ith AF performs preying behavior.
Random behavior: Each AF makes its random search process and lets the fish swim freely or follow a swarm in a larger space. The next state of AF is Xnext and defined as follows:
5.
The proposed modified artificial fish swarm algorithm
In standard AFSA, AF typically randomly searches its visual range for the next state before proceeding to the next position. This method is particularly time-consuming. The AF must explore every direction until it finds its position. To address this weakness, we incorporate aspiration behavior into the four primary behaviors of the AFSA, which are influenced by the best position of AFs. The proposed algorithm starts by initializing the population size of a fish swarm, followed by the initiation of the AFSA and the proposed AFSA parameters. Every AF signifies a solution to the problem, receives a fitness value to assess its performance, and records its results on the bulletin board following each iteration. Like standard AFSA, each AF in the proposed algorithm changes its position based on its individual best solution for the whole swarm through each iteration. However, there is a major difference in how the best solution is updated. The modified algorithm compares the current position of an AF with the best position achieved across all behaviors. This enhances the search process and helps AFs to escape from the local optimums. Figure 3 illustrates the flowchart of the modified algorithm, highlighting the modified steps in yellow. Creating new behavior depends on the best, current, and random movement solutions. The update processes are formulated as Eq (27).
Suppose that Xbest represents the potential position of AF in the step range and ∥Xbest−Xi∥≤Step, which can be stated as:
The aspiration behavior guarantees that the computing time is greatly reduced because AF can determine the best position in just one cycle of calculations.
However, through iterative processes, the visual and step parameters in the standard AFSA are fixed. The algorithm's convergence speed is increased at the beginning with large visual and step values. Nevertheless, the large values will result in problems like local optimum or iterative jumps when AFs approach the final position. However, values that are too low reduce effectiveness [24,25]. As a result, there are specifications for the algorithm for the visual's size and step at various phases. To achieve a balance between convergence rate and global search capability, the improved adaptive parameters (visual, step) utilized in [25] were adapted by the modified algorithm and are given as follows:
where visualmin is the minimum visual value; stepmin is the minimum step value; t = (1, 2, …, tmax) is the index number of iterations; 0.5<σ<1 at any stage.
The AFSA was originally created to address continuous problems; solving combinatorial optimization problems such as UPMSP remains challenging. Therefore, it is crucial to make the algorithm suitable for solving discrete mathematical scheduling problems and improving the original algorithm's search capabilities. The major contribution of the proposed algorithm is the use of the transformation method to transform the continuous solution into a discrete solution. To achieve this, the modified algorithm's continuous solution was encoded, and the fractional parts were sorted in a non-decreasing order. Let us illustrate the proposed procedure as follows: Assume that a UPMSP has five jobs and three machines and let the lower bound for algorithm search space be equal to 0 and the upper bound be equal to 1. Let the generated solution by AFSA, S = [0.23 0.43 0.1 0.7 0.2], be continuous, and then encode the solution by integer numbers N = [1 2 3 4 5]. After a combination of solution and index, the solution turns out to be:
Now, the solution is sorted by increasing order, and the index is arranged based on the solution. After sorting, the corresponding solution should be:
Thus, the discrete solution D = [3 5 1 2 4].
This method is used to compute the best solution for each solution in the population, and then the best solution is selected according to the value of the multi-objective function. The entire optimization process is performed and runs simultaneously by employing the three proposed modification steps, which are interconnected and depend on the quality of the solution.
The proposed algorithm was applied for each machine and job combination, which were randomly generated, with three types of problem instances: small, medium, and large size. Each instance was repeated 10 times, and the results were recorded. The smallest minimum value is determined to be the optimum value for each instance. The details of the results and comparisons are discussed in the following section.
6.
Results and discussion
Various experiments were conducted on three differently sized problem instances to confirm the proposed algorithm's performance for the multi-objective UPMSP. Each size of the problem consists of 10 instances and was run 10 times. Small size problems consist of the number of jobs N = [5, 10, 15, 20, 25, 30, 35, 40, 45, 50] and the number of machines M = [3, 3, 4, 4, 5, 5, 6, 6, 7, 7]. Medium size problems instances had N = [60, 80,100,120,140,160,180,200,220,240] and M = [8, 8, 9, 9, 10, 10, 11, 11, 12, 12], while large size problems had N = [250,270,290,310,330,350,370,390,410,430] and M = [13, 13, 15, 15, 16, 16, 17, 17]. The proposed AFSA results are compared with standard AFSA, other versions of modified AFSA (presented in previous works by Zhao et al [24] and Tan & Mohamad-Saleh [25]), and three methods outlined by Huang et al [26]. The performance evaluation of the solution methodology is made based on the minimum values, mean, and standard deviation of the objective function obtained. Further analysis of the proposed algorithm's performance was also conducted using the Wilcoxon signed-rank test. The experiments were conducted based on different parameter values, as given in Table 1, using 12th Gen Intel(R) Core (TM) i7-1280P 2.00 GHz and 16 GB RAM under Windows 11 (64-bit) with MATLAB R2023a.
a) Comparison of results based on the minimum values
In minimization problems, the minimum values are used to determine the best performance of the proposed solution approach. Tables 2, 3, and 4 illustrate the minimum values of the proposed algorithm for 10 instances of different size problems. The results are then compared with the standard AFSA, Modified 1 [24], Modified 2 [25], and three methods presented in Modified 3 [26].
As shown in Tables 2, 3 and 4, the bold value is the minimum value obtained that represents the best-found solution in comparison with all seven versions of AFSA. The proposed algorithm exhibits relative performance improvements when dealing with small-sized problems, as demonstrated by the results in Table 2. It is notable that the best minimum values that the proposed algorithm yields are 23.25, 42, and 47.25, which happened in the instances of (N = 5, M = 3), (N = 10, M = 3), and (N = 15, M = 4), respectively. However, as the number of jobs and machines increases to medium and large sizes (as seen in Table 3 and Table 4), the algorithm demonstrates an even more pronounced enhancement in its superior performance. We noticed that the proposed algorithm provides the best minimum values in nine instances of medium-sized problems, 62.5,105.5,123.5,136.5,161.5,154,181.5,205,251.5, which happened in the instances of (N = 60, M = 8), (N = 100, M = 9), (N = 120, M = 9), (N = 140, M = 10), (N = 160, M = 10), (N = 180, M = 11), (N = 200, M = 11), (N = 220, M = 12), and (N = 240, M = 12), respectively. Meanwhile, the standard AFSA provides the best minimum values in the second instance when (N = 80, M = 8). In large-sized problems, the proposed algorithm also provides the best minimum values in nine instances and gives the values 262,270,409,303,565,449.5,847,517,696.5, which happened in the instances of (N = 250, M = 13), (N = 270, M = 13), (N = 290, M = 14), (N = 310, M = 14), (N = 350, M = 15), (N = 370, M = 16), (N = 390, M = 16), (N = 410, M = 17), and (N = 430, M = 17), respectively. The standard AFSA provides the best minimum value in the fifth instance when (N = 330, M = 15). We observe that in medium and large size problems, the AFSA algorithm converges with an unsatisfactory solution. However, when modifications are added to the AFSA, the proposed modified algorithm converges to the best solutions in 9 out of 10 instances for each problem for the proposed multi-objective function. This reflects the effectiveness of the proposed modifications, making the modified algorithm more effective in solving the proposed multi-objective UPMSP.
b) Comparison of results based on statistical values
A descriptive statistical analysis of the performance of AFSA and several modified AFSA algorithms was conducted to demonstrate the superior accuracy and computational efficiency of the proposed algorithm. The results in Tables 5, 6, and 7 present the numerical outcomes of all algorithms after 10 independent runs of the proposed UPMSP model. In the tables, "Mean" refers to the average value, and "STD" refers to the standard deviation, which was used to verify the reliability of the performance of the proposed algorithm. The results show that as more jobs and machines are added to the problem, the mean and STD of all algorithms increase. A smaller mean value represents the best average solution performed by the algorithms, and a lower STD indicates that the results are closer to the mean, suggesting more consistent or stable performance.
Table 5 demonstrates that the proposed algorithm produced the best mean values of the proposed model in the first three instances, with values of 23.475, 43.275, and 51.975. Additionally, the algorithm achieved the best STD value in six instances: 0.711512, 1.589025, 1.852363, 1.371587, 2.243045, and 1.864135, for (N = 5, M = 3), (N = 20, M = 4), (N = 25, M = 5), (N = 30, M = 5), (N = 40, M = 5), and (N = 50, M = 6), respectively, for small-sized problems. Table 6 and Table 7 show that the proposed algorithm achieved the best mean values in six instances, such as 110 and 336.15 for (N = 100, M = 9), and (N = 270, M = 13), respectively, and the best STD values in four instances, such as 3.146427 and 79.19822 for (N = 100, M = 9), and (N = 330, M = 15), respectively, compared to the other algorithms for medium and large-sized problems. The summarized results based on the mean criterion indicate that the superiority and efficiency of the proposed algorithm improves as the number of machines and jobs increases and low values of STD imply more consistency in the performance of the algorithm.
The best possible solutions for the proposed model are analyzed and illustrated in figures after 10 runs of each algorithm. It is guaranteed that the proposed algorithm will converge to the best domain solutions for each of the three size test problems. The provided graph samples illustrate the performance of the proposed algorithm in Figures 4, 5, and 6, on two instances of each size problem, clarifying the best convergence to the best solution and demonstrating that the proposed algorithm can stably converge when compared to other algorithms. Small-sized problems are illustrated in Figure 4, with (N = 10, M = 3) and (N = 15, M = 4); medium-sized problems are illustrated in Figure 5, with (N = 60, M = 8) and (N = 220, M = 12); and large-sized problems are illustrated in Figure 6, with (N = 290, M = 14) and (N = 370, M = 18). In all figures, the x-axis represents the number of iterations used in the comparison process, and the y-axis represents the function evaluation in terms of getting closer to minimum values. As the number of jobs and iterations increases, the proposed algorithm has a notable impact when approaching the best values. As shown in Figure 4, the proposed algorithm has a slight impact on getting close to the best values. Figures 5 and 6 demonstrate a significant impact, confirming the effectiveness of the proposed algorithm. This is evident from the smaller minimum values of the objective function, which expanded the convergence range and accelerated the algorithm toward the best feasible solutions. Additionally, the update process is guided to enhance the global search ability. As a result, the convergence results and quality of the solutions produced by the proposed algorithm improve as the number of jobs and iterations increase.
c) Comparison of results based on the Wilcoxon signed-ranks test
A common practice in computational intelligence is to use statistical tests as part of the performance evaluation process of a new method [54]. Therefore, the Wilcoxon signed-ranks test [55] is utilized in this research since it is non-parametric, meaning it does not assume a normal distribution of the data and is appropriate for small sample sizes. It is specifically formulated for pairwise comparisons to determine significant differences between the proposed algorithm and the algorithms under comparison, which is advantageous when evaluating two related samples. It is also robust, safe, and easy to use. Tables 11, 12, and 13 summarize the results for small, medium, and large instances, respectively, in comparison of the proposed algorithm with other AFSA versions
Tables 11, 12, and 13 present the results of the Wilcoxon signed-rank test obtained by the proposed algorithm, AFSA, Modified 1, Modified 2, Modified 3-method 1, Modified 3-method 2, and Modified 3- method 3. The p-value is the assessment index between zero and one, carried out with a significance level of 0.05. R+ represents the total ranking indicating that the first method is superior to the second one, while R− represents the total ranking indicating that the second method is superior to the first one. Indicate (Ind) denotes a difference in performance scores between the two algorithms; if Ind = +1, the proposed modified AFSA is superior to the other; if Ind = -1, the other algorithm is superior to the proposed modified AFSA; and if Ind = 0, the performance of the two algorithms is equal.
Subsequently, Table 11 shows that the p-value in most pairwise comparisons is lower than the significance level of 0.05. For instance, the p-value in all ten instances in the comparison between the proposed algorithm and AFSA is lower than 0.05, which proves that the proposed algorithm outperforms AFSA. The comparison results with other algorithms based on the Wilcoxon signed-ranks test demonstrate that, except for the results with AFSA for small-size problems and the results with AFSA and Modified 3-method 3 for medium-size problems, the proposed algorithm outperforms the other compared algorithms and has great significant differences in performance. Furthermore, the proposed algorithm outperforms all compared algorithms and shows great significant differences for large-sized problems in each pairwise comparison.
To sum up the discussions above, it is evident that the proposed algorithm's effectiveness stems from leveraging AFSA's advantages, including its multi-stage solution updates and search domain exploration. The algorithm enhances the exploitation and exploration phases by utilizing the best solution extracted from AFSA. Additionally, by adapting improved visual and step parameters, it balances global search capability with convergence speed and effectively applies AFSA to machine scheduling problems. However, the proposed algorithm has limitations, particularly in achieving optimal results for machines 4 to 10. Thus, improvements are necessary to solve small-sized jobs and machine problems. While the stability of the proposed algorithm is commendable, further enhancements are required.
7.
Conclusions and future research
This research adopts UPMSP to minimize multi-objective makespan and total tardiness. A fuzzy programming model is presented, which is transformed into a deterministic model using the total integral value defuzzification method. The proposed algorithm is developed by adding aspiration behavior to improve the performance of AFSA. Visual and step are crucial parameters for optimizing AFSA; thus, improved visual and step parameters are adopted into the modified algorithm. Additionally, transforming the continuous solution of AFSA into a discrete solution enables the algorithm to handle the discrete model of UPMSP. Three sets of problem sizes, each including 10 randomly generated instances, are used to evaluate the performance of the algorithm. The proposed algorithm's best performance metrics on the test problems are determined by the minimum values in the proposed minimization problem. The first three instances provide good performance for small-sized problems with up to 50 jobs and up to 7 machines, whereas the best performance is achieved in nine instances for medium and large-sized problems with up to 240 jobs and 12 machines, and up to 430 jobs and 17 machines, respectively. According to computational results, the proposed algorithm improves the exploitation capability of the AFSA and demonstrates superior performance compared to the AFSA and other modified AFSA variants in identifying the best solutions for almost all test problems. The Wilcoxon signed-rank test supports the conclusion that the proposed algorithm significantly outperforms the other algorithms. Based on the good performance of the proposed modified algorithm, it might be used in the future to solve more complex scheduling problems, such as job shop machine scheduling or flow shop scheduling, as well as various performance measures.
Author contributions
Azhar Mahdi Ibadi conceptualized the research methodology and led the development of the algorithm and programming, focusing on results analysis and writing the initial draft. Rosshairy Abd Rahman led the supervision and validation, thoroughly checking it for significant conceptual content. All authors participated in carefully editing the manuscript. All authors have read and approved the final version of the manuscript for publication.
Acknowledgments
The authors are deeply grateful to the School of Quantitative Sciences, Universiti Utara Malaysia, for their invaluable support in facilitating this research.
Conflict of interest
The authors declare no conflicts of interest.
Use of AI tools declaration
The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.









 DownLoad:
DownLoad:
















