Asymptotic behavior of plate equations with memory driven by colored noise on unbounded domains

1.   Introduction

The finite secant series and the Hurwitz-Lerch zeta function are mathematical concepts that are used in different areas of mathematics. The finite secant series is a generalization of the regular secant series, which is defined as the power series expansion of the secant function. The secant function is the reciprocal of the cosine function, and its series expansion involves powers of the variable raised to even positive integers. This series expands the secant function using powers of the variable raised to non-negative real numbers, which allows for a broader range of values. This series is typically used in mathematical analysis and approximation theory to approximate the secant function for a wider class of arguments. The Hurwitz-Lerch zeta function, is named after the Czech mathematician Mathias Lerch, who who published about 250 papers, largely on mathematical analysis and number theory. Lerch's transcendental function ^[1] was introduced in his work in Acta math. 1887. V. 11. P. 19–24. At this time, he had just started working at the University of Prague. The Hurwitz-Lerch zeta function is a complex-valued function that generalizes several other mathematical functions, such as the Hurwitz zeta function and the polylogarithm function. This function has various applications in number theory, mathematical physics, and special functions theory. It appears in the study of Riemann zeta function, modular forms, and quantum statistical mechanics, among other areas. It has connections to other important functions, such as the polylogarithm function, and the Hurwitz zeta function for special cases of the parameters involved.

Finite sums involving special functions are of high interest in the science community. A few notable examples of this interest are exemplified in the work by Kim et al. ^[2], where a finite summation formula and an infinite summation formula involving Harmonic numbers of order up to some order by means of several definite integrals was derived. In the work by Kim et al. ^[3] an investigation of some properties, recurrence relations and identities involving degenerate Stirling numbers of both kinds associated with degenerate hyperharmonic numbers and also with degenerate Bernoulli, degenerate Euler, degenerate Bell, and degenerate Fubini polynomials was conducted. In the work by Kim at al. ^[4] a study of some results on degenerate harmonic numbers, degenerate hyperharmonic numbers, degenerate Fubi polynomials and degenerate r-Fubini polynomials from a general identity which is valid for any two formal power series and involves the degenerate r-Stirling numbers of the second kind was published. Finite secant series and contour integration have various applications in mathematics and physics. One area where they prove useful is in the calculation of special functions. By utilizing finite secant series and contour integrals, values of special functions like the gamma function, Bessel functions, and hypergeometric functions can be determined numerically. These functions can be expressed in terms of contour integrals, and the residue theorem is employed to evaluate them accurately. Another significant application lies in the evaluation of real integrals that are challenging to compute using standard methods. By combining contour integration techniques with finite secant series, complex integrals can be simplified. Appropriate contour choices and utilization of the integrand's properties facilitate the calculation process, ultimately leading to finite secant series representations. Finite secant series also offer an alternative representation for certain series, aiding in their analysis and summation. By expressing a given series as a finite secant series, closed-form expressions can potentially be derived, patterns can be identified, and convergence properties can be explored.

Contour integration techniques, in conjunction with finite secant series, can be applied to solve differential equations. Transforming a given differential equation into an integral equation through contour integration allows for the utilization of finite secant series methods in solving it. This approach is particularly advantageous when dealing with linear differential equations that have special functions as solutions. In the realm of theoretical physics, contour integration plays a vital role in the formulation and evaluation of scattering amplitudes in quantum field theory. Contour integration techniques enable the calculation of loop integrals encountered in perturbative expansions. Finite secant series offer compact and efficient representations of these loop integrals, assisting in higher-order calculations in quantum field theory. While there are numerous references on the applications of finite secant series and contour integration, here are a few notable sources that provide detailed information are recorded in ^[5,6,7,8]. In this work, we apply the contour integral method from ^[9], to the finite sum of the secant function where the general derivation is given on page 90 in ^[10], resulting in

where $a, m, k\in\mathbb{C}, Re(m+w) > 0, n\in\mathbb{Z^{+}}$. Using Eq (1.1) the main Theorem to be derived and evaluated is given by

where the variables $k, a, m$ are general complex numbers and $n$ is any positive integer. This new expression is then used to derive special cases in terms of trigonometric functions. The derivations follow the method used by us in ^[9]. This method involves using a form of the generalized Cauchy's integral formula given by

where $y, w\in\mathbb{C}$ and $C$ is in general an open contour in the complex plane where the bilinear concomitant ^[9] is equal to zero at the end points of the contour. This method involves using a form of Eq (1.3) then multiplies both sides by a function, then takes the finite sum of both sides. This yields a finite sum in terms of a contour integral. Then we multiply both sides of Eq (1.3) by another function and take the infinite sum of both sides such that the contour integral of both equations are the same.

2.   The Hurwitz-Lerch zeta Function

In the Prudnikov paper ^[11], the contour integral method, ^[9] was applied to a finite sum involving the product of the cosecant and cosine functions to derive a generalized finite sum in terms of the Hurwitz-Lerch zeta function. The variables in the special function were 2 raised to an integer power times a complex number. In this current paper we are able to expand upon this previous work by deriving a finite sum involving the Hurwitz-Lerch zeta function with variables involving 5 raised to an integer power times a complex number. One of the interesting findings of this work is the derivation of the finite product involving the gamma function. This application of the contour integral method to finite sum of trigonometric functions is another way deriving these interesting formulae which have been around since Catalan's work in 1875 ^[12]. This method can perhaps be used to generalize these finite products which in some cases can be extended the infinite case. This work in our opinion can assist fellow researchers with deriving other closed forms involving finite sums and products of Hurwitz-Lerch zeta functions and its composite functions. In this work we expand upon previous work in ^[11], where a Prudnikov et al. finite sum was extended to derive the Hurwitz-Lerch zeta function. The contour integral method in ^[9] was employed to achieve this goal and a similar process is employed in this current article. This article expands evaluations of the Hurwitz-Lerch zeta function to functions involving the gamma function which was not present in our previous work.

Let $\lambda \in \mathbb{R}$ and $0 < \alpha \leq 1$. The Hurwitz-Lerch Zeta function $L(\lambda, \alpha, s)$ given in ^[13], is defined by

for $\sigma > 1$ if $\lambda > 0$ if $\lambda \notin \mathbb{Z}$. For $\lambda \in \mathbb{Z}$ the Hurwitz-Lerch Zeta function reduces to the Hurwitz zeta function $\zeta(s, \alpha)$:

Moreover, we have $L(\lambda, 1, s) = \zeta(s)$, $\lambda\in\mathbb{Z}$, where $\zeta(s)$ denotes the classical Riemann zeta function,

and, for $k\in\mathbb{Z}$,

Thus we see that the Hurwitz-Lerch zeta function is the special case of a general Dirichlet series.

with $a_{m} = e^{2\pi i \lambda m}$ and $\lambda_{m} = \log(m+\alpha)$. This Dirichlet series converges uniformly on compact subsets of the half-plane $\sigma > 1$, therefore the Hurwitz-Lerch zeta function is analytic in the latter region. In more general setting it is assumed that $\sigma > 0$.

First we consider the case $\lambda \in \mathbb{Z}$, i.e. we consider the Hurwitz zeta function $\zeta(s, a)$. We have the Eq (5.2.1) in ^[14] for $\sigma > 0$

Hence, for $\sigma > 1$,

Here the interchange of the order of integration and summation is justified by absolute convergence of the series

Consequently, we have proved that, for $\sigma > 1$,

With the conditions of (25.14.1) in ^[14] and $m = 1, 2, 3, ...,$

where $Re(s) > 1$, $Re(a) > 0$ if $z = 1$; $Re(s) > 0$, $Re(a) > 0$ if $z\in\mathbb{C} \setminus [0, \infty)$. For these and further properties see Erdélyi et al. ^[15], (1953a, pp. 27–31).

3.   Contour integral representation for the finite sum of the Hurwitz-Lerch zeta functions

In this section we derive the contour integral representations of the left-hand side and right-hand side of Eq (1.1) in terms of the Hurwtiz-Lerch zeta and trigonometric functions.

3.1.   Derivation of the generalized Hurwitz-Lerch contour integral for the secant function

We use the method in ^[9]. Using Eq (1.3) we first replace $\log (a)+i b (2 y+1)$ and multiply both sides by $-2 i (-1)^y e^{i b m (2 y+1)}$ then take the finite and infinite sums over $p\in[0, n]$ and $y\in [0, \infty)$ and simplify in terms of the Hurwitz-Lerch zeta function to get

from Eq (1.232.2) in ^[16] where $Re(w+m) > 0$ and $Im\left(m+w\right) > 0$ in order for the sums to converge. We apply Tonelli's theorem for multiple sums, see page 177 in ^[17] as the summands are of bounded measure over the space $\mathbb{C} \times [0, n] \times [0, \infty)$.

3.2.   Derivation of a generalized Hurwitz-Lerch zeta function in terms of the product of the cosine and secant function contour integral

We use the method in ^[9]. Using a generalization of Cauchy's integral formula (1.3) we first replace $y$ by $\log (a)+i x+y$ then multiply both sides by $e^{mxi}$ then form a second equation by replacing $x$ by $-x$ and add both equations to get

Next we replace $y$ by $i b (2 y+1)$ and multiply both sides by $(-1)^y e^{i b m (2 y+1)}$ and take the infinite sum over $y\in[0, \infty)$ and simplify in terms of the Hurwitz-Lerch zeta function to get

from Eqs (1.232.2) and (1.411.3) in ^[16] where $Re(w+m) > 0$ and $Im\left(m+w\right) > 0$ in order for the sums to converge. We apply Tonelli's theorem for sums and integrals, see page 177 in ^[17] as the summand and integral are of bounded measure over the space $\mathbb{C} \times [0, \infty)$.

3.3.   Derivation of the contour integrals

In this section we will use Eqs (3.1) and (3.3) by simple substitution to derive the contour integrals in Eq (1.1).

3.3.1.   Derivation of the left-hand first contour integral

Use Eq (3.1) and replace $b$ by $5^p$ then multiply both sides by $-4 i 5^{-p}$ and take the finite sum over $p\in[0, n]$ to get;

3.3.2.   Derivation of the left-hand second contour integral

Use Eq (3.3) and replace $x$ by $2\times 5^{p-1}$, $b$ by $5^p$ then multiply both sides by $2\times 5^{1-p}$ and take the finite sum over $p\in[0, n]$ to get:

3.3.3.   Derivation of the left-hand third contour integral

Use Eq (3.3) and replace $x$ by $4\times 5^{p-1}$, $b$ by $5^p$ then multiply both sides by $-2\times 5^{1-p}$ and take the finite sum over $p\in[0, n]$ to get:

3.3.4.   Derivation of the right-hand first contour integral

Use Eq (3.1) and replace $b$ by $5^n$ then multiply both sides by $-5^n/i$ to get:

3.3.5.   Derivation of the right-hand second contour integral

Use Eq (3.1) and replace $b$ by $1/5$ then multiply both sides by $5/i$ to get:

4.   Evaluations and derivations involving special functions

The Lerch transcendent or Hurwitz-Lerch zeta function is a special function that appears in number theory, complex analysis, and other areas of mathematics. Its symbol is $\Phi(z, s, a)$. The Hurwitz-Lerch zeta function is derived in this section by determining the function's derivatives with respect to the given variables. We also derive gamma function-related infinite and finite products.

Theorem 4.1. For all $k, a, m\in \mathbb{C}$ then,

Proof. Since the addition of the right-hand side of Eqs (3.4)–(3.6) is equal to the addition of right-hand sides of Eqs (3.7) and (3.8) relative to Eq (1.1), we may equate the left-hand sides to yield the stated result. □

Example 4.2. The degenerate case.

Proof. Use Eq (4.1) and set $k = 0$ and simplify using entry (2) in Table below (64:12:7) in ^[18]. □

Example 4.3. Finite product of the fifth roots of product quotient gamma functions.

Proof. Use Eq (4.1) and set $m = 0$ and simplify to yield the Hurwitz zeta function using entry (4) in Table below (64:12:7) in ^[18]. Next we take the first partial derivative with respect to $k$ and set $k = 0$ and simplify in terms of the log-gamma function, using Eq (64:10:2) in ^[18]. Next we take the exponential function of both sides and simplify in terms of the gamma function. The $\log\Gamma(z)$ is analytic throughout the complex $z$ plane, except for a single branch cut discontinuity along the negative real axis. The $\log(\Gamma(z))$ has a more complex branch cut structure. Similar forms of this interesting formula are recorded in ^{[19,20,21,22,23]}. □

The $\sqrt{5}$ finds its application in diverse fields, including mathematics, physics, engineering, finance, and computer science. In mathematics, it is extensively used in equations and formulas, particularly in geometry and trigonometry. It enables the calculation of distances, angles, and proportions in various geometric shapes and calculations. In physics, the $\sqrt{5}$ plays a role in determining quantities related to wave propagation, resonance, and harmonic oscillators. Equations that describe wave behavior, such as those concerning sound waves and electromagnetic waves, incorporate the $\sqrt{5}$. Engineers frequently employ the $\sqrt{5}$ in vibrations and structural mechanics calculations. It is significant in determining natural frequencies, resonance points, and damping ratios of mechanical systems. In the realm of finance, the $\sqrt{5}$ is employed in diverse calculations associated with risk and volatility. For instance, it is used in calculating the standard deviation, which measures the dispersion of data points from their mean. Additionally, financial models like the Black-Scholes formula for option pricing utilize the $\sqrt{5}$. Computer scientists also leverage the $\sqrt{5}$ in algorithms and computational techniques. It is commonly utilized in numerical analysis and optimization algorithms, where iterative methods may depend on square root calculations to converge towards desired solutions.

Example 4.4. The product of quotient of gamma functions in terms of the square root of $5$. The square root of $5$ and its applications are recorded in the works of Campbell ^[24], Magnus et al. ^[25] and Lewis ^[26].

Proof. Use Eq (4.3) and set $n = 0$ and simplify using Eq (3.323.2) in ^[16]. □

Example 4.5. The infinite product of the fifth roots of product quotient gamma functions. This infinite product of the gamma function has also be recorded in the works of Davis ^[27], Duke ^[28], Adamchik ^[29] and Borwein et al. ^[30]. The right-hand side of Eq (4.5) can also be used in the solution of Legendre and related functions and their differential equation form see Eq (14.2.11) in ^[14]. The right-hand side of Eq (14.2.11) in ^[14] can be replaced by an infinite product by setting $u = \frac{5 a}{4}+\frac{1}{2}, v = -\frac{1}{4}$ where the resulting product form is given by Eq (4.5). We can also equate this infinite product to a double infinite sum. This double infinite sum involving the Laguerre polynomial is derived by applying the method in ^[9] to Eqs (5.2.11.17) and (5.11.4.8) in ^[31] and ^[32] respectively.

Proof. Use Eq (4.3) and take the limit as $n\to \infty$ and simplify the right-hand side using Eq (2) in ^[33]. □

Example 4.6. A functional equation for the Hurwitz-Lerch zeta function. This type of equation is also recoded in the work by Oberhettinger ^[34].

Proof. Use Eq (4.1) and set $n = 0$ and simplify. Next replace $m\to 5\log(z)/(2i), k\to -s, a\to e^{ai}$ and simplify. Next replace $a\to 2(a-1/2)/5, z = -z$ and simplify. □

Example 4.7. Special case of the first partial derivative of the Hurwitz-Lerch zeta function in terms of the log-gamma function. This form is useful in simplifying definite integrals expressed in terms of the Hurwitz-Lerch zeta function and its derivatives. Definite integrals expressed in terms of the log-gamma function were first studied by Malmsten ^[35].

Proof. Use Eq (4.6) and set $z = i^{2/5}$ and simplify in terms of the Hurwitz zeta function using Eq (25.14.2) in ^[14] and then take the first partial derivative with respect to $s$ and set $s = 0$ and simplify in terms of the log-gamma function using (25.11.18) in ^[14]. □

Example 4.8. A finite sum involving sine and cosine functions.

Proof. Use Eq (4.1) and set $k = 1, a = 1, m = x$ and simplify. □

Example 4.9. Finite product involving the fifth roots of the product of quotient sine functions.

Proof. Use Eq (4.1) and set $k = 1, a = 1, m = x$ and simplify using the method in section (8.1) in ^[36]. □

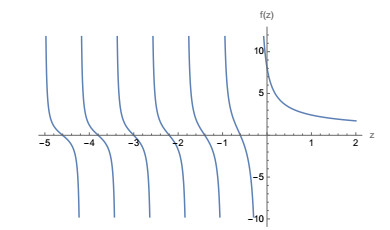
Example 4.10. The infinite case of the product involving the fifth roots of the product of quotient sine functions. Note here $-1 < Re(x) < 1, -1 < Im(x) < 1$.

Proof. Use Eq (4.9) and applying the limit as $n\to \infty$ along with analyzing a plot of the right-hand side over $x\in\mathbb{R}$, we can write down the stated result. □

5.   Conclusions

In this research paper, we presented formulas using trigonometric and special functions, and methods that can obtain formulas similar to those previously published previously. Our method is based on contour integration. The results of numerical calculations for a variety of parameters in mathematical expressions, including real, imaginary, and complex numbers, were verified with the help of the Wolfram software Mathematica.

Use of AI tools declaration

The author declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

The author thanks the anonymous referee for helpful comments and suggestions on the initial and final form of the manuscript.

Conflict of interest

The author declares no conflict of interest with this paper.