Quasi-MV algebras for complex fuzzy logic

1.   Introduction

Complex fuzzy logic (CFL), along with complex fuzzy sets (CFS), proposed by Ramot et al. ^[1,2], is an extension of fuzzy logic and sets. They have found numerous practical applications. However, due to the circle structured codomain of the complex membership function, the study of formal CFL in the narrow sense is developing slowly. Inspired by the assertion "phase is relative" in ^[2], Dick ^[3] developed the concept of rotational invariance and introduced an order for CFL. Dai ^[4] extended Dick's rotational invariance but showed that Dick's order is not a partial order ^[5]. In 2016, Dick, Yager and Yazdanbahksh ^[6] introduced a new order for CFL based on the order in Pythagorean fuzzy sets (PFS). However, the foundations are flawed, their order in PFS is not a partial order ^[7]. In 2020, Dick ^[8] proposed a complex fuzzy S-implication operator based on absmax() and absmin() functions in ^[6]. However, Dick's complex fuzzy S-implication operator is not continuous but is semi-continuous. So algebraic structure in "traditional" fuzzy logic cannot be easily transplanted to CFL.

As is well-known, MV-algebra ^[9] plays a special role in fuzzy logic. This raises an interesting problem: Can we define an MV-algebra in CFL. In this paper, we construct quasi-MV algebras in CFL. Quasi-MV algebras was introduced by Ledda et al. ^[10] for the algebraic structures of quantum logical gates. A qMV algebra is a weaker algebra than MV algebra, the former satisfies the axioms of MV algebra except for the condition $\alpha\oplus\textbf{0} = \alpha$. Later, $\sqrt{\neg}$ quasi-MV algebras were introduced by Giuntini et al. ^[11] who added an operator of square root of the negation. Paoli et al. ^[12,13,14] investigated the structure theory of quasi-MV algebras and $\sqrt{\neg}$ quasi-MV algebras. Bou et al. ^[15] studied the logics underlying the quasi-MV algebras. After that, Paoli et al. ^[16] extended the investigations of Bou et al. to the case of $\sqrt{\neg}$ qMV algebras and axiomatised several logics arising out of the variety of $\sqrt{\neg}$ qMV algebras.

In the paper "MV algebra and quantum computation'' by Ledda et al., the universe of quasi-MV algebra is the following set of complex numbers:

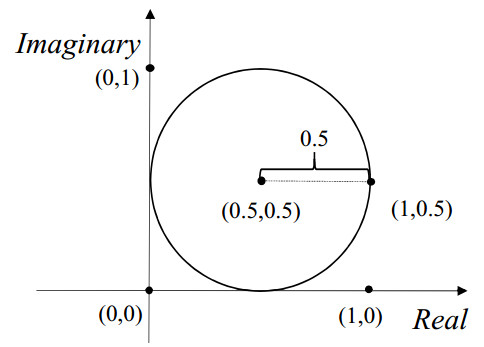
where $i = \sqrt{-1}$. The geometric representation of $\textbf{D}$ is the closed $disc$ with centre $(\dfrac{1}{2}, \dfrac{1}{2})$ and radius $\dfrac{1}{2}$, as shown in Figure 1. Moreover, let minimum element $\textbf{0}^{\textbf{D}} = (0, \frac{1}{2})$, maximum element $\textbf{1}^{\textbf{D}} = (1, \frac{1}{2})$, and define

Negation: $\neg^{\textbf{D}}(a, b) = (1-a, 1-b);$

Trunvated sum: $(a, b)\oplus^{\textbf{D}}(c, d) = \big((a+c)\wedge 1, \frac{1}{2}\big);$

then the set $\textbf{D}$ with these operations $\langle \textbf{D}, \oplus^{\textbf{D}}, \neg^{\textbf{D}}, \textbf{0}^{\textbf{D}}, \textbf{1}^{\textbf{D}} \rangle$ is a quasi-MV algebra, called Disc standard quasi-MV algebra. Later, Giuntini et al ^[11] defined an operator of square root of the negation and a fixed point as follows:

Square root of the negation: $\sqrt{\neg}^{\textbf{D}}(a, b) = (b, 1-a)$;

Fixed point: $\kappa^{\textbf{D}} = (\frac{1}{2}, \frac{1}{2})$.

They called $\langle \textbf{D}, \oplus^{\textbf{D}}, \sqrt{\neg}^{\textbf{D}}, 0^{\textbf{D}}, 1^{\textbf{D}}, \kappa^{\textbf{D}} \rangle$ a standard $\sqrt{\neg}$ quasi-MV algebra.

Interesting enough, the universe of complex fuzzy logic $\textbf{S}$ is a closed unit circle with centre $(0, 0)$ and radius $1$ in the complex plane, as shown in Figure 2, that is,

Then the question are: Which is the minimum element, which is the maximum element, how to define the operations over $\textbf{S}$. Many scholars investigated these issues ^{[1,2,3,6,8,17]}. In some initial works ^[1,2,17], operations over $\textbf{S}$ are isomorphic to those over $[0, 1]\times [0, 1)$, which ignored circle structure of CFL. And these works does not strictly consider the algebraic structure over $\textbf{S}$. Dick, Yager, and Yazdanbakhsh ^[6,8] introduced several complex fuzzy operations, but these operations are discontinuous. Dai ^[5] showed that the lattice in ^[3] used algebraic product as meet operation over $\textbf{S}^{\circ}\cup\{1\}$, not the closed unit disc $\textbf{S}$, where $\textbf{S}^{\circ}$ is the interior of $\textbf{S}$ i.e.,

In this paper, we consider the algebraic structures over $\textbf{S}$. We can define a bijection between $\textbf{D}$ and $\textbf{S}$, then combined with the algebraic structures over $\textbf{D}$, we get a quasi-MV algebra, a $\sqrt{\neg}$ quasi-MV algebra and a quasi-Wajsberg algebra over $\textbf{S}$.

The remainder of this paper is organized as follows.

In Section 2, the algebraic structure of quasi-MV algebras is used in $\textbf{S}$ for CFL. In Section 3, the algebraic structure of $\sqrt{\neg}$ quasi-MV algebras is used in $\textbf{S}$ for CFL. In Section 4, the algebraic structure of quasi-Wajsberg algebras is used in $\textbf{S}$ for CFL. In Section 5, we give a generalized construction method of algebraic structures in $\textbf{S}$ based on homeomorphisms between $\textbf{D}$ and $\textbf{S}$. Conclusions are presented in Section 6.

2.   Quasi-MV algebras

Definition 1. ^[10] A quasi-MV algebra is an algebra $\boldsymbol{A} = \langle A, \oplus, \neg, \boldsymbol{0}, \boldsymbol{1}\rangle$ of type (2, 1, 0, 0) in which the following conditions are satisfied for any $\alpha, \beta, \gamma \in A$:

(qMV1) $\alpha\oplus(\beta\oplus\gamma) = (\alpha\oplus\beta)\oplus\gamma,$

(qMV2) $\neg\neg\alpha = \alpha,$

(qMV3) $\alpha\oplus\boldsymbol{1} = \boldsymbol{1},$

(qMV4) $\neg(\neg\alpha\oplus\beta)\oplus\beta = \neg(\neg\beta\oplus\alpha)\oplus\alpha,$

(qMV5) $\neg(\alpha\oplus\boldsymbol{0}) = \neg\alpha\oplus\boldsymbol{0},$

(qMV6) $(\alpha\oplus\beta)\oplus\boldsymbol{0} = (\alpha\oplus\beta),$

(qMV7) $\neg\boldsymbol{0} = \boldsymbol{1}.$

Of course, an MV algebra is a quasi-MV algebra. But a quasi-MV algebra is an MV algebra if the condition $\alpha\oplus\textbf{0} = \alpha$ holds. $\langle \textbf{D}, \oplus^{\textbf{D}}, \neg^{\textbf{D}}, \textbf{0}^{\textbf{D}}, \textbf{1}^{\textbf{D}} \rangle$ is a quasi-MV algebra. Now we try to give a quasi-MV algebra over $\textbf{S}$.

Clearly, $\textbf{D}$ is homeomorphic to $\textbf{S}$, we can define a function $F:\textbf{D} \rightarrow \textbf{S}$ as

Moreover, the inverse function $F^{-1}:\textbf{S}\rightarrow \textbf{D}$ is

Lemma 1. The functions $F$ and $F^{-1}$ are continuous and one to-one.

Based on the homeomorphisms $F$ and $F^{-1}$, we define the minimum element, maximum element, negation and trunvated sum as follow:

Minimum element: $\textbf{0}^{\textbf{S}} = F^{-1}(\textbf{0}^{\textbf{D}}) = (-1, 0);$

Maximum element: $\textbf{1}^{\textbf{S}} = F^{-1}(\textbf{0}^{\textbf{D}}) = (1, 0);$

Negation: $\neg^{{\textbf{S}}}(a, b) = F\Big(\neg^{\textbf{D}}F^{-1}(a, b)\Big) = (-a, -b);$

Trunvated sum:

Lemma 2. $\oplus^{\boldsymbol{S}}$ and $\neg^{\boldsymbol{S}}$ are continuous on $\boldsymbol{S}$.

Theorem 1. $\langle \boldsymbol{S}, \oplus^{\boldsymbol{S}}, \neg^{\boldsymbol{S}}, \boldsymbol{0}^{\boldsymbol{S}}, \boldsymbol{1}^{\boldsymbol{S}}\rangle$ is a quasi-MV algebra.

Proof. For convenience, we denote $\langle \textbf{S}, \oplus^{\textbf{S}}, \neg^{\textbf{S}}, \textbf{0}^{\textbf{S}}, \textbf{1}^{\textbf{S}}\rangle$ by $\langle \textbf{S}, \oplus, \neg, \textbf{0}, \textbf{1}\rangle$.

(qMV1) $\alpha\oplus(\beta\oplus\gamma) = (\alpha\oplus\beta)\oplus\gamma$. We have

Hence, property (qMV1) is proven.

(qMV2) is trivially true.

(qMV3) $\alpha\oplus\textbf{1} = \textbf{1}$. Since $a+1+1\geq 1$ for any $a\in[-1, 1]$, then $(a, b)\oplus(1, 0) = \big((a+1+1)\wedge 1, 0\big) = (1, 0)$.

(qMV4) $\neg(\neg\alpha\oplus\beta)\oplus\beta = \neg(\neg\beta\oplus\alpha)\oplus\alpha$. We have

Hence, property (qMV4) is proven.

(qMV5) $\neg(\alpha\oplus\textbf{0}) = \neg\alpha\oplus\textbf{0}$. We have

Hence, property (qMV5) is proven.

(qMV6) $(\alpha\oplus\beta)\oplus\textbf{0} = (\alpha\oplus\beta)$. We have

Hence, property (qMV6) is proven.

(qMV7) $\neg^{\textbf{S}}\textbf{0}^{\textbf{S}} = \neg(-1, 0) = (1, 0) = \textbf{1}^{\textbf{S}}$.

This concludes the proof of the theorem.

Example 1. Consider two elements $0.1-0.2i$ and $-0.3+0.4i$ of $\boldsymbol{S}$, then $\neg^{\boldsymbol{S}}(0.1-0.2i) = -0.1+0.2i$, $\neg^{\boldsymbol{S}}(-0.3+0.4i) = 0.3-0.4i$ and $(0.1-0.2i)\oplus^{\boldsymbol{S}}(-0.3+0.4i) = (0.1-0.3+1)\wedge1+0i = 0.8.$

Since there exists $(a, b)\in\textbf{S}$ such that $(a, b)\oplus(-1, 0) = ((a-1+1)\wedge1, 0) = (a, 0)\neq(a, b)$, then $\langle \textbf{S}, \oplus, \neg, \textbf{0}, \textbf{1}\rangle$ is a "pure" quasi-MV algebra, is not an MV algebra.

Corollary 1. $\langle \boldsymbol{S}, \oplus, \neg, \boldsymbol{0}, \boldsymbol{1}\rangle$ is isomorphic to $\langle \boldsymbol{D}, \oplus^{\boldsymbol{D}}, \neg^{\boldsymbol{D}}, 0^{\boldsymbol{D}}, 1^{\boldsymbol{D}} \rangle$.

3.   $\sqrt{\neg}$ quasi-MV algebra

Definition 2. ^[11] A $\sqrt{\neg}$ quasi-MV algebra is an algebra $\boldsymbol{A} = \langle A, \oplus, \sqrt{\neg}, \boldsymbol{0}, \boldsymbol{1}, \kappa\rangle$ of type (2, 1, 0, 0, 0) such that, upon defining $\neg\alpha = \sqrt{\neg}\sqrt{\neg}\alpha$ for $\alpha\in A$, the following conditions are satisfied:

(Q1) $\langle A, \oplus, \neg, \boldsymbol{0}, \boldsymbol{1}\rangle$ is a quasi-MV algebra.

(Q2) $\sqrt{\neg}\kappa = \kappa.$

(Q3) $\sqrt{\neg}(\alpha\oplus\beta)\oplus\boldsymbol{0} = \kappa$.

$\langle \textbf{D}, \oplus^{\textbf{D}}, \sqrt{\neg}^{\textbf{D}}, 0^{\textbf{D}}, 1^{\textbf{D}}, \kappa^{\textbf{D}} \rangle$ is a standard $\sqrt{\neg}$ quasi-MV algebra. Based on the homeomorphisms $F$ and $F^{-1}$, we define a fixed point and the square root of the negation sum on $\textbf{S}$ as follow:

Square root of the negation:

Fixed point: $\kappa^{\textbf{S}} = F^{-1}\Big(F\big(\kappa^{\textbf{D}}\big)\Big) = (0, 0)$.

Lemma 3. $\sqrt{\neg}^{\boldsymbol{S}}$ is continuous on $\boldsymbol{S}$.

Theorem 2. $\langle \boldsymbol{S}, \oplus^{\boldsymbol{S}}, \sqrt{\neg}^{\boldsymbol{S}}, \boldsymbol{0}^{\boldsymbol{S}}, \boldsymbol{1}^{\boldsymbol{S}}, \kappa^{\boldsymbol{S}}\rangle$ is a $\sqrt{\neg}$ quasi-MV algebra.

Proof. For convenience, we denote $\langle \textbf{S}, \oplus^{\textbf{S}}, \sqrt{\neg}^{\textbf{S}}, \textbf{0}^{\textbf{S}}, \textbf{1}^{\textbf{S}}, \kappa^{\textbf{S}}\rangle$ by $\langle \textbf{S}, \oplus, \sqrt{\neg}, \textbf{0}, \textbf{1}, \kappa\rangle$.

We prove $\langle \textbf{S}, \oplus, \sqrt{\neg}, \textbf{0}, \textbf{1}, \kappa\rangle$ is a $\sqrt{\neg}$ quasi-MV algebra. Obviously, $\sqrt{\neg}\sqrt{\neg}(a, b) = \sqrt{\neg}(b, -a) = (-a, -b) = \neg(a, b)$. Then (Q1) is true.

(Q2) $\sqrt{\neg}\kappa = \kappa$. $\sqrt{\neg}(0, 0) = (0, 0)$, property (Q2) is proven.

(Q3) $\sqrt{\neg}(\alpha\oplus\beta)\oplus\textbf{0} = \kappa$.

This concludes the proof of the theorem.

Example 2. Consider the element $-0.3+0.4i$ of $\boldsymbol{S}$, then $\sqrt{\neg}^{\boldsymbol{S}}(-0.3+0.4i) = 0.4+0.3i$ and $\sqrt{\neg}^{\boldsymbol{S}}\sqrt{\neg}^{\boldsymbol{S}}(-0.3+0.4i) = \sqrt{\neg}^{\boldsymbol{S}}(0.4+0.3i) = 0.3-0.4i$. And since $\neg^{\boldsymbol{S}}(-0.3+0.4i) = 0.3-0.4i$, it is easy to verify

Corollary 2. $\langle \boldsymbol{S}, \oplus^{\boldsymbol{S}}, \sqrt{\neg}^{\boldsymbol{S}}, \boldsymbol{0}^{\boldsymbol{S}}, \boldsymbol{1}^{\boldsymbol{S}}, \kappa^{\boldsymbol{S}}\rangle$ is isomorphic to $\langle \boldsymbol{D}, \oplus^{\boldsymbol{D}}, \sqrt{\neg}^{\boldsymbol{D}}, \boldsymbol{0}^{\boldsymbol{D}}, \boldsymbol{1}^{\boldsymbol{D}}, \kappa^{\boldsymbol{D}}\rangle$.

4.   Quasi-Wajsberg algebras

In the above sections, quasi-MV algebras are presented with connectives $\oplus$ and $\neg$. Since we are especially interested in the logical aspects of CFS, it is desirable to consider implication as a primitive connective which seems to better suit logical purposes ^[15]. We reconsider the classes of algebras in which implication is a primitive operation. Similar to the relationship between MV algebras and Wajsberg algebras ^[18], we can replace quasi-MV algebras by the term equivalent variety of quasi-Wajsberg algebras:

Definition 3. ^[15] A quasi-Wajsberg algebra is an algebra $\boldsymbol{A} = \langle A, \rightarrow, \neg, \boldsymbol{1}\rangle$ of type (2, 1, 0) in which the following conditions are satisfied for any $\alpha, \beta, \gamma \in A$:

(qW1) $\boldsymbol{1}\rightarrow (\alpha\rightarrow \beta) = \alpha\rightarrow \beta,$

(qW2) $(\alpha\rightarrow \beta)\rightarrow ((\beta\rightarrow \gamma)\rightarrow (\alpha\rightarrow \gamma)) = \boldsymbol{1},$

(qW3) $(\alpha\rightarrow \beta)\rightarrow \beta = (\beta\rightarrow \alpha)\rightarrow \alpha,$

(qW4) $(\neg\alpha\rightarrow \neg\beta)\rightarrow (\beta\rightarrow \alpha) = \boldsymbol{1},$

(qW5) $\neg\neg\alpha = \alpha,$

(qW6) $\boldsymbol{1}\rightarrow \neg(\boldsymbol{1}\rightarrow \alpha) = \neg(\boldsymbol{1}\rightarrow \alpha).$

Theorem 3. ^[15]

(1) If $\boldsymbol{A} = \langle A, \rightarrow, \neg, \boldsymbol{1}\rangle$ is a quasi-Wajsberg algebra then it is a quasi-MV algebra if $\boldsymbol{0}$ and $\oplus$ are defined as $\boldsymbol{0} = \neg\boldsymbol{1}$ and $\alpha\oplus\beta = \neg\alpha\rightarrow \beta$.

(2) If $\boldsymbol{A} = \langle A, \oplus, \neg, \boldsymbol{0}, \boldsymbol{1}\rangle$ is a quasi-MV algebra then it is a quasi-Wajsberg algebra if $\rightarrow$ is defined as $\alpha\rightarrow \beta = \neg\alpha\oplus\beta$.

Clearly, a quasi-Wajsberg algebra is a weaker algebra than Wajsberg algebra, the former satisfies the axioms of Wajsberg algebra except for the condition $1 \rightarrow x = x$.

Based on the $\neg^{\textbf{D}}$ and $\oplus^{\textbf{D}}$, the following connective $\rightarrow ^{\textbf{D}}$ is

Then $\langle \textbf{D}, \rightarrow ^{\textbf{D}}, \neg^{\textbf{D}}, \textbf{1}^{\textbf{D}}\rangle$ is a quasi-Wajsberg algebra.

Based on the homeomorphisms $F$ and $F^{-1}$, we define the implication connective $\rightarrow ^{\textbf{S}}$ as follow:

Implication:

Lemma 4. The connective $\rightarrow ^{\boldsymbol{S}}$ is also induced by $\neg^{\boldsymbol{S}}$ and $\oplus^{\boldsymbol{S}}$, that is, $(a, b)\rightarrow ^{\boldsymbol{S}}(c, d) = \neg^{\boldsymbol{S}}(a, b)\oplus^{\boldsymbol{S}}(c, d).$

Lemma 5. $\rightarrow ^{\boldsymbol{S}}$ is continuous on $\boldsymbol{S}$.

Theorem 4. $\langle \boldsymbol{S}, \rightarrow ^{\boldsymbol{S}}, \neg^{\boldsymbol{S}}, \boldsymbol{1}^{\boldsymbol{S}}\rangle$ is a quasi-Wajsberg algebra.

Proof. It follows from Theorems 1 and 3.

Thus we get a quasi-Wajsberg algebra over $\textbf{S}$ in which implication is a primitive operation.

Corollary 3. $\langle {\boldsymbol{S}}, \rightarrow ^{{\boldsymbol{S}}}, \neg^{{\boldsymbol{S}}}, {\boldsymbol{1}}^{{\boldsymbol{S}}}\rangle$ is isomorphic to $\langle {\boldsymbol{D}}, \rightarrow ^{{\boldsymbol{D}}}, \neg^{{\boldsymbol{D}}}, {\boldsymbol{1}}^{{\boldsymbol{D}}}\rangle$.

Since there exists $(a, b)\in\textbf{S}$ such that $\textbf{1}\rightarrow (a, b) = \neg(1, 0)\oplus(a, b) = (-1, 0)\oplus(a, b) = ((a-1+1)\\\wedge1, 0) = (a, 0)\neq(a, b)$, then $\langle \textbf{S}, \oplus, \neg, \textbf{0}, \textbf{1}\rangle$ is not a Wajsberg algebra.

Based on the implication on $\textbf{S}$, we can define a preordering $\leq$ on $\textbf{S}$ as follows:

Theorem 5. We define the relation $\leq$ on ${\boldsymbol{S}}$:

Then the relation $\leq$ is a preordering, is not a partial ordering in ${\boldsymbol{S}}$.

Proof. (i) Reflexivity is from $(a, b)\rightarrow (a, b) = \big((1-a+a)\wedge1, 0\big) = (1, 0) = \textbf{1}$.

(ii) If $(a, b)\leq(c, d)$ and $(c, d)\leq(e, f)$, then we have $(1-a+c)\geq1$ and $(1-c+e)\geq1$ from the definition of $\leq$. Then $1-a+e = (1-a+c)+(1-c+e)-1\geq1$, so $(a, b)\rightarrow (e, f) = \big((1-a+e)\wedge1, 0\big) = (1, 0) = \textbf{1}$.

(iii) We give a counterexample to antisymmetry is given. For example, we have $(0.5, 0.3)\leq(0.5, 0.4)$ and $(0.5, 0.4)\leq(0.5, 0.3)$, but $(0.5, 0.3)\neq(0.5, 0.4)$.

This concludes the proof of the theorem.

Theorem 6. The functions $F$ and $F^{-1}$ is order-preserving, that is, for all

Lemma 6. ^[12] Let ${\boldsymbol{A}}$ be a quasi-MV algebra, if the connective $\otimes$ is given as follows:

Then the preordering relation $\leq$ given by Eq (4) has the following property:

Based on the homeomorphisms $F$ and $F^{-1}$, we define the connective $\otimes^{\textbf{S}}$ as follow:

Product:

Lemma 7. $\otimes^{\boldsymbol{S}}$ is continuous in ${\boldsymbol{S}}$.

Theorem 7. For any $(a, b), (c, d), (e, f)\in {\boldsymbol{S}}$, we have

Proof. It follows from Lemma 6.

Example 3. Consider two elements $0.1-0.2i$ and $-0.3+0.4i$ of $\boldsymbol{S}$, then $(0.1-0.2i)\rightarrow ^{\boldsymbol{S}}(-0.3+0.4i) = (1-0.1-0.3)\wedge1+0i = 0.6$. Since $\neg^{\boldsymbol{S}}(0.1-0.2i) = -0.1+0.2i$ and $\neg^{\boldsymbol{S}}(0.1-0.2i)\oplus^{\boldsymbol{S}}(-0.3+0.4i) = (-0.1+0.2i)\oplus^{\boldsymbol{S}}(-0.3+0.4i) = (-0.1-0.3+1)\wedge1+0i = 0.6$, it is easy to verify

Moreover, $(0.1-0.2i)\otimes^{\boldsymbol{S}}(-0.3+0.4i) = (0.1-0.3-1)\vee(-1)+0i = -1$. And since $\neg^{\boldsymbol{S}}(0.1-0.2i)\oplus^{\boldsymbol{S}}\neg^{\boldsymbol{S}}(-0.3+0.4i) = (-0.1+0.2i)\oplus^{\boldsymbol{S}}(0.3-0.4i) = (-0.1+0.3+1)\wedge1+0i = 1+0i$ and $\neg^{\boldsymbol{S}}(1+0i) = -1-0i = -1$, it is easy to verify

In this quasi-Wajsberg algebra over $\textbf{S}$, implication $\rightarrow ^{\textbf{S}}$ and negation $\neg^{\textbf{S}}$ are two basic connectives. Then derived connectives $\otimes^{\textbf{S}}$ and $\oplus^{\textbf{S}}$ are defined over $\textbf{S}$. From above results, we know that the DeMorgan laws hold for $\otimes^{\textbf{S}}$, $\oplus^{\textbf{S}}$ and $\neg^{\textbf{S}}$. Based on the implication on $\textbf{S}$ a preordering $\leq$ is defined in Eq (4). Moreover, we show that $\otimes^{\textbf{S}}$ and $\rightarrow ^{\textbf{S}}$ satisfies the residuation principle.

Note that Kreinovich et al. ^[19] showed that there is no continuous square root of negation in [0,1]. In the $\sqrt{\neg}$ quasi-MV algebra $\langle \textbf{S}, \oplus^{\textbf{S}}, \sqrt{\neg}^{\textbf{S}}, \textbf{0}^{\textbf{S}}, \textbf{1}^{\textbf{S}}, \kappa^{\textbf{S}}\rangle$, the connective $\sqrt{\neg}^{\textbf{S}}$ can viewed as a continuous square root of negation for CFL.

5.   A generalized construction method

Our construction method is based on the homeomorphism $F$ and its inverse $F^{-1}$, as shown in Figure 3. Based on the quasi-MV algebra over $\textbf{D}$, and combined with the bijection between $\textbf{D}$ and $\textbf{S}$, a quasi-MV algebra over $\textbf{S}$ is constructed for CFL. Clearly, there are many homeomorphisms between $\textbf{D}$ and $\textbf{S}$.

For example, we can define a function $f:\textbf{D} \rightarrow \textbf{S}$ as

Moreover, the inverse function $f^{-1}:\textbf{S}\rightarrow \textbf{D}$ is

Based on the homeomorphisms $f$ and $f^{-1}$, we define

Minimum element: $\textbf{0}_{f} = f(\textbf{0}^{\textbf{D}}) = (0, -1);$

Maximum element: $\textbf{1}_{f} = f(\textbf{0}^{\textbf{D}}) = (0, 1);$

Negation: $\neg_{f}(a, b) = f\Big(\neg^{\textbf{D}}f^{-1}(a, b)\Big) = (-a, -b);$

Trunvated sum:

Square root of the negation:

Implication:

Then $\langle \textbf{S}, \oplus_{f}, \neg_{f}, \textbf{0}_{f}, \textbf{1}_{f}\rangle$ is a quasi-MV algebra, $\langle \textbf{S}, \oplus_{f}, \sqrt{\neg}_{f}, \textbf{0}_{f}, \textbf{1}_{f}, \kappa^{\textbf{S}}\rangle$ is a $\sqrt{\neg}$ quasi-MV algebra, and $\langle \textbf{S}, \rightarrow_{f}, \neg_{f}, \textbf{1}_{f}\rangle$ is a quasi-Wajsberg algebra.

Since $\textbf{S}$, the form $a+bi\in\textbf{S}$ is equivalent to $a(1+0i)+b(0+1i)$, where $(1+0i)$ and $(0+1i)$ the standard basis of complex plane. If we use $\cos\theta+i\sin\theta$ and $-\sin\theta+i\cos\theta$ as the basis and denote

New basis can be obtained from the standard basis by rotating $\theta$ degrees, its the rotation matrix is

Based on the new basis $\cos\theta+i\sin\theta$ and $-\sin\theta+i\cos\theta$, we define the minimum element, maximum element, negation, trunvated sum, square root of the negation, and implication as follow:

Minimum element: $\textbf{0}^{\theta} = \langle-1, 0\rangle = -\sin\theta+i\cos\theta;$

Maximum element: $\textbf{1}^{\theta} = \langle1, 0\rangle = \cos\theta+i\sin\theta;$

Negation: $\neg^{\theta}\langle a, b) = \langle-a, -b\rangle = -a(\cos\theta+i\sin\theta)-b(-\sin\theta+i\cos\theta);$

Trunvated sum:

Square root of the negation:

Implication:

When $\theta = 0$, above elements and operations are reduce to $\textbf{0}^{\textbf{S}}$, $\textbf{1}^{\textbf{S}}$, $\neg^{\textbf{S}}$, $\oplus^{\textbf{S}}$, $\sqrt{\neg}^{\textbf{S}}$ and $\rightarrow_{\textbf{S}}$.

Obviously, $\langle \textbf{S}, \oplus_{\theta}, \neg_{\theta}, \textbf{0}_{\theta}, \textbf{1}_{\theta}\rangle$ is a quasi-MV algebra, $\langle \textbf{S}, \oplus_{\theta}, \sqrt{\neg}_{\theta}, \textbf{0}_{\theta}, \textbf{1}_{\theta}, \kappa^{\textbf{S}}\rangle$ is a $\sqrt{\neg}$ quasi-MV algebra, and $\langle \textbf{S}, \rightarrow_{\theta}, \neg_{\theta}, \textbf{1}_{\theta}\rangle$ is a quasi-Wajsberg algebra.

6.   Conclusions

In this paper, we constructed quasi-MV algebras, $\sqrt{\neg}$ quasi-MV algebra and quasi-Wajsberg algebras in the closed unit circle of complex plane. Moreover, operations defined in these algebras are continuous. Our results can be summarized as follow.

● $\langle \textbf{S}, \oplus^{\textbf{S}}, \neg^{\textbf{S}}, \textbf{0}^{\textbf{S}}, \textbf{1}^{\textbf{S}}\rangle$ is a quasi-MV algebra.

● $\langle \textbf{S}, \oplus^{\textbf{S}}, \sqrt{\neg}^{\textbf{S}}, \textbf{0}^{\textbf{S}}, \textbf{1}^{\textbf{S}}, \kappa^{\textbf{S}}\rangle$ is a $\sqrt{\neg}$ quasi-MV algebra.

● $\langle \textbf{S}, \rightarrow ^{\textbf{S}}, \neg^{\textbf{S}}, \textbf{1}^{\textbf{S}}\rangle$ is a quasi-Wajsberg algebra.

As we known, there are relations between quantum and fuzzy logic. On the one hand, with the rapid development of quantum computation, quantum computational logics (or quantum computational algebras ^[20]) have been studied. On the other hand, complex fuzzy logic was developed in the context of complex fuzzy sets. Analogue to relations between orthodox quantum logic and traditional fuzzy logic, the interaction between quantum computational logic and complex fuzzy logic shows in many aspects in terms of ideas, methods and algebraic structure.

Acknowledgments

This research was funded by the National Science Foundation of China under Grant No. 62006168, Natural Science Foundation of Zhejiang Province of China under Grant No. LQ21A010001.

Conflict of interest

The author declares no conflict of interest.