Numerical approach for approximating the Caputo fractional-order derivative operator

Ramzi B. Albadarneh; Iqbal Batiha; A. K. Alomari; Nedal Tahat; Ramzi B. Albadarneh; Iqbal Batiha; A. K. Alomari; Nedal Tahat

doi:10.3934/math.2021735

AIMS Mathematics

2021, Volume 6, Issue 11: 12743-12756. doi: 10.3934/math.2021735

Previous Article Next Article

Research article Special Issues

Numerical approach for approximating the Caputo fractional-order derivative operator

1.
Department of Mathematics, Faculty of Science, The Hashemite University, P.O Box 330127, Zarqa 13133, Jordan
2.
Department of Mathematics, Faculty of Science and Technology, Irbid National University, Irbid 2600, Jordan
3.
Nonlinear Dynamics Research Center (NDRC), Ajman University, Ajman 346, UAE
4.
Department of Mathematics, Yarmouk University, Irbid 211-63, Jordan

Received: 09 July 2021 Accepted: 27 August 2021 Published: 06 September 2021
MSC : 34A08, 65Y99, 65H05, 65L05

This work aims to propose a new simple robust power series formula with its truncation error to approximate the Caputo fractional-order operator $D_{a}^{\alpha}y(t)$ of order $m-1 < \alpha < m$ , where $m\in\mathbb{N}$ . The proposed formula, which are derived with the help of the weighted mean value theorem, is expressed ultimately in terms of a fractional-order series and its reminder term. This formula is used successfully to provide approximate solutions of linear and nonlinear fractional-order differential equations in the form of series solution. It can be used to determine the analytic solutions of such equations in some cases. Some illustrative numerical examples, including some linear and nonlinear problems, are provided to validate the established formula.

Keywords:

Citation: Ramzi B. Albadarneh, Iqbal Batiha, A. K. Alomari, Nedal Tahat. Numerical approach for approximating the Caputo fractional-order derivative operator[J]. AIMS Mathematics, 2021, 6(11): 12743-12756. doi: 10.3934/math.2021735

Related Papers:

[1]	Zahra Pirouzeh, Mohammad Hadi Noori Skandari, Kamele Nassiri Pirbazari, Stanford Shateyi . A pseudo-spectral approach for optimal control problems of variable-order fractional integro-differential equations. AIMS Mathematics, 2024, 9(9): 23692-23710. doi: 10.3934/math.20241151
[2]	Najat Almutairi, Sayed Saber . Chaos control and numerical solution of time-varying fractional Newton-Leipnik system using fractional Atangana-Baleanu derivatives. AIMS Mathematics, 2023, 8(11): 25863-25887. doi: 10.3934/math.20231319
[3]	Fawaz K. Alalhareth, Seham M. Al-Mekhlafi, Ahmed Boudaoui, Noura Laksaci, Mohammed H. Alharbi . Numerical treatment for a novel crossover mathematical model of the COVID-19 epidemic. AIMS Mathematics, 2024, 9(3): 5376-5393. doi: 10.3934/math.2024259
[4]	Fatmawati, Muhammad Altaf Khan, Ebenezer Bonyah, Zakia Hammouch, Endrik Mifta Shaiful . A mathematical model of tuberculosis (TB) transmission with children and adults groups: A fractional model. AIMS Mathematics, 2020, 5(4): 2813-2842. doi: 10.3934/math.2020181
[5]	Sumbal Ahsan, Rashid Nawaz, Muhammad Akbar, Saleem Abdullah, Kottakkaran Sooppy Nisar, Velusamy Vijayakumar . Numerical solution of system of fuzzy fractional order Volterra integro-differential equation using optimal homotopy asymptotic method. AIMS Mathematics, 2022, 7(7): 13169-13191. doi: 10.3934/math.2022726
[6]	Peijiang Liu, Taj Munir, Ting Cui, Anwarud Din, Peng Wu . Mathematical assessment of the dynamics of the tobacco smoking model: An application of fractional theory. AIMS Mathematics, 2022, 7(4): 7143-7165. doi: 10.3934/math.2022398
[7]	Shuqin Zhang, Jie Wang, Lei Hu . On definition of solution of initial value problem for fractional differential equation of variable order. AIMS Mathematics, 2021, 6(7): 6845-6867. doi: 10.3934/math.2021401
[8]	Jagdev Singh, Jitendra Kumar, Devendra Kumar, Dumitru Baleanu . A reliable numerical algorithm for fractional Lienard equation arising in oscillating circuits. AIMS Mathematics, 2024, 9(7): 19557-19568. doi: 10.3934/math.2024954
[9]	Hassan Khan, Umar Farooq, Fairouz Tchier, Qasim Khan, Gurpreet Singh, Poom Kumam, Kanokwan Sitthithakerngkiet . The analytical analysis of fractional order Fokker-Planck equations. AIMS Mathematics, 2022, 7(7): 11919-11941. doi: 10.3934/math.2022665
[10]	Amjid Ali, Teruya Minamoto, Rasool Shah, Kamsing Nonlaopon . A novel numerical method for solution of fractional partial differential equations involving the $ \psi $-Caputo fractional derivative. AIMS Mathematics, 2023, 8(1): 2137-2153. doi: 10.3934/math.2023110

Abstract

1. Introduction

At present, the fractional calculus field is extensively developed to support and describe a wide variety of complex real-world phenomena. This filed, which is dated back to the 17th century, is a standard extension of the well-known formal calculus in which it can convert the integer-order integrals and derivatives into their fractional-order cases to gain additional degrees of freedom ^[1,2]. At the end of the 19th century, many theoretical and applied contributions were included to improve the knowledge and the perceptions of such field (see e.g.: ^[3,4,5,6]). In particular, the theory of fractional calculus was mostly established through several research papers conducted by Marchaud ^[7,8], Grünwald ^[9], Letnikov ^[10,11], Riemann ^[12], and Liouville ^[13]. In the past few decades, the fractional calculus has confirmed its significant role and its contribution in applied sciences such as cosmic rays, plasma dynamics, quantum mechanics, electrodynamics, thermodynamics, porous media, continuum mechanics, and rheology ^[14,15].

The Fractional-order Differential Equations (FoDEs) are undoubtedly considered the core of the fractional calculus. From this standpoint, numerous widely known approaches for offering approximate solutions to the traditional differential equations are numerically developed to meet solving the FoDEs. Adomian decomposition method ^[16], perturbation method ^[17], extrapolation method ^[18], homotopy analysis method ^[19], homotopy Sumudu transform method ^[20], and variational iteration method ^[21] are some of these numerical approaches. Different fractional-order derivative/integral operators are employed for expressing the FoDEs such as the Riemann-Liouville operators ^[12], the Atangana-Baleanu operators ^[1,22], the Caputo operators ^[23], the Caputo-Fabrizio operators ^[24], the Hadamard operators ^[25], the Caputo-Hadamard operators ^[26], the generalized Caputo type non-classical derivative ^[27], and many others. In fact, the most notable definitions among these operators are those given by Reimann-Liouville, Caputo, and recently those given by Caputo-Fabrizo and Atangana-Baleanu type fractional-order operators. Such operators have their characteristics in using. Since in the past two decades, Caputo operator has adopted mostly to handle several real-life models ^[27,28]. Therefore by using fractional-order differential operator, we state that in the fields of continuous-time modeling, various researchers have pointed out that fractional-order derivative operators are better tools in describing acoustics, rheology, polymeric chemistry, linear viscoelasticity, and many more such type of sciences ^[27,28]. Thus, establishing an appropriate numerical formula to introduce an accurate approximation of any of these operators is deemed necessary to solve these FoDEs. Given this pioneering idea, the discretization of the fractional-order integral operators and/or the fractional-order derivative operators will undoubtedly yield a series of quadrature formulae, as can be seen in the Grünwald-Letnikov approach. It has been recently reported in ^[15] that once the coefficients and nodes of these formulae are varied, different accuracies will be gained. For instance, several numerical approaches that depend on the order of differentiation and integration can be established in view of the so-called polynomial interpolation. Besides, the convolution quadratures can be also considered as other numerical approaches used for approximating the operators at hand ^[15]. In references ^[29,30,31], some $(3-\alpha)$ -order formulae were established for approximating the Caputo fractional-order operator through implementing a higher-order interpolant instead of the linear interpolant. This operator with order $(3-\alpha)$ was approximated by using a three-point $L1$ approach in ^[32], and also by using a high-order algorithm with convergence order $(4-\alpha)$ in ^[33]. In ^[6], a numerical algorithm for approximating the Caputo operator of a function was proposed and verified by taking some applications. Recently, Mokhtari and Mostajeran in ^[34] have introduced a new different $(4-\alpha)$ -order technique for approximating the Caputo operator. They have also implemented it on some schemes in order to solve some FoDEs numerically ^[34]. In view of all these pioneer works, we can report that if a continuous function can be expressed using an explicit formula, the Caputo fractional-order derivative operator will be computed. Therefore, throughout this work, we will attempt to propose new explicit formulae for approximating the Caputo fractional-order derivative operator with the help of the Weighted Mean Value Theorem (WMVT).

The remainder of this paper is structured as follows: Section 2 provides some basic definitions. Section 3 presents a robust power series formula with its error term for approximating the Caputo fractional-order operator. Section 4 illustrates some applications to verify the proposed formula. Section 5 summarizes the key conclusions of this paper.

2. Basic definitions and preliminaries

Non-integer calculus is based on the concept of non-integer derivative and even non-integer integral. The Caputo differential operator, as one of the most significant operators of the fractional derivatives, meets all mathematical basics that lie under umbrella of fractional calculus. In the following content, some definitions and properties related to the operator at hand will be demonstrated for completeness. Let us, firstly, assume that $[a, b]$ is a finite interval, where $a, b\in \mathbb{R}$ and $-\infty < a < b < \infty$ . In this regard, when a function belongs to the class of absolutely continuous functions, then we define the left-sided Caputo fractional-order derivative operator of order $\alpha\in \mathbb{R}_+$ as ^[35]:

$\begin{equation} D_{a+}^{\alpha}f(t) = \frac{1}{\Gamma (m-\alpha)}\int_{a}^{t}\frac{f^{(m)}(x)}{(t-x)^{\alpha-m+1}}\;dx,\;m-1 < \alpha < m,\ m\in\mathbb{N},\ t > a. \end{equation}$

(2.1)

On the other hand, the right-sided Caputo fractional-order derivative operator of order $\alpha\in \mathbb{R}_+$ is defined as:

$\begin{equation} D_{b-}^{\alpha}f(t) = \frac{(-1)^m}{\Gamma (m-\alpha)}\int_{t}^{b}\frac{f^{(m)}(x)}{(x-t)^{\alpha-m+1}}\;dx,\;m-1 < \alpha < m,\ m\in\mathbb{N},\ b < t. \end{equation}$

(2.2)

Although the formulas (2.1) and (2.2) are critically significant in fractional calculus, only (2.1) is commonly employed in calculus. Actually, it is for this reason that we have narrowed our focus to the formula (2.1). So, from now on we will only adopt this formula in the rest of this work, and we will assume $a = 0$ to simplify the symbol $D_{a}^{\alpha}(\cdot)$ to be as $D^{\alpha}(\cdot)$ . Besides, in connection with the operator at hand, it should be mentioned its inverse operator, the Riemann-Liouville fractional-order integral operator, which has the form ^[35]:

$\begin{equation} J_{a}^\alpha f(x) = \frac{1}{\Gamma(\alpha)} \int_{a}^{x}\frac{f(\tau)}{(x-\tau)^{1-\alpha}}d\tau, \end{equation}$

(2.3)

where $\alpha\in \mathbb{R}_+$ , $m\in\mathbb{N}$ . Next, certain significant properties related to the Caputo differential operator are stated for more clarification.

Lemma 2.1. ^[35] Let $m-1 < \alpha < m$ , $m\in\mathbb{N}$ , $\alpha\in \mathbb{R}_+$ and $f(t)$ be such that $D^{\alpha}f(t)$ exists, then we have:

$\begin{equation} D^{\alpha}f(t) = J^{m-\alpha}D^{\alpha}f(t). \end{equation}$

(2.4)

Lemma 2.2. ^[35] Let $m-1 < \alpha < m$ , $m\in\mathbb{N}$ , $\alpha\in \mathbb{R}_+$ and $f(t)$ be such that $D^{\alpha}f(t)$ exists, then we have:

● $\lim_{\alpha\rightarrow m}D^{\alpha}f(t) = f^{(m)}(t)$ ,

● $\lim_{\alpha\rightarrow m-1}D^{\alpha}f(t) = f^{(m-1)}(t)-f^{(m-1)}(0)$ .

Lemma 2.3. ^[35] Let $m-1 < \alpha < m$ , $m\in\mathbb{N}$ and $\alpha, \lambda\in \mathbb{C}$ . Let the two functions $f(t)$ and $g(t)$ be such that $D^{\alpha}f(t)$ and $D^{\alpha}g(t)$ exist. Then the Caputo fractional-order derivative is a linear operator. That is,

$\begin{equation} D^{\alpha}(\lambda f(t)+g(t)) = \lambda D^{\alpha}f(t)+D^{\alpha}g(t). \end{equation}$

(2.5)

Lemma 2.4. ^[35] Let $m-1 < \alpha < m$ , $m, n\in\mathbb{N}$ , $\alpha, \lambda\in \mathbb{R}_+$ and the function $f(t)$ be such that $D^{\alpha}f(t)$ exists. Then we have:

$\begin{equation} D^{\alpha}D^{n}f(t) = D^{\alpha+n}f(t)\neq D^{n}D^{\alpha}f(t). \end{equation}$

(2.6)

The variable-order fractional derivative is one of the operators of interest; for additional information, see ^[36,37]. The variable-order fractional derivative, in the sense of Caputo, is defined as

$\begin{equation} D_{a+}^{\alpha (t)}f(t) = \frac{1}{\Gamma (m-\alpha(t))}\int_{a}^{t}\frac{f^{(m)}(x)}{(t-x)^{\alpha (t)-m+1}}\;dx,\;m-1 < \alpha (t) < m,\ m\in\mathbb{N},\ t > a, \end{equation}$

(2.7)

and

$\begin{equation} D_{b-}^{\alpha (t)}f(t) = \frac{(-1)^m}{\Gamma (m-\alpha (t))}\int_{t}^{b}\frac{f^{(m)}(x)}{(x-t)^{\alpha (t)-m+1}}\;dx,\;m-1 < \alpha (t) < m,\ m\in\mathbb{N},\ b < t. \end{equation}$

(2.8)

3. Theoretical study

This part intends to introduce a power series formula to approximate the Caputo operator when its fractional-order is $\alpha\in(m-1, \ m)$ , where $m\in\mathbb{N}$ , see ^[38].

Theorem 3.1. Let $y\in C^{n+m}[a, b]$ , $m-1 < \alpha < m$ ; where $m, n\in\mathbb{N}$ , and $a\geq 0$ , then for every $t\in (a, b]$ , there exist $\xi \in (a, b)$ such that the Caputo fractional-order operator can be written in terms of a fractional-order series and its reminder term as follows:

$\begin{equation} D_{a}^{\alpha }y(t) = \frac{1}{\Gamma (m-\alpha )}\sum\limits_{i = 1}^{n}\frac{y^{(m+i-1)}\;(a)(t-a)^{m-\alpha +i-1}}{\Pi _{j = 1}^{i}\;(m-\alpha +j-1)} +\frac{y^{(m+n)}\;(\xi )(t-a)^{m+n-\alpha -1}}{\Gamma (m-\alpha )\Pi_{j = 1}^{n+1}\;(m-\alpha +j-1)}. \end{equation}$

(3.1)

Proof. By applying the integration by parts to (2.1), we obtain:

$\begin{equation} D_{a}^{\alpha }y(t) = \frac{1}{\Gamma (m-\alpha )}\left( \frac{y^{(m)}\;(a)(t-a)^{m-\alpha }}{m-\alpha }+\int_{a}^{t}\frac{(t-x)^{m-\alpha}\;y^{(m+1)}\;(x)}{(m-\alpha )}dx\right). \end{equation}$

(3.2)

If one applies the integration by parts $n$ -times to the second part of (3.2), then the following assertion will be obtained:

$\begin{equation*} \begin{aligned} D_{a}^{\alpha }y(t) = &\frac{1}{\Gamma (m-\alpha )}\Bigg(\frac{y^{(m)}(t-a)^{m-\alpha }}{m-\alpha }+\frac{y^{(m+1)}(a)(t-a)^{m-\alpha+1}}{(m-\alpha )(m-\alpha +1)}+\cdots \\ & +\frac{y^{(m+n-1)}(a)(t-a)^{m-\alpha +n-1}}{\Pi _{j = 1}^{n}(m-\alpha +j-1)}+\int_{a}^{t}\frac{(t-x)^{m-\alpha +n-1}y^{(m+n)}(x)}{\Pi_{j = 1}^{n}(m-\alpha +j-1)}dx\Bigg). \end{aligned} \end{equation*}$

That is,

$\begin{equation} \begin{aligned} D_{a}^{\alpha }y(t) = \frac{1}{\Gamma (m-\alpha )}&\Bigg(\sum\limits_{i = 1}^{n}\frac{y^{(m+i-1)}(a)(t-a)^{m-\alpha +i-1}}{\Pi_{j = 1}^{i}(m-\alpha +j-1)} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \\ & +\int_{a}^{t}\frac{(t-x)^{m-\alpha+n-1}y^{(m+n)}(x)}{\Pi _{j = 1}^{n}(m-\alpha +j-1)}dx\Bigg). \end{aligned} \end{equation}$

(3.3)

Again, since $y\in C^{m+n}[a, b]$ and due to the term $(t-x)^{m-\alpha +n-1}$ does not change its sign on $[a, t]$ , and also by the WMVT, we conclude that there exist $\xi \in(a, t)$ such that:

$\begin{equation*} \int_{a}^{t}\frac{(t-x)^{m-\alpha +n-1}y^{(m+n)}(x)}{\Pi _{j = 1}^{n}(m-\alpha+j-1)}dx = \frac{y^{(m+n)}(\xi )}{\Pi _{j = 1}^{n}(m-\alpha +j-1)} \int_{a}^{t}(t-x)^{m-\alpha +n-1}dx \end{equation*}$

$\begin{equation*} { \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ } = \frac{y^{(m+n)}(\xi )(t-a)^{m-\alpha+n}}{\Pi _{j = 1}^{n+1}(m-\alpha +j-1)}. \end{equation*}$

This leads us, consequently, to the desired result.

Corollary 3.2. Let $y\in C^{n+m}[a, b]$ , $m-1 < \alpha (t) < m$ ; where $m, n\in\mathbb{N}$ , and $a\geq 0$ , then for every $t\in (a, b]$ , there exist $\xi \in (a, b)$ such that the variable-order fractional operator given in (2.7) can be written in terms of a fractional variable-order series and its reminder term as follows:

$\begin{equation} D_{a}^{\alpha (t) }y(t) = \frac{1}{\Gamma (m-\alpha (t) )}\sum\limits_{i = 1}^{n}\frac{y^{(m+i-1)}(a)(t-a)^{m-\alpha (t) +i-1}}{\Pi _{j = 1}^{i}(m-\alpha (t) +j-1)} +\frac{y^{(m+n)}(\xi )(t-a)^{m+n-\alpha (t) -1}}{\Gamma (m-\alpha (t) )\Pi_{j = 1}^{n+1}(m-\alpha (t) +j-1)}. \end{equation}$

(3.4)

Remark 3.3. In view of Theorem 3.1, if $y\in C^{\infty }[a, b]$ and if $|y^{(n)}(t)|$ is bounded for all $n \in \mathbb{N}$ , then the power series:

$\begin{equation} D_{a}^{\alpha }y(t) = \frac{1}{\Gamma (m-\alpha )}\sum\limits_{i = 1}^{\infty }\frac{y^{(m+i-1)}(a)(t-a)^{m-\alpha +i-1}}{\Pi _{j = 1}^{i}(m-\alpha +j-1)}, \end{equation}$

(3.5)

is convergent for any $t\in[a, \ b]$ and $m-1 < \alpha < m$ , where $m\in\mathbb{N}$ .

Moreover,

$\begin{equation} D_{a}^{\alpha }y(t)\approx \frac{1}{\Gamma (m-\alpha )}\sum\limits_{i = 1}^{n }\frac{y^{(m+i-1)}(a)(t-a)^{m-\alpha +i-1}}{\Pi _{j = 1}^{i}(m-\alpha +j-1)}. \end{equation}$

(3.6)

The next corollary is a special case of Theorem 3.1 when $m$ = 1.

Corollary 3.4. Let $y\in C^{n+1}[a, b]$ , $0 < \alpha < 1$ , and $a\geq 0$ , then for every $t\in(a, b]$ there exist $\xi \in (a, b)$ such that the Caputo fractional-order operator $D_{a}^{\alpha }y(t)$ can be written in terms of a fractional-order series and its reminder term as follows:

$\begin{equation} D_{a}^{\alpha }y(t) = \frac{1}{\Gamma (1-\alpha )}\left( \sum\limits_{i = 1}^{n}\frac{y^{(i)}(a)(t-a)^{i-\alpha }}{\Pi _{j = 1}^{i}(j-\alpha )}+\frac{y^{(n+1)}(\xi )(t-a)^{n+1-\alpha }}{\Pi _{j = 1}^{n+1}(j-\alpha )}\right) . \end{equation}$

(3.7)

4. Illustrative numerical applications

In this section, some numerical examples are taken into account to validate the proposed power series formula. The first example is formulated to offer an accurate approximation for the Caputo fractional-order derivative of a certain function, while the remain examples address some linear and nonlinear FoDEs.

Example 4.1. Given the function $y(t) = 5t^{3}-2t+4\cos (2t+3)+e^{2t+1}$ . Through using Mathematica software package, we obtain results presented in that illustrates different approximations for $D^{\alpha }y(t)$ according to various values of $\alpha$ using formula (3.6). For example, if $a = 0$ , $\alpha = 1.4$ , $m = 2$ , and $n = 15$ , the approximated fractional derivative function is

$\begin{equation} \begin{aligned} D^{1.4 }y(t)\approx &\\ &0.671505 (-2.75960010968 \times 10^{-7} t^{14.6}+5.32593489839\times 10^{-6} t^{13.6}+7.36764\times 10^{-5} t^{12.6}&\\ &+1.49697\times 10^{-4} t^{11.6}-5.00549\times 10^{-4} t^{10.6}+7.01373\times 10^{-3} t^{9.6}&\\ &+6.84879\times 10^{-2} t^{8.6}+9.49785\times 10^{-2} t^{7.6}-0.208073 t^{6.6}+1.81533 t^{5.6}&\\ &+10.3404 t^{4.6}+7.67023 t^{3.6}-7.95954 t^{2.6}+58.6063 t^{1.6}+44.5217 t^{0.6}).& \end{aligned} \end{equation}$

(4.1)

Table 1. Exact value and absolute errors for Example 4.1.

$t_{i}$	$\alpha =0.5,$ $n=15$		$\alpha =1.4,$ $n=15$		$\alpha =2.7,$ $n=15$
$t_{i}$	Exact	$Abs. Error$	Exact	$Abs. Error$	Exact	$Abs. Error$
$0$	$0.000000$	$0.000000$	$0.000000$	$0.000000$	$0.000000$	$0.000000$
$0.1$	$1.511909$	$6.66\times 10^{-16}$	$8.486253$	$1.77\times 10^{-15}$	$30.719270$	$3.55\times 10^{-15}$
$0.2$	$3.259715$	$2.22\times 10^{-15}$	$14.317880$	$5.32\times 10^{-15}$	$37.463010$	$7.10\times 10^{-15}$
$0.3$	$5.545301$	$8.88\times 10^{-16}$	$20.113280$	$1.06\times 10^{-14}$	$42.704250$	$7.10\times 10^{-15}$
$0.4$	$8.405971$	$8.88\times 10^{-15}$	$26.143210$	$2.13\times 10^{-14}$	$48.122780$	$4.97\times 10^{-13}$
$0.5$	$11.880960$	$2.93\times 10^{-13}$	$32.560140$	$9.87\times 10^{-13}$	$54.656340$	$1.49\times 10^{-11}$
$0.6$	$16.020670$	$4.82\times 10^{-12}$	$39.515800$	$1.75\times 10^{-11}$	$63.069360$	$2.44\times 10^{-10}$
$0.7$	$20.892110$	$5.07\times 10^{-11}$	$47.194130$	$2.00\times 10^{-10}$	$74.094510$	$2.60\times 10^{-9}$
$0.8$	$26.584550$	$3.85\times 10^{-10}$	$55.827170$	$1.66\times 10^{-9}$	$88.490060$	$2.02\times 10^{-8}$
$0.9$	$33.215780$	$2.28\times 10^{-9}$	$65.706490$	$1.07\times 10^{-8}$	$107.074900$	$1.23\times 10^{-7}$
$1.0$	$40.939220$	$1.11\times 10^{-8}$	$77.193930$	$5.74\times 10^{-8}$	$130.759200$	$6.20\times 10^{-7}$

| Show Table

DownLoad: CSV

Based on the above results, one may observe that the error terms can be reduced by increasing the value of $n$ or by reducing the error in the round of error that appears in the calculations.

From now on, we intend to address some linear and nonlinear FoDEs. In particular, we attempt to offer accurate approximations for FoDEs using (3.6) to estimate the Caputo operator. For this purpose, we first suppose:

$\begin{equation} y(t) = \sum\limits_{i = 0}^{n}c_{i}(t-a)^{i}. \end{equation}$

(4.2)

Then, we set $D_{a}^{\alpha}y(t)$ as:

$\begin{equation} D_{a}^{\alpha }y(t) = \frac{1}{\Gamma (m-\alpha )}\sum\limits_{i = 1}^{n}\frac{c_{i+m-1}(m+i-1)!(t-a)^{m-\alpha +i-1}}{\Pi _{j = 1}^{i}(m-\alpha +j-1)}. \end{equation}$

(4.3)

Consequently, we substitute the above two relations (4.2) and (4.3) into the required FoDE to generate a system of linear or nonlinear equations, which can be solved by many methods. However, this manner can be further generalized to generate a proper power series formula for handling linear and nonlinear FoDEs having several variables with high accuracy results (see ^[39]).

Example 4.2. Consider the following linear FoDE ^[40]:

$\begin{equation} D_{a}^{1/2}y(t)-\frac{8}{3}\sqrt{\frac{t^{3}}{\pi }}+2\sqrt{\frac{t}{\pi }} = 0,{ \ \ }y(a) = 0. \end{equation}$

(4.4)

Note that the exact solution of (4.4) when $a = 0$ is: $y(t) = t^{2}-t.$ To solve (4.4), $D^{1/2}y(t)$ can be replaced by the formula (3.6), we have

$\begin{equation} \begin{aligned} \frac{t^{1-\alpha } y'(0)}{\Gamma (2-\alpha )} +\frac{t^{2-\alpha } y''(0)}{\Gamma (3-\alpha )} +\frac{y^{(3)}(0) t^{3-\alpha }}{\Gamma (4-\alpha )} +\frac{y^{(4)}(0) t^{4-\alpha }}{\Gamma (5-\alpha )} +\frac{y^{(5)}(0) t^{5-\alpha }}{\Gamma (6-\alpha )}+... = \frac{8}{3}\sqrt{\frac{t^{3}}{\pi }}-2\sqrt{\frac{t}{\pi }}. \end{aligned} \end{equation}$

(4.5)

For $\alpha = 1/2$ and by equating the coefficients of $t^j$ in (4.5) yields: $y'(0) = -1, y''(0) = 2$ , and $y^{(n)}(0) = 0$ , for $n = 3, 4, ...$ .

Hence, the solution can be written in term of the power series $y(t) = \sum_{k = 0}^{\infty}\frac{y^{(k)}t^k}{k!} = -t+t^2$ , which coincides with the exact solution.

Example 4.3. Consider the following nonlinear FoDE:

$\begin{equation} D^{\alpha }y(t) = \left(\frac{1}{2}t^{1-\alpha}-t^{1-\alpha}y(t)\right) \frac{1}{\sqrt[4]{2-y(t)}},{ \ \ }y(0) = 1. \end{equation}$

(4.6)

In order to solve this nonlinear problem, we first use the formula (3.6) in the left hand side of (4.6) and taking the Taylor series for the right hand side about $t = 0$ where $y(0) = 1$ , yields:

$\begin{equation} \begin{aligned} \frac{1}{\Gamma (1-\alpha )}\sum\limits_{i = 1}^{\infty }\frac{y^{(i)}(a)(t-a)^{i-\alpha }}{\Pi _{j = 1}^{i}(j-\alpha )} = &\\& -\frac{t^{1-\alpha }}{2}-\frac{9}{8} t^{2-\alpha } y'(0)+t^{3-\alpha } (\frac{1}{64} (-21) y'(0)^2-\frac{9 y''(0)}{16})&\\ &+t^{4-\alpha } \left(-\frac{3}{16} y^{(3)}(0)+\frac{1}{256} (-55) y'(0)^3-\frac{21}{64} y'(0) y''(0)\right)&\\ &+t^{5-\alpha } (-\frac{3}{64} y^{(4)}(0)-\frac{21}{256} y''(0)^2-\frac{675 y'(0)^4}{4096}&\\ &-\frac{7}{64} y^{(3)}(0) y'(0)-\frac{165}{512} y'(0)^2 y''(0))+... \rm{ .}& \end{aligned} \end{equation}$

(4.7)

Equating the coefficient of $t^{1-\alpha}$ in (4.7) yields:

$\begin{equation*} y'(0) = -\frac{\Gamma (2-\alpha )}{2}, \end{equation*}$

Again, equating the coefficient of $t^{2-\alpha}$ in (4.7) then substituting the previous value of $y'(0)$ yields:

$\begin{equation*} y''(0) = \frac{9}{16} \Gamma (2-\alpha ) \Gamma (3-\alpha ). \end{equation*}$

In the same manner, we can find $y'''(0)$ , $y^{(4)}(0)$ , .... Consequently, the general solution can be written as:

$\begin{equation*} A_0(t) = \left(\frac{1}{2}-y(t)\right) \frac{1}{\sqrt[4]{2-y(t)}}, \end{equation*}$

$\begin{equation*} A_k(t): = \frac{d}{dt}A_{k-1}(t), \end{equation*}$

$\begin{equation*} B_0 = \Gamma(2-\alpha) A_0(0), \end{equation*}$

and

$\begin{equation*} B_k: = \frac{\Gamma(k+2-\alpha) A_k(0)}{k!},y^{(k)} \rightarrow B_{k-1}. \end{equation*}$

Hence, the general solution for (4.6) in the form of power series would be in the following form:

$\begin{equation} z(t,\alpha) = y(0)+\sum\limits_{k = 1}^{\infty}\frac{B_k t^k}{k!}. \end{equation}$

(4.8)

Moreover, the power series solution would be consequently as:

$\begin{equation} \begin{aligned} z(t,\alpha) = &\\ &1-\frac{t \Gamma (2-\alpha )}{2}+\frac{9}{32} t^2 \Gamma (2-\alpha ) \Gamma (3-\alpha )-\frac{1}{128} t^3 (\frac{7 \Gamma (2-\alpha )^2}{4}+\frac{27}{4} \Gamma (3-\alpha ) \Gamma (2-\alpha )) \Gamma (4-\alpha )&\\ &+\frac{1}{6144} t^4 (\frac{55 \Gamma (2-\alpha )^3}{8}+\frac{189}{8} \Gamma (3-\alpha ) \Gamma (2-\alpha )^2&\\ &+\frac{9}{4} (\frac{7 \Gamma (2-\alpha )^2}{4}+\frac{27}{4} \Gamma (3-\alpha ) \Gamma (2-\alpha )) \Gamma (4-\alpha )) \Gamma (5-\alpha )&\\ &-\frac{1}{491520}t^5 (\frac{675 \Gamma (2-\alpha )^4}{16}+\frac{1485}{8} \Gamma (3-\alpha ) \Gamma (2-\alpha )^3+\frac{1701}{16} \Gamma (3-\alpha )^2 \Gamma (2-\alpha )^2&\\ &+\frac{21}{2} (\frac{7 \Gamma (2-\alpha )^2}{4}+\frac{27}{4} \Gamma (3-\alpha ) \Gamma (2-\alpha )) \Gamma (4-\alpha ) \Gamma (2-\alpha )&\\ &+\frac{3}{4} (\frac{55 \Gamma (2-\alpha )^3}{8}+\frac{189}{8} \Gamma (3-\alpha ) \Gamma (2-\alpha )^2&\\ &+\frac{9}{4} (\frac{7 \Gamma (2-\alpha )^2}{4}+\frac{27}{4} \Gamma (3-\alpha ) \Gamma (2-\alpha )) \Gamma (4-\alpha )) \Gamma (5-\alpha )) \Gamma (6-\alpha )+...\ .& \end{aligned} \end{equation}$

(4.9)

In particular, the solution of (4.6) when $\alpha = 1$ using formula (4.8) in the power series form would be:

$\begin{equation*} 1-\frac{t}{2}+\frac{9 t^2}{32}-\frac{1}{128} \left(17 t^3\right)+\frac{275 t^4}{4096}-\frac{411 t^5}{10240}+\frac{4533 t^6}{163840}-\frac{95937 t^7}{4587520}+\frac{985563 t^8}{58720256}-\frac{8250131 t^9}{587202560}+\frac{570105539 t^{10}}{46976204800}+..., \end{equation*}$

which coincides with the exact solution of (4.6) when $\alpha = 1$ .

Example 4.4. Consider the following nonlinear Riccati FoDE:

$\begin{equation} D_{a}^{\alpha }y(t) = (t-a)^{1-\alpha}(1+2y(t)-y(t)^{2}),\rm{ \ \ }y(a) = b,\rm{ }0 < \alpha \leq 1. \end{equation}$

(4.10)

The exact solution of (4.10) when $\alpha = 1$ , $a = 0$ , and $b = 0$ is:

$\begin{equation*} y(t) = \frac{e^{2 \sqrt{2} t}-1}{\sqrt{2} e^{2 \sqrt{2} t}-e^{2 \sqrt{2} t}+\sqrt{2}+1}. \end{equation*}$

In order to solve (4.10), we first use formula (3.6) in the left hand side of (4.10) and taking the Taylor series for the right hand side about $t = a$ . That is,

$\begin{equation} \frac{1}{\Gamma (1-\alpha )}\sum\limits_{i = 1}^{\infty }\frac{y^{(i)}(a)(t-a)^{i-\alpha }}{\Pi _{j = 1}^{i}(j-\alpha )} = \left(-y(a)^2+2 y(a)+1\right) (t-a)^{1-\alpha } +(t-a)^{2-\alpha } \left(2 y'(a)-2 y(a) y'(a)\right) \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+ (t-a)^{3-\alpha } \left(-y(a) y''(a)+y''(a)-y'(a)^2\right)\\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+\frac{1}{3} (t-a)^{4-\alpha } \left(-y(a) y^{(3)}(a)+y^{(3)}(a)-3 y'(a) y''(a)\right) \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+\frac{1}{12} (t-a)^{5-\alpha } \left(-y(a) y^{(4)}(a)+y^{(4)}(a)-3 y''(a)^2-4 y^{(3)}(a) y'(a)\right) \\\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;+\frac{1}{60} (t-a)^{6-\alpha } \left(-y(a) y^{(5)}(a)+y^{(5)}(a)-5 y^{(4)}(a) y'(a)-10 y^{(3)}(a) y''(a)\right)+...\rm{ .} \end{equation}$

(4.11)

Equating the coefficient of $t^{1-\alpha}$ in (4.11) yields:

$\begin{equation*} y'(a) = \left(1+2y(a)-y(a)^2\right) \Gamma (2-\alpha )\rm{.} \end{equation*}$

By equating the coefficient of $t^{2-\alpha}$ in (4.11) and substituting the previous value of $y'(a)$ we get:

$\begin{equation*} y''(a) = 2 \left(y(a)^3-3 y(a)^2+y(a)+1\right) \Gamma (2-\alpha ) \Gamma (3-\alpha ). \end{equation*}$

In the same manner, we can find $y'''(a)$ , $y^{(4)}(a)$ , .... Consequently, the general solution can be written as:

$\begin{equation*} A_0(t) = 1+2y(t)-y(t)^2, \end{equation*}$

$\begin{equation*} A_k(t): = \frac{d}{dt}A_{k-1}(t), \end{equation*}$

$\begin{equation*} B_0 = \Gamma(2-\alpha) A_0(a), \end{equation*}$

and

$\begin{equation*} B_k: = \frac{\Gamma(k+2-\alpha) A_k(a)}{k!},y^{(k)} \rightarrow B_{k-1}. \end{equation*}$

Hence, the general solution of (4.10) in the form of power series would be in the following form:

$\begin{equation} z(t,\alpha) = y(a)+\sum\limits_{k = 1}^{\infty}\frac{B_k (t-a)^k}{k!}. \end{equation}$

(4.12)

In addition, the solution when $y(a) = 0$ would be:

$\begin{equation} z(t,\alpha) = t \Gamma (2-\alpha )+t^2 \Gamma (2-\alpha ) \Gamma (3-\alpha )-\frac{1}{6} t^3 \left(\Gamma (2-\alpha )^2-2 \Gamma (2-\alpha ) \Gamma (3-\alpha )\right) \Gamma (4-\alpha )\\\;\;\;\;\;-\frac{1}{72} t^4 \left(6 \Gamma (3-\alpha ) \Gamma (2-\alpha )^2+\left(\Gamma (2-\alpha )^2-2 \Gamma (2-\alpha ) \Gamma (3-\alpha )\right) \Gamma (4-\alpha )\right) \Gamma (5-\alpha )+...\ . \end{equation}$

(4.13)

In particular, the solution of (4.10) when $a = 0$ , $b = 0$ , and $\alpha = 1$ using formula (4.12) in the power series form would be as follows:

$\begin{equation*} t+t^2+\frac{t^3}{3}-\frac{t^4}{3}-\frac{7 t^5}{15}-\frac{7 t^6}{45}+\frac{53 t^7}{315}+\frac{71 t^8}{315}+\frac{197 t^9}{2835}-\frac{1213 t^{10}}{14175}+..., \end{equation*}$

which coincides with the exact solution of (4.10) when $a = 0$ , $b = 0$ , and $\alpha = 1$ .

Example 4.5. Consider the following nonlinear FoDE:

$\begin{equation} D^{\alpha }y(t) = y(t)^2+t,\rm{ \ \ }y(0) = 0, y'(1) = 0,1 < \alpha < 2. \end{equation}$

(4.14)

In order to solve (4.14), we first suppose that $y(t) = \sum _{i = 0}^n c(i) t^i$ , then we use formula (3.6) into the left hand side of (4.14) to generate a new equation with the unknowns $c_i, \;i = 1, 2, ..., n$ :

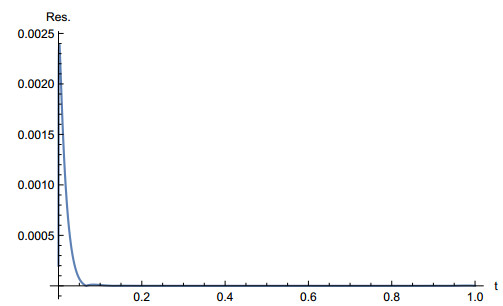
$\begin{eqnarray*} t+\left(\sum\limits_{i = 1}^nc(i)t^i\right)^2& = & 0.551631 c(2) t^{0.25} +6.61958 c(3) t^{1.25} +21.1826 c(4) t^{2.25} +47.0725 c(5) t^{3.25}\\ && +86.9032 c(6) t^{4.25}+143.135 c(7) t^{5.25} +218.11 c(8) t^{6.25} +314.078 c(9) t^{7.25}\\ && + 433.211 c(10) t^{8.25} +... \end{eqnarray*}$

then substitute different values of $t = 0.1, 0.2, ..., 1$ into the resulting equation to generate a nonlinear system that can be solved numerically. The solution and the residual errors obtained are shown in Table 2, and in Figures 1 and 2 where the residual error is given by:

$\begin{equation*} Res(t) = \left| D_{app.}^{\alpha }y(t)-y(t)^2-t \right|,{\rm{ where }}\; D_{app.}^{\alpha }y(t) \;\rm{ is\; the\; approximating \;solution\; function.} \end{equation*}$

Table 2. Approximation solution and residual error for Example 4.5.

t	exact $\alpha$ =2	app. $\alpha$ =1.75	app. $\alpha$ =1.9	app. $\alpha$ =1.75	Res. $\alpha$ =1.75	Res. $\alpha$ =1.9	Res. $\alpha$ =1.99
$\rm{ 0.1}$	$-0.01659675$	$-0.0224054$	$-0.0187648$	$-0.0168044$	$2.262\times 10^{-8}$	$5.702\times 10^{-9}$	$4.334\times 10^{-10}$
$\rm{ 0.2}$	$-0.03219034$	$-0.0429012$	$-0.0362256$	$-0.0325787$	$1.712\times 10^{-7}$	$4.788\times 10^{-8}$	$3.874\times 10^{-9}$
$\rm{ 0.3}$	$-0.04577333$	$-0.0601248$	$-0.0512319$	$-0.0463013$	$6.192\times 10^{-7}$	$1.839\times 10^{-7}$	$1.543\times 10^{-8}$
$\rm{ 0.4}$	$-0.05633536$	$-0.0728892$	$-0.0626911$	$-0.0569532$	$1.345\times 10^{-6}$	$4.171\times 10^{-7}$	$3.591\times 10^{-8}$
$\rm{ 0.5}$	$-0.06286591$	$-0.0801116$	$-0.0695491$	$-0.0635188$	$1.908\times 10^{-6}$	$6.119\times 10^{-7}$	$5.376\times 10^{-8}$
$\rm{ 0.6}$	$-0.06435742$	$-0.0807880$	$-0.0707837$	$-0.0649884$	$1.822\times 10^{-6}$	$6.008\times 10^{-7}$	$5.366\times 10^{-8}$
$\rm{ 0.7}$	$-0.05980816$	$-0.0739803$	$-0.0654020$	$-0.0603601$	$1.169\times 10^{-6}$	$3.944\times 10^{-7}$	$3.571\times 10^{-8}$
$\rm{ 0.8}$	$-0.04822370$	$-0.0588047$	$-0.0524380$	$-0.0486416$	$4.843\times 10^{-7}$	$1.667\times 10^{-7}$	$1.528\times 10^{-8}$
$\rm{ 0.9}$	$-0.02861621$	$-0.0344183$	$-0.0309479$	$-0.0288485$	$1.175\times 10^{-7}$	$4.119\times 10^{-8}$	$3.816\times 10^{-9}$
$\rm{ 1.0}$	$\rm{ 4.821}\times 10^{-9}$	$-4.821\times 10^{-13}$	$-4.518\times 10^{-14}$	$-8.031\times 10^{-16}$	$1.272\times 10^{-8}$	$4.529\times 10^{-9}$	$4.236\times 10^{-10}$

| Show Table

DownLoad: CSV

Figure 1. Res. for Example 4.5 for n = 10 and

$\alpha$ = 1.75.

DownLoad: Full-Size Img PowerPoint

Figure 2. Approximation solution for Example 4.5 for different values of

$\alpha$ .

DownLoad: Full-Size Img PowerPoint

Example 4.6. Consider the nonlinear Riccati differential equation:

$\begin{equation} D^{\alpha }y(t) = 1+2y(t)-y(t)^{2},\rm{ \ \ }y(0) = 0,0 < \alpha < 1. \end{equation}$

(4.15)

The exact solution for $\alpha = 1$ is given by

$\begin{equation*} y(t) = 1+\sqrt{2}\tanh \left[ \sqrt{2}t+\frac{1}{2}log\left( \frac{(-1+\sqrt{2} )}{(1+\sqrt{2})}\right) \right]. \end{equation*}$

To solve (4.15), suppose that

$\begin{equation} y(t) = \sum\limits_{j = 0}^{n}c_{j}t^{j}, \end{equation}$

(4.16)

then set $D^{\alpha }y(t)$ to be as:

$\begin{equation} \frac{1}{\Gamma (1-\alpha )}\sum\limits_{i = 1}^{n}\frac{(i)!c_{i}(t)^{-\alpha +i}}{ \Pi _{j = 1}^{i}(j-\alpha )}. \end{equation}$

(4.17)

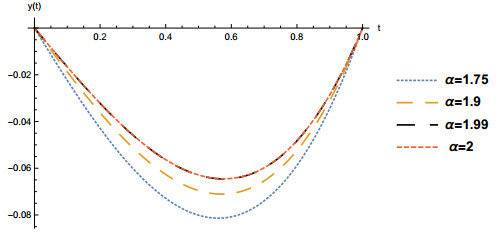
By substituting (4.16) and (4.17) into the Ricatii equation (4.15) for different values of $t$ , we generate a system of nonlinear equations which solved numerically. However, the numerical solutions and the residual error for different values of $\alpha$ are given in . The result shows that our numerical solution converges to the exact solution as $\alpha$ approaches 1. shows a comparison results for different values of $\alpha$ and as $\alpha$ approaches 1 with the results given in ^[41].

Table 3. Approximation solution and residual error for Example 4.6.

t	exact $\alpha$ =1	app. $\alpha$ =0.99	app. $\alpha$ =0.9	app. $\alpha$ =0.75	Res. $\alpha$ =0.99	Res. $\alpha$ =0.9	Res. $\alpha$ =0.75
$\rm{ 0.10}$	$\rm{ 0.11029519}$	$\rm{ 0.1133960}$	$\rm{ 0.1461280}$	$\rm{ 0.2291660}$	$2.220\times 10^{-16}$	$0$	$4.441\times 10^{-16}$
$\rm{ 0.20}$	$\rm{ 0.24197683}$	$\rm{ 0.2479170}$	$\rm{ 0.3097370}$	$\rm{ 0.4585910}$	$0$	$8.882\times 10^{-16}$	$4.441\times 10^{-16}$
$\rm{ 0.30}$	$\rm{ 0.39510486}$	$\rm{ 0.4038300}$	$\rm{ 0.4930100}$	$\rm{ 0.6935230}$	$4.441\times 10^{-16}$	$0$	$8.882\times 10^{-16}$
$\rm{ 0.40}$	$\rm{ 0.56781225}$	$\rm{ 0.5790880}$	$\rm{ 0.6915440}$	$\rm{ 0.9229300}$	$4.441\times 10^{-16}$	$8.882\times 10^{-16}$	$4.441\times 10^{-16}$
$\rm{ 0.50}$	$\rm{ 0.75601450}$	$\rm{ 0.7692950}$	$\rm{ 0.8975900}$	$\rm{ 1.1350300}$	$8.882\times 10^{-16}$	$4.441\times 10^{-16}$	$4.441\times 10^{-16}$
$\rm{ 0.60}$	$\rm{ 0.95356638}$	$\rm{ 0.9679840}$	$\rm{ 1.1019700}$	$\rm{ 1.3222100}$	$4.441\times 10^{-16}$	$7.994\times 10^{-15}$	$1.377\times 10^{-14}$
$\rm{ 0.70}$	$\rm{ 1.15294913}$	$\rm{ 1.1674200}$	$\rm{ 1.2959700}$	$\rm{ 1.4817500}$	$4.441\times 10^{-16}$	$5.773\times 10^{-15}$	$4.885\times 10^{-15}$
$\rm{ 0.80}$	$\rm{ 1.34636378}$	$\rm{ 1.3597500}$	$\rm{ 1.4728100}$	$\rm{ 1.6146000}$	$0$	$1.288\times 10^{-14}$	$4.263\times 10^{-14}$
$\rm{ 0.90}$	$\rm{ 1.52691142}$	$\rm{ 1.5382500}$	$\rm{ 1.6285100}$	$\rm{ 1.7237400}$	$3.553\times 10^{-15}$	$3.553\times 10^{-15}$	$2.753\times 10^{-14}$
$\rm{ 1.00}$	$\rm{ 1.68949852}$	$\rm{ 1.6981200}$	$\rm{ 1.7617000}$	$\rm{ 1.8129300}$	$2.665\times 10^{-15}$	$1.776\times 10^{-15}$	$7.105\times 10^{-15}$

| Show Table

DownLoad: CSV

Table 4. Comparison of absolute errors and approximation solution with the method given in ^[41] for Example 4.6.

t	Abs. Error $\alpha$ =1		App. $\alpha$ =0.9		App. $\alpha$ =0.75
t	Our	Method in ^[41]	Our $\alpha$ =0.9	Method in ^[41]	Our	Method in ^[41]
$\rm{ 0.2}$	$2.45\times 10^{-5}$	$9.23\times 10^{-5}$	$\rm{ 0.309737}$	$\rm{ 0.314571}$	$0.458591$	$0.473076$
$\rm{ 0.4}$	$3.50\times 10^{-5}$	$7.35\times 10^{-5}$	$\rm{ 0.691544}$	$\rm{ 0.697246}$	$0.922930$	$0.936880$
$\rm{ 0.5}$	$3.87\times 10^{-5}$	$7.26\times 10^{-5}$	$\rm{ 0.897590}$	$\rm{ 0.903363}$	$1.135030$	$1.147576$
$\rm{ 0.6}$	$4.05\times 10^{-5}$	$7.56\times 10^{-5}$	$\rm{ 1.101970}$	$\rm{1.107569}$	$1.322210$	$1.333068$
$\rm{ 0.8}$	$3.81\times 10^{-5}$	$3.94\times 10^{-5}$	$\rm{ 1.472810}$	$\rm{ 1.477434}$	$1.614600$	$1.622033$
$\rm{ 1.0}$	$2.79\times 10^{-5}$	$7.12\times 10^{-5}$	$\rm{ 1.761700}$	$\rm{ 1.765103}$	$1.812930$	$1.817550$

| Show Table

DownLoad: CSV

5. Conclusions

In this paper, an efficient power series formula with its error term for approximating the Caputo fractional-order derivative operator has been introduced with the help of the weighted mean value theorem. It has been shown that this formula can be used to solve many linear and nonlinear problems in fractional calculus as exhibited in several examples taken into account.

Acknowledgments

We are grateful to the anonymous referee for his or her useful remarks that have improved the manuscript's quality.

Conflict of interest

The authors declare that they have no competing interests.

References

[1]	A. Atangana, K. M. Owolabi, New numerical approach for fractional differential equations, Math. Model. Nat. Phenom., 13 (2018), 3. doi: 10.1051/mmnp/2018010
[2]	R. B. Albadarneh, I. M. Batiha, M. Zurigat, Numerical solutions for linear fractional differential equations of order $1 < \alpha < 2$ using finite difference method (ffdm), Int. J. Math. Comput. Sci., 16 (2016), 103–111.
[3]	I. M. Batiha, R. El-Khazali, A. AlSaedi, S. Momani, The general solution of singular fractional-order linear time-invariant continuous systems with regular pencils, Entropy, 6 (2018), 1–14.
[4]	R. B. Albadarneh, I. M. Batiha, N. Tahat, A. K. Alomari, Analytical solutions of linear and non-linear incommensurate fractional-order coupled systems, Indones. J. Electr. Eng. Comput. Sci., 21 (2021), 776–790. doi: 10.11591/ijeecs.v21.i2.pp776-790
[5]	I. M. Batiha, R. B. Albadarneh, S. Momani, I. H. Jebril, Dynamics analysis of fractional-order Hopfield neural networks, Int. J. Biomath., 13 (2020), 2050083. doi: 10.1142/S1793524520500837
[6]	F. Zeng, C. Li, Numerical approach to the Caputo derivative of the unknown function, Cent. Eur. J. Phys., 11 (2013), 1433–1439.
[7]	F. Ferrari, Weyl and Marchaud derivatives: A forgotten history, Mathematics, 6 (2018), 1–25.
[8]	S. Rogosin, M. Dubatovskaya, Letnikov vs. Marchaud: A survey on two prominent constructions of fractional derivatives, Mathematics, 6 (2018), 1–15.
[9]	A. K. Grünwald, Über "begrenzte" derivationen und deren Anwendung, Z. Angew. Math. Und Phys., 12 (1867), 441–480.
[10]	A. V. Letnikov, Theory of differentiation with an arbitrary index, Sb. Math., 3 (1868), 1–66.
[11]	A. V. Letnikov, On explanation of the main propositions of differentiation theory with an arbitrary index, Sb. Math., 6 (1872), 413–445.
[12]	B. Riemann, Versuch einer allgemeinen auffassung der integration und differentiation, In: Gesammelte mathematische werke und wissenschaftlicher nachlass, Leipzig: Druck Und Verlag Von B. G. Teubner, 1876.
[13]	J. Liouville, Mémorie sur une formule d'analys, J. Reine Angew. Math., 1834 (1834), 273–287. doi: 10.1515/crll.1834.12.273
[14]	V. V. Uchaikin, Application, In: Fractional derivatives for physicists and engineers, 1Eds., Beijing: Higher Education Press, 2013.
[15]	M. Cai, C. Li, Numerical approaches to fractional integrals and derivatives: A review, Mathematics, 8 (2020), 1–53.
[16]	V. Daftardar-Gejji, H. Jafari, Solving a multi-order fractional differential equation using adomian decomposition, Appl. Math. Comput., 189 (2007), 541–548.
[17]	O. Abdulaziz, I. Hashim, S. Momani, Solving systems of fractional differential equations by homotopy-perturbation method, Phys. Lett. A, 372 (2008), 451–459. doi: 10.1016/j.physleta.2007.07.059
[18]	K. Diethelm, G. Walz, Numerical solution of fractional order differential equations by extrapolation, Numer. Algorithms, 16 (1997), 231–253. doi: 10.1023/A:1019147432240
[19]	A. K. Alomari, M. S. M. Noorani, R. Nazar, Adaptation of homotopy analysis method for the numeric-analytic solution of Chen system, Commun. Nonlinear Sci., 14 (2009), 2336–2346. doi: 10.1016/j.cnsns.2008.06.011
[20]	A. K. Alomari, M. I. Syam, N. R. Anakira, A. F. Jameel, Homotopy Sumudu transform method for solving applications in physics, Results Phys., 18 (2020), 103265. doi: 10.1016/j.rinp.2020.103265
[21]	G. C. Wu, E. W. M. Lee, Fractional variational iteration method and its application, Phys. Lett. A, 374 (2010), 2506–2509. doi: 10.1016/j.physleta.2010.04.034
[22]	M. I. Syam, M. Al-Refai, Fractional differential equations with Atangana-Baleanu fractional derivative: Analysis and applications, Chaos, Solitons Fract.: X, 2 (2019), 100013. doi: 10.1016/j.csfx.2019.100013
[23]	B. R. Sontakke, A. S. Shaikh, Properties of Caputo operator and its applications to linear fractional differential equations, Int. J. Eng. Res. Appl., 5 (2015), 22–27.
[24]	V. E. Tarasov, Caputo-Fabrizio operator in terms of integer derivatives: Memory or distributed lag, Comput. Appl. Math., 38 (2019), 1–15. doi: 10.1007/s40314-019-0767-y
[25]	B. Ahmad, A. Alsaedi, S. K. Ntouyas, J. Tariboon, Hadamard-type fractional differential equations, inclusions and inequalities, Switzerland: Springer International Publishing, 2017.
[26]	R. Zafar, M. ur Rehman, M. Shams, On Caputo modification of Hadamard-type fractional derivative and fractional Taylor series, Adv. Differ. Equ., 2020 (2020), 1–13. doi: 10.1186/s13662-019-2438-0
[27]	P. Kumar, V. S. Erturk, H. Abboubakar, K. S. Nisar, Prediction studies of the epidemic peak of coronavirus disease in Brazil via new generalised Caputo type fractional derivatives, Alex. Eng. J., 60 (2021), 3189–3204. doi: 10.1016/j.aej.2021.01.032
[28]	K. S. Nisar, S. Ahmad, A. Ullah, K. Shah, H. Alrabaiah, M. Arfan, Mathematical analysis of SIRD model of COVID-19 with Caputo fractional derivative based on real data, Results Phys., 21 (2021), 103772. doi: 10.1016/j.rinp.2020.103772
[29]	J. Y. Cao, C. J. Xu, Z. Q. Wang, A high order finite difference/spectral approximations to the time fractional diffusion equations, Adv. Mater. Res., 875–877 (2014), 781–785.
[30]	G. H. Gao, Z. Z. Sun, H. W. Zhang, A new fractional numerical differentiation formula to approximate the Caputo fractional derivative and its applications, J. Comput. Phys., 259 (2014), 33–50. doi: 10.1016/j.jcp.2013.11.017
[31]	J. P. Roop, Computational aspect of FEM approximation of fractional advection dispersion equation on bounded domains in $R^2$ , J. Comput. Appl. Math., 193 (2006), 243–268. doi: 10.1016/j.cam.2005.06.005
[32]	Y. Dimitrov, Three-point approximation for Caputo fractional derivative, Commun. Appl. Math. Comput., 31 (2017), 413–442.
[33]	J. X. Cao, C. P. Li, Y. Q. Chen, High-order approximation to Caputo derivatives and Caputo-type advection-diffusion equations (Ⅱ), Fract. Calc. Appl. Anal., 18 (2015), 735–761. doi: 10.1515/fca-2015-0045
[34]	R. Mokhtari, F. Mostajeran, A high order formula to approximate the Caputo fractional derivative, Commun. Appl. Math. Comput., 2 (2020), 1–29. doi: 10.1007/s42967-019-00023-y
[35]	J. S. Leszczyński, An introduction to fractional mechanics, Czȩstochowa: Publishing Office of Czȩstochowa University of Technology, 2011.
[36]	X. C. Zheng, H. Wang, A hidden-memory variable-order time-fractional optimal control model: Analysis and approximation, SIAM J. Control Optim., 59 (2021), 1851–1880. doi: 10.1137/20M1344962
[37]	X. C. Zheng, H. Wang, Optimal-order error estimates of finite element approximations to variable-order time-fractional diffusion equations without regularity assumptions of the true solutions, IMA J. Numer. Anal., 41 (2021), 1522–1545. doi: 10.1093/imanum/draa013
[38]	R. B. Albadarneh, I. Batiha, A. Adwai, N. tahat, A. B. Alomari, Numerical approach of riemann-liouville fractional derivative operator, Int. J. Electr. Comput. Eng., 11 (2021), 5367–5378.
[39]	R. B. Albadarneh, N. T. Shawagfeh, Z. S. Abo Hammour, General $(n+1)$ -explicit finite difference formulas with proof, Appl. Math. Sci., 6 (2012), 995–1009.
[40]	R. B. Albadarneh, M. Zurigat, I. M. Batiha, Numerical solutions for linear and non-linear fractional differential equations, Int. J. Pure Appl. Math., 106 (2016), 859–871.
[41]	M. G. Sakar, A. Akgül, D. Baleanu, On solutions of fractional Riccati differential equations, Adv. Differ. Equ., 2017 (2017), 1–10. doi: 10.1186/s13662-016-1057-2

This article has been cited by:

1.	Bohui Yang, Ziyang Luo, Xindong Zhang, Quan Tang, Juan Liu, Mohammad Alomari, Trajectories and Singular Points of Two-Dimensional Fractional-Order Autonomous Systems, 2022, 2022, 1687-9139, 1, 10.1155/2022/3722011
2.	Iqbal M. Batiha, Abeer A. Al-Nana, Ramzi B. Albadarneh, Adel Ouannas, Ahmad Al-Khasawneh, Shaher Momani, Fractional-order coronavirus models with vaccination strategies impacted on Saudi Arabia's infections, 2022, 7, 2473-6988, 12842, 10.3934/math.2022711
3.	MAHDI SHADABFAR, MOJTABA MAHSULI, ARASH SIOOFY KHOOJINE, VAHID REZA HOSSEINI, ANYU HONG, RANDOMIZED FRACTIONAL SEIR-VQHP MODEL WITH APPLICATIONS IN COVID-19 DATA PREDICTION, 2023, 31, 0218-348X, 10.1142/S0218348X23400649
4.	Ramzi B. Albadarneh, Abderrahmane Abbes, Adel Ouannas, Iqbal M. Batiha, Taki-Eddine Oussaeif, 2023, 2849, 0094-243X, 030014, 10.1063/5.0162686
5.	Iqbal M. Batiha, Shameseddin Alshorm, Abdallah Al-Husban, Rania Saadeh, Gharib Gharib, Shaher Momani, The n-Point Composite Fractional Formula for Approximating Riemann–Liouville Integrator, 2023, 15, 2073-8994, 938, 10.3390/sym15040938
6.	Suhail Saleem, Muhammad Rafiq, Nauman Ahmed, Muhammad Shoaib Arif, Ali Raza, Zafar Iqbal, Shafiullah Niazai, Ilyas Khan, Fractional epidemic model of coronavirus disease with vaccination and crowding effects, 2024, 14, 2045-2322, 10.1038/s41598-024-58192-7
7.	Iqbal M. Batiha, Ahmad A. Abubaker, Iqbal H. Jebril, Suha B. Al-Shaikh, Khaled Matarneh, A Numerical Approach of Handling Fractional Stochastic Differential Equations, 2023, 12, 2075-1680, 388, 10.3390/axioms12040388
8.	Shaher Momani, Iqbal M. Batiha, Amira Abdelnebi, Iqbal H. Jebril, A powerful tool for dealing with high-dimensional fractional-order systems with applications to fractional Emden–Fowler systems, 2024, 12, 25900544, 100110, 10.1016/j.csfx.2024.100110
9.	U.H.M. Zaman, Mohammad Asif Arefin, Md. Akram Hossain, M. Ali Akbar, M. Hafiz Uddin, Nonlinear dynamic wave characteristics of optical soliton solutions in ion-acoustic wave, 2024, 451, 03770427, 116043, 10.1016/j.cam.2024.116043
10.	Ramzi B. Albadarneh, Ahmad M. Adawi, Sa’ud Al-Sa’di, Iqbal M. Batiha, Shaher Momani, 2023, Chapter 6, 978-981-99-0446-4, 65, 10.1007/978-981-99-0447-1_6
11.	haojie yu, guoliang cai, huimin liu, wenjun shi, M. A. Jabbar , Pascal Lorenz, 2024, Dynamics and synchronization of a fractional-order hyperchaotic financial system, 9781510680531, 3, 10.1117/12.3032791
12.	Iqbal M. Batiha, Shaher Momani, Shameseddin Alshorm, Adel Ouannas, 2023, Numerical Solutions of Stochastic Differential Equation Using Modified Three-Point Fractional Formula, 979-8-3503-2168-5, 1, 10.1109/ICFDA58234.2023.10153192
13.	Iqbal M. Batiha, Rania Saadeh, Iqbal H. Jebril, Ahmad Qazza, Abeer A. Al-Nana, Shaher Momani, Composite Fractional Trapezoidal Rule with Romberg Integration, 2024, 140, 1526-1506, 2729, 10.32604/cmes.2024.051588
14.	Junseok Kim, A normalized Caputo–Fabrizio fractional diffusion equation, 2025, 10, 2473-6988, 6195, 10.3934/math.2025282

Reader Comments

Your name:*

Email:*
© 2021 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(3925) PDF downloads(388) Cited by(14)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Mathematics

Numerical approach for approximating the Caputo fractional-order derivative operator

Related Papers:

Abstract

1. Introduction

2. Basic definitions and preliminaries

3. Theoretical study

4. Illustrative numerical applications

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. Basic definitions and preliminaries

3. Theoretical study

4. Illustrative numerical applications

5. Conclusions

Acknowledgments

Conflict of interest

References

AIMS Mathematics

Numerical approach for approximating the Caputo fractional-order derivative operator

Related Papers:

Abstract

1. Introduction

2. Basic definitions and preliminaries

3. Theoretical study

4. Illustrative numerical applications

5. Conclusions

Acknowledgments

Conflict of interest

References

This article has been cited by:

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Basic definitions and preliminaries

3. Theoretical study

4. Illustrative numerical applications

5. Conclusions

Acknowledgments

Conflict of interest

References