The inverse Frobenius-Perron problem: A survey of solutions to the original problem formulation

1.   Introduction

In the first half of the 20$^{\text {th}}$ century, Borel ^[1], Rényi ^[2], and Ulam and von Neumann ^[3] revealed that nonlinear deterministic systems with unsophisticated evolution rules may exhibit complex and seemingly random behavior. Initially regarded as mathematical curiosities, these systems started to attract greater attention when, with the advent of modern, powerful computing technology in the 1970s, it was discovered that systems with chaotic behavior are more prevalent and widespread than initially thought. The same period witnessed growing interest in the application of concepts from ergodic theory to study chaotic systems from a probabilistic perspective (see, for instance, ^[4,5]). This approach has proven successful in numerous application areas and its maturation has led not only to deeper understanding of how chaotic dynamics emerge in systems, but also to powerful tools and methods for analyzing and modeling chaotic systems.

The probabilistic approach to the analysis of chaotic systems considers the temporal evolution of state probability density functions, instead of individual state trajectories. Rechard ^[6] investigated what became known as the Frobenius-Perron operator (FPO) of a one-dimensional discrete-time system. This operator maps a state density function at one time instant to the evolved density function at the next time instant. Subsequent analysis of the FPO and its properties answered fundamental questions on the existence and uniqueness of state density functions that remain unchanged from one time instant to the next (i.e., invariant density functions), which play a central role in ergodic theory ^[7,8,9]. In turn, this led to the derivation of sufficient criteria for the ergodicity of certain families of systems ^[4,5]. Armed with Birkhoff's ergodicity theorem ^[10,11] and robust methods for approximating the FPO ^[12,13,14], analysts gained the capability to compute statistics and approximate the invariant density of ergodic systems without the troublesome issue of numerical inaccuracy associated with sensitive dependence on the initial state.

Whereas techniques for the probabilistic analysis of chaotic systems have matured over the years, the modeling problem (specifically, the synthesis of a dynamical system model such that it exhibits prescribed statistical characteristics) has only received attention in the research literature from the 1980s onwards. Multiple formulations of this problem, which collectively became known as the inverse Frobenius-Perron problem (IFPP) ^{[15,16,17,18,19,20,21,22,23,24,25,26,27,28]}, have been considered. Solutions to this family of problems are of interest from both theoretical and practical perspectives. These solutions not only provide insight into bifurcation routes and the transition from the non-chaotic to the chaotic regime, but also reveal how structural features of a map give rise to certain statistical characteristics ^[29,30]. Solutions to the IFPP have also been successfully applied to model systems and processes encountered in practice, such as the motion of fluids ^[31] and neural processes pertaining to the olfactory system ^[32]. In addition, these solutions have led to the design of more robust cogged bits for rock drills ^[33], more efficient random signal generators ^[34] and improved radar waveforms ^[35].

The original and most widely considered formulation of the IFPP requires the construction of a one-dimensional ergodic map with a prescribed invariant state density function ^{[15,16,17,18]}. Solutions to this problem formulation may, in general, be divided into three categories according to the strategy employed to construct the map. These are the topological conjugation ^[15], direct solution ^[16] and matrix solution ^[17,18] strategies. The solution strategies have revealed that maps which are structurally distinct and possess different higher-order statistics may share the same invariant density. In these cases, the original formulation of the IFPP does not have a unique solution. This observation, together with the growing need for simulation environments that provide more realistic models of systems and processes, have stimulated interest in solving a more general formulation of the IFPP ^[19]. This formulation involves the prescription of both the invariant density and autocorrelation function (or equivalently, by the Wiener-Khinchin theorem, the power spectrum) of an ergodic map. Several steps have been taken towards solving this more general problem ^{[19,20,21,22,23]}; however, theory regarding the capacity of certain map families to simultaneously realize a prescribed invariant density and autocorrelation function is currently incomplete, and a general analytical solution that permits the independent selection of these functions remains elusive.

More recently, a third formulation of the IFPP, which requires the derivation of a one-dimensional ergodic map from causal sequences of observed density functions, has emerged ^{[24,25,26,27,28,36]}. This problem is encountered in applications where individual trajectories of the system state cannot be observed directly, such as particle image velocimetry for flow visualization ^[37] and flow cytometry ^[38]. A matrix solution to this problem formulation has been proposed ^[24,25] and generalized to stochastically perturbed systems ^[26] and systems driven by an external input ^[27,28]. This solution generates semi-Markov maps with piecewise constant invariant density functions that approximate the invariant density of the system that generated the observed densities (refer to sections 2.2.1 and 5 for details). In the absence of noise and under the assumption of perfect density estimation, the approximation error can be made arbitrarily small by refining the partition^*. This approach provides the opportunity to model not only the asymptotic behavior of the unknown system, but also its transient dynamics; by only considering the invariant density, solutions to the first formulation of the IFPP do not necessarily produce maps with dynamical properties (such as the Lyapunov exponent and fixed points) that are consistent with those of the unknown system. In contrast, the solution to the third problem formulation ^{[25,26,27,28]} has been shown to successfully recover the true structure of continuous nonlinear maps, thereby demonstrating its potential to produce more faithful models when compared to earlier solutions.

^* The solution proposed in ^[25] (and its generalization in subsequent works) addresses the problem of estimating the unknown Markov partition. Other matrix-based reconstruction techniques assume this partition is known.

In this paper, we review the strategies and methods that have been proposed for solving the original formulation of the IFPP. With reference to the wide dispersal of these solutions across literature in diverse technical domains such as physics, engineering, biology and economics, the objective of this survey is to provide an information source that unifies these contributions, thereby improving accessibility to the corresponding modeling tools and methods. Furthermore, we illustrate several of the solution strategies and methods using examples, with the aim of promoting their practical application. The paper is concluded by discussing possible avenues for future work.

The remainder of this paper is set out as follows. Background on the probabilistic characterization of ergodic maps, as required to solve the original problem formulation, as well as the definition of the class of piecewise monotonic maps, which are typically constructed during the solution of the IFPP, are provided in section 2. Section 3 presents the original formulation of the IFPP. Strategies for solving this problem formulation, together with a review of existing techniques, are presented in section 4. Section 5 presents a brief overview of recent developments in the domain. Section 6 considers future research topics.

2.   Background

This section presents the necessary background on the probabilistic analysis of one-dimensional maps. The reader is referred to ^[4,5] for a comprehensive treatment of the subject. The class of piecewise monotonic maps is subsequently defined; in general, solutions to the IFPP construct ergodic maps from this large family of maps. Two subsets of these maps, the Markov and semi-Markov maps, allow a matrix solution to the IFPP.

2.1.   Probabilistic analysis of one-dimensional maps

We consider a one-dimensional dynamical system with a nonlinear evolution rule $S: \Omega \to \Omega$, where $\Omega$ is the state space which, for simplicity without any loss of generality, is assumed to be the unit interval $\Omega = [0, 1]$ (note that any map defined on an arbitrary, compact interval of $\mathbb{R}$ may be transformed to a map on $\Omega$ via topological conjugation with a linear mapping). Systems which exhibit sensitive dependence on the initial state are considered. This implies continual repulsion of a trajectory by almost every state in $\Omega$; consequently, almost all trajectories are aperiodic. In this case, the system gives rise to behavior that appears stochastic, and may be investigated using concepts from ergodic theory. To accommodate this investigation, let $X_1$ denote a real random variable on the probability space $(\Omega, \mathcal{B}, P_1)$, which represents the initial state of the dynamical system. Here, $\mathcal{B}$ denotes the Borel $\sigma$-algebra on $\Omega$ and $P_1$ is a probability measure. We assume that $S$ is surjective and measurable on $\mathcal{B}$. It follows that the random variables $X_2, X_3, \dots$, defined by $X_{n+1} = S(X_n)$ for $n \geq 1$, have corresponding probability measures

We only consider probability measures that are absolutely continuous with respect to the Borel measure $\mu$. From the Radon-Nikodym theorem, this implies the existence of a function $f_1 \in \mathcal{D}(\Omega)$ associated with $X_1$, where $\mathcal{D}(\Omega) = \{f \in L^1(\Omega): f \geq 0 \quad \text { and } \quad \|f\| = 1\}$ denotes the set of all probability density functions on $\Omega$. The density function $f_1$ satisfies $P_1(B) = \int_Bf_1(x)d\mu(x)$ for all $B \in \mathcal{B}$. We require that $S$ is nonsingular with respect to the Borel measure $\mu$; this implies that each measure $P_n, \quad n > 1$, is also absolutely continuous with respect to $\mu$, and is associated with a corresponding density $f_n \in \mathcal{D}(\Omega)$.

We consider the linear operator $\mathcal{P}_S: L^1(\Omega) \to L^1(\Omega)$, referred to as the Frobenius-Perron operator (FPO). This operator characterizes the evolution of densities under iteration of the map $S$ according to the expression $f_{n+1} = \mathcal{P}_Sf_n$ for $n \geq 1$. The FPO is uniquely defined by the expression

It can be shown that $\mathcal{P}_S$ is a Markov operator, in the sense that $f \geq 0$ implies $\mathcal{P}_Sf \geq 0$ and $\|\mathcal{P}_S f\| = \|f\|$; these properties imply that $\mathcal{P}_S$ maps from one density function to another, as expected.

We restrict our attention to ergodic systems. Formally, a map $S$ is referred to as ergodic if every $S$-invariant set $B \in \mathcal{B}$ is a trivial subset of $\Omega$; i.e., $S^{-1}(B) = B$ implies either $\mu(B) = 0$ or $\mu(\Omega \setminus B) = 0$. Ergodicity corresponds to the property that almost every trajectory visits every infinitesimal neighborhood of every state in the state space. It can be shown that an ergodic system permits at most one absolutely continuous invariant (ACI) measure $P_*$, where $P_*(B) = P_*(S^{-1}(B))$ for all $B \in \mathcal{B}$. This measure corresponds to the asymptotic likelihood of a trajectory passing through a particular region $B \subset \Omega$ of the state space at a fixed time instant. Moreover, ergodicity implies asymptotic independence of measurable sets (events) ^[4].

Let $f_*$ denote the density function corresponding to the measure $P_*$. A measure $P_*$ is $S$-invariant if and only if $f_*$ is a fixed point of the FPO $\mathcal{P}_S$; i.e., $\mathcal{P}_{S}f_* = f_*$. We refer to $f_*$ as an invariant density of $S$. The concept of an invariant density is important when investigating the convergence properties of the FPO. In general, it can be shown that the FPO is non-expansive; i.e., $\|\mathcal{P}_{S}f - \mathcal{P}_{S}g\| \leq \|f - g\|$ for $f, g \in L^1(\Omega)$. This property is not sufficient to guarantee the existence of a unique fixed point of $\mathcal{P}_S$ (in contrast, the stronger requirement of contractiveness guarantees, by the Banach fixed point theorem, the existence of a unique fixed point ^[39]). However, if the map $S$ is ergodic, it follows that a fixed point $f_*$ of the FPO is unique. Furthermore, ergodicity is equivalent to the sequence $\{\mathcal{P}^n_Sf\}$ converging in the Cesàro sense to the invariant density $f_*$ for all $f \in \mathcal{D}(\Omega)$.

One consequence of ergodicity is the asymptotic equivalence of averages computed over trajectories of the map and ensemble averages. More formally, we have

for any integrable function $h$ and almost all starting points $x_1$. The practical utility of (2.1), which is an often-quoted extension of Birkhoff's individual ergodic theorem (see, for instance, ^[4]), is that it provides a means for computing averages without suffering from inaccuracy due to finite precision arithmetic and the sensitivity of $S$ on the initial state. Instead of computing averages over individual trajectories, one may alternatively compute ensemble averages.

Equation (2.1) has a further consequence. If we set $h(x) = \chi_{B}(x)$, where

is the characteristic function of the set $B$, then the asymptotic fraction of trajectory points that fall within $B$ is equal to $P_*(B)$ for almost every trajectory. In an asymptotic sense this implies that the distribution of points in almost every trajectory is consistent with the invariant density.

We conclude this section by observing that it is not always feasible to derive an expression for the invariant density function of an ergodic map. To overcome this problem, Ulam ^[12] proposed a numerical method whereby a matrix representation of the FPO is constructed over a partition of the state space, and the invariant density is approximated with a piecewise defined function that coincides with the leading eigenvector of this matrix. Li ^[13] proved that this approximation converges to the true invariant density function as the partition becomes finer. The method was later generalized to multi-dimensional maps ^[14].

2.2.   Piecewise monotonic maps

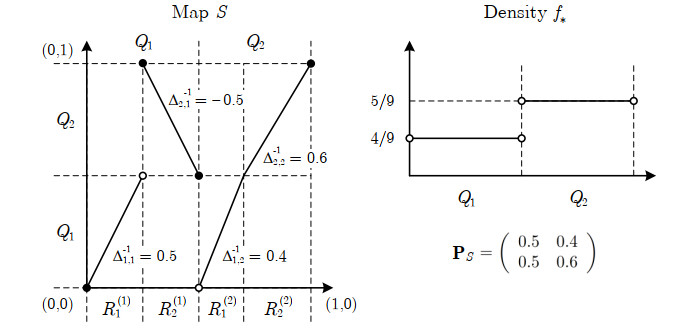
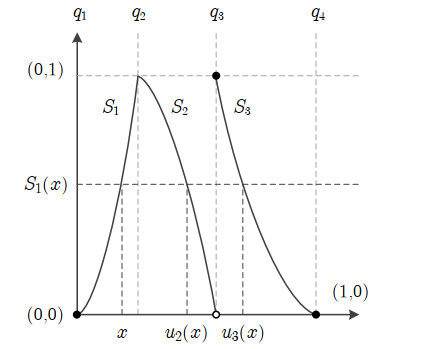
Now we introduce the class $\Gamma(\mathcal{Q})$ of piecewise monotonic and surjective maps. These maps are defined over a partition of the map domain. Let $P(\mathcal{Q}) = \{q_1, q_2, \dots, q_{M+1}\}$ denote the partition points of the partition $\mathcal{Q} = \{Q_1, Q_2, \dots, Q_{M}\}$, where $Q_m = (q_m, q_{m+1})$ denotes the partition intervals and $0 = q_1 < q_2 < \dots < q_{M+1} = 1$ with integer $M > 1$.

Definition 2.1 (Class $\Gamma(\mathcal{Q})$). A surjective map $S: \Omega \to \Omega$ is piecewise monotonic ^[5] (i.e., $S \in \Gamma(\mathcal{Q})$) if there exists a partition $\mathcal{Q}$ of the unit interval such that (i) each branch function $S_m \triangleq S|_{(q_{m}, q_{m+1})}$ is a $C^r$ function, for some $r \geq 1$, that can be extended to a $C^{r}$ function over $[q_{m}, q_{m+1}]$, and (ii) $|S'_m| > 0$ for $m = 1, 2, \dots, M$, where $S'_m \triangleq dS_m/dx$.

Let $S \in \Gamma(\mathcal{Q})$ (an example is plotted in Figure 1). The pre-image $S^{-1}(B)$ of any Borel set $B \in \mathcal{B}$ can then be expressed as a finite union of Borel sets, which implies that $S^{-1}(B) \in \mathcal{B}$. Hence, $S$ is a Borel measurable function. Furthermore, it follows from Villani's lemma ^[40] that $S$ is nonsingular with respect to the Borel measure; i.e., $\mu(B) = 0, \quad B \in \mathcal{B}$ implies $\mu(S^{-1}(B)) = 0$. Since each branch function $S_m$ is strictly monotonic and continuous, it also follows that $S_m$ is invertible over its image.

Sufficient conditions for the existence of ACI measures were derived in ^[5,7].

Theorem 2.1 (Existence of ACI measures ^[5,7]). Let $S \in \Gamma(\mathcal{Q})$. If $|S_{m}'| \geq \alpha > 1$ over all partition intervals $Q_m$, and the function $h(\cdot) \triangleq 1/|S'(\cdot)|$ is of bounded variation, where $S'$ is the appropriate one-sided derivative at the partition points $P(\mathcal{Q})$, then $S$ admits an ACI measure with a corresponding invariant density of bounded variation.

An expression may be derived for the evolution of distribution functions under iteration of a piecewise monotonic map, in addition to an explicit representation of the FPO; these expressions are manipulated to solve the IFPP directly in section 4.2.

The distribution function $F_n$ evolves under iteration of $S \in \Gamma(\mathcal{Q})$ according to ^[23]

where $N(x) \triangleq \{m: x \in S(Q_m)\}$, $M(x) \triangleq \{m: x \geq y'_m\}$, $y'_m \triangleq \sup\{S(Q_m)\}$ and

The FPO $\mathcal{P}_S$ corresponding to a map $S \in \Gamma(\mathcal{Q})$ has the explicit representation ^[5]

2.2.1.   Markov and semi-Markov maps

We introduce two subsets of the piecewise monotonic map family, namely the Markov and semi-Markov maps. The structures of these maps accommodate matrix solutions to the IFPP, as illustrated in section 4.3.

Informally, a map $S \in \Gamma(\mathcal{Q})$ is $\mathcal{Q}$-Markov if the image of each partition interval $Q_m \in \mathcal{Q}$ under $S$ can be expressed as a union of intervals from the same partition $\mathcal{Q}$. A formal definition, which takes into account that the partition intervals $Q_m$ are open, is provided in what follows. We use $\bar{Q}_m = \text {cl}\{Q_m\}$ to denote the closure of interval $Q_m$.

Definition 2.2 ($\mathcal{Q}$-Markov map). A map $S \in \Gamma(\mathcal{Q})$ is $\mathcal{Q}$-Markov if

for each $Q_m \in \mathcal{Q}$, where $W(m) \subseteq \{1, 2, \dots, M\}$ for $m = 1, 2, \dots, M$.

The Folklore theorem establishes conditions for both the existence and uniqueness of ACI measures for $\mathcal{Q}$-Markov maps that are piecewise $C^2$. This theorem originated from the work of Rényi ^[2], who considered piecewise onto transformations. The Folklore theorem refers to the aperiodicity property of a map. The map $S \in \Gamma(\mathcal{Q})$ is aperiodic if, for each $m = 1, 2, \dots, M$, there exists some $q > 0$ such that $S^q(\bar{Q}_m) = \Omega$.

Theorem 2.2 (Folklore theorem ^[5]). Let $S \in \Gamma(\mathcal{Q})$ denote an aperiodic $\mathcal{Q}$-Markov map, where each branch function $S_m$ can be extended to a strictly monotonic $C^2$ function on the closed interval $\bar{Q}_m$. If $S$ satisfies $|S_m'| \geq 1 + \varepsilon$ for all $m$ and some $\varepsilon > 0$ (i.e., $S$ is piecewise expanding), then it has a unique ACI measure $P_*$.

A $\mathcal{Q}$-Markov map $S \in \Gamma(\mathcal{Q})$ that satisfies the conditions of the Folklore theorem is necessarily ergodic, since its invariant measure $P_*$ is unique. Furthermore, since the measure is absolutely continuous, there exists a corresponding invariant density function $f_*$. This density function can be chosen as a piecewise continuous function with discontinuities only at the partition points $P(\mathcal{Q})$, and satisfying $K^{-1} \leq f_*(x) \leq K$ for some $K > 0$.

We next consider the semi-Markov maps, first introduced in ^[18].

Definition 2.3 ($\mathcal{R}(\mathcal{Q})$-semi-Markov map). Let $\mathcal{Q}$ denote a partition of $\Omega$, and let the non-empty set of open intervals $\{R^{(m)}_{1}, R^{(m)}_{2}, \dots, R^{(m)}_{c(m)}\}$ constitute a partition of $\bar{Q}_m$ for each $m$. Let $\mathcal{R}$ denote the unit-interval partition containing the intervals $R^{(m)}_j$ for all $m = 1, 2, \dots, M$ and $j = 1, 2, \dots, c(m)$. The map $S \in \Gamma(\mathcal{R})$ is $\mathcal{R}(\mathcal{Q})$-semi-Markov if the image of each of the intervals $R^{(m)}_{j}$ under $S$ is an interval of the partition $\mathcal{Q}$; i.e.,

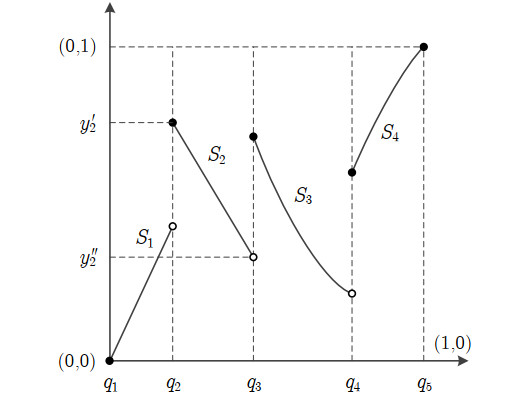
Let $S \in \Gamma(\mathcal{R})$ denote an $\mathcal{R}(\mathcal{Q})$-semi-Markov map (an example is plotted in Figure 2). Since the closure of each $Q_m \in \mathcal{Q}$ has a partition consisting of intervals in $\mathcal{R}$, and each of the intervals in $\mathcal{R}$ is mapped to an interval in $\mathcal{Q}$, the map $S$ is also $\mathcal{R}$-Markov. Hence, $S$ is ergodic if it satisfies the conditions of the Folklore theorem.

We consider ergodic Markov and semi-Markov maps with linear branch functions and ACI measure $P_*$ in the remainder of this section. Each of these piecewise linear maps possesses a piecewise constant invariant density function. In particular, Boyarsky ^[41] and Góra ^[18] proved that any such $\mathcal{Q}$-Markov or $\mathcal{R}(\mathcal{Q})$-semi-Markov map has an invariant density function $f_*$ that is piecewise constant over the intervals of the partition $\mathcal{Q}$. Furthermore, these maps permit a matrix representation of the corresponding FPO if involvement is restricted to density functions that are piecewise constant on $\mathcal{Q}$. Let $f_n$ denote such a density function, and let $S \in \Gamma(\mathcal{R})$ denote a piecewise linear $\mathcal{R}(\mathcal{Q})$-semi-Markov map with branches $S_{j, m} \triangleq S|_{R^{(m)}_j}$ given by

where $\Delta_{j, m}, b_{j, m} \in \mathbb{R}$, $m = 1, 2, \dots, M$ and $j = 1, 2, \dots, c(m)$. It can be verified using (2.4) that the density $f_{n+1} = \mathcal{P}_{S}f_{n}$ is also piecewise constant on $\mathcal{Q}$. We introduce the column vector $\mathbf{f}_n \triangleq [f_{n, 1}, f_{n, 2}, \dots, f_{n, M}]^{T}$ as the explicit representation of the density $f_n$, where $f_{n, m} \triangleq f_{n}|_{Q_m}$; the representations $f_n$ and $\mathbf{f}_n$ will be used interchangeably. Using (2.4) it can be shown that vector $\mathbf{f}_{n+1}$, which represents density $f_{n+1}$, is given by

where $\mathbf{P}_S = [p_{k, m}]$ is the $M \times M$ matrix representation of the FPO $\mathcal{P}_S$, with elements

and

The matrix $\mathbf{P}_S$ is referred to as the Frobenius-Perron matrix (FPM).

The FPM of a piecewise linear $\mathcal{R}(\mathcal{Q})$-semi-Markov map $S$ has several properties that are relevant to the matrix strategy for solving the IFPP. In what follows, we assume that the map satisfies the conditions of the Folklore theorem and is therefore ergodic. In the case where the partition $\mathcal{Q}$ is uniform, the map structure imposed by the semi-Markov property leads to a FPM $\mathbf{P}_S$ that is column stochastic (this term implies that the matrix has elements which satisfy $0 \leq p_{j, m} \leq 1$, and each matrix column sums to unity). Selecting $\mathbf{v}_1 = [1, 1, \dots, 1]^T$ reveals that $\mathbf{v}_1^T = \mathbf{v}_1^T\mathbf{P}_S$; this implies that $\mathbf{P}_S$ has at least one eigenvalue $\lambda_1$ equal to unity. Furthermore, since $S$ is aperiodic, there exists some natural number $t$ such that $\mathbf{P}_S^t$ is positive. Hence, $\mathbf{P}_S$ is primitive, and the Perron-Frobenius theorem ^[42,43,44] may be used to characterize the matrix. It follows that the unity eigenvalue $\lambda_1$, referred to as the Perron eigenvalue, is a simple root of the characteristic polynomial of the matrix. All remaining eigenvalues of $\mathbf{P}_S$ are strictly smaller than $\lambda_1$ in absolute value, which implies that the matrix has a spectral radius of unity. The right eigenvector $\mathbf{w}_1$ associated with the Perron eigenvalue, referred to as the right Perron eigenvector, satisfies $\mathbf{w}_1 = \mathbf{P}_S \mathbf{w}_1$; hence, $\mathbf{w}_1 \equiv \mathbf{f}_*$ coincides with the unique piecewise constant invariant density function $f_*$. The Perron-Frobenius theorem guarantees that the elements of $\mathbf{f}_*$ are positive.

In the more general case of a piecewise linear $\tilde{\mathcal{R}}(\tilde{\mathcal{Q}})$-semi-Markov map $\tilde{S}$ defined over a nonuniform partition $\tilde{\mathcal{Q}}$, it can be shown that the FPM $\mathbf{P}_{\tilde{S}}$ has a unity eigenvalue $\tilde{\lambda}_1$. This eigenvalue is associated with a left eigenvector $\tilde{\mathbf{v}}_1$ that coincides with the lengths of the intervals in $\tilde{\mathcal{Q}}$. It follows that $\mathbf{P}_{\tilde{S}}$ is similar to a stochastic matrix; specifically, $\mathbf{P}_{\tilde{S}} = \mathbf{D}^{-1}\mathbf{PD}$, where $\mathbf{D}$ is a diagonal matrix with diagonal elements equal to the lengths of the intervals in $\tilde{\mathcal{Q}}$, and $\mathbf{P}$ is a column stochastic matrix^†. Since similar matrices share the same characteristic polynomial, prior observations regarding the eigenvalue spectrum of $\mathbf{P}_S$ (the FPM corresponding to a semi-Markov map $S$ over a uniform partition $\mathcal{Q}$) also apply to $\mathbf{P}_{\tilde{S}}$, provided that $\mathbf{P}$ is a primitive matrix.

^† In this case, map $\tilde{S}$ is a topological conjugate of another semi-Markov map $S$ over a uniform partition and with FPM $\mathbf{P}_S = \mathbf{P}$.

3.   The original problem formulation: IFPP-I

In this paper we consider the original formulation of the IFPP, denoted by IFPP-I. Let $f_P \in \mathcal{D}(\Omega)$, where $f_P > 0$ a.e., denote a probability density function (the subscript indicates that the density function is prescribed). IFPP-I requires the construction of a nonsingular map $S: \Omega \to \Omega$ with ACI measure $P_*$ that satisfies

The measure $P_*$ is required to be the unique $S$-invariant measure. This implies that the map $S$ must be ergodic with invariant density function $f_* = f_P$, which is the unique fixed point of the FPO $\mathcal{P}_S$ corresponding to $S$.

4.   Solution strategies

Solutions to IFPP-I may generally be divided into three categories with respect to the strategy employed to construct the ergodic map. These are the topological conjugation, direct solution and matrix solution strategies. Each strategy is outlined in a separate section below. We present examples that illustrate how IFPP-I is solved using each strategy and review the relevant literature.

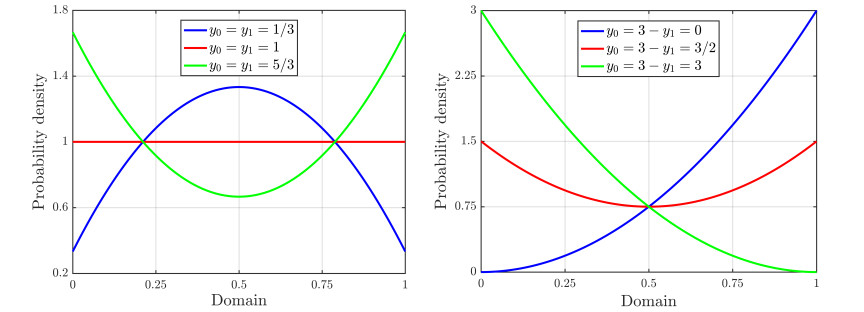
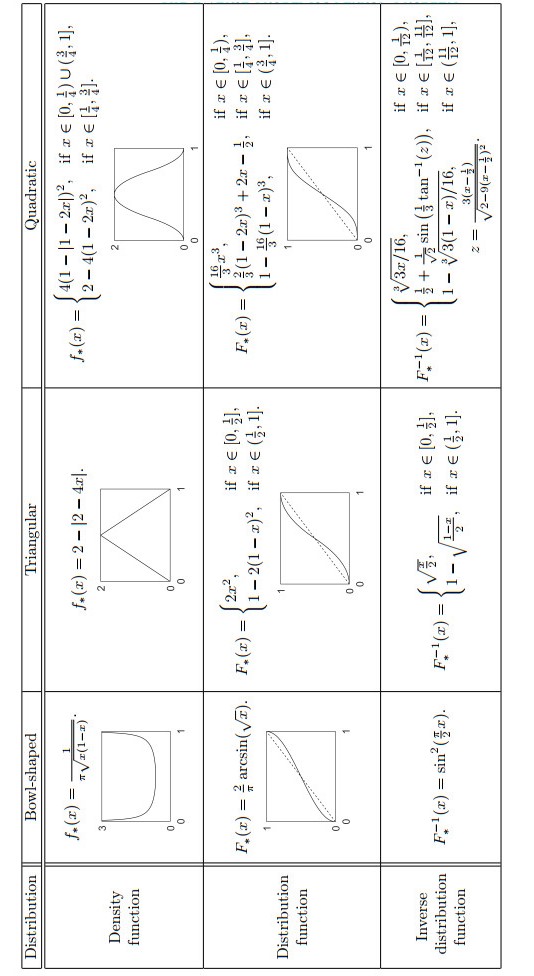
The examples provided in the following sections involve the construction of ergodic maps with invariant densities from the family of quadratic polynomials

defined over the unit interval, with coefficients

where $y_0 \triangleq f_P(0)$ and $y_1 \triangleq f_P(1)$ are free parameters to be prescribed. The corresponding distribution function is given by

and the region of valid parameter pairs $(y_0, y_1)$ is defined by

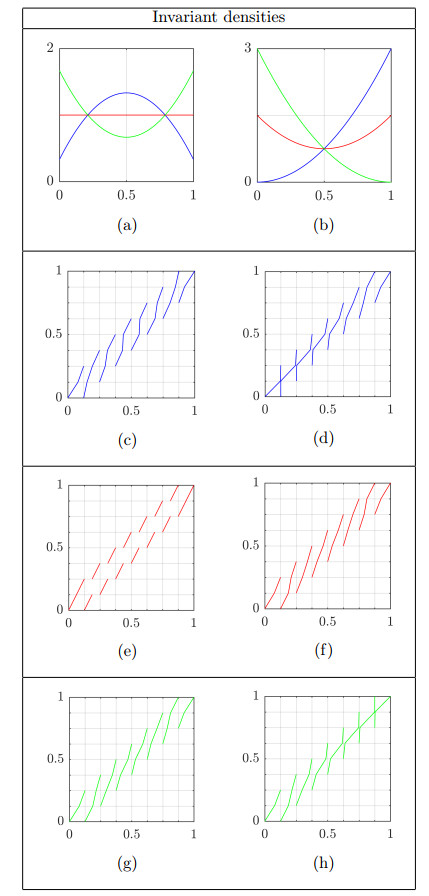
The density functions considered in the examples, with the corresponding parameter pairs $(y_0, y_1)$, are presented in Figure 3.

4.1.   Topological conjugation solution strategy

4.1.1.   Outline

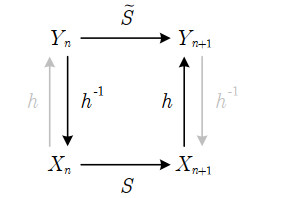
Let $X_1$ denote a random variable on the probability space $(\Omega, \mathcal{B}, P_1)$, where the measure $P_1$ is absolutely continuous with respect to the Borel measure $\mu$. Suppose that $S: \Omega \to \Omega$ is a measurable and nonsingular map, and let $X_{n+1} = S \circ X_n$, where $n \geq 1$. Define a homeomorphism $h: \Omega \to \Omega$ with derivative that satisfies $|h'| > 0$ a.e. Since $h$ is continuous, it is Borel measurable, and hence the functions defined by

are random variables on $(\Omega, \mathcal{B}, \tilde{P}_n)$, where $\tilde{P}_{n} = P_{n} \circ h^{-1}$. Furthermore, since $h$ is nonsingular ^[40], the absolute continuity of $P_n$ implies that the measures $\tilde{P}_n$ are also absolutely continuous. Hence, each $Y_n$ has a corresponding density function $\tilde{f}_n$.

The invertibility of $h$ implies that the sequence of random variables $\{Y_n\}$ may be interpreted as representing the evolution of the unknown state of a one-dimensional dynamical system having the map $\tilde{S}$ as evolution rule, such that $Y_{n+1} = \tilde{S}(Y_n)$. In particular, with reference to Figure 4, we have

The maps $\tilde{S}$ and $S$ are referred to as topological conjugates with $h$ as the conjugating function or transformation ^[15,45,46]. Topological conjugation establishes an equivalence relation between maps, such that the maps of any class generated by topological conjugation share the same properties of ergodicity, mixing and exactness (a definition of the latter two concepts may be found in ^[4]). The property that ergodicity is preserved under conjugation is proved in the following theorem.

Theorem 4.1 (Conjugation preserves ergodicity).

Proof. Let $S$ be ergodic with ACI measure $P_*$ and invariant density $f_* > 0$ a.e. The measure $\tilde{P}_* = P_* \circ h^{-1}$ then satisfies, for any $B \in \mathcal{B}$,

where the second step follows from the $S$-invariance of $P_*$. It follows that $\tilde{P}_*$ is $\tilde{S}$-invariant. We now prove that $\tilde{P}_*$ is unique by contradiction. Assume that a second distinct $\tilde{S}$-invariant measure $\tilde{U}_*$ exists. Then, due to $S$ being the topological conjugate of $\tilde{S}$ with conjugating function^‡ $g = h^{-1}$, the corresponding measure $U_* = \tilde{U}_* \circ g^{-1}$ is necessarily $S$-invariant and distinct from $P_*$. However, since $S$ is ergodic, the $S$-invariant measure is unique. The assumption that $\tilde{U}_*$ is $\tilde{S}$-invariant then contradicts the original statement that measure $P_*$ is $S$-invariant. Hence, there exists no measure other than $\tilde{P}_*$ that is $\tilde{S}$ invariant. Theorem 4.2.2 from ^[4] then implies that $\tilde{S}$ is ergodic.

^‡ It is assumed here that $|g'| > 0$ a.e.

Topological conjugation presents a means for solving IFPP-I. Suppose that $S$ is an ergodic map with a known ACI measure $P_*$ and $f_* > 0$ a.e. To solve IFPP-I, we design an ergodic map $\tilde{S}$ that is a topological conjugate of $S$ and with invariant density function $\tilde{f}_*$ equal to the prescribed density $f_{P}$. This is achieved by deriving a conjugating transformation $h$ such that the invariant measure $\tilde{P}_* = P_* \circ h^{-1}$ corresponds to $f_{P}$. To illustrate how the transformation $h$ may be derived, we consider the distribution functions $F_*$ and $\tilde{F}_*$ associated with measures $P_*$ and $\tilde{P}_*$, respectively. From (2.2) we have, for an increasing function $h$,

Assume that the distribution functions $F_*$ and $F_P$, where $F_P$ is associated with the prescribed density $f_P$, are both homeomorphisms from $\Omega$ onto itself. Selecting $\tilde{F}_* = F_P$ leads to

If $h' > 0$ a.e., $h$ is nonsingular and satisfies the conditions for a conjugating transformation. The ergodic map $\tilde{S}$ is then given by (4.3). The topological conjugation solution strategy is illustrated in the following example.

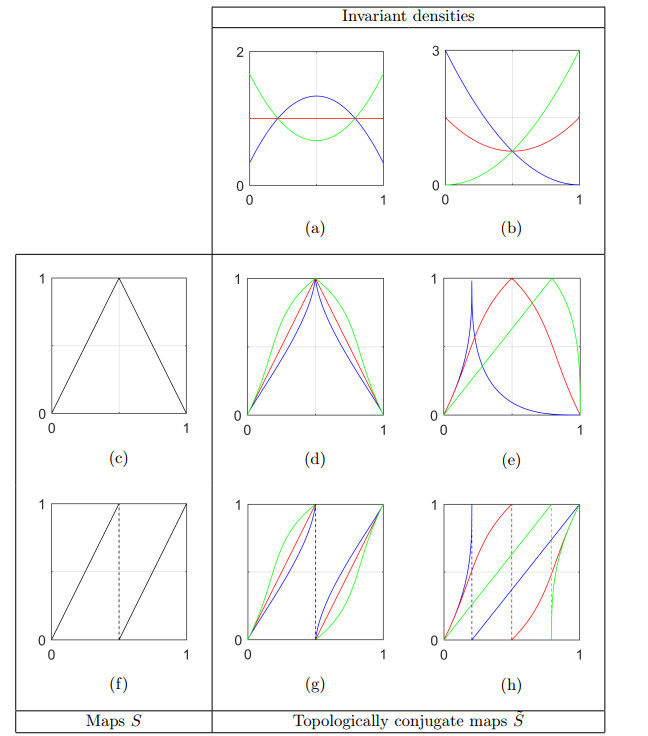
Example 4.1 (Topological conjugation solution). Ergodic maps $\tilde{S}$ with the invariant density functions plotted in Figure 3 are constructed. We consider the ergodic maps $S = S_T$ and $S = S_B$, defined by

and

These maps are referred to as the tent map and Bernoulli map, and are plotted in Figures 5(c) and 5(f), respectively. Both of these maps possess a uniform invariant density function, which corresponds to a distribution function $F_*(x) = x$. Substitution of (4.4) into (4.3) then produces the map $\tilde{S}_T$, a topological conjugate of the tent map, given by

and the map $\tilde{S}_B$, a topological conjugate of the Bernoulli map, given by

where $F_P$ is defined in (4.2). The maps $\tilde{S}_T$ and $\tilde{S}_B$ are plotted in Figures 5(d, e) and Figures 5(g, h) respectively, and the invariant density function of each conjugate map is plotted, in the same color, at the top of the same column (Figures 5(a, b)). Due to the strict monotonicity and smoothness of $F_P$ and $F_P^{-1}$, the conjugate maps $\tilde{S}$ have the same number of branches as the underlying map $S$; furthermore, the positivity or negativity of each branch slope is also preserved under conjugation with $h = F_P^{-1}$. In certain cases, topological conjugation also preserves symmetry. We refer to a function $G: \Omega \to \Omega$ as symmetric around $x = x_0$ if it satisfies

antisymmetric around $x = x_0$ if it satisfies

and translationally symmetric around $x = x_0$ if

Maps that are symmetric, antisymmetric or translationally symmetric around $x_0 = 1/2$ are simply referred to as symmetric, antisymmetric or translationally symmetric. The tent map is an example of a symmetric map, whereas the Bernoulli map is both antisymmetric and translationally symmetric. For the symmetric density functions in the example, it is found that (i) the corresponding map $\tilde{S}_T$, which is conjugate to the tent map, is also symmetric (Figure 5(d)), and (ii) the map $\tilde{S}_B$, which is conjugate to the Bernoulli map, is also antisymmetric (Figure 5(g)). In general, any map $\tilde{S}$ with symmetric invariant density function $f_P$, where $\tilde{S}$ is conjugate to a symmetric (antisymmetric) map $S$ with symmetric invariant density function $f_*$ via the conjugating transformation of (4.4), is also symmetric (antisymmetric). However, in the case where the density function $f_P$ lacks symmetry, the domain of each branch of the map $S$ may change under conjugation (blue and green maps of Figures 5(e, h)).

Apart from selecting the number of branches of the conjugate map $\tilde{S}$ (in the case of a smooth conjugating transformation) and the sign of each branch slope through the choice of the underlying map $S$, the topological conjugation strategy provides no direct opportunity to select structural characteristics such as the branch domains of $\tilde{S}$. In contrast, the direct solution and matrix solution strategies discussed in sections 4.2 and 4.3 provide greater opportunity to select the characteristics of each map branch. This implies that the topological conjugation strategy is a less attractive option for solving the more general formulations of the IFPP, where the ability to prescribe the branch structure of the resulting map becomes relevant. However, with topological conjugation, the conjugate map is guaranteed to be ergodic provided that the underlying map $S$ is itself ergodic.

4.1.2.   Literature

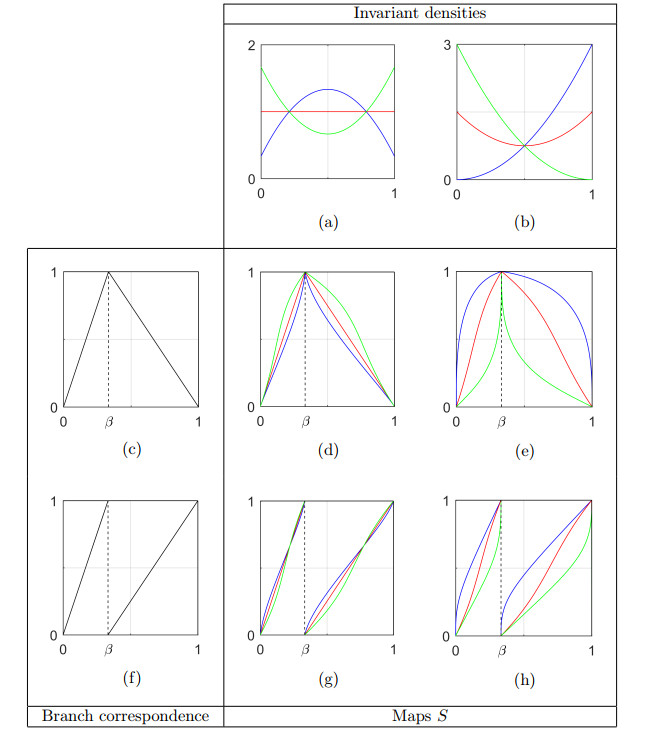
Grossman and Thomae ^[15] formally introduced topological conjugation as an approach towards solving IFPP-1. The authors constructed equivalence classes of ergodic maps that are conjugate to maps from the family of piecewise linear transformations $S_v: \Omega \to \Omega$, defined by

where $v \in \mathbb{R}$ and $[\cdot]$ denotes the integer part of its argument. These maps are ergodic for all $v > 1$ and possess a uniform invariant density function for integer $v \geq 2$. Maps $\tilde{S} = F_P^{-1} \circ S_v \circ F_P$ with the invariant densities listed in Figure 6 were derived; for convenience, we provide expressions for the distribution functions and their inverses.

Using topological conjugation to design chaotic noise generators, van Wyk and Steeb ^[47] derived an expression that may be solved for the required conjugating transformation $h$. This expression contains both the invariant density $f_*$ of the underlying map $S$ and the prescribed invariant density $f_P$, and is given by

The expression was solved analytically to obtain (4.4). A map topologically conjugate to a Bernoulli-type map with selectable discontinuity (as studied in ^[48]), and with an exponential invariant density, was constructed.

Berlinet and Biau ^[49] constructed exact maps with prescribed invariant density functions for the purpose of nonuniform random variate generation (in this approach, map trajectories are used as random variate sequences^$\S$). These maps are topologically conjugate to the maps $S(x) = vx \quad (\mod 1)$ with integer $v > 1$. The maps obtained via topological conjugation preserve the number of branches and the positivity of the branch slopes of the underlying map, and may therefore be interpreted as a generalization of the class of linear congruential random number generators from uniform to nonuniform distributions. The statistics of maps with invariant density corresponding to the Gumbel probability distribution, with distribution function given by $F_P = \exp(-\exp(-x))$, $x \in \mathbb{R},$ were investigated numerically.

^$\S$ From Birkhoff's ergodic theorem it follows that the distribution of the random variates produced using this technique is asymptotically consistent with the invariant density of the map (see, for instance, ^[4]).

Pingel et al. ^[30] demonstrated a technique for constructing symmetric maps with asymmetric invariant density functions that is related to topological conjugation (see also ^[50]). This approach was first considered in ^[51]. Let $S = S_T$ denote the tent map. Now, consider the map

where $u:\Omega \to \Omega$ is a conjugating transformation that is antisymmetric and satisfies $u'(x) > 0$ for all $x \in \Omega$, and where $U(x) = u(x) + v(x)$, such that $v$ is symmetric and $v(0) = 0$. The functions $u$ and $v$ may be (uniquely) selected to realize a symmetric map $\tilde{S}$ with a prescribed invariant density $f_P$. In particular, if we select $U = F_P$, where $F_P$ is the distribution function corresponding to the prescribed invariant density, and decompose $F_P$ into antisymmetric and symmetric components according to

and

then $\tilde{S}$ is symmetric with invariant density function $\tilde{f}_* = dU/dx$ that need not be symmetric. However, as the mapping between trajectories of $S$ and $\tilde{S}$ is no longer one-to-one, the uniqueness of the invariant density (and hence the ergodicity of $\tilde{S}$) cannot be guaranteed.

4.2.   Direct solution strategy

4.2.1.   Outline

In general, direct solutions to IFPP-I encountered in the literature construct complete^¶ maps from the class of piecewise monotonic maps $\Gamma(\mathcal{Q})$ (refer to Definition 2.1). The direct solution strategy involves the solution of either expression (2.2) or (2.4), which characterizes the evolution of distribution and density functions (respectively), under the unknown map $S \in \Gamma(\mathcal{Q})$. We outline the direct solution strategy using (2.2); equivalent expressions that involve density functions are provided towards the end of the section.

^¶ Each of the branches of a complete map stretches over the entire codomain of the map.

In the case of a complete piecewise monotonic map $S$ with $M$ partition intervals, (2.2) may be simplified to obtain

where $P(\mathcal{Q}) = \{q_1, q_2, \dots, q_{M+1}\}$ and $d_m$ is defined in (2.3). Now assume that $S$ is ergodic with unique ACI measure $P_*$ and corresponding distribution function $F_*$. Substituting $y = S_1(x)$ and setting $F_{n+1} = F_{n} = F_*$ leads to

Consider the case where $P_*(B) = 0 \Leftrightarrow \mu(B) = 0$, such that $F_*$ is monotonically increasing and continuous, and therefore invertible. Equation (4.5) may then be manipulated to obtain

This expression for the first branch $S_1$ of the map $S$ is dependent on the remaining branches of the map, as well as the partition points of $\mathcal{Q}$ and the constants $d_1, d_2, \dots, d_M$. We observe that each of the functions

appearing in (4.6) maps branch domain $Q_1$ onto $Q_m$. Considering the expression $S_m \circ u_m(x) = S_1(x)$, we recognize that each function $u_m$ defines an implicit relationship between branches $S_1$ and $S_m$. This is illustrated in Figure 7; we refer to these functions as inter-branch correspondence functions. Now, assume that the first branch $S_1$ is to be monotonically increasing, such that $d_1 = 0$. In the direct solution strategy we select the partition $\mathcal{Q}$ and specify each of the inter-branch correspondence functions $u_m$, thereby also specifying the value of $d_m$ for all $m > 1$ (i.e., the function $u_m$ implicitly determines whether the slope of branch $S_m$ is positive or negative). Equation (4.6) may then be solved for the first branch $S_1$; setting $F_* = F_P$ leads to

where $u_1(x) \triangleq x$ and $d_1 = 0$. The remaining branches are then given by

Inter-branch correspondence functions provide control over the structure of the map. These functions may, for example, be selected as to introduce symmetry between map branches. This is illustrated in the following example.

Example 4.2 (Direct solution). Consider the two-interval partition $\mathcal{Q} = \{Q_1, Q_2\}$, where $Q_1 = (0, \beta)$, $Q_2 = (\beta, 1)$ and $0 < \beta < 1$. We construct two sets of complete maps $S$ with branch functions $S_1 = S|_{Q_1}$ and $S_2 = S|_{Q_2}$, such that each map in the first set is symmetric around $x = \beta$, and each map in the second set is translationally symmetric around $x = \beta$. We require branch $S_1$ of each map to be monotonically increasing. Using piecewise linear maps, the expected branch correspondence of these symmetric and translationally symmetric maps is illustrated in Figures 8(c, f) respectively. In order to preserve symmetry, it is expected that the branch functions satisfy

and

We first consider the symmetric maps of set 1. From (4.9), the function $u_2(x) = S_2^{-1} \circ S_1(x)$ is derived as

Since $S_1$ and $S_2$ are monotonically increasing and decreasing, respectively, we have that $d_1 = 0$ and $d_2$ = 1. Observing that $F_P(0) = 0$ and $F_P(1) = 1$, we have, from (4.7),

and, from (4.8),

Substituting the distribution function of (4.2) into these expressions leads to the maps of Figures 8(d, e). These maps possess the invariant densities of Figures 8(a, b), which correspond to the parameter sets indicated in Figure 3.

Considering the translationally symmetric maps of set 2, we derive $u_2(x) = S_2^{-1} \circ S_1(x)$ from (4.10),

Since both branches of each map are monotonically increasing, we have that $d_1 = 0$ and $d_2 = 0$. It follows that

and

Substitution of (4.2) into these expressions leads to the maps plotted in Figures 8(g, h), with corresponding invariant densities plotted in Figures 8(a, b).

The example illustrates that the direct solution of IFPP-I, unlike the topological conjugation strategy, provides the opportunity to specify not only the domain of each branch function (through the choice of partition $\mathcal{Q}$), but also the functional relationship between the branches.

The direct solution strategy presented thus far involves the solution of (2.2) for the unknown map $S$. An alternative approach is the solution of (2.4), which characterizes the evolution of density functions under $S$. In this approach, the partition $\mathcal{Q}$ and inter-branch correspondence functions $u_m$ of the map are again selected. We assume that the first branch $S_1$ of the map is monotonically increasing. An expression for $S_1$ may then be obtained by solving the differential equation

where $u'_m \triangleq du_m/dx$ and $f_P$ is the prescribed invariant density function (as before, $d_1 = 0$ and $u_{1}(x) \triangleq x$). The remaining branches may then be derived from (4.8). Whereas this approach leads to the same map as obtained by solving (2.2), the differential equation of (4.11) may be solved numerically if expressions for the distribution function and its inverse are unavailable.

The topological conjugation solution strategy may be interpreted as a special case of the direct solution strategy. Let $\tilde{S} = h \circ S \circ h^{-1}$ denote a topological conjugate to $S$, and assume that $h: \Omega \to \Omega$ and its inverse are $C^r$ functions, where $r \geq 1$. Suppose that $S \in \Gamma(\mathcal{Q})$ is a complete map. Then $\tilde{S} \in \Gamma(\tilde{\mathcal{Q}})$ is also a complete map, where $\tilde{\mathcal{Q}} \triangleq \{\tilde{Q}_1, \tilde{Q}_2, \dots, \tilde{Q}_M\}$ and $\tilde{Q}_m \triangleq (h(q_m), h(q_{m+1}))$. We define the inter-branch correspondence functions $\tilde{u}_m: \tilde{Q}_1 \to \tilde{Q}_m$ of this map as

It can then be shown that

Hence, the inter-branch correspondence functions of $\tilde{S}$ are topological conjugates of the inter-branch correspondence functions of the underlying map $S$. The topological conjugation solution strategy is thus equivalent to the direct solution strategy with a particular set of inter-branch correspondence functions.

We conclude this section by observing that maps constructed using the direct solution strategy are not necessarily guaranteed to be ergodic, unlike maps obtained via topological conjugation. However, if the map $S \in \Gamma(\mathcal{Q})$ is complete, it is necessarily $\mathcal{Q}$-Markov. If $S$ then satisfies the remaining conditions of the Folklore theorem, it is ergodic and the invariant density is unique.

4.2.2.   Literature

Ershov and Malinetskii ^[5,16] solved IFPP-I directly for unimodal maps with an arbitrary invariant density function $f_P > 0$. The authors derived an expression for $S$ that contains the complementary distribution function corresponding to the prescribed density. It was proved that the map is the unique unimodal solution for the prescribed inter-branch correspondence function and invariant density. However, the authors do not state conditions under which the map is ergodic.

Koga ^[52] solved IFPP-I directly for two-branch maps that are either symmetric or translationally symmetric (with inter-branch correspondence functions $u_2(x) = 1 - x$ and $u_2(x) = x + 1/2$, respectively). The maps were derived by solving

and

for the symmetric and translationally symmetric maps, respectively. Expressions were derived for maps with sinusoidal and polynomial invariant densities, and maps with invariant density that corresponds to the truncated Gaussian distribution were obtained numerically. It was verified that all maps are ergodic, which implies that the invariant density of each map is unique.

Diakonos and Schmelcher ^[29] solved IFPP-I directly for symmetric unimodal maps with the symmetric beta density as invariant density (this is commonly referred to as the doubly symmetric case in the literature). The authors derived an implicit defining equation for the maps; this expression is identical to that obtained using the technique of Ershov and Malinetskii ^[5,16] with an inter-branch correspondence function $u_2(x) = 1 - x$. Hence, these are the unique unimodal and symmetric maps with the symmetric beta invariant density. The authors investigated the analytical properties of each map in the region around its maximum, as well as the bifurcation routes of the maps.

Pingel et al. ^[30] generalized the work of Diakonos and Schmelcher ^[29] to asymmetric unimodal maps by defining an explicit inter-branch correspondence function. These maps are equivalent to those obtained using the technique from ^[5,16], and are therefore the unique unimodal maps with the prescribed invariant density and branch correspondence. The technique was applied to construct maps with invariant density functions corresponding to the beta distribution with arbitrary choice of parameters. The analytical and dynamical properties of the maps were characterized, and their Lyapunov exponents and autocorrelation functions were investigated.

In a series of papers, Huang used the direct solution strategy to design unimodal maps with branches that have a reciprocal relationship ^[53], unimodal maps with closed functional forms ^[54] and complete maps with more than two branches ^[55,56]. Venegeroles ^[57] used the direct solution strategy to construct maps with branches that are related by explicit inter-branch correspondence functions. More recently, Boyarsky et al. ^[58] considered approximate solutions to IFPP-I for the case where the map $S$ is restricted to a specific region of the codomain, as defined by 'lower' and 'upper' maps $S_L, S_U: \Omega \to \Omega$ such that $S_L(x) \leq S(x) \leq S_U(x)$ for all $x \in \Omega$. An algorithm was provided for directly solving an expression containing the explicit form of the corresponding FPO for a sequence of piecewise defined maps, thereby approximating a prescribed invariant density. These maps are appropriate for situations where the trajectories of the system should not evolve in a free and unrestricted manner over time, such as the modeling of gross domestic product growth.

4.3.   Matrix solution strategy

4.3.1.   Outline

Matrix solutions to IFPP-I construct ergodic and piecewise linear $\mathcal{Q}$-Markov and $\mathcal{R}(\mathcal{Q})$-semi-Markov maps (refer to section 2.2.1 and Definitions 2.2 and 2.3). These maps possess invariant density functions that are piecewise constant over the partition $\mathcal{Q}$. Hence, we can only approximate a prescribed invariant density function $f_P$ that is not piecewise constant when constructing these maps. However, these matrix solutions provide considerable freedom to select the structural characteristics of the map (i.e., the number of branches, the partitions of the map domain and the image of each branch), thereby allowing us to construct a family of distinct maps that approximate the same prescribed invariant density. This capability is relevant when solving more general formulations of the IFPP, as control over the map's structure affords us the opportunity to select the characteristics of the map's power spectrum ^[23].

We proceed by describing a process that several matrix solutions to IFPP-I follow to construct piecewise linear $\mathcal{R}(\mathcal{Q})$-semi-Markov maps. This process consists of three steps, namely (i) the prescription of a density function $\hat{\mathbf{f}}_P$ that is piecewise constant over a selected partition $\mathcal{Q}$, such that $\hat{\mathbf{f}}_P$ approximates the required invariant density $f_P$ and has elements strictly greater than zero, (ii) the generation of a matrix $\mathbf{P}$ with the characteristics required of an FPM, in addition to the appropriate left and right Perron eigenvectors, and (iii) the subsequent construction of a map $S$ with FPM $\mathbf{P}_S$ equal to $\mathbf{P}$. The left Perron eigenvector of the FPM belonging to an ergodic $\mathcal{R}(\mathcal{Q})$-semi-Markov map has elements that coincide with the lengths of the intervals in partition $\mathcal{Q}$, whereas the right Perron eigenvector coincides with $\mathbf{f}_*$, the map's invariant density. Hence, the matrix $\mathbf{P}$ has to be constructed with left and right Perron eigenvectors that are consistent with the approximation $\hat{\mathbf{f}}_P$. The construction of a map $S$ with FPM equal to $\mathbf{P}$ is achieved by using (2.5), which relates the slopes of the linear map branches to the entries of the FPM.

The generation of matrix $\mathbf{P}$ in step (ii) above is first considered in the case of a uniform partition $\mathcal{Q}$ of the unit interval; generalization to a nonuniform partition is considered thereafter. In the uniform case, the FPM $\mathbf{P}_S$ of a piecewise expanding and aperiodic (and therefore ergodic) $\mathcal{R}(\mathcal{Q})$-semi-Markov map is necessarily column stochastic and primitive. We may then design matrix $\mathbf{P}$ to be column stochastic and primitive, and to possess the prescribed right Perron eigenvector. This problem has been considered in the literature and different approaches to solving it have been proposed (see, for instance, ^[18,50,59])^||. In general, there exist multiple stochastic matrices with the same right Perron eigenvector, and any of the different techniques for constructing these matrices may be applied in the context of solving IFPP-I.

^|| In contrast to the conventional linear inverse problem, where the matrix equation $\mathbf{y} = \mathbf{P}\mathbf{x}$ is to be solved for unknown $\mathbf{x}$, the problem considered here does not involve matrix inversion. Rather, the goal is to construct a stochastic matrix $\mathbf{P}$ that satisfies $(\mathbf{P}-\mathbf{I})\mathbf{x} = \mathbf{0}$ for a given $\mathbf{x} \neq \mathbf{0}$.

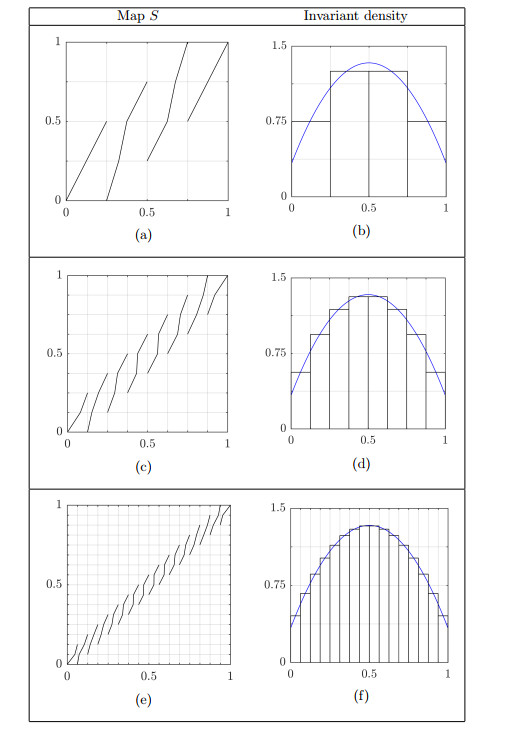
In the following example, we illustrate the matrix solution of IFPP-I by constructing ergodic and piecewise linear $\mathcal{R}(\mathcal{Q})$-semi-Markov maps over a uniform partition $\mathcal{Q}$. The invariant densities of the maps are selected to approximate the quadratic polynomial densities defined in (4.1) and Figure 3.

Example 4.3 (Matrix solution). Let $\mathcal{Q} = \{Q_1, Q_2, \dots Q_M\}$ denote the uniform partition with $M$ intervals, such that $Q_m = (q_m, q_{m+1})$, and $q_m = (m-1)/M$ for $m = 1, 2, \dots, M+1$. The piecewise constant invariant density prescribed for $S$, denoted by $\hat{\mathbf{f}}_{P} = [\hat{f}_{P, 1}, \hat{f}_{P, 2}, \dots, \hat{f}_{P, M}]^T$, is chosen to approximate $f_P$. The elements $\hat{f}_{P, m}$ are selected as

thereby ensuring that the distributions corresponding to $\hat{\mathbf{f}}_{P}$ and $f_{P}$ assign equal probability to each interval $Q_m$.

Using the technique proposed by Góra and Boyarsky ^[18], we now derive a column stochastic matrix $\mathbf{P}$ with right Perron eigenvector equal to $\hat{\mathbf{f}}_P$. This technique produces a three-band stochastic matrix, which is a square stochastic matrix having nonzero elements only in the main diagonal and the diagonals immediately above and below the main diagonal. We first define $\mathbf{g} = [g_1, g_2, \dots g_M]^T$ as $\mathbf{g} = [2 \max\{f_{P, m}\}]^{-1}\hat{\mathbf{f}}_P$. The nonzero entries in the first and last columns of the matrix $\mathbf{P} = [p_{k, m}]$ are then given by

The remaining matrix entries are given by

where $m = 2, 3, \dots, M-1$. Having generated the matrix $\mathbf{P}$, we construct an $\mathcal{R}(\mathcal{Q})$-semi-Markov map $S$ with FPM $\mathbf{P}_S$ equal to $\mathbf{P}$. This involves the selection of a partition $\mathcal{R}^{(m)} = \{R_1^{(m)}, R_2^{(m)}, \dots, R_{c(m)}^{(m)}\}$ for each interval $Q_m$ (refer to Figure 2 for a guiding example). In general, there exist multiple valid partitions of each $Q_m$. Equation (2.5) implies that each nonzero entry in column $m$ of the FPM requires at least one subinterval in $\mathcal{R}^{(m)}$ to be mapped to the corresponding interval in $\mathcal{Q}$ (specifically, if the nonzero entry is the $k$th element of column $m$, the subinterval is mapped to interval $Q_k$). Each zero entry in column $m$ requires that no subinterval in $\mathcal{R}^{(m)}$ must be mapped to the corresponding interval in $\mathcal{Q}$. We choose $\mathcal{R}^{(m)}$ so that each consecutive subinterval in this partition is mapped to a unique interval $Q_k$, but in the same order as the corresponding nonzero entries appear in column $m$ of the FPM. Let $v_{1, m} < v_{2, m} < \dots < v_{w(m), m}$ denote the indices of the $w(m)$ nonzero entries in column $m$ of $\mathbf{P}$. We select $c(m) = w(m)$ and $T(k, m) \triangleq \{j:S(R_{j}^{(m)}) = Q_k\}$ as

for $k, m = 1, 2, \dots, M$. Let the branch functions $S_{j, m}(x) \triangleq S|_{R_{j}^{(m)}}$ be given by $S_{j, m}(x) = \Delta_{j, m}x + b_{j, m}$. Equation (2.5) then implies that $|\Delta_{j, m}|^{-1} = p_{i, m}$, where $i = v_{j, m}$; we select the branch slopes as $\Delta_{j, m} = p_{i, m}^{-1}$. Finally, we derive the $y$-intercept $b_{j, m}$ of each branch. Since

where $R_{j}^{(m)} \triangleq (r_{j}^{(m)}, r_{j+1}^{(m)})$, we find that

Figure 9 contains plots of semi-Markov maps that were constructed with invariant densities that approximate the quadratic polynomial density $f_P$ of (4.1) with parameters $y_0 = y_1 = 1/3$ (this density is plotted in blue). Three maps with uniform partitions of 4, 8 and 16 intervals were constructed. These maps are plotted in Figures 9(a, c, e), respectively. The piecewise constant invariant density function of each map is plotted in black in Figures 9(b, d, f). The three-band property of the FPM is reflected by the structure of each map, where branches are concentrated around the line $y = x$. This observation reveals that the approach towards constructing matrix $\mathbf{P}$ has a direct impact on the structure of the resulting map. The plots also reveal that a finer partition produces a more accurate fit to the prescribed invariant density function.

To illustrate how the choice of invariant density affects the structure of the map, the matrix solution strategy was used to construct maps with invariant densities that approximate the quadratic polynomial invariant density functions $f_P$ of Figure 3. The resulting maps are plotted in Figures 10(c) to 10(h). These maps were designed with a uniform partition of eight intervals, and possess the invariant densities plotted in Figures 10(a, b).

We conclude this section by considering the construction of $\tilde{\mathcal{R}}(\tilde{\mathcal{Q}})$-semi-Markov maps $\tilde{S}$ with invariant density $\mathbf{f}_*$ that is equal to some prescribed piecewise constant density $\hat{\mathbf{f}}_{P}$ defined over a nonuniform partition $\tilde{\mathcal{Q}}$. The steps for solving this problem are similar to the solution steps in the case of a uniform partition. In the nonuniform case, the map $\tilde{S}$ is also designed such that its FPM $\mathbf{P}_{\tilde{S}}$ is equal to a matrix $\tilde{\mathbf{P}}$, which is similar to a column stochastic matrix. The matrix $\tilde{\mathbf{P}}$ is selected such that its left and right Perron eigenvectors are consistent with the required invariant density $\hat{\mathbf{f}}_P$ over the nonuniform partition. However, $\tilde{\mathbf{P}}$ is obtained in a different manner than the uniform case. Consider an approach whereby the nonuniform partition is obtained by stretching or contracting the corresponding intervals of a uniform partition. This is achieved by the similarity transformation

where $\mathbf{P}_{S}$ is the column stochastic FPM of an ergodic $\mathcal{R}(\mathcal{Q})$-semi-Markov map $S$ with uniform partition $\mathcal{Q}$, and $\mathbf{D}$ is a diagonal matrix with positive entries along the diagonal that determine the degree of stretching or contraction of each interval. Since similar matrices share the same characteristic polynomial, $\tilde{\mathbf{P}}$ and $\mathbf{P}_{S}$ share the same eigenvalues. Let the left and right Perron eigenvectors of $\mathbf{P}_S$ be denoted by $\mathbf{v}_1$ and $\mathbf{w}_1$, and the same eigenvectors of $\tilde{\mathbf{P}}$ by $\tilde{\mathbf{v}}_1$ and $\tilde{\mathbf{w}}_1$. It follows that

and

Recall that $\mathbf{v}_1 = [1, 1, \dots, 1]^T$. Since the left Perron eigenvector $\tilde{\mathbf{v}}_1$ of $\tilde{\mathbf{P}}$ must be a nonzero scalar multiple of $\mathbf{q}$, where $\mathbf{q}$ is a column vector with entries equal to the lengths of the intervals in the nonuniform partition $\tilde{\mathcal{Q}}$, we have from (4.13) that the diagonal of $\mathbf{D}$ must equal $\mathbf{q}$. In order to ensure that $\tilde{\mathbf{w}}_1 = \hat{\mathbf{f}}_P$, we then consider (4.14) and require that $\mathbf{w}_1 = \mathbf{D}\hat{\mathbf{f}}_P$. We construct a column stochastic matrix $\mathbf{P}_{S}$ with right Perron eigenvector $\mathbf{w}_1$ using any of the proposed techniques, and then compute $\tilde{\mathbf{P}}$ from (4.12). The map $\tilde{S}$ is then designed with FPM $\mathbf{P}_{\tilde{S}}$ equal to $\tilde{\mathbf{P}}$ using the relationship between the slopes of the map branches and the entries of the FPM, as set out in (2.5); further details are provided in ^[18].

4.3.2.   Literature

Friedman and Boyarsky ^[17] proposed a matrix technique for constructing ergodic maps with invariant densities from a class of piecewise constant density functions with relative minima equal to zero. The technique uses methods from the domain of graph theory. However, due to the restrictiveness of the class of achievable invariant densities, this technique was found to be of limited practicality.

Consider any density function $f_P$ that is piecewise constant over a partition of a compact real interval. Góra and Boyarsky ^[18] proved that there exists at least one piecewise linear and expanding semi-Markov map with an invariant density equal to $f_P$. The proof is constructive and therefore presents a solution to IFPP-I. This solution^** requires the generation of a three-band stochastic matrix $\mathbf{P}$ and the construction of a piecewise linear semi-Markov map on a uniform partition such that its FPM matches $\mathbf{P}$. The solution was generalized to piecewise constant invariant densities on nonuniform partitions using topological conjugation. Recently, this solution was generalized further by introducing $K$-band matrices, where $K > 3$ ^[50].

^** This solution was demonstrated in example 3.

Rogers et al. ^[60] proposed a matrix solution to IFPP-I that involves the construction of semi-Markov ergodic maps with piecewise constant invariant densities over a uniform partition. The proposed solution uses an $M \times M$ FPM with a predefined structure that is fully specified by a set of $2M$ real valued parameters. This structure leads to a simplified expression for the right Perron eigenvector of the FPM, which coincides with the invariant density of the map. Rogers ^[61] demonstrated how a suitable choice of parameters allows for the selection of an arbitrary right Perron eigenvector and piecewise constant invariant density, and generalized the solution to nonuniform partitions. The correlation properties of trajectories generated by the resulting maps were investigated numerically in ^[62]. The solution was also extended to randomly switched chaotic maps and chaotic maps of higher dimensions. Convergence properties of Rogers' solution to IFPP-I ^[60], together with further examples of ergodic maps that were constructed using this solution, were provided in ^[63].

5.   Brief overview of recent developments

In this section we present a brief excursion into the more recent developments. Due to significant additional analytical machinery of a rather sophisticated nature required, as well as space limitations, a full discussion would require an independent survey in its own right. Hence, we forgo a detailed review and only provide a summary of several key contributions.

McDonald and van Wyk ^[21] addressed the problem of constructing an ergodic map with a prescribed invariant density and a multimodal power spectrum that has prescribed mode center frequencies and bandwidths. The authors proposed a technique for generating a column stochastic matrix $\mathbf{P}$ that involves recursive Markov state disaggregation ^[59]. Starting with an elementary one-state Markov chain, this algorithm recursively divides (or disaggregates) each state of the Markov chain into a pair of equiprobable states, thereby constructing a Markov chain with an arbitrary number of states. The state transition matrix of the final Markov chain is then selected as the matrix $\mathbf{P}$. Using this algorithm, the authors generated several column stochastic matrices with distinct eigenvalue spectra^†† and constructed semi-Markov maps with matching FPMs. It was shown that these maps possess time correlation functions with distinct characteristics and different rates of decay. The authors also constructed topological conjugates of these maps with invariant densities that are piecewise constant approximations of the beta density function.

^†† It can be shown that each eigenvalue belonging to the (non-defective) second-order FPM of a semi-Markov map corresponds to a particular mode of the power spectrum ^[64]. More specifically, the modulus of the eigenvalue is inversely proportional to the mode's bandwidth, and its argument coincides with the center frequency of the mode.

McDonald and van Wyk ^[22] constructed ergodic semi-Markov maps with the uniform invariant density and power spectra consisting of five modes. These maps possess $3 \times 3$ column stochastic first-order FPMs with a predefined expression formulated in terms of the eigenvalue spectrum of the matrix. It was proved that any of the possible column stochastic matrix eigenvalue spectra may be chosen for these matrices. It was also shown that the bandwidths and center frequencies of two power spectrum modes may be prescribed through selection of the FPM eigenvalue spectrum.

More recently, McDonald and van Wyk ^[23] introduced a new collection of semi-Markov maps that is referred to as the family of hat maps. Following a matrix approach, the authors constructed piecewise linear hat maps with piecewise constant invariant densities and multimodal power spectra. It was demonstrated that the structure of hat maps affords the opportunity to select the bandwidth and center frequency of each mode in the map's power spectrum. A nonlinear branch transformation that allows for the construction of piecewise nonlinear hat maps with prescribed invariant densities was proposed. This transformation was used to construct maps with invariant density equal to the beta density function and two-mode power spectra with prescribed mode center frequencies and bandwidths.

Nie and Coca ^[24,25] proposed a technique for modeling the unknown evolution rule of a one-dimensional dynamical system from causal sequences of state density functions generated by the system. This technique assumes that the unknown map $S$ is $\mathcal{R}(\mathcal{Q})$-semi-Markov, and involves estimation of the unknown partition $\mathcal{Q}$ from the invariant density function of $S$. A piecewise constant approximation of each state density function is then constructed over this partition. After substituting the vectors corresponding to these density functions into the matrix equation for density evolution, the equation is solved for the matrix representing the unknown map's FPO (i.e., the FPM of $S$). The ergodic map is then reconstructed in the same manner as the third step of the matrix solution strategy for IFPP-I (see also ^[18]). The authors also extended the technique by constructing semi-Markov approximations of unknown ergodic maps that are continuous and asymptotically stable from sequences of state density functions. This was achieved using a novel algorithm for deciding whether each branch of the map is monotonically increasing or decreasing (recall that the entries of the FPM are nonnegative; hence, it cannot be deduced whether the branch corresponding to each entry has a positive or negative slope from the FPM alone). The authors provided examples that demonstrate the technique's ability to reconstruct unknown piecewise linear semi-Markov maps, as well as the logistic map $S(x) = 4x(1-x)$, from sequences of density functions.

Nie and Coca ^[26] generalized the technique proposed in ^[25] to approximate the evolution rule of an unknown stochastically perturbed dynamical system, which is of practical relevance when constructing models from measurements that are corrupted by noise. Under the assumption that the unknown map is semi-Markov, the authors formulated a matrix representation of the system's transfer operator in terms of the map's FPM. An algorithm was proposed for estimating this FPM from sequences of causal density functions generated by the stochastically perturbed system, where it is assumed that the density function of the perturbation is known. The unknown map is reconstructed from the estimate of the FPM as before. The technique was also extended to approximate continuous nonlinear maps. Examples were presented that demonstrate the improved accuracy of the technique when used to approximate an unknown semi-Markov map and the logistic map in higher noise levels, as compared to the original technique presented in ^[25].

Nie et al. ^[27] considered the problem of constructing a semi-Markov map that approximates the unknown map of a one-dimensional dynamical system that is driven by an external control input and subjected to an additive stochastic perturbation. Following a similar approach as in ^[26], the authors formulated a matrix representation of the system's transfer operator in terms of the FPM corresponding to the semi-Markov map. An algorithm was proposed for estimating the latter matrix from sequences of density functions generated by the system (here it is assumed that the density functions of the noise and control inputs are both known a priori). The map is constructed from the FPM as before. It is noteworthy that this solution to the IFPP presents a new approach to solving the control problem for stochastically perturbed autonomous systems, where the goal is to determine the optimal input density function such that the dynamical system has the desired equilibrium distribution.

Nie et al. ^[28] proposed a technique for inferring the evolution rule of an unknown one-dimensional dynamical system driven by an external stochastic input from stationary densities generated by the system. In this scenario the density function of the input is varied, and the stationary density of the system is observed in each case. Conditions under which each input density leads to a unique stationary density were stated. The proposed technique constructs a matrix approximation of the unknown map's FPO, and generates a semi-Markov map with FPM equal to this matrix. An example was presented wherein a semi-Markov approximation of the logistic map was obtained from stationary density functions generated by the map.

6.   Conclusions and future work

In this paper we surveyed the inverse Frobenius-Perron problem, its formulations, as well as three solution strategies to the original problem formulation (IFPP-I). Several examples were provided to illustrate the techniques, with the aim of promoting their practical application.

In the topological conjugation strategy, IFPP-I is solved by transforming an existing ergodic map with known invariant density to an ergodic map with the prescribed invariant density. We proved that this strategy is a special case of the direct solution strategy. Due to the one-to-one nature of the mapping between the trajectories of the original map and those of its topological conjugates, ergodicity can be guaranteed when solving IFPP-I. However, this strategy provides less freedom to select the structure of the map, as compared to the other solution strategies.

The direct solution strategy produces complete maps that are unique for a prescribed invariant density, branch structure and set of inter-branch correspondence functions. Unlike the topological conjugation solution strategy, ergodicity of the direct solution is not necessarily guaranteed; further investigation of this topic may lead to relaxed criteria for ergodicity. Furthermore, the direct solution strategy has, to the best of our knowledge, not yet been generalized to the case of incomplete maps. We anticipate that such a generalization would prove useful when solving more general formulations of the IFPP, where the power spectrum characteristics of the map are prescribed. Another topic for future work in this context is the uniform approximation of singular maps by locally "sterile" expansive maps ^[65].

The matrix solution strategy has the limitation of only producing maps with piecewise constant invariant densities, which can only approximate nonuniform and continuous density functions. However, this strategy provides more freedom to select the structure of the map, and may be used to generate multiple distinct maps with the same invariant density. This characteristic is of interest when solving the more general problem formulations. Whereas the matrix solution strategy demonstrated here only generates maps with linear branch functions, it was recently shown that the generalization of this solution to piecewise nonlinear semi-Markov maps leads to a broader class of attainable invariant density functions. This allows for an exact match to a prescribed invariant density while retaining some control over the structure of the map and thereby its power spectrum characteristics.

Acknowledgments

This work was jointly supported by the Key-Area Research and Development Program of Guangdong Province, China, under Grant 2019B010157002, the Carl and Emily Fuchs Foundation's Chair in Systems and Control Engineering, University of the Witwatersrand, Johannesburg, South Africa, the Hong Kong Research Grants Council through GRF under Grant CityU11206320, and by the Innovation and Technology Fund of the Hong Kong Special Administrative Region, China, under Grant ITS/359/17.

Conflict of interest

All authors declare no conflicts of interest in this paper.