A study on a line congruence as surface in the space of lines

1.   Introduction

Differential line geometry examines the set of lines in space with 3-dimension. The ambient space can be an Euclidean or a non-Euclidean space. It is one of the interesting subdivision of differential geometry since it is directly connected with the spatial motion (kinematics) and get therefore a lot of application in mechanism design ^{[1,2,3,4,5,6,7,8,9]}.

A line congurence is a two-parameter set of lines in three-dimensional space- is a classical part of differential geometry, whose origins can be traced to Kummer in his memoir; Allgemeine Theorie der Gradlinigen Strahen system ^[1]. The normal vector field of a surface could be given as an example of line congruence. In this way the line congruence formed by the normal vector field of the surface constructs a special class, which is called normal line congruence. However, the line congruence does not usually need to consist only of normal vector field. The lines of the line congruence which pass through a curve on the surface form a one-parameter family of lines in the space or ruled surface (parameter ruled surface). Recently, line congruence has become relevant for practical applications (See for instance ^{[2,3,4,5,6,7]}).

As it is known, the most analytical tool in the study of three-dimensional kinematics and differential line geometry is based upon the so-called E. Study's map: The set of all oriented lines in Euclidean 3-space $\mathbb{E} {{}^3}$ is in one-to-one correspondence with set of points of the dual unit sphere in the dual 3-space $\mathbb{D} {{}^3}$. It allows a complete generalization for the spherical point geometry to the spatial line geometry by means of dual-number extension, i.e. replacing all ordinary quantities by the corresponding dual-number quantities. Hence, the ruled surfaces and line congruence obtained by the motion of a line, depending on one and two parameters, respectively. There exists a vast literature on the subject including several monographs, such as ^{[6,8,9,10,11]}.

This work develops the kinematic-geometry for line congruence in the space of lines by using the analogy with theory of surfaces. Then the well known formulae of J. Liouville, Hamilton, and Mannheim of surfaces theory are proved for the line congruence. Moreover, a new geometrical interpretation of J. Liouville formula has been defined for a given closed ruled surface in the line congruence. The Plücker conoid associated with the line congruence has been derived and it is shown that the principal axes of it are located at its center and at right angles. Finally, an example of application is investigated and explained in detail.

2.   Preliminaries

In this section we list some notions, formulas of dual numbers and dual vectors (See for instance ^{[1,2,3,4,5,6]}). Therefore we start with recalling the use of appropriate line coordinates: An oriented line $L$ in the Euclidean 3-space $\mathbb{E}^{3}$ can be determined by a point $\mathbf{p} \in L$ and a normalized direction vector $\mathbf{x}$ of $L$, i.e. $\left\Vert \mathbf{x}\right\Vert = 1$. To obtain components for $L$, one forms the moment vector

with respect to the origin point in $\mathbb{E}^{3}$. If $\mathbf{p}$ is substituted by any point

on $L,$ then Eq (2.1) implies that $\mathbf{x}^{\ast }$ is independent of $\mathbf{p}$ on $L$. The two vectors $\mathbf{x}$ and $\mathbf{x}^{\ast }$ are not independent of one another; they satisfy the following relationships:

The six components $x_{i}, \; x_{i}^{\ast }(i = 1, 2, 3)$ of $\mathbf{x}$ and $\mathbf{x}^{\ast }$are called the normalized Plűcker coordinates of the line $L$. Hence the two vectors $\mathbf{x}$ and $\mathbf{x}^{\ast }$ determine the oriented line $L.$

In line geometry, from a kinematic point of view, a line congruence (congruence for shortness) is a two-parameter set of lines in $\mathbb{E} ^{3}$ generated by a straight line $L$ moving along a surface. The various positions of the generating lines are called the rulings or generators of the congruence. This congruence holds a parameterization as form

Here $\mathbf{y} = \mathbf{y}(u_{1}, u_{2})$ is called the director surface, $\mathbf{r} = \mathbf{r}(u_{1}, u_{2})$ is the unit vector giving the direction of generating line of the congruence, $u_{1},$ $u_{2}$ are the motion parameters, and $v$ is the parameter of its points indicating the singed distance of the corresponding point on $\mathbf{y} = \mathbf{y}(u_{1}, u_{2})$. The equations

define a ruled surface belonging to the congruence. It is a developable if and only if the determinate

Ruled surfaces (such as cylinders and cones) contain rulings where the tangent plane touches the surface along the entire line. Such rulings are called torsal lines, to distinguish them from the common case of the non-torsal generators ^[6,11,12,13]:

$\bullet$ Ruled surfaces with exclusively torsal generators are called developable surfaces;

$\bullet$ Ruled surfaces consisting largely of non-torsal generators are called skew ruled surfaces (or warped ruled surfaces);

$\bullet$ Cylinders, cones, and ruled surfaces that consist of tangents of a spatial curve are developable surfaces.

Definition 1. The singular surface points of a torsal generator is called its cuspidal point, and the tangent plane in its other direction is called torsal plane.

2.1.   E. Study's map

The set of dual numbers is

This set is a commutative ring under addition and multiplication. This set cannot be a field under these operations, because $0+\varepsilon x^{\ast }$ has no multiplication inverse in $\mathbb{D}$. But this ring has a unit element according to multiplication. A dual number $X = x+\varepsilon x^{\ast }$, is called proper if $x\neq 0.$ An example of dual number is the dual angle subtended by two skew lines in the Euclidean 3-space $\mathbb{E}^{3}$ and defined as $\Theta = \vartheta +\varepsilon \vartheta ^{\ast }$ in which $\vartheta$ and $\vartheta ^{\ast }$ are, respectively, the projected angle and the minimal distance between the two lines.

For all pairs $\left(\mathbf{x}, \mathbf{x}^{\ast }\right) \in \mathbb{E} ^{3}\times \mathbb{E}^{3}$ the set

together with the scalar product

forms the dual 3-space $\mathbb{D}^{3}.\;$Thereby a point $\mathbf{X} = (X_{1}, X_{2}, X_{3})^{t}$ has dual coordinates $X_{i} = (x_{i}+\varepsilon x_{i}^{\ast })\in \mathbb{D}.$ The norm is defined by

In the dual 3-space $\mathbb{D}^{3}$ the dual unit sphere is defined by

Definition of dual unit sphere gives us that all points $\mathbf{X}$ of $\mathbb{K}$ must satisfy two equations

Via this we have the following map (E. Study's map): The set of all oriented lines in the Euclidean 3-space $\mathbb{E}^{3}$ is in one-to-one correspondence with the set of points of dual unit sphere in the dual 3-space $\mathbb{D}^{3}$. By using this correspondence, one can derive the properties of the spatial motion of a line. Hence, the geometry of ruled surface is represented by the geometry of curves on the dual unit sphere in $\mathbb{D}^{3}$. Therefore, the dual curve and ruled surfaces are synonymous in this paper.

2.2.   Line congruence as a dual region on $\mathbb{K}$

The E. Study's map admits us to revision Eq (2.4) using the dual vector function as

where $\mathbf{r}^{\ast }$ is the moment of $\mathbf{r}$ about the origin in $\mathbb{E}^{3}$. Since the spherical image $\mathbf{r}(u_{1}, u_{2})$ is a unit vector, then the dual vector $\mathbf{R}(u_{1}, u_{2})$ also has unit magnitude as is seen from the computations:

Thus the line congruence fills a domain on dual unit sphere $\mathbb{K}$ in $\mathbb{D}^{3}$. Hence, the line congruence can be viewed as a two-dimensional surface in $\mathbb{D}^{3}$-space. It follows that there are resemblances between theory of surface and theory of line congruence.

A relationship such as $f(u_{1}, u_{2}) = 0$ between the parameters $u_{1},$ $u_{2}$ reduces the congruence to a one-parameter set of lines (a ruled surface) in the congruence $\mathbf{R}(u_{1}, u_{2})$. The equations $u_{2} = c_{2}$ and $\ u_{1} = c_{1}($real constants) determines parameter ruled surfaces given by the parameter dual curves $\mathbf{R} = \mathbf{R} (u_{1}, c_{2})$ and $\mathbf{R} = \mathbf{R}(c_{1}, u_{2})$, respectively.

Definition 2. A line congruence is torsal, if the ruled surfaces defined by $u_{1} =$const. are developable, and so are the ones defined by $u_{2} =$const.

If $L$ any function, scalar or vector, defined for the line congruence, we shall denote $L_{u_{1}}$, and $L_{u_{2}}$ by $\partial L/\partial u_{1},$ and $\partial L/\partial u_{2}$, respectively. Thus $\mathbf{R}_{u_{1}}$ is a dual tangent vector in direction which $u_{1}$ alone varies, similarly for $\mathbf{R}_{u_{2}}$. Therefore,

Thus, we arrive by means of the real and dual parts of Eq (2.14), at

Now we consider two neighboring dual points, with position vectors $\mathbf{R }$ and $\mathbf{R+}d\mathbf{R}$, from $(u_{1}, u_{2})$ to $(u_{1}+du_{1}, u_{2}+du_{2})$, respectively. Then

Since the two dual points are adjacent points on a dual curve passing through them, the dual arc length $dS( = ds+\varepsilon ds^{\ast })$ is

or finally,

By separating the real and dual parts of this equation, respectively, we get

and

The forms $I$ and $II$ are called the first and second fundamental forms of the line congruence, respectively. The distribution parameter of a ruled surface belong to the congruence is given by ^[10,11]

A ruled surface belong to the congruence for which

is a developable surface. If we let $\eta = du_{1}/du_{2}$, we can write

For developable surfaces of the congruence, we equate the coefficients of the Eq (2.22) to zero identically, and we can write

2.3.   Blaschke moving frames

Through every line in the congruence there pass two principal surfaces whose images on the dual unit sphere we take as parameter curves. For this special system we assume that $u_{1}$, and $u_{2}$ dual curves of $\mathbf{R} (u_{1}, u_{2})$ are principal ruled surfaces, i.e., the elements $f$ and $f^{\ast }$ of the first and second fundamental forms vanish identically $(f = f^{\ast } = 0)$. So, according to Eq (2.17), the dual arc length of the dual curves $u_{2} = c_{2}$(real const.), and $u_{1} = c_{1}$(real const.), respectively are $dS_{1} = ds_{1}+\varepsilon ds_{1}^{\ast } = \sqrt{E}du_{1}$ and $dS_{2} = ds_{2}+\varepsilon ds_{2}^{\ast } = \sqrt{G}du_{2}$.

In order to examine the geometrical properties of the congruence, we set up a moving frame coincident with the point on the sphere. If we label the point on the sphere, the generator as $\mathbf{R}(u_{1}, u_{2})$, then the Blaschke frame can be set up ^[10,11,15]

which are invariants vector functions on the congruence $Q$; we fix det$(\mathbf{R}$, $\mathbf{R}_{12}\mathbf{, R}_{22}) = +1$ and consequently

The extreme values of the distribution parameter, corresponding to the principal surfaces $\mathbf{R}(u_{1}, c_{2})$, and $\mathbf{R}(c_{1}, u_{2})$, respectively, are obtained by

According to the elements of spherical kinematics, the motion of the frame $\{\mathbf{O; }$ $\mathbf{R},$ $\mathbf{R}_{12}\mathbf{, }$ $\mathbf{R}_{22}\}$ at any instant is a rotation around the Darboux vector of this frame. Hence, by means of the derivatives with respect to the dual arc-length parameter of the dual curves $u_{2} = c_{2}$ with tangent $\mathbf{R}_{12}$, the derivative formula is ^[10,15]

where

$\Sigma _{1} = \sigma _{1}+\varepsilon \sigma _{1}^{\ast } = -\frac{E_{u_{2}}}{2E \sqrt{G}}$ is the geodesic curvature of the dual curves $\mathbf{R} (u_{1}, c_{2})$. Similarly, the derivative formula of the Blaschke frame of the dual curves $\mathbf{R}(c_{1}, u_{2})$, with tangent $\mathbf{R}_{22}$ is

where

$\Sigma _{2} = \sigma _{2}+\varepsilon \sigma _{2}^{\ast } = \frac{G_{u_{1}}}{2G \sqrt{E}}$ has the same meaning as in Eq (2.27). In other words, dual geodesic curvatures of the dual curves $\mathbf{R}(u_{1}, c_{2})$, and $\mathbf{R}(c_{1}, u_{2})$, respectively, are

3.   Main results

Consider $u_{i}=u_{i}(t),~(i=1,2)$ as functions of real parameter $t\in \mathbb{R}$. Then $\mathbf{R} = \mathbf{R}(u_{1}(t), u_{2}(t))\;$represents a ruled surface in the congruence $Q$. The dual vector $\mathbf{R}_{t} = (\partial \mathbf{R}/\partial t)\;$is tangent to this dual curve;

If $< \mathbf{R}_{t}, \mathbf{R}_{t} > \neq 0$, then we have a dual unit vector

where $P = p+\varepsilon p^{\ast } = \left\Vert \mathbf{R}_{u_{1}}\frac{du_{1}}{ dt}+\mathbf{R}_{u_{2}}\frac{du_{2}}{dt}\right\Vert = \sqrt{EG}$. Hence, the dual arc length of the dual curve $\mathbf{R} = \mathbf{R}(u_{1}(t), u_{2}(t))$ is given by

In order to research the properties of $\mathbf{R} = \mathbf{R} (u_{1}(t), u_{2}(t))$, the Blaschke frame relative to $\mathbf{R}(t)$ will be defined as the frame of which this line and the central normal $\mathbf{R} _{2}$ to the ruled surface at the central point of $\mathbf{R}$ are two edges. The third edge $\mathbf{R}_{3}$ is the central tangent to the ruled surface $\mathbf{R}(t)$. Likwise, the frame $\{\mathbf{R}_{1} = \mathbf{R}(t),$ $\mathbf{R}_{2} = \frac{\mathbf{R}_{t}}{\left\Vert \mathbf{R}_{t}\right\Vert },$ $\mathbf{R}_{3}(t) = \mathbf{R}_{1}\times \mathbf{R}_{2}\}$ is called Blaschke frame. Then we have

where

$\Sigma = \sigma +\varepsilon \sigma ^{\ast }$ is the dual geodesic curvature of the dual curve $\mathbf{R}(t) = \mathbf{R}(u_{1}(t), u_{2}(t))$. It is easily seen from the last two equations that

Referring to the congruence $Q$, since $\mathbf{R}_{t}$ is tangent of the dual curve $\mathbf{R}(t)$, then Eq (3.2) rewritten as

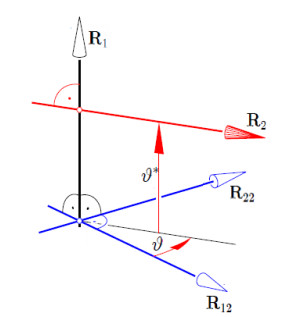
So, we can find a dual angle $\Theta = \vartheta +\varepsilon \vartheta ^{\ast }$ such that (Figure 1)

where

By simple verification, it follows that

we get

From Eqs (2.27), (2.29) and (3.8) it follows that

Thus, from Eqs (3.4) and (3.12), one finds that

This formula has the same nature of J. Liouville's formula in surface theory ^[1,6,9].

3.1.   The dual angle of pitch

In this subsection we give a geometric characterization of the of J. Liouvile's formula. For this purpose, if $\mathbf{R}_{1}(t) = \mathbf{R} _{1}(t+2\pi)$ then $\mathbf{R}_{1}(t)$ is called a closed differentiable curve. According to E. Study's map, this corresponds to $\mathbf{R}_{1}(t)$ -closed ruled surface belong to the line congruence. Also, let $\mathbf{R} _{2}$ generates a developable ruled surface (torse) along the orthogonal trajectory of the $\mathbf{R}_{1}(t)$-closed ruled surface. From Eq (3.12), this is expressed by

Then we call the total differential of $\Theta$ as the dual angle of pitch of the $\mathbf{R}_{1}(t)$-closed ruled surface. Thus, if it is denoted the dual angle of pitch of the $\mathbf{R}_{1}(t)$-closed ruled surface by the symbol $\Lambda _{1}$, then it can be written

where $\lambda _{r}$ is the angel of pitch and $L_{r}$ is the pitch of the $\mathbf{R}_{1}(t)$-closed ruled surface. The pitch and the angle of pitch are well-known real integral invariants of a closed ruled surface ^{[10,14,15,16]}. Equations (3.14) and (3.15) shown that

We found by application of Green's formula, that

Since the Gaussian curvature of the dual unit sphere can be written by

So that, we obtain as a result the formula

where $dA_{1} = \sqrt{EG}du_{1}du_{2}$ is the dual area on the dual unit sphere enclosed by the closed dual curve $\mathbf{R}_{1}(t) = \mathbf{R} _{1}(t+2\pi)$. Hence the following theorem is proved.

Theorem 1. For a closed ruled surface in the Euclidean 3-space $\mathbb{E}^{3}$. The dual angel of pitch is equal to minus the total dual spherical area of its dual image.

In fact from Eqs (3.9) and (3.19), we have that

If we separate the real and dual parts of Eq (3.20), then we find

where $a_{1}$ is the element of area on real unit sphere enclosed by the real spherical curve $\mathbf{r}_{1}(t) = \mathbf{r}_{1}(t+2\pi)$. More explicitly, we can rewrite Eq (3.16) as

and shown that

where $\Lambda _{r_{1}}$, and $\Lambda _{r_{2}}$ are the dual angel of pitches of the principal ruled surfaces $\mathbf{R} = \mathbf{R}(u_{1}, c_{2})$ and $\mathbf{R} = \mathbf{R}(c_{1}, u_{2})$, respectively.

3.2.   Plücker conoid and Dupin's indicatrix

By separating the real and dual parts of Eq (3.9), bearing in mind Eqs (2.25) and (2.26), we get

These formulas are Hamilton and Mannhiem formulae of surfaces theory in Euclidean 3-space, respectively ^[1]. The surface described by $\vartheta ^{\ast }$ in Eq (3.24) is the Plücker conoid. The Plücker conoid is a smooth regular ruled surface sometimes also called the cylindroid ^[1,6,9].

The parametric form can also be given in terms of point coordinates. We may choose $\mathbf{R}_{1}$ is coincident with the $z-$axis of a fixed frame $(\mathbf{o}xyz),$ while the position of the dual unit vector $\mathbf{R}_{2}$ is given by angle $\vartheta$ and distance $\vartheta ^{\ast }$ along the positive $z-$axis. The oriented lines $\mathbf{R}_{12}$ and $\mathbf{R}_{22}$ can be selected in sense of $x$ and $y-$axes, respectively, as depicted in Figure 2. Clearly, Hamilton's formula shows that the angle $\vartheta$ varies from $0$ to $\frac{\pi }{2}$ as $\lambda$ varies from $\lambda _{1}$ to $\lambda _{2}$, the principal surfaces being perpendicular to each other. This shows that the oriented lines $\mathbf{R}_{12}$ and $\mathbf{R}_{22}$ are the principal axes and together with the oriented line $\mathbf{R}_{1}$ create the fundamental coordinate system of the Plücker's conoid. Let $\mathbf{ \pmb{\mathsf{ ζ}} }$ denote a point on this surface, it is possible to have the following point coordinates:

Thus, the $z-$axis acts as base curve and the circle $\vartheta \rightarrow \left(\cos \vartheta, \sin \vartheta, 0\right)$ as director curve for the parametrization. Using this parametrization, the rulings are clearly visible passing through the $z-$axis, namely,

which gives us the intersection point of the principal axes $\mathbf{R}_{12}$ and $\mathbf{R}_{22}$ lies at a half of the conoid height $\vartheta ^{\ast }$. It can easily be verified by direct computations that

The Eq (3.27) shows that the Plücker's conoid has two integral invariants of the first order, $\lambda _{1}$, and $\lambda _{2}$. It is assumed by convention that $\lambda _{1} > \lambda _{2}$. The Plücker's conoid depends only on their difference; $\lambda _{1}-\lambda _{2} = 1, \ \vartheta \in \lbrack 0, 2\pi]$, $\upsilon \in \lbrack -1, 1]$ (Figure 2). This surface has two torsal planes $\pi _{1}$, $\pi _{2}$ and each of which contains one torsal line $L$ as follow: Solving for $\frac{y}{x}$, one obtains a second-order algebraic equation, whose roots are:

The limit points of the Plücker's conoid can be determined by the vanishing of the discriminant of Eq (3.19), which leads to the two extreme positions, that is,

According to the value of $\lambda$ in Eq (3.28), the geometric properties of the Plücker's conoid are discussed as follows:

A- If the parameter ruled surface $\mathbf{R}(t) = \mathbf{R} (u_{1}(t), u_{2}(t))$ is a non-developable surface, i.e. $\lambda \neq 0$, then there are two real generators passing through the point $(0, 0, z)$ only if $z < \left(\lambda _{2}-\lambda _{1}\right) /2$; for the two limit points $z = \pm \left(\lambda _{2}-\lambda _{1}\right) /2$ they coincide with the principal axes $\mathbf{R}_{12}$ and $\mathbf{R}_{22}$.

B- If the parameter ruled surface $\mathbf{R}(t) = \mathbf{R} (u_{1}(t), u_{2}(t))$ is a developable surface, i.e. $\lambda = 0,$ then their two torsal lines $L_{1}$, $L_{2}$ are represented by

Thus the two torsal lines $L_{1},$ and$\ L_{2}$ are perpendicular each other, however, only real if $\lambda _{1}\lambda _{2}\leq 0$. Hence, in this special case, if $\lambda _{1}$ and $\lambda _{2}$ have the same value, it follows that the Plücker's conoid degenerates into the pencil of lines through "$\mathbf{o"}$ in the torsal plane $z = 0$ (and the two isotropic planes through $z-$axis). Such a line congruence is called an elliptic line congruence. If, however, $\lambda _{1}$ and $\lambda _{2}$ have opposite signs, the lines $L_{1}$ and $L_{2}$ are real and they coincide with the generating lines $\mathbf{R}_{12}$ and $\mathbf{R}_{22}$. Such a line congruence is a hyperbolic line congruence. If either $\lambda _{1}$ or $\lambda _{2}$ is zero the line congruence is a parabolic line congruence, the lines $L_{1}$ and $L_{2}$ both coincide with $x-$axis; for $\lambda _{1}\neq 0$, and $\lambda _{2} = 0$ they coincide with $y-$axis.

Transition from polar coordinates to Cartesian coordinates could be performed by substituting

into Hamilton's formula, one obtain the equation

of a conic section. As for theory of surfaces, this conic section is the Dupin's indicatrix of the line congruence. We now examine three cases in detail:

(1) If $\lambda _{1}$, and $\lambda _{2}$ are both positive, the Dupin's indicatrix is an ellipse has the principal semi-axes are $\frac{1}{\sqrt{ \lambda _{1}}}$, and $\frac{1}{\sqrt{\lambda _{2}}}$. The lines through the center intersects the ellipse in the points

The distance intercepted by the ellipse on the line $\frac{y}{x} = \tan \vartheta$ is (See Figure 3):

(2) If $\lambda _{1}$, and $\lambda _{2}$ have opposite signs the Dupin's indicatrix is set of conjugate hyperbolas

shown in Figure 4. The two asymptotic directions of the hyperbolas represent the torsal lines at which $\lambda = 0$.

(3) If either $\lambda _{1}$ or $\lambda _{2}$ is zero the Dupin's indicatrix is a set of parallels lines corresponding to one of the forms

3.3.   Developable ruled surfaces

The parametric equation of the dual unit sphere $\mathbb{K} = \{\mathbf{R\in } \mathbb{D}^{3}\mid R_{1}^{2}+R_{2}^{2}+R_{3}^{2} = 1\}$, may be given by the equations

where $\Theta = \vartheta +\varepsilon \vartheta ^{\ast }$, and $\Phi = \varphi +\varepsilon \varphi ^{\ast }$ are dual angles with $-\pi \leq \vartheta \leq \pi$, and $-\frac{\pi }{2}\leq \varphi \leq \frac{\pi }{2}$. Separating Eq (3.36) into real and dual parts we obtain

and

These coordinates represent the four parameter family of lines in $\mathbb{E} ^{3}$. To form line congruence, which describes a two-real parameter motion on the dual unit sphere, we may assume that $\vartheta ^{\ast } = \vartheta ^{\ast }\left(\vartheta, \varphi \right)$, and $\varphi ^{\ast } = \varphi ^{\ast }\left(\vartheta, \varphi \right)$. Thus, the line congruence is given by

According to Eqs (2.15) and (2.23), we obtain that

Thus,

In order to identify the principal ruled surfaces of the line congruence, from Eq (3.40), we have

which yields $\lambda = e^{\ast } = g^{\ast } = f^{\ast } = 0$. Therefore, the principal ruled surfaces are developable ruled surfaces of the line congruence.

Now we may calculate the equation of the developable ruled surfaces of the congruence $\mathbf{R} = \mathbf{R}(\vartheta, \varphi)$ in terms of the Pl ücker coordinates as follows: Since $\mathbf{y\times r} = \mathbf{r}^{\ast }$ we have the system of linear equations in $y_{1},$ $y_{2}$ and $y_{3}$ ($y_{is}$ are the coordinates of $\mathbf{y}$)

The matrix of coefficients of unknowns $y,$ $y_{2}$ and $y_{3}$ is the skew-symmetric matrix

and therefore its rank is 2 with $\varphi \neq 0$, and $\vartheta \neq 0$. Also the rank of the augmented matrix

is 2. Hence this system has infinite solutions given by

Since $y_{3}(\vartheta, \varphi)$ can be chosen arbitrarily, then we may take $y_{3}-\vartheta ^{\ast } = 0$. In this case, Eq (3.44) reduces to

According to Eqs (3.37) and (3.45) we obtain

It is very clear that if the functions $\vartheta$, and $\varphi$ are given, then the following developable can be determined. The developable of the congruence is obtained for $\vartheta (t) = \varphi (t) = t\in \mathbb{R}$, $\vartheta = const$, and $\varphi = const$, see Figure 5.

4.   Conclusions

This work mainly deals with the dual representation of line congruence and explains the resemblance between theory of surfaces and theory of line congruences. In terms of this, several some new and well-known formulae of line congruence in the Euclidean 3-space have been introduced. Furthermore, we determine kinematic-geometry of the Plucker conoid and its characterization. In addition, the degenerated cases of the Plücker conoid are discussed according to the Dupin's indicatrix having specific trajectories. We hope that this work will lead to a wider usage in the differential line geometry and rational design of space mechanisms.

Conflict of interest

The authors declare that they have no conflict of interest.