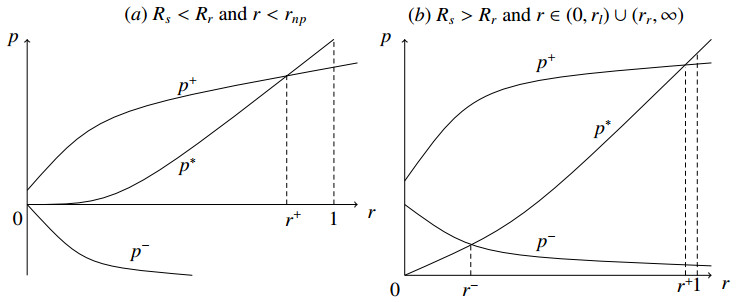Assessing the role of bacterial plasmid replication in a competition model of sensitive and resistant bacteria to antibiotics

1.   Introduction

Just as vaccines have saved the lives of millions of children and contributed to the eradication of diseases around the world, antibiotics have been effective in curing different types of infection caused by bacteria. Currently, antibiotics are the medications most prescribed by doctors to treat diseases caused by bacteria, and although it has not been a century since Sir Alexander Fleming discovered penicillin in 1928, there is already a global threat caused by the resistance of certain bacteria to first-line antibiotics.

Bacteria can acquire antibiotic resistance by transferring genetic material. They can be classified as vertical gene transfer (including spontaneous or acquired mutations) and horizontal gene transfer, which can occur through the transformation, conjunction, or transduction of mobile genetic elements that function as vehicles. Such elements include plasmids, transposons, integrons, and integrative conjugative elements.

Plasmid-mediated resistance (due to the transfer of antibiotic resistance genes carried on plasmids) is increasing worldwide. Bacterial plasmids are circular or linear extrachromosomal DNA molecules. They carry antimicrobial resistance genes coding for proteins such as colistin, ESBL (extended-spectrum $\beta$-lactamases), carbapenemases, fluoroquinolones, and aminoglycosides. This resistance has resulted in a global epidemic ^[1,2]. A plasmid is between 1 and 250 kb long (one kilobase is 1000 base pairs of DNA or RNA). A cell can have from a single copy of a plasmid to a few hundred copies ^[3]. Multi-drug resistance caused by plasmids has been reported for several bacterial strains ^[4,5].

Much are still unknown about the biology of plasmids. However, since they are associated with antibiotic resistance, a considerable amount of research has been conducted to establish their role in this process. Identification of the characteristics and properties of plasmids has contributed to our understanding of the dynamics of the acquisition of antibiotic resistance ^[6]. In particular, plasmid-mediated resistance has been studied by isolating E. coli strains in vitro, and interesting results have been obtained from experiments on the replication, transfer, and propagation of plasmids, which have implications in bacterial growth ^[7,8,9,10]. The results of research at the biological level can be complemented or used as a basis for new studies. In this sense, we find mathematical modeling mainly focuses on PMAR ^{[11,12,13,14]}.

In particular, Ibarguen et al.^[15] developed a model of the interactions between bacteria sensitive and resistant to antibiotics. The model considers the acquisition of resistance due to plasmids. From a qualitative analysis of this model, we obtained three steady states: (1) a bacteria-free state, $E_0$, (2) a state where only resistant bacteria are present, $E_1$, and (3) a state where sensitive and resistant bacteria coexist, $E_2$. Additionally, a stability region was determined for each equilibrium that depends on the values of parameters similar to basic reproductive numbers for sensitive and resistant bacteria. Ibarguen et al.^[16] modified the model to use a dynamic variable for the acquisition of resistance due to plasmids. The results obtained from the qualitative analysis of this model were interesting because in addition to the previously mentioned scenarios, there was a new scenario in which a limit cycle emerges around a coexistence equilibrium (Hopf bifurcation). The limit cycle corresponds to the self-regulation of bacterial growth, which could minimize the transmission of plasmids between bacteria. In the previous model, the functional response for plasmid replication was key in the appearance of the limit cycle. These results confirm self-regulation processes in the dynamics of bacterial growth ^[17]. Furthermore, different studies reveal that plasmids play a fundamental role in PMAR ^[18,19].

In this work, we formulate and analyze a generalization of the model developed in ^[16], in which the plasmid replication rate is defined using a $\mathcal{C}^1$-function.

2.   The model

The World Health Organization has declared antimicrobial resistance among the top 10 global threats to public health. In this sense, the fact that aggravates the situation is the use of antibiotics for treating humans and animals. The above has allowed the horizontal transmission of resistance genes, driving the growing trend of PMAR. However, due to the lack of knowledge about the biology of the plasmids, many gaps are related to their role in antimicrobial resistance. This has led to the development of scientific production that reveals the importance of the transfer and replication of plasmids in biological phenomena. Nevertheless, discovering the properties and factors of the interaction dynamics of bacteria and plasmids is still a challenge. In particular, the form of plasmids replication is not yet clear. The above motivated us to study the role played by plasmids replication in the plamid-meadiated resistance. In ^[16,20] we formulated mathematical models considering specific functional responses for the plasmids growth rate. In the first one we supposed that plasmids growth rate, $G$, is proportional to the resistant bacteria; that is, $G(R, P) = \sigma_pR$ where $\sigma_p$ is a constant plasmid reproduction rate, and in the second one, we supposed that the plasmids replication rate follows a generalized law of mass action, $G(R, P) = \sigma_pP^aR^b$ where $a, b\in\mathbb{R}$ are constants. We obtained consistent results with the biological phenomenon.

In this work, we develop a mathematical model that describes the interaction dynamics between bacteria and plasmids in which the plasmid replication rate is an undefined function that satisfies the common properties of the plasmid replication rate defined in ^[16,20].

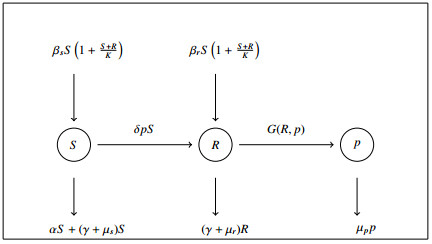
In this section, we formulate a model on bacterial resistance that describes the interaction of susceptible bacteria, resistant bacteria and plasmids populations. Let us denote by $S(t)$, and $R(t)$ the population sizes of susceptible, and resistant bacteria to antibiotics at time $t$, respectively; and $p(t)$ the number of plasmids at time $t$. As in ^[21], we assume that bacteria follow a logistic growth with carrying capacity $K$. Let $\beta_s$ and $\beta_r$ the birth rate of susceptible and resistant bacteria, respectively. Specific mutations that confer resistance to chemical control often have an inherent fitness cost which may be manifested through reduced reproductive capacity or competitive ability ^[22]. In this work, we quantify fitness cost as a reduction in the reproduction rate of the resistant strain, therefore $\beta_r\leq\beta_s$. Susceptible and resistant bacteria have per capita natural death rates $\mu_s$, and $\mu_r$, respectively. Susceptible bacteria also die due to the action of the antibiotics, and we assume that the rate at which they are killed by the antibiotic is equal to $\alpha S$. Further, it is assumed that during treatment with antibiotics, the process of bacterial conjugation for the transfer of resistant plasmids is conducted. In this process, susceptible bacteria are reservoir and resistant bacteria are donors of genetic material which is represented by the term $\delta PR$, with $\delta$ the rate of transfer of resistant plasmids among bacteria. Susceptible and resistant bacteria are eliminated by the host immune system at per capita rate $\gamma$. The plasmids degrade at a constant rate $\mu_p$. There is a symbiosis between plasmids and host cells. Plasmids replicate autonomously in the bacterial cell and use them for their propagation. Plasmid replication is a function of the plasmid and the host cell ^[23]. Since we are only interested in the replication of resistant plasmids, we assume that plasmid replication rate is given by the functional response $G(R, p)$ where $G:\mathbb{R}^2\to \mathbb{R}_0^+$ is a $\mathcal{C}^1$ function. Under the abovementioned assumptions, we obtain the following system of ordinary differential equations:

The Figure 1 shows the flow diagram of system (2.1). With the following change of variables $s = S/K$ and $r = R/K$ the system (2.1) is reduced to

where $g(r, p) = G(Kr, p)$.

3.   Invariant set

The matrix form of (2.2) is given by

where

and

where

The parameter $R_r$ defined in (3.4) is interpreted as the number of bacteria produced by the fraction of resistant bacteria that evade the immune response, and $R_s$ is interpreted as the number of bacteria generated by the fraction of sensitive bacteria that survive the effects due to antibiotics and the immune system response.

Since $g\in\mathcal{C}^1(\mathbb{R}^2)$, then $f\in\mathcal{C}^1(\mathbb{R}^3)$. Therefore, there exists an $\varepsilon > 0$ such that the initial value problem (ivp) defined by (3.1) and $x(0) = x^0\in\mathbb{R}^3$, has a solution $x(t)$ on the interval $[0, \varepsilon]$ (Fundamental theorem of existence and uniqueness, ^[24]). In addition, for a compact set $\Omega\subset E$ such that

it follows that $\varepsilon = \infty$. In consequence, the ivp has a solution $x(t)$ for all $t\geq0$ (Corollary 2, page 91, ^[24]). Now, we will prove the existence of bounded solutions. To this end, we will use the results developed by W. Karpińska in ^[25], about bounded solutions of dynamical systems, which establish that under the following assumptions,

1. $A\in\left(\mathbb{R}^3\right)$ defined in (6) is a self-adjoint operator, and 0 is its eigenvalue, and

2. $h:\mathbb{R}\times\mathbb{R}^3\to\mathbb{R}^3$ defined in (3.2) is a Carathéodory function; that is,

(a) $h$ is a map measurable with respect to the first variable.

(b) $h$ is continuous with respect to the second one, and

(c) for any $l\in\mathbb{R}$ there exists a locally integrable function $M_l:\mathbb{R}\to\mathbb{R}$ that satisfies $\|h(t, x)\|\leq M_l(t)$ for $\|x\|\leq l$.

The existence and uniqueness of bounded solutions on $\mathbb{R}$ of system (3.1) were obtained. Since $A$ is a diagonal matrix, the first item is satisfied. On the other hand, $h(\cdot, x)$ is constant function which implies that $h$ is measurable with respect to $t$. Since the function $g$ is continuous with respect to $x$, then $h$ is continuous with respect to $x$. By adding the first two equations of (2.2) we obtain

where $\beta = \max\left(\beta_s, \beta_r\right)$. The solution of inequality (3.5) satisfies $0\leq s(t)+r(t)\leq1$ for $t\geq0$. Now, for $t\in\mathbb{R}$ we have

where

Since $g\in\mathcal{C}^{1}(\mathbb{R})$, then $M_l$ is a locally integrable function. Thefere, the item 2 is satisfied. The above implies the existence of an unique bounded solution of ivp defined by (3.1) and $x(0) = x_0$. Let

The invariant set of system (2.2) is given by the following compact set

where $M = \sup\{|\tilde{p}(t)|:t\geq0\}$. The results of this section are summarized in the following lemma, which assures that system (2.2) is well posed in the sense that solutions with initial conditions in $\Omega$ remain there for all $t\geq 0$.

Lemma 3.1. The set $\Omega$ defined in (3.8) is positively invariant with respect to system (2.2).

4.   Equilibrium points

At biological level, there are inhibition mechanisms of the host cell that control the plasmid replication rate, which allows reaching steady state conditions for the plasmid copy number ^[23]. The plasmid replication rate and inhibition period directly affect one another ^[18]. Since the reciprocal of the inhibition period is the degradation rate of plasmids, then a necessary condition for the existence of equilibria is $g(r, p) = \mu_pp$. Another necessary condition is that the previous equation has at least one solution. For convenience, we suppose that the solution is a function of plasmids $p^*$ in terms of resistant bacteria $r$. Plasmid is generally replicated on constant average per cell and cell cycle, which implies that $p^*$ follows an exponential growth. This behavior has been experimentally verified in several research works ^[18,23]. Finally, since plasmids cannot replicate in the absence of resistant bacteria, then we assume $p^*(0) = 0$. From the above, we obtain the following assumption.

$C_1:$ the equation $g(r, p) = \mu_pp$ has unique non-negative solution $p^*(r)$ which is a increasing convex function that satisfies $p^*(0) = 0$.

In this section, we will determine the equilibrium points of system (2.2) under the condition $C_1$. The equilibria of system (2.2) are given by the solutions of the algebraic equations

Now, we will find the equilibrium points for which $s = 0$. In this case, the system (4.1) is reduced to

The condition $C_1$, implies the existence of an unique solution $p(r)$ of the second equation of (4.2) that satisfies $p(0) = 0$. Solutions of the first equation of (4.2) are $r = 0$ and $r = r_1$, where

By substituting $r = r_1$ in $p^*(r)$, we obtain $p_1 = p^*(r_1)$, which implies the exitence of the equilibrium point $x_1 = (0, r_1, p_1)^T$. By substituting $r = 0$ we obtain the equilibrium $x_0\equiv(0, 0, 0)^T$. The above results are summarized in the following proposition.

Proposition 4.1. If condition $C_1$ is satisfied, then the systen (2.2) always has the equilibrium $x_0\equiv0$ in $\Omega$, and if $R_1 > 1$, in addition there exists an equilibrium point $x_1 = (0, r_1, p_1)^T\in\Omega$.

Now, for $s\neq0$ the system (4.1) is reduced to

From the first equation of (4.4) we obtain

From (4.5) is concluded that a necessary condition for the existence of plasmids, susceptible and resistant bacteria is $R_s > 1$. Solving for $s$ in (4.5) we obtain

Note that a necessary and sufficient condition such that $s$ defined in (4.6) be positive is

By Substituting (4.6) in the second equation of (4.4) we obtain

From (4.8) we obtain the following equation

where

being

The solutions of (4.9) are given by

Now, we will determine the conditions for the existence of coexistence equilibria. To this end, we will analyze the requirements for which $p^{\pm}$ defined in (4.12) are positive, negative or complex functions, considering the following cases $R_s > R_r$, $R_s = R_r$ and $R_s < R_r$, and we will find the number of positive solutions of the following equations

in the interval $(0, 1)$, where $p^*(r)$ is the function of hypothesis $C_1$ that satisfies $p^*(0) = 0$.

Condition $R_s < R_r$ : In this case $c(r) < 0$, which implies that $p^{\pm}$ are real value functions. On the other hand, the sign of $b(r)$ depends on the value of $r_{np}$. In consequence:

1. If $r < r_{np}$, then $b(r) < 0$ which implies that $p^{+}$ is a positive and increasing concave function ($p^+(r) > 0$), and $p^-$ is a negative and decreasing convex function ($p^-(r) < 0$). Since $p^-(0) = 0$ and $p^+(0) = -b(0) > 0$, then the functions $p^-$ and $p^*$ intersect at $r = 0$ and the functions $p^+$ and $p^*$ intersect at $r^{+}\in(0, 1)$ if and only if $p^+(1) < p^*(1)$ (See Figure 2a). In consequence, the equation $p^-(r) = p^{*}(r)$ does not have a positive solution, and the equation $p^+(r) = p^*(r)$ only has one positive solution $r^+$ if and only if $p^+(1) < p^*(1)$. Therefore, if $R_s < R_r$ and $p^+(1) < p^*(1)$ there exists an equilibrium point $x^+ = (s^+, r^+, p^+)$ in the subset $\Omega_1\subset\Omega$ given by

2. If $r = r_{np}$, then $b(r) = 0$ which implies that $p^{+}(r) = \sqrt{-c(r)}$ is a positive and increasing concave function, and $p^{-}(r) = -\sqrt{-c(r)}$ is a negative and decreasing convex function. Following a procedure similar to the previous case, we conclude that if $R_s < R_r$ and $p^+(1) < p^*(1)$ there exists an equilibrium point $x^+ = (s^+, r^+, p^+)$ in the subset $\Omega_2\subset\Omega$ given by

3. If $r > r_{np}$, then $b(r) > 0$. We verify that if $R_s < R_r$ and $p^+(1) < p^*(1)$, there exits an equilibrium point $x^+ = (s^+, r^+, p^+)$ in the subset $\Omega_3\subset\Omega$ given by

Condition $R_s = R_r$ : In this case $c(r) = 0$, which implies that $p^{\pm}$ are reduced to real value functions

Newly,

1. If $r < r_{np}$, then $b(r) < 0$ which implies that $p^{+}(r) = -b(r)$ is a positive and increasing linear function, and $p^-(r) = 0$. Since $p^-(0) = 0$ and $p^+(0) = -b(0) > 0$, then the functions $p^-$ and $p^*$ intersect at $r = 0$ and the functions $p^+$ and $p^*$ intersect at $r^{+}\in(0, 1)$ if and only if $p^+(1) < p^*(1)$. In consequence, the equation $p^-(r) = p^{*}(r)$ does not have positive solutions, and the equation $p^+(r) = p^*(r)$ only has a positive solution $r^+$ if and only if $p^+(1) < p^*(1)$. Therefore, if $R_s = R_r$ and $p^+(1) < p^*(1)$ there exists an equilibrium point $x^+ = (s^+, r^+, p^+)$ in the subset $\Omega_1\subset\Omega$ given by

2. If $r = r_{np}$, then $b(r) = 0$ which implies that $p^{+}(r) = p^-(r) = 0$. In consequence, there are not positive solutions of the equations $p^+(r) = p^*(r)$ and $p^-(r) = p^*(r)$. Therefore, there are not coexistence equilibria.

3. If $r > r_{np}$, then $b(r) > 0$ which implies that $p^{-}(r) = -b(r) < 0$, and $p^+(r) = 0$. Therefore, there are not coexistence equilibria.

Condition $R_s>R_r$ : In this case $c(r) > 0$, which implies that $p^{\pm}$ could be real or complex value functions. Therefore, the values of $p^{\pm}$ depend on of the sign of $b(r)$ and the sign of

where

Eq (4.15) is equivalent to

where

Observe that $0 < r_l < r_{np} < r_r$. In consequence

Now, since the sign of $b(r)$ depends on $r_{np}$ we have the following options.

● For $r\in(0, r_l)\cup(r_r, \infty)$ we have:

1. If $r < r_{np}$, then $b(r) < 0$ which implies that $p^{+}$ is a positive and increasing concave function ($p^+(r) > 0$), and $p^-$ is a positive and decreasing convex function ($p^-(r) < 0$). Since $p^-(0) = (\beta_s-\beta_r)r_{np}/(2\delta) > 0$ and $p^+(0) = 3(\beta_s-\beta_r)r_{np}/(2\delta) > 0$, then the functions $p^-$ and $p^*$ intersect at positive root $r^- > 0$ and the functions $p^+$ and $p^*$ intersect at positive root $r^{+} > 0$, which satisfy $r^- < r^+$ (See Figure 2b). In consequence, if $p^+(1) < p^*(1)$ there are two coexistence equilibria $x^+$ and $x^-$, if $p^-(r^-) < p^*(1) < p^+(r^+)$ there exists an unique equilibrium $x^-$, and if $p^*(1) > p^-(r^-)$ there are nor equilibria. Therefore, if $R_s > R_r$ and $p^+(1) < p^*(1)$ there are two equilibrium points $x^+$ and $x^-$ in the subset $\Omega'_1\subset\Omega_1$ given by

If $R_s > R_r$ and $p^-(r^-) < p^*(1) < p^+(r^+)$ there exists an unique equilibrium $x^-\in\Omega'_1$.

2. If $r = r_{np}$, then $b(r) = 0$ which implies that $p^{+}(r) = \sqrt{-c(r)}$ is a positive and increasing concave function, and $p^{-}(r) = -\sqrt{-c(r)}$ is a negative and decreasing convex function. Following a procedure similar to the previous cases, we conclude that if $R_s > R_r$ and $p^+(1) < p^*(1)$ there exists an unique equilibrium point $x^+$ in the subset $\Omega'_1\bigcap\Omega_2\subset\Omega_1$.

3. If $r > r_{np}$, then $b(r) > 0$ which implies that $p^{-}(r) < 0$, and $p^+(r) < 0$. Therefore, there are not coexistence equilibria.

● For $r = r_l$ or $r = r_r$ we have $p^{\pm}(r) = -b(r)/2$. In consequence, if $r < r_{np}$, then $b(r) < 0$ which implies that $p^{\pm}$ is a positive and increasing linear function. Therefore, if $R_s > R_r$ and $p^{\pm}(1) < p^*(1)$ there is an unique equilibrium $x^+$ in the subset $\Omega''_1\bigcap\Omega_1\subset\Omega_1$ given by

We can verify, that if $r\geq r_{np}$ there are not coexistence equilibria.

● For $r\in(r_l, r_r)$, is follows that $p^{\pm}$ are complex value functions. Therefore, there are not coexistence equilibria.

The existence results of coexistence equilibrium points are summarized in the following proposition.

Proposition 4.2. By assuming that the functions $p^*$ defined in the hypothesis $C_1$ and $p^+$ defined in (4.12) satisfy $p^+(1) < p^*(1)$, $R_s > 1$ and $R_r > 1$ we have the following results:

1. If $R_s < R_r$, there exists an equilibrium $x^+\in\Omega$.

2. If $R_s = R_r$, there exists an equilibrium $x^+\in\Omega_1$.

3. If $R_{s} > R_r$ then

● there are two equilibrium points $x^+$ and $x^-$ in $\Omega'_1\subset\Omega_1$.

● there exists an equilibrium point $x^+$ in the subset $\Omega'_1\cap\Omega_2\subset\Omega_1$.

● there is an equilibrium $x^+$ in the subset $\Omega''_1\cap\Omega_1\subset\Omega_1$.

On the other hand, If $R_s > R_r$ and $p^-(r^-) < p^*(1) < p^+(r^+)$ there exists an unique equilibrium $x^-\in\Omega'_1$.

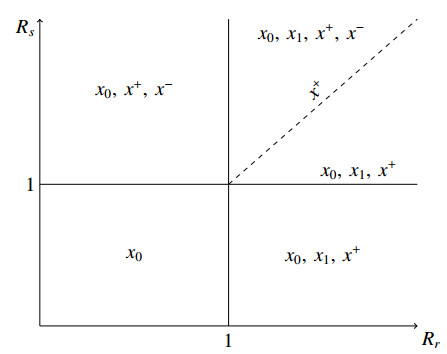
Figure 3 shows the existence region of the equilibria. The equilibrium $x_0$ represents the state without bacterial load, $x_1$ represents the state of resistant bacteria, $x^+$ represents the coexistence state with high bacterial load, and $x^-$ represents the coexistence state with low bacterial load.

5.   Stability analysis

In this section, we determine the stability of the equilibrium points of the system (2.2). The linearization of the system (2.2) around of an equilibrium point $\bar x$ is given by $x' = J(\bar x)x$, where the Jacobian matrix $J$ evaluated at $x$ is given by

The eigenvalues of $J(0)$ are given by $\partial g(0, 0)/\partial p-\mu_p$, $(\gamma+\mu_r)(R_r-1)$ and $(\alpha+\gamma+\mu_s)(R_s-1)$ which are negative if and only if $R_s < 1$, $R_r < 1$ and $\partial g(0, 0)/\partial p < \mu_p$. In consequence, $x_0$ is locally asymptotically stable (l.a.s). Similarly, the eigenvalue of $J(x_1)$ are $-\beta_rr_1$, $\beta_s(1/R_r-1/R_s-\delta p_1/\beta_s)$ and $\partial g(r_1, p_1)/\partial p-\mu_p$. In consequence, it is verified that $x_1$ is l.a.s when $R_s < (1+\delta p_1/(\alpha+\gamma+\mu_s))R_r$ and $\partial g(r_1, p_1)/\partial p < \mu_p$.

The Jacobian $J$ evaluated $x^{\pm}$ is given by

The characteristic polynomial of $J(x^{\pm})$ is given by

where

The Routh-Hurwitz criterium establish that the roots of a polynomial $p(\lambda)$ have negative real part if and only if their coefficients satisfy $D_1 = a_1 > 0$, $D_2 = a_1a_2-a_3$ and $a_3 > 0$. Now, $D_3$ is rewritten as

If

then $a_1$ defined in (5.4) and $D_3$ defined in (5.5) are positive, and since $p^{\pm}\leq M$ then $a_3$ defined in the second equation of (4.1) satisfies

From (5.7), for $\delta$ small enough we have $\delta M\ll1$ which implies $a_3 > 0$. Therefore, if (5.6) holds then $x^+$ and $x^-$ are l.a.s. The results about local stability are summarized in the following proposition.

Proposition 5.1. If $R_s < 1$, $R_r < 1$ and $\partial g(0, 0)/\partial p < \mu_p$, then $x_0$ is l.a.s in $\Omega$. If $R_r > 1$ and $R_s < (1+\delta p_1/(\alpha+\gamma+\mu_s))R_r$ and $\partial g(r_1, p_1)/\partial p < \mu_p$, then $x_1$ is l.a.s in $\Omega$. If $g$ satisfies the conditions (5.6), $\delta\ll1$ and under hypothesis of Proposition 4.2 it follows that $x^+$ is l.a.s in $\Omega$ and $x^-$ is l.a.s in $\Omega'_1$.

Empirically, the existence of a control system for plasmid replication that depends on the genetics, molecular biology and physiology of both plasmids and host cells has been demonstrated. Much is still unknown about the mechanisms underlying this theory. However, the first evidence that plasmids control, at least partially, their own replication rate was the isolation of copy mutants, which have a higher steady-state copy number than the wild-type parent. Under steady state conditions, the plasmid concentration is constant and therefore the size of the plasmid population must double every time the cell population doubles. This means that each plasmid molecule must, on average, replicate once per cell and cell cycle. In our model, this property was analyzed by means of the gradient vector of the function that defines the plasmids replication rate. Specifically, for the stability of the equilibria $x_0$ and $x_1$ it is required that $\partial g(0, 0)/\partial p < \mu_p$ and $\partial g(r_1, p_1)/\partial p < \mu_p$, respectively. For the equilibria $x^{\pm}$ is required that $g$ satisfies the conditions (5.6). As we can see, to control the replication of plasmids in the cases of equilibrium points $x_0$ and $x_1$, it is necessary to limit the variation of the plasmid replication rate with respect to plasmids. In the case of $x^{\pm}$, in addition to the above, it is necessary that the plasmid replication rate be decreasing with respect to resistant bacteria.

The global stability of $x_0$ is presented in the following proposition

Proposition 5.2. If $R_s\leq1$ and $R_r\leq1$, then $x_0$ is globally asymptotically stable in $\Omega$ defined in (3.8).

Proof. Since $g\in\mathcal{C}^1(\Omega)$, then there exists $L\geq0$ such that $\dfrac{\delta}{\mu_p\beta_r}\int_{0}^tg(x(\tau))d\tau = L$. The function $V$ defined by

satisfies $V(x_0) = 0$ and $V(x)\geq0$ for all $x\in\Omega$. The orbital derivative of $V$ is given by

For $R_s\leq1$ and $R_r\leq1$ we obtain

In consequence $\dot{V}(x) < 0$ for all $x\in\Omega$. Therefore, $x_0$ is globally asymptotically stable in $\Omega$.

6.   Hopf bifurcation

In the last section, we verified that the equilibria $x^{\pm}$ are l.a.s when the conditions defined in (5.6) are satisfied. In this section, we will verify that if

then there exists a Hopf bifurcation for a suitable parameter of system (2.2). In this case, a change of stability of $x^{+}$ or $x^-$ occur, and a limit cycle appears with amplitude and frequency depending on the value of the bifurcation parameter. To this end, we will use the following version of the Hopf theorem

Theorem 6.1 (Hopf Theorem). Let n-dimensional autonomous system of differential equation given by

which depends on the real parameter $\mu$, and where $F(x, u)$ is twice differentiable in both variables. We suppose that

1. The system (6.1) possess an analytic family $x(\mu)$ of equilibrium points; that is $F(x(\mu), \mu) = 0$.

2. For certain value of $\mu$, say $\mu_0$, the jacobian matrix $J(x(\mu_0), \mu_0) = F_x\left(x(\mu_0), \mu_0\right)$ has two purely imaginary eigenvalues $\lambda^{\pm}(\mu_0) = \pm i\beta$ and no other eigenvalue of $J(x(\mu_0), \mu_0)$ is an integral multiple of $i\beta$.

3. If $\lambda(\mu) = \alpha(\mu)+i\beta(\mu)$ is the continuation of eigenvalue $i\beta$, then $\alpha'(\mu_0) = d\left(\mathrm{Re}(\lambda)(\mu_0)\right)/d\mu\neq0$.

Under the above conditions there exists differentiable functions $\mu(\epsilon)$ and $T(\epsilon)$ depending on a parameter $\epsilon$ with $\mu_0$ and $T(0) = 2\pi\beta^{-1}$ such that there are nonconstant periodic solutions $x(t, \epsilon)$ of (6.1) with period $T(\epsilon)$ which collapse into $x(\mu)$ as $\epsilon\to0$.

See Schmidt ^[26] for a prove of Theorem 6.1. From (3.1) we observe that $\mu$ is one of the following parameters $\beta_s$, $\beta_r$, $\alpha$, $\delta$, $\gamma$, $\sigma_p$, $\mu_s, \; \mu_r,$ or $\mu_p$, and $F(x, \mu) = A(\mu)x+h(x, \mu)$. In the Proposition 5.1 we proved the existence of equilibriium $x^{+}$ which depends of $\mu$, and satisfies $F(x^+, \mu) = 0$. Consequently the first item of the Theorem 6.1 is satisfied. For convenience we choose the bifurcation parameter $\mu = \beta_s$, which implies $x(\mu) = x^{+}(\beta_s)$.

Now, we will prove that the Jacobian matrix at $x^{+}(\beta_s)$ has a negative real eigenvalue and a pair of eigenvalues on the imaginary axis. To this end, we define

In term of the parameter $\xi$, the constants $a_1$, $a_2$ and $a_3$ defined in (5.4) are rewritten as

Now, $D_2$ in terms of $\xi$ is given by

where

Observe that $D_2(\xi)$ defined in (6.2) can be rewritten as $D_2(\xi) = (\xi-\xi^{+}(\beta_s))(\xi-\xi^{-}(\beta_s))$ where

Observe that $c_2 > 0$, if $\partial g/\partial p < \mu_p$ then $c_1 > 0$, in addition, if $\partial g/\partial r > 0$ then $c_3 < 0$, which implies that $\xi^{+}$ is the only positive solution of $D_2(\xi) = 0$. If $\partial g/\partial p = \mu_p$, then $c_1 = 0$ and $c_3 < 0$, then the solution of $D_2(\xi) = 0$ is $\xi = -c_3/c_2 > 0$. In consequence, for $\xi = \xi^{+}(\beta_s)$ or $\xi = -c_3(\beta_s)/c_2(\beta_s)$ we obtain $D_2(\xi) = 0$ which implies $a_1(\beta_s)a_(\beta_s) = a_3(\beta_s)$ for some $\beta_s = \beta_s^0$. By substituting the previous equation in $p_1(\lambda)$ we obtain

From (6.4) we establish that the eigenvalues of $J(x^{+})$ are $-a_1(\beta_s^0)$ and $\lambda^{\pm}(\beta_s^0) = \pm\sqrt{- a_2(\beta_s^0)}$. Since $a_1(\beta_s^0) > 0$ and $a_2(\beta_s^0) > 0$ then $- a_1(\beta_s^0)$ is a negative real number and $\lambda^{\pm}(\beta_s^0) = \pm i\sqrt{a_2(\beta_s^0)}$ are imaginary numbers which implies that the second item of the Theorem 6.1 is satisfied.

Since $s$, $r$ and $p$ implicitly depend on all parameters of mathematical model (2.2), then the constants $a_1$, $a_2$ and $a_3$ defined in (5.4) implicitly depend on the same parameters. In consequence, the calculation of the crossing speed is cumbersome, no matter which bifurcation parameter is chosen. From Lemma 8.1 (appendix), it is verified the existence of an unique function $v:\mathbb{R}^{7}\to \mathbb{R}$ such that $\beta_s = v(\beta_r, \alpha, \delta, \gamma, \mu_s, \mu_r, \mu_p)$. On the other hand, since the eigenvalues of Jacobian matrix defined in (5.2) are given by $- a_1(\beta_s^0)$ and $\lambda^{\pm}(\beta_s^0) = \pm i\beta(\beta_s^0)$ where $\beta(\beta_s^0) = \sqrt{a_2(\beta_s^0)}$, then using the canonical form theory of Jordan (See Hirsch and Smale^[27]) we obtain

with $\beta_0 = \beta(\beta_s^0)$ and $a_1^0 = a_1(\beta_s^0)$. Suppose that for $\beta_s\approx\beta_s^0$ we have

being $\bar\alpha(\beta_s^0) = 0$ and $\beta(\beta_s^0) = \beta_0$. Since we wish to calculate

which is the crossing speed of the eigenvalues $\lambda^{\pm}(\beta_s)$ in the imaginary axis. For $\beta_s\approx\beta_s^0$ the characteristic polynomial associated with the Jacobian matrix

is

where

Since the coefficients $L_1$, $L_2$ and $L_3$ must satisfy the same conditions that the coefficients $a_1$, $a_2$ and $a_3$ of the characteristic equation of $J(x(\sigma_p))$; that is, $L_3(\beta_s)-L_1(\beta_s)L_2(\beta_s) = 0$. Substituting (6.6) in above equation we obtain the followin equation

For $\bar\alpha(\mu)\neq0$, then (6.7) is rewritten as

Applying implicit differentiation in (6.8) with respect to $\beta_s$ we obtain

Evaluating (6.9) in $\beta_s = \beta_s^0$ we obtain

In consequence, there exits a a Hopf bifurcation to the system (2.2) in the endemic equilibrium $x(\beta_s) = x^{+}$. Similar way, we verify the existence of a Hopf bifurcation around $x^-$.

7.   Discussion

Currently, plasmid-mediated resistance is a threat to humanity. One of the key factors in tackling this challenge is to understand the replication dynamics of resistance plasmids. However, the lack of knowledge about the biology of plasmids makes this task difficult. In this regard, efforts by researchers in different fields have clarified some aspects of plasmids. The replication rate has been modeled as a Holling type II functional response ^[28]. However, it is still unclear which functional responses best fit the relevant rates. In this work, we studied the functional response of plasmid replication on antibiotic resistance. Thus, we modeled the competitive interaction between plasmids, sensitive and resistant bacteria with a system of three nonlinear ordinary differential equations. We used a function $g\in\mathcal{C}^1(\mathbb{R}^2)$ for the plasmid replication rate.

We proved the existence of bounded solutions of system (2.2) in the set $\Omega$ defined in (3.8). Qualitative analysis was made under hypothesis $C_1$; the equation $g(r, p) = \mu_pp$ has unique non-negative solution $p^*(r)$ which is a increasing convex function that satisfies $p^*(0) = 0$. The system (2.2) always has the bacteria-free equilibrium, $x_0\equiv0\in\Omega$, if $R_r > 1$ there exists a resistant bacteria equilibrium $x_1\in\Omega$ where $R_r$ represents the number of bacteria produced by the fraction of resistant bacteria that evade the immune response, the existence results of coexistence equilibrium points, $x^{\pm}$, are summarized in the Proposition 4.2. This proposition explicitly determines the regions of existence of $x^{\pm}$. For example, if $R_s > R_r$ then the equilibria $x^+$ and $x^-$ coexist in the subset $\Omega'_1\subset\Omega$, where $R_s$ represents the number of bacteria generated by the fraction of sensitive bacteria that survive the effects due to antibiotics and the immune system response, $x^+$ and $x^-$ are associated with high and low bacterial load, respectively. If $R_s < 1$, $R_r < 1$ and $\partial g(0, 0)/\partial p < \mu_p$, then $x_0$ is l.a.s. In addition, we proved that $x_0$ is globally asymptotically stable when $R_s\leq1$ and $R_r\leq1$. In consequence, if each bacterium (sensitive or resistant) produces at most one new bacteria, then the infection will be controlled or eliminated. If $R_r > 1$, $R_s < (1+\delta p_1/(\alpha+\gamma+\mu_s))R_r$ and $\partial g(r_1, p_1)/\partial p < \mu_p$, then $x_1$ is l.a.s in $\Omega$. In this scenario, the infection is caused only by resistant bacteria. For $\delta\ll1$ and under hypothesis of Proposition 4.2 we proved that $x^+$ is l.a.s in $\Omega$ and $x^-$ is l.a.s in $\Omega'_1$. Furthermore, we verified the existence of a Hopf bifurcation when $\beta_s\ll1$, $\partial g(r^+, p^+)/\partial p < \mu_p$ and $\partial g(r^+, p^+)/\partial r > 0$. In this cases, when $x^+$ loses its stability, a stable limit cycle appears. The growth of plasmids, sensitive and resistant bacteria have an oscillatory behavior with initial period $T = 2\pi\beta_S^{-1}$.

The analysis of the model shows three possible scenarios in the outcome of the infection; bacterial progression is cleared, persists only with resistant bacteria, or persists with both of them. The only equilibrium point in the region

is $x_0$. Since $x_0$ is globally asymptotically stable in $U_1$, then regardless of the initial conditions or the plasmid replication rate, the bacterial progression is always eliminated in $U_1$. The region

contains the equilibria $x_0$ and $x_1$. The point $x_0$ is unstable and $x_1$ is l.a.s when tha plasmid replication rate satisfies $\partial g(r_r, p_1)/\partial p < \mu_p$. Therefore, in the subregion $W_1\subset U_2$ defined by

$x_0$ is unstable and $x_1$ is l.a.s, which implies that the infection tends to spread only with resistant bacteria. For $R_s > 1$ and $R_r > 1$ there are several regions. In the region

the equilibrium $x_0$ is unstable, $x^+$ and $x_1$ are l.a.s. In consequence, $U_3$ is a region of bi-stability in which infection progresses with resistant bacteria or with high levels of both bacterial populations. In the region

the equilibrium $x_0$ is unstable $x_1$ is l.a.s and $x^+$ does not exist. Then, in $U_4$ the bacterial progression is only with resistant bacteria. In the regions

the equilibria $x_0$ and $x_1$ are unstable $x^+$ is l.a.s. Then, in the regions $U_5-U_8$ the infection progresses with high levels of both bacterial populations. In the region

the equilibria $x_0$ and $x_1$ are unstable, $x^+$ and $x^-$ are l.a.s, which means that the infection progresses with high and low levels of both bacterial populations. In the region

the equilibrium $x_0$ and $x^+$ are unstable, and there are limit cycles.

The results of the analysis of the model (2.2) confirm that the form of replication of bacterial plasmids plays a fundamental role in PMAR. Under hypothesis $C_1$ and additional conditions of $\partial g/\partial p$ and $\partial g/\partial r$ we obtained results similar to those presented in ^[16]. However, since the number of equilibrium solutions of (2.2) depends on the number of solutions of the equations defined in (4.13) we can modify $C_1$ to obtain new scenarios on the set of equilibrium points. For the following hypothesis

$C_2:$ the equation $g(r, p) = \mu_pp$ has unique non-negative solution $p^*(r)$ such that the equations $p^+(r) = p^*(r)$ and $p^-(r) = p^*(r)$ have $n$ and $m$ solutions in $(0, 1)$, respectively.

we have the following existence results for the coexistence equilibria.

Proposition 7.1. By assuming that the hypothesis $C_2$ is satisfied, $R_s > 1$ and $R_r > 1$ we have the following results:

1. If $R_s < R_r$, then there are $n$ coexistence equilibria $x_1^+, \ldots, x_n^+\in\Omega$.

2. If $R_s = R_r$, there are $n$ coexistence equilibria $x_1^+, \ldots, x_n^+\in\Omega_1$.

3. If $R_{s} > R_r$, then

● there are $n+m$ coexistence equilibria $x_1^+, \ldots, x_n^+$ and $x_1^-, \ldots, x_m^-$ in $\Omega'_1\subset\Omega_1$.

● there are $n$ coexistence equilibria $x_1^+, \ldots, x_n^+\in\Omega'_1\cap\Omega_2\subset\Omega_1$.

● there are $n$ coexistence equilibria $x_1^+, \ldots, x_n^+\in\Omega''_1\cap\Omega_1\subset\Omega_1$.

Proof. The same procedure carried out to prove the Proposition 4.2.

The stability results for the coexistence equilibria of Proposition 7.1 are summarized in the following proposition.

Proposition 7.2. If $g$ satisfies the conditions (5.6), $\delta\ll1$ and under hypothesis of Proposition 7.1 it follows that $x_1^+, \ldots, x_n^+$ are l.a.s in $\Omega$ and $x_1^-, \ldots, x_m^-$ are l.a.s in $\Omega'_1$.

Proof. The same procedure carried out to prove the Proposition 5.1.

Now, under following hypothesis,

$C_3:$ the equation $g(r, p) = \mu_pp$ has unique non-negative solution $p^*(r)$ such that the equations $p^{\pm}(r) = p^*(r)$ have an infinite countable number of equilibrium solutions $\{r_i\}_{i = 1}^{\infty}\in(0, 1)$.

It is follows the next proposition.

Proposition 7.3. By assuming that the hypothesis $C_3$ is satisfied, $R_s > 1$ and $R_r > 1$, then there are an infinite countable number of non isolated equilibrium points $\{x_i\}_{i = 1}^{\infty}\subset\Omega$ and a isolated equilibrium point $\bar x\in\Omega$ of system (2.2) such that $x_i\to\bar x$ when $i\to\infty$. In addition,

1. If $R_s < R_r$, then $\{x_i\}_{i = 1}^{\infty}\in\Omega$ and $\bar x\in\Omega$.

2. If $R_s = R_r$, then $\{x_i\}_{i = 1}^{\infty}\in\Omega_1$ and $\bar x\in\Omega_1$.

3. If $R_{s} > R_r$, then

● $\{x_i\}_{i = 1}^{\infty}\in\Omega'_1\subset\Omega_1$ and $\bar x\in\Omega'_1\subset\Omega_1$.

● $\{x_i\}_{i = 1}^{\infty}\in\Omega'_1\cap\Omega_2\subset\Omega_1$ and $\bar x\in\Omega'_1\cap\Omega_2\subset\Omega_1$.

● $\{x_i\}_{i = 1}^{\infty}\in\Omega''_1\cap\Omega_1\subset\Omega_1$ and $\bar x\in\Omega''_1\cap\Omega_1\subset\Omega_1$.

Proof. If we assume that the Eq (4.13) has an infinite countable set of solutions $\{r_i\}_{i = 1}^{\infty}\in(0, 1)$, then there exits $\bar r\in[0, 1]$ such that $r_i\to\bar r$ when $i\to\infty$. Therefore, the system (2.2) have an infinite countable set of equilibrium solutions $\{x_i\}_{i = 1}^{\infty}$ such that $x_i\to\bar x$ when $i\to\infty$, where $\bar x$ is an equilibrium point of system (2.2). Following a similar idea, we could obtain continuous curves of non-isolated equilibria of (2.2).

8.   Conclusions

The elimination of the bacterial population is the most relevant scenario to the host. In this regard, the qualitative analysis reveals that to reach this objective in a neighborhood of $x_0$, $N(x_0)$, it is necessary that the surviving bacteria of both the effect of antibiotic and the immune response do not generate new bacteria, and the variation of the plasmid replication rate respect to plasmids would be less than its degradation rate. While eliminating the bacterial population in $\Omega$, it is required only that each bacterium mentioned above generates at most one new bacterium. Here, the plasmid replication rate plays no role. These results suggest that within the host plasmid replication produces local effects on the outcome of infection. Now, when each surviving bacterium generates more than one bacterium, different types of bacterial spread occur, and although the effect of plasmid replication remains local, the plasmid replication rate is essential to determine the type of spread.

Acknowledgments

The authors acknowledges support from projects No 106-25/09/2018 (1678) and No.118-25/09/2018 (1669) financed by Vicerectoría de Investigaciones e Interacción Social (VIIS)-Universidad de Nariño.

Conflict of interest

The authors declare that they have no competing interests.

Appendix

Lemma 8.1. There exists an unique function $v:\mathbb{R}^{7}\to \mathbb{R}$ that satisfies $\beta_s = v(\beta_r, \alpha, \delta, \gamma, \mu_s, \mu_r, \mu_p)$.

Proof. Let $D_2(z, \beta_S) = a_2(z, \beta_s)a_1(z, \beta_s)-a_3(z, \beta_s)$ where $z = (\beta_r, \alpha, \delta, \gamma, \mu_s, \mu_r, \mu_p)$, then we had verified that $D_2(z_0, \beta_s^0) = 0$ where $z_0$ is the vector corresponding to the parameter $\beta_s^0$. In addition, from (5.5) we verify

Observe that $\partial D_2\left(z_0, \beta_s^0\right)/\partial\beta_s\neq0$ for $\beta_s^0\ll1$. In consequence, the Implicit function theorem implies the existence of an open ball $U\in\mathbb{R}^7$ containing $z_0$ and an interval $V\subset\mathbb{R}$ containing $\beta_s^0$ such that there is an unique function $\beta_s = v(z)$ defined for $z\in U$ and $\beta_s\in V$ which satisfies $F(x(\beta_s^0), \beta_s^0) = 0$, where $F$ is the right side of the system (2.2) ^[29].