Dynamics of drug on-drug off models with mutations in morbidostat — Dedicated to the seventieth birthday of Professor Gail Wolkowicz

1.   Introduction and models

1.1.   Introduction

Antibiotic drug resistance is a global health problem ^[9]. Five years after the clinical application of penicillin, staphylococcus aureus with penicillin resistance ^[8] was found in humans, which caused penicillin to fail in some patients. These years, human beings may face the dilemma of infecting multiple drug-resistant bacteria (commonly known as superbugs) without any help of antibiotics because of the antibiotic drug resistance.

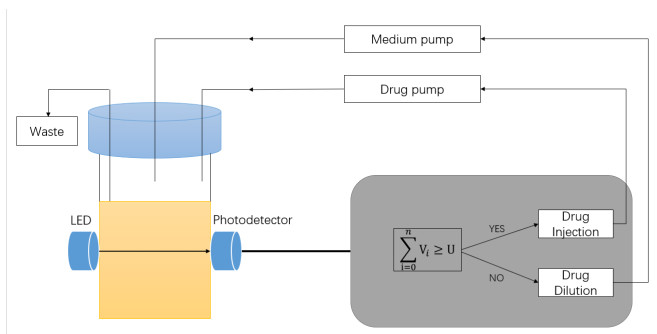
In ^[10,11] the authors presented a devices for building and operating an automated fluid system for continuous culture called "morbidostat" (See Figure 1.1). The morbidostat is used to study evolution of mircobial drug resistance in real time, It constantly measure the growth rates of evoluting mircobial populations inside culture in order to maintain a constant drug-induced inhibition. The growth rate measurements are done by using an optical detection system. Similar to chemostat rate $D$ lower than the maximal growth rate of population in morbidostat. In contrast to a chemostat in which the bacterial growth in inherently the cell density is kept low such that the population in not nutrient limited, its growth rate is also controlled by externally adjusting drug concentration.

In this work, we follow the same mathematical model of morbidostat in ^[5,6]. When the total population of all bacteria are less than a threshold value U, there is no drug injection into the morbidostat and $\frac{dP}{dt} = -DP$. However if the total population of all bacteria reaches over the threshold value U, there will be continuous drug injection into morbidostat. The growth rate of species $i$ will be $g_{i}(S)f_{i}(P)$ where $S$ is the concentration of nutrient, $g_{i}(S)$ takes the form of Holling type Ⅱ $g_{i}(S) = \frac{m_{i}S}{a_{i} + S}$ and $P$ is the concentration of drug, the inhibition $f_{i}(P)$ takes the form of Hill function $f_{i}(P) = \frac{1}{1 + (\frac{P}{K_{i}})^{L}}$ and $\frac{dP}{dt} = D\left(P^{(0)} - P\right)$.

Remark: We note that in ^[5,6], we assume

i.e, the $n$-th mutant has largest growth rate.

In ^[6] we consider periodic resetting for nutrient and drug; while in ^[5] we consider drug on-drug off mechanism.

In this paper we relax the assumption ($H^{*}$) with drug on-drug off dynamics in the morbidostat.

1.2.   Description of the models

In this work, we analyze the transition between the population of wild type u and those of mutant $v_i$ $(i = 1.2, \cdots, n)$. Consider the drug on-drug off model with forward mutations(see Figure $1.2$) and forward-backward mutations(see Figure $1.3$).

The growth dynamics with the nutrient substrate $S$ in a chemostat under the influence of the drug inhibitor $P$ with forward mutations and forward-backward mutations are given by $(1)$ and $(2)$ respectively:

where $i = 1, 2, 3, \cdots, n-1$. Let $v_0 = u$ and $v_i$ are the volume densities of the wild type and mutant populations, respectively. $\gamma$ denotes the yield constant, reflecting the conversion of nutrient to bacteria. S is the concentration of nutrient, while $S^{(0)}$ is the input concentration of nutrient. D is the dilution rate. $g_0(S)$ and $g_i(S)$ are the growth rates of the wild type and mutants, which satisfy $g_i(0) = 0$, $g_i^\prime(S) > 0$ for $i = 0, 1, 2, \cdots, n$. It implies that bacteria grows only when there has nutrient substrate in the device, and a higher concentration of nutrient leads to the bacteria's higher growth rates. Here we consider the important special case $g_i{(S)} = \frac{m_i{S}}{a_i+S}$. $q_{i}$ denotes the forward mutation from $v_i$ to $v_{i+1}$, and $\widetilde {q_{i}}$ is the backward mutation from $v_{i+1}$ to $v_i$. $q_{i}$ and $\widetilde {q_{i}}$ are small positive quantities. Besides, the drug inhibitions for $v_i$ are described by $f_i(P)$ for $i = 0, 1, 2, \cdots, n$. It is easy to know, the higher concentration of drug leads to a stronger inhibition to the growth of bacteria. Based on the fact that mutants always have stronger resistances to the inhibitor than wild-type, and the $i$-th mutant $v_i$ has stronger resistances than the $(i-1)$-th mutant $v_{i-1}$. So we assume

for $i = 0, 1, 2, \cdots, n$.

Let $g_i(\lambda_i) = D$, i.e. $\lambda_i = \frac{a_i}{(\frac{m_i}{D}-1)}$. We also assume that:

which implies the wild type $u$ which has smallest break-even concentration, is the most superior species than the mutants $v_i$ in the absence of drug inhibition ^[1].

The rest of this paper is organized as follows. In Section 2 we study the dynamics of drug on-drug off models with no mutations, In Section 3 we study the dynamics of drug on-drug off models with forward mutations. In Section 4 we study the dynamics of drug on-drug off models with forward-backward mutations. Section 5 is a section of numerical simulations for various threshold parameters $U$. Section 6 is the discussion section.

2.   Dynamics of drug on-drug off model with no mutations

Without loss of generality by scaling, we assume the yield constant, $\gamma = 1$.

Lemma 2.1. (Conservation Property) $S(t)+ \sum_{i = 0}^{n}{v_i(t)} \to S^{(0)}$ as $t \to \infty$.

Proof. Let $M(t) = S(t) + \sum_{i = 0}^{n}{v_i(t)}$.

Adding the first $n+2$ equations of $(1)$ and $(2)$, yields

So $M(t) = S(t)+ \sum_{i = 0}^{n}{v_i(t)} \to S^{(0)}$ as $t \to \infty$. □

For simplicity in $(1)$ we assume that $q_i = 0$ for all $i = 0, 1, 2, \cdots, n$. Let $u = v_0$, the system $(1)$ becomes

Next we state two theorems which will be used in Section 2.1 below.

Theorem A (Competitive exclusion in simple chemostat) (^[1] p. 30 or p. 35)

Consider the simple chemostat equation

with $S(0)\geq 0$ and $v_{i}(0) > 0$. Let (H2) hold. Then

□

Consider two systems of ordinary differential equations of the form

and

where

We assume $A$ is an $m\times m$ matrix, $f$ is continuous differentiable, $D$ is positively invariant for (F.1) and (F.2) is dissipative. Let (B1)-(B5) be additional hypothesis:

(B1) All of eigenvalues of $A$ have negative real parts.

(B2) Equation (F.2) has finite number of rest points in $\Omega$, each of which is hyperbolic (^[2], p. 88) for (F.2). Denote these rest points by $x_{1}, \dots, x_{p}$.

(B3) The dimension of the stable manifold {(^[2], p. 88)} is $n$ for $1\leq i\leq r$, and the dimension of the stable manifold of $x_{j}$ is less than $n$ for $j = r+1, \dots, p$. In symbols, dim($M^{+}(x_{j})$)$= n, i = 1, \dots, r$; dim$(M^{+}(x_{j})) < n$ for $j = r+1, \dots, p$.

(B4) $\Omega = \cup_{i = 1}^{p}M^{+}(x_{j})$.

(B5) Equation (F.2) does not possess a cycle of rest points.

Theorem B (A convergence theorem)(^[1], p. 294)

Let (B1)-(B5) hold and $(y(t), z(t))$ be a solution of (F.1). Then, for some $i$,

2.1.   The behavior of solutions of the system (3)

For the solution of the system (3), we discuss the following three cases:

Case 1 : $\sum_{i = 0}^{n}{v_i{(t)}} < U$ for all $t > t_0 > 0$ for some $t_0 > 0$. Then we have

it is obvious that

Let

Then by Lemma 2.1, we have

and $\Sigma_{1}(t)\to 0$ and $\Sigma_{2}(t)\to 0$ as $t\to \infty$. Rewrite the system (3) with $\frac{dP}{dt} = -DP$ as

The system corresponding to (F.2) in Theorem B is

Apply Theorem B with $A = {\text{diag}}(-D, -D), m = 2$ and

Under the hypothesis (H2), we apply Theorem A and obtain a result of global stability,

Now we verify the hypothesis (B1)-(B5) holds for the systems (2.1) and (2.2). Obviously the $2\times 2$ matrix $A$ satisfies hypothesis (B1). For hypothesises (B2), (B3), (B4), equation (2.2) has finite number of rest points in $\Omega$, namely, $O = (0, 0, \dots, 0)$, $E_{0} = (v_{0}^{*}, 0, \dots, 0)$, $E_{i} = (0, \dots, v_{i}^{*}, \dots, 0)$, $v_{i}^{*} = S^{(0)} - \lambda_{i}, i = 1, 2, \dots, n$. dim$(M^{+}(E_{0})) = n+1$, dim$(M^{+}(E_{i})) = n - (i-1), i = 1, 2, \dots, n$. To verify the cyclic condition (B5), we note that from (H2) $E_{j}$ is chained to $E_{i}$, $E_{j}\to E_{i}, j > i, i, j = 0, 1, 2, \dots, n$ if and only if $\lambda_{j} < \lambda_{i}$ and $E_{i}\to O$ for all $i = 1, 2, \dots, n$. Suppose there is a cycle in $\Omega$, $E_{k(1)}\to E_{k(2)} \to \dots \to E_{k(1)}$ then it follows that $\lambda_{k(1)} < \lambda_{k(2)} < \dots < \lambda_{k(1)}$ which is obviously a contradiction to $(H2)$

Case 2 : $\sum_{i = 0}^{n}{v_i{(t)}}\geq U$ for all $t > t_0 > 0$ for some $t_0 \geq 0$. Then we have

we have

Let

Then we have

and $\Sigma_{1}(t)\to 0$ and $\Sigma_{2}(t) \to 0$ as $t\to \infty$. Rewrite the system (3) with $\frac{dP}{dt} = \left(P^{(0)} - P\right)$,

The system corresponding to (F.2) in Theorem B is

We may verify the hypothesises (B1)-(B5) as in the Case 1.

If $m_i f_i(P^{(0)}) \leq D$, then it is easy to show $\lim_{t \to \infty}v_i{(t)} = 0$. Thus we assume that

Replace $m_i$ in $g_i(S)$ by $m_if_i(P^{(0)})$, we have a new simple chemostat equation.

Let

then

as $t \to \infty$ or

Case 3 : $\sum_{i = 0}^{n}{v_i} < U$ at some sequence $\{ t_k \}$, $t_k \to \infty$ and $\sum_{i = 0}^{n}{v_i}\geq U$ at some other sequence $\{t_l\}$, $t_l \to \infty, k = 1.2.\cdots$, $l = 1, 2, \cdots$, $k \not = l$, $\sum_{i = 0}^{n}{v_i}$ oscillates around $U$.

2.2.   The results of the asymptotic behavior of the solutions of model with no mutations

Lemma 2.2. Let $v_{i}, i = 0, \dots, n$ be the solution of system (2.4). Let $(H1)$, $(H2)$, $(H3)$ hold, then $\hat{v_k^*} < v_0^*$.

Proof. Since

and $0 < f_i(P^{(0)}) < 1$, then $\hat{\lambda_k} > \lambda_k$.

Obviously, we obtain

Hence,

□

In the following Theorem 2.3 we shall give sufficient conditions for the Case 1, Case 2 and Case 3 for the solutions of the system (3).

Theorem 2.3. Let $(H1)$, $(H2)$, $(H3)$ hold and $v_{i}, i = 0, 1, \dots, n$ be the solutions of the system (3), then

(I) if $U > v_0^*$, then there exists $t_0 > 0$, such that for all $t \geq t_0$, $\sum_{i = 0}^{n}{v_i(t)} < U$. From Case 1 in section 2.1, $\lim\limits_{t\rightarrow \infty}S(t) = \lambda_{0}$, $\lim\limits_{t\rightarrow \infty}u(t) = S^{(0)} - \lambda_{0}$, $\lim\limits_{t = \rightarrow \infty}v_{i}(t) = 0$, $i = 1, 2, \dots, n$.

(II) Let $\hat{\lambda_l} = \max_{0 \leq i \leq n}{\hat \lambda_i}$ and $\hat{v_l^*} = S^{(0)} - \hat{\lambda_l} < \hat{v_k^*}$. If $U < \hat{v_l^*}$, then there exists $t_0 > 0$, such that for all $t \geq t_0$, $\sum_{i = 0}^{n}{v_{i}(t)} \geq U$. From Case 2 in section 2.1, $\lim\limits_{t\rightarrow \infty}S(t) = \hat{\lambda_{k}}$, $\lim\limits_{t\rightarrow \infty}v_{k}(t) = \hat{v_{k}^{*}} = S^{(0)} - \hat{\lambda_{k}}$, $\lim\limits_{t\rightarrow \infty}v_{i}(t) = 0, i\neq k, i = 0, 1, 2, \dots, n$.

(III) if $\hat{v_k^*} < U < v_0^*$, then $\sum_{i = 0}^{n}{v_i(t_k)} \geq U$ for some $\{t_k\}$, $t_k \to \infty$ and $\sum_{i = 0}^{n}{v_i(t_l)} < U$ for some other sequence $\{ t_l \}$, $t_l \to \infty$. This is Case 3 in section 2.1, $\sum_{i = 0}^{n}v_{i}(t)$ oscillates around $U$.

Proof.

1. We shall exclude the following two cases:

(i) $\sum_{i = 0}^{n}{v_i(t)} \geq U$ for all $t > 0$.

From Case 2 in section 2.1, we have $v_k \to \hat{v_k^*}$, $v_i \to 0$, where $i \neq k$.

So $\sum_{i = 0}^{n}{v_i} \to \hat{v_k^*} < U$ as $t \to \infty$. By Lemma 2.2 $\sum_{i = 1}^{n}v_{i}(t)\to \hat{v_{0}^{*}} < v_{0}^{*} < U$ a contradiction to $\sum_{i = 0}^{n}v_{i}(t)\geq U$ for all $t\geq 0$.

(ii) There exists $\hat {t} > 0$, such that

In this case, consider the system $(2.1)$,

we obtain that

It follows that $S^{(0)} - \sum_{i = 1}^{n}{v_i}(\hat{t}) = S^{(0)} - U < \lambda_0 < \lambda_1 < \cdots < \lambda_n$,

$g_i(S^{(0)}-\sum_{i = 0}^{n}{v_i}(\hat{t})) < g_i(\lambda_i)$ for all $i = 0, 1, \dots, n$.

Hence $\frac{d}{dt}(\sum_{i = 0}^{n}{v_i})|_{t = \hat t} < 0$.

This is a contradiction to (2.6).

Hence, we exclude (i) and (ii). It follows that $\sum_{i = 0}^{n}{v_i} < U$ for $t\geq t_{0}$ for some $t_{0} > 0$.

2. We shall exclude the following two cases:

(i) $\sum_{i = 0}^{n}{v_i(t)} \leq U$ for all $t > 0$.

In this case, we have $v_0 \to v_0^*$, $v_i \to 0$, where $i \not = k$.

So $\sum_{i = 0}^{n}{v_i} \to v_0^* > U$ as $t \to \infty$. Since $U < \hat{v_{l}^{*}} < \hat{v_{k}^{*}} < v_{0}^{*}$, we obtain a contradiction to $\sum_{i = 0}^{n}v_{i}(t)\leq U$ for all $t > 0$

(ii) There exists $\bar{t} > 0$, such that

In this case, we consider the system (3),

we obtain that

Let

When $U \leq \hat{v_l^*}$, $\sum_{i = 0}^{n}{v_i(\bar{t})} = U \leq \hat{v_l^*} = S^{(0)} - \hat{\lambda_l}$

It follows that $S^{(0)}- \sum_{i = 0}^{n}{v_i(\bar{t})} \geq \hat{\lambda_l} > \hat{\lambda_i}$, $i = 0, 1, \cdots, n$ and $i \not = l$

The monotonicity of $g_i(S)$ implies that $g_i(S^{(0)} - \sum{v_i}) \geq g_i(\hat{\lambda_i})$, from (2.8)

This is a contradiction to (2.7)

Hence $\sum_{i = 0}^{n}{v_i(t)} \geq U$ for all $t$ large.

3. Assume $\hat{v}_{k}^{*} < U < \hat{v_{0}^{*}}$, $\sum_{i = 0}^{n}{v_i} \geq U$ for all $t > 0$.

Then from $(H3)$ and $(2.6)$, $v_k \to \hat{v_k^*}$, $v_i \to 0$, where $i \not = k$.

So $\sum_{i = 0}^{n}{v_i} \to \hat{v_k^*} < U$ as $t \to \infty$, a contradiction to the assumption $\sum_{i = 0}^{n}v_{i}\geq U$ for all $t$ large.

Suppose $\sum_{i = 0}^{n}{v_i} < U$ for $t$ large.

Then from $(H2)$ $v_0 \longrightarrow v_0^*$, $v_i \longrightarrow 0$, $i = 1, 2, \cdots, n$, as $t \to \infty$.

So $\sum_{i = 0}^{n}{v_i} \longrightarrow v_0^* > U$ as $t \to \infty$, a contradiction.

Hence $\sum_{i = 0}^{n}{v_i}$ oscillates around U.

□

Remark 2.4. When $\hat{v_l^*} \leq U < \hat{v_k^*}$, from the numerical studies in section 5, we conjecture that the conclusion in (Ⅱ) in Theorem 2.3 holds, i.e. $\lim\limits_{t\rightarrow \infty}S(t) = \hat{\lambda_{k}}$, $\lim\limits_{t\rightarrow \infty}\hat{v_{k}(t)} = \hat{v_{k}^{*}} = S^{(0)} - \hat{\lambda_{k}}$, $\lim\limits_{t\rightarrow \infty}v_{i}(t) = 0$ for $i\neq k$, $i = 0, 1, \dots, n$.

Remark 2.5. When the threshold value $U$ satisfies $\hat{v}_{k}^{*} < U < \hat{v}_{0}^{*}$, we conjecture that the competitive exclusion principle holds. In this case, we conjecture that there exist a bifurcation point $U^{*}$ such that for $\hat{v}_{k}^{*} < U < U^{*}$, species $v_{k}$ wins the competition; for $U^{*} < U < v_{0}^{*}$ the wild type species $u: = v_{0}$ wins the competition. We note that from (Ⅲ) of Theorem 2.3 for $\hat{v}_{k}^{*} < U < \hat{v}_{0}^{*}$, $\sum_{i = 0}^{n}v_{i}$ oscillates around $U$. Thus the solution of the system (3) will not tend to equilibrium $E_{0} = (\lambda_{0}, \hat{v}_{0}^{*}, 0, \dots, 0)$ or $E_{1} = (\hat{\lambda}_{0}, 0, \dots, 0, \hat{v}_{k}^{*}, 0, \dots, 0)$. See Figure 5.3 (a), 5.3 (b), 5.3 (c) and Figure 5.4(a), 5.4(b), 5.4(c) in Section 5.

3.   Dynamics of drug on-drug off model with forward mutations

Consider the following drug on-drug off model with forward mutation:

3.1.   The behavior of the solutions of the system (1)

As we did in Section 2, we discuss three cases.

Case 1 : $\sum_{i = 0}^{n}{v_i{(t)}} < U$ for all $t > t_0$ for some $t_0 > 0$. Then we have

It is obvious that

As we did in case 1 in Section 2.1, it suffices to consider the limiting system of (1)

Theorem 3.1. Let $q = (q_0, q_1, \cdots, q_n)$, then (3.1) has a unique positive equilibrium $E(q) = (v_{0}^{*}(q), \cdots, v_n^*(q))$ satisfying

Proof. Consider the first equation of (3.1) :

Then the positive equilibrium, $v_{0} = v_{0}^{*}(q) > 0$, satisfies

The monotocity of $g_0(S)$ implies that $S^* = g_0^{-1}(D+q_{0})$ is unique.

Since $q_{0}$ is close to 0, we have $S^*$ is close to $g_0^{-1}(D) = \lambda_0$.

Let $S^* = \lambda_0 + \epsilon$, $\epsilon > 0$ is small enough.

From $(H2)$, it follows that $g_i(S^*) = g_i(\lambda_0+ \epsilon) < g_i(\lambda_i) = D$, $i = 1, 2, \dots, n-1$.

Then we have for $i = 1, 2, \dots, n-1$,

Consider the $n+1$ equations in (3.2), we denote them in the form of $Ax = y$ as following,

Let $A^{(0)}$ =

We apply the following elementary transformations on $A^{(0)}$.

(Step 1) Consider the $(n+1)$-th row in $A^{(0)}$, multiplying $\frac{g_0(S^*)}{q_0}$ to 1st row and subtracting it from $(n+1)$-th row, and we have

$A^{(1)} =$

where $m_1 = g_1(S^*)-\frac{g_0(S^*)}{q_0}\cdot (g_1(S^*)-D-q_{1})$

Since $g_1(S^*) > 0$, $g_0(S^*) > 0$, $q_0 > 0$, we have $m_1 > 0$.

After $n$ elementary transformations, we get an upper triangular matrix

$A^{(n)} =$

So the solution $(v_{0}^{*}, v_1^*, v_2^*, \cdots, v_n^*)$ exists and is unique.

By mathematical induction, we can show that, $m_n$ in $A^{(n)}$ is positive.

From (3.4), we have

and it follows that $v_{n}^{*} > 0$

From (3.2), we obtain

For each $1 \leq i \leq n-1$,

${\text{Hence }} v_i^* > 0 {\text{ for all }} 0 \leq i \leq n.$

and the equilibrium $E(q) = (v_{0}^{*}(q), v_{1}^{*}(q), v_{2}^{*}(q), \cdots, v_{n}^{*}(q))$ is positive.

□

Since $q \approx 0$, $E(q)$ is closed to $E_0$, so we use the following perturbation theory to discuss the local and global stability of $E(q)$.

Theorem 3.2. ^[4] Let $A, B \in \mathbb{C}^{n\times n}$, with A simple. If A has eigenvalues $\lambda_1, \lambda_2, \cdots, \lambda_n$ and $\mu$ is an eigenvalue of $A+B$, and if for a matrix norm induced by an absolute vector norm $\|\|_v$, we have $r = \|B\|\|A\|_v$, then $\mu$ lies in at least one of the disks ${z:|z- \lambda_j| \leq r}$, $j = 1, 2, \cdots, n$, of the complex z-plane.

Theorem 3.3. ^[7] Assume that $(x_0, \lambda_0) \in U \times \Lambda$, $x_0 \in Int U$, $f(x_0, \lambda_0) = 0$, all eigenvalues of $D_x f(x_0, \lambda_0)$ have negative real part, and $x_0$ is globally attracting for solutions of $x^\prime = f(x, \lambda)$ with $\lambda = \lambda_0$. If there exists a compact set $D \subset U$ such that for each $\lambda \in \Lambda$ and each $z \in U$, $x(t, z, \lambda) \in D$ for all large t, then there exists $\epsilon > 0$, and a unique point $\hat {x(\lambda)} \in U$ for $\lambda \in B_\Lambda (\lambda_0, \epsilon)$ such that $f(\hat{x}(\lambda), \lambda) = 0$ and $x(t, z, \lambda) \longrightarrow \hat{x}(\lambda)$ as $t \longrightarrow \infty$ for all $z \in U$.

Theorem 3.4. $E(q)$ is locally stable.

Proof. From $(2.2)$ in Section 2, $E_0$ is a stable equilibrium where $E_{0} = (v_{0}^{*}, 0, \dots, 0), v_{0}^{*} = S^{(0)} - \lambda_{0}$. The Jacobi matrix of system $(2.2)$ evaluated at $E_0$, is

The eigenvalues $\mu_0, \mu_2, \cdots, \mu_{n+1}$ of $J(E_{0})$ are $\mu_{0} = -v_{0}^{*}g_{0}'(\lambda_{0}) < 0, \mu_{1} = g_{1}(\lambda_{0}) - D < 0, \dots, \mu_{n} = g_{n}(\lambda_{0}) - D < 0$.

From (3.2), we have the Jacobi matrix of system (3.1) evaluated at $E(q)$,

$J(E(q)) =$

Since $q_{i}$ is sufficiently small,

we have $g_i(S^*) \approx g_i(\lambda_0)$ and $g_i^\prime(S^*) \approx g_i^\prime (\lambda_0)$.

Let $J(E(q)) = J(E_0)+ B$, then $|B| \approx 0$.

From Theorem 3.2, the eigenvalues of $J(E(q))$ lies in at least one of the disks $z: |z - \mu_i| \leq \epsilon, i = 0, 1, \cdots, n$ ($\epsilon$ is small enough).

Since $\mu_i < 0$ for all $i = 0, 1, \cdots, n$, all eigenvalues of $J(E(q))$ have negative real part.

Hence $E(q)$ is locally stable. □

Theorem 3.5. $E(q)$ is globally stable.

Proof. Write $(3.2)$ as $\frac{dx}{dt} = f(x, q)$, when $x = (S, u, v_1, \cdots, v_n)$ and $q = (q_{0}, q_{1}, \cdots, q_{n-1})$.

Take $U = \mathbb{R}_+ \cup B_\epsilon(E_0)$, and $\Lambda(q) = [0, \delta]^{n-1}$.

when $q = 0$, i.e. all the $q_{i} = 0$ for each $0\leq i\leq n$, $f(E_0, 0) = 0$, and $D_x f(E_0, 0)$ has all negative eigenvalues.

Take $D = [0, S^{(0)}]^{n+2}$, then D is compact.

when $q_{i} \approx 0$, and $x = E(q)$, we have $f(E(q), q) = 0$.

By Theorem 3.3, $x(t, z, q) \to E(q)$ as $t \to \infty$ for all $z \in U$.

This concludes that $E(q)$ is globally stable. □

Next we discuss Case 2.

Case 2 : $\sum_{i = 0}^{n}{v_i{(t)}}\geq U$ for all $t > t_0$ for some $t_0 > 0$.

Then

and hence

As we did in Case 2 in Section 2.1, it suffice to consider the limiting system of (1)

We shall study (3.7) by using the same method for the system (2.4) in section 2.1,

Suppose $(H3)$ holds, let

Theorem 3.6.

1. System (3.7) has an equilibrium $E_* = (v_{0*}, \cdots, v_{n*})$.

(i) If $\hat {\lambda_0} = \min_{0 \leq i \leq n}{\hat \lambda_i}$, then $v_{i*} > 0$ for all $i = 0, 1, \cdots, n$. Write $E_* = (\bar{v_{0}}, \bar{v_1}, \cdots, \bar{v_n})$ satisfying

(ii) If $\hat {\lambda_k} = \min_{0 \leq i \leq n}{\hat \lambda_i}$ for some $k$, $0 < k < n$, then $v_{i*} = 0$ for $i = 0, 1, \cdots, k-1$ and $v_{j*} > 0$ for $k \leq j \leq n$. Write $E_* = (0, \cdots, \widetilde{v_k}, \cdots, \widetilde{v_n})$ satisfying

(iii) If $\hat {\lambda_n} = \min_{0 \leq i \leq n}{\hat \lambda_i}$, then $v_{i*} = 0$ for all $i = 0, 1, \cdots, n-1$ and $v_{n*} > 0$. Write $E_* = (0, 0, \cdots, 0, v_{n*})$, $v_{n*} = S^{(0)} - \hat{\lambda}_{n}$.

2. For the system (3.7), $E_*$ is global stable. \end{enumerate}

Proof.

1.

(i) Since $\hat{\lambda}_{0} < \hat{\lambda}_{i}, i = 1, 2, \dots, n,$ replacing $g_{i}(S)$ by $f_{i}(P^{(0)})g_{i}(S)$ in Theorem 3.1, we complete the proof of (i).

(ii) Consider the steady state of the first equation in (3.7),

Claim: $v_{0}^{*}$ = 0

if not, $v_{0}^{*} > 0$ then $g_{0}(S^{*})f_{0}(P^{(0)}) - D - q_{0} = 0$. Since the mutation rate $q_{i}, i = 0, 1, \dots, n$ are sufficiently small, $g_{0}(S^{*})\approx g_{0}(\hat{\lambda_{k}})$.

This leads to a contradiction $g_{0}(S^{*})f_{0}(P^{(0)}) - D - q_{0} = 0$. Hence we have $v_{0}^{*} = 0.$

Similarly from the steady state equation of (3.7)

we obtain $v_{i*} = 0, i = 1, 2, \dots, k-1$. Thus $E_{*} = (0, \dots, 0, \hat{v}_{k}, \dots, \hat{v}_{n})$ satisfies (3.9).

Consider the $n-k+1$ equations in (3.9), we denote them in the form of $Ax = y$ as following,

Since $q_{k}$ is close to 0, we have $\widetilde S$ is close to $g_k^{-1}(\frac{D}{f_k(P^{(0)})}) = \hat{\lambda_k}$.

Let $\widetilde S = \hat{\lambda_k} + \epsilon$, $\epsilon$ is small enough,

From $(H2)$, get $g_i(\widetilde S)f_i(P^{(0)}) = g_i(\hat{\lambda_k}+ \epsilon)f_i(P^{(0)}) < g_i(\hat{\lambda_i})f_i(P^{(0)}) = D$.

It follows that $g_i(\widetilde S)f_i(P^{(0)})-D -q_{i} < 0$, and $g_n(\widetilde S)-D < 0$.

Use the same method as Theorem 3.1, we have $\widetilde v_i > 0$ when $k \leq i \leq n$.

(iii) Particularly, when $\hat {\lambda_n} = \min_{0 \leq i \leq n}{\hat \lambda_i}$,

Let $g_n(S)f_n(P^{(0)})-D = 0$, we can get $S = \hat{\lambda_n}$.

Similarly, we can use mathematical induction as the second part of Theorem 3.6 to prove that $v_{i*} = 0$ for all $0 \leq i \leq n-1$, and then $v_{n*} = S^{(0)}- \lambda_n$.

2. Since $q_i$ is small enough and close to 0, $E_*$ is close to $E_1$.

We can also use the perturbation theory (Theorem 3.2 and Theorem 3.3) to prove the local and global stability of $E_*$. The proof is similar to Theorem 3.4 and Theorem 3.5.

□

Case 3 :

If $\sum_{i = 0}^{n}{v_i(t_k)} < U$ at some sequence $\{t_k\}$, $t_k \to \infty$ and $\sum_{i = 0}^{n}{v_i(t_l)}\geq U$ at some other sequence $\{t_l\}$, $t_l \to \infty$, $k = 1.2.\cdots$, $l = 1, 2, \cdots$, $k \not = l$, $\sum_{i = 0}^{n}{v_i}$ oscillates around $U$.

3.2.   The results of the asymptotic behavior of the solutions of model with forward mutations

From Lemma 2.1, we have $S(t) + \sum_{i = 0}^{n}{v_i(t)} \longrightarrow S^{(0)}$ as $t \to \infty$.

In case 1, $S(t) \to S^* = g_0^{-1}(D+q_{0})$, which is close to $\lambda_0$.

So $\sum_{i = 0}^{n}{v_i(t)}$ is close to $S^{(0)} - \lambda_0$ ($= v_0^*$) as $t \to \infty$.

In case 2, $S \to S_* = g_k^{-1}(D+q_{k})$, which is approximately equal to $\hat{\lambda_k}$, but a little greater than $\hat{\lambda_k}$.

So $\sum_{i = 0}^{n}{v_i(t)}$ is close to $S^{(0)} - \hat{\lambda_k}$ ($= \hat{v_k^*}$) as $t \to \infty$.

By the theory of perturbation, we can get the same relation between $\sum_{i = 0}^{n}{v_i}$ and $U$ as Theorem 2.3 in Section 2.

Theorem 3.7. Let $(H1)$, $(H2)$, $(H3)$ hold, then

(I) if $U > v_0^*$, then there exists $t_0$, such that for all $t \geq t_0$, $\sum_{i = 0}^{n}{v_i(t)} < U$

(II) Let $\hat{\lambda_l} = \max_{0 \leq i \leq n}{\hat \lambda_i}$ and $\hat{v_l^*} = S^{(0)} - \hat{\lambda_l} < \hat{v_k^*}$. If $U < \hat{v_l^*}$, then there exists $t_0 > 0$, such that for all $t \geq t_0$, $\sum_{i = 0}^{n}{v_i(t)} \geq U$.

(III) if $\hat{v_k^*} < U < v_0^*$, then $\sum_{i = 0}^{n}{v_i(t_k)} \geq U$ for some sequence $\{t_k\}$, $t_k \to \infty$ and $\sum_{i = 0}^{n}{v_i(t_l)} < U$ for some other sequence $\{ t_l \}$, $t_l \to \infty$.

Proof.

(I) Assume $U > v^{*}_{0}$, we shall exclude the following two cases.

(i) $\sum_{i = 0}^{n}v_{i}(t)\geq U$ for $t > 0$. Then $P(t)\rightarrow P^{(0)}$ as $t\rightarrow \infty$. Consider the limiting system (3.7). By perturbation method in Theorem 3.3 and the result in Case 2 of section 2.1, we have

where $i\neq k$, $c_{1}(q)$ and $c_{i}(q)$ are small, $q = (q_{1}, \dots, q_{n})$. Then

and it follows that

This is a contradiction to the assumption (i):

(ii) There exists $\hat{t} > 0$ such that

From the system (1),

It follows that

Hence

This is a contradiction. Excluding (i) and (ii), we obtain $\sum_{i = 0}^{n}v_{i} < U$ for $t$ large.

(II) Assume $U < \hat{v}_{l}^{*}$. Then $\sum_{i = 0}^{n}v_{i}(t) \geq U$ for $t\geq t_{0}$. Applying the perturbation method and the method in Theorem 2.3 (Ⅱ), we finish the proof of (Ⅱ).

(III) Assume $v_{k}^{*} < U < v_{0}^{*}$. Suppose $\sum_{i = 0}^{n}v_{i}\geq U$ for $t$ large. Then by perturbation method in Theorem 3.3 and the results in Case 2 of section 2.1,

a contradiction.

Suppose $\sum_{i = 0}^{n}v_{i} < U$ for $t$ large. Then

Hence $\sum v_{i}\rightarrow v_{0}^{*} + c_{0}(q) + \sum_{i = 1}^{n}c_{i}(q) > U$, a contradiction.

Hence $\sum_{i = 0}^{n}v_{i}$ oscillates around $U$.

□

4.   Dynamics of drug on-drug off model with forward-backward mutations

Consider the model

Lemma 4.1. (^[3], p. 141) If $y(t)$ has a finite limit as $t\rightarrow \infty$ and $y^{(n)}$ is bounded for $t\geq t_{0}$, then $y^{(k)}(t)\rightarrow 0$ as $t\rightarrow \infty$ for $0 < k < n$.

In this section we only consider Case 1 and Case 2, i.e. we assume either $U > v_{0}^{*}$ or $U < \hat{v}_{l}^{*}$. Then the solutions of (2) are smooth.

Lemma 4.2. In (2), if $v_m(t) \to 0$ as $t \to \infty$ for some m, $0 \leq m \leq n$, then we can get $v_k(t) \to 0$ as $t \to \infty$, for all $k \not = m$ and $0 \leq k \leq n$.That means all the species will go extinction as long as one of them goes extinction when time is long enough. Otherwise, all species coexists.

Proof. We just prove the cases when $0 < m < n$, since $m = 0$ and $m = n$ are similar.

Consider the model (2), we have

From Lemma 2.1, we have

and $0 < S \leq S^{(0)}$ and $0 < P \leq P^{(0)}$.

From the first equation in (2),

For $1\leq i \leq n-1$,

from (4.2),

it is easy to see that $|v_{i}'|$, $|P'| \leq DP^{(0)}$, $|S'|$, $|f'_{m}(P)|$, $|g'_{m}(S)|$ are bounded.

It follows from (4.1), we conclude that $|\frac{d^{2}v_{m}}{dt^{2}}|$ is bounded.

Since $v_m \to 0$ as $t \to \infty$, and $|\frac{d^2 v_m}{d t^2}|$ is bounded.

From Lemma 4.1, we have $\frac{d v_m}{d t} \to 0$ as $t \to \infty$.

It implies that $q_{m-1} v_{m-1} + \widetilde{q_{m}}v_{m+1} \to 0$ as $t \to \infty$, $v_{m-1}\rightarrow 0$, $v_{m+1}\rightarrow 0$ as $t\rightarrow \infty$.

Hence $v_k \to 0$ as $t \to \infty$ for $k \neq m$. □

From Lemma 4.2, there are two cases: Either all the bacteria $v_i$ $(0 \leq i \leq n)$ go extinction or all of them coexist. In the drug on-drug off model with forward-backward mutations, we get the next results.

Theorem 4.3. Let the hypothesis $(H1)$ and $(H2)$ hold and $v_i$ $(0 \leq i \leq n)$ be the solutions of system (2), then the species $v_i$ $(0 \leq i \leq n)$ coexists.

Proof. If all the species $v_i$ $(i = 0, 1, \cdots, n)$ go extinction, then $\sum_{i = 0}^{n}{v_i} \to 0 < U$ as $t \to \infty$.

We have

Consider the second equation of the system (2):

Since $g_0(S^{(0)}) - D = g_0(S^{(0)}) - g_0(\lambda_0) > 0$ and $q_i$, $\widetilde{q_i}$ are sufficiently small.

$\frac{d u}{d t} > 0$ as $t \to \infty$, which contradicts to $u \to 0$ as $t \to \infty$.

Hence all the species $v_i$ $(i = 0, 1, \cdots, n)$ coexist for t large in the system (2) with forward-backward mutation.

□

Remark 4.4. We note that since the mutant rates $\widetilde{q_i}$ are quite small, the most resistant $v_k$ whose $\hat{\lambda_k} = \min_{0 \leq i \leq n}{\hat \lambda_i}, {\text{ }} where {\text{ }} \hat{\lambda_i} = \frac{a_i}{\frac{m_i f_i(P)}{D}-1}$ dominates the rest species.

5.   Numerical simulations

In this numerical simulation, we consider the case $n = 2$ and verify the conjecture in Remark 2.4 and Remark 2.5.

For simplicity, we assume $S^{(0)} = 10$, $D = 0.9$ and

where $a_0 = 2$, $a_1 = 2$, $a_2 = 3$, $m_0 = 3$, $m_1 = 2$, $m_2 = 1.5$.

Since $g_i(\lambda_i) = D$, we have $\lambda_0 \approx 0.86$, $\lambda_1 \approx 2.44$ and $\lambda_2 = 4.5$.

Hence $v_0^* = S^{(0)}-\lambda_0 \approx 9.14$.

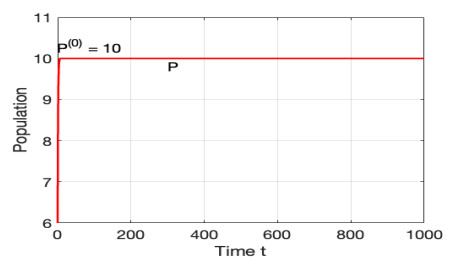
Let $P^{(0)} = 10$ and

where $L = 1$, $K_0 = 6$, $K_1 = 15$, $K_2 = 40$.

After calculations, we have $\hat{\lambda_0} = 8$, $\hat{\lambda_1} = 6$, $\hat{\lambda_2} = 9$, Then $\hat{\lambda}_{1} = \min(\hat{\lambda_{0}}, \hat{\lambda_{1}}, \hat{\lambda_{2}})$, $\hat{\lambda}_{2} = \max(\hat{\lambda_{0}}, \hat{\lambda_{1}}, \hat{\lambda_{2})}$, and

$\hat{v_k^*} = \hat{v_1^*} = 4$, and $\hat{v_l^*} = \hat {v_2^*} = 1$.

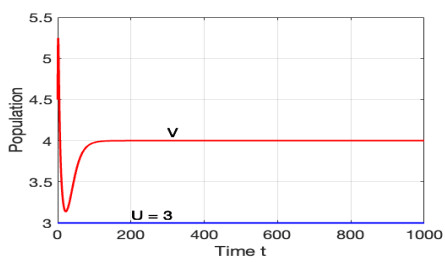
Take $U = 3$, then $\hat{v_2^*} \leq U < \hat{v_1^*}$.

1. When there is no mutation, under the assumption $(H3)$, (2.5), the mutant $v_{2}$ survives, but the wide type $v_{0}$ and the other mutant $v_{1}$ go extinct. $V: = \sum_{i = 0}^{2}{v_i(t)} \geq U$ for time $t$ large, satisfying the conjecture in Remark 2.4.

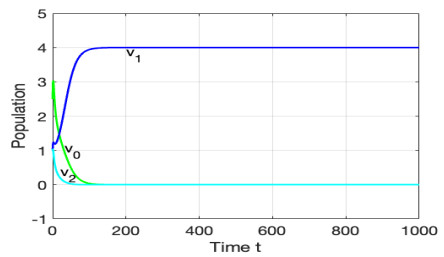
In Figure 5.1 (a), (b), (c) we verify the conjecture that if $\hat{v}_{l}^{*} < U < \hat{v}_{k}^{*}$ then $v_{k}(t) \to \hat{v}_{k}^{*}, v_{i}\to 0$ for $i\neq k$.

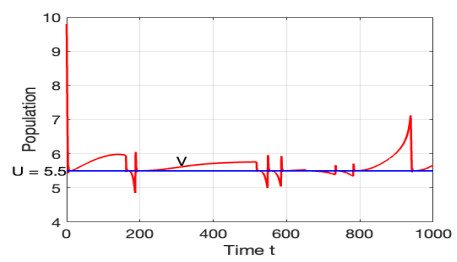
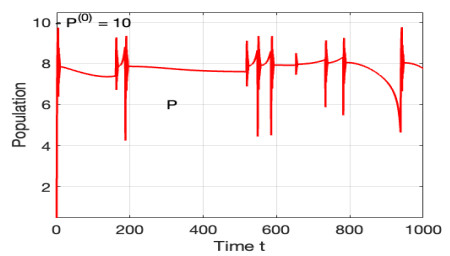
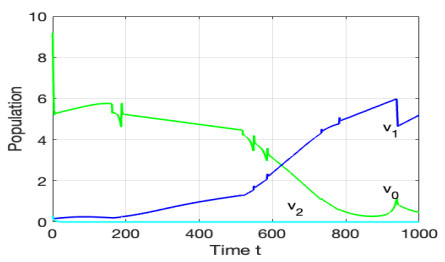
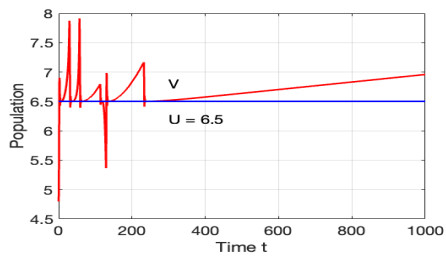
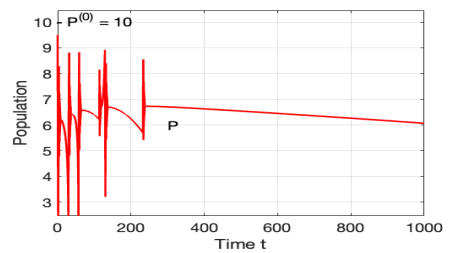
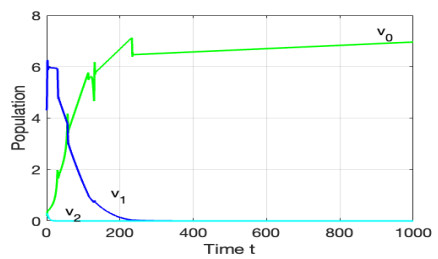
In the following Figure 5.2 and Figure 5.3, $U$ satisfies $\hat{v}_{k}^{*} < U < v_{0}^{*}$. Thus the total population $V = \sum_{i = 0}^{n}v_{i}$ oscillates around $U$. We conjecture that there exists $U^{*}$ between $\hat{v}_{k}^{*}$ and $v_{0}^{*}$ such that species $v_{k}$ win the competition when $\hat{v}_{k}^{*} < U < U^{*}$ and species $v_{0}$ (wild Type) win the competition when $U^{*} < U < v_{0}^{*}$, For the numerical data is $n = 2$, $\hat{v}_{k}^{*} = 4$, $v_{0}^{*} = 9.14$, we compute the value $U^{*}$, $U^{*}\approx 5.846$.

2. Let $U = 5.5$, $\hat{v}_{k}^{*} < U < U^{*}$, $\hat{v}_{k}^{*} = 4$, $U^{*}\approx 5.846$ and the initial data $(9.2, 0.3, 0.3, 0.2)$ near equilibrium $E_{0} = (v_{0}^{*}, 0, 0, 0) = (9.14, 0, 0, 0)$, then the trajectories of the system (3) are shown in Figure 5.2 (a), 5.2 (b), 5.2 (c).

3. Let $U = 6.5$, $U^{*} < U < v_{0}^{*}$, $U^{*}\approx 5.846$, $v_{0}^{*} = 9.14$, and the initial data $(6.2, 0.2, 4.3, 0.3, 9.5)$ near equilibrium $E_{1} = (0, v_{1}^{*}, 0, P^{(0)}) = (0, 4, 0, 10)$, then the trajectories of the system (3) are shown in Figure 5.3 (a), 5.3 (b), and 5.3 (c).

Acknowledgment

The authors would like to give their sincere thanks to the anonymous referee for his/her valuable suggestions to improvement of the paper. The second author's research is supported by MOST 111-2115-M-007-011.

Conflict of interest

There is no conflict of interest.